
A Task Space Approach for Planar Optimal Robot Tube Following
Matthias Oberherber, Hubert Gattringer, Andreas M¨uller and Michael Schachinger
Institute of Robotics, Johannes Kepler University Linz, Altenberger Str. 69, Linz, Austria
Keywords:
Robotics, Optimal Path Planning, Optimal Tube Following, Dynamic Modeling, Polygonal Paths.
Abstract:
The classical optimal path following problem considers the problem of moving optimally along a predefined
geometric path under technological restrictions. In contrast to optimal path following, optimal tube following
allows deviations from the initial path within a predefined tube to reduce cost even more. The present paper
proposes a modern approach that treats this non-convex problem in task space. This novel method also pro-
vides a simple way to derive optimal trajectories withina tube described in terms of polygonal lines. Numerical
examples are presented that allow to compare the proposed method to existing joint space approaches.
1 INTRODUCTION
Intelligent path planning and motions exploiting the
existing hardware in an optimal way are essential for
modern production lines. Nevertheless, it is still com-
mon to use lines as geometric paths and motion pro-
files like trapezoidal acceleration or minimum jerk to
follow these lines (Siciliano et al., 2009). An im-
provement for tasks with a defined robot motion can
be achieved by the optimal path following problem.
The latter consist in following a given path in short-
est time possible under kinematic and dynamic con-
straints. It is an established approach to divide the
problem into the geometric path planning followed by
a subsequent optimization of the path following tra-
jectory (Bobrow et al., 1985) (Pfeiffer and Johanni,
1987). Nowadays very efficient algorithms are avail-
able to solve this kind of problem like (Pham, 2013;
Reynoso-Mora et al., 2013; Verscheure et al., 2009b).
If only the start and end points are defined, optimal
point-to-point motion planning can be used. In this
course the path is no longer defined fix, it is optimized
under various restrictions. Beside the kinematic and
dynamic restrictions of the robot, also obstacles have
to be considered (Shiller and Dubowsky, 1988). The
optimization can be performed in task space (Rajan,
1985) or joint space (Antonelli et al., 2005). Usu-
ally the calculation times for this kind of problem are
rather high, compared to the execution times.
Often a predefined path do not have to be fol-
lowed exactly, but within a certain surrounding. (De-
brouwere et al., 2014) proposed a method called opti-
mal tube following, where the path can vary within
a predefined tube around an initial path to reduce
the costs compared to the initial path. They solved
the problem by introducing a joint angle parametriza-
tion, tube approximation and optimization of the path
within the tube to reduce execution times.
Robotic tasks are typically given in task space,
why the paths are usually also planed there. Due
to this the approach proposed in the present paper
is based on an optimization of the geometric end-
effector (EE) path. This path is defined via splines,
which provide many useful properties concerning op-
timization. We will give a comparison to the joint
space approach in (Debrouwere et al., 2014). Further
we show how this idea can be extended to achieve op-
timal trajectories starting with polygonal lines as ge-
ometric path, as they are used e.g. in mobile robotics
(Zou et al., 2006; Zaverucha, 2005).
The focus of the present paper lies on time optimal
trajectories. Nevertheless, the proposed approaches
can also be used for other optimality criteria like en-
ergy consumption.
In the course of this paper derivatives with respect
to the path parameter are marked with a prime x
′
=
dx
ds
,
time derivatives with a dot ˙x =
dx
dt
. Small bold letters
are used for vectors, capital bold letters for matrices.
The paper is organized as follows: Section 2 starts
with the geometric path planning followed by the
kinematic and dynamic modeling of the robot. The
time-optimal path following problem is introduced in
section 3. Afterwards, the tube restriction is defined in
section 4. The joint space time-optimal tube follow-
ing is briefly introduced in section 5. Our task space
approach is proposed in section 6. In section 7 we
Oberherber, M., Gattr inger, H., Müller, A. and Schachinger, M.
A Task Space Approach for Planar Optimal Robot Tube Following.
DOI: 10.5220/0005980303270334
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 327-334
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
327

give a comparison between the joint space and task
space approach. Further we present a numerical ex-
ample for an industrial robot to show the approach’s
functionality concerning polygonal initial paths. Fi-
nally, we conclude our paper and give an insight into
future work in section 8.
2 PATH PLANNING AND
MODELING
The following section briefly covers the geometric
path planning, the kinematic and dynamic modeling
of the manipulator. Further, the parametrization of
the Equations of Motion (EoM) along the scalar path
parameter is introduced.
2.1 Geometric Path Planning
Spline functions provide many useful properties like
the convex hull property, local support property, con-
tinuity or the invariance against translation, rotation
and scaling (Piegl and Tiller, 1997). These proper-
ties, and the existence of very fast algorithms for nu-
merically calculations, like de Boor’s algorithm (De-
Boor, 1978), make splines to an interesting tool in the
fields of robotics. A three-dimensional spline curve,
describing e.g. the EE-position r
r
r
E
of a robot can be
written as
r
r
r
E
(s) =
n
D
∑
l=1
d
d
d
l
N
d
l
(s), (1)
with the scalar path parameter s = [s
B
,s
E
] (s
B
- be-
gin of the path, s
E
- end of the path). N
d
l
(s) denote
the B-spline basis functions of degree d, while d
d
d
l
are
the control points (CPs). There are different ways
to define the basis functions as local or global sup-
port functions. Once the path is defined, the deriva-
tives of the path with respect to the path parameter
r
r
r
′
E
(s),r
r
r
′′
E
(s) can be calculated easily by differentia-
tion of the basis functions. For details we refer to
(DeBoor, 1978) and (Piegl and Tiller, 1997). An ex-
emplary spatial EE-path, defined via splines, is shown
Figure 1.
2.2 Kinematic Model
The forward kinematics of a manipulator provides the
EE- coordinates z
z
z
T
E
(s) = [r
r
r
T
E
(s),ϕ
ϕ
ϕ
T
E
(s)] (position r
r
r
E
, orientation ϕ
ϕ
ϕ
E
, e.g. in Cardan angles) as a func-
tion of the joint positions q
q
q of the robot. Conversely,
the inverse kinematicsq
q
q(s) = f
f
f
−1
(z
z
z
E
(s)) provides the
joint angles as a function of desired EE - coordinates.
There are different ways to solve the locally, but not
q
1
q
2
q
3
q
4
q
5
q
6
d
d
d
0
d
d
d
1
d
d
d
j
d
d
d
n
D
−1
d
d
d
n
D
I
x
I
y
I
z
E
x
E
y
E
z
s
s
B
s
E
r
r
r
E
(s)
ϕ
ϕ
ϕ
E
(s)
Figure 1: Six-axis industrial robot with joint positions q
q
q.
globally unique problem of the inverse kinematics.
We use a numerical approach (Siciliano et al., 2009)
based on the relation
v
v
v
E
ω
ω
ω
E
= J
J
J(q
q
q)
˙
q
q
q, (2)
with the EE - velocities v
v
v
E
, ω
ω
ω
E
represented in the in-
ertial frame and the geometric Jacobian
J
J
J =
∂v
v
v
E
∂
˙
q
q
q
∂ω
ω
ω
E
∂
˙
q
q
q
!
. (3)
With the Jacobian and r
r
r
′
E
(s), r
r
r
′′
E
(s), the prime quanti-
ties of the joint angles can be calculated as
q
q
q
′
= J
J
J
−1
r
r
r
′
E
(4)
q
q
q
′′
= J
J
J
−1
r
r
r
′′
E
−J
J
J
′
q
q
q
′
. (5)
Near to singularities the Jacobian gets singular. Due
to this a robust inversion J
J
J
+
= (J
J
J
T
J
J
J + δ
2
I)
−1
J
J
J
T
is
used, with the identity matrix I and a damping fac-
tor δ that is only active near to singularities.
Using the chain rule for differentiation
dx
dt
=
dx
ds
ds
dt
= x
′
˙s (6)
and the identity ¨s = (d˙s/ds)(ds/dt) = ( ˙s
2
)
′
/2, the
joint velocities and accelerations are
˙
q
q
q(s) = q
q
q
′
(s)˙s (7)
¨
q
q
q(s) = q
q
q
′′
(s)˙s
2
+
1
2
q
q
q
′
(s)(˙s
2
)
′
. (8)
2.3 Dynamic Model
A dynamic model of the robot is necessary to be able
to include torque constraints in the optimization. It
is also used for simulation purposes. The dynamic
model can be written in form of the EoM as
M
M
M(q
q
q)
¨
q
q
q+g
g
g(q
q
q,
˙
q
q
q) = τ
τ
τ (9)
with the position dependent positive definite mass
matrix M
M
M(q
q
q). Joint angles q
q
q are the minimal coor-
dinates of the system. The vector g
g
g(q
q
q,
˙
q
q
q) contains all
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
328

nonlinear terms, like Coriolis-, centrifugal-, friction-,
or gravitational forces. The motor torques are denoted
withτ
τ
τ. We derive the EoM with the help of the Projec-
tion Equation (Bremer, 2008). For the path tracking
problem a representation of the EoM in the parameter
range is necessary, and can be written as
τ
τ
τ = a
a
a(s) ( ˙s
2
)
′
+b
b
b(s) ˙s
2
+c
c
c(s) +d
d
d
v
(s)˙s. (10)
A method, based on the Projection Equation, to de-
rive the parameters a
a
a, b
b
b, c
c
c and d
d
d
v
analytically is pro-
posed in (Gattringer et al., 2014). Numerical methods
to derive them are presented in (Johanni, 1988) and
(Geu Flores and Kecskemthy, 2012).
3 PATH FOLLOWING PROBLEM
The time optimal robot path following (PF) problem
regards the problem of generating trajectories that fol-
low predefined EE paths in shortest possible time, tak-
ing into account kinematic and dynamic constraints.
Since the path is defined in the parameter range, the
aim is to calculate an optimal relation t(s) between
time and path parameter. We are looking for optimal
solutions for the cycle time t
E
of a process. Since this
time is the solution of the optimization, it is a priori
unknown. A change of the integration variable from t
to s leads to
t
E
=
Z
t
E
0
1dt =
Z
s
E
s
B
1
˙s(s)
ds. (11)
By introducing the abbreviation z = ˙s
2
the following
optimization problem in parameter space
min
z(·)
Z
s
E
s
B
1
p
z(s)
ds (12)
s.t.
˙
q
q
q
≤ q
q
q
′
(s)
p
z(s) ≤
˙
q
q
q
¨
q
q
q
≤ q
q
q
′′
(s)z(s)+
1
2
q
q
q
′
(s)z
′
(s) ≤
¨
q
q
q
τ
τ
τ
≤ a
a
a(s)z
′
(s) +b
b
b(s)z(s)+c
c
c(s) +d
d
d
v
(s)
p
z(s) ≤ τ
τ
τ.
has to be solved. It is assumed that the joint velocity
restrictions
˙
q
q
q
,
˙
q
q
q, joint acceleration restrictions
¨
q
q
q
,
¨
q
q
q and
torque restrictions τ
τ
τ
, τ
τ
τ are constant along the path.
There exist several different approaches to solve
the classical path following problem. In the 1980’s
(Bobrow et al., 1985) proposed a method based on nu-
merical integration and the search of switching points
in the phase plane, while (Shin and McKay, 1986)
used a dynamic programming approach to solve this
kind of problem. Current works in this research field
are for example an online log-barrier optimization
(Verscheure et al., 2009b), or a Second Order Cone
Program (SOCP) reformulation of the problem (Ver-
scheure et al., 2009a). These approaches make use of
a convex formulation of the optimization problems.
Nevertheless, (12) is non-convex, due to the inclu-
sion of viscous friction (parameter d
d
d
v
). (Reynoso-
Mora et al., 2013) proposed a method called convex-
relaxation, that empowers them to reformulate the op-
timization as a SOCP anyway.
4 TUBE-RESTRICTION
The tube should constrain the EE-position within a
defined distance r
T
(s
i
) to the initial path. Debreuwere
et al. proposed different ways to approximate the
tube. They show, that a linear approximation is com-
putationally more expensive than a quadratic approx-
imation, see Figure 2. In this paper we will use the
quadratic approximation, defined as
C
r
E
= {r
r
r
E
(s
i
)| (13)
(r
r
r
E
(s
i
) −r
r
r
E,0
(s
i
))
T
(r
r
r
E
(s
i
) −r
r
r
E,0
(s
i
)) ≤ r
T
(s
i
)
2
,
where C
r
E
is the defined space of the tube. The better
performance of the quadratic approximation goes in
contrast with a higher deviation of the approximated
to the original tube. An approximation of the tube
is necessary to allow a tangential relocation of a dis-
crete path point r
r
r
E
(s
i
) against the initial path r
r
r
E,0
(s
i
),
see Figure 2. For a detailed explanation of the tube
definitions we refer to (Debrouwere et al., 2014).
s
i
s
i−1
s
i+1
r
T
(s
i
)
Figure 2: Quadratic approximation of the tube with the ini-
tial path r
r
r
E,0
(s) in black and a modified path r
r
r
E
(s) in blue.
5 JOINT SPACE APPROACH
(Debrouwere et al., 2014) solves the time optimal PF
problem in joint space, with the joint anglesq
q
q ∈ R
n
DOF
as minimal coordinates. These are parametrized along
the path within an upper
q
q
q and a lower q
q
q boundary
using a parameter 0 ≤ λ
λ
λ(s) ≤ 1. Thus, they can be
written as
q
q
q(s) = λ
λ
λ(s)q
q
q(s) + (1−λ
λ
λ(s))q
q
q(s). (14)
Parameter λ
λ
λ(s) = [λ
1
(s),... ,λ
n
DOF
(s)]
T
can be de-
fined as a spline curve with k
c
CPs γ
γ
γ. These CPs rep-
resent the optimization variables and the optimization
A Task Space Approach for Planar Optimal Robot Tube Following
329

problem can be written as
min
z(·),γ
γ
γ
Z
s
E
s
B
1
p
z(s)
ds (15)
s.t.
˙
q
q
q
≤ q
q
q
′
(s)
p
z(s) ≤
˙
q
q
q
¨
q
q
q
≤ q
q
q
′′
(s)z(s)+
1
2
q
q
q
′
(s)z
′
(s) ≤
¨
q
q
q
τ
τ
τ
≤ a
a
a(s)z
′
(s) +b
b
b(s)z(s)+c
c
c(s) +d
d
d
v
(s)
p
z(s) ≤ τ
τ
τ
0 ≤ λ
λ
λ(s) ≤ 1
r
r
r
E
(λ
λ
λ(s)) ∈ C
r
E
r
r
r
E
(s
B
) = r
r
r
E,B
r
r
r
E
(s
E
) = r
r
r
E,E
.
The last two equality constraints indicate that the start
point (r
r
r
E,B
) and end point r
r
r
E,E
of the path are fixed.
6 TASK SPACE APPROACH
The following section introduces the task space ap-
proach. The discussion is limited to planar paths.
First the method for general planar paths is intro-
duced. Following, this section shows how this ap-
proach can be used to deriveoptimal trajectories when
the initial path is described in terms of polygonal
lines.
6.1 General Solution Strategy
The solution strategy of the proposed task space ap-
proach is based on a separation of path planning and
the calculation of an optimal motion profile. The
idea is similar to the one proposed in (Rajan, 1985).
First an initial path for the EE of the robot r
r
r
E,0
(s) is
planned via the CPs D
D
D = [d
d
d
0
,.. . ,d
d
d
j
,d
d
d
n
D
]
T
using (1).
A time optimal solution for this PF problem is calcu-
lated. In a next step, a path optimization algorithm in
the sense of variation of the CPs is used to get even
faster overall trajectories. Therefore, with the new
CPs, a new EE-path is calculated and again a time
optimal PF problem for this path is solved. This is
repeated till convergence (no further improvement of
the execution time t
E
) is achieved.
Figure 3 shows a flow-chart of this two-stage op-
timization strategy. An advantage of this method is,
that, depending on the restrictions that have to be con-
sidered, any of the consisting and well tested time op-
timal PF-algorithms like (Bobrow et al., 1985), (Shin
and McKay, 1986), (Verscheure et al., 2009b), (Ver-
scheure et al., 2009a), (Reynoso-Mora et al., 2013),
(Pham, 2013) can be used. The choice of the path op-
timization algorithm is not easy since the problem is
non-convex.
initial path
time optimal PF-optimization
time optimal PF-optimization
path-optimization (optimize CPs)
calculate new path
convergence?
yes
no
t
E,0
t
E
d
d
d
j
r
r
r
E
r
r
r
E,0
optimal trajectory
Figure 3: Solution strategy for the multistage optimization.
6.2 Task Space Approach for Planar
Spline Paths
The following procedure can not only be used for pla-
nar robots, but also for multi-axis robots, when the
EE-path is defined within a plane. In this plane the
path, as well as the tube boundaries can be repre-
sented by splines. The CP locations can be defined
as a convex combination
d
d
d
j
= d
d
d
j
α
j
+d
d
d
j
(1− α
j
) for j = 1.. .n
D
− 1. (16)
of the bounding CPs d
d
d
j
and d
d
d
j
of the tube curves
r
r
r
E
and r
r
r
E
, as shown in Figure 4. The parameters
0 < α
j
< 1 represent the optimization variables for
the path optimization. Thus, the optimization prob-
lem for the two-stage approach can be written as
min
α
α
α
J (17)
s.t. 0 < α
j
< 1 for j = 1.. .n
D
− 1
r
r
r
E
(s,α
α
α) ∈ C
r
E
,
wherein the time optimal PF optimization (12) has to
be solved in every iteration of the path optimization.
d
d
d
0
d
d
d
0
d
d
d
0
d
d
d
1
d
d
d
1
d
d
d
1
d
d
d
2
d
d
d
2
d
d
d
2
d
d
d
3
d
d
d
3
d
d
d
3
r
r
r
E,0
(s)
r
r
r
E
(s)
r
r
r
E
(s)
Figure 4: Task space approach: Planar tube and path.
6.3 Tube Following with Polygonal
Lines
In (16) bounding CPs D
D
D
= [d
d
d
0
,.. . ,d
d
d
j
,d
d
d
n
D
]
T
and D
D
D =
[
d
d
d
0
,.. . ,d
d
d
j
,d
d
d
n
D
]
T
are defined. Nevertheless, the tube
restriction (13) has to be considered in the optimiza-
tion problem (17). Now, one may ask how they should
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
330
be defined to guarantee that the resulting curve with
the CPs d
d
d
j
= d
d
d
j
α
j
+
d
d
d
j
(1− α
j
) lies within the tube.
Unfortunately it is not straight forward to calculate in-
tersection points of splines (Mørken et al., 2009), and
following it is hard to define the CPs boundings in a
reasonable way for splines.
But, as mentioned in section 1, the usage of
straight lines with subsequent edge combining is still
a wide spread approach for path planning in industrial
applications nowadays. Also the global path planner
of mobile robots often provide polygonal lines, see
e.g. (Zou et al., 2006). For such cases it is a manage-
able problem to define the position of the bounding
CPs in a reasonable way. In the course of this section
we will present an approach to achieve optimal trajec-
tories along continuous paths, starting with polygonal
lines surrounded by polygonal tube restrictions.
6.3.1 Local Convex Hull Property
To eliminate the possibility of an intersection between
the resulting spline and the tube, we will use the lo-
cal convex hull property, as for example proposed in
(Mørken et al., 2009):
If the unions of all local convex hulls of two
spline curves are disjunct, so are the splines.
If we are able to define the bounding CPs in a way
that this condition holds, the tube approximation (13)
and the related restriction in the optimization problem
(17) can be omitted.
The local convexhull of a spline curve with degree
d is the smallest convex set, that contains the points
d
d
d
j−d
...d
d
d
j
. In Figure 5 the local convex hulls (exem-
plary for d = 3) of the bounding CPs D
D
D and D
D
D are
shown. The presence of multiple CPs let the convex
hull degenerate to lines or points in some cases. The
spline curves r
r
r
(s) and r
r
r(s) defined by D
D
D and D
D
D lie
within the union of the local convex hulls. If an in-
tersection between these two curves can be excluded,
the resulting spline r
r
r
E
(s), whose CPs are calculated
as a convex combination of D
D
D
and D
D
D, lies guaranteed
within ther
r
r
(s) andr
r
r(s) and following within the tube.
d
d
d
1
d
d
d
1
d
d
d
1
d
d
d
1
d
d
d
2
d
d
d
2
d
d
d
2
d
d
d
2
d
d
d
3
d
d
d
3
d
d
d
3
d
d
d
3
d
d
d
4
d
d
d
4
d
d
d
4
d
d
d
4
d
d
d
5
d
d
d
5
d
d
d
5
d
d
d
5
d
d
d
1
d
d
d
1
d
d
d
1
d
d
d
1
d
d
d
234
d
d
d
234
d
d
d
234
d
d
d
234
d
d
d
5
d
d
d
5
d
d
d
5
d
d
d
5
r
r
r
T,1
r
r
r
T,2
r
r
r(s)
r
r
r
T,1
r
r
r
T,2
r
r
r
(s)
Figure 5: Local convex hulls for
r
r
r(s) (gray), r
r
r(s) (yellow).
6.3.2 Control Point Placement
We will use the knowledge from section 6.3.1 to de-
fine the CPs positions in a way that the resulting curve
guaranteed lies within the defined tube. For a reason-
able definition followingpoints have to be considered:
• The polygonal path is defined by the points p
p
p
j
in
task space coordinates. The angle between two
lines is denoted as ϕ.
• The combination of two lines is called segment.
Following a path consists of n
L
lines, respectively
n
S
= n
L
− 1 segments.
• The descriptions ’inner’ and ’outer’ corner refer
to a movement along the path from s
B
to s
E
.
• The local convex hulls of r
r
r(s) and r
r
r(s) must not
intersect.
• The necessary number of CPs for one segment de-
pends on the spline degree d.
• No overlaps between CPs are allowed.
• The projected tube lengths l
T,i
and l
T,i
denote the
projection of r
r
r
T,i
on r
r
r
T,i
and conversely the pro-
jection of
r
r
r
T,i
on r
r
r
T,i
, as shown in Figure 6 right.
ϕ
1
ϕ
2
l
T,1
l
T,2
l
T,3
l
T,1
l
T,2
l
T,3
p
p
p
0
p
p
p
0
p
p
p
2
p
p
p
1
p
p
p
1
p
p
p
3
r
T0,1
r
T0,1
r
TE,1
r
TE,1
Figure 6: Left: Tube distance definition. Right: polygonal
path with tube restrictions and projected tube lengths.
Algorithm:
For all lines k = 1...n
L
1. Treat special cases
: For ϕ = π the lines are com-
bined to one, the case ϕ = 0 is excepted. Assum-
ing long lines in comparison to the tube distances
avoids the case that a line lies completely within
the tube of an adjacent line.
2. Define the tubes
: The tubes are defined as lines
with orthogonal distances to the line r
T0,k
and
r
T0,k
at the start and r
TE,k
and
r
TE,k
at the end of
the line as shown in Figure 6 left.
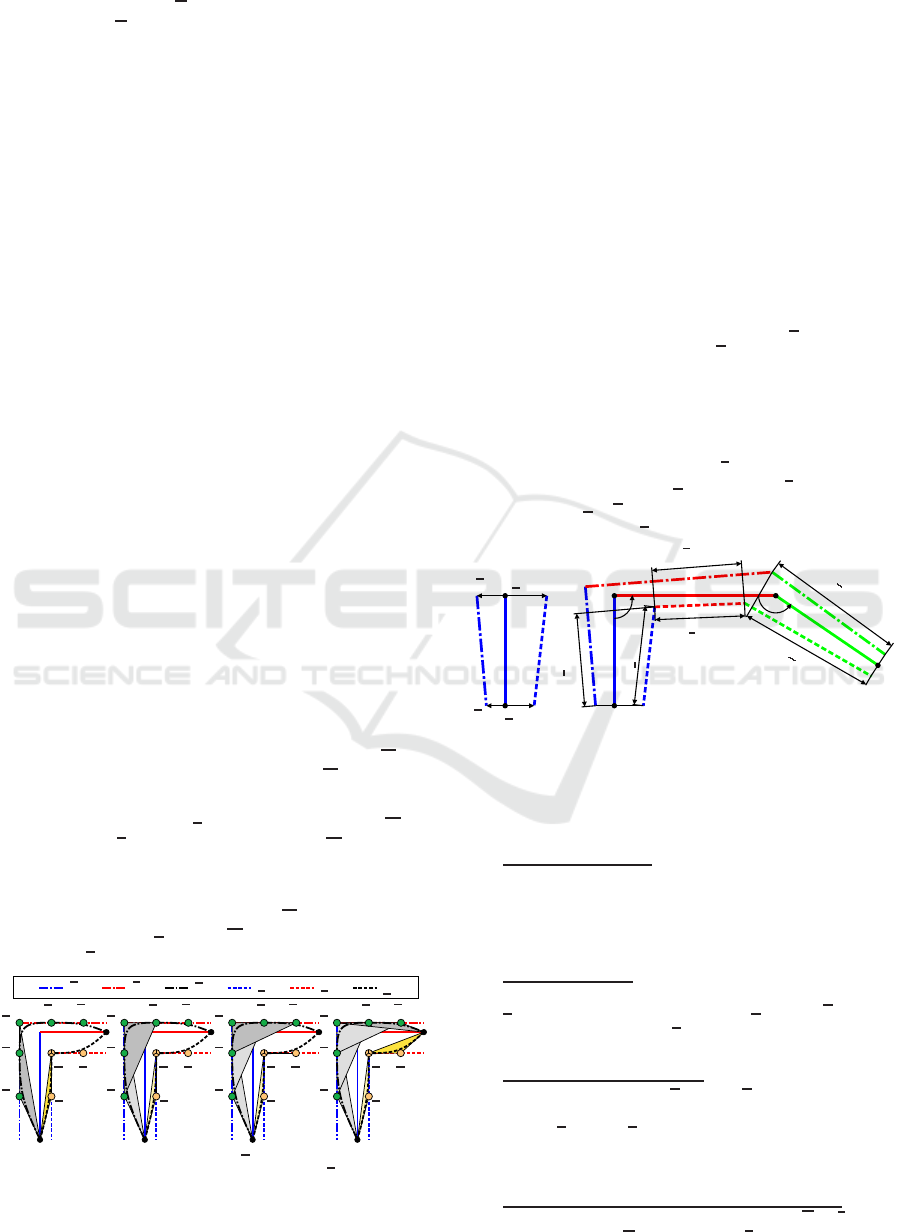
3. Generate the overall tube: Calculate the intersec-
tion points between r
r
r
T,k
and r
r
r
T,k+1
and also be-
tween r
r
r
T,k
and r
r
r
T,k+1
. Complete the tube by ex-
trapolating and cutting the particular tubes at in-
tersection points as shown in Figure 6 right.
4. Place CPs at half of projected tube lengths:
Bounding CPs d
d
d
are placed at l
T,k
/2,
d
d
d at l
T,k
/2.
A Task Space Approach for Planar Optimal Robot Tube Following
331

5. Place CPs around the corners: Determine the
connection line between the outer CPs (dotted and
dotdashed in Figure 7 left). If this connection line
lies within the tube (dotdashed), the outer CPs are
also placed there. Otherwise (dotted), the line is
parallel shifted to the inner corner and the outer
CPs are placed at the intersection points of the line
with the outer tube. The inner bounding CPs are
placed at the inner tube corner.
6. Place CPs at the tube corners
: At the tube corners
bounding control points of multiplicity d − 1 are
placed. The number of optimization variables can
be reduced by placing the outer CPs onto the inner
tube corner, as shown in Figure 7 right. Then it
is guaranteed that the path touches the inner tube
corner. This should be an advantage in most cases,
except if the inner corner lies near to a singularity.
D
D
D
D
D
D
d
d
d
j
d
d
d
j.. j+3
= d
d
d
j
d
d
d
j.. j+1
= d
d
d
j
d
d
d
j
(α
j
)
Figure 7: Left: Control point placement for d = 3. Right:
Reduction of optimization variables.
7 EXAMPLES AND RESULTS
At first this section gives a comparison of the pro-
posed task space approach with the joint space ap-
proach in terms of a 2D-example defined in (De-
brouwere et al., 2014). Additionally, an example with
polygonal line paths for the industrial robot St¨aubli
RX130L is presented. The following examples are
programmed in Matlab and run on a standard PC with
a 3.4 GHz processor.
7.1 General Planar Paths
The parameters of the 2DOF serial manipulator in
Figure 8 are: l
1
= l
2
= 1m, r
s,1
= r
s,2
= 0.5m and
m
1
= m
2
= 1kg. With
τ
τ
τ = [30,10] Nm and τ
τ
τ = −τ
τ
τ, the
motor torque restrictions are given, see (Debrouwere
et al., 2014) for details. The initial joint motion is
defined as
q
q
q
0
(s) =
−4π(s
2
− s)
−πs
. (18)
The resulting EE path, see Figure 8, is discretized
into n = 100 pieces. The joint angle restrictions are
q
q
q
(s) =
1
2
q
q
q
0
(s) and
q
q
q(s) = 2q
q
q
0
(s), the spline λ
λ
λ(s) is
linear (degree 1). With r
T
(s) = 0.1(1 − s
4
) the posi-
tion dependent tube size is defined. For the task space
approach the tube and the EE path have to be approx-
imated by splines, which can be achieved in a satisfy-
ing manner with n
D
> 10.
In Table 1 a listing of resulting execution and cal-
culation times is given. It should be mentioned that
the calculation times strongly depend on the chosen
path discretization and chosen optimization criteria.
To allow a fair comparison we defined them equally
as much as possible for both approaches. The abbre-
viations are TF TS for tube-following task space, and
TF JS for tube-following in the joint space. These
results show, that both approaches perform nearly
equally for this very simple example. The percent-
age savings in execution time (last column in Table 1)
of the joint space approach are comparable to those
presented in (Debrouwere et al., 2014). Since we use
non-optimized Matlab code for the optimization, cal-
culation times are slightly higher. With the number
of CPs the quality of the solution can be modified.
The decrease in execution time stands in contrast to a
higher calculation time. A view on Figure 8 shows,
that the optimal paths of the two approaches are quite
different, in spite of the similar execution times. This
is also an evidence on the non-convex characteristic
of the problem. The resulting motor torques normal-
ized on the maximum values as well as the optimal
trends z
opt
(s) are shown in Figure 9.
r
E,0
r
E,JS
r
E,TS
x in m
y in m
r
E
r
E
−1.5
−1
−0.5
0
0.5
1
1.5
2
0
0.5
1
1.5
2
g
r
s,1
r
s,2
m
1
m
2
q
1
q
2
Figure 8: Optimal end-effector paths and tube constraints.
Table 1: Calculation t
CPU
and execution times t
E
.
Approach n
D
, k
c
t
E
in s t
CPU
in s TF/PF
PF - 2.30 0.334 -
TF TS 11 2.20 4.16 4.35%
TF TS 13 2.19 3.81 4.78%
TF TS 15 2.17 5.36 5.65%
TF JS 11 2.17 3.98 5.65%
TF JS 13 2.14 5.46 6.96%
Comparison. Both approaches have their certain
pros and cons. The task space approach does not re-
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
332

τ
JS
τ
TS
τ
PF
τ
2
/
τ
2
s
τ
1
/
τ
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
−1
0
1
−1
0
1
z
JS
z
TS
z
PF
z(s)
s
0
0.1
0.2
0.3
0.4
0.5 0.6
0.7
0.8
0.9
1
0
0.2
0.4
0.6
0.8
Figure 9: Top: Normalized torques τ
τ
τ/τ
τ
τ. Bottom: Optimal
trends z
opt
(s) for all approaches.
quire a joint angle parametrization, which drives up
the optimization time if chosen too big, or addition-
ally restrict the problem if chosen too small. The
number of optimization variables for the path opti-
mization depends on the path length, respectively the
number of chosen CPs for the task space approach
n
opt
≤ n
D
−2. While the number of optimization vari-
ables for the path optimization at the joint space ap-
proach also depends on the number of degrees of free-
dom n
opt
= n
DOF
k
c
. The necessity of the inverse kine-
matics may be seen as disadvantage of the task space
approach. But, it empowers us to simply include de-
sired EE-orientations ϕ
ϕ
ϕ
E
(s) along the path. While
an additional equality constraint has to be added to
the optimization problem (15) for the joint space ap-
proach to consider a desired EE-orientation.
A big advantage of the task space approach is
that optimal trajectories defined in terms of polygonal
lines as shown in section 6.3 can be derived,where the
tube approximation can be omitted due to an intelli-
gent placement of the CPs, as shown in the following
example.
7.2 Polygonal Lines
The following example is implemented for the indus-
trial robot St¨aubli RX130L in Figure 1. For simplic-
ity, joints q
4
, q
5
and q
6
are locked. In contrast to
the simple example in the section before, several ef-
fects like viscous and Coulomb friction are consid-
ered. The time optimal PF optimization is done with
a dynamic programming approach. Three lines, in the
y - z plane in front of the robot with the points
p
p
p
0
= [0.75 − 0.5 0.1] m p
p
p
1
= [0.75 − 0.5 1] m
p
p
p
2
= [0.75 0.5 1] m p
p
p
3
= [0.75 0.7 0.1] m
represent the initial path, shown in Figure 10. This
path is discretized into n = 150 equidistant pieces.
The robot’s hardware restrictions for the joint veloci-
z in m
y in m
r
r
r
E,0
r
r
r
T
r
r
r
T
r
r
r
E
d
d
d
d
d
d
d
d
d
p
p
p
0
p
p
p
1
p
p
p
2
p
p
p
3
−0.6
−0.4
−0.2
0.2
0.4
0.6
0.8
0
0.2
0.4
0.6
0.8
1
1.2
Figure 10: Polygonal path with tube restrictions and result-
ing optimal path with the associated CPs.
ties and motor torques are given as
˙
q
q
q = −
˙
q
q
q
= [4.45, 4.45, 5.7]rad/ s (19)
τ
τ
τ = −τ
τ
τ = [9.05, 9.05, 6.4]Nm. (20)
To show some special cases, different tube distances
are chosen for the lines:
r
T0
= {10, 1, 10} cm, r
T0
= {5, 15, 1} cm
r
TE
= {5, 2, 20} cm, r
TE
= {5, 25, 5} cm.
The BOBYQA algorithm from NLOPT library (John-
son, 2011) was used via the Matlab interface for path
optimization. For validation purposes several other
algorithms from the NLOPT library were proved, re-
sulting in nearly the same trajectory within differ-
ent calculation times, strongly depending on the dis-
cretization. Resulting joint velocities and torques are
shown in Figure 11. Execution and calculation times
are given in Table 2. Where r
r
r
E,0
, indicates the line
path, r
r
r
E
the optimal and r
r
r
E,α
α
α
0
the initial path with
α
j
= 0.5, j = 1..n
opt
. Fixed corner CPs, as described
in section 6.3.2, reduce the number of optimization
variables from n
opt
= 9 to 7. This influences not only
the calculation times, but also generates a better ini-
tial solution. The percentage time savings refer to the
time optimal motion along the three lines, where the
robot has to stop after each line.
Table 2: Execution and calculation times.
r
r
r
E,0
r
r
r
E,α
α
α
0
r
r
r
E
r
r
r
E,α
α
α
0
r
r
r
E
n
opt
= 9 n
opt
= 7
t
E
in s 1.46 1.46 1.14 1.13 1.05
t
CPU
in s 0.85 0.72 18 0.73 12
save in % — 0 21.7 14.82 22.8
8 CONCLUSIONS
In the present paper we proposed a task space ap-
proach to solve the planar optimal tube following
problem. The focus is on time optimality, neverthe-
less other optimality criteria like energy consump-
tion or path length can also be considered with this
A Task Space Approach for Planar Optimal Robot Tube Following
333

˙q
3
˙q
2
˙q
1
˙
q
q
q/
˙
q
q
q
s
0
0.2
0.4
0.6
0.8
1
−1
−0.5
0
0.5
1
τ
3
τ
2
τ
1
τ
τ
τ/
τ
τ
τ
s
0
0.2
0.4
0.6
0.8
1
−1
−0.5
0
0.5
1
Figure 11: Top: Normalized joint velocities. Bottom: Nor-
malized motor torques.
method. By means of numerical examples we have
shown that the proposed approach performs nearly
equally to an existing one, with the benefit that opti-
mal trajectories from polygonal paths without an ad-
ditional tube restriction can be derived. Future works
will include among other things further improvements
of the algorithm, an automatism for the tube genera-
tion and the extension to spatial paths.
ACKNOWLEDGEMENTS
This work has been supported by the Linz Center of
Mechatronics (LCM) in the framework of the Aus-
trian COMET-K2 program.
REFERENCES
Antonelli, G., Chiaverini, S., Palladino, M., Gerio, G. P.,
and Renga, G. (2005). Joint space point-to-point mo-
tion planning for robots: An industrial implementa-
tion. In Ztek, P., editor, Proceedings of the 16th IFAC
World Congress.
Bobrow, J. E., Dubowsky, S., and Gibson, J. S. (1985).
Time-optimal control of robotic manipulators along
specified paths. International Journal Robotics Re-
sarch, 4:3–17.
Bremer, H. (2008). Elastic Multibody Dynamics: A Direct
Ritz Approach. Springer Verlag, Heidelberg.
DeBoor, C. (1978). A practical guide to splines. Springer.
Debrouwere, F., Van Loock, W., Pipeleers, G., and Sw-
evers, J. (2014). Time-optimal tube following for
robotic manipulators. In Advanced Motion Control
(AMC),2014 IEEE 13th International Workshop on,
pages 392–397.
Gattringer, H., Oberherber, M., and Springer, K. (2014).
Extending continuous path trajectories to point-to-
point trajectories by varying intermediate points.
International Journal of Mechanics and Control,
15(01):35–43.
Geu Flores, F. and Kecskemthy, A. (2012). Time-optimal
path palanning along specified trajectories. In Gat-
tringer, H. and Gerstmayr, J., editors, Multibody Sys-
tem Dynamics, Robotics and Control, pages 1–15.
Johanni, R. (1988). Optimale Bahnplanung bei Industrier-
obotern. Technische Universit¨at M¨unchen.
Johnson, S. G. (2011). The NLopt nonlinear-optimization
package.
Mørken, K., Reimers, M., and Schulz, C. (2009). Com-
puting intersections of planar spline curves using knot
insertion. Comput. Aided Geom. Des., 26(3):351–366.
Pfeiffer, F. and Johanni, R. (1987). A concept for manipula-
tor trajectory planning. IEEE Journal of Robotics and
Automation, 3(2):115 –123.
Pham, Q. (2013). A general, fast, and robust implementa-
tion of the time-optimal path parameterization algo-
rithm. CoRR, abs/1312.6533.
Piegl, L. A. and Tiller, W. (1997). The NURBS book (2. ed.).
Monographs in visual communication. Springer.
Rajan, V. (1985). Minimum time trajectory planning. In
Robotics and Automation. Proceedings. 1985 IEEE
International Conference on, volume 2, pages 759–
764.
Reynoso-Mora, P., Chen, W., and Tomizuka, M. (2013).
On the time-optimal trajectory planning and control of
robotic manipulators along predefined paths. In Amer-
ican Control Conference (ACC), 2013, pages 371–
377.
Shiller, Z. and Dubowsky, S. (1988). Global time optimal
motions of robotic manipulators in the presence of ob-
stacles. In Robotics and Automation, 1988. Proceed-
ings., 1988 IEEE International Conference on, pages
370–375 vol.1.
Shin, K. G. and McKay, N. D. (1986). A dynamic pro-
gramming approach to trajectory planning of robotic
manipulators. Automatic Control, IEEE Transactions
on, 31(6):491–500.
Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G.
(2009). Robotics - Modelling, Planning and Control.
Advanced Textbooks in Control and Signal Process-
ing series. Springer.
Verscheure, D., Demeulenaere, B., Swevers, J., De Schutter,
J., and Diehl, M. (2009a). Time-optimal path tracking
for robots: A convex optimization approach. Auto-
matic Control, IEEE Transactions on, 54(10):2318–
2327.
Verscheure, D., Diehl, M., De Schutter, J., and Swevers,
J. (2009b). Recursive log-barrier method for on-line
time-optimal robot path tracking. In American Con-
trol Conference, 2009. ACC ’09., pages 4134 –4140.
Zaverucha, G. (2005). Approximating polylines by curved
paths. In Mechatronics and Automation, 2005 IEEE
International Conference, volume 2, pages 758–763
Vol. 2.
Zou, A.-M., Hou, Z.-G., Tan, M., and Liu, D. (2006). Path
planning for mobile robots using straight lines. In Net-
working, Sensing and Control, 2006. ICNSC ’06. Pro-
ceedings of the 2006 IEEE International Conference
on, pages 204–208.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
334
