3D Path Following with Remote Center of Motion Constraints
Bassem Dahroug, Brahim Tamadazte and Nicolas Andreff
FEMTO-ST Institute, AS2M department, Univ. Bourgogne Franche-Comt
´
e/CNRS/ENSMM,
4 Rue Alain Savary, 25000 Besanc¸on, France
Keywords:
Bilateral Remote Center of Motion Constraints, 3D Path Following, Medical Robotics.
Abstract:
The remote center of motion (RCM) is an essential issue during minimal invasive surgery where the surgeon
manipulates a medical instrument inside the human body. It is important to assure that the tool should not
apply forces on the incision wall in order to prevent patient harm. The paper shows a geometric method
computing the intended robot velocity vector for respecting the RCM constraints. In addition, the proposed
solution deals with the latter constraints as the highest task priority. A second task function is added, which
is projected in the null space on the first task, to follow a 3D path inside the cavity. As result, this method
helps the surgeon to execute more sophisticated motion within the patient body with high accuracy; since the
results shows standard deviation around 0.004mm and 0.089mm of RCM task error and positioning task error,
respectively.
1 INTRODUCTION
The surgical assisted-robotics have been getting more
demands over the last years as they help by providing
ergonomic conditions for increasing accuracy and re-
ducing fatigue. Moreover, the patients benefit from a
reduced invasion, time and costs. The assistance will
help the surgeon in performing more complex mo-
tion inside the patient’s body, getting over the phys-
ical constraints and navigating in unknown environ-
ment. In fact, the robot not only needs information
about its internal state, which is the pose of its end-
effector with respect to its base, but it is also required
information regarding the relative pose of the organs.
During the navigation phase, visual servoing con-
trol approach (Azizian et al., 2014) allows to mimic
the perception sense for the surgeon. This approach
uses real-time imaging (e.g., endoscope, optical co-
herence tomography or ultrasound) to detect, track
and guide the instrument (Krupa et al., 2002) (Du-
flot et al., 2016). The navigation software may in-
clude other advanced options such as virtual- and
augmented- reality to enhance the visualization and
guidance process. But the essential control task is
guiding the instrument motion for following a desired
geometric path or trajectory. The difference between
these two latter notations is the solution convergence.
In case the tool is retarded to reach the scheduled
point due to any throughout the previous point. On
one hand, the trajectory following controller tends to
accelerates its velocity and to shortcut the desired tra-
jectory, especially when it is defined with acute cur-
vature, in order to reduce the time delay. On the other
hand, path following controller maintains its motion
along the geometric path with the intended velocity
profile even in lag conditions. The latter controller is
useful for medical applications, especially during ab-
lation process. Since path following controller guar-
antees independent instrument velocity from the ge-
ometric path and depend on the interaction between
the ablation tool and the tissue type. Path following is
widely used for mobile robot but it is not frequently
applied into medical application. A 2D path following
proposed (Seon et al., 2015) for laser surgery. They
applied non-holonomic control for executing a uni-
cycle path following with high frequency. A 3D tra-
jectory following and pose estimation methods (Na-
geotte et al., 2006) proposed for controlling an in-
strument to perform automatic suturing during laparo-
scopic surgery. In general, surgical assisted-robots
help the surgeon to perform more complex gestures
and become less invasive.
Minimal invasive robotic systems enter into the
human body from a small incision which presents
physical constraints on the surgical tool motion.
These constraints are created by the incision wall
which reduces the tool degrees of freedom (DOF) to
four DOF (three rotations and one translation). The
resultant motion from these constraints is called re-
mote center of motion (RCM), trocar constraints, bi-
84
Dahroug, B., Tamadazte, B. and Andreff, N.
3D Path Following with Remote Center of Motion Constraints.
DOI: 10.5220/0005980900840091
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 84-91
ISBN: 978-989-758-198-4
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

lateral constraints or fulcrum effect. This type of mo-
tion could be achieved either with specific kinematic
robot structure (Kuo et al., 2012) or with software
control (Dalvand and Shirinzadeh, 2012). This arti-
cle is focusing on the software control type because it
is a generic method that could be applied regardless
of the robot structure, in condition that the robot DOF
should be greater than 4-DOF. This condition ensures
that the robot kinematic structure is redundant. The
redundancy occurs when the manipulator joints num-
ber (i.e., its DOF) is greater than those required to
execute a desired task. Such task could be any kine-
matic or dynamic goal. The advantage of redundancy
is increasing the robot manoeuvrability and dexterity
that could be useful to avoid singularity, joints lim-
its, workspace obstacles and it provides the concept
of task priority (Nakamura et al., 1987).
For software RCM resolution, there are different
reported methods in the literature: extended Jacobian
with quadratic optimization (Funda et al., 1996), arti-
ficial intelligence based heuristic search (Boctor et al.,
2004), analytical solution based on trocar modelling
with Euler angle representation (Mayer et al., 2004),
isotropy-based kinematic optimization (Locke and
Patel, 2007), gradient projection approach in closed-
loop form (Azimian et al., 2010), dual quaternion-
based kinematic controller (Marinho et al., 2014), and
constrained Jacobian represented with Lie algebra
(Pham et al., 2015). For solving RCM with a visual
servoing scheme, the reported methods are: geomet-
ric constraint with stereo visual servoing for control-
ling the robot position from point-to-point (Osa et al.,
2010), and extended Jacobian solution for manipu-
lating serial end-effector (Aghakhani et al., 2013).
These presented techniques are used to maintain the
task function of fulcrum effect and additional tasks
may be added to extend the robot functionality.
As far as we know, the problem of RCM con-
straints combined with the 3D path following has not
been properly addressed yet.The previous researches
discussed the modelling of trocar kinematics only or
combined with trajectory following. However, the
main new add value of this article is formulating a
new method to maintain bilateral constraints while
following a 3D pre-defined path. The method controls
the motion of rigid tool with visual feedback and it
describes the bilateral constraints in vector form with
task hierarchy, as shown in Section 2. The control
laws are tested in simulator and the results are pre-
sented in Section 3.
2 CONTROL DESIGN
The proposed controller commands the robot velocity
for performing 3D path following with bilateral con-
straints. It achieves the objective with two task errors:
(i) the first prior task is the alignment of the tool with
incision point, and (ii) the second task error is the po-
sition of tool tip with respect to the required path. It
is also has two operation modes to accomplish a de-
sired 3D path: (i) approaching phase where the tool
aligns itself with the trocar point, and (ii) insertion
phase where the trocar point should be located along
the tool.
2.1 Notation
The notations used within the paper are summarized
in Table 1, for a better understanding.
2.2 Remote Center of Motion
Constraints
2.2.1 Problem Statement
On one hand, the tool is free to move when it is out-
side the incision point. On the other hand, the tool
movement is restricted when it passes the incision
hole. During the latter motion, the RCM constraints
allow the tool translation along the y-component of
the current RCM frame (
r
v) and angular rotation (
r
ω)
around the latter frame axes. The y-component of
RCM frame (
r
y) is assumed to be perpendicular to the
tissue surface (Figure 1). The tool tip velocity with
respect to the medical imaging system (
c
v
t
) is deter-
mined by the position-based path following control
(see Section 2.3). Therefore, the problem becomes to
achieved this motion by applying the adequate end-
effector velocity (
r
v and
r
ω) while maintaining the
RCM constraints.
In (Boctor et al., 2004), two heuristic functions
were used to define the RCM constraints. The first
one is the distance (e
1
= T −P) between the tool tip
(T ) and the target point (P) inside the cavity. The sec-
ond function is the cross-product (e
2
= ET ∧RP) be-
tween the rigid tool vector (ET) and the vector from
RCM to the target point (RP). The weakness of this
method is not arranging the heuristic functions in task
priority mode. Therefore, the system could converge
to a solution to satisfy the one function without re-
specting the other one (i.e., (e
1
, e
2
) = (e
1
6= 0, 0) or
(e
1
, e
2
) = (0, e
2
6= 0)).
3D Path Following with Remote Center of Motion Constraints
85

Table 1: Symbols summary.
Symbol Description
ℑ
W
world frame with the origin point W
ℑ
B
robot base frame with the origin point B
ℑ
E
end-effector frame with the origin point E
ℑ
T
tool tip frame with the origin point T
ℑ
R
RCM frame with the origin point R
ℑ
C
camera frame with the origin point C
w
M
e
homogeneous transformation matrix that
describes the pose of ℑ
E
in ℑ
W
c
v
e
linear velocity of ℑ
E
that is expressed in
ℑ
C
c
ω
e
angular velocity of ℑ
E
that is expressed
in ℑ
C
c
τ
e
velocity vector of ℑ
E
that groups its linear
and angular velocities
I
3×3
identity matrix
r
y the y-component of ℑ
R
r
v linear velocity of any point (subscript)
that is expressed in ℑ
R
c
τ
t
linear velocity of ℑ
T
that is expressed in
ℑ
C
e
ER vector between the origin points of ℑ
E
and ℑ
R
, expressed in ℑ
E
e
u
er
unit vector of
e
ER and expressed in ℑ
E
e
v
r
linear velocity of ℑ
R
that is expressed in
ℑ
E
e
v
e
linear velocity of ℑ
E
that is expressed in
its frame
e
ω
e
angular velocity of ℑ
E
that is expressed
in its frame
e
1
and e
2
alignment task error and second task error
L
T
e
1
interactive matrix of alignment task error
λ gain factor for alignment task error
u
e
1
unit vector of alignment task error
γ gain factor for second task error
v
⊥
y
linear velocity perpendicular on
e
y
Γ geometric path to be followed
M
k
k
th
point on the path
d and
˙
d projection distance between the tool tip
and the path, and its time-derivative
S the projected point on the path
v
s
linear velocity of S along the path
˙s the speed of S along the path
K
s
unit vector between two consecutive
points along the path
v
tissue
desired linear velocity along the tissue
β gain factor for reducing d
α gain factor for v
tissue
2.2.2 Case 1: Tool Outside Incision Point
This is the first phase for getting close to the fulcrum
point. It is required to align the rigid tool with the
incision point. To achieve this task, the error between
the y-component of end-effector frame (
e
y) and the
unit vector oriented from end-effector origin point to
incision origin point (
e
u
er
) should be equal to zero
(1), where (∧) is the cross product between these two
Y
X
Z
W
E
R
Path
C
T
Body surface
Robot
end-effector
Incision
point
Medical
imaging
Tool
M
k
Figure 1: Representation of different reference frames used
in the modelling of the whole system.
vectors.
e
1
=
e
y ∧
e
u
er
= 0 (1)
This task tracks the incision point and the end-effector
in order to align both of them. In order to ensure expo-
nential error decay, the control equation is
˙
e
1
= −λe
1
,
thereby the time-derivative of (1) is calculated as:
˙
e
1
=
e
y ∧
e
˙
u
er
+
e
˙
ER
|{z}
=0
∧
e
u
er
|
{z }
=0
(2)
the time-derivative of vector
e
ER represents the linear
velocity of incision point expressed in end-effector
frame (
e
˙
ER =
e
v
r
). This velocity must be equiva-
lent to zero, and consequently the formulation (2) is
reduced. The derivative of unit vector
e
u
er
with re-
spect to time is calculated as follows:
e
˙
u
er
=
k
e
ERk
e
˙
ER −
e
ER
dk
e
ERk
dt
k
e
ERk
2
where
d
dt
k
e
ERk =
e
ER
T
e
˙
ER
√
e
ER
T
e
ER
(3)
and it is simplified as follows:
e
˙
u
er
=
e
˙
ER
k
e
ERk
−
e
ER
e
ER
T
e
˙
ER
k
e
ERk
3
= (
I
k
e
ERk
−
e
u
er
e
u
T
er
k
e
ERk
)
e
˙
ER
(4)
The trocar velocity can be expressed in terms of end-
effector velocity as:
e
v
r
= −(
e
v
e
+
e
ω
e
∧
e
ER) (5)
By putting (5) in (4), the derivative of unit vector
(
e
˙
u
er
) is represented as:
e
˙
u
er
=
−1
k
e
ERk
(I −
e
u
er
e
u
T
er
)[I −[
e
ER]
∧
]

e
v
e
e
ω
e

(6)
where −[
e
ER]
∧
is the skew matrix of vector
e
ER and
I
3×3
is the identity matrix. By substituting (6) in (2),
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
86

the derivative of first error is defined as:
˙
e
1
=
−1
k
e
ERk
[
e
y]
∧
(I −
e
u
er
e
u
T
er
)[I −[
e
ER]
∧
]
| {z }
L
T
e
1

e
v
e
e
ω
e

| {z }
e
τ
e
(7)
˙
e
1
= L
T
e
1
e
τ
e
= −λe
1
(8)
where (L
T
e
1
) is the interaction matrix, (λ) is a gain fac-
tor for alignment task and (
e
τ
e
) is the control veloc-
ity of end-effector which gather the linear and angu-
lar velocities (
e
τ
e
=

e
v
e
ω

). This control velocity is
achieved by inverting the interaction matrix (L
T
†
e
1
) by
singular value decomposition (SVD) in (8):
e
τ
e
= −λL
T
†
e
1
e
1
(9)
A possible solution of end-effector velocity vector is
calculated in (10) to bring the alignment error task in
the null space.
L
T
e
1

0
λ
e
y
T e
ER
e
1

= −λe
1
(10)
The constraints are extended by adding another
task (e
2
=
e
R −
e
T ) that brings the tool tip (T ) to the
incision point (R). The second task error is projected
in the null space of first task error that its interaction
matrix in nullity (L
T
e
1
Ker
) is defined as:
L
T
e
1
Ker
=

e
u
er
0 k
e
Rk∗(
e
u
er
∧u
e
1
) −k
e
Rk∗u
e1
0
e
u
er
u
e
1
e
u
er
∧u
e
1

(11)
The latter projection is also valid for the second case
where the tool moves inside the hole, where (k
e
Rk) is
the euclidean norm of R, and (u
e
1
) is the unit vector
of e
1
.
2.2.3 Case 2: Tool Inside Incision Point
During this phase, the tool follows a pre-defined path
and its velocity (
e
v
t
) is determined by the path follow-
ing algorithm (see Section 2.3). The tool tip velocity
is transmitted to the end-effector as:
e
v
t
=
e
v
e
+
e
ω ∧
e
ET (12)
The incision wall allows only the tool translation
along the y-component of end-effector frame (Figure
2). The mathematical representation of RCM con-
straint is:
e
v
r
∧
e
y = 0 (13)
The linear velocity vector of incision point is pro-
jected on the y-component of end-effector in order to
find its solution and maintain the bilateral constraint
(13):
(I −
e
y
e
y
T
)
e
v
r
= 0 (14)
e
v
r
=
e
v
e
+
e
ω ∧
e
ER (15)
Putting (12) in (15), the RCM velocity is described in
terms of tool tip velocity:
e
v
r
=
e
v
t
+
e
ω ∧
e
ER −
e
ET
| {z }
=
e
TR
(16)
By substituting (16) in (14), the equation (17) is di-
vided into two parts. The first one is the linear veloc-
ity perpendicular to
e
y and the second is the angular
velocity that is reduced because
e
ω ∧
e
TR is perpen-
dicular to
e
y.
(I −
e
y
e
y
T
)
e
v
t
| {z }
v
⊥
y
+ (I −
e
y
e
y
T
)(
e
ω ∧
e
TR)
| {z }
−
e
TR ∧
e
ω
= 0 (17)
The angular velocity of end-effector (
e
ω) is calculated
by:
e
ω =
v
⊥
y
∧
e
TR
k
e
TRk
2
=
v
⊥
y
∧
e
y
k
e
TRk
(18)
Thereby, the linear velocity of end-effector is deter-
mined by replacing (18) into (12) and accordingly this
will result to the following:
e
v
e
=
e
v
t
−
e
ω ∧
e
ET (19)
The second task error in this case is determined by
the path following (e
2
=
e
T −
e
T
∗
) that is the error
between the actual tool tip position vector (
e
T) and
the desired one (
e
T
∗
). The error is projected in the
null space of first task as used in (11).
2.3 3D Path Following
2.3.1 Problem Statement
The desired geometric path is generally defined by
a planning algorithm (Gasparetto et al., 2015), for
avoiding obstacles and generating the shortest dis-
tance between the initial point and the target one, or
simply by the surgeon drawing on input device, such
as tablet
1
.
During the robot motion, the perpendicular dis-
tance (d) between the tool tip and the desired path
points should be maintained to zero (Figure 2). In
addition, it is required to determine the tool velocity
along the desired path.
2.3.2 Problem Resolution
The projection of tool tip on the path provides the
point (S) and the projected distance (20) which is re-
quired to be as minimal as possible.
d = T −S (20)
1
µRALP (Micro-technologies and Systems for Robot-
Assisted Laser Phonomicrosurgery). [online]. http://
www.microralp.eu/
3D Path Following with Remote Center of Motion Constraints
87

E
R
Path
T
K
S
d
V
t
s
Figure 2: Representation of different reference frames used
in the path following.
The time-derivative of (20) is obtained in (21). The
projected point velocity (v
s
) is defined as the speed (˙s)
in the direction of the instantaneous unit vector (K
s
)
that is tangent to the path.
˙
d =
˙
T −
˙
S
= v
t
−v
s
= v
t
− ˙sK
s
(21)
The instantaneous tangential vector (K
s
) is calculated
in (22). (K
+
s
) and (K
−
s
) are the previous and next tan-
gential vectors, respectively, and (M
k
) is the k
th
point
on the geometric path.
K
s
=
M
k+1
−M
k
kM
k+1
−M
k
k
K
+
s
=
M
k+2
−M
k+1
kM
k+2
−M
k+1
k
K
−
s
=
M
k
−M
k−1
kM
k
−M
k−1
k
(22)
The derivative of instantaneous tangential vector is
computed as:
˙
K
s
=
dK
s
dt
=
∂K
s
∂s
ds
dt
=
K
+
s
−K
−
s
2 M s
˙s (23)
The latter time-derivative is the instantaneous velocity
vector to move from point M
k
to M
k+1
. It is also the
perpendicular resultant (25) from the cross product of
the unit vector K
s
and the angular velocity ω, which
depends on the speed along the path and its curvature:
ω = ˙sC(s) (24)
˙
K
s
= ˙sC(s) ∧K
s
(25)
From (23) and (25), the path curvature (C(s)) is cal-
culated as:
C(s) = −K
s
∧
K
+
s
−K
−
s
2 M s
(26)
Since the projected distance is perpendicular on
the tangential vector (d
T
K
s
= 0), then the time-
derivative of the latter expression is concluded as:
˙
d
T
K
s
+ d
T
˙
K
s
= 0 (27)
In order to calculate the required speed along the path,
(21) is modified to:
˙
dK
s
= v
t
K
s
− ˙sK
s
K
s
(28)
By putting (25) and (28) in (27), the speed along the
path is determined as:
˙s =
v
T
t
K
s
1 −d
T
(C(s) ∧K
s
)
(29)
Back substituting (29) in (21), the velocity required to
bring the tool tip on the path is defined as following
which is the kinematic state-space representation:
˙
d =

I −
K
s
K
T
s
1 −d
T
(C(s) ∧K
s
)

v
t
(30)
The velocity profile of tool is to be set freely. A
possible solution (31) is describing the tool velocity
as two components: the first one to advance the tool
along the path, and the second to reduce the distance
between the tool and the path.
v
t
= αK
s
+ βd (31)
Thereby, (31) gets into (30):
˙
d = α[1 −
1
1 −d
T
(C(s) ∧K
s
)
]K
s
+ βd (32)
As result the control problem becomes to determine
the gain coefficients (α and β).
3 VALIDATION
3.1 Implementation
Algorithm 1 realizes the RCM motion and it is
divided mainly into two phases. The first phase
is getting the robot close to the incision point
and align the tool with the y-component of RCM
frame. The second phase is guiding the robot to
perform the pre-defined 3D path. The function
generate geometric path() creates the path with re-
spect to the incision point. The first task error is com-
puted as shown in (1). In the control loop, the robot
velocity is obtained analytically (10) and the projec-
tion in the null space of first task (11). The projected
velocity control vector is:
e
τ
e
ker
= L
e
1
Ker
∗L
T
e
1
Ker
∗
e
τ
e
(33)
During the first phase, the second task error brings
the tool tip to the incision point and the interaction
matrix of this task is determined as, where its dimen-
sion is 3 ×6:
L
T
e
2
= −[I
3×3
[
e
R]
∧
] (34)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
88

The control velocity is computed to ensure exponen-
tial decay of second task error that is projected in the
null-space of first task error, and (γ) is a gain factor of
second task:
e
τ
e
= −λγL
T
†
e
2
e
2
(35)
During the insertion phase, the second task is the path
following error and the control velocity is considered
as mentioned in (18) and (19).
Algorithm 1: Control loop for RCM constraints.
w
M
e
← initalization re f erence f rames(W, R, E,T )
Γ ← generate geometric path()
(e
1
,e
2
) ← initial task errors(
e
y,
e
u
r
,
e
TR)
(approaching,inserting) ← (true, f alse)
while not path end do
e
τ
e
control
← analytical solution(λ, e
1
,
e
y,
e
ER)
if approach & (norm(e
2
) < 0.0001) then
(approaching,inserting) ← ( f alse,true)
end if
if approaching then
e
2
←
e
TR
L
T
e
2
← interactive matrix(I,[
e
R]
∧
)
e
τ
e
← control law(λ, γ, e
2
,L
T
†
e
2
)
else
e
2
←
e
T −
e
T
∗
w
v
t
← path f ollowing(Γ,
w
T)
w
ω
e
← explicit solution(
e
TR,
e
y,
e
v
⊥
y
)
e
τ
e
← control law(
e
v
t
,
e
ω
e
,
e
ET)
end if
L
e
1
Ker
← pro jection null space(
e
u
r
,
e
~
R,u
e
1
)
e
τ
e
ker
← pro jected velocities(L
e
1
Ker
,
e
τ
e
)
e
τ
e
control
← send robot velocities(
e
τ
e
ker
,
e
τ
e
)
e
1
← update variables(
e
y,
e
u
r
)
end while
Algorithm 2 computes the linear velocity of tool
tip to follow the desired path. It gives priority to reach
the path when the tool is far from it. When the error is
relatively small, the calculated velocity (31) is the re-
sultant velocity between that of tool tip and that along
the path. The parameter (α) is obtained in the latter
case as follows:
α =
q
(βkdk)
2
+ v
2
tissue
(36)
Algorithm 2: Control loop for 3D path following.
(M
k
,M
k+1
) ← nearest point(Γ, T)
(K
s
,S,d) ← pro jection(M
k
,M
k+1
,T)
if (βkdk)
2
> v
2
tissue
then
α ← 0
else
α ← compute(β,d,v
tissue
)
end if
v
t
← required velocity(α, β, d)
3.2 Results
A spherical workspace was chosen (Figure 3.a) in
which the rigid tool navigates. The RCM will produce
a conical workspace within the spherical one. There-
fore, the desired 3D curve is defined as straight line
from the incision point to the starting point of helical
path. Figure 3.b presents the resultant tool tip posi-
tion with respect to the 3D geometric path (in blue)
and the shortest way between the initial position of
tool tip and the incision point (in green). Through-
out the tested simulation, the standard deviation er-
ror of RCM constraints during the insertion phase is
around 0.004mm and that of path following is ap-
proximately 0.089mm. These results in figure 4 are
obtained with parameters values λ = 0.3, γ = 0.3,
β = −10, v
tissue
= 0.001m/sec and sampling time
0.1sec. Figure 4.a shows the RCM constraints error
and positioning error during the approaching phase.
Both errors are decreased exponentially as designed.
Figure 4.b presents the same errors during the inser-
tion phase where the RCM error is stable and the posi-
tioning error is oscillating due to the gain parameters.
−0.1
−0.05
0
0.05
0.1
0.15
−0.2
−0.15
−0.1
−0.05
0
0.05
0.1
0.15
−0.1
−0.05
0
0.05
0.1
x (m)
RCM motion
y (m)
z (m)
Incision
point
(a)
−0.05
−0.04
−0.03
−0.02
−0.01
0
0.01
−0.1
−0.08
−0.06
−0.04
−15
−10
−5
0
5
x 10
−3
x (m)
3D path following
y (m)
z (m)
Path outside RCM
Path inside RCM
Actual path
(b)
Figure 3: (a) The end-effector motion during approach
phase (doted blue) and insertion phase (doted black); (b)
the position of tool tip with respect to the path.
3D Path Following with Remote Center of Motion Constraints
89

0 100 200 300 400 500 600 700
0
0.01
0.02
0.03
0.04
0.05
0.06
Approach phase error
iteration
error (m)
RCM constraint error
approach error
(a)
600 700 800 900 1000 1100 1200 1300 1400
0
1
2
3
4
5
6
7
8
x 10
−4
Inserstion phase error
iteration
error (m)
RCM constraint error
path following error
(b)
Figure 4: Motion error during (a) approach phase and (b)
path following.
These coefficients effect the system performance and
the problem becomes to choose the right values for
these system variables. In order to visualize this effect
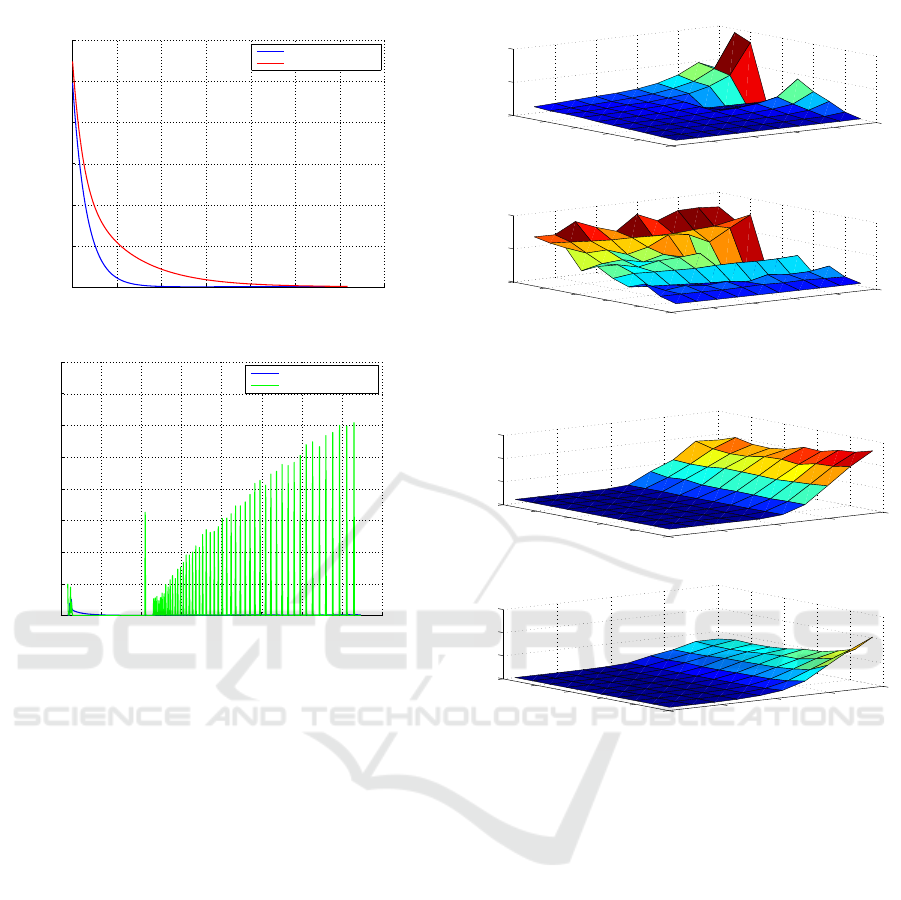
in 3D surface, the error is calculated while varying
two parameters and the others are fixed. In Figure 5.a,
the variables β and v
tissue
are varied from −1∗10
−6
to
−10 and 0.1 to 1 ∗10
−3
m/sec, respectively. In Figure
5.b, the results are obtained by changing λ and γ from
2 to −0.1 and 2.5 to −0.1, respectively.
4 CONCLUSIONS
The article presented a detailed method to arrange
more than one task in hierarchical form, whereby the
highest priority is the bilateral constraints and the sec-
ond one is 3D path following task. The proposed
method implements the controller for the usage of
rigid tool but it could be modified easily in order to
be adapted with other tool shape. This controller is
useful for medical application, such as ENT (ear, nose
and throat) surgeries and laparoscopic surgery; since
it is accurate to follow the 3D path and maintain the
0
0.02
0.04
0.06
0.08
0.1
−10
−8
−6
−4
−2
0
0
0.02
0.04
V
tissue
(m/s)
β
path following error (m)
0
0.02
0.04
0.06
0.08
0.1
−10
−8
−6
−4
−2
0
0
1
2
x 10
−3
V
tissue
(m/s)
β
RCM error while path following (m)
(a)
0
0.5
1
1.5
2
0
0.5
1
1.5
2
2.5
0
1
2
3
x 10
−3
λ
γ
path following error (m)
0
0.5
1
1.5
2
0
0.5
1
1.5
2
2.5
0
2
4
6
x 10
−3
λ
γ
RCM error while path following (m)
(b)
Figure 5: Effect of system variables on the error (a)v
tissue
vs β and (b)λ vs γ.
trocar kinematics. It will be extended to consider uni-
lateral RCM constraints where the incision hole is
bigger than the tool diameter and the instrument has
more space to move before it hits the incision wall.
ACKNOWLEDGEMENTS
This work is conducted with a financial support
from the project NEMRO (ANR-14-CE17-0013-01)
funded by the ANR and the financial support of the
Franche-Comt
´
e region (FRANCHIR), France. It is
also performed in the framework of the Labex AC-
TION (ANR-11-LABEX-01-001).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
90

REFERENCES
Aghakhani, N., Geravand, M., Shahriari, N., Vendittelli,
M., and Oriolo, G. (2013). Task control with re-
mote center of motion constraint for minimally in-
vasive robotic surgery. In IEEE International Con-
ference on Robotics and Automation (ICRA), pages
5807–5812.
Azimian, H., Patel, R. V., and Naish, M. D. (2010). On
constrained manipulation in robotics-assisted mini-
mally invasive surgery. In IEEE RAS and EMBS In-
ternational Conference on Biomedical Robotics and
Biomechatronics (BioRob), pages 650–655.
Azizian, M., Khoshnam, M., Najmaei, N., and Patel, R. V.
(2014). Visual servoing in medical robotics: a sur-
vey. part i: endoscopic and direct vision imaging–
techniques and applications. The International Jour-
nal of Medical Robotics and Computer Assisted
Surgery, 10(3):263–274.
Boctor, E. M., Webster III, R. J., Mathieu, H., Okamura,
A. M., and Fichtinger, G. (2004). Virtual remote
center of motion control for needle placement robots.
Computer Aided Surgery, 9(5):175–183.
Dalvand, M. M. and Shirinzadeh, B. (2012). Remote
centre-of-motion control algorithms of 6-rrcrr paral-
lel robot assisted surgery system (pramiss). In IEEE
International Conference on Robotics and Automation
(ICRA), pages 3401–3406.
Duflot, L.-A., Krupa, A., Tamadazte, B., and Andreff, N.
(2016). Towards ultrasound-based visual servoing us-
ing shearlet coefficients. In IEEE International Con-
ference on Robotics and Automation (ICRA).
Funda, J., Taylor, R. H., Eldridge, B., Gomory, S., and
Gruben, K. G. (1996). Constrained cartesian motion
control for teleoperated surgical robots. IEEE Trans-
actions on Robotics and Automation, 12(3):453–465.
Gasparetto, A., Boscariol, P., Lanzutti, A., and Vidoni, R.
(2015). Path planning and trajectory planning algo-
rithms: A general overview. In Motion and Operation
Planning of Robotic Systems, pages 3–27. Springer.
Krupa, A., Doignon, C., Gangloff, J., and De Mathelin,
M. (2002). Combined image-based and depth visual
servoing applied to robotized laparoscopic surgery.
In IEEE/RSJ International Conference on Intelligent
Robots and Systems, volume 1, pages 323–329.
Kuo, C.-H., Dai, J. S., and Dasgupta, P. (2012). Kinematic
design considerations for minimally invasive surgi-
cal robots: an overview. The International Journal
of Medical Robotics and Computer Assisted Surgery,
8(2):127–145.
Locke, R. C. and Patel, R. V. (2007). Optimal remote center-
of-motion location for robotics-assisted minimally-
invasive surgery. In IEEE International Conference
on Robotics and Automation, pages 1900–1905.
Marinho, M. M., Bernardes, M. C., and B
´
o, A. P. (2014). A
programmable remote center-of-motion controller for
minimally invasive surgery using the dual quaternion
framework. In 5th IEEE RAS & EMBS International
Conference on Biomedical Robotics and Biomecha-
tronics, pages 339–344.
Mayer, H., Nagy, I., and Knoll, A. (2004). Kinematics and
modelling of a system for robotic surgery. In On Ad-
vances in Robot Kinematics, pages 181–190. Springer.
Nageotte, F., Zanne, P., Doignon, C., and de Mathe-
lin, M. (2006). Visual servoing-based endoscopic
path following for robot-assisted laparoscopic surgery.
In IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 2364–2369.
Nakamura, Y., Hanafusa, H., and Yoshikawa, T. (1987).
Task-priority based redundancy control of robot ma-
nipulators. The International Journal of Robotics Re-
search, 6(2):3–15.
Osa, T., Staub, C., and Knoll, A. (2010). Framework of
automatic robot surgery system using visual servoing.
In IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS), pages 1837–1842.
Pham, C. D., Coutinho, F., Leite, A. C., Lizarralde, F.,
From, P. J., and Johansson, R. (2015). Analysis of a
moving remote center of motion for robotics-assisted
minimally invasive surgery. In IEEE/RSJ Interna-
tional Conference on Intelligent Robots and Systems
(IROS), pages 1440–1446.
Seon, J.-A., Tamadazte, B., and Andreff, N. (2015). De-
coupling path following and velocity profile in vision-
guided laser steering. IEEE Transactions on Robotics,
31(2):280–289.
3D Path Following with Remote Center of Motion Constraints
91