Balancing Skew-Hamiltonian/Hamiltonian Pencils

With Applications in Control Engineering

Vasile Sima

National Institute for Research & Development in Informatics, 8–10 Bd. Mares¸al Averescu, Bucharest, Romania

Keywords:

Deﬂating Subspaces, Generalized Eigenvalues, Numerical Methods, Skew-Hamiltonian/Hamiltonian Matrix

Pencil, Software, Structure-preservation.

Abstract:

Badly-scaled matrix pencils could reduce the reliability and accuracy of computed results for many numeri-

cal problems, including computation of eigenvalues and deﬂating subspaces, which are needed in many key

procedures for optimal and H

∞

control, model reduction, spectral factorization, and so on. Standard balancing

techniques can improve the results in many cases, but there are situations when the solution of the scaled

problem is much worse than that for the unscaled problem. This paper presents a new structure-preserving

balancing technique for skew-Hamiltonian/Hamiltonian matrix pencils, and illustrates its good performance

in solving eigenvalue problems and algebraic Riccati equations for large sets of examples from well-known

benchmark collections with difﬁcult examples.

1 INTRODUCTION

Computing eigenvalues and bases of certain associ-

ated invariant or deﬂating subspaces of matrices or

matrix pencils is central to various numerical tech-

niques in control engineering and other domains.

When the corresponding eigenproblems have special

structure, implying structural properties of their spec-

tra, it is important to use structure-preserving and/or

structure-exploiting algorithms. General numerical

algorithms cannot ensure that the theoretical prop-

erties are preserved during computations (Paige and

Van Loan, 1981; Van Loan, 1984; Kressner, 2005).

Common special structures are Hamiltonian and sym-

plectic matrices or matrix pencils, which are encoun-

tered in optimal or H

∞

control (e.g., solution of alge-

braic Riccati equations, or evaluation of the H

∞

- and

∞

-norms of linear dynamic systems), spectral factor-

ization, model reduction, etc., see, for instance, (Bru-

insma and Steinbuch, 1990; Laub, 1979; Mehrmann,

1991; Sima, 1996). While structured matrices are en-

countered for standard linear dynamic systems, gen-

eralized and descriptor systems may involve struc-

tured matrix pencils. Often such pencils can be re-

cast as skew-Hamiltonian/Hamiltonian pencils, for

which dedicated algorithms have been developed, see

e.g., (Benner et al., 2007; Benner et al., 2002; Ben-

ner et al., 2005; Benner et al., 2012a; Benner et al.,

2012b; Benner et al., 2013a; Benner et al., 2013b;

Jiang and Voigt, 2013), and the references therein.

Quite often, the pencil matrices have large norms

and elements with highly different magnitude. Such

pencils imply potential numerical difﬁculties for

software implementations of eigensolvers, with

negative consequences on the reliability and accuracy

of the results, see, e.g., (Sima and Benner, 2015a).

Balancing procedures can be used to improve the

numerical behavior. Ward (1981) proposed a bal-

ancing technique for general matrix pencils, which

has been incorporated in state-of-the-art software

packages, such as LAPACK (Anderson et al., 1999).

(This will be referred below as standard balancing.)

The data matrices are preprocessed by equivalence

transformations, in two optional stages: the ﬁrst

stage uses permutations to ﬁnd isolated eigenvalues

(which are available by inspection, with no rounding

errors), and the second stage uses diagonal scaling

transformations to make the row and corresponding

column 1-norms as close as possible. Balancing

may reduce the 1-norm of the scaled matrices, but

there is no guarantee in general. This is the reason

why full balancing is either avoided or provided as

an option in the LAPACK subroutines; some expert

driver routines, such as DGEES, DGEESX, DGGES,

DGGESX, and DGGEV use permutations only, while

other drivers, e.g., DGEEVX and DGGEVX, have an

input argument allowing either permutations, scaling,

both permutations and scaling, or no balancing at all.

Sima, V.

Balancing Skew-Hamiltonian/Hamiltonian Pencils - With Applications in Control Engineering.

DOI: 10.5220/0005981201770184

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 177-184

ISBN: 978-989-758-198-4

177

A structure-preserving balancing technique for

Hamiltonian matrices has been developed in (Benner,

2001), but no special procedure has been available

for skew-Hamiltonian/Hamiltonian matrix pencils.

This paper presents a new, structure-preserving

balancing procedure for skew-Hamiltonian/Hamil-

tonian pencils, and illustrates its performance for

some control engineering applications, in comparison

with the general approach, and with the case when

no balancing is used. This procedure includes several

optional enhancements which allow to get meaning-

ful results when standard balancing (possibly even a

structured variant) fails, as shown for some numerical

examples.

2 BALANCING

SKEW-HAMILTONIAN/

HAMILTONIAN PENCILS

Let αS − βH be a complex skew-Hamiltonian/

Hamiltonian pencil, with α, β ∈ C, S ∈ C

2n×2n

skew-Hamiltonian matrix and H ∈ C

2n×2n

a Hamil-

tonian matrix, i.e.,

(SJ )

= −SJ , (H J )

= H J , J :=



0 I

−I



(1)

where M

denotes the conjugate transpose of a ma-

trix M, M

, the overbar denotes the complex

conjugate, M

denotes the transpose of M, and I

the identity matrix of order n. These deﬁnitions imply

the following structure for S and H :

S =



A D

E A



, H =



C V

W −C



, (2)

where D and E are skew-Hermitian, i.e., D

= −D,

= −E, and V and W are Hermitian matrices.

When S and H are real matrices, then D and E are

skew-symmetric, V and W are symmetric, the H su-

perscript is replaced by T, and some derivations be-

low simplify.

When the matrices S and H are badly scaled, e.g.,

when their elements have moduli with highly differ-

ent magnitude, the accuracy of computed solutions of

related eigenproblems can be very poor. The accuracy

may be improved by using a balancing procedure, as

described in (Ward, 1981) for general matrix pencils,

and implemented in the LAPACK package (Anderson

et al., 1999). Similarly to the techniques in (Anderson

et al., 1999; Benner, 2001; Ward, 1981), a structure-

exploiting balancing procedure for the structured pen-

cil matrices in (2) would involve, in a ﬁrst step,

permuting αS − βH by a symplectic equivalence

transformation to isolate eigenvalues in the elements

1 : ℓ−1 and n+1 : n+ℓ−1 on the diagonals of S and

H , and in a second step, applying a diagonal equiva-

lence transformation to rows and columns ℓ : n and

n + ℓ : 2n, to make the rows and columns as close

in 1-norm as possible. (A MATLAB-style notation

for array indexing (MATLAB, 2016) is used.) Both

steps above are optional. Balancing may reduce the

1-norms of the matrices S and H .

Note that it is enough to equilibrate the 1-norms

of the rows and columns 1:n of the matrices S and H ,

since kS

i+n,:

= kS

:,i

and kS

:,i+n

= kS

i,:

, for

any p-norm, for p ≥ 1, and similarly for H (see (Ben-

ner, 2001)). The balancing procedure performs the

following transformation:

S = LS R ,

H = LH R , (3)

where

L = L

···L

ℓ

ℓ−1

···P

, R = P

···P

ℓ−1

ℓ

···R

(4)

where P

, k = 1 : ℓ− 1, are symplectic permutation or

J -permutation matrices (Benner, 2001), and L

and

are left and right diagonal scaling matrices (with

(k,k), L

(k+n,k+n), R

(k,k), and R

(k+n,k+n)

the only diagonal elements different from 1), chosen

to equilibrate the 1-norms of the k-th row and col-

umn of S and H , for k = ℓ, · · · ,n. A permutation

matrix has exactly one nonzero entry, which is 1, in

each row and column. A J -permutation matrix has a

similar structure, but the nonzero entries may also be

−1. When possible, the permutations are chosen in

the form

P =



P 0

0 P



, (5)

where P is an n×n permutation matrix (hence, P

P =

= I

). Clearly, P is symplectic, since P J P

J . As shown in (Benner, 2001), it is generally not

possible to preserve the (skew-)Hamiltonian structure

using symplectic permutations only, but symplectic

J -permutations are also needed.

Applying a permutation (5) in (3) is easy. Speciﬁ-

cally, the transformedmatrices become P

AP, P

DP,

EP, P

CP, P

VP, and P

WP.

Consider applying a J -permutation, P, which has

the following structure, deﬁned by an index i, i ≤ n,

P =







i−1

0 0 0 0 0

0 0 0 0 1 0

0 0 I

n−i

0 0 0

0 0 0 I

i−1

0 0

0 −1 0 0 0 0

0 0 0 0 0 I

n−i







, (6)

to the skew-Hamiltonian matrix S, and Hamiltonian

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

178

matrix H . Using the partition of H in (2), the trans-

formed matrix P

H P is

H P =







⋆ −v

1:i−1,i

⋆

−w

i,1:i−1

− ¯c

−w

i+1:n,i

⋆ −v

i,i+1:n

⋆

⋆ c

i,1:i−1

⋆

i,1:i−1

−v

i,i+1:n

⋆ c

i,i+1:n

⋆

⋆ c

1:i−1,i

⋆

1:i−1,i

−w

i+1:n,i

⋆ c

i+1:n,i

⋆

⋆ w

i,1:i−1

⋆

1:i−1,i

i,i+1:n

⋆ w

i+1:n,i

⋆







, (7)

where ⋆ denotes submatrices which do not change.

Matrix S is transformed similarly.

The permutation procedure ﬁrst scans the columns

1 : n and then the rows 1 : n of S and H , and uses

row and column permutations with matrices of the

form (5) and (6) so that

S and

H ﬁnally have the

ﬁrst ℓ − 1 columns upper triangular, i.e., with zeros

below the diagonals. This way, the ﬁrst ℓ − 1 eigen-

values of the pencil are deﬁned by the diagonal ele-

ments 1 :ℓ−1 in

S and

H . The upper triangular struc-

ture is built column by column, starting from the ﬁrst.

Therefore, the permutationsabove can take advantage

of the zero subdiagonal part in the already processed

columns. For instance, when a J -permutation (6) is

formed and applied, the vectors c

i,1:i−1

, and w

i,1:i−1

in (7) (and similarly for a

i,1:i−1

, e

i,1:i−1

in S), as well

as all ⋆ vectors under the diagonals in the ﬁrst i − 1

columns are already zero.

The balancing procedure for (skew-)Hamiltonian

matrices must use symplectic scaling matrices as well,

in order to preserve the structure (Benner, 2001). For-

tunately, this is not needed for skew-Hamiltonian/Ha-

miltonian pencils, if diagonal scaling is used, as men-

tioned above. Indeed, without loss of generality, con-

sider that permutations are not wanted, and only scal-

ing should be applied. Let L and R be the real diago-

nal matrices which scale the ﬁrst n rows and the ﬁrst

n columns, respectively, of S and H . Since R and L

will be the scaling matrices for the last n rows and

columns, respectively, the global scaling transforma-

tion is

S =



L 0

0 R



A D

E A



R 0

0 L



H =



L 0

0 R



C V

W −C



R 0

0 L



. (8)

Then,

SJ =



LAR LDL

RER RA



0 I

−I





−LDL LAR

−RA

L RER



= −(

SJ )

, (9)

since D = −D

, E = −E

. Similarly,

H J =



LCR LVL

RWR −RC



0 I

−I





−LVL LCR

L RWR



= (

H J )

, (10)

since V = V

and W = W

. Therefore, the struc-

ture of S and H is preserved for the transformation

in (8). Note that the left and right transformations

are not symplectic if L 6= R

−1

, but they are structure-

preserving, for diagonal L and R. The permutations

used for isolating the eigenvalues must, however, be

symplectic.

As described above, the elementary scaling matri-

ces in (4) are, for k = ℓ, · ·· ,n,

= bl

diag(I

k−1

n−1

n−k

= bl diag(I

k−1

n−1

n−k

), (11)

where bl

diag(X,Y,...) denotes a bloc-diagonal ma-

trix with diagonal blocks X, Y, etc. Note that

−1

= P

···P

ℓ−1

−1

ℓ

···L

−1

. (12)

Formula (12) can be used to apply, from the left, the

back balancing transformations to a given 2n×m ma-

trix. Since L

−1

has a formula similar to R , to obtain

R , one can apply to I

the transformations in (12),

with scaling factors l

and r

replaced by 1/r

and

1/l

, respectively. There is no need for an algorithm

to apply the right back transformation.

A special case of application of the balancing

transformations appears when computing the solu-

tion of algebraic Riccati equations (AREs) using the

skew-Hamiltonian/Hamiltonian approach, see (Ben-

ner et al., 2013a), and the references therein. This

approach uses a basis for the stable right deﬂating

subspace of the matrix pencil αS − βH , where S

and H are suitably deﬁned in terms of the dynamic

system and performance index matrices. For conve-

nience, assume that S = I

, which is the case for stan-

dard continuous-time dynamic systems, e.g., when

the control weighting matrix of the performance index

is well-conditioned. (The general case will be brieﬂy

described below.) Let

U =





be a ba-

sis of the stable right deﬂating subspace of α

S − β

H ,

corresponding to the balanced pencil. The stabilizing

solution of the balanced ARE is given by

X =

−1

Balancing Skew-Hamiltonian/Hamiltonian Pencils - With Applications in Control Engineering

179

Note that

U is related to a basis, U, of the stable right

deﬂating subspace of the original pencil, αS −βH , by

the transformation

U = bl

diag(R

−1

)U, hence





:= U = bl

diag(R,L)

U. Therefore,

the stabilizing solution of the original ARE can be

computed as follows

X = U

−1

= L

−1

. (13)

Formula (13) allows to represent and use the solution

X in a factored form, which may be useful for nu-

merical reasons. If balancing also involves symplec-

tic permutations of the form (5) only, then the right

hand side in (13) becomes PL

−1

, where

P denotes here the product of the ℓ − 1 permutations

performed. Such factorization, is, however, not possi-

ble if J -permutations are also needed, in which case

it is necessary to apply the balancing transformations

before solving the set of linear systems giving

If S is a general matrix, the order of S and H is

2(n+ p), where n is the dimension of the state vector,

and p may be chosen as p = ⌈m/2⌉ (i.e., p = m/2, if

m is even, and p = (m+ 1)/2, otherwise), with m the

number of system inputs. In this case, the computa-

tions are similar, but

and U

, i = 1,2, refer to the

lines 1 : n and n + p + 1 : 2n+ p of the matrix bases

U and U, respectively.

3 IMPLEMENTATION ISSUES

The developed balancing algorithm operates only on

the matrices A, D, E, C, V, and W, and preserves

the pencil structure. Moreover, the pairs of skew-

Hermitian matrices, D and E, and Hermitian matri-

ces, V andW, are stored compactly in two n× (n+1)

arrays,

and

. Speciﬁcally, the lower triangle of

E and the upper triangle of D are concatenated along

their main diagonals, and similarly for W and V:

= e

, j = 1 : n, i ≥ j,

i, j+1

= d

, j = 1 : n, i ≤ j,

= w

, j = 1 : n, i ≥ j,

i, j+1

= v

, j = 1 : n, i ≤ j. (14)

This way, the storage requirements are reduced by

− 2n memory locations, in comparison with the

general algorithm in (Anderson et al., 1999), which

needs 8n

storage space for S and H . Note that in

the real case, the diagonal elements of D and E, d

and e

, i = 1 : n, which should be zero, by deﬁnition,

are not stored and not used. However, in the complex

case, d

and e

, i = 1 : n, should have zero real parts,

while the imaginary parts might be nonzero; more-

over, the diagonal elements of V and W should have

zero imaginary parts, but possibly nonzero real parts.

The implementation takes care of the compact storage

scheme when computing P

DP, ..., P

WP.

Consider a structured pencil, (S ,H ), and assume

that S = I

. The order of magnitude of the dif-

ferences in size of the nonzero elements in the H

matrix can be huge. For instance, for the CM6

and CM6

IS examples from the COMPl

ib collec-

tion (Leibfritz and Lipinski, 2003), the maximum

and minimum absolute values of the nonzero en-

tries are about 2.53· 10

and 4.9407 · 10

−324

, hence

their ratio is not representable in the usual double

precision representation, and it is evaluated as Inf

(∞). The standard balancing algorithm implemented

in the LAPACK Library subroutine

DGGBAL

(for ma-

trix pencils) returns scaling factors covering a very

large range of magnitudes, namely with maximum

and minimum values 10

159

and 10

−47

, respectively,

for both left and right scaling factors. No eigenvalue

can be isolated. The scaling transformation matrices,

L and R , have condition numbers with values 10

206

The 1-norms of scaled matrices,

H and

S, are about

228

and 10

184

, respectively, while the 1-norms of

the original H and S are 6.9123· 10

and 1. Com-

puting the eigenvalues or deﬂating subspaces using

the balanced matrices would return results very far

from the true ones. CM6 and CM6

IS are not the only

examples in the COMPl

ib collection which produce

numerical troubles for eigenproblem-related compu-

tations. The CM5 and CM5

IS examples have also

a huge ratio, 10

279

, between the magnitudes of their

elements. Other very large ratios are 10

141

, for CM4

and CM4

IS, 10

, for CM3 and CM3 IS, or 10

, for

CM2 and CM2 IS.

The proposed algorithm uses an adaptation of

the basic LAPACK procedure for ﬁnding the scaling

factors, but optionally limits the range of their

variation, possibly via an outer loop. Speciﬁcally,

the user can set a threshold value, τ; if τ ≥ 0,

the entries whose absolute values are smaller than

τM

, where M

= max(kH (s,s)k

,kS(s,s)k

), with

s := ℓ : n ∪ n + ℓ : 2n, are considered negligible,

and do not count for computing the scaling factors.

(For the CM6 and CM6 IS examples, ℓ = 1, and

setting τ = 10

−20

, all entries with magnitude less

than about 7 · 10

−15

will be taken as zero by the

procedure.) If τ < 0 on entry, an outer loop over a set

of values τ

> 0 will enable to select a set of scaling

factors which, if possible, ensure the reduction of a

desired norm-related measure for the scaled matri-

ces. For τ = −1, this measure is the minimum of

max

(kH

(s,s)k

/kS

(s,s)k

,kS

(s,s)k

/kH

(s,s)k

)

where H

(s,s) and S

(s,s) are the scaled submatrices

corresponding to the threshold τ

. This strategy

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

180

tries to balance H and S, but also have comparable

1-norms. For τ = −2, the same measure is used, but if

max(k

H (s,s)k

S(s,s)k

) > cM

and t > T, where

c and T are given constants (c possibly larger than

1), and t is the maximum ratio of the scaling factors

found (the maximum of the condition numbers of

L and R ), then the scaling factors are set to 1 and

a warning indicator is set; here, the matrices with

tilde accent are the solution of the above norm ratio

reduction problem. This approach avoids to obtain

scaled matrices with too large norms, compared to

the given ones, and also limits the range of the scaling

factors. For τ = −3, the measure used is the smallest

product of norms, min

(kH

(s,s)k

), over

the sequence of τ

values tried, while for τ = −4,

the condition numbers of the scaling transformations

are additionally supervised, and the scaling factors

are set to 1 if the “optimal” scaling has a condition

number larger than T. This tends to reduce the

1-norms of both matrices. Finally, if τ = −10

, the

condition numbers of the acceptable scaling matrices

are bounded by 10

4 NUMERICAL RESULTS

An extensive testing has been performed to assess the

performance of the new balancing solver for skew-

Hamiltonian/Hamiltonian matrix pencils. Computa-

tion of eigenvalues, as well as solution of AREs, have

been considered as main applications. This section

summarizes part of the results.

The COMPl

ib collection (Leibfritz and Lipin-

ski, 2003) is taken here as a benchmark for eigen-

value computations. All 151 problems with n < 2000

have been tried. For testing purposes, the balancing

algorithms have been used in combination with the

MATLAB eigensolvers

eig

(H ), when S = I

, and

eig

(H ,S), when S is general, or, for small-size prob-

lems, with the symbolic solvers

eig(vpa

(H )) (with

default number of digits, i.e., 32), or

eig(sym

(H )).

Usually,

eig(vpa

(H )) and

eig(sym

(H )) have been

used for examples with n ≤ 200 and n ≤ 30, respec-

tively. Examples with larger orders need signiﬁcant

CPU times for symbolic solvers, e.g., over one hour

for CM4 or CM4

IS (n = 240) using

vpa

, or much

longer for

sym

. But a comparison between the eigen-

values computed by

eig(vpa

(H )) and

eig(sym

(H ))

has shown a very good agreement between their re-

sults. The maximum absolute difference between

the relative errors of

eig

(H ) in comparison with

eig(vpa

(H )) and

eig(sym

(H )) for 100 COMPl

examples with n ≤ 30 is 3.0292· 10

−28

. (Examples

JE2 and JE3, with n = 21 and n = 24, respectively,

have been excluded, since

eig(sym

(H )) needed un-

reasonably large CPU time.) However, the rela-

tive errors of

eig

(H ,S), when S = I

, compared

eig(vpa

(H )) and

eig(sym

(H )), for example PAS

have been 1.2798· 10

−6

, and 1.4432 · 10

−6

, respec-

tively. Omitting PAS, the norm of the differences

between relative errors of

eig

(H ,S) compared to

eig(vpa

(H )) and

eig(sym

(H )) was 5.8491· 10

−25

There are 18 examples with ratios between the

magnitude of the largest and smallest moduli of

their elements larger than 10

. Besides exam-

ples CM2* – CM6*, this set also includes AC10,

BDT2, PAS, TL, CDP, NN16, ISS1, and ISS2 ex-

amples. Most of these are difﬁcult examples for

any balancing algorithm, and for generalized eigen-

solvers using standard balancing. For instance, for

CDP example, even the structure-exploiting skew-

Hamiltonian/Hamiltonian solver with standard bal-

ancing, for S = I

, returns eigenvalues with a relative

error of 0.19172 (when compared to

eig

(H )), and

of 0.24788 (when compared to

eig(vpa

(H )), while

the same solver without scaling delivers relative er-

rors 1.0476 · 10

−14

and 1.3064 · 10

−14

, respectively.

These values are close to the error obtained using

eig

(H ), 4.9248· 10

−15

, compared to

eig(vpa

(H )).

The structure-exploiting solver with balancing option

τ < 0 returns a relative error of 5.4838 · 10

−15

(when

compared to

eig

(H )), and of 3.9091· 10

−15

(when

compared to

eig(vpa

(H )), even more accurate than

eig

(H ).

Figure 1 shows the relative errors of eigenval-

ues computed using

eig

(Hl,Sl), where Hl :=

H , Sl

S, with LAPACK balancing (using DGGBAL)

and

eig

(H ,S ), in comparison with

eig

(H ) for 151

COMPl

ib examples. The error is inﬁnite for CDP,

CM3, CM4, CM3

IS, and CM4 IS examples. There

are also several large errors using LAPACK balanc-

ing. However, for many examples, balancing im-

proves the accuracy of the computed eigenvalues.

Similar results have been obtained using the struc-

tured balancing solver with option τ = 0. Speciﬁcally,

except for ﬁve examples, the differences between the

relative errors of eigenvalues computed using LA-

PACK balancing and the new balancing solver with

option τ = 0 have been less than about 3.64· 10

−3

Figure 2 shows the relative errors of eigenvalues

computed using

eig

(Hl,Sl) with the new balancing

solver with option τ = −1 and

eig

(H ,S), in compari-

son with

eig

(H ) for 151 COMPl

ib examples. There

are no inﬁnite errors. The errors are smaller for many

examples than when using LAPACK balancing. Note

that the ordinate axes have different scales. Note also

that

eig

(H ,S ) has often larger errors than

eig

(Hl,Sl)

with the new solver. The behaviorfor τ= −3 has been

Balancing Skew-Hamiltonian/Hamiltonian Pencils - With Applications in Control Engineering

181

0 20 40 60 80 100 120 140 160

Example #

-20

-15

-10

-5

Relative errors

eig(H,S) and eig(Hl,Sl), after LAPACK balancing compared to eig(H)

eig(H,S)

eig(Hl,Sl)

Figure 1: Relative errors of eigenvalues computed using

eig

(Hl,Sl) with LAPACK balancing and

eig

(H,S), com-

pared to

eig

(H), for COMPl

ib examples.

0 20 40 60 80 100 120 140 160

Example #

-20

-15

-10

-5

Relative errors

Structured solver (τ = -1) and eig(H,S) compared to eig(H)

eig(H,S)

new solver

Figure 2: Relative errors of eigenvalues computed us-

ing

eig

(Hl,Sl) with new balancing solver, τ = −1, and

eig

(H,S), compared to

eig

(H), for COMPl

ib examples.

almost the same (the maximum differencebetween er-

rors for the two options has been of order 10

−9

Figure 3 illustrates the relative errors of eigen-

values of αS + βH , computed using

eig

and

the SLICOT structured eigensolver MB04BD (see

www.slicot.org), without balancing, in comparison

with

eig

(H ). The structured eigensolver is more ac-

curate than

eig

for almost all examples and compa-

rable with

eig

for the remaining examples. Figure 4

uses similarly the structured eigensolver applied to

and

H , obtained with balancing option τ = −1. It can

provide even more accurate results than

eig

(H ,S ),

see Fig. 2. For comparison, Fig. 5 shows results for

option τ = 0. Clearly, standard balancing does not

provide good results in all cases, even using a struc-

tured solver.

The remaining of this section considers the per-

formance of the new balancing solver, in combina-

tion with the structured SLICOT routine MB03LD,

to compute the deﬂating subspaces of skew-

Hamiltonian/Hamiltonian pencils, for solving AREs

0 20 40 60 80 100 120 140 160

Example #

-20

-15

-10

-5

Relative errors

Structured eigensolver on (H,S), no balancing, and eig(H,S) compared to eig(H)

eig(H,S)

structured eigensolver

Figure 3: Relative errors of eigenvalues computed by

SLICOT structured eigensolver without balancing and

eig

(H,S), compared to

eig

(H), for COMPl

ib examples.

0 20 40 60 80 100 120 140 160

Example #

-20

-15

-10

-5

Relative errors

Structured eigensolver (τ = -1) and eig(H,S) compared to eig(H)

eig(H,S)

structured eigensolver

Figure 4: Relative errors of eigenvalues computed by

SLICOTstructured eigensolver with balancing, τ = −1, and

eig

(H,S), compared to

eig

(H), for COMPl

ib examples.

0 20 40 60 80 100 120 140 160

Example #

-20

-15

-10

-5

Relative errors

Structured eigensolver (τ = 0) and eig(H,S) compared to eig(H)

eig(H,S)

structured eigensolver

Figure 5: Relative errors of eigenvalues computed by

SLICOT structured eigensolver with balancing, τ = 0, and

eig

(H,S), compared to

eig

(H), for COMPl

ib examples.

from the SLICOT CAREX collection (Abels and

Benner, 1999). This combination is referred to as

skHH

in the legends of the following ﬁgures. Both

pencils of order 2n (with S = I

) and extended pen-

cils of order 2(n + p) have been tried. The com-

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

182

0 2 4 6 8 10 12 14 16 18

Example #

-20

-15

-10

-5

Relative errors

Relative errors to care solution using balancing

skHH

Figure 6: Relative errors of the stabilizing ARE solutions

computed by SLICOT structured eigensolver (for extended

pencil), with balancing option τ = 0, compared to

care

, for

examples from the SLICOT CAREX collection.

0 2 4 6 8 10 12 14 16 18

Example #

-16

-14

-12

-10

-8

-6

-4

-2

Relative errors

Relative errors to care solution using balancing

skHH

Figure 7: Relative errors of the stabilizing ARE solutions

computed by SLICOT structured eigensolver (for 2n-order

pencil), with option τ = −1, compared to

care

, for exam-

ples from the SLICOT CAREX collection.

0 5 10 15

Example #

-30

-25

-20

-15

-10

-5

Relative errors

Relative errors using balancing

skHH

care

Figure 8: Relative errors of the stabilizing ARE solutions

computed by

care

and SLICOT structured eigensolver (for

extended pencil), with option τ = 0, compared to exact so-

lution, for examples from the SLICOT CAREX collection.

puted solutions are compared with the exact ones,

when known, or with the solutions returned by the

MATLAB function

care

. Note that

care

uses a

special balancing procedure, and Hamiltonian ma-

trices, instead of pencils, for all examples, except

for CAREX example 2.2 with default parameter, for

which the control weighting matrix tends to be sin-

gular. This creates an advantage for

care

over the

new solver. However, both solvers produce compa-

rable results, when the balancing option τ = −1 is

used. See (Sima and Benner, 2015b) for a compari-

son between a Hamiltonian-based solver and

care

for

CAREX examples.

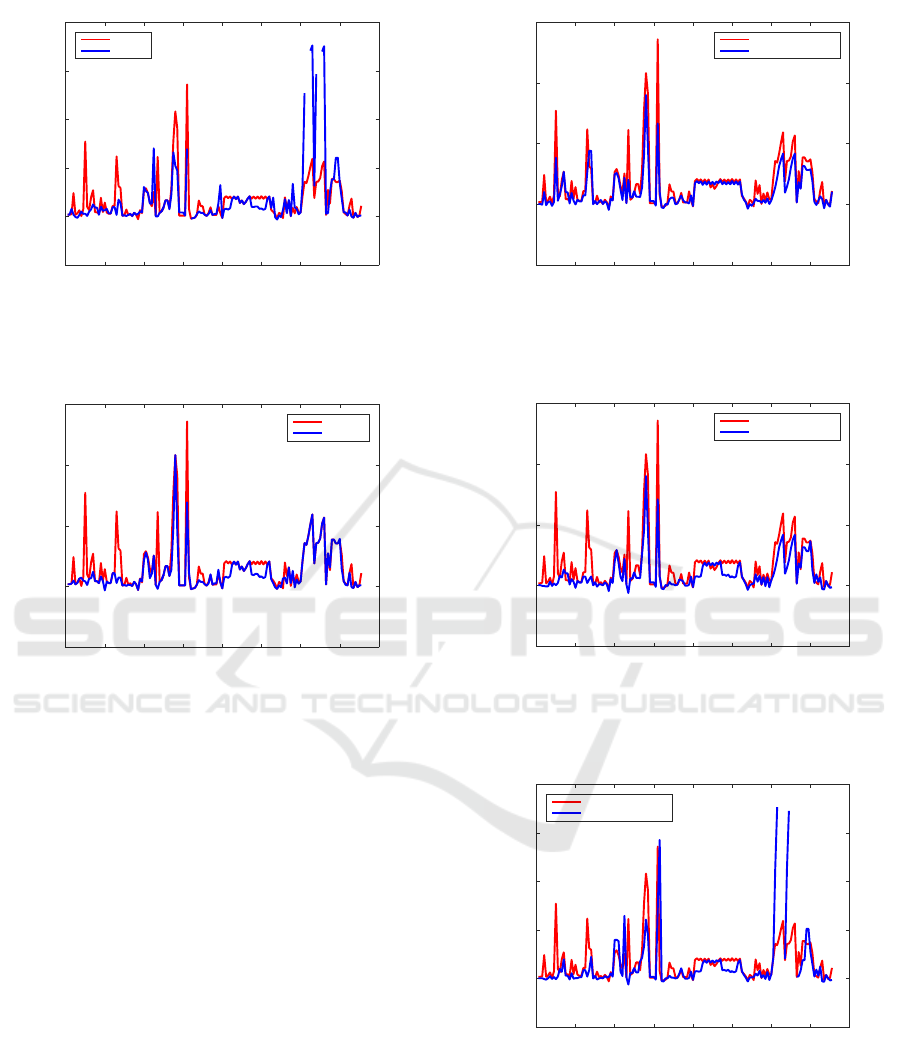
Figure 6 shows the relative errors of the stabiliz-

ing solution of the AREs computed using SLICOT

structured eigensolver (for extended pencil), with bal-

ancing option τ = 0, in comparison with

care

, while

Fig. 7 plots similarly the relative errors when option

τ = −1 is used. Moreover,Fig. 8 and Fig. 9 present in

the same manner the relative errors compared to the

known, exact solutions. The balancing option τ = −1

ensures better results than the standard balancing (for

τ = 0). Finally, Fig. 10 plots the relative residuals for

care

and the structured solver.

0 5 10 15

Example #

-30

-25

-20

-15

-10

-5

Relative errors

Relative errors using balancing

skHH

care

Figure 9: Relative errors of the stabilizing ARE solutions

computed by

care

and SLICOT structured eigensolver (for

2n-order pencil), with option τ = −1, compared to exact so-

lution, for examples from the SLICOT CAREX collection.

0 5 10 15 20 25 30 35

Example #

-25

-20

-15

-10

-5

Relative errors

Relative residuals using balancing

skHH

care

Figure 10: Relative residuals of the stabilizing ARE so-

lutions computed by

care

and SLICOT structured eigen-

solver (for 2n-order pencil), with option τ = −1, for exam-

ples from the SLICOT CAREX collection.

Balancing Skew-Hamiltonian/Hamiltonian Pencils - With Applications in Control Engineering

183

5 CONCLUSIONS

A new structure-preserving balancing technique for

skew-Hamiltonian/Hamiltonian matrix pencils is pre-

sented. Symplectic (J -)permutations and equivalence

scaling transformations are used. Several enhance-

ments are described, which avoid a large increase of

the norms of the pencil matrices, and/or of the con-

dition numbers of the scaling transformations, which

can appear when using the standard balancing pro-

cedure. The numerical results show a good perfor-

mance of the new technique in comparison with state-

of-the-art solvers. Tens of examples from well-known

benchmark collections have been investigated.

ACKNOWLEDGEMENTS

The NICONET support is highly acknowledged.

REFERENCES

Abels, J. and Benner, P. (1999). CAREX—A collection

of benchmark examples for continuous-time algebraic

Riccati equations (Version 2.0). SLICOT Working

Note 1999-14.

Anderson, E., Bai, Z., Bischof, C., Blackford, S., Dem-

mel, J., Dongarra, J., Du Croz, J., Greenbaum, A.,

Hammarling, S., McKenney, A., and Sorensen, D.

(1999). LAPACK Users’ Guide: Third Edition. SIAM,

Philadelphia.

Benner, P. (2001). Symplectic balancing of Hamiltonian

matrices. SIAM J. Sci. Comput., 22(5):1885–1904.

Benner, P., Byers, R., Losse, P., Mehrmann, V., and

Xu, H. (2007). Numerical solution of real skew-

Hamiltonian/Hamiltonian eigenproblems. Technical

report, Technische Universit¨at Chemnitz, Chemnitz.

Benner, P., Byers, R., Mehrmann, V., and Xu, H. (2002).

Numerical computation of deﬂating subspaces of

skew Hamiltonian/Hamiltonian pencils. SIAM J. Ma-

trix Anal. Appl., 24(1):165–190.

Benner, P., Kressner, D., and Mehrmann, V. (2005). Skew-

Hamiltonian and Hamiltonian eigenvalue problems:

Theory, algorithms and applications. In Proceedings

of the Conference on Applied Mathematics and Scien-

tiﬁc Computing, 3–39. Springer-Verlag, Dordrecht.

Benner, P., Sima, V., and Voigt, M. (2012a). L

∞

-norm com-

putation for continuous-time descriptor systems us-

ing structured matrix pencils. IEEE Trans. Automat.

Contr., AC-57(1):233–238.

Benner, P., Sima, V., and Voigt, M. (2012b). Robust and

efﬁcient algorithms for L

∞

-norm computations for de-

scriptor systems. In 7th IFAC Symposium on Robust

Control Design (ROCOND’12), 189–194. IFAC.

Benner, P., Sima, V., and Voigt, M. (2013a). FOR-

TRAN 77 subroutines for the solution of skew-

Hamiltonian/Hamiltonian eigenproblems. Part I: Al-

gorithms and applications. SLICOT Working Note

2013-1.

Benner, P., Sima, V., and Voigt, M. (2013b). FOR-

TRAN 77 subroutines for the solution of skew-

Hamiltonian/Hamiltonian eigenproblems. Part II: Im-

plementation and numerical results. SLICOT Working

Note 2013-2.

Bruinsma, N. A. and Steinbuch, M. (1990). A fast algo-

rithm to compute the H

∞

-norm of a transfer function.

Systems Control Lett., 14(4):287–293.

Jiang, P. and Voigt, M. (2013). MB04BV — A FOR-

TRAN 77 subroutine to compute the eigenvectors as-

sociated to the purely imaginary eigenvalues of skew-

Hamiltonian/Hamiltonian matrix pencils. SLICOT

Working Note 2013-3.

Kressner, D. (2005). Numerical Methods for General and

Structured Eigenvalue Problems. Springer-Verlag,

Berlin.

Laub, A. J. (1979). A Schur method for solving algebraic

Riccati equations. IEEE Trans. Automat. Contr., AC–

24(6):913–921.

Leibfritz, F. and Lipinski, W. (2003). Description of the

benchmark examples in COMPl

ib. Technical report,

Department of Mathematics, University of Trier, D–

54286 Trier, Germany.

MATLAB (2016). MATLAB



Primer. R2016a. The Math-

Works, Inc., 3 Apple Hill Drive, Natick, MA.

Mehrmann, V. (1991). The Autonomous Linear Quadratic

Control Problem. Theory and Numerical Solution.

Springer-Verlag, Berlin.

Paige, C. and Van Loan, C. F. (1981). A Schur decomposi-

tion for Hamiltonian matrices. Lin. Alg. Appl., 41:11–

32.

Sima, V. (1996). Algorithms for Linear-Quadratic Opti-

mization. Marcel Dekker, Inc., New York.

Sima, V. and Benner, P. (2015a). Pitfalls when solving

eigenproblems with applications in control engineer-

ing. In Proceedings of the 12th International Con-

ference on Informatics in Control, Automation and

Robotics (ICINCO-2015), 21-23 July, 2015, Colmar,

France, volume 1, 171–178. SciTePress.

Sima, V. and Benner, P. (2015b). Solving SLICOT bench-

marks for continuous-time algebraic Riccati equa-

tions by Hamiltonian solvers. In Proceedings of the

2015 19th International Conference on System The-

ory, Control and Computing (ICSTCC 2015), October

14-16, 2015, Cheile Gradistei, Romania, 1–6. IEEE.

Van Loan, C. F. (1984). A symplectic method for approx-

imating all the eigenvalues of a Hamiltonian matrix.

Lin. Alg. Appl., 61:233–251.

Ward, R. C. (1981). Balancing the generalized eigenvalue

problem. SIAM J. Sci. Stat. Comput., 2:141–152.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

184