
Robust Control of Uncertain Linear Plants in Conditions of Signal
Quantization and Time-delay
Alexey Margun
1
and Igor Furtat
1,2
1
Control Systems and Informatics Department, ITMO University, 49 Kronveksky av., 197101, Saint Petersburg, Russia
2
Control of Complex Systems Lab., Institute for Problems of Mechanical Engineering,
V.O., 61 Bolshoy str., 199178, Saint Petersburg, Russia
Keywords:
Robust Cotrol, Quantizer, Time-delay, Parametric Uncertainties.
Abstract:
The paper is aimed to the robust control of parametric uncertain linear plants in conditions of signal quantiza-
tion with time delay and bounded external perturbations. State vector of control plant is unmeasured. Output
of control plant is measured only via quantizer with transport delay. Control algorithm is based on consecutive
compensator method. Proposed algorithm provides convergence of tracking error to the reference signal with
prespecified accuracy for bounded time delay in quantizer. Limitations on value of delay providing stability
of closed-loop system are obtained.
1 INTRODUCTION
The great amount of modern electronic and comput-
ing devices uses digital technologies for data transfer
and processing due to its high reliability and stability
with respect to noises. However, digital technologies
have several disadvantages: loss of information due to
the time discretization, signal level quantization and
other problems caused by channel restrictions.
Most of physical and technical processes have a
continuous nature. Usually discrete models are used
for description of such systems and their implemen-
tation on digital devices. High-performance comput-
ing systems allow to realize the discrete in time trans-
formation of continuous signal with a prescribed ac-
curacy for a large number of cases (Shannon, 1949).
Quantization of signal level is a more difficult prob-
lem in practice because of the limited sensors accu-
racy and the high cost of precision measuring devices.
Most researches consider signal discretization as
a random discrete noise in system (Widrow, 1961),
(Gray and Neuhoff, 1988). However, such assump-
tion is inapplicable if the quantization step is compa-
rable with the range of signal variation (Delchamps,
1989).
The paper (Liberzon, 2003) is devoted to the syn-
thesis of control law for providing of global asymp-
totic stabilization of continuous linear systems with
known parameters in conditions of quantized estima-
tion of state-space vector.
In (Sharon and Liberzon, 2013) the method of sta-
bility achieving for linear plants with known param-
eters and perturbations in the quantized state vector
measurement is considered.
The results (Liberzon, 2003), (Brockett and Liber-
zon, 2000), (Sharon and Liberzon, 2013) and the al-
gorithm of robust discrete control (Tsykunov, 2014)
have been summarized in (Furtat et al., 2015). Pro-
posed discrete robust controller is designed for con-
tinuous linear parametrically uncertain plants exposed
to external disturbances when only quantized output
measurements are available.
In (Margun and Furtat, 2015b) the consecu-
tive compensator control law, which is described in
(Bobtsov, 2008), is applied to the control of the class
of linear continuous parametric uncertain plants in
condition of external disturbances and quantized out-
put measurement. This result is extended for the case
of MIMO systems in (Margun and Furtat, 2015a).
The paper (Wang and Xue, 2010) proposes output
feedback control method for time-delay systems with
measurements quantized by logarithmic quantizer. In
order to analyze the influence of the quantizer on the
system the sector bound method is introduced. Quan-
tization problem is considered as robustness problem.
Condition of exponential stability is obtained using
linear matrix inequalities techniques.
The paper (Mahmoud et al., 2011) proposes a
quantized feedback stabilization algorithm for a class
of interconnected continuous time-delay systems. H
∞
514
Margun, A. and Furtat, I.
Robust Control of Uncertain Linear Plants in Conditions of Signal Quantization and Time-delay.
DOI: 10.5220/0005981405140520
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 514-520
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
approach and LMI-based method is used for synthesis
of decentralized controller.
However, the problem of controller synthesis for
uncertain systems with signal quantizing and time-
delay remains urgent. The present research is devoted
to the control of parametric uncertain plants in condi-
tions of bounded external disturbances, unmeasured
state vector, output signal time-delay and quantizing.
The paper is organized as follows: Section II
describes mathematical problem statement, in Sec-
tion III controller synthesis is considered, Section IV
contains stability analysis with using of Lyapunov-
Krasovskii function. An academic example confirm-
ing performance of proposed controller is given in
Section V.
2 PROBLEM STATEMENT
Consider the control plant described by linear differ-
ential equation
Q(p)y(t) = R(p)u(t) +
˜
f (t), (1)
where Q(p),R(p) are linear differential operators
with known degrees n and m respectively and un-
known coefficients, y(t) ∈ R is an output signal,
u(t) ∈ R is a control signal, p = d/dt is a differen-
tial operator, ρ = n − m ≥ 1 is a relative degree of a
plant,
˜
f (t) is a bounded external disturbance.
A reference model is described by linear differen-
tial equation
Q
m
(p)y
m
(t) = R
m
(p)r(t), (2)
where Q
m
(p),R
m
(p) are linear differential operators
with known coefficients, y
m
(t) ∈ R is an output sig-
nal of a reference model, r(t) is a piecewise smooth
bounded reference signal, Q
m
(λ) and R
m
(λ) are Hur-
witz polynomials, λ is a complex variable.
Assume, that the state vector of control plant is
unmeasured and the plant output is measured only
via quantizer (Liberzon, 2003) that converts the sig-
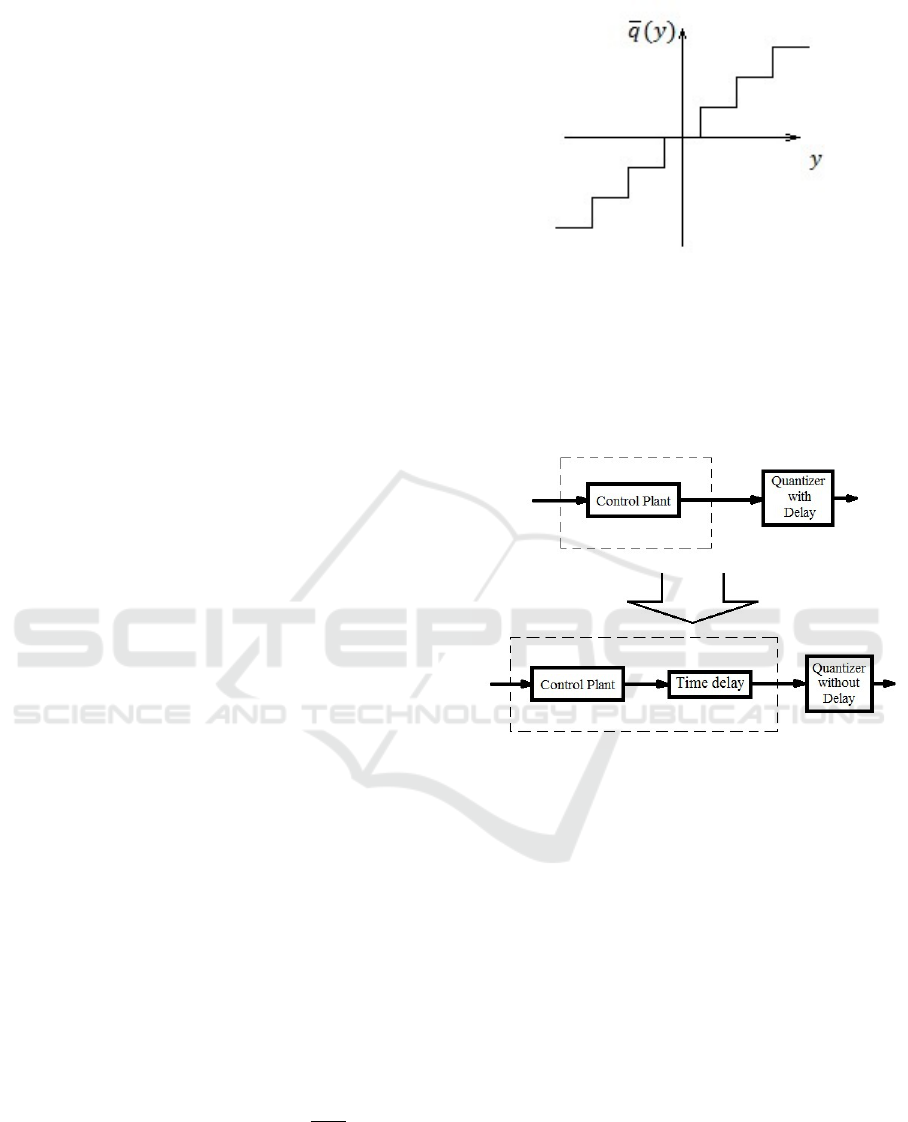
nal y(t) according to (3):
q(y(t)) =
˜q(y(t − τ)),|y(t − τ)| ≤ ¯y,
¯ysign(y(t − τ)),|y(t − τ)| > ¯y,
(3)
where ¯y > 0 is a quantizer saturation value, τ is a
bounded unknown time delay, ˜q(y) =
1
χp+1
¯q(y), ¯q(y)
is a quantizer function illustrated on Fig. 1, χ > 0 is
a some positive number. It should be noted that sig-
nals ¯q(y) and ˜q(y) are almost the same in the case of
sufficiently small χ in comparison with quantization
step, but ˜q(y) is differentiable in contradistinction to
¯q(y). The presence of transport delay represents time
Figure 1: Quantizer output.
which is necessary for signal processing in quantizer.
In practice such plants are actual in technical systems
with analog-digital converters.
It is possible to represent structure of the system
in the form of plant with time delay in output channel
and quantizer without delay (Fig. 2).
Figure 2: Plant structure transformation.
In this case, the control plant is described by the
equation
Q(p)y(t − τ) = R(p)u(t) +
˜
f (t). (4)
Let the system (4) with quantizer (3) satisfies follow-
ing assumptions.
Assumptions
1. Quantizer satisfies condition:
| ˜q(y(t)) − y(t)| ≤ δ
1
,
(5)
where δ
1
is a some positive number.
2. Unknown coefficients of the operators Q(p)
and R(p) belong to the known bounded set Ξ.
3. Control plant (4) is minimum phase.
4. Initial conditions of output signal satisfies in-
equality
|y(0), ˙y(0),...,y
n−1
(0)| ≤ ¯y.
It is necessary to synthesize control system that en-
sures the implementation of the goal condition:
|q(y(t)) −y
m
(t)| < δ, ∀t > T, (6)
Robust Control of Uncertain Linear Plants in Conditions of Signal Quantization and Time-delay
515

where δ > 0 is a prespecified required accuracy, T > 0
is a transient time.
3 CONTROL LAW
Introduce consecutive compensator control law
(Bobtsov, 2008) for plant (4) with quantization and
time delay similarly to (Margun and Furtat, 2015b):
u(t) = −(α + β)D(p)ˆe(t), (7)
where α and β are some positive numbers, D(λ)
is Hurwitz polynomial of degree ρ − 1 such that
(2Q(λ) + αR(λ)D(λ)) is Hurwitz polynomial, λ is a
complex variable, ˆe(t) is estimation of error e(t) =
q(y) −y
m
(t).
Rewrite control plant (4) in the form
Q(p)y(t) = R(p)u(t) +
˜
f (t) + Q(p)(y(t) − y(t − τ))
(8)
Taking into account (2), (7) and (8) error dynamics
can be represented as
(2Q(p) +αR(p)D(p))e(t) = R(p)D(p)×
((α +β)(e(t) − ˆe(t) − βe(t)) +
˜
f (t)+
+ 2Q
1
(q(y(t)) −y(t)) + Q
2
(p)( ˙q(y(t)) − ˙y(t))
− 2Qy
m
(t) +Qy
m
(t − τ) −Q(q(y(t − τ))−
− y(t − τ))+ Qe(t − τ),
(9)
where Q(p) = Q
1
(p) + pQ
2
(p), degQ
2
(p) = n − 1,
degQ
1
(p) ≤ n − 1.
Rewrite equation (9) in state-space form
˙
ε(t) = Aε(t) + B(−βe(t) +(α + β)(e(t)−
− ˆe(t))) + B
1
(q(y(t)) −y(t)) + B
2
×
× ( ˙q(y(t)) − ˙y(t))+ B
3
ϕ(t) +B
4
ε(t − τ),
e(t) =
¯
Lε(t),
(10)
where ε(t) ∈ R
n
is an error state vector, A ∈ R
n×n
,
B ∈ R
n
, B
1
∈ R
n
, B
2
∈ R
n
, B
3
∈ R
n
, B
4
∈ R
n×n
are
matrices obtained from (9) to (10) transition,
¯
L =
[1 0 ... 0], ϕ(t) =
˜
f (t)−2Qy
m
(t)+Qy
m
(t − τ)−
Q(q(y(t − τ)) −y(t − τ)) is a bounded function.
For implementation of control law (7) we use the
observer algorithm
(
˙
ξ(t) = σΓξ(t) + σGe(t),
ˆe(t) = Lξ(t),
(11)
where ξ(t) ∈ R
ρ−1
is an observer state vector,
Γ =
0 I
ρ−2
−k
1
... −k
ρ−1
is Hurwitz matrix, G =
[0 ... 0 k]
T
, I
ρ−2
is identity matrix of ρ − 2
order, k
i
,i =
1,ρ − 1 are positive numbers, L =
[1 0 ... 0], σ > α + β.
Introduce estimation error
η(t) = L
T
e(t) −ξ(t), (12)
where L = [1 0 ... 0].
Yield derivative of estimation error (12)
˙
η(t) = σΓη(t) + L
T
˙e(t). (13)
Closed loop system is described by equations
˙
ε(t) = Aε(t) + B(−βe(t) +(α + β)(e(t)−
− ˆe(t))) + B
1
(q(y(t)) −y(t))+
+ B
2
( ˙q(y(t)) − ˙y(t)) + B
3
ϕ(t) +B
4
ε(t − τ),
˙
η(t) = σΓη(t) + L
T
˙e(t),
(14)
Taking into account
ε(t − τ) = ε(t) −
Z
t
t−τ
˙
ε(s)ds, (15)
closed loop system takes the form
˙
ε(t) = (A + B
4
)ε(t) +B(−β
¯
Lε(t)+
+ (α + β)Lη(t) + B
1
(q(y(t)) −y(t))+
+ B
2
( ˙q(y(t)) − ˙y(t)) + B
3
ϕ(t)−
− B
4
Z
t
t−τ
˙
ε(s)ds,
˙
η(t) = σΓη(t) + L
T
˙e(t).
(16)
Rewrite (16) for brevity
˙
ε(t) =
˜
Fε(t) +
¯
Fη + F
1
Z
t
t−τ
˙
ε(s)ds + F
2
φ(t),
˙
η(t) = σΓη(t) + L
T
˙e(t),
(17)
where
˜
F = A + B
4
− βB
¯
L,
¯
F = (α + β)BL,F
1
=
−B
4
,F
2
φ(t) = B
1
(q(y(t)) − y(t)) + B
2
( ˙q(y(t)) −
˙y(t)) + B
3
ϕ(t) is a bounded perturbation function
which depends on quantizer parameters, and external
disturbances.
4 STABILITY ANALYSIS
Theorem.
Let Assumptions 1-4 hold. Then there exist poly-
nomial D(λ) and positive numbers α,β,σ > 0 and
¯
τ > τ > 0 such that the control system consisting of
control law (7) and estimation algorithm (11) pro-
vides goal (6).
Proof of the Theorem.
Consider Lyapunov-Krasovskii functional V =
V
1
+ V
2
, where V
1
is a functional for part of system
without delay and V
2
is a functional for delay depen-
dent part:
V
1
= ε
T
(t)H
1
ε(t) +η(t)H
2
η(t),
V
2
=
Z
0
−τ
Z
t
t−µ
˙
ε
T
(s)N
˙
ε(s)dsdµ,
(18)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
516

where H
1
and H
2
are solutions of Lyapunov equations
˜
F
T
H
1
+H
1
˜
F = −Q
1
and Γ
T
H
2
+H
2
Γ = −Q
2
respec-
tively, Q
1
,Q
2
and N are symmetric positive defined
matrices.
In the case of the absence of the time-delay closed
loop system takes the form
(
˙
ε(t) =
˜
Fε(t) +
¯
Fη(t) + F
2
φ,
˙
η(t) = σΓη(t) + L
T
˙e(t).
(19)
Let us use the results of Theorem proof in (Margun
and Furtat, 2015b). According to (Margun and Furtat,
2015b), the derivative of Lyapunov function V
1
along
the trajectories of (19) is bounded by inequality
˙
V
1
≤ −ε
T
(t)R
1
ε(t) −η
T
(t)R
2
η(t) +θ, (20)
where R
1
= Q
1
− 2υH
1
B
¯
L − υH
1
¯
F
¯
F
T
H
1
−
υ
˜
F
¯
L
T
LL
T
¯
L
˜
F − βH
1
B
1
B
T
1
H
1
− βH
1
B
2
B
T
2
H
1
−
βH
1
B
3
B
T
3
H
1
− βυ, R
2
= σQ
2
− 2L
T
˜
F
T
¯
L
T
LH
2
−
1
υ
LL
T
−
1
υ
H
2
H
T
2
− βH
2
L
T
¯
LB
1
B
T
1
¯
L
T
LH
2
−
βH
2
L
T
¯
LB
2
B
T
2
¯
L
T
LH
2
− βH
2
L
T
¯
LB
3
B
T
3
¯
L
T
LH
2
−
β
υ
H
2
L
T
¯
LB
¯
L
¯
L
T
B
T
¯
L
T
LH
2
, θ =
2
υ
sup(ϕ
2
(t)) +δ
2
1
,
υ > 0 is a sufficiently small number. R
1
and R
2
are
positive defined matrices due to the choose of υ, Q
1
and Q
2
.
Differentiating Lyapunov-Krasovskii function
along the trajectories (17) we obtain
˙
V = −ε
T
R
1
ε − η
T
R
2
η + θ + 2ε
T
H
1
F
1
Z
t
t−τ
˙
ε(s)ds+
+ 2ε
T
H
1
F
2
φ + τ
˙
ε
T
N
˙
ε −
Z
t
t−τ
˙
ε
T
N
˙
εds.
(21)
Using Jensen inequality
−
Z
t
t−τ
˙
ε
T
(s)N
˙
ε(s)ds ≤ −
1
τ
Z
t
t−τ
˙
ε
T
(s)dsN
Z
t
t−τ
˙
ε(s)ds
(22)
bound Lyapunov-Krasovskii function:
˙
V ≤ −ε
T
R
1
ε − η
T
R
2
η + θ + 2ε
T
H
1
F
1
Z
t
t−τ
˙
ε(s)ds+
+ 2ε
T
H
1
F
2
φ + τ(ε
T
˜
F
T
N
˜
Fε + η
T
¯
F
T
N
¯
Fη+
+
Z
t
t−τ
˙
ε
T
(s)dsF
T
1
NF
1
Z
t
t−τ
˙
ε(s)ds + φ
T
F
T
2
NF
2
φ+
+ 2ε
T
˜
F
T
N
¯
Fη + 2η
T
˜
F
T
NF
1
Z
t
t−τ
˙
ε(s)ds+
+ 2ε
T
˜
F
T
NF
2
φ + 2η
T
¯
F
T
NF
2
φ + 2η
T
¯
F
T
NF
1
×
×
Z
t
t−τ
˙
ε(s)ds + 2φ
T
F
T
2
NF
1
Z
t
t−τ
˙
ε(s)ds)−
−
1
τ
Z
t
t−τ
˙
ε
T
(s)dsN
Z
t
t−τ
˙
ε(s)ds.
(23)
The terms of the right side of (23) are bounded by the
inequalities
2ε
T
H
1
F
1
Z
t
t−τ
˙
ε(s)ds ≤ υεH
1
F
1
F
T
1
H
1
ε+
+
1
υ
Z
t
t−τ
˙
ε
T
(s)ds
Z
t
t−τ
˙
ε(s)ds,
2ε
T
H
1
F
2
φ ≤ υε
T
H
1
F
2
F
T
2
H
1
ε +
1
υ
φ
T
φ,
2ε
T
˜
F
T
N
¯
Fη ≤ υε
T
˜
F
T
N
¯
F
¯
F
T
N
˜
Fε +
1
υ
η
T
η,
2η
T
˜
F
T
NF
1
Z
t
t−τ
˙
ε(s)ds ≤ υη
T
˜
F
T
NF
1
F
T
1
N
˜
Fη+
+
1
υ
Z
t
t−τ
˙
ε
T
(s)ds
Z
t
t−τ
˙
ε(s)ds,
2ε
T
˜
F
T
NF
2
φ ≤ υε
T
˜
F
T
NF
2
F
T
2
N
˜
Fε +
1
υ
φ
T
φ,
2η
T
¯
F
T
NF
2
φ ≤ υη
T
¯
F
T
NF
2
F
T
2
N
¯
Fη +
1
υ
φ
T
φ,
(24)
2η
T
¯
F
T
NF
1
Z
t
t−τ
˙
ε(s)ds ≤ υη
T
¯
F
T
NF
1
F
T
1
N
¯
Fη+
+
1
υ
Z
t
t−τ
˙
ε
T
(s)ds
Z
t
t−τ
˙
ε(s)ds,
2φ
T
F
T
2
NF
1
Z
t
t−τ
˙
ε(s)ds ≤ υφ
T
F
T
2
NF
1
F
T
1
NF
2
φ+
+
1
υ
Z
t
t−τ
˙
ε
T
(s)ds
Z
t
t−τ
˙
ε(s)ds.
where υ is a some positive number.
In accordance with (24) rewrite (23)
˙
V ≤ −ε
T
(R
1
− τ
˜
F
T
N
˜
F − υH
1
(F
1
F
T
1
+ F
2
F
T
2
)H
1
−
− τυ
˜
F
T
N(
¯
F
¯
F
T
+ F
2
F
T
2
)N
˜
F)ε − η
T
(R
2
− τ(
¯
F
T
N
¯
F+
+
1
υ
I + υ
˜
F
T
NF
1
F
T
1
N
˜
F + υ
¯
F
T
NF
2
F
T
2
N
¯
F+
+ υ
¯
F
T
NF
1
F
T
1
N
¯
F))η +
Z
t
t−τ
˙
ε
T
(s)ds(τF
T
1
NF
1
+
+
1
υ
I +
3τ
υ
−
1
τ
N)
Z
t
t−τ
˙
ε(s)ds + θ + φ
T
(τF
T
2
NF
2
+
+ τυF
T
2
NF
1
F
T
1
F
2
+
1 + 2τ
υ
I)φ.
(25)
Assume that τ satisfies conditions
R
1
> τ
˜
F
T
N
˜
F,
R
2
> τ
¯
F
T
N
¯
F +
τ
υ
I,
1
τ
N > τF
T
1
NF
1
+
1 + 3τ
υ
I.
(26)
Robust Control of Uncertain Linear Plants in Conditions of Signal Quantization and Time-delay
517

Rewrite (25) in the form
˙
V ≤ −ε
T
R
1τ
ε − η
T
R
2τ
η −
Z
t
t−τ
˙
ε
T
(s)dsR
3τ
×
×
Z
t
t−τ
˙
ε(s)ds + θ
τ
,
(27)
where R
1τ
= R
1
− τ
˜
F
T
N
˜
F − υH
1
(F
1
F
T
1
+
F
2
F
T
2
)H
1
− τυ
˜
F
T
N(
¯
F
¯
F
T
+ F
2
F
T
2
)N
˜
F, R
2τ
= R
2
−
τ(
¯
F
T
N
¯
F +
1
υ
I + υ
˜
F
T
NF
1
F
T
1
N
˜
F + υ
¯
F
T
NF
2
F
T
2
N
¯
F +
υ
¯
F
T
NF
1
F
T
1
N
¯
F) and R
3τ
= τF
T
1
NF
1
+
1
υ
I +
3τ
υ
−
1
τ
N
are positive defined matrices due to the (26) and
choose of Q
1
,Q
2
and υ.
Transform (27) to the form
˙
V ≤ −ςV + θ
τ
(28)
where ς =
λ
min
(R
1τ
)
λ
max
(M)
Solving inequality (28) with respect to the V we
obtain
V ≤
V (0) −
θ
τ
ς
e
ςt
−
θ
τ
ς
. (29)
Taking into account λ
min
(P)e
2
≤ λ
min
(P)ε
T
ε ≤ V we
obtain tracking error bound:
|e| ≤
s
1
λ
min
(M)
V (0) −
θ
τ
ς
e
−ςt
+
θ
τ
ς
(30)
From (30) follows that the control system (7), (11)
provides the execution of goal condition (6) for a time
T with accuracy
δ =
s
1
λ
min
(M)
V (0) −
θ
τ
ς
e
−ςT
+
θ
τ
ς
. (31)
In infinite time control algorithm provides tracking of
output for the reference signal with accuracy
δ
∞
=
s
1
λ
min
(M)
θ
τ
ς
. (32)
It follows from (31) that goal condition (6) holds.
Theorem is proved.
Note.
Despite the fact that there is a quite rough esti-
mates in proof of theorem, it is follows that the track-
ing error depends on quantizer parameter δ
1
, external
disturbances bounds sup
˜
f (t) and value of time delay
τ.
5 EXAMPLE
Consider numerical example. Control plant is de-
scribed by equation
(p
3
+ q
1
p
2
+ q
2
p + q
3
)y(t) = bu(t) +
˜
f (t).
Set of plant coefficients possible values is defined by
inequalities:
1 ≤ q
1
≤ 5,
− 10 ≤ q
2
≤ 10,
− 10 ≤ q
3
≤ 10,
1 ≤ b ≤ 10.
Plant state vector is unmeasured. Plant output is mea-
sured only via quantizer q(y) with quantization step
δ
1
= 0.05 and time delay τ = 1 ms.
Reference model is described by equation
(p
3
+ 2p
2
+ 2p + 1)y
m
(t) = r(t),
where r(t) = 1.
Choose controller parameters α = 340, β = 10 and
D(p) = p
2
+ 12p + 35. In this case control law (7)
takes the form
u(t) = −350(p
2
+ 12p + 35) ˆe(t).
Choose parameters σ = 700, k
1
= 1, k
2
= 15. Ob-
server algorithm (11) takes the form
(
˙
ξ
1
(t) = 700ξ
2
(t)
˙
ξ
2
(t) = 700(−ξ
1
(t) −15ξ
2
(t) +e(t)).
Let plant parameters are chosen as follows:
b = 3,
q
1
= 2,
q
2
= −2,
q
3
= 1.
Bounded external disturbance has a form of biased
multiharmonic signal
˜
f (t) = 0.5 + sin(t − 0.5)+ 0.2 sin(5t + 0.15).
Output transients of quantizer and reference model
are illustrated on Fig. 3. Plant and reference model
output transients are illustrated on Fig. 4. Tracking er-
ror transient is illustrated on Fig. 5. Modeling results
show that tracking error is comparable with quantiza-
tion step after 8 seconds.
6 CONCLUSIONS
Robust control algorithm for parametric uncertain
plants in conditions of external perturbations and sig-
nal quantizing is considered. In the paper it is as-
sumed that state vector of control plant is unmeasured
and output of control plant is measured only via quan-
tizer with bounded transport delay (transport delay is
a time necessary for signal processing in quantizer).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
518
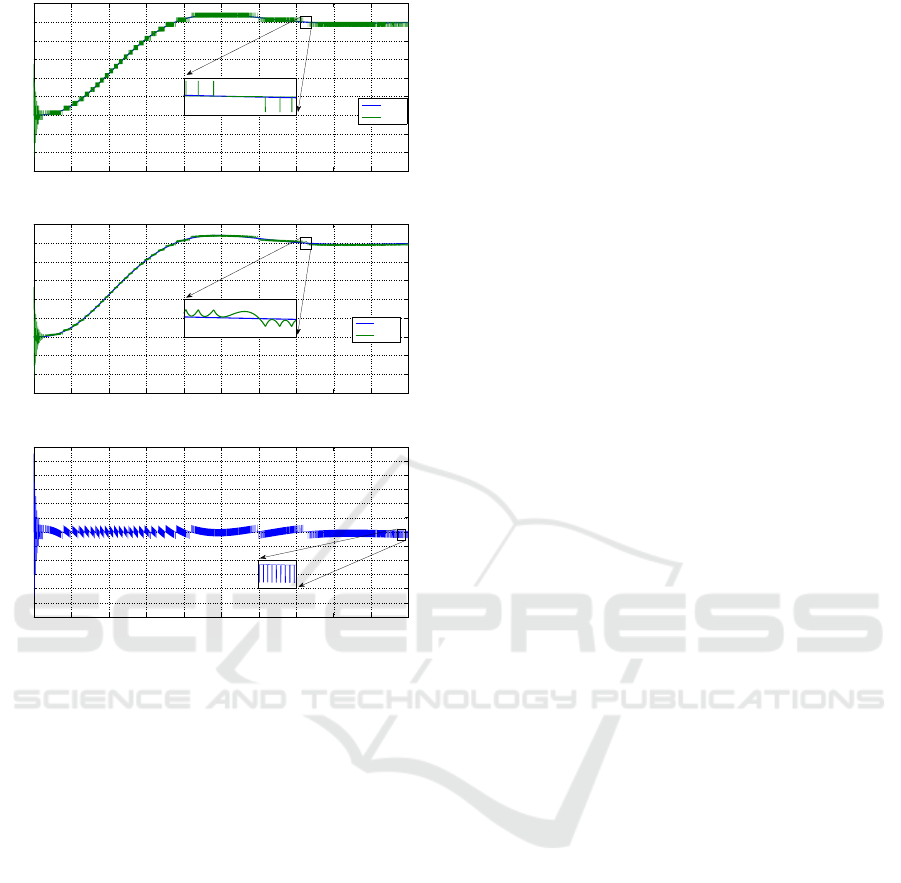
0 1 2 3 4 5 6 7 8 9
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
t
y
m
(t)
q(y)
Figure 3: Quantizer and reference model output.
0 1 2 3 4 5 6 7 8 9
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
t
y
m
(t)
y(t)
Figure 4: Plant and reference model output.
0 1 2 3 4 5 6 7 8 9
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
t
e(t)
Figure 5: Tracking error.
Such system can be represented as a plant with trans-
port delay in output channel and quantizer without de-
lay. Proposed control algorithm provides convergence
of tracking error to the reference signal with prespeci-
fied accuracy. Limitations on value of transport delay
are obtained.
There are several advantages of the proposed
method in comparison with classic controllers:
• for controller synthesis we need to know only rel-
ative degree of plant;
• only quantized output measurement is necessary
for controller;
• algorithm provides prespecified accuracy for
bounded time delay.
Numerical example confirms performance of pro-
posed control method.
ACKNOWLEDGEMENTS
This work was partially financially supported by Gov-
ernment of Russian Federation, Grant 074-U01
This work was supported by the Ministry of Ed-
ucation and Science of Russian Federation (Project
14.Z50.31.0031).
The work was supported by the Russian Federa-
tion President Grant (No. MD-6325.2016.8).
This work was supported by the Russian Federa-
tion President Grant 14.Y31.16.9281.
REFERENCES
Bobtsov, A. (2008). Output control algorithm with the com-
pensation of biased harmonic disturbances. In Au-
tomation and Remote Control. V. 69. Issue 8. P. 1289–
1296.
Brockett, R. and Liberzon, D. (2000). Quantized feedback
stabilization of linear systems. In IEEE Trans. on Au-
tomatic Control. V. 45. P. 1279–1289.
Delchamps, D. (1989). Extracting state information from a
quantized output record. In System Control Letters. V.
13. P. 365–372.
Furtat, I., Fradkov, A., and Liberzon, D. (2015). Compensa-
tion of disturbances for mimo systems with quantized
output. In Automatica. Vol. 60. P. 239244.
Gray, R. and Neuhoff, D. (1988). Quantization. In IEEE
Transaction on Information Theory. V. 44. P. 2325-
2383.
Liberzon, D. (2003). Hybrid feedback stabilization of sys-
tems with quantized signals. In Automatica. V. 39. P.
1543–1554.
Mahmoud, M., Al-Rayyah, A., and Xia, Y. (2011). Quan-
tized feedback stabilization of interconnected contin-
uous time-delay systems. In IMA Journal of Mathe-
matical Control and Information. V.2. P. 1–17.
Margun, A. and Furtat, I. (2015a). Robust control of linear
mimo systems in conditions of parametric uncertain-
ties, external disturbances and signal quantization. In
Proc. of the 20th International Conference on Meth-
ods and Models in Automation and Robotics. P. 341–
346.
Margun, A. and Furtat, I. (2015b). Robust control of un-
certain linear systems in conditions of output quanti-
zation. In 1st Conference on Modelling, Identification
and Control of Nonlinear Systems (MICNON-2015).
P. 853-857.
Shannon, C. (1949). Communication in the presence of
noise communication in the presence of noise. In
Proc. Institute of Radio Engineers. V. 37. No. 1. P.
10–21.
Sharon, Y. and Liberzon, D. (2013). Input to state stabilizat-
ing controller for systems with coarse quantization. In
IEEE Trans. on Automatic Control. V. 57. No. 4. P.
830–844.
Tsykunov, A. (2014). Robust control with compensation
of bounded perturbations and noise. In International
Journal of Computer and Systems Sciences. V. 53. No.
3. P. 320–326.
Robust Control of Uncertain Linear Plants in Conditions of Signal Quantization and Time-delay
519

Wang, J.-H. and Xue, A.-K. (2010). Output feedback con-
trol for time-delay system with quantized measure-
ment. In Journal of Zhejiang University (Engineering
Science). V. 44. P. 1418–1422.
Widrow, B. (1961). Statistical analysis of amplitude-
quantized sampled-data systems. In Transaction on
AIEE. V. 79. No. 2. P. 555-567.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
520
