Integrated Object Segmentation and Tracking for 3D LIDAR Data

Mehmet Ali C¸ a

grı Tuncer and Dirk Schulz

Cognitive Mobile Systems, Fraunhofer FKIE, Fraunhoferstr. 20, 53343 Wachtberg, Germany

Keywords:

Motion Segmentation, Object Tracking, Distance Dependent Chinese Restaurant Process, 3D LIDAR Data.

Abstract:

This paper proposes a novel method for integrated tracking and segmentation of 3D Light Detection and

Ranging (LIDAR) data. The conventional processing pipeline of object tracking methods performs the seg-

mentation and tracking modules consecutively. They apply a connected component algorithm on a grid for

object segmentation. This results in an under-segmentation and in turn wrong tracking estimates when there

are spatially close objects. We present a new approach in which segmentation and tracking modules proﬁt

from each other to resolve ambiguities in complex dynamic scenes. A non-parametric Bayesian method, the

sequential distance dependent Chinese Restaurant Process (s-ddCRP), enables us to combine segmentation

and tracking components. After a pre-processing step which maps measurements to a grid representation, the

proposed method tracks each grid cell and segments the environment in an integrated way. A smoothing algo-

rithm is applied to the estimated grid cell velocities for better motion consistency of neighboring dynamic grid

cells. Experiments on data obtained with a Velodyne HDL64 scanner in real trafﬁc scenarios illustrate that

the proposed approach has a encouraging detection performance and conclusive motion consistency between

consecutive time frames.

1 INTRODUCTION

A very important task of intelligent mobile vehicles is

that being capable of a reliable perception of their en-

vironment. They decide the movements and other ac-

tions by considering the evaluated state of their envi-

ronment so close objects in complex dynamic scenes

need to be tracked in the high volume 3D point cloud

data. For a reliable evaluation of dynamic environ-

ments, data provided by sensors need to be processed.

3D Light Detection and Ranging (LIDAR) sen-

sors are being used to obtain the necessary observa-

tions. These 3D sensors provide a huge amount of

point cloud data to allow more thorough representa-

tion of the environment and less noisy distance mea-

surements in comparison to other types of sensors

such as stereo cameras which exhibit measurement er-

ror growing quadratic with the distance and depend on

external lighting.

A multi-object tracking problem with 3D laser

data can be decomposed as a processing pipeline of

point cloud segmentation and object tracking. Typical

approaches perform these steps consecutively with an

assumption that objects are well segmented from each

other. However, this assumption does not hold under

the circumstances of complex dynamic scenes. For

instance, pedestrians often get very close to static ob-

stacles such as parking cars or buildings. That causes

to accidental segmentation errors which lead to inac-

curate or wrong tracking estimates.

This paper presents a framework to replace the

consecutive processing pipeline and solve the track-

ing and segmentation steps simultaneously. Different

parts of the pipeline structure proﬁt from each other

to resolve ambiguities in complex dynamic scenes.

Using a non-parametric Bayesian method, the se-

quential distance dependent Chinese Restaurant Pro-

cess (s-ddCRP), enables us to integrate segmentation

and tracking components in a single coherent frame-

work. The proposed method tracks each grid cell and

segments the environment in an integrated way. A

smoothing algorithm is applied to the estimated grid

cell velocities for better motion consistency of neigh-

boring dynamic grid cells. We present experimental

results achieved using data collected with a Velodyne

scanner in real trafﬁc to show the feasibility and ben-

eﬁt of the proposed approach.

The layout of this paper is as follows. It starts

with a discussion of related work in Section 2. In

Section 3, the proposed method is described in detail.

Section 4 evaluates the performance of the presented

framework on real trafﬁc data. Section 5 recapitulates

the most important ﬁndings and gives an outlook on

future work.

344

Tuncer, M. and Schulz, D.

Integrated Object Segmentation and Tracking for 3D LIDAR Data.

DOI: 10.5220/0005982103440351

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 344-351

ISBN: 978-989-758-198-4

Figure 1: Architecture of the proposed framework for integrated segmentation and tracking of 3D LIDAR data.

2 RELATED WORK

Estimating the states of moving objects has been stud-

ied for a long time. 3D LIDAR data is projected on a

2D representation (Urmson et al., 2008; Montemerlo

et al., 2008). Given a known segmentation, tracking

becomes a problem of motion estimation and data as-

sociation (Douillard et al., 2011; Moosmann et al.,

2009).

Typical approaches perform the segmentation and

tracking components consecutively (Petrovskaya and

Thrun, 2009; Morton et al., 2011; Choi et al., 2013;

Azim and Aycard, 2012). However this does not hold

in case of complex dynamic surroundings. Under

these circumstances, segmentation gets difﬁcult and

results in an under-segmentation of objects and inac-

curate tracking estimates. In the 3D LIDAR based

tracking approach by Li et al. (Li et al., 2014), the seg-

mentation step is completely eliminated by estimating

a motion ﬁeld of the 3D LIDAR data. This avoids

tracking errors caused by the segmentation compo-

nent, but the detection of nearby objects in the data re-

mains problematic. As a solution, distance dependent

Chinese Restaurant Process (ddCRP) (Blei and Fra-

zier, 2011) is applied to 3D LIDAR data of the traf-

ﬁc scenes by Tuncer and Schulz (Tuncer and Schulz,

2015). The ddCRP is an extension of the Chinese

Restaurant Process (CRP) (Pitman et al., 2002), an hi-

erarchical non-parametric Bayesian clustering model.

The method of Tuncer and Schulz estimates the mo-

tion ﬁeld of the scene and exploits spatial and motion

features together for 3D point cloud segmentation. In

this work, we utilize segmentation and tracking mod-

ules in an integrated way to detect and isolate objects

in the data by using a sequential variant of the distance

dependent Chinese Restaurant Process (ddCRP).

3 PROPOSED METHOD

This section explains our novel approach that solves

the tracking and segmentation tasks simultaneously.

Avoiding under-segmentations of objects in 3D LI-

DAR data incorporating state information from track-

ing promotes consistent and better tracking results.

The architecture of the proposed method is shown in

Figure (1). Each block is described in the following

sections.

3.1 Pre-processing

Recent 3D LIDAR sensors provide huge amounts of

data which poses a challenge on the processing algo-

rithms. For an efﬁcient approach, measurements are

mapped to a grid gr

which has 0.2 m grid cell reso-

lution in x and y dimensions. It stores the height of

objects in each cell as well.

The center of mass of points p = (g

, g

) of a grid

cell is determined. In addition, the average height of

points H and variance of height of points 4H falling

into the grid cell are calculated. Then, a grid cell i at

time frame t is represented as gr

t,i



, g

, H,4H



To classify the grid cells as either a ground or an ob-

stacle cell, we use the decision rule,

= {gr ∈

| H(gr) ≥ tr

∧ 4H(gr) ≥ tr

}

(1)

where tr

and tr

are empirically learned thresh-

olds. They are chosen as 30 cm height above ground

level and 3 cm variance in height measurements re-

spectively. Then, a connected components algo-

rithm (Bar-Shalom, 1987) using 8 neighborhood on

the grid is applied to extract segmentation blobs of

the scene.

Integrated Object Segmentation and Tracking for 3D LIDAR Data

345

3.2 Kalman Filtering

It is assumed that dynamic objects move homoge-

neously, which means that motion states of cells be-

longing to the same object are similar. Therefore grid

cells are treated as the basic elements of motion and

each cell is assigned its own motion vector. Instead

of tracking the centroid of a moving object, we ap-

ply independent linear Kalman ﬁlters to each grid cell

belonging to the extracted segmentation blobs in the

pre-processing step. A typical Kalman ﬁlter with con-

stant velocity model is used for estimation and pre-

diction of each cell’s location at the succeeding time

frames.

If a grid cell gr

t,i

is associated with a cell gr

t−1, j

from the previous scan, its Kalman ﬁlter is replaced

with the last Kalman ﬁlter of grid cell gr

t−1, j

. Then

it is updated with the coordinates of gr

t,i

. The Fil-

tering approach yields the motion state vector x



ˆgr

, ˆgr

, v



, which consists of the estimated cen-

ter of mass of the grid cells and their velocities .

3.3 Grid Cell Association

Grid cells of previous and current scans are assigned

with a Gating and Nearest Neighbor (NN) ﬁlter. The

gating strategy prunes candidates. Cell locations pre-

dicted from the state vectors of the previous time

frames provide a validation gate. If there are candi-

dates lying in the gate, the nearest one is accepted

based on the Euclidean distances of the centers of

mass of points p. Otherwise the current grid cell is

not associated with any previous measurements and a

new Kalman ﬁlter is initialized.

3.4 Smoothing Process

Applying a simple Gating and Nearest Neighbor ﬁl-

ter for grid cell association might result in association

errors. Considering the assumption of homogeneous

movement of grid cells belonging to the same object,

a smoothing process (Alparone et al., 1996) is ap-

plied to the estimated grid cell velocities of extracted

segmentation blobs for better motion consistency of

neighboring dynamic grid cells. If the motion vector

of a grid cell gr

t,i

is denoted as v

, then we can show

the motion feature of its N neighboring cells gr

t,n

with

. The mean square deviation MS

t,i

of grid cell gr

t,i

can be computed as below,

t,i

∑

n=1

− v

(2)

For the smoothing process, we also need to cal-

culate the mean square MS

t,n

of each N neighboring

cells as follows,

t,n

∑

j=1



− v



(3)

If the condition in Equation (4) holds, the algo-

rithm detects that the motion vector of the grid cell in

query is abnormal.

max(MS

t,n

) < MS

t,i

(4)

In this case, the motion vector v

of the grid cell gr

t,i

replaced by the motion vector of the cell with the min-

imum value of MS

t,n

, which is calculated in Equa-

tion (3).

3.5 Object Segmentation

This subsection explains the partitioning process of

the 3D LIDAR data into objects. In the pre-processing

step, point cloud data is coarsely segmented into blobs

using a connected components algorithm based on

an 8 neighborhood of the 2D grid cells. However,

when objects get close to each other, this approach

might lead to under-segmentation. That means that

two or more objects are part of a single blob, which

induces inaccurate tracking estimates. Under these

circumstances, it is not sufﬁcient to rely on the spa-

tial distance of grid cells alone for the segmenta-

tion. This paper therefore aims to show that integrat-

ing segmentation and tracking components increases

the performance of the general tracking system. We

present a sequential variant of distance dependent

Chinese Restaurant Process (ddCRP) method, which

ﬁnds contiguous grid cell regions and determines the

unknown number of clusters (objects) in the extracted

blobs. Assigned grid cells are then sequentially used

in the following time frames.

3.5.1 Chinese Restaurant Process

The sequential-ddCRP (s-ddCRP) algorithm is an ex-

tension of the Chinese Restaurant Process (CRP). The

generative process of CRP is assumed with an inﬁ-

nite number of tables in a restaurant. Costumers enter

the restaurant one by one. Either a customer takes a

seat at a table z (c

) with a probability proportional to

the number of people already sitting at that table or

takes a new table with a probability proportional to

a scaling parameter α. The seating plan provides the

clustering of data. CRP is an exchangeable model,

i.e. the order of the data does not affect the posterior

distribution over partitions. However, exchangeabil-

ity does not hold for point cloud data because the co-

ordinates of grid cells need to be considered for spa-

tially contiguous segmentations. For the task of 3D

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

346

LIDAR data segmentation, each extracted blob repre-

sents a restaurant; tables denote the clusters (objects)

and customers are grid cells. We aim to estimate the

number of clusters in each extracted blob.

3.5.2 Sequential Distance Dependent Chinese

Restaurant Process

The sequential ddCRP method is able to cluster non-

exchangeable point cloud data into objects. It deﬁnes

a distribution over partitions indirectly via distribu-

tions over links between grid cells. This leads to a

biased clustering: nearby grid cells are more likely to

be clustered as an object. A grid cell gr

has a link

variable c

which links to another cell gr

or to itself

according to the distribution below,

p(c

= j|A, α) ∝

(

i j

if i 6= j,

α if i = j.

(5)

where the afﬁnity A

i j

= f (d

i j

) depends on a dis-

tance d

i j

between cells and a window decay function

f (d) = 1 [d < a] with a value of a = 1, which con-

nects adjacent grid cells. Grid cells link together with

a probability proportional to A

i j

or cell gr

can stay

alone and link itself with a probability proportional to

α. Then the generative process is as follows:

1. For each grid cell gr

, sample its link assignment

v s −ddCRP(A, α)

2. Assign the customer links c

to the cluster assign-

ments (object assignments) z

. Then draw param-

eters θ

v G

for each cluster.

3. For each grid cell, sample data x

v F(θ

) inde-

pendently. The k represents a cluster.

Here, the F(θ

) is a Gaussian distribution with θ



, σ



. The base distribution G

deﬁnes the mixture

model of extracted segmentation blobs. It is selected

as a conjugate prior of the data generating distribu-

tion with Θ =



, σ



. While nearby grid cells are

linked probabilistically to Equation (5), the estimated

motion features are sampled according to the cell as-

signments as described above.

3.5.3 Posterior Inference

The key problem of inference is to compute the poste-

rior distribution of the latent variables conditioned on

the estimated motion features. However, the posterior

is intractable to directly evaluate because of the huge

combinatorial number of cluster structures. Therefore

we resort to a Gibbs sampling, which iteratively sam-

ples each latent variable c

conditioned on other latent

variables c

−i

and the state vector x as below,

p(c

−i

, x, Ω) ∝ p (c

|A, α) p (x|z(c) , Θ) (6)

where Ω =

{

A, α, Θ

}

. The ﬁrst term of Equation (6) is

the s-ddCRP prior given in Equation (5). The second

one is the likelihood, which is factorized according to

the cluster index as follow,

p(x|z (c), Θ) =

∏

k=1



z(c)=k

|Θ



. (7)

K denotes the number of clusters and x

z(c)=k

rep-

resents the motion vectors of grid cells assigned to

cluster k. This factorization allows us to apply a

block-wise sampling because we do not need to re-

evaluate terms which are unaffected as the sampler

reassigns c

. Equation (8) shows the computation of

the marginal probability.



z(c)=k

|Θ



∏

i∈z(c)=k

p(x

|θ)

p(θ|Θ)dΘ

(8)

Selecting conjugate p(x

|θ) and G

enables the

marginalization of θ. Then Equation (8) can be com-

puted analytically (Gelman et al., 2003).

The sampling algorithm explores the space of pos-

sible clusterings by reassigning links c

. If c

is the

only link connecting two clusters, they split. When

there are other alternative links connecting those clus-

ters, the partitions of data stay unchanged. Reassign-

ing the link c

might newly connect two clusters as

well. The sampler considers how the likelihood is af-

fected by removing and randomly reassigning the cell

links. It needs to consider the current link c

and all its

connected cells, because if a cell gr

connects to a dif-

ferent cluster, then all cells which are linked to it also

move to that cluster. The sampler explores the space

of possible segmentations with these reassignments.

The sampling approach considers different cluster

layouts. Assuming cluster indices m and l joined to

cluster r, a Markov chain can be speciﬁed as follows,

p(c

−i

, x, Ω) ∝

(

p(c

|A, α)Λ (x, z, Θ) if m ∪l,

p(c

|A, α) otherwise,

(9)

where

Λ (x, z, Θ) =



z(c)=r

|Θ





z(c)=m

|Θ





z(c)=l

|Θ



(10)

The sampler generates different segmentation hy-

potheses and decides on the most probable ones by

using motion and spatial features together. The sam-

pling procedure is initialized with a priori clusterings

obtained in the previous time step. The mean value of

smoothed motion vectors of grid cells which form an

object is assigned as a motion feature of the object.

Integrated Object Segmentation and Tracking for 3D LIDAR Data

347

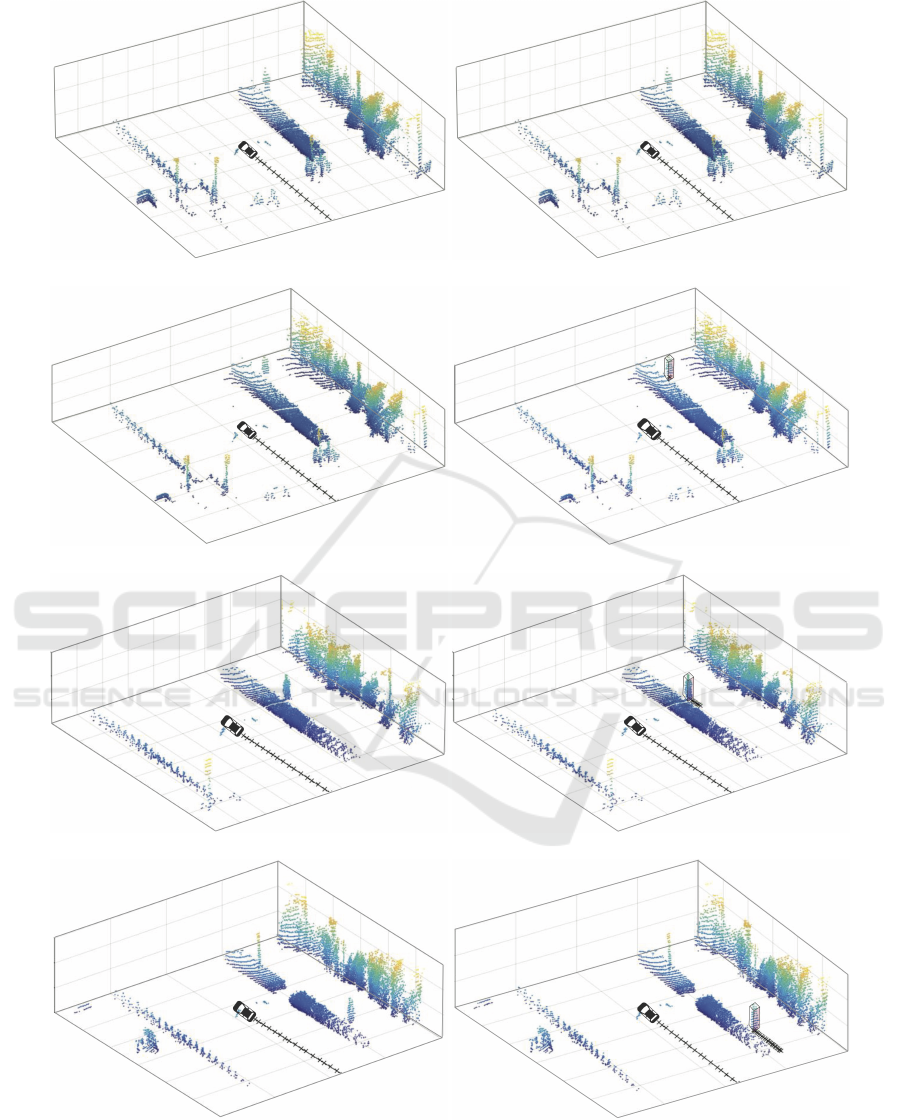
(a) (b)

(e) (f)

(g) (h)

Figure 2: From left to right, the columns display the scene segmented by the connected components algorithm and the

proposed method. From top to bottom, each raw represents the scene at different time frames t = 119, t = 121, t = 129 and

t = 144. For better visualization, the 3D bounding box is applied only for the detected pedestrian. Black solid lines show the

trajectories of the EGO vehicle and the pedestrian.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

348

3.6 Track Management

Two main objectives of track management are: initial-

ization of a new track when the s-ddCRP algorithm

detects a new object and removing spurious tracks.

As the s-ddCRP algorithm exploits spatial and motion

features together, it delivers the information of seg-

mented objects and the features of their corresponding

grid cells. The data association unit sends information

only when there is no grid cell for an association to a

track. Whenever the grid cells of an object are not

associated to an existing object’s cells, the track man-

agement module creates a new track and waits for the

next time frame. If it also gets associated in the fol-

lowing frame, it is a new object. Otherwise a false de-

tection occurs. When the data association unit doesn’t

ﬁnd any grid cell for association of an existing track,

it is deleted.

4 EXPERIMENTAL RESULTS

The proposed method was evaluated on a real world

data set (Geiger et al., 2013). That was recorded us-

ing a Velodyne HDL-64D LIDAR sensor and a high

precision GPS/IMU inertial navigation system. The

LIDAR sensor has a frame rate of 10 Hz, a 360 de-

gree horizontal ﬁeld of view and it produces approx-

imately 1.1 million point measurements per second.

Estimated grid cell velocities are transformed to one-

dimensional movement directions for the inference

step of s-ddCRP. Larger α values bias the algorithm

towards more clusters so we set α = 10

−4

. The s-

ddCRP sampler is run with 20 iterations for each ex-

tracted segmentation blob.

Table 1: Performance of the smoothing algorithm. A

smaller SD value means better motion consistency of neigh-

boring grid cells.

Without Smoothing 46.2

Smoothing 35.8

In order to evaluate the beneﬁt of the smoothing

algorithm, the standard deviation SD

of velocities of

moving grid cells constituting an object is computed.

The average of the computed value SD is considered

as the effect of smoothing. Table (1) shows that the

smoothing algorithm results in a better motion con-

sistency of clustered grid cells.

The ground truth for evaluating the tracker work-

ing on the LIDAR data set which is used for experi-

ments is not available, so we have performed a qual-

itative evaluation. Performance of the proposed ap-

proach has been tested with different data sequences.

A representative one is shown in Figure (2). For com-

parison, we also applied a conventional segmentation

method of 3D LIDAR data which includes a con-

nected components algorithm on a grid (Bar-Shalom,

1987). A pedestrian walking close to a wall gets into

the perception ﬁeld of the laser scanner equipped on a

moving car at time frame t = 119 in Figure (2). Both

the pedestrian and the car are heading in the same

direction. Although the typical object segmentation

method is not able to segment the pedestrian, the pro-

posed approach can detect and start tracking after two

frames in Figure (2) (d). Beside the spatial features,

the segmentation unit also exploits the motion vec-

tors sent by the ﬁltering module. The left column

of Figure (2) illustrates that the pedestrian can not

be detected by the connected component algorithm.

However, the proposed method successfully contin-

ues tracking the pedestrian during the data sequence

as shown in the right column of Figure (2).

Figure (3) displays a scene sequence where the

door of a car is opened and a person suddenly gets

out of the car. In Figure (3) (a) and Figure (3) (b), the

scene at time frame 288 is displayed by a RGB image

and 3D LIDAR data for a better visualization. The

person goes out of his car and starts walking. It is

illustrated in Figure (3) (c) that the tracking system

which uses a connected components algorithm for

segmentation is not able to detect the person. How-

ever, the proposed method detects and starts tracking

the person as shown in Figure (3) (d).

Table 2: The averaged standard deviation SD of velocity

differences between consecutive time frames.

Kalman Filter 34.6

The proposed method 22.1

Because of the lack of ground truth, we mea-

sured the motion consistency of the proposed tracker.

For comparison, we applied an independent Kalman

ﬁlter for each well segmented vehicle (Bar-Shalom,

1987). It tracks the centroid of the objects for a

data sequence. Then we have measured the aver-

aged standard deviation SD of velocity differences be-

tween consecutive time frames. Object velocities are

expected to change smoothly in successive scans so

smaller SD value means better motion consistency of

the tracker. Table (2) tells that the proposed method

has a good motion consistency as well.

Integrated Object Segmentation and Tracking for 3D LIDAR Data

349

(a) (b)

Figure 3: The scene at the time frame t = 288 is displayed by (a) a RGB image (for better understanding of the scene) and

(b) 3D LIDAR data. The black solid line shows the trajectory of the EGO vehicle. The result at t = 313 is obtained by (c) a

connected components algorithm and (d) the proposed method. For better visualization, the 3D bounding box is applied only

for the detected pedestrian.

5 CONCLUSIONS

We proposed a novel method for integrated tracking

and segmentation of 3D LIDAR data. It replaces the

consecutive processing pipeline with a simultaneous

tracking and segmentation framework. The conven-

tional processing pipeline of object tracking methods

performs the segmentation and tracking modules con-

secutively, e.g., they ﬁrst apply a connected compo-

nent algorithm on a grid for object segmentation and

then track the segmented objects. However, when ob-

jects get close to each other, this approach might lead

to under-segmentation, which in turn induces inaccu-

rate tracking estimates. Therefore we present a new

approach in which segmentation and tracking mod-

ules proﬁt from each other to resolve ambiguities in

complex dynamic scenes. Using a non-parametric

Bayesian method, the sequential distance dependent

Chinese Restaurant Process (s-ddCRP), enables us to

combine segmentation and tracking components in a

single coherent framework. After the pre-processing

step which maps measurements on a grid representa-

tion, the proposed method tracks each grid cell and

segments the environment in an integrated way. A

smoothing algorithm is applied to the estimated grid

cell velocities for better motion consistency of clus-

tered dynamic grid cells. Experiments on data ob-

tained with a Velodyne HDL64 scanner in real trafﬁc

scenarios illustrate that the proposed approach has a

satisfactory detection performance and good motion

consistency between consecutive time frames. As a

future work, we plan to add an integrated classiﬁca-

tion step to the proposed framework. Also, applying

a more stochastic tracking module, e.g. including oc-

clusion likelihood, would be interesting. In addition

to the connected components algorithm, we intend

to compare the performance of the proposed method

with other novel algorithms from the state of the art.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

350

ACKNOWLEDGEMENTS

We acknowledge the support by the EU’s

Seventh Framework Programme under grant

agreement no 607400 (TRAX, Training net-

work on tRAcking in compleX sensor systems)

http://www.trax.utwente.nl/.

REFERENCES

Alparone, L., Barni, M., Bartolini, F., and Cappellini, V.

(1996). Adaptively weighted vector-median ﬁlters

for motion-ﬁelds smoothing. In Acoustics, Speech,

and Signal Processing, 1996. ICASSP-96. Conference

Proceedings., 1996 IEEE International Conference

on, volume 4, pages 2267–2270. IEEE.

Azim, A. and Aycard, O. (2012). Detection, classiﬁcation

and tracking of moving objects in a 3d environment.

In Intelligent Vehicles Symposium (IV), 2012 IEEE,

pages 802–807. IEEE.

Bar-Shalom, Y. (1987). Tracking and data association.

Academic Press Professional, Inc.

Blei, D. M. and Frazier, P. I. (2011). Distance dependent

chinese restaurant processes. The Journal of Machine

Learning Research, 12:2461–2488.

Choi, J., Ulbrich, S., Lichte, B., and Maurer, M. (2013).

Multi-target tracking using a 3d-lidar sensor for au-

tonomous vehicles. In Intelligent Transportation

Systems-(ITSC), 2013 16th International IEEE Con-

ference on, pages 881–886. IEEE.

Douillard, B., Underwood, J., Kuntz, N., Vlaskine, V.,

Quadros, A., Morton, P., and Frenkel, A. (2011).

On the segmentation of 3d lidar point clouds. In

Robotics and Automation (ICRA), 2011 IEEE Inter-

national Conference on, pages 2798–2805.

Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).

Vision meets robotics: The kitti dataset. International

Journal of Robotics Research (IJRR).

Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B.

(2003). Bayesian data analysis. Chapman and

Hall/CRC Texts in Statistical Science.

Li, Q., Zhang, L., Mao, Q., Zou, Q., Zhang, P., Feng, S.,

and Ochieng, W. (2014). Motion ﬁeld estimation for a

dynamic scene using a 3d lidar. Sensors, 14(9):16672–

16691.

Montemerlo, M., Becker, J., Bhat, S., Dahlkamp, H., Dol-

gov, D., Ettinger, S., Haehnel, D., Hilden, T., Hoff-

mann, G., Huhnke, B., et al. (2008). Junior: The

stanford entry in the urban challenge. Journal of ﬁeld

Robotics, 25(9):569–597.

Moosmann, F., Pink, O., and Stiller, C. (2009). Segmen-

tation of 3d lidar data in non-ﬂat urban environments

using a local convexity criterion. In Intelligent Vehi-

cles Symposium, 2009 IEEE, pages 215–220. IEEE.

Morton, P., Douillard, B., and Underwood, J. (2011). An

evaluation of dynamic object tracking with 3d lidar.

In Proc. of the Australasian Conference on Robotics

& Automation (ACRA).

Petrovskaya, A. and Thrun, S. (2009). Model based vehicle

detection and tracking for autonomous urban driving.

Autonomous Robots, 26(2-3):123–139.

Pitman, J. et al. (2002). Combinatorial stochastic processes.

Technical Report 621, Dept. Statistics, UC Berkeley,

2002. Lecture notes for St. Flour course.

Tuncer, M. A. C. and Schulz, D. (2015). Monte carlo based

distance dependent chinese restaurant process for seg-

mentation of 3d lidar data using motion and spatial

features. In Information Fusion (Fusion), 2015 18th

International Conference on, pages 112–118. IEEE.

Urmson, C., Anhalt, J., Bagnell, D., Baker, C., Bittner, R.,

Clark, M., Dolan, J., Duggins, D., Galatali, T., Geyer,

C., et al. (2008). Autonomous driving in urban envi-

ronments: Boss and the urban challenge. Journal of

Field Robotics, 25(8):425–466.

Integrated Object Segmentation and Tracking for 3D LIDAR Data

351