
µAUV
2
- Development of a Minuscule Autonomous Underwater Vehicle
Hendrik Hanff
1,∗
, Korbinian Schmid
2,∗
, Philipp Kloss
1
and Sven Kroffke
1
1
DFKI GmbH − Robotics Innovation Center Bremen, Robert-Hooke Str. 1, 28359 Bremen, Germany
2
RoboCeption GmbH, Kaflerstr. 2, 81241 Munich, Germany
Keywords:
Underwater Robotics, System Design, Miniature Robotics, System Parameter Identification, Control of
Underwater Robots, Robot Development.
Abstract:
Small sized robotic systems have operational advantages compared to large systems. They can also operate
in fields of application where bigger systems would fail. This paper describes the specifications and the
design of the autonomous underwater vehicle µAUV
2
. Technical details of the system regarding sensor setup,
motorization and computing power are given. Furthermore, we present details about the system identification
process and the implemented controller structure. Possible scopes of the µAUV
2
are underwater exploration,
inspection tasks, development and evaluation of algorithms, education and competitions.
1 INTRODUCTION
Autonomous underwater vehicles (AUVs) are robotic
systems which do not depend on any input from an
operator. Typical fields of application include com-
mercial uses e.g. in the oil and gas industry (Albiez
et al., 2015) or the inspection of different underwa-
ter structures, research purposes like the autonomous
investigation of the ice ocean interface, (Dowdeswell
et al., 2008) or even military purposes (Nicholson and
Healey, 2008) like autonomous surveillance tasks.
The development of AUVs is of great interest to all
above mentioned groups. Possible benefits range
from monetary advantages to extended capabilities
due to the extended range of operation.
Dimensions of AUVs range from small, portable
and lightweight to large systems with several meters
length. Large systems offer advantages concerning
payload capacity, range of operation and the ability to
operate when exposed to water currents. In contrast,
small systems offer significant advantages during the
launch and recovery process due to their small foot-
print. With their comparably low production and ser-
vice costs, such systems could even be used as dispos-
able sensor units in situations where a recovery is not
possible. Despite these advantages, there only exists a
few small and even less minuscule AUVs. The small
dimensions enable fields of applications where big-
ger AUVs would fail. One domain might be the ex-
∗
These authors contributed equally to this work.
ploration of underwater cave systems or archaeologi-
cal sites which are too small or too fragile for normal
sized AUVs. Pipeline or wreck inspection could also
be addressed by systems like the presented µAUV
2
(see Figure 1) or similar systems. Swarms can be real-
ized more easily due to the potentially lower costs per
system. The described system is based on knowledge
from previous projects and the experiences gained
with the µAUV 1 (Fechner et al., 2007) which can
be regarded as the predecessor of the µAUV
2
.
The µAUV
2
, developed at the German Research
Centre for Artificial Intelligence (DFKI), combines
small dimensions (270x182x156mm
3
(LxHxW)), a
weight of 1.2kg and a maximum speed of 1.5m/s
with a unique propulsion concept, and high process-
ing power. This paper presents the system design and
development, the identification of system parameters
and first control approaches.
The main objectives of the µAUV
2
are the develop-
ment of control and autonomy algorithms. Further-
more the µAUV
2
represents an easy to use evaluation
platform for swarm algorithms in the underwater area.
2 STATE OF THE ART
In this section, we give an overview of state-of-the-
art AUVs and their unique features which inspired the
development of the µAUV
2
. A small form factor, an
interesting sensor setup and a streamlined hull are just
Hanff, H., Schmid, K., Kloss, P. and Kroffke, S.
µAUV2 - Development of a Minuscule Autonomous Underwater Vehicle.
DOI: 10.5220/0005982201850196
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 185-196
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
185

Figure 1: µAUV
2
- A: DC motor (Maxon motor with in-
tegrated encoder and gear) driven thruster, blue are the 3D
printed protection frames, each of the three thrusters can
be turned ±90
◦
, 3rd thruster cannot be seen in this picture;
B: Front sphere made from acrylic glass; C: battery pack
mounted below the AUV for easy trimming and a low centre
of mass (CM); D: IMU, developed at DFKI GmbH, E: peri-
staltic (buoyancy) pump, a commercialy available product;
F: Optical communication platform; G: Rear sphere made
from acrylic glass; H: Central piece of aluminium which
connects the acrylic spheres and serves as a mounting point
for the three thrusters and the battery pack; I: Printed Circuit
Board (PCB) stack (Microcon1..5) ; J: Connector for the
battery pack. Hidden on the other side of the AUV is the
JTAG connector which permits reprogramming the FPGA
without opening the hull.
some of these features.
The CoCoRo project (Mintchev et al., 2014) has
developed the autonomous underwater vehicles Jeff
and Lily which interact with each other. Each ot the
two AUVs fullfills a different task in a swarm. The 3
degrees of freedom (DOF) Jeff system contains cus-
tom magnetically coupled thrusters and a custom de-
signed rolling diaphragm buoyancy system. A blue-
light sensor system for short-range distance measure-
ment and short-range communication enables the Lily
AUV to fullfill swarm operations.
Another example of a small AUV is Monsun
(Meyer et al., 2014). Monsun is a small and inexpen-
sive AUV. Just like CoCoRo, Monsun was designed
to operate in a swarm. Being equipped with an ac-
celerometer, IMU, compass and a camera makes it
ideal for environmental monitoring. Running Linux
and ROS on an ARM based microcontroller provides
a lot of possibilities concerning camera vision. 6
thrusters enable the system to accelerate in all direc-
tions.
Stingray (Barngrover et al., 2011) is a 6 DOF
system and was developed by the San Diego iBotics
group. It consists of a carbon fibre hull which mimics
the shape of the cartilaginous fish. The streamlined
shape enables the underwater vehicle to maneuver
very energy efficient. In contrast to other small AUVs,
this system makes use of two Voith-Schneider pro-
pellers which make this AUV highly agile. The PC-
104 form factor computer from Kontron comprises an
Intel Core Duo (1.2GHz) with 2Gb of DDR2 RAM
and 100Mbps Ethernet. Being equipped with a cam-
era and a low-cost sonar, the Stingray system is able
to detect underwater objects.
3 SYSTEM DESIGN
Designing a minuscule underwater vehicle poses hard
challenges since commercial of the shelf components
(COTS) do generally not meet the design objectives
mentioned in the introduction. Therefore, hardware
components, electronics as well as mechanics have to
be miniaturized. The system has to provide sufficient
computational power on strictly limited space, ther-
mal and power constraints. Sensors such as cameras
have to be mounted in a way that the acquired data
can be used for navigation as well as inspection tasks.
Electronics has to be protected from water while fast
reprogramming should be possible in a fully assem-
bled state. In the following we describe our system
design considering these aforementioned aspects.
3.1 Mechanics
The main body of the µAUV
2
consists of three parts:
• 2 hollow acrylic glass domes, one at the front of
the system and one at the back. These two domes
build the hull protecting the inner part of the AUV
from water up to a depth of 2.5 m. Both domes are
transparent to allow optical sensors to monitor the
environment.
• 1 central base frame made of aluminium which
connects the two acrylic domes. This frame also
serves as a carrier for all three thrusters and the
battery pack, see Figure 1, label H.
The AUV has the dimensions 270x182x156mm
3
(Lx-
HxW).
3.1.1 Propulsion
3 thrusters are responsible for moving the µAUV
2
in
all directions. The top thrusters can be turned in-
dependently ±90
◦
. The two side thrusters can be
synchronously turned ±90
◦
. All thrusters are pro-
pelled by Maxon RE 10 DC motors in a 6V/1.5W
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
186

configuration. In combination with the epicyclic 16:1
gear Maxon GP10a1 and the Maxon quadrature en-
coder MR S 16 they actuate the µAUV
2
. All three
thrusters can be rotated by Krick micro pile gear mo-
tors whose current angle of rotation is measured with
potentiometers (Schmid, 2008). The configuration
and the high flexibility of the thrusters make the AUV
highly agile compared to miniaturized AUVs in its
class (see Section 2))
3.1.2 Buoyancy Tank
Like the CoCoRo system (see Section 2 ) the µAUV
2
also contains a buoyancy tank. This buoyancy or bal-
last water tank enables the µAUV
2
to float energy ef-
ficiently at a certain depth in the water column. The
tank can be filled and emptied with a peristaltic pump.
The ballast water tank itself is a simple convoluted
rubber gaiter. To prevent an overfilled water tank,
the status (full/not full) of the water tank is measured
with an ordinary mini push-button switch. The fill
level is determined by measuring the time the pump
is switched on while the throughput of the peristaltic
pump is known.
3.2 Electronics
The main electronics were designed with modularity
and miniaturization in mind. It consists of 5 stackable
PCBs (Printed Circuit Boards) named Microcon 1, 2,
3, 4 and 5 respectively. All PCBs have the same form
factor and are thus stackable . This concept enables
an easy extension by further electronic components if
needed. Microcon1 is responsible for driving the mo-
tors, generating the system voltage and for determin-
ing the motor current. The second board contains the
communication hardware: 4 UARTs for serial com-
munication, 8 GPIOs and in addition 3 eight channel
ADCs. Microcon3 is the processing board. It em-
beds a Xilinx Virtex 4 FPGA (XC4VLX25) with an
8Mbit configuration Flash and 512k x 8 bit low volt-
age SRAM. Microcon4 houses a Blackfin DSP, static
memory and flash memory. Microcon5 houses a cam-
era (see Section 3.2.1) and the corresponding elec-
tronics. All PCBs offer a small form factor of only
35x80mm.
The µAUV
2
contains several complementary sen-
sors to control the thrusters and to navigate au-
tonomously under water.
3.2.1 Camera
For environmental perception the µAUV
2
is equipped
with two ON Semiconductor MT9V022 digital cam-
eras, one pointing downward and one pointing ahead.
With a wide VGA resolution (752Hx480V), global
shutter, a frame rate of 60fps and optional 8 bit serial
(LVDS) or 10 bit parallel video data output, the cam-
era is ideal for machine vision tasks. Being connected
to an FPGA, the machine vision algorithms can be
accelerated with minimum power consumption com-
pared to CPU or GPU computation.
3.2.2 IMU
To measure the attitude of the vehicle, an Inertial
Measurement Unit (IMU) was developed. The µIMU
has a size of 20x20x20mm and consists of 1 gyro-
scope per axis, a three-axis acceleration sensor and a
three-axis magnetometer . An on-board controller fil-
ters and fuses the sensor values with a Kalman filter
(Kalman, 1960) and calculates the quaternions to de-
termine the actual attitude of the system. The data is
sent to the central processing unit via UART.
3.2.3 Differential Pressure Sensor
The differential pressure sensor Freescale
MPX5100DP is used to determine the depth of
the vehicle. With a sensitivity of 45mV/kPa and
a range from 0 to 100kPa the sensor will deliver
4.5mV/cm. The 12 bit ADC which transforms the
analog output into the digital domain has a resolution
of 240µV /bit leading to a depth resolution of 1.8mm
per bit.
3.2.4 Thruster Attitude Sensor
The current inclination of the thrusters can be mea-
sured by potentiometers (Piher N15TV) which are
mounted on the turning axis. Linear potentiometers
change their voltage division ratio proportional to the
angle of rotation of the shaft of the potentiometer. Us-
ing an analog to digital converter (ADC) the output
voltage of the potentiometer can be converted into the
digital domain. Thus the determined inclination of the
thrusters is used for control.
3.2.5 Thruster and Pump Speed Sensors
The speed of the thruster and pump motors is mea-
sured with quadrature encoders.
As already mentioned in Section 3.1.1, the used
quadrature encoder is a Maxon MR S 16. The sensor
delivers 16 counts per turn and in combination with
the used 16:1 Maxon gear, 256 counts are produced
for one 360
◦
shaft revolution. Maximum electrical
and mechanical speeds are 30000rpm.
µAUV2 - Development of a Minuscule Autonomous Underwater Vehicle
187

3.2.6 Communication Module
Underwater wireless communication is still an area of
research. Depending on the transmission power, high
speed communication methods like WLAN or Blue-
tooth usually last less then 10cm. This is because the
attenuation of frequencies in the range of radio waves
in water is very high compared to the attenuation in
air due to the dipol nature of the water molecules
(Bryant, 2002) . Long range communication channels
like Long Baseline Modems (LBLs) are too bulky for
a miniaturized AUV and due to their low frequency
range acoustic methods do not have the capability to
transmit a huge amount of data in an appropriate time.
In contrast, optical communication methods pro-
vide a throughput which is high for certain wave-
lengths. A very low attenuation (2 · 10
−2
/m) appears
for a wavelength of 480nm. Thus the µAUV
2
is
equipped with an optical communication module that
was developed at the DFKI. This means of communi-
cation was also chosen because the range that is cov-
ered by optical underwater communication modules
easily covers the dimensions of the basin that is avail-
able for tests at the DFKI GmbH. Data is sent with
a green (530nm) LED. An OTS IrDa (infrared data)
transceiver (Maxim Integrated MAX3120) physical
layer is used for controlling the LEDs. The complete
OptCom module is UART compatible and fits on one
of the PCBs mentioned in section 3.2. The datarate
achieved is 19.2kbps with a range of approximately
2.5m.
4 SYSTEM PARAMETER
IDENTIFICATION
The system model introduced by (Fossen, 2002)
builds the basis for the controller. The identification
process of the corresponding model parameters as de-
scribed in (Indiveri, 1998) and (Ridao et al., 2001) is
described in this Section.
4.1 Pressure Sensor
The diving depth of an underwater vehicle can be cal-
culated by Equation 1, where p is the hydrostatic pres-
sure [Pa], h is the depth in meter, ρ is the density of
water [kg/m
3
] and g is the gravitational acceleration
(9.81 m/s
2
).
p = hρg (1)
The pressure sensor provides information about
the current pressure surrounding the AUV. Equation
2 is used to convert sensor output data into depth
information,
d(V ) = C
1
V +C
2
(2)
where d(V) is the depth, V is the output voltage of
the sensor, C
1
is a constant factor and C
2
is an offset.
For identifying the constants C
1
and C
2
, the µAUV
2
is manually submerged to a depth of 50cm which is
the maximum depth of the available pool. The system
was then ascended in steps of 5cm.
We used linear regression to identify the constants
(see Table 1 and Figure 2).
Figure 2: The sampled pressure sensor output data with lin-
ear resgression (Schmid, 2008).
Table 1: Results of the system identification of the pressure
sensor.
C
1
1.920m/V
C
2
-486.4mm
R
2
static 0.993
4.2 Thrusters
The following one-state thruster model was proposed
by (Yoerger and Slotine, 1991)
τ = C
t
n|n| (3)
˙n = βT − αn|n| (4)
where τ is the output force, C
t
, α and β are sys-
tem constants, n is the propeller revolution rate and
T is the input torque. Due to the usage of small
and lightweight propellers, the time constant of the
thrusters is assumed to be very small compared to the
time constant of the system. Therefore the thruster
dynamics can be neglected. C
t
varies depending on
the sign of the revolution rate (forward/backward) and
is thus denoted as C
+
t
and C
−
t
. The experimental set-
up to identify the thruster force parameters is depicted
in Figure 3. The µAUV
2
is in the middle of the pool
while it is attached to an aluminium rod. Outside of
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
188

the pool is a scale on which the µAUV
2
generates a
force when the thrusters are turned on. This is due
to a mechanical connection between the AUV and the
scale via a lever arm.
The speed of the side thrusters is increased syn-
chronously from −100% to +100% in steps of 5%
while the related weight on the scale is saved. The
torque that is generated in point O by the force of the
two side thrusters can be calculated using Equation 5.
τ
O
= 2 f
t
d
t
(5)
τ
O
is the torque in point O, f
t
is the thrust of one
thruster and d
t
is the perpendicular distance of the
thrusters from O. On the scale a force f
s
is induced by
the torque τ
O
which can be determined by equation 6
τ
O
= m
s
gd
s
(6)
where m
s
is the measured weight on the scale, g is
the gravitational constant and d
s
is the length of the
arm between O and the point of contact on the scale.
Using Equations 5 and 6, the resulting thruster force
can be calculated as
f
t
=
d
s
2d
t
m
s
g (7)
With f
t
= τ from Equation 3 we find
d
s
2d
t
m
s
g = C
t
n|n| (8)
Linear regression on the measured (m
s
,n) tuples (see
Figure 4) reveals the parameter C
±
t
.
Scale
Figure 3: Thruster force identification experiment set-up
(Schmid, 2008).
Table 2: Results of the experiments with the thrusters.
C
+
t
13.2 · 10
−06
Nm(
s
U
)
2
C
−
t
−8.32 · 10
−06
Nm(
s
U
)
2
R
2+
static 0.9990
R
2−
static 0.9989
4.3 Damping Coefficient
The motion of a moving, submerged object is damped
by friction generated by the surrounding liquid parti-
cles (Fossen, 2002). The following assumptions are
Figure 4: Thruster force over revolution rate including lin-
ear regression(Schmid, 2008)).
made to reduce the complexity such that the damping
coefficients can be determined experimentally.
1. Only steady state movements without linear ac-
celerations are considered
2. Only linear movements are considered
3. The AUV is stable with zero buoyancy and no roll
and pitch are assumed
4. In contrast to the definition by (Fossen, 2002)
where D is a complex function depending on ν,
we use the approximation of (Leonessa, 2008)
in Equation 9 for linear and quadratic damping
(Christensen et al., 2009).
ν = [u v w p q r]
T
represents the position in
a body fixed system {B
xyz
} in all 6 degrees of free-
dom.
D = − diag(X
u
,Y
v
,Z
w
,K
p
,M
q
,N
r
)
D(ν) = − diag(X
u|u|
|u|,Y
v|v|
|v|,Z
w|w|
|w|,
K
p|p|
|p|,M
q|q|
|q|,N
r|r|
|r|)
(9)
D(ν)ν = τ
=
X
Y
Z
K
M
N
=
X
u
0 0 0 0 0
0 Y
v
0 0 0 0
0 0 Z
w
0 0 0
0 0 0 K
p
0 0
0 0 0 0 M
q
0
0 0 0 0 0 N
r
u
v
w
p
q
r
+
X
u|u|
|u| 0 0 0 0 0
0 Y
v|v|
|v| 0 0 0 0
0 0 Z
w|w|
|w| 0 0 0
0 0 0 K
p|p|
|p| 0 0
0 0 0 0 M
q|q|
|q| 0
0 0 0 0 0 N
r|r|
|r|
u
v
w
p
q
r
(10)
X
u
,Y
v
,Z
w
,K
p
,M
q
,N
r
are linear and
X
u|u|
|u|,Y
v|v|
|v|,Z
w|w|
|w|,K
p|p|
|p|,M
q|q|
|q|,N
r|r|
|r|
µAUV2 - Development of a Minuscule Autonomous Underwater Vehicle
189

are quadratic damping factors. Under the mentioned
assumptions the six degrees of freedom can be
separated such that each degree of freedom is an
equation of the form
D
ν
ν
max
+ D
ν|ν|
ν
max
|ν
max
| = τ
(11)
with v
max
as the constant maximum velocity at an
input force/torque of τ. Because only heave and
yaw will be controlled actively in a closed loop
configuration, the only parameters that need to be
identified to determine suitable controller parameters
are Z
w
, Z
w|w|
, N
r
and N
r|r|
.
The experimental setup for the identification of
the heave parameters was as follows: The µAUV
2
was submerged to the bottom of the pool. Then it
emerged with a constant thruster force which was
varied in subsequent experiment runs. The diving
speed is determined by the derivation of the pressure
sensor data. The (w
max
,Z) tuples are the sampling
data for a linear regression on Equation 11. The
heave position was measured with varying values for
Z = [0.0238 0.0324 0.0423 0.0535
0.0661 0.08 0.0952 0.1117 0.1295]N. Figure
5 shows the result of the regression and the maximum
reachable heave speed over the applied force. The
results can be seen in Table 3.
Figure 5: Maximum heave speed over driving force
((Schmid, 2008)).
To identify the yaw damping, the experimental
setup starts with positioning the µAUV
2
in the mid-
dle of the pool. Then a defined and constant torque
is applied to both side thrusters. The torque is varied
with each consecutive run of the experiment. The yaw
turning speed is logged from the IMU. Different yaw
speeds were measured for the corresponding torques
τ = [0.0013 0.0020 0.0027 0.0033 0.0040
0.0047 0.0053]Nm.
Figure 6 shows the resulting regression function
and the measured maximum yaw speed samples.
Figure 6: Maximum yaw speed over driving force with re-
gression function ((Schmid, 2008)).
The results of the experiments are summarized in
Table 3.
Table 3: Results of the damping experiments.
Z
w
204 · 10
−3
Ns
m
Z
w|w
|w| 6.28
Ns
m
ZR
2
static 0.9902
N
r
251 · 10
−6
Ns
m
N
r|r|
|r| 3.54 · 10
−3
Ns
m
NR
2
static 0.9990
4.4 Additive Mass
In this section, the added mass of the vehicle is esti-
mated. The added mass is an extra virtual mass term,
since an accelerating or decelerating body must move
some volume of the surrounding fluid as it moves
through it (Fossen, 2002).
If we assume that:
1. The vehicle is accelerating such that ˙v 6= 0
2. The movement of the AUV is linear along one
axis
3. Buoyancy, roll and pitch are zero
the system equation from (Fossen, 2002) can be sim-
plified to
τ − D(ν)ν = (M
RB
+ M
A
)
˙
ν (12)
with M
RB
+ M
A
= M (M
RB
= mass of the rigid body
and M
A
=additive mass) being the only parameter, be-
cause the damping coefficients were already identified
in Section 4.3. τ are the forces/torques in a body fixed
system {B
xyz
}. The degrees of freedom in Equation
12 are assumed to be separable resulting in Equation
13
τ − D(ν)ν − D
ν|ν|
ν|ν| = M
˙
ν (13)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
190
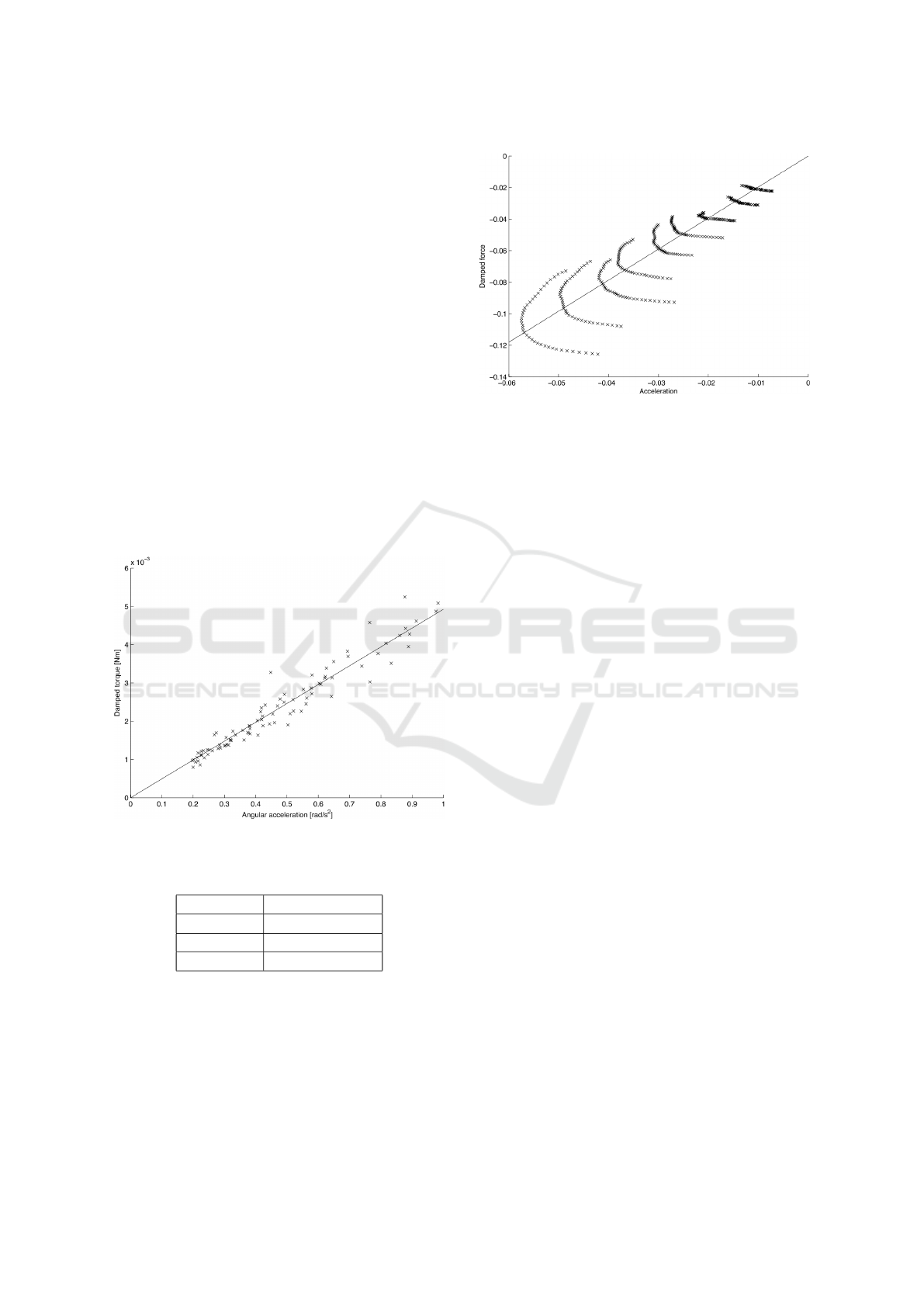
The total effective mass parameter M can be identi-
fied with a linear regression on Equation 13 and the
data tuples (τ − D(ν)ν − D
ν|ν|
ν|ν|,
˙
ν). Measurements
show that the above mentioned condition
˙
ν 6= 0 is
true between t = 1.5s and t = 3s. Figure 7 shows the
fitted regression result with the regression input data
tuples. Table 4 lists the regression results.
Identifying the effective mass for heave is more
critical than for yaw because the current depth is the
only measurable system state and Equation 13 needs
the first and second derivative of the depth. The IMU
acceleration sensors do not permit to detect small
changes in acceleration due to a low resolution and
noisy signals of the sensors. Therefore, the second
derivative needs to be determined numerically which
is badly conditioned as high frequency noise is am-
plified. Measurements showed that the acceleration
phase is between t = 2.5s and t = 3.5s. A regression
line through the data tuples can be seen in Figure 8.
The coefficient of determination R
2
is very bad with a
value of 0.80.
Figure 7: Damped yaw torque over acceleration ((Schmid,
2008)).
Table 4: Additive mass parameters.
I
zz
4.9 · 10
−3
kg · m
2
I
zz
R
2
static 0.9990
m
z
1.96kg
m
z
R
2
static 0.80
5 SYSTEM CONTROL
The system model and the identified parameters are
the basis for the layout of the controller system. This
section will begin with defining the system properties.
Then the controller structure will be explained in de-
Figure 8: Damped heave force over acceleration ((Schmid,
2008)).
tail providing both information about the simulation
and information about the implemented controller.
5.1 µAUV
2
System Properties
Tests showed that the µAUV
2
is stable concerning roll
and pitch as long as the thruster controllers only gen-
erate low frequency thruster angle changes. Thus both
roll and pitch are controlled passively. In the follow-
ing the angles α and β are related to the orientataion
of the top- and side thrusters respectively. The follow-
ing modes were defined to control the µAUV
2
:
1. Diving mode, α = 0,β = −π/2. Top thruster
turned off. Used for pure heave control
2. Buoyancy mode: diving with pump control
3. Turning mode: α = 0,β = 0 Top thruster turned
off. Used for pure yaw control
4. Drift mode: α = π/2,β = 0. Top thruster turned
off. Used for pure yaw control
5. Auto mode: α = 0,β ∈ [−π/4;π/4]. Used for
concurrent heave, yaw and surge control
5.2 Controller Structure
We first designed a simulation to test the AUV con-
trollers: Figure 9 shows the block diagram of the sim-
ulated control system.
Inputs are in absolute values for heave and yaw in
{W
xyz
}, desired thruster forces for surge and sway in
{B
xyq
} and the mode of the controller. The block la-
beled CTRL1 is the implementation of the controller.
It will be described in detail in this paragraph. Con-
troller output thrust is limited by the saturation block
to the maximum thrust of the used thrusters. A mov-
ing average lowpass filter is used to suppress fast
thruster movements related to the fast changes in the
µAUV2 - Development of a Minuscule Autonomous Underwater Vehicle
191
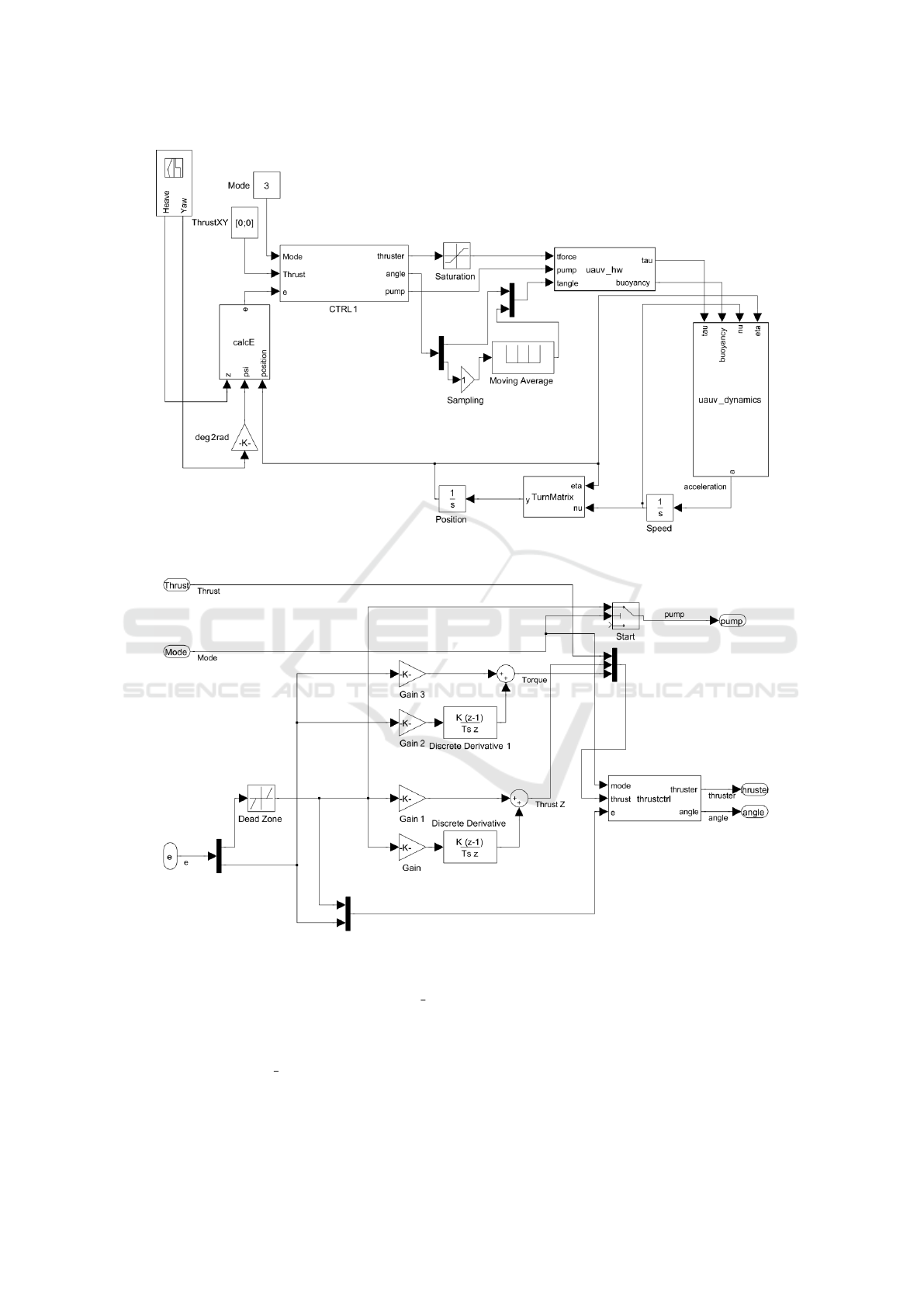
Figure 9: Block diagram of the complete control system ((Schmid, 2008)). Inputs are on the left and outputs are on the right.
Figure 10: Detailed CTRL1 block diagram (Schmid, 2008).
output of the related controller because these might
destabilize the µAUV
2
. The block labeled uauv hw
transforms thruster force to applied force in {B
xyq
}.
In addition it is responsible for controlling the buoy-
ancy state. The system equation from (Fossen, 2002)
is modeled in block uauv dynamics to determine the
system acceleration against the current system states.
To get the system speed the acceleration state is inte-
grated over time. This value is fed back to the system
dynamic block. A transformation matrix is used to
transform the system speed from {B
xyq
} to {W
xyq
}.
This speed vector is integrated to determine the posi-
tion of the system. The resulting value is fed back to
both the turning matrix and the AUV dynamics block.
To calculate the heave and yaw controller error the
position is used. Please keep in mind that the system
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
192

only implements the actively controlled DOF.
Figure 10 shows a detailed block diagram of the
implemented controller block CTRL1. The error in-
puts for heave and yaw are used as inputs for two PD
controllers. A heuristic method was used to estimate
the values for P- and D in simulation. Fine tuning of
the parameters was done in the water basin. Depend-
ing on the controller mode, the PD controller outputs
as well as the rest of the CTRL1 block inputs are used
for thrust and angle calculation. In buoyancy mode,
a bang-bang controller was used for the pump with a
dead zone on the heave error.
5.3 RESULTS
A minuscule AUV named µAUV
2
has been techni-
cally described in this paper. The system was suc-
cessfully tested in waterbasins at the DFKI GmbH
in Bremen, Germany. System parameters have been
identified experimentally. They have been the basis
for the controller design. This section presents the
main simulation and experimental results.
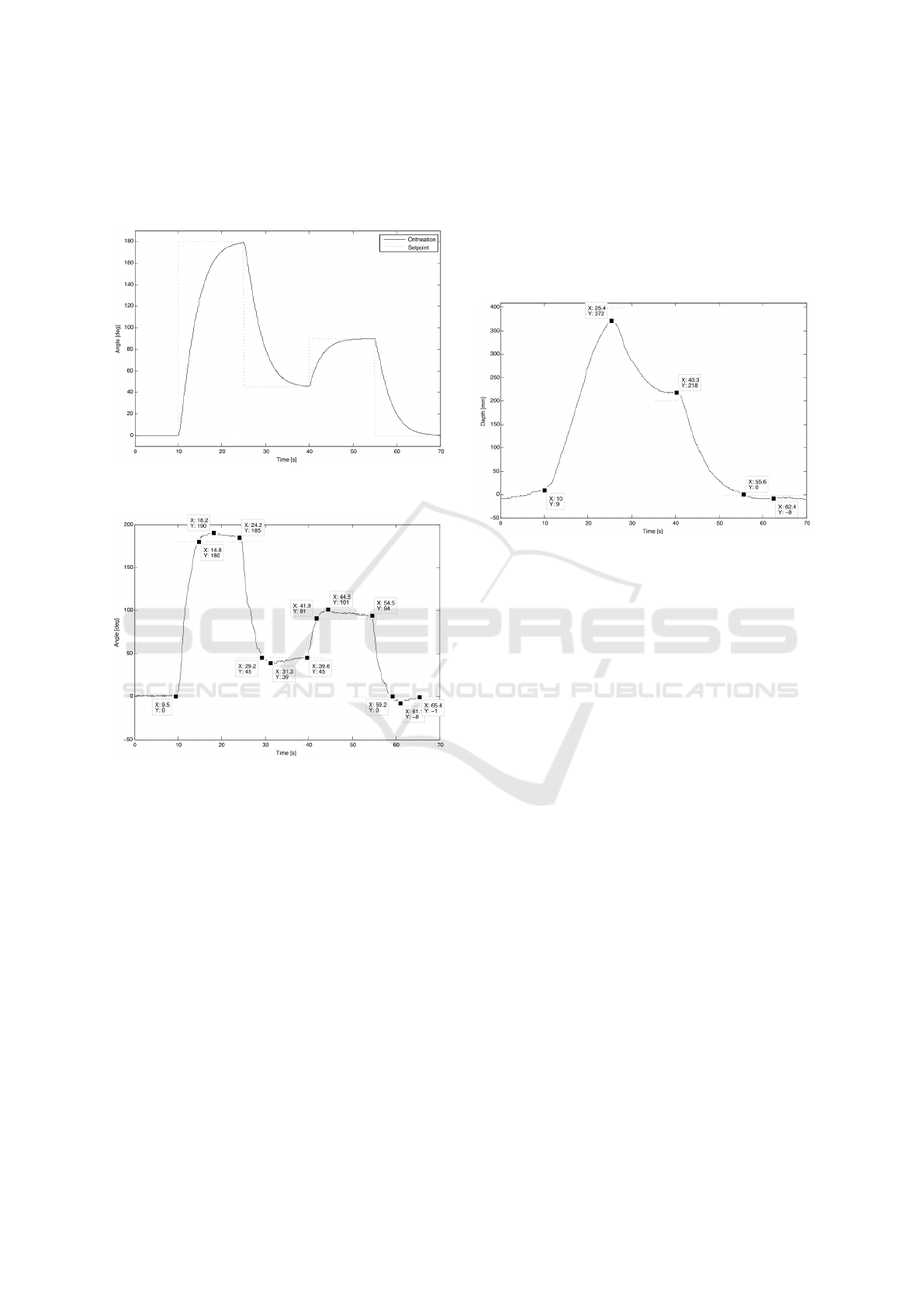
5.4 Diving Control
To analyse the performance of the diving controller, a
diving trajectory was defined. Starting at the surface
of the water, a new depth value of 0.4m is set after
t=10s. 15s later the value is changed to 0.2m. At
t=40s the depth is set to 0m.
Figure 11: Diving controller in simulation (Schmid, 2008).
The trajectory was used for simulation (Figure 12)
and real runs (Figure 12). In simulation the system
shows no overshoot for ω
z
= 0.6 as ζ
z
= 1. The sys-
tem successfully reaches the setpoints after 15s. In
reality the system reacts much faster. Setpoints are
reached after 7s. The determined error of 8mm is very
low.
Figure 12: Diving controller on a real run (Schmid, 2008).
5.5 Buoyancy Control
A buoyancy calibration run before each system start
is crucial because the depth controller is designed for
zero buoyancy.
Figure 13: Buoyancy compensation run (Schmid, 2008).
The calibration can be seen in Figure 13. It starts
by setting the depth to 0.2m while the µAUV
2
has a
positive buoyancy. A depth of 0.15m is reached af-
ter 16s. The PD controller has a steady state error of
0.05m. After 51s the pump has reduced buoyancy so
much that the dead zone is reached. 2s later the dead
zone is left again because a negative buoyancy was
reached. The system reacts by increasing the buoy-
ancy such that the system re-enters the dead zone.
Now a zero buoyancy state is reached.
The control effort was chosen low (ω
z
= 0.4) on
purpose to avoid large overshoots which could even
lead to oscillations. Once the dead zone is reached
the system stays in the dead zone of 8mm for at least
30s.
µAUV2 - Development of a Minuscule Autonomous Underwater Vehicle
193
5.6 Turning Control
Again a trajectory was defined to evaluate the turning
control mode.
Figure 14: Simulation results of the turn controller (Schmid,
2008).
Figure 15: Turning control with ω
Ψ
= 0.6 and increased
K
DΨ
= 0.016 (Schmid, 2008).
The simulation can be seen in figure 14. It starts at
an orientation of 0
◦
. After 10s, the set point becomes
180
◦
, 15s later it is set to 45
◦
for 15s to jump to 90
◦
at a time of 40s. At 55s the orientation is reset to
0
◦
. To reduce overshoots the K
Dψ
part was increased.
The maximum overshoot is 10
◦
which corresponds to
2.8% of the total angle range of 360
◦
. The controller
reaches a maximum average turning speed of 34
◦
/s
which is about 60% of the maximum possible turning
speed of the µAUV
2
(see Figure 15).
5.7 Auto Mode Control
To compare both the diving and turning controllers
with the auto mode controller the same trajectories
mentioned in the corresponding sections were created
for the auto mode controller. Surge and sway mo-
tion should be suppressed by the controller. The side
thruster angle does not permit high frequency move-
ments (except for the steps at a set point change which
is acceptable). Surge and sway stayed at zero for
the whole simulation time. The top thruster could
perfectly compensate the surge force of the two side
thrusters. In reality, the auto heave controller is a lot
slower than the diving controller, see Figure 16.
Figure 16: Performance of the auto mode controller, heave
(Schmid, 2008).
The maximum average speed of 0.0024m/s is less
than the half of the depth control performance. The
effect can be explained with the thruster saturation.
The total surge force that is produced by the side
thrusters is limited to the maximum thrust level that
the top thruster can produce to compensate the surge
motion and stay at the same place. This also reduces
the thrust that is used for diving. It can also be seen
that overshoots mentioned before disappeared and a
steady state error of a maximum of 0.018m could be
reached. In relation to the total pool depth of 0.6m,
the error is still acceptable.
The maximum average turning speed is only
slightly reduced to 28
◦
/s (compared to 34
◦
/s in turn-
ing mode), see Figure 17. The overshoot rates are also
similar to the diving mode. This result was expected
as the turning force is prioritized when the total side
thruster force is calculated. Another effect that can
be seen is the oscillation of the yaw angle. A possi-
ble reason might be water turbulence that is produced
by the different turning directions of the side thrusters
and the top thruster. It should be mentioned that the
system did not exactly stay at the original surge and
sway position in contrast to simulations. This might
also be caused by non linear turbulence effects that
were not considered. Without an exact knowledge of
the actual position in surge and sway it would not be
possible to control the system and prevent this move-
ment.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
194

Figure 17: Performance of the auto mode controller, yaw
(Schmid, 2008).
6 DISCUSSION
6.1 System Design
The mechanical part of the µAUV
2
has proven to be
very robust and the propulsion system has sufficient
power to propel the system. One drawback of the
thrusters is the fact that the thrusters have an insuf-
ficient sealing concept. This leads to the problem
that over time water accumulates in the inside of the
thrusters. An ideal solution for hovering in the water
column is the use of a buoyancy tank. All sensors ful-
fill their requirements and espescially the IMU which
outputs quaternions, even though there is a need for
a more accurate acceleration, speed and position val-
ues. Being extendable and providing a lot of compu-
tational power makes the µAUV
2
an ideal platform for
the purposes mentioned in section 1. Communication
via an optical link has proven to be very robust even
though the data rate should be increased in the future.
A very useful feature is the possibility to program the
system when it is fully assembled.
6.2 Identification of System Parameters
The presented simplified model is a good start but can
be improved in the future. It is used as a first pass at-
tempt and the results are still useful for control. The
correlated errors in Figure 8 imply an error, where re-
gression fails. The bad conditioning cannot be fully
explained by high frequency noise as hypothesised.
Regression may try to average out the errors, but the
R
2
metric and the method itself expects white noise,
uncorrelated errors. Assuming that the total mass is
constant leads to a modelling error. The thrust mod-
elling might be too simplistic for the dynamic case
because static thrust does not equal dynamic thrust.
This also impacts the thrust vs. damping force re-
sults. Another cause could be laminar flow in all di-
rections except for the heave direction where turbu-
lent flow might dominate due to the non-streamline
battery pack.
6.3 Controller
The simulated controller has proven to work in the
real system. A major problem is the lag of position in-
formation in surge and sway and imprecise position,
speed and acceleration data.
One of the reasons for the gap between simulation
and reality (see Section 5.4) is the simplified system
model used throughout this paper. Other possible rea-
sons could be an inaccuracy in the experiments (see
Section 4) or the fully charged battery pack which
might lead to a motor speed slightly over the theo-
retical speed.
7 CONCLUSION AND FUTURE
WORK
This paper has presented a minuscule AUV named
µAUV
2
. As soon as basic autonomous behavior is
implemented, the µAUV
2
could be tested in outside
watercourses. Its behavior in water currents would
shed light on the feasibility of the application of
µAUV
2
in open water. It would also be very inter-
esting to implement a controller for the µAUV
2
to do
a roll or a loop around the y-axis. The thrusters would
have to produce a sinusoidal force with the resonance
frequency of the system on the corresponding axis. In
any case, there are a lot of conceivable functions that
could be implemented in the future.
An interface for easily equipping the µAUV
2
with
new sensors could accelerate many tasks. Hull im-
provements are mainly focused on the thrusters and
the battery pack. The thrusters are the weak point in
the design concerning maximum dive depth. Due to
the thruster design, the dive depth is currently lim-
ited to approximately 2m. This together with the fact
that water accumulates in the thrusters will make a
redesign of the thrusters necessary. A possible im-
provement could be a magnetically coupled thruster.
A further step towards a streamlined hull will require
a redesign of the battery pack,
A major problem of the controller, the lag of posi-
tion information in surge and sway, could be solved
with the camera on the bottom. An algorithm for op-
tical flow could be implemented to calculate the ac-
tual moving speed. Furthermore, the absolute posi-
µAUV2 - Development of a Minuscule Autonomous Underwater Vehicle
195

tion could be calculated by integrating the speed. Ad-
ditionally, optical markers on the ground of the pool
further improve the position estimate. The second
camera might be used for obstacle detection. With
this additional sensor information it would be possi-
ble to create a map of the area the AUV is moving
in.
As said before, the presented simplified model is
a good start. But e.g. the error in Figure 8, implies
that the system modell can be improved.
ACKNOWLEDGEMENTS
The project DAEDALUS is funded by the German
Space Agency (DLR, Grant number: 50NA1312)
with federal funds of the Federal Ministry of Eco-
nomics and Technology (BMWi) in accordance with
the Bundestag resolution of the German Parliament.
REFERENCES
Albiez, J., Gaudig, C., Hilljegerdes, J., and Kirchner, F.
(2015). FlatFish A compact subsea-resident inspec-
tion AUV. Unknown, 1(November).
Barngrover, C., Kastner, R., Denewiler, T., and Mills, G.
(2011). The stingray auv: A small and cost-effective
solution for ecological monitoring. In OCEANS 2011,
pages 1–8.
Bryant, S. (2002). Ice-embedded transceivers for europa
cryobot communications. IEEE Aerospace Confer-
ence Proceedings, 1(1):349–356.
Christensen, L., Kampmann, P., Hildebrandt, M., Albiez, J.,
and Kirchner, F. (2009). Hardware rov simulation fa-
cility for the evaluation of novel underwater manipula-
tion techniques. In OCEANS 2009 - EUROPE, pages
1–8.
Dowdeswell, J., Evans, J., Mugford, R., Griffiths, G.,
McPhail, S., Millard, N., Stevenson, P., Brandon, M.,
Banks, C., Heywood, K., Price, M., Dodd, P., Jenk-
ins, A., Nicholls, K., Hayes, D., Abrahamsen, E.,
Tyler, P., Bett, B., Jones, D., Wadhams, P., Wilkin-
son, J., Stansfield, K., and Ackley, S. (2008). In-
struments and methodsautonomous underwater vehi-
cles (auvs) and investigations of the ice/ocean inter-
face in antarctic and arctic waters. Journal of Glaciol-
ogy, 54(187):661–672.
Fechner, S., Kerdels, J., Albiez, J., and Kirchner, F. (2007).
Design of a uauv. In Autonomous Minirobots for Re-
search and Edutainment (AMiRE-2007). Proceedings
of the 4th International AMiRE Symposium (AMiRE-
2007), Heinz Nixdorf Institut Universit Paderborn,
pages 99-106.
Fossen, T. I. (2002). Marine control systems: guidance,
navigation and control of ships, rigs and underwater
vehicles. Marine Cybernetics AS.
Indiveri, G. (1998). Modelling and identification of under-
water robotic systems. Computer Science.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems. Transactions of the ASME–
Journal of Basic Engineering, 82(Series D):35–45.
Leonessa, A. (2008). Underwater robots: Motion and
force control of vehicle-manipulator systems (g. an-
tonelli; 2006) [book review]. IEEE Control Systems,
28(5):138–139.
Meyer, B., Ehlers, K., Isokeit, C., and Maehle, E. (2014).
The development of the modular hard- and software
architecture of the autonomous underwater vehicle
monsun. In ISR/Robotik 2014; 41st International
Symposium on Robotics; Proceedings of, pages 1–6.
Mintchev, S., Donati, E., Marrazza, S., and Stefanini, C.
(2014). Mechatronic design of a miniature underwater
robot for swarm operations. In Robotics and Automa-
tion (ICRA), 2014 IEEE International Conference on,
pages 2938–2943.
Nicholson, J. and Healey, A. (2008). The present state
of autonomous underwater vehicle (auv) applications
and technologies. Marine Technology Society Journal,
42(1):44–51.
Ridao, P., Batlle, J., and Carreras, M. (2001). Model identi-
fication of a low-speed uuv. IFAC Conference Control
Applications in Marine Systems, Glasgow, Scotland.
Schmid, K. (2008). Embedded system and controller
design for a micro AUV Diploma thesis. The-
sis, University of Bremen, TU Hamburg Harburg.
https://www.researchgate.net/publication/299283880
Embedded system and controller design for a
micro AUV.
Yoerger, D. and Slotine, J.-J. (1991). Adaptive sliding
control of an experimental underwater vehicle. In
Robotics and Automation, 1991. Proceedings., 1991
IEEE International Conference on, pages 2746–2751
vol.3.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
196
