
Recognition of Affective State for Austist from Stereotyped Gestures
Marcos Yuzuru O. Camada
1
, Diego St´efano
2
, J´es J. F. Cerqueira
2
, Antonio Marcus N. Lima
3
,
Andr´e Gustavo S. Conceic¸˜ao
2
and Augusto C. P. L. da Costa
2
1
IFbaiano, Rua Baro de Camac¸ari, 118, Centro, 48110-000, Catu, Bahia, Brazil
2
Electrical Engineering Department, Federal University of Bahia, Rua Arstides Novis, 02, Federac¸ ˜ao,
40210-630, Salvador, Bahia, Brazil
3
Electrical Engineering Department, Federal University of Campina Grande, Aprigio Veloso, 882, Bodocongo,
58109-100, Campina Grande, Para´ıba, Brazil
Keywords:
HRI, HMM, Fuzzy Inference System, Autism, Stereotyped Gesture, Assistive Robotic.
Abstract:
Autists may exhibit difficulty in interaction (social and communication) with others and also stereotyped
gestures. Thus, autists have difficulty to recognize and to express emotions. Human-Robot Interaction (HRI)
researches have contributed with robotic devices able to be mediator among autist, therapists and parents. The
stereotyped behaviors of these individuals are due to their defense mechanism from of their hypersensitivity.
The affective state of a person can be quantify from poses and gestures. This paper proposes a system is able
to infer the defense level of autists from their stereotyped gestures. This system is part of the socially assistive
robot project called HiBot. The proposed system consist of two cognitive subsystems: Hidden Markov Models
(HMM), in order to determine the stereotyped gesture, and Fuzzy Inference System (FIS), to infer activation
level of these gestures. The results of these simulations show this approach is able to infer the defense level
for an task or the presence of the robot.
1 INTRODUCTION
Autism Spectrum Disorder (ASD) belongs to the
group of pervasive developmental disorders which is
characterized by deficits in social interaction, com-
munication, and stereotyped (or unusual) behaviors
(Levy et al., 2009). The autist has difficulty to express
and to recognize social cues, as emotion through fa-
cial and body expression and gaze eyes. The major
treatments for ASD rely on psychiatric medications,
therapies and behavioral analysis (or both).
Both software (Parsons et al., 2004) and robotic
devices (Goodrich et al., 2012) have been developed
to aid the treatment of autism. The design of such
robotic devices is naturally demand for multidisci-
plinary teams, because they may involve different
fields of health, engineering and computing.
The use of robots as social partners for autis-
tic children has already been proposed (Dautenhahn,
2003; Goodrich et al., 2012) within the field of Hu-
man Robot Interface (HRI). Theses devices can be-
have as mediators among autists, therapist, parents.
The affective state recognition of a person is essential
for a social partner robot.
A human can express himself through verbal and
non-verbal, such as face, body and voice (Zeng et al.,
2009). Researches have focused on face expression,
but studies have also shown body cues are as powerful
as facial cues in conveying and recognizing of emo-
tions. The quantification of the human affective state
from the poses and gestures (Camurri et al., 2003) has
been proposed as a way to recognize emotions. In ad-
dition, (Kuhn, 1999) assumes stereotyped gestures
are defense mechanisms of autists due to their hyper-
sensitivity.
For these reasons, we propose a system to affec-
tive state recognition from the stereotyped gestures
of autists in this paper. The gestures are recognized
using Hidden Markov Models (HMM). A Fuzzy In-
ference System (FIS) is used to infer the affective
state (defense level) of the autist from the gesture rec-
ognized and kinetic of joint groups.
This paper is organized as follows. In Section 2,
we define affective state, body expression, and the re-
lationship between autism. Classification and infer-
ence tools are described in Section 3. Details of the
proposed system architecture is presented in the Sec-
tion 4. Experiments of proposed model and their re-
sults are discussed in Section 5. Finally, a general
discussions about the contributions of this paper and
Camada, M., Stéfano, D., Cerqueira, J., Lima, A., Conceição, A. and Costa, A.
Recognition of Affective State for Austist from Stereotyped Gestures.
DOI: 10.5220/0005983201970204
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 197-204
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
197

future works are present in Section 6.
2 BACKGROUND
2.1 Affective State
Although the human emotional state is present only
in mind, and some unconscious signals from body al-
low us to infer the mood. Particular models are es-
sential to define the human affective state. There are
two major approaches (Russell, 2003): (i) the dis-
crete approach considers the human experiences can
be expressed by a small set of emotions (e.g. hap-
piness, sadness, fear, anger, surprise and tenderness)
and these emotions are basic and experimented inde-
pendently from each other; and (ii) affective dimen-
sions approach, also called Core Affective by (Rus-
sell, 2003), assumes that emotions are appropriately
represented in an emotional plan of Valence/Arousal.
2.2 Body Expressions
Studies on body language have advanced, though they
are still few if compared with researches on facial ex-
pressions or voice. Two properties about emotional
quality from body expression are considered (Wall-
bott, 1998): (i) static configuration (posture), and (ii)
dynamic or movement configuration (gesture). How-
ever, most of body cues may indicate only activation
level of the person. Thus, these cues just work to
differentiate emotions. The energy (power) of move-
ments is of these cues. The highest values related to
hot anger, elated joy and terror emotions, the lowest
values corresponded to sadness and boredom.
A way to get relevant emotional features from the
full-body movements is through the Quantity of Mo-
tion (QoM) (Camurri et al., 2003). QoM can revel ac-
tivation level, for example, during dance performance
showed that movements of the limbs associated with
anger and joy are significantly high values of QoM.
Now, let v
l
(f) denote the module of velocity of
each limb l at time frame f as
v
l
( f) =
p
˙x
l
( f) + ˙y
l
( f) + ˙z
l
( f), (1)
where ˙x
l
( f), ˙y
l
( f) and ˙z
l
( f) are cartesian velocities.
The body kinematic energy, E
tot
( f), can be an ap-
proximated by sum of the kinematic energy of each
limb as
E
tot
( f) =
1
2
n
∑
l=1
m
l
v
l
( f)
2
, (2)
where m
l
is the approximated of the limb mass based
on biometrics anthropometric tables (Dempster and
Gaughran, 1967).
2.3 Autism Spectrum Disorders
Autism Spectrum Disorder (ASD) is a neuropsychi-
atric disorder characterized by severe damage in the
socialization and communication processes. Gener-
ally, autist may also have a unusual pattern or stereo-
typed behaviors (Levy et al., 2009). Novel researches
have been indicated that several factors are associated
with the autism. Some of these known factors are ge-
netic, neurological anomalies and psychosocial risks
(Levy et al., 2009).
(Kuhn, 1999) assumes that the stereotypic behav-
iors in autists are defense mechanism due to their hy-
persensitivity. Some stereotyped gestures that can
be noted are: (i) Body Rocking (repetitive move-
ment to forward and backward of the upper torso); (ii)
Top Spinning (walk in a circle); (iii) Hand Flapping
(swing motion of the hands up and down); (iv) Head
Banging (hitting head on the floor or wall). The Head
Banging was not considered in this papers specially
because the trajectory of their movement is similar to
Body Rocking.
3 CLASSIFICATION AND
INFERENCE TOOLS
In this paper, we propose the use of two cognitive
tools for recognizing the stereotyped gesture and in-
ference of autist defense level: HMM (Subsection
3.1) and FIS (Subsection 3.2), respectively. Figure
1 (B) shows this proposed model.
3.1 Hidden Markov Models
Hidden Markov Models (HMM) are doubly stochas-
tic models, because they have an underlying Markov
chain and to transit their stochastic states symbols
need to be emitted. This emitting process is itself
a stochastic process, once it has a probability dis-
tribution over the states and to following the timing
of the transitions. Since the symbol output probabil-
ity distribution of a continuous HMM is given by a
mixture of Gaussians, a HMM can be expressed as
λ = (A, c, µ, U), where: A is the matrix of transition
probabilities; c is a set of coefficients (weights for
each Gaussian in the mixture of Gaussians); µ rep-
resents the averages of each Gaussian in the mixture
and U also represents the covariance matrices of the
Gaussians.
The HMM can be applied for supervised learn-
ing pattern recognition tasks. The training process of
the HMM consists of the presentation of sequences of
outputs (training sequences) from a particular system.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
198

A training algorithm adjusts the HMM’s parameters
in such a way that when a new observation sequence
from the system being modelled is given as input to
the HMM, the probability that the model was gener-
ated will be presented in output. This discussion leads
to the three basic problems of the HMM (Rabiner,
1989; Fink, 2008):
Problem 1 - To find the probability that the HMM λ
generated a given sequence of observation sym-
bols O = O
1
, O
2
, ..., O
T
, where T is the length of
the sequence (P(O|λ));
Problem 2 - To find the underlying optimal state se-
quence Q = q
1
, q
2
, ..., q
T
of λ that was needed to
generate O
1
, O
2
, ..., O
T
(P(Q|O, λ));
Problem 3 - To adapt the model parameters in order
to maximize P(O|λ).
3.2 Fuzzy Inference System
Fuzzy Inference Systems (FIS) are widely used for
problems what the variables of the real worlds are
complex or unclear. These systems are knowledge-
based (or rule-based) and such knowledge can be ob-
tained from human experts. It can be defined by fuzzy
rules of IF − THEN type. Each IF− THEN rule is
a statement in which some words are represented by
continuous membership functions (Wang, 1997). The
value of the membership function informs the degree
of membership into a fuzzy set.
(Wang, 1997) indicates three types of fuzzy sys-
tems. They differ basically about how they deal with
inputs and outputs variables of the system:
Pure Fuzzy System - It is a generic model with in-
puts and outputs based on words of natural lan-
guage;
TSK (Takagi-Sugeno-Kang) Fuzzy System - It has
input variables combine words of natural lan-
guage and Real values, but output variables are
only real values;
Mamdani - Both Fuzzifier and Defuzzifier asso-
ciates translate real input to output variables into
natural language.
Fuzzyfier and Defuzzifier are based on member-
ship functions. The membership functions translate
variable values from one universe to another. There
are different membership functions, such as Single-
ton, Gaussian, S-Shape and Z-Shape.
A Singleton membership, µ
I
, represents a set I
which is associated to a crisp number α
I
, such that,
µ
I
(x) =
(
1, if x = α
I
0, otherwise.
(3)
A Gaussian membership, µ
G
, represents a set G,
where G is a gaussian curve, and it is defined by aver-
age
X and standard deviation σ,
µ
G
(x) = e
−
(x−
X)
2
2σ
2
. (4)
A S-shape membership, µ
S
, represents a set S,
where S is a “S” curve, and it is defined two parame-
ters α
S
and β
S
such that,
µ
S
(x) =
0, x ≤ α
S
2
x− α
S
β
S
− α
S
2
, α
S
≤ x ≤
α
S
+ β
S
2
1− 2
x− β
S
β
S
− α
S
2
,
α
S
+ β
S
2
≤ x ≤ β
S
1, x ≥ β
S
.
(5)
A Z-shape membership, µ
Z
, represents a set Z,
where Z is a “Z” curve , and it is defined two param-
eters α
Z
and β
Z
such that,
µ
Z
(x) =
1, x ≤ α
Z
1− 2
x− α
β
Z
− α
Z
2
, α
Z
≤ x ≤
α
Z
+ β
Z
2
2
x− β
β
Z
− α
Z
2
,
α
Z
+ β
Z
2
≤ x ≤ β
Z
0, x ≥ β
Z
.
(6)
4 SYSTEM OVERVIEW
This paper is part of the robotics project called HiBot
(see Figure 1 (A)). The HiBot has been developing in
the laboratory of robotics at the Electrical Engineer-
ing Department, Federal University of Bahia. It aims
to be a platform for experiments on Human Robot In-
teraction (HRI).
The HiBot has a sets of affective actuators and
sensors. These sets are arranged by modules. The
affective actuators aim to promote interaction with
through social protocols (face and voice expressions).
That way, we define two modules: (i) Voice Synthe-
sis Module (VSM) and (ii) Facial Expression Module
(FEM). The affective sensors aim to get affective cues
conveyed by different modais, such as face, body,
voice and electroencephalography (EEG). Thus, Hi-
bot has four affective sensory modules: (i) Facial
Expression Recognition Module (FERM); (ii) Body
Expression Recognition Module (BERM); (iii) Voice
Expression Recognition Module (VERM); and (iv)
EEG Recognition Module (EEGRM). We focus on
the BERM in this paper.
The BERM gets stereotyped gestures from
autists to recognize his affective stare (defense level).
Recognition of Affective State for Austist from Stereotyped Gestures
199
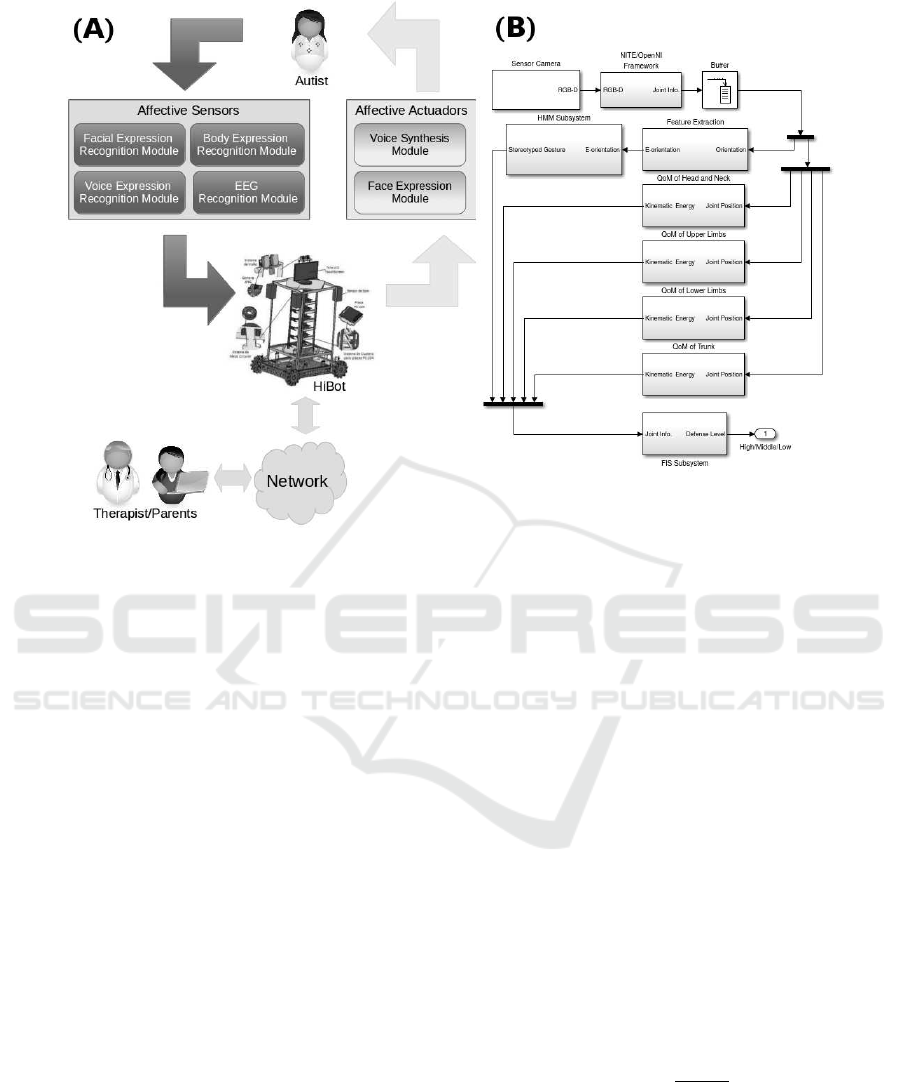
Figure 1: (A) General model of HiBot project and (B) Body Expression Recognition Module architecture.
The architecture of this module is shown in of Figure
1(B). The camera sensor is a Kinect
R
. This device
has a set of sensors (RGB and IR cameras, accelerom-
eter, and microphone array) and also a motorized tilt
(Microsoft, 2013). We used the RGB and IR cameras
in this paper. The IR camera provides depth infor-
mation of environment and objects. The IR Emitter
projects on the environment (and objects) several in-
frared lasers. The IR Sensor captures the IR lasers
projected. Due to this, Kinect
R
is able to infer the
distance (depth) between objects and IR sensor.
OpenNI/NITE frameworks are used for develop-
ment of 3D sensing middleware and applications.
Currently, they are maintained by Structure Sensor
(Structure, 2013). These software extract information
about position and orientation of the joint of an at-
tending person. The joint considered in this paper are:
head, neck, shoulders, elbows, hands (wrists), trunk,
hips, knees and foots (ankles).
The joint data (orientation and position) from 40
frames are stored in a Buffer. Joint orientation data are
processed by feature extraction algorithm (Subsection
4.1). Likewise, Quantity of Motion (Equation 2) is
applied on the joint position data.
The feature extraction algorithm results are used
by HMM Subystem (Subsection 4.2). Thus, the in-
puts of FIS Subsystem are the stereotyped gesture rec-
ognized by HMM Subsystem and the QoMs of each
joint group. FIS Subsystem must infer the defense
(stress) level of target autist.
4.1 Feature Extraction
The joint orientation data are computed by a algo-
rithm of feature extractions. This procedure was ap-
plied in order to both reduce the dimensionality (from
4 to 3) of the acquired input data and obtain a mean-
ingful representation of this data. Results from this
algorithm are the input to HMM subsystem.The fol-
lowing subsections describe the step-by-step this al-
gorithm.
4.1.1 Merging
The first step of feature extractions algorithm consist
in merging the four quaternion streams into only one
stream. This was achieved by averaging the compo-
nents. So, let s
i
, for 1 ≤ i ≤ 4, denote the i-th quater-
nion stream. The resulting signal is given by
¯s =
∑
4
i=1
s
i
4
(7)
4.1.2 Frequency Spectrum
After the merging step, the frequency spectrum of the
signal ˜s, evaluated from the Fast Fourier Transform
(FFT) algorithm, is appended to it, to generate the sig-
nal s = [ ˜s FFT( ˜s)].
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
200

4.1.3 Short-Time Analysis
The Short-Time Analysis is performed with the signal
s divided in segments having M = M
1
+ M
2
samples
centered at the ˆn-th sample, given by s
ˆn
(m) = s( ˆn +
m), with −M
1
≤ m ≤ M
2
. This segment is further
multiplied (element-wise) with a Hamming window
function given by
w(n) =
(
0.54− 0.46cos(
2πn
M−1
), if 0 ≤ n ≤ M − 1
0, otherwise
,
(8)
being the segments obtained with an overlapping
of 30%.
The energy of each segment s
ˆn
is then calculated
as
E
ˆn
=
M
2
∑
j=−M
1
s
ˆn
( j), (9)
that is the first component of the observation vectors.
Second and third componentsare respectively the first
and second derivatives of this energy with respect to
ˆn.
4.2 HMM Subsystem Setup
In this work, the HMMs is applied to recognize ges-
tures from sequences of joint orientation acquired
with sensor camera Kinect
R
and stored in Buffer of
size 40. The features are extracted (see Subsection
4.1) from these sequences to generate arrays of fea-
ture vectors. These arrays, in turn, will represent the
sequence of observation symbols O. Each gesture is
associated with a HMM.
The training procedure is given by the solution
to the third problem. Let λ
i
= (A
i
, c
i
, µ
i
, U
i
) denote
the HMM associated to the i-th gesture, with a given
initial condition, the training procedure should adapt
these parameters using enough (typically several) ob-
servation symbols sequences O
i
train
from the i-th ges-
ture such that the likelihood that the resulting model
is given by
¯
λ
i
= (
¯
A
i
, ¯c
i
, ¯µ
i
,
¯
U
i
). (10)
The mechanism to evaluate the aforementioned
likelihood is given by the solution to the first problem.
The HMM training uses 200 samples by stereotyped
gesture (100 for each activation group).
Each gesture has an HMM where Body Rocking
and Hand Flapping have 3 states, and Top Spinning
has 4 states. The number of Gaussian mixtures was
the same in all three case is 3.
4.3 FIS Subsystem Setup
FIS Subsystem infers the state of defense from the
stereotyped gesture recognized by HMM Subsys-
tem. Modelof FIS subsystem has 5 inputs: (i) Stereo-
typed Gesture, (ii) QoM Head/Neck, (iii) QoM Upper
Limbs, (iv) QoM Lower Limbs and (v) QoM Trunk.
The output of this model is Defense Level.
The first input of the fuzzifies is the stereotyped
gesture recognized by HMM subsystem. Thus, this
fuzzifier has 3 linguistic variables: (i) Body Rocking
(BR), (ii) Hand Flapping (HF) and (iii) Top Spin-
ning (TS). These linguistic variables are defined by
Singleton membership function (Equation 3). The pa-
rameters α
I
for these linguistic variables are respec-
tively 1, 2 and 3. Figure 2 (A) shows these linguistic
variables and its values.
The processing of QoM (see Equation (2)) is exe-
cuted in the following joint groups: Head/Neck, Up-
per Limbs,Lower Limbs and Trunk. Thus, the inputs
QoM Head/Neck, QoM Upper Limbs, QoM Lower
Limbs and QoM Trunk maps QoM of joint groups.
Figure 2(B)-(E) show 4 inputs of FIS Subsystem
with three linguistic variables: Low, Middle and High.
Linguistic variable Low is defined by Z-Shape mem-
bership function (see Equation (6)). The values of pa-
rameters α
Z
and β
Z
are as follows,
[α
Z
, β
Z
] = [
¯
X
Low
, Max
Low
], (11)
where
¯
X
Low
, Max
Low
are average and maximum val-
ues of low subgroup related to the training samples.
Linguistic variable Middle is represented by
Gaussian membership function. The values of its pa-
rameters σ and
¯
X are defined as,
[σ,
¯
X] = [σ
LH
,
¯
X
LH
], (12)
where σ
LH
,
¯
X
LH
are standard deviation and average
related to high and low subgroups of the training sam-
ples.
Finally, linguistic variable High is defined by S-
Shape membership function (Equation (5)). The val-
ues of the parameters α
S
and β
S
are as follows,
[α
S
, β
S
] = [Min
High
,
¯
X
High
], (13)
where Min
High
and
¯
X
High
are respectively minimum
and average values of high subgroup related to the
training samples.
FIS Subsystem is based on Mamdani. That way,
we define 15 weighted rules. Table 1 shows these
rules and their respective weights.
Body Rocking and Hand Flapping are defined
respectively by head/neck and upper limbs. Top
Spinning is defined by lower limbs and trunk. Be-
sides that, a weight is assigned to each rule. The last
Recognition of Affective State for Austist from Stereotyped Gestures
201
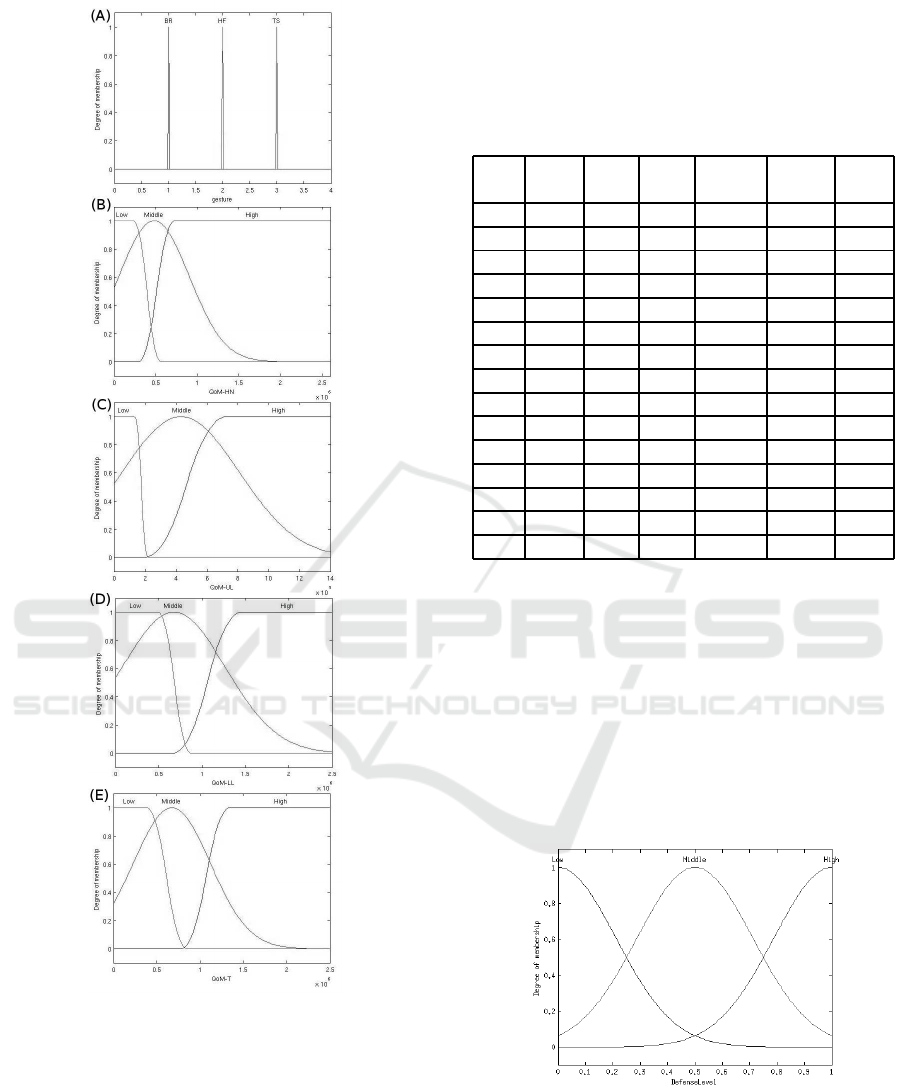
Figure 2: Input of FIS Subsystem: (A) Gesture, (B) QoM
of Head and Neck, (C) QoM of Upper Limbs, (D) QoM of
Lower Limbs, and (E) QoM of Trunk.
column (W.) in Table 1 define the values of weight of
rules. The weight is a real value that can be 0.25, 0.50
or 1.00.
The value 1.00 is assigned to the weights of the
rules related to Body Rocking and Hand Flapping
gestures. The weight values for rules of the gesture
Top Spinning depends on the difference of activation
Table 1: Defining the rules and their weights (W.) with
Defense Level (D. Level) for stereotyped gestures (Ge.):
Body Rocking (BR), Hand Flapping (HF) and Top Spinning
(TS). Linguistic variables HIGH (HI.), MIDDLE (MI.) and
LOW (LO.) are defined according to each QoM (Q.) of joint
groups Head/Neck (H/N), Upper Limbs (UL), Lower Limbs
(LL) and Trunk.
Ge. Q. Q. Q. Q. D. W.
H/N UL LL Trunk Level
BR HI. any any any HI. 1.00
BR MI. any any any MI. 1.00
BR LO. any any any LO. 1.00
HF any HI. any any HI. 1.00
HF any MI. any any MI. 1.00
HF any LO. any any LO. 1.00
TS any any HI. HI. HI. 1.00
TS any any HI. MI. HI. 0.50
TS any any HI. LO. MI. 0.25
TS any any MI. HI. HI. 0.50
TS any any MI. MI. MI. 1.00
TS any any MI. LO. LO. 0.50
TS any any LO. HI. MI. 0.25
TS any any LO. MI. LO. 0.50
TS any any LO. LO. LO. 0.50
level between joint groups upper limb and trunk. It
is assigned to the maximum, medium ad minimum
differentiation, 0.25, 0.50 and 1.00, respectively.
The output of the FIS Subsystem has three Gaus-
sian membership function: Low, Middle and High
(see Figure 3). The defuzzifier uses Centroid method,
aggregation Maximum and implication Minimum.
These membership functions are equally distributed
on the universe of values. The output of defuzzifier
represents the defense level of a person with autism.
Figure 3: Defuzzifier (defense level) with 3 Gaussian mem-
bership function: Low, Middle or High.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
202
5 EXPERIMENTS
Simulations of the BERM allow us to analyzing its
behavior and also expected results. MATLAB
R
and
HMM/FIS toolboxes (Murphy, 1998) were used to
simulate the BERM. MATLAB
R
is a high-level lan-
guage and interactive environment well known by the
community of scientists and engineers.
5.1 Methodology
For each gesture, we defined two simulation scenar-
ios: high and low activation. In this way, an actor
performed repeatedly each scenarios of the stereo-
typed gestures. These gestures were recorded us-
ing Kinect
R
device and OpenNI/NiTE frameworks.
Thus, the RGB-D image frames were stored together
with position and orientation metadada of each joint.
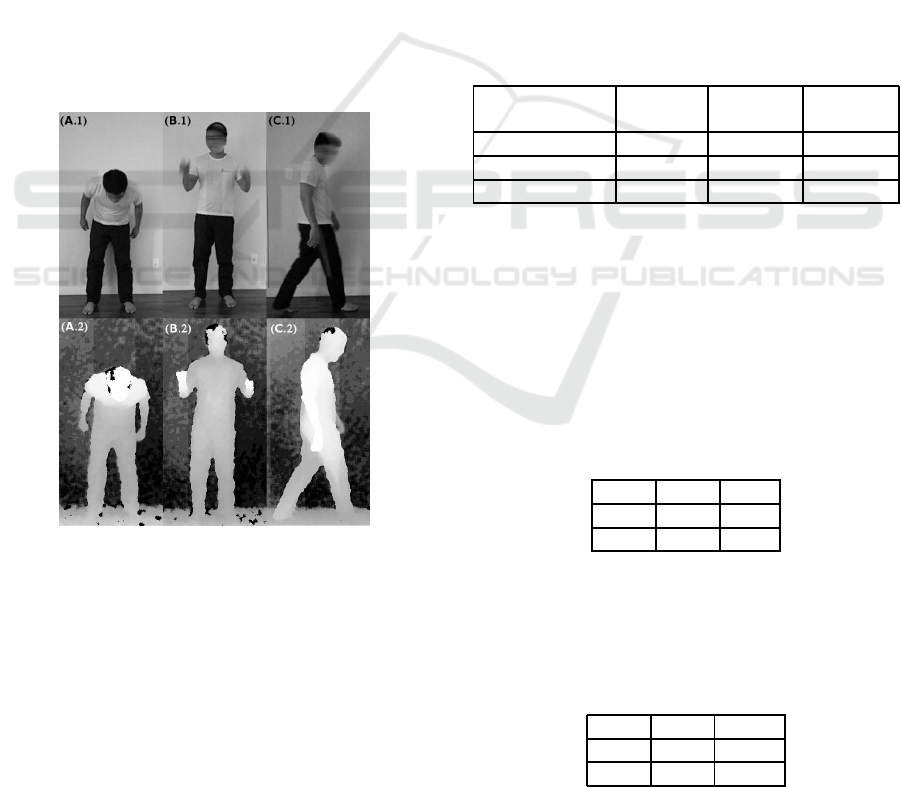
Figure 4 shows RGB-D images of stereotyped
gestures: Body Rocking (A.1 and A2), Hand Flap-
ping (B.1 and B.2) and Top Spinning (C.1 and C.2).
Figure 4: RGB-D images of stereotyped gestures performed
by an actor.
After that, the samples were manually extract.
Each sample has data about joints (position and ori-
entation) of 40 image frames. The scenarios of each
stereotyped gesture have 150 samples of which: 100
samples were used to training and other 50 were used
to simulation.
The parameter values of QoM membership func-
tion high (Equation (13)), middle (Equation (12)) and
low (Equation (11)) were defined from the training
samples of HMM.
Results of these simulations present the defense
level for each gesture. In this way, we analyze
whether these results coincided with expected defense
level. These results are discussed in the followingsec-
tion.
5.2 Results and Discussion
In order to represent the statistics of the simulations
results, we use the confusion matrix. Simulation
results show the HMM Subsystem recognized all
stereotyped gestures Hand Flapping and Top Spin-
ning. Although the results for Body Rocking lower
than the other gestures, their performance was 86%
hit (see Table 2). The efficiency of the HMM is due
to two reasons: (i) stereotyped gestures are well-
defined and distinct from themselves. (ii) the HMM
Subsystem should not differentiate among subgroups
of gestures (high or low activation).
Table 2: Confusion matrix of recognition stereotyped ges-
ture by HMM Subsystem.
Body Hand Top
Rocking Flapping Spinning
Body Rocking 86% 0% 14%
Hand Flapping 0% 100% 0%
Top Spinning 0% 0% 100%
Tables 3, 4, 5 show the performance of FIS Sub-
system for each stereotyped gesture. We consider
defense level is high for values above or equal to 0.5.
Therefore, the defense level is low for values below
0.5.
Table 3 shows the defense level for gesture Body
Rocking presents better adjustments values for high
activation (98%) than for low activation (82%).
Table 3: Confusion matrix of activation level for Body
Rocking.
High Low
High 98% 2%
Low 18% 82%
However, Table 4 shows gesture Hand Flapping
presents better adjustments values of defense level for
low activation (100%) than for high activation (96%).
Table 4: Confusion matrix of activation level for Hand Flap-
ping.
High Low
High 96% 4%
Low 0% 100%
The defense level for the gesture Top Spinning
Recognition of Affective State for Austist from Stereotyped Gestures
203

showed positive performance for the two activation
levels (see Table 5).
Table 5: Confusion matrix of activation level for Top Spin-
ning.
High Low
High 100% 0%
Low 0% 100%
The results of simulations in Tables 2, 3, 4 and 5
show relevant results for the proposed model. How-
ever, the proposed model may present lower perfor-
mance with a autist in real world than with an actor.
The idiosyncrasy of each person may influence the
gesture recognition process and inference of defense
level. In addition, the ASD (Autism Spectrum Disor-
der) presents different behavioral aspects which may
vary according to the severity. Thus, it necessary to
specify the target autistic spectrum.
Although the confusion matrix does not show the
variation in trend of defense level, this is a major re-
quirement in the process of interaction between the
robot and autistic. Thus, it is possible to analyze the
interactive process is effective or not.
6 CONCLUSION
This paper proposed a system model to infer the de-
fense level of autist from the stereotyped gestures
(body rocking, hand flapping and top spinning).
These gestures were performed by an actor. The cog-
nitive model consists of HMM and FIS Subsystems.
The simulation results demonstrate this approach
is adequate and promising to recognize the defense
level from stereotyped gestures. HMM Subsystem
classifies these gestures correctly. FIS Subsystem is
able to correctly infer for most simulations, showing
better results for Top Spinning.
The BERM will be used in the HiBot to recognize
the affective state of the autist, more precisely during
interaction with others sensors.
The next steps after this paper are:
1. Creating and using a database with genuine autis-
tic gestures (not actors);
2. Specifying the target autistic spectrum;
3. Integrating this module Body Expression Recog-
nition Module (BERM) with the other modules of
HiBot.
REFERENCES
Camurri, A., Lagerlof, I., and Volpe, G. (2003). Recog-
nizing emotion from dance movement: Comparison
of spectator recognition and automated techniques.
International Journal of Human Computer Studies,
59(1–2):213–225.
Dautenhahn, K. (2003). Roles and functions of robots in
human society- implications from research in autism
therapy. Robotica, 21(4):443–452.
Dempster, W. and Gaughran, G. (1967). Properties of body
segments based on size and weight. American Journal
of Anatomy, 120(7414):33–54.
Fink, G. (2008). Markov Model for Pattern Recognition:
From Theory to Applications. Berlin: Springer.
Goodrich, M., Colton, M., Brintonand, B., Fujiki, M.,
Atherton, J., and Robinson, L. (2012). Incorporating
a robot into an autism therapy team. IEEE Intelligent
Systems, 27(2):52–59.
Kuhn, J. (1999). Stereotypic behavior as a defense mecha-
nism in autism. Harvard Brain Special, 6(1):11–15.
Levy, S., Mandell, D., and Schultz, R. (2009). Autism. The
Lancet, 374(9701):1627–1638.
Microsoft (2013). Kinect for windows sensor components
and specifications. https://msdn.microsoft.com/en-
us/library/jj131033.aspx. Last accessed on Oct 21,
2013.
Murphy, K. (1998). Hidden markov model (hmm)
toolbox for matlab. http://www.cs.ubc.ca/ mur-
phyk/Software/HMM/hmm.html. Last accessed on
Jan 10, 2015.
Parsons, S., Mitchell, P., and Leonard, A. (2004). The
use and understanding of virtual environments by ado-
lescents with autistic spectrum disorders. Journal of
Autism and Developmental Disorders, 34(4):449–466.
Rabiner, L. (1989). A tutorial on hidden markov models
and selected applications in speech recognition. Pro-
ceedings of the IEEE, 77(2):257–286.
Russell, J. (2003). Core affect and the psychologi-
cal construction of emotion. Psychological Review,
110(1):145–172.
Structure (2013). Support openni.
http://structure.io/openni. Last accessed on Nov
21, 2013.
Wallbott, H. (1998). Bodily expression of emotion. Euro-
pean Journal of Social Psychology, 28(6):879–896.
Wang, L. (1997). A Course in Fuzzy Systems and Control.
PTR, Prentice Hall.
Zeng, Z., Pantic, M., Roisman, G., and Huang, T. (2009). A
survey of affect recognition methods: Audio, visual,
and spontaneous expressions. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 31(1):39–
58.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
204
