Pedestrian Trajectory Prediction in Large Infrastructures

A Long-term Approach based on Path Planning

Mario Garz

on, David Garz

on-Ramos, Antonio Barrientos and Jaime del Cerro

Centro De Autom

atica y Rob

otica UPM-CSIC,

Calle Jos

e Guti

errez Abascal, 2, 28006 Madrid, Spain

Keywords:

Pedestrian Trajectory Prediction, Planning-based Prediction, Trajectory Forecast.

Abstract:

This paper presents a pedestrian trajectory prediction technique. Its mail novelty is that it does not require any

previous observation or knowledge of pedestrian trajectories, thus making it useful for autonomous surveil-

lance applications. The prediction requires only a set of possible goals, a map of the scenario and the initial

position of the pedestrian. Then, it uses two different path planing algorithms to ﬁnd the possible routes and

transforms the similarity between observed and planned routes into probabilities. Finally, it applies a motion

model to obtain a time-stamped predicted trajectory. The system has been used in combination with a pedes-

trian detection and tracking system for real-world tests as well as a simulation software for a large number of

executions.

1 INTRODUCTION

Predicting the future trajectory of a pedestrian in a

given environment is a very useful task for many ap-

plications, both in the robotics world as in social sci-

ences. This work presents a novel approach for this

task, that can be used in any given scenario without

previous observation or data-collection.

This work is focused on a very common appli-

cation of pedestrian trajectory prediction: the au-

tonomous surveillance of critical infrastructures, such

as harbours, power plants or security facilities. Nowa-

days, surveillance systems are mostly static and they

require continuous monitoring by a human. More-

over, they are usually limited to provide reactive in-

formation (e.g. motion sensors, alarms on doors and

windows, etc). Therefore, they require a response

from the users which in some cases may not have

enough time to effectively address the incident. In this

context, predicting the possible goal of a given pedes-

trian, as well as the route and time that will take him

or her to the goal can help to increase the effectiveness

of the surveillance system because the prediction can

provide the ability of responding efﬁciently and on

time to potential vulnerabilities, such as the presence

or approximation of intruders to restricted or vulnera-

ble locations.

When performing autonomous surveillance of a

critical infrastructure, a series of important or vulner-

able locations can be clearly deﬁned. Moreover, it can

be assumed that an intruder moving on the infrastruc-

ture has a knowledge of the complete map, and there-

fore it can also perform a long-term planning of his or

her own route. Furthermore, the prediction does not

need to be highly accurate, because the objective of

the prediction algorithm will be to ﬁnd the most prob-

able destination and its route so a robot can be sent to

obtain a detailed image of the intruder. Moreover, in

order to obtain the prediction, only a few requisites,

analogous those required by any path planning algo-

rithm, are needed. Namely: The initial position of the

pedestrian, a map of the scenario and a list of possible

goals.

Once the initial position, and the set of possible

goals are deﬁned, an efﬁcient route to each one of

them can be obtained. Those possible routes depend

on the cost-map and they are the base of the trajectory

prediction. After this, the objective of the prediction

algorithm will be to ﬁnd the probability of the pedes-

trian following any of the possible trajectories. This

probability can be computed based on the similarity

between the observed trajectory and each one of the

possible routes. The probability distribution, as well

as the prediction output, can be updated every time a

new observation arrives or at a ﬁxed time-step.

For this work, two different planning techniques

are used and compared: Fast Marching Method

(FMM) (Sethian, 1999) and the widely used A Star

Garzón, M., Garzón-Ramos, D., Barrientos, A. and Cerro, J.

Pedestrian Trajectory Prediction in Large Infrastructures - A Long-term Approach based on Path Planning.

DOI: 10.5220/0005983303810389

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 381-389

ISBN: 978-989-758-198-4

381

Algorithm (A

∗

). Both of them take into account the

map of the scenario and the possible destination of

the pedestrians but differ on the optimal solution ob-

tained due the heuristically component of A

∗

and the

fact that FMM uses only a 4-connected neighbour-

hood to obtain the route.

The main novelty in this work is that is does

not require any previous observation of pedestrian

trajectories to obtain the prediction, and it can be

adapted to any scenario by requiring only a cost-map,

making it useful for security applications where it

is not likely to have previous observations. Further-

more, the prediction presented is integrated with a

previously-developed pedestrian detection and track-

ing algorithm, so it is capable of handling errors or

noisy measurements present in any real-world detec-

tion system. Finally, by integrating a motion model of

the pedestrian, it is possible to obtain a time-stamped

prediction, which is required for its integration with

autonomous surveillance with mobile robots.

2 RELATED WORK

Most of the pedestrian trajectory prediction tech-

niques that have been proposed are focused on obtain-

ing a short-time prediction, mainly for robot naviga-

tion in scenarios where people and robots may found

themselves together.

An early work was based on multi-layer Bayesian

dynamic structures, where each layer represents a

path trough the environment (Bui et al., 2001). A

different work was based on Hidden Markov Models,

using clustering obtained form expectation maximiza-

tion (Bennewitz et al., 2005). However, it requires a

high load of previous observations, it is scenario de-

pendent and it does not consider time or velocities. A

prediction based on genetic algorithms and an agent-

based was tested on a large shopping centre, however,

it does not take into account any time constraint be-

cause it is oriented to recreate trajectories in social

studies (Kitazawa and Batty, 2004).

Some works have proposed to predict the pedes-

trian trajectory using a goal-directed prediction. The

goals may be obtained from clustering large amounts

of observations (Yen et al., 2008) or by topological

places in a map (Ikeda et al., 2012). Then data from

observations was used to obtain probability of transi-

tion between sub-goals. The main drawback of these

works is their dependence on scenario speciﬁc infor-

mation and their limitation on time and length of the

prediction.

A two level prediction process has been also pro-

posed (Foka and Trahanias, 2010), it deﬁnes a short-

term prediction based on Polynomial Neural Net-

works, and a long-term prediction based on the prob-

ability of transition between a series of manually de-

ﬁned ”Hot Points”. This technique however only di-

rects the future position of the pedestrian and does not

take into account time or velocity issues.

A more recent approach proposes a probabilistic

method of determining pedestrian trajectory (Tamura

et al., 2013). It classiﬁes the behaviours of pedes-

trians into deﬁnite patterns, learned through observa-

tion. Then compares a new one by likelihood cal-

culation. This technique however does not take into

account the environment and it only predicts simple

trajectories based on the direction of the movement.

A more complex algorithm models goal-directed

trajectories of pedestrians using maximum entropy in-

verse optimal control (Ziebart et al., 2009). This ap-

proach describes the environment by using generic

features, which then can be moved. Then, it cre-

ates a cost-map based on previously observed trajec-

tories, and uses it to plan a future trajectory of the

newly observed pedestrian. This work was later ex-

tended by adding vision based physical scene features

and noisy tracker observations (Kitani et al., 2012).

Those works are similar to the one proposed in this

paper in the sense that they also use a planning step

to predict the future position of the pedestrian, how-

ever, their long-term prediction is not very clear, be-

cause it only directs its future position and therefore

it is only valid in relatively short distances, further-

more, time or velocity issues are not accounted for,

and as with all other prediction techniques they re-

quire a large amount of observations.

The main novelty of the prediction technique pro-

posed in this paper, is that it does not require any

previous observations of pedestrians in order to ob-

tain the prediction, as does every previous work. This

means that can be used in any scenario, only having

its map. Another difference with previous works is

that the work presented here uses a Kalman ﬁlter to

obtain the pedestrian velocity and combines it with

a path planning based prediction. This combination

results in a long-term prediction that can take into ac-

count not only the position but also time and velocity

constraints. Finally, it is possible to obtain predictions

that model the different behaviours of pedestrians by

modifying the cost-map and using different path plan-

ning techniques, therefore increasing the adaptability

of the prediction to any infrastructure or depending on

the user’s necessities.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

382

3 METHODOLOGY OVERVIEW

As aforementioned, the prediction process has three

inputs: The list of possible goals, the map of the sce-

nario and the pedestrian position. The process is ini-

tialized by deﬁning the ﬁrst two while the third one

will change continuously as the pedestrian moves.

Moreover, the other two are only processed once at

the initialization of the algorithm and then only if a

re-initialization is executed.

Two independent threads are used, one for pro-

cessing the income data and other for computing the

prediction. Therefore the predicted trajectory can be

produced at a constant frequency, independently from

the rate at which observations are received. Once the

target position is received, it is sent simultaneously to

both the Kalman ﬁlter and the prediction process.

When the ﬁrst position is received an instance of a

Kalman ﬁlter is created. Then, every time a new ob-

servation arrives, the ﬁlter is updated and a new cycle

of its loop is executed, this allows to keep an accurate

model of the movement of the pedestrian.

The prediction process also receives the initial po-

sition, then it uses a planner (A

∗

or FMM) to obtain

an efﬁcient path from the initial position to each one

of the possible destinations, the initialization is com-

pleted by assigning an equal probability value to each

one of the possible routes. Then, when new observa-

tions arrive, the trajectory followed by the pedestrian

is compared to the possible routes. The result of this

comparison is translated into probabilities so the most

similar route will have the highest probability.

Finally, the long-term prediction is obtained by

projecting the position and velocity observed into the

planned route. The prediction can be as long as the

complete route or according to a given parameter. In

order to account for changes in the direction or un-

predicted movements, the process is restarted if the

pedestrian moves far away from the route or after a

given lapse of time. The complete prediction process

is summarized in Figure 1.

Figure 1: Overview of the proposed approach. The inputs

of the algorithm are shown in blue, the main components,

as well as the trajectory output, are highlighted.

4 TRAJECTORY PREDICTION

BASED ON PATH PLANNING

The core of the prediction algorithm is the use of a

path planning strategy. Its main objective is to obtain

the most likely destination of the pedestrian as well

as its possible trajectory towards it. The problem is

simpliﬁed by deﬁning a ﬁxed number of possible des-

tinations, and then compare the observed trajectory of

the pedestrian with the possible routes obtained from

a path planning algorithm. After this, the similarities

are translated into probabilities and the most likely

route is extracted out and considered as the predicted

trajectory. The main components of the algorithm will

be described next.

4.1 Obtaining the Cost-map

The ﬁrst input to be processed is the map of the sce-

nario, which is used to obtain the cost-map required

for the path planner. This cost-map is of high impor-

tance, because it will determine the behaviour of the

trajectory prediction. Moreover, the process used to

obtain it can be taken as a replacement to the observa-

tions of past pedestrian trajectories required by most

of the prediction algorithms in the literature.

The algorithm uses the standard ROS map format

which deﬁnes the map in two ﬁles: a yaml ﬁle which

contains the meta-data and deﬁnes the name of the

map image. The second ﬁle is the image, which de-

scribes the occupancy state of each cell of the map.

It marks free cells with whiter colours and occupied

ones with black. The map can be obtained from a

SLAM algorithm or it can be created using informa-

tion from a Geographical Information System (GIS).

The ﬁrst step in processing the map is to scale it

(i.e change its resolution). Maps used in ROS have

usually high resolution because they are used for au-

tonomous navigation (e.g. 0.05m per pixel). How-

ever, a much lower resolution can be used for this

task. Taking into account the frequency of the de-

tection algorithm, the expected mean size of pedes-

trians and the required precision of the algorithm, the

resolution can be much lower, for the presented ex-

periments a value of 0.35m per pixel was deﬁned.

This decrease in resolution will speed up and facili-

tate the complete process, moreover other prediction

techniques also use low resolution maps(Ikeda et al.,

2012). The scaling process is done by using a bilinear

interpolation technique, ensuring that positions in the

resulting map have a correct translation to the original

one. This allows using the result of the prediction in

the original, unscaled, map.

http://wiki.ros.org/map server

Pedestrian Trajectory Prediction in Large Infrastructures - A Long-term Approach based on Path Planning

383

The second step in processing the map is to mod-

ify it by incorporating additional obstacles. Those ob-

stacles may represent static objects not included in the

original map, or they can also represent virtual obsta-

cles used to deﬁne zones where the pedestrian is not

expected to cross, or to block passages that need to

be avoided. This obstacles can be manually added by

deﬁning its position and radius, or they can be given

as a new map of obstacles that can be added to the

original one.

After the obstacles map is completed, the map is

modiﬁed by applying transformations or ﬁlters, such

as a distance transformation, median or low pass ﬁl-

ters as well as any other geometrical transformation.

This transformation allows to change the costs in the

surroundings of the obstacles, and therefore modi-

fying the planned routes to common pedestrian be-

haviours (i.e. generate trajectories by the center of

halls, closer to walls, or avoid crossroads or areas

where other pedestrians may be found). This transfor-

mations are applied homogeneously to the complete

map, so it does not include any preference on the pre-

dicted trajectories. An example of the map processing

with an artiﬁcial map is presented on Figure 2.

(a) Original map (b) Scaled map

Figure 2: Steps in the process of obtaining the prediction

cost-map from a given (artiﬁcial) map.

4.2 Path Planning for Prediction

Since this work is not focused on developing a new

planning technique, two well known planners (A

∗

and

Fast Marching Method) have been used. However, as

aforementioned, any planner based on a cost-map can

be used. It should be clariﬁed that the implementation

of the path planning algorithms used here does not

take into account the orientation of the pedestrian, nor

it poses any kinematic restriction to its movements.

There are two reasons for this: First, pedestrians can

move in any direction in a plane and second, the de-

tection and tracking algorithm used does not provide

information about the pedestrian orientation.

The planner uses the same three inputs as the com-

plete algorithm: The list of possible goals, which are

deﬁned in map coordinates and can be pre-ﬁxed or

given manually to the algorithm. The second input is

the cost-map, which is received after the pre-process

described in Section 4.1. The third input is the ﬁrst

position received from the detection algorithm.

Once these inputs are deﬁned, the planner obtains

an effective route from the initial position to each one

of the possible goals in a sequential manner. Each

time a route is found, it is stored and the algorithm re-

mains on stand-by until all possible routes are found.

An example of the result using the A

∗

planner, which

uses the euclidean distance to the goal as heuristic

cost, is depicted on Figure 3.

Figure 3: Possible pedestrian routes (shown in colours)

from an initial position (red rectangle) towards different

possible goals.

4.3 Comparing Two Trajectories

Once the possible routes are deﬁned, the next step is

to compare them with the trajectory that pedestrian

is following so the results can be later translated into

probabilities. There are several issues to take into ac-

count when comparing the trajectories, the ﬁrst one is

that the possible routes may have different length and

they do not have any time constraints. Also, the dis-

tance should be computed with the information avail-

able at each moment (i.e. the trajectory observed so

far) and it should be updated every time a new obser-

vation arrives.

It was necessary to deﬁne a method to measure

the similarity between two trajectories, one that can

be used without requiring time-stamped positions, or

complex computations. The measurement technique

used is based on the Fr

echet distance (Fr

echet, 1906),

which can be deﬁned as follows: “A man is walking

a dog on a leash: the man can move on one curve,

the dog on the other; both may vary their speed, but

backtracking is not allowed. What is the length of

the shortest leash that is sufﬁcient for traversing both

curves?”(Alt and Godau, 1995).

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

384

The distance computation proposed here also re-

lies on the sum of the point-to-point distance between

each of possible routes. However some differences

are introduced. First of all, since the planned routes

do not have time constraints, and their length can be

different, the minimum distance between each point

in the pedestrian trajectory and the routes is used. An-

other difference is that the distance values are updated

every time a new observation arrives, meaning that

the distance between the trajectories D

tra j

changes ac-

cordingly at every time-step, as deﬁned in Equation

(1).

tra j

(n − 1) =

n−1

∑

i=0

tra j

(n) = D

tra j

(n − 1)+ d

(1)

Where d

represents the distance from the observa-

tion i to the possible route. D

tra j

(n−1) is the distance

up to the n − 1 observation. The complete distance

tra j

(n) is obtained by adding the distance from the

last observation to the predicted route d

whenever a

new observation is received

4.4 Obtain Likelihood and Probabilities

The next step in the algorithm is to translate the simi-

larities into probabilities. A ﬁrst approach was to nor-

malize them so the result can be directly translated

to probability values. Taking into account that the

distance value is punctual and deﬁned at each time-

step, the normalization is straightforward. First, the

total distance value D

total

is obtained, by adding the

distance to each one of the possible routes D

. Then

the probability of each route P

will be the ratio be-

tween each distance and the total distance value, as

expressed by (2).

total

; P

total

; . . . P

total

;

(2)

However, after some initial tests, it was found that

using the similarity of all the observed trajectory in-

duce errors, because the pedestrians may not follow

the predicted route, they can change direction or even

go back. In order to solve this, it was necessary to

propose a different computation, one that allows to

give more relevance to the more recent observations

without completely disregarding the previous ones.

The new approach consists on using a memory of

the trajectory observed so far, which will slowly fade

as new observations arrive. To obtain this, a combined

probability with two components is computed. The

ﬁrst component will be obtained from the last obser-

vation only, and the second one will be the memory of

the previous prediction. This approach has a twofold

advantage, ﬁrstly it uses a very simple computation.

Secondly, it allows to control the weight of both cur-

rent and previous values, so as to adapt them to differ-

ent types of behaviours or scenarios. The combined

probability computation is expressed in Equation (3).

(t) = αP

(t − 1) + (1 − α)

(3)

Where P

(t) represents the probability of the

pedestrian following any given trajectory P

at time

t. And α is the weight factor (0.6 for the experi-

ments) that allows to take into account the previously

observed trajectory, and ﬁnally

is the probability

value obtained using only the last observation. This

process is also illustrated in Figure 4.

Figure 4: Current and previous distances from pedestrian

position to possible routes, clearer colours represent the

lower weight of those values in the probability computation.

4.5 Create Predicted Trajectory

After the probability computations, the trajectory

with higher value is selected as the predicted

route/goal. In order to generate the trajectory predic-

tion, it is necessary to take into account not only the

goal but also the velocity of the pedestrian. Further-

more, it should be possible to control the time step

and the temporal scope of the prediction.

This is achieved by projecting the current position

and velocity of the pedestrian, extracted from the state

of the Kalman ﬁlter, into the route with the higher

probability. The (x, y) velocity is added to the position

on the path previously found, this results in a new po-

sition that is projected back to the planned route. This

procedure is repeated until the length of the prediction

is achieved, this process is depicted in ﬁgure 5.

Although this trajectory may introduce some de-

viation or inaccuracies, its prediction is valid for the

Figure 5: Generation of the predicted trajectory, clear blue

shows the most probable route. The predicted trajectory is

shown with connected purple dots.

Pedestrian Trajectory Prediction in Large Infrastructures - A Long-term Approach based on Path Planning

385

security application, because the objective is not to

collide with the pedestrian but rather be able to reach

it with a mobile robot. Furthermore, changes on di-

rection or variation of velocity can be correctly han-

dled by continuously updating the prediction.

5 EXPERIMENTS AND RESULTS

This section describes the experiments performed to

evaluate the proposed prediction method. Both sim-

ulations and real-world pedestrian trajectories have

been tested. First, the scenario and common features

for both experiments are described. Then, the acqui-

sition of simulated and real trajectories is explained,

along with the performance of the prediction system

in every case.

5.1 Scenario

The same scenario was used in both simulated and

real experiments. The location is a real street inter-

section with many obstacles and possible routes for

pedestrian motion. The 2D map was pre-built using

SLAM algorithms. Then, the cost-map was generated

from the map, as described in Section 4.1, and it was

used for getting the predicted routes in simulated and

real-world tests. The original scenario, the map re-

construction as well as the cost-map and the possible

goals are shown in Figure 6.

5.2 Simulations

The pre-built map and a mobile robot, acting as simu-

(a) Aerial view (b) SLAM map

Figure 6: Scenario for simulations and real world tests.

lated pedestrian, were loaded in Stage simulator. Five

positions, according to their proximity to important

locations or exits, were selected as possible goals (See

Figure 6(d)). Then, the trajectories were obtained by

teleoperating the pedestrian from one possible goal

to each one of the other four. In all cases the opera-

tor knew the map of the infrastructure and choose the

route for the simulated pedestrian, thus resulting in ar-

bitrary suboptimal routes. This process was repeated

ﬁve times for each possible combination, resulting on

a total of 100 recorded trajectories. Finally, the A

∗

and Fast Marching planners to generate the predicted

routes, and the prediction algorithm was applied, re-

sulting in a total of 200 simulations.

This amount of registers allows obtaining valid

information about the efﬁciency of the prediction

methodology as well as its behaviour when it is used

in conjunction with the A

∗

or the FMM planner.

Three parameters were studied to validate the results:

the number of changes in the most probable route over

the time, the percentage of trajectory covered before

ﬁnding the correct route/goal and the percentage of

trajectory covered before the probability of the correct

route reaches 0.5. Moreover, the mean and standard

deviation were calculated for all parameters named

above. The results for the complete data are shown

in Table 1.

Table 1: Results for trajectory prediction. A changes in the

most probable route; B Trajectory covered (%) before ﬁnd-

ing the correct route/goal; C Trajectory covered (%) before

probability of route reaches 0.5.

∗

Planner FMM Planner

µ σ µ σ

A 4.93 2.79 3.01 1.64

B 51.81% 18.58% 50.46% 18.71%

C 61.61% 13.91% 58.39% 16.27%

It was found that the A

∗

planner have more

changes selecting the most probable route over the

time. This fact was associated to the heuristic com-

ponent of this technique. The euclidean distance min-

imization derives in early differentiation of the possi-

ble routes to reach every goal, which causes that ran-

domly movements of the pedestrian have high impact

in the probability distribution since the ﬁrst time of

the displacement. On the other hand, due to the shared

starting point for the FMM plans, they tend to follow

the same routes for a considerable percentage of the

displacement, resulting in a more stable probability

distribution.

In both cases, the percentage of trajectory covered

before ﬁnding the correct route and the percentage be-

fore its probability reaches 0.5 is nearly 50%. This

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

386

value is related to the goals positions in the map (Fig-

ure 6(d)). Several plans go through the intersection at

the centre of the scenario before they split into very

distinct paths. It can be said that this result is strongly

dependent on the map and for that reason this is not

signiﬁcant to determinate the speed of achieving a

deﬁnitive prediction. However, it gives relevant qual-

itative information about high interest positions in the

scenario.

5.3 Real World Experiments

As aforementioned, in order to use the prediction al-

gorithm, it is necessary to have the pedestrian position

in a given map. This was achieved by using a previous

work, where pedestrians are detected by fusing infor-

mation of a camera and a laser scanner, and their po-

sition on a map is given by a tracking algorithm run-

ning on-board a mobile robot (Garz

on et al., 2015).

An image of the detection and tracking algorithm and

the corresponding position in the map is presented on

Figure 7.

Figure 7: Screen capture of the pedestrian detection and

tracking algorithm and the corresponding position on the

map.

Several experiments, having similar start and end

points as with the simulations were carried out. The

prediction algorithm was executed on-board the mo-

bile robot, thus testing the real-time capabilities of the

implementation, and the observed results were consis-

tent to those of the simulations.

The behaviour of prediction based on the A

∗

plan-

ner algorithm could be observed in Figure 8(b) where

the most probable route changes several times due to

unexpected variations in the direction of the pedes-

trian at the intersection, as can be seen in Figure 8(a).

The results for the prediction based on the FMM

algorithm were also consistent with the simulations,

the number of changes in the predicted route is lower

because the possible routes share the same path for a

longer period. This can be seen in Figures 9(b) and

9(a) respectively.

In order to compare the proposed prediction with

previous works, the Modiﬁed Hausdorff Distance

(a) Possible routes and

pedestrian trajectory

Displacement(m)

0 5 10 15 20 25 30

Probability

0.2

0.4

0.6

0.8

Route 1

Route 2

Route 3

Route 4

(b) Probabilities evolution

Figure 8: Real experiments using A

∗

Planner.

(a) Possible routes and

pedestrian trajectory

Displacement(m)

0 5 10 15 20 25 30

Probability

0.2

0.4

0.6

0.8

Route 1

Route 2

Route 3

Route 4

(b) Probabilities evolution

Figure 9: Real experiments using FMM Planner.

(MHD) can be computed. This measurement provides

a standardized a-posteriori information about the sim-

ilarity of the predicted routes and the trajectory fol-

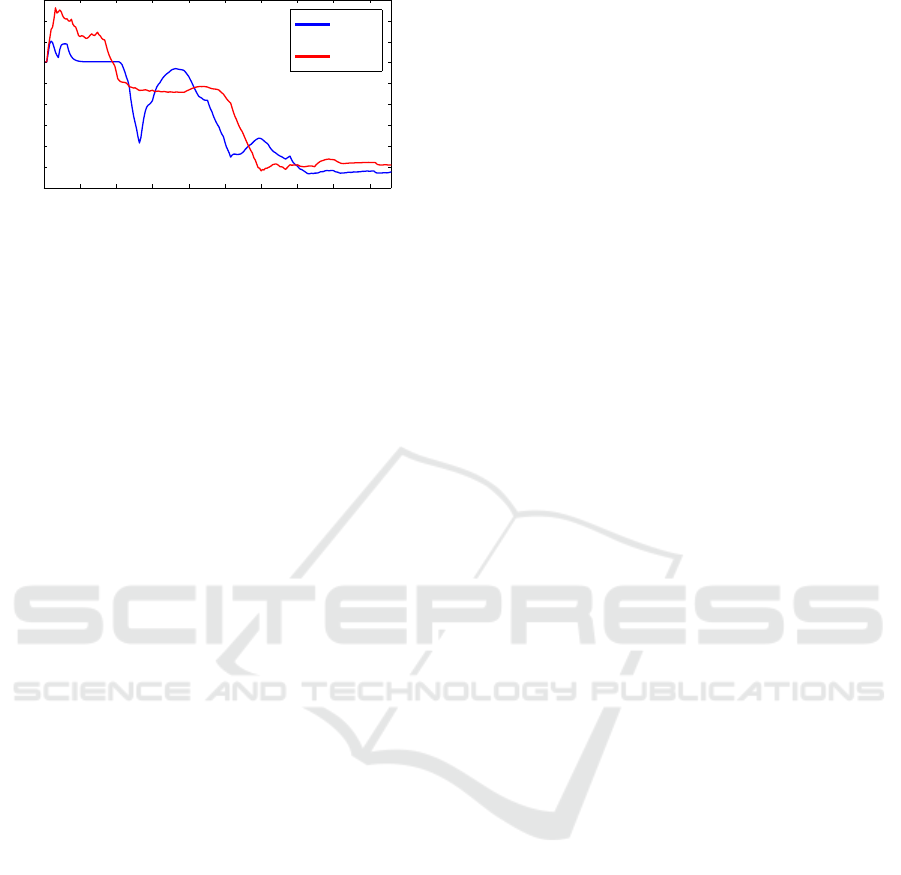
lowed by the pedestrian. Figure 10 shows the evo-

lution of the MHD for the prediction using A

∗

and

FMM, which has an analogous behaviour as that of

the prediction, which was expected because of the

probability computation process is based on compar-

ing distances.

A comparison with previous works can not be di-

rectly performed, because they provide their results in

pixels, not it meters as is done here. However, a rel-

ative estimation could be calculated based on the dif-

ference between maximum and minimum MHD. The

work of (Kitani et al., 2012) has a relative reduction

of 75% and in the results presented here, this relative

reduction is 86%. Although this is not conclusive, it

shows that the proposed technique produces a useful

prediction, even when working in large scenarios.

6 CONCLUSIONS

An approach for pedestrian trajectory prediction was

presented. The proposed methodology, as well as the

experiments and results obtained show that it is pos-

Pedestrian Trajectory Prediction in Large Infrastructures - A Long-term Approach based on Path Planning

387

0 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

Observations Available

Modified Hausdorff Distance (MHD)

A Star

FMM

Figure 10: Modiﬁed Hausdorff Distance evolution with the

observations available for A

∗

and FMM planners.

sible to model the approximate behaviour of pedestri-

ans based on using path planning techniques.

The tests have shown that a valid pedestrian tra-

jectory prediction can be obtained without requiring

a large set of previously observed trajectories. This

allows to use the proposed algorithm in any scenario,

requiring only a map and a list of possible goals.

The prediction algorithm was successfully inte-

grated with a pedestrian detection system and it was

executed on-board a mobile robotic platform, thus

validating its capabilities of working in real-time in

both simulations and real-world applications.

Two different path planning algorithms (A

∗

and

FMM) were implemented and tested for prediction.

It was shown that the prediction based on the A

∗

plan-

ner is more prone to be affected by variations in the

movement of the pedestrian, whereas the FMM based

prediction is more stable in this sense. Moreover, it

can be concluded that in terms of the length of the tra-

jectory required to determine the correct route, both

planning techniques produce a similar result, requir-

ing about 50% of the trajectory, although this results

are may be conditioned by the test scenario.

Furthermore, it was possible to use a simple mo-

tion model, based on a Kalman ﬁlter to estimate the

time it will take to reach any given goal, thus mak-

ing the time-stamped prediction very useful for any

autonomous surveillance system.

This work has two main lines for future work, the

ﬁrst one is to try to autonomously ﬁnd the possible

destinations and the second is to provide a map or set

of maps of predictions where the or different possibil-

ities, uncertainties or variances of the prediction can

be expressed in a better way.

ACKNOWLEDGEMENTS

This work was partially supported by the Robotics

and Cybernetics Group at Universidad Polit

ecnica de

Madrid (Spain), and it was funded under the projects:

PRIC (Protecci

on Robotizada de Infraestructuras

ıticas; DPI2014-56985-R), sponsored by the Span-

ish Ministry of Economy and Competitiveness and

RoboCity2030-III-CM (Rob

otica aplicada a la mejora

de la calidad de vida de los ciudadanos. fase III;

S2013/MIT-2748), funded by Programas de Activi-

dades I+D en la Comunidad de Madrid and co-funded

by Structural Founds of the EU.

REFERENCES

Alt, H. and Godau, M. (1995). Computing the fr

echet dis-

tance between two polygonal curves. International

Journal of Computational Geometry & Applications,

5(01n02):75–91.

Bennewitz, M., Burgard, W., Cielniak, G., and Thrun, S.

(2005). Learning motion patterns of people for com-

pliant robot motion. The International Journal of

Robotics Research, 24(1):31–48.

Bui, H. H., Venkatesh, S., and West, G. (2001). Tracking

and surveillance in wide-area spatial environments us-

ing the abstract hidden markov model. International

Journal of Pattern Recognition and Artiﬁcial Intelli-

gence, 15(01):177–196.

Foka, A. and Trahanias, P. (2010). Probabilistic au-

tonomous robot navigation in dynamic environments

with human motion prediction. International Journal

of Social Robotics, 2(1):79–94.

echet, M. M. (1906). Sur quelques points du calcul

fonctionnel. Rendiconti del Circolo Matematico di

Palermo (1884-1940), 22(1):1–72.

Garz

on, M. A., Barrientos, A., Cerro, J. D., Alacid, A., Fo-

tiadis, E., Rodr

ıguez-Canosa, G. R., and Wang, B.-C.

(2015). Tracking and following pedestrian trajecto-

ries, an approach for autonomous surveillance of criti-

cal infrastructures. Industrial Robot: An International

Journal, 42(5):429–440.

Ikeda, T., Chigodo, Y., Rea, D., Zanlungo, F., Shiomi, M.,

and Kanda, T. (2012). Modeling and prediction of

pedestrian behavior based on the sub-goal concept. In

Proceedings of Robotics: Science and Systems, Syd-

ney, Australia.

Kitani, K. M., Ziebart, B. D., Bagnell, J. A., and Hebert, M.

(2012). Computer Vision – ECCV 2012: 12th Euro-

pean Conference on Computer Vision, Florence, Italy,

October 7-13, 2012, Proceedings, Part IV, chapter

Activity Forecasting, pages 201–214. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Kitazawa, K. and Batty, M. (2004). Pedestrian behaviour

modelling. In Developments in Design and Decision

Support Systems in Architecture and Urban Planning,

pages 111–126.

Sethian, J. A. (1999). Fast marching methods. SIAM Re-

view, 41(2):199–235.

Tamura, Y., Terada, Y., Yamashita, A., and Asama, H.

(2013). Modelling behaviour patterns of pedestrians

for mobile robot trajectory generation. International

Journal of Advanced Robotic Systems, 10(301):1–11.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

388

Yen, H. C., Huang, H. P., and Chung, S. Y. (2008). Goal-

directed pedestrian model for long-term motion pre-

diction with application to robot motion planning.

In Advanced robotics and Its Social Impacts, 2008.

ARSO 2008. IEEE Workshop on, pages 1–6.

Ziebart, B., Ratliff, N., Gallagher, G., Mertz, C., Peterson,

K., Bagnell, J., Hebert, M., Dey, A., and Srinivasa,

S. (2009). Planning-based prediction for pedestrians.

In Intelligent Robots and Systems, 2009. IROS 2009.

IEEE/RSJ International Conference on, pages 3931–

3936.

Pedestrian Trajectory Prediction in Large Infrastructures - A Long-term Approach based on Path Planning

389