A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System

Mounir Hammouche

, Samir Sakhi

, Mahmoud Belhocine

, Abdelhafid Elourdi

and Samir Bouaziz

Laboratoire Systèmes Numériques, Ecole Militaire Polytechnique, BP 17, Bordj El Bahri, Algiers, Algeria

Centre for Development of Advanced Technologies, Algiers, Algeria

Laboratoire SATIE - CNRS UMR 8029, Université Paris Saclay, F-91405 Orsay, France

Keywords: GPS, INS, Reduced Inertial Sensor System (RISS), Kalman Filter, Fuzzy Controller.

Abstract: Navigation technology has an important role in designing intelligent vehicles and advanced robots. To have

a continuous navigation solution that does not suffer from interruption, GPS (Global Positioning System)

data is merged with relative positioning techniques such as inertial navigation system (INS) or odometry

(Odm). To accomplish the reliability and integrity desired, it is therefore necessary to take into account

physical capabilities and limitations of each sensor during navigation. A fuzzy switcher controller (FSC) is

well suited for this task. FSC is an Expert rule-based method for choosing the best fusion from multiple

redundant integration methodologies (GPS/INS, GPS/Odometry, Odometry/INS or GPS/INS/Odometry)

based on navigation conditions and accuracy of the navigation systems.

1 INTRODUCTION

Road navigation systems are one of the main field of

interest in the intelligent transport domain such as

advanced driver assistance, route guidance or

traveller information which require a Road Side

Equipment (RSE) able to provide an accurate

position at low price (Boysen,2004). The commonly

used sensors in these applications may be divided

into two categories, external sensors and Dead

Reckoning Sensors (DRS) such as Inertial

Navigation System (INS) and Odometry.

The common external sensors for land vehicle

positioning are satellite navigation systems such as

Global Positioning Systems (GPS). However, in

GPS-denied environments (tunnels, canyons urban)

the GPS satellite signal is not often available. Hence

the positioning information provided is not accurate.

To achieve continuous navigation solution even

during GPS outages, the GPS is augmented with

dead reckoning sensors.

Inertial Navigation Systems and Odometry have

always been presented as valuable sensors in many

applications. Their advantages are well known: high

update rates; position and heading accuracy in short

time. However, Combining odometry with INS

which is called in the literature “Reduced Inertial

Sensor System –RISS- (North, 2012)” can enhance

the positioning accuracy compared to INS or

odometry alone. Indeed, odometry and INS have, to

some degree, complementary characteristics: INS can

provide the heading/attitude information (Xiaochuan,

2009), while odometry can remarkably limit the

position error accumulation of INS with respect to

time. To design more precise systems, external

sensors are usually integrated with dead reckoning

sensors taken on many forms, such as GPS/INS

integration, GPS/Odm integration or integrating the

three sensors together (GPS/RISS) (North, 2012).

This latter gives the best solution when the three

sensors are used in best conditions. In the case of

failure of one of them the position accuracy

decreases (North, 2012).

To accomplish the best reliability and integrity

desired, it is therefore necessary to choose which

sensors integration gives the best result. A Fuzzy

Logic based on expert rules derived from careful

observations of the physical functioning of each

sensor is certainly required to process the available

data. The algorithms must provide fault detection and

data fusion capabilities to make the best use of the

available information (Xiaochuan, 2009), (Singhala,

2014).

390

Hammouche, M., Sakhi, S., Belhocine, M., Elourdi, A. and Bouaziz, S.

A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System.

DOI: 10.5220/0005984103900397

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 390-397

ISBN: 978-989-758-198-4

To fuse information coming from sensors

different approaches can be found in the literature.

Many of them rely on the implementation of an

Extended Kalman Filter (EKF) (Boysen, 2004),

(Boucher, 2004), (Hay, 2005), (Sukkarieh, 2000).

The performance of the EKF is reliable in many

practical situations, but the non-linear state equations

may lead to instability problems. Other ﬁltering

methods can be found in the literature, such as the

Unscented Kalman Filter (St-Pierre, 2004) and

particle based solution (Boucher, 2004).

This paper aims to develop an experimental

approach of GPS/INS/Odometry data fusion that uses

fuzzy rule-based system. It is divided into four (4)

main sections. Section 2 presents different integration

methodologies (GPS/INS, GPS/Odometry,

GPS/INS/Odometry and Odometry/ INS integration)

and a brief description of Fuzzy Switcher. Finally

section 3 presents the results and discussion with a

hardware implementation. A conclusion is given in

Section 4.

2 INTEGRATION ALGORITHMS

The concept of integrating GPS and dead reckoning

sensors (INS or Odometry) has been well discussed

in the research community. Different integration

strategies have been developed and tested with

different grades of INS. Typically; three main

strategies are used, namely loose integration, tight

integration and ultra-tight (or deep) integration. We

have chosen the loose coupling integration scheme

with close-loop. This schema lets control the

navigation accuracy and reduce the cost of design

(Sakhi, 2014).

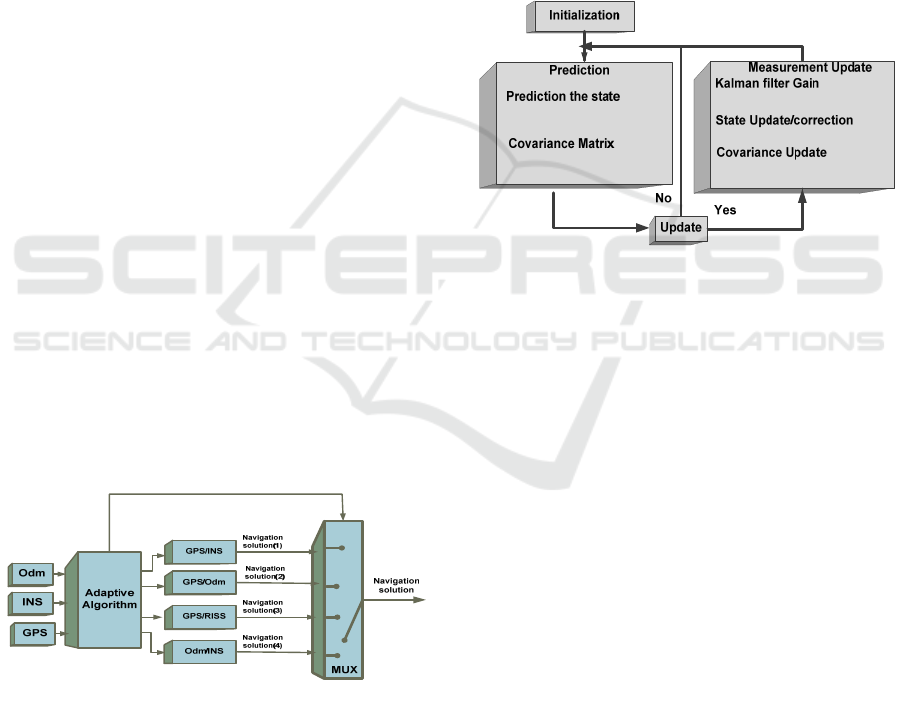
Figure 1: Architecture of proposed integrated

GPS/INS/Odm system.

The implemented algorithms consist of four (4)

filters. The first filter fuses the INS and GPS

measures, the second filter fuses the odometry and

GPS measures, and the third filter fuses odometry

and inertial data, while the fourth filter fuses the three

sensors data together. Then, an adaptive algorithm,

based on signal degradation conditions of the

different navigation systems, is used to choose the

best combination that gives the best navigation

solution. These algorithms are summarized in the

following diagram (Figure 1).

Kalman filter is a suitable filter used to integrate

sensors information. The prediction step, of the used

filter, is based on a kinematics model of motion.

Because of the non-linearity of the process model, we

have used an EKF filter.

The Extended Kalman filter (EKF) proceeds by

linearizing the model about the latest estimate to

meet the Kalman Filter assumptions (Boucher, 2004).

EKF is summarized by the flow chart showed in

Figure 2.

Figure 2: Kalman Filter Algorithm.

: state vector of the process at epoch t

k+1

: actual observation,

k+1/k

: state transition matrix from time t

to t

k+1,

: measurement and process covariance matrix,

: error covariance matrix,

k+1

: Kalman gain matrix,

k+1

observation matrices,

Where , represent a prior and a posterior

estimated state vector.

The implemented algorithms consist of an

Extended Kalman filter of 5-states including position,

velocity, and angular velocity in two (2) dimensions

for GPS/INS integration. However, for both

INS/Odm and GPS/RISS integration we have used a

Kalman filter of 3-state. The three integrated

algorithms are summarized in the following.

2.1 INS/GPS Integration Algorithm

Several techniques are proposed in the literature for

inertial and GPS fusion (Xiaochuan, 2009),

(Quinchia, 2011), (North, 2009). We have chosen the

loose coupling integration scheme with close-loop, as

shown in Figure 3, in order to reduce inertial unit

1111111

()

kkkkkkk

KPHHPHR

−−−

+++++++

11/

ˆˆ

kkk

−+

=Φ

1111

()

kkkk

Ik H P

+−

++++

=−

11 1

111

()

ˆˆ ˆ

kk k

kkk

+−

++ +

−

+++

=+ −

11/ 1/

kkkkkkk

−+

++ +

=Φ Φ +

−

A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System

391

errors. This has implications for inertial units of low

and medium precision (Sakhi, 2014).

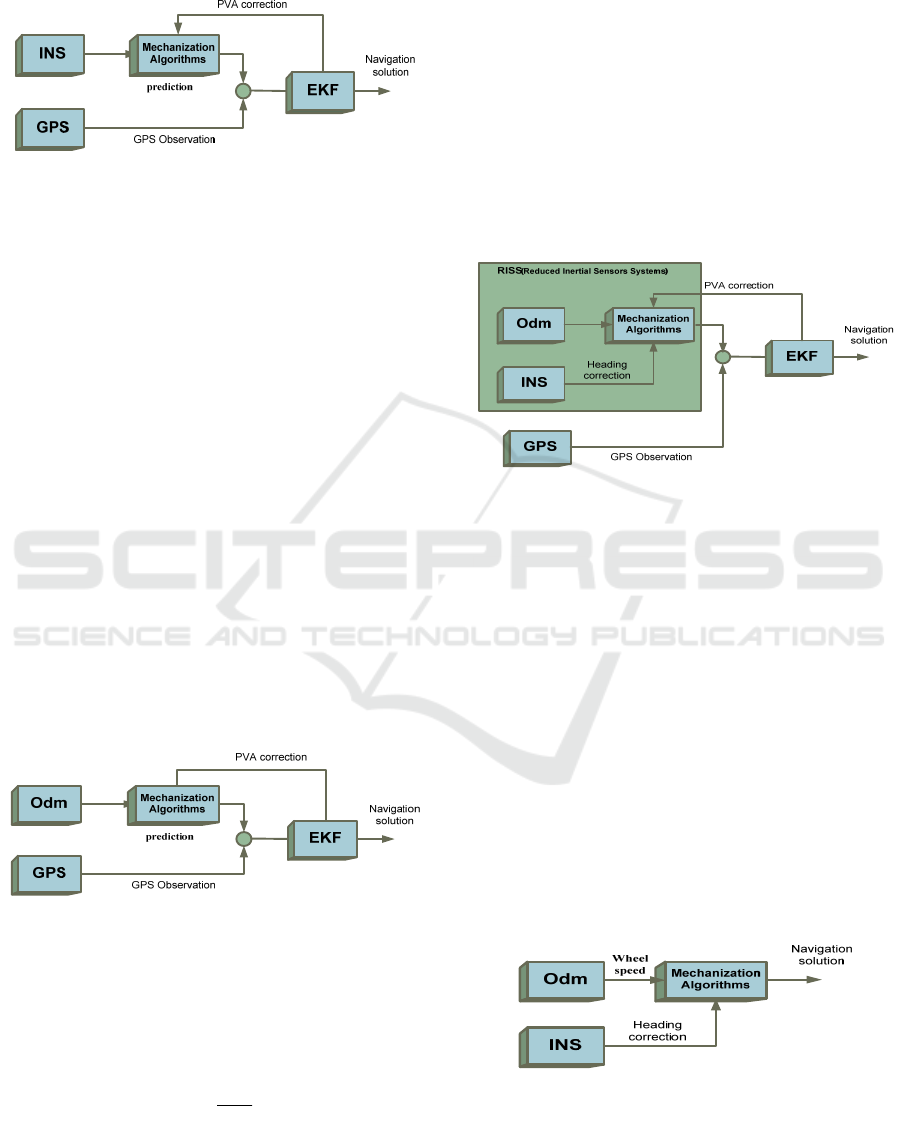
Figure 3: Loose coupling integration scheme (INS/GPS).

We have used the kinematics model which is

defined by the following equations (Kubrak, 2007)

instead of using dynamics model of a robot in order

to reduce the complexity of calculations.

(1)

2.2 Odometry/GPS Integration

Algorithm

Many techniques are proposed for integrating

Odometry with GPS (Lamon, 2004). We have

chosen a loose coupling integration scheme with

close-loop, where the state feedback PVA (Position,

Velocity and Attitude) correction to the Odometry

system, as shown in Figure 4 in order to reduce scale

factor errors.

Figure 4: Loose coupling integration scheme (GPS/Odm).

The motion model equations that transform

odometer measures in the navigation frame are

equations expressing the predicted function:

(2)

Where this state is defined by the coordinates of

its center M and the angle relative to , the

velocity of the center based on the average wheel

speeds and the steering angle of wheels .

2.3 RISS/GPS Integration Algorithm

The concept of RISS (Reduced Inertial Sensor

System ) was used in vehicle navigation in order

to further higher the accuracy of the positioning

solution. The RISS used in (North, 2009) involves a

single-axis gyroscope and the vehicle odometer

model to provide 2-D navigation solution , with

the assumption that the vehicle mostly stays in

the horizontal plane.

Figure 5: Schematic diagram of the RISS/GPS Integration.

The discrete form of Mechanization equations is:

(1) () ()cos(())

(1) () ()sin(())

(1) ()

kxkTVk k

yk yk TV k k

kkTWz

θθ

+= +

(3)

Where Wz is the gyroscope measurement (rate of

turns) in radium/second.

2.4 Odometry/INS Integration

Algorithm

Different configurations are proposed in the

literature (North, 2012), (Rogers, 2012) for

integrating Odometers and INS. In (North, 2012), N.

Eric used an IMU and the information delivered by

odometry as measurement update of the Kalman

filter .

Figure 6: Schematic diagram of the Odm/INS Integration.

In our work, after testing several methods we

have chosen the RISS configuration which gives a

−

•

••

•

••

•

(1) () ()0.5 ()

(1) () ()

(1) () ()0.5 ()

(1) () ()

mme exm

exm

mme eym

eym

mme

kxkTxkTak

xk xk Ta k

yk yk Tyk Ta k

yk yk Ta k

kkTk

θθθ

+= + +

+= +

+= + +

+= +

−

(1) () ()cos(())

(1) () ()sin(())

()

( 1) () tan(())

kxkTVk k

yk yk TV k k

kkT k

θθ φ

+= +

−

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

392

good positioning accuracy with simple integration

strategies without the need of filter. The system

model based on inertial and Odometry data is

depicted in (Figure 6).

2.5 Fuzzy Switcher Controller (FSC)

When designing a fusion system, we must take into

consideration the multi-rate sensor data collection,

and implement the integration algorithm

appropriately. Here, the term “fusion” refers

generally to the process of combining three sets of

measures to produce a consistent solution. That is,

we need to fuse odometry, inertial and GPS data

when all sensors perform well, but in the case of a

sensor failure, which may lead to degradation of

overall system performance, we have to eliminate its

use.

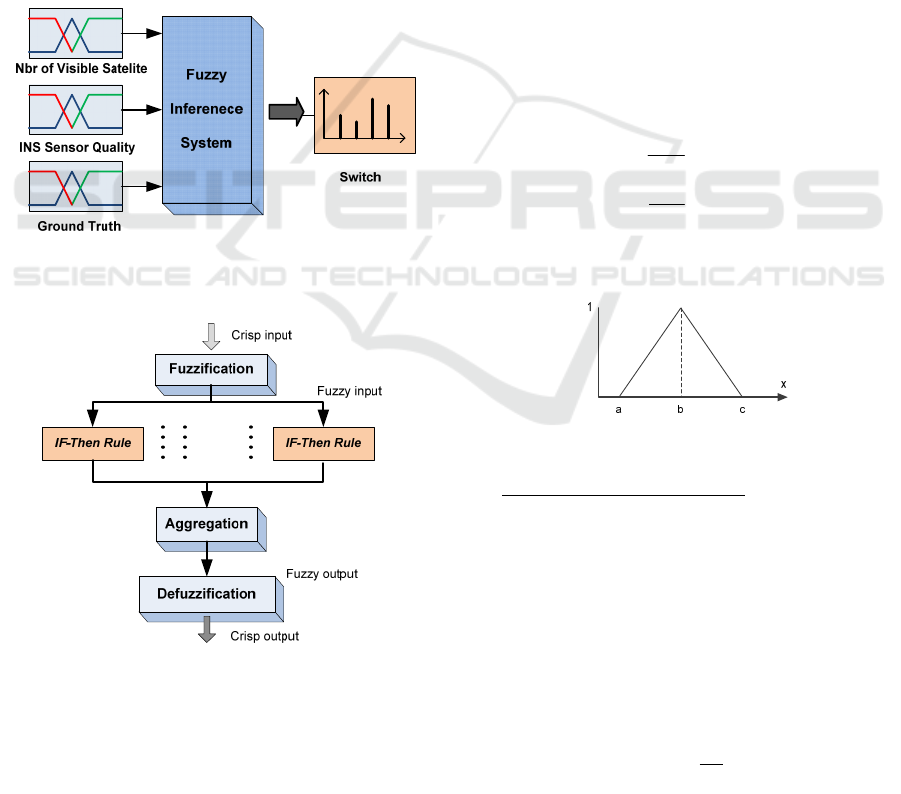
Figure 7: Architecture of the fuzzy logic data classification

system.

Figure 8: Block diagram of the fuzzy inference system

(Wang, 2006).

A fusion algorithm that takes into accounts the

physical capabilities and limitations of each sensor is

therefore necessary. A Fuzzy Logic is well suited for

this task. The down-mentioned expert rule-based

method for choosing best fusion result from multiple

redundant algorithms can help in selecting the most

accurate fusion algorithm. Our fuzzy algorithm uses

three fuzzy membership function inputs and one

output, as shown in Figure 7.

In a typical fuzzy system (Figure 8) the crisp

inputs are first converted to the input fuzzy sets

using the membership functions. Then, the input

fuzzy sets are mapped into a consequent fuzzy set

based on the adopted fuzzy logic operators, if-then

rules and aggregation strategy. Finally, the

consequent fuzzy set is converted into a scalar

quantity as the system output using a defuzzification

method.

2.5.1 Fuzziﬁcation Interface

It transforms crisp data (GPS data, Ground Truth,

and sensor’s data quality) into fuzzy sets. The

assignment of membership values to fuzzy variables

are based on experimental testing and logical

operations. For a computational simplicity, the

triangle membership function (equation 4) , shown

in Figure 9, is used.

() ,

axb

xbxc

otherwise

−

⎧

<≤

⎪

−

⎪

−

⎪

=<≤

⎨

−

⎪

⎩

(4)

Figure 9: Trapezoidal fuzzy membership function.

Path Condition Fuzzification: It is beneficial to

know if a robot (or vehicle) is crossing sandy

surfaces in order to eliminate the use of odometers

and reduce positioning errors. For the detection of

sandy surfaces, the robot literally bounces on the

ground when the rear bogie wheels go through rough

terrain. Shocks occurring during the experiment are

easily identified when looking at the roll angel

variation. The equations used to calculate roll from

accelerometers are based on the idea presented in

(Kubrak, 2007).

tan

−

⎛⎞

⎜⎟

⎝⎠

(5)

: , are the accelerometer readings.

where a a

()

A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System

393

An effective method for estimating the ground

truth is to calculate the current roll angle of the land

vehicle displacements. The Variation of this angle is

beings used to select the appropriate fuzzy decision

to the navigated terrain.

In our case the roll angle is the mean computed

for a period of 1 second (which corresponding to 40

samples of odometer’s data). After experiments test

we have assigned our membership function of path

condition as shown in Figure 10.

Figure 10 : The first input variable (Path Condition).

Number of Satellite Fuzzification: The second

input (Figure 11) represents the number of satellites.

As we have seen in experiments, RISS outperforms

all the other compared solutions when the number of

visible satellites is less than tree (3). Furthermore,

the RISS solution provides very good results,

compared to IMU or Odometer alone. So it is very

important to detect degradations of GPS signal to

use RISS for position estimation.

Figure 11: The second input variable (number of satilites).

IMU‘s Data Quality Fuzzification: Our fusion

algorithm takes into account the physical capabilities

and limitations of each sensor.

Figure 12: The third input variable (number of satellites).

Therefore, it is necessary to determine the quality

of IMU data during experiments. Since we are

looking to produce a simple and flexible algorithm

suitable for any IMU quality, we took into account

this point by giving users the possibility to predefine

the quality of the IMU before starting experiments.

Users can a score from 0 (very bad) to 10 (good), as

shown in Figure 12, based on the bias and scale

factor of the used inertial navigation sensor.

2.5.2 Inference System

To describe the relationship between the input and

the output, a set of rules is applied as shown in Table

1. The fuzzy rules are derived directly from the three

basic rules defined at the beginning of this section

and they cover all possible combinations of input

variables.

Table 1: If-then rules used in the fuzzy inference system

for data classification.

Inputs Output

NVS PAC SQ SW

1 Low Low Bad

INS/Odm

2 Low Low Good

INS/Odm

3 Low Med Bad

INS/Odm

4 Low Med Good

INS/Odm

5 Low High Bad

INS/Odm

6 Low High Good

INS/Odm

7 Med Low Bad

GPS/INS

8 Med Low Good

GPS/INS

9 Med Med Bad

GPS/INS

10 Med Med Good

GPS/INS

11 Med High Bad

GPS/Odm

12 Med High Good

RISS

13 Med Low Bad

GPS/INS

14 High Low Good

GPS/INS

15 High Med Bad

GPS/Odm

16 High Med Good

GPS/INS

17 High High Bad

GPS/Odm

18 High High Good

RISS

NVS: Nbr of visible satellites, PAC: path condition

SQ: sensor quality, SW: Switch data fusions.

2.5.3 Defuzziﬁcation Interface

Several popular methods exist for defuzzification

such as max-membership principle, centroid method,

weighted average method, centre of sums (Singhala,

2014). In our algorithm, the result of the

defuzzification has to be a single value that

determines which sensors integration is used to give

the best results, as shown in Figure 13.

In our case, outputs of the fuzzy fusion system,

SW (switch) are dimensionless weighting factors that

emphasize either the 1

(GPS/INS), 2

(GPS/Odm),

(GPS/RISS) or 4

(RISS) solution is the best in

terms of accuracy. The weighted average

defuzzification technique is the most prevalent and

widely adopted defuzzification method. The centroid

method is given by the following algebraic

expression:

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

394

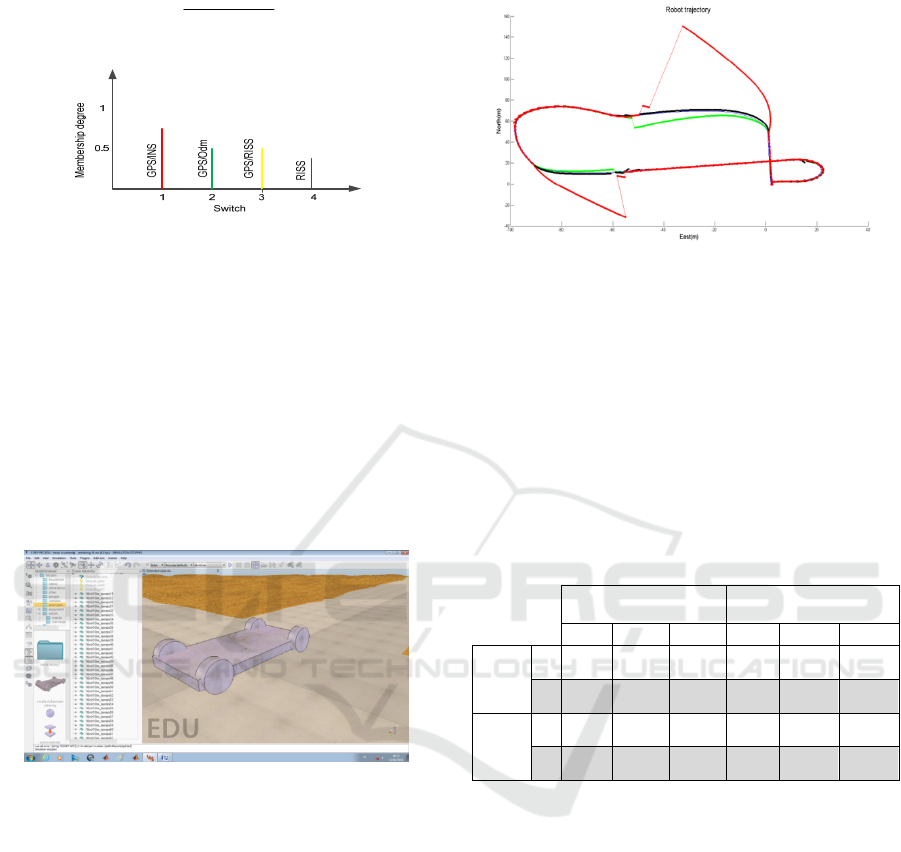
(6)

Figure 13: The output variable (Switch).

3 RESULTS AND DISCUSSION

In order to evaluate the FSC performances, several

driving were performed using data of a driving

simulator framework called Virtual Robot

Experimentation Platform (V-REP). The V-REP is a

very versatile and ideal for multi-robot applications.

This software is an open source for use in research

or academic environments which can model

dynamics of several robots (Tharin, 2012).

Figure 14: Screen shot of V-REP’s application main

window.

We have used a Simple Ackermann steering

mobile robot. It has four-wheel drive and a steered

locomotion system. The sensor part includes two

encoders measuring rear wheels rotation at 20Hz.

The system provide also GPS (1HZ) data and

inertial (acceleration and gyroscope) at 40Hz.

3.1 Evaluation of Algorithms during

GPS Outages

This section aims to evaluate the "standalone"

performances of the different integrations by

simulating a long GPS outage in sensor’s data

acquisition. During a period without GPS signal, no

updates are performed. The resulting trajectory is

built using only the prediction. Therefore, difference

in terms of positions is well highlighted.

Figure 15: Estimated and reference trajectories: bleu for

reference, Red for GPS/INS, Green for GPS/Odm, black

for the GPS/RISS integration.

Table 2 presents difference in terms of position,

resulting from a comparison of trajectories computed

with the various GPS outages. These divergences are

expressed using Root Mean Square (RMS). The

maximum diﬀerences is also listed. Note that these

different integrations are computed using only the

trajectory diﬀerences during the outages.

Table 2: Comparison of trajectories computed with GPS

outages of various duration. ( 5 s and 10 s).

First GPS outage

for 10s

Second GPS outage

for 5s

GPS/INS GPS/Odm GPS/RISS GPS/INS GPS/Odm GPS/RISS

East

errors

(m)

Max

16.25 1.21 3.42 4.11 1.50 2.11

10.85 0.64 3.64 1.12 0.16 0.85

North

errors

(m)

Max

70.23 11.26 2.05 43.29 2.41 1.55

24.28 6.04 1.32 11.72 1.48 0.69

Outages of short duration (5 seconds) are well

bridged by the Odometry navigation system. Indeed,

the maximum position deference ranges from 1.5 m

to 11 m. But the range of errors proportionally

increases with the GPS outages duration due to

accumulation of errors which appears clearly in the

first case when the outages is 10s. Moreover, the

position accuracy of a GPS/RISS trajectory ranges

from 1 m to 3 m. These results show that the

reduced inertial navigation system (RISS) is able to

bridge GPS outages of long duration or short

duration with best position accuracy.

3.2 Evaluation of Fuzzy Switcher

Controller

Several experiments with GPS outages and rough

terrain condition, using good and bad quality of

[] []

[]

Pi W i

Defuz

∑

A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System

395

IMU, were processed to evaluate FSC performances.

We did a comprehensive set of tests in V-REP using

different speeds varying between 5-25 m/s. The

deferent characteristics, i.e. the RMS, and the max

are well presented.

The trajectory used for this evaluation is similar

to the applied in section A. Here, we introduced a

variation in the number of satellites (on view) to see

the functionality of the FSC during GPS signal

degradation. However, we have simulated four GPS

outages as shown in Figure 17.

The potential parameter used to detect the

surface condition is computed from the variance of

the roll angle using 40 last samples of the

acceleration corresponding to 1s which is the

frequency of GPS, as mentioned before. The rough

terrain is easily detected as show in the Figure 16.

In the down-mentioned simulation results we

have presented only the case of a medium Quality of

inertial navigation system. However, we have given

a mark of “6”. Figure 18 shows the output of Fuzzy

switcher controller. Hence we are using an IMU

with a good quality, the FSC switches to GPS/RISS

during good surface and good GPS signal, but when

the vehicle go by a rough surface the FSC

eliminates the use of odometers measures by

switching to GPS/INS. The same case is produced

during GPS signals degradation. The FSC eliminate

the use of GPS by switching to RISS.

Figure 16: Variance of the roll angle during trajectory.

Figure 17: Variation of number of satellites.

Figure 18: Outputs of the FSC during trajecory.

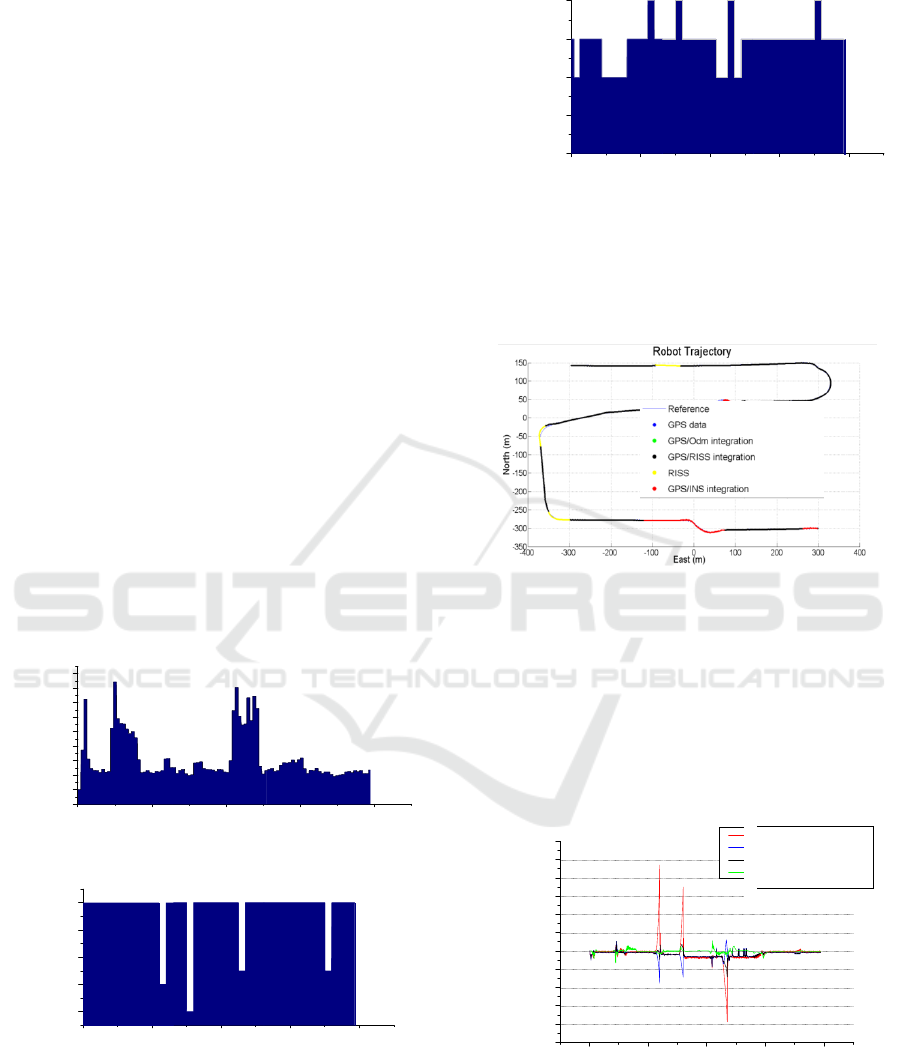
Figure 19 shows the estimated trajectory of the

robot and the ground truth during the simulation.

The trajectory is portion-colored to easily see the

different integrations used during the trajectory.

Figure 19: Trajectory plot using FSC.

Simulation results (Figure 20 and Figure 21 )

clearly show the advantage of FSC over GPS/RISS,

GPS/Odm and GPS/IMU. However there is a big

difference in 2-D positional errors when we compare

GPS/INS and GPS/Odometry with results of FSC

integration during GPS outages. This later has an

average of the maximum positional error off 3m as

shown in Table 4.

Figure 20: East position Error computed by different

integrations.

0 2000 4000 6000 8000

-0,05

0,00

0,05

0,10

0,15

0,20

0,25

0,30

0,35

0,40

The Var i anc e( r ad)

Samples

0 2000 4000 6000 8000

Nbr of vi si ble satel l ite

Samples

0 2000 4000 6000 8000

(RISS)

(

GPS/RISS)

(GPS/INS)

Samples

Fuzzy Output(Switch)

(

GPS/Odm)

0 2000 4000 6000 8000

-25

-20

-15

-10

-5

Error in East(m)

Samples

GPS/INS errors

GPS/Odm errors

GPS/RISS errors

AFSA errors

GPS/INS errors

GPS/Odom errors

GPS/RISS errors

FSC errors

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

396

Figure 21: North position error computed by different

integrations.

Table 3: Simulation measurements.

Errors during GPS outages

Outage .N° 1 2 3 4

Duration (s) 10 10 10 10

East

errors (m)

Max

2.709 2.801 4.617 1.565

RMS

1.969 1.778 2.042 0.547

North

errors (m)

Max

3.070 3.299 3.188 1.011

RMS

2.159 1.188 1.588 0.996

4 CONCLUSIONS

In this paper we introduced a Fuzzy Switcher

Controller (FSC) for navigation systems. Several

methodologies of integrating inertial sensors,

Odometry and GPS data using a loosely coupled

integration techniques are also presented. Results

show that the Fuzzy switcher controller has a

powerful adaptability to physical capabilities and

limitations of navigation systems which improves

the navigation positioning accuracy. Compared to

others integration methods, the new position errors

are controlled within ± 3m even during a GPS

outages or a rough terrain condition.

REFERENCES

Boysen, P.A. and Zunker, H. ,2004. Low Cost Sensor

Hybridisation and Accuracy Estimation for Road

Applications. ESA Conference Navitec 2004.

Noordwijk, The Netherlands. .

North, E., et al., 2012. Improved Inertial/Odometry/GPS

Positioning of Wheeled Robots Even in GPS-Denied

Environments," InTech Europe.

Xiaochuan, Z. et al., 2009. A Novel Information Fusion

Algorithm for GPS/INS Navigation System. In

Proceedings of the IEEE International Conference on

Information and Automation, Zhuhai/Macau, China,

pp. 818-823.

Singhala, P. et al., 2014. Temperature Control using Fuzzy

Logic International Journal of Instrumentation and

Control Systems (IJICS) vol. 4.

Boysen, P. A. and Zunker, H., 2004. Low Cost Sensor

Hybridisation and Accuracy Estimation for Road

Applications. In ESA Conference Navitec, Noordwijk,

The Netherlands.

Boucher, C., et al., 2004. Non-linear filtering for land

vehicle navigation with GPS outage. in IEEE

International Conference on Systems, pp. 1321 -1325.

Hay, C., et al., 2005. Wheel-Speed Dead Reckoning for

Vehicle Navigation. In GPS World, p. 37 42.

Sukkarieh, 2000. Low Cost, High Integrity, Aided Inertial

Navigation Systems for Autonomous Land Vehicles.

PhD. Thesis, Sydney. Sydney, Australia.

St-Pierre, M. and Ing, D. G. D., 2004. Comparison

between the unscented Kalman filter and the extended

Kalman filter for the position estimation module of an

integrated navigation information system," in IEEE

Intelligent Vehicles Symposium Parma, Italy, 2004.

Sakhi, S., 2014. Centrale d'acquisition pour le trace

d'engins mobiles Thèse doctorat, Ecole Militaire

Polytechnique d'Alger, Algérie.

Quinchia, A. G. and Ferrer, C., 2011. A Low-Cost

GPS&INS Integrated System Based on a FPGA

Platform. In International Conference on Localization

and GNSS, ICL-GNSS, Tempere, Finland.

North, E. et al., 2009. Enhanced Mobile Robot Outdoor

Localization Using INS/GPS Integration. In

International Conference on Computer Engineering &

Systems ( ICCES), Cairo, Egypt.

Lamon, P. and Siegwart, R., 2004. Inertial and 3D-

odometry fbsion in rough terrain-Towards real 3D

navigation. In International Conference On intelligent

Robots and Systems (IEEE/RSJ), Sendai, Japan.

Rogers-Marcovitz, F., et al., 2012. Aiding Off-Road

Inertial Navigation with High Performance Models of

Wheel Slip. In International Conference on Intelligent

Robots and Systems (IEEE/RSJ), Vilamoura, Algarve,

Portugal.

Wang, J.-H., 2006. Intelligent MEMS INS/GPS

Integration For Land Vehicle Navigation. PHD,

Department of Geomatics Engineering Calgary,

Alberta. Canada.

Kubrak, D., 2007. Etude de l’hybridation d’un récepteur

GPS avec des capteurs bas coûts pour la navigation

personnelle en milieu urbain. Thèse de Doctorat,

l’École Nationale Supérieure des Télécommunications

Paris, France.

Tharin, J., et al., 2012. V-REP User manual . Switzerland,

4 edition.

0 2000 4000 6000 8000

-20

-15

-10

-5

Error in North(m)

Samples

GPS/INS errors

GPS/Odm errors

GPS/RISS errors

AFSA errors

GPS/INS errors

GPS/Odom errors

GPS/RISS errors

FSC errors

A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System

397