Mechatronics Design, Modeling and Preliminary Control of a 5 DOF

Upper Limb Active Exoskeleton

Abdelkrim Abane

1,2,3

, Mohamed Guiatni

, Djahid Fekrache

, Saad Merouche

Abdelouahab Otmani

, Mouloud Tair

and Noureddine Ababou

Control Laboratory, Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria

Hopital Militaire Universitaire Sp

ecialis

e, Bouchaoui, Algiers, Algeria

Instrumentation Laboratory, Universit

e des Sciences et Technologie Houari Boumedienne, Beb Ezzouar, Algiers, Algeria

Keywords:

Mechatronics Design, Upper Limb Exoskeleton, Robot Modeling, PD Controller.

Abstract:

In this paper, we present the mechatronics design, modeling and preliminary control of a new 5 degrees of

freedom (DoF) exoskeleton, dedicated for the upper limb rehabilitation. The designed exoskeleton allows

the shoulder rotations as well as the elbow movements. It combines the advantages of both parallel and

serial mechanisms. It has been designed by considering the main factors in designing a general use robotic

force-feedback device and the human upper limb specications. This active device, as a kind of haptic device,

provides two ways communication in both position and force, and allows patients to interact with the virtual

reality system and practice activities of daily living (ADL) assistance. The kinematic model of the exoskeleton

is presented. In order to evaluate the performance of the exoskeleton, a preliminary position and torque

controllers have been implemented.

1 INTRODUCTION

Due to the increasing need of physical rehabilitation

of the upper extremity, many research groups have

proposed robotic devices with the potential to facil-

itate the rehabilitation process. Many devices for up-

per limb rehabilitation have already been proposed.

These devices have the potential to address this prob-

lem as noted by the results of recent research stud-

ies. An excellent survey and a state-of-the-art on

robotic devices for upper limb rehabilitation is com-

piled in (Maciejasz et al., 2014) in which more than

200 references and more than 100 devices have been

cited and compared in terms of number of degrees of

freedom (DOF), actuation, supported movements of

the limb (shoulder, elbow, forearm, wrist and ﬁngers),

control inputs, type and ﬁeld of application and their

stage of development. A vast majority of these pro-

posed devices are technically advanced and are de-

signed for clinical settings. However, there is still

signiﬁcant need to improve efﬁciency and reduce cost

of home-based devices for therapy and ADLs assis-

tance. The effectiveness of robotic over conventional

therapy is arguable and the best therapy strategy is

still not clear (Maciejasz et al., 2014) (Jarrassee et al.,

2014). The situation may change soon, because more

and more devices are being commercialized and more

scientiﬁc results will be available. It may encourage

next groups to propose their own solutions. Devel-

oping new devices and improving those already in the

market will be easier, when taking advantage from the

already existing solutions (Gopura et al., 2011) (Jar-

rassee et al., 2014) (Chay et al., 2014).

The aim of this work is to propose a new de-

vice for the upper limb rehabilitation. The proposed

exoskeleton-based devices have a mechanical struc-

ture that mirrors the skeletal structure of patients limb.

Therefore movement in the particular joint of the de-

vice directly produces a movement of the speciﬁc

joint of the limb. The use of exoskeleton-based reha-

bilitation allows for independent and concurrent con-

trol of particular movement of patients arm in many

joints, even if the overall number of assisted move-

ments is higher than six. However, in order to avoid

patient injury, we have taken care in our device to ad-

just lengths of particular segments of the manipula-

tor to the lengths of the segments of the patient arm.

Therefore setting-up such device for a particular pa-

tient, especially if the device has many segments, may

take a signiﬁcant amount of time.

This paper is organized as follows: Section 2

presents the mechanical design methodology of the

398

Abane, A., Guiatni, M., Fekrache, D., Merouche, S., Otmani, A., Tair, M. and Ababou, N.

Mechatronics Design, Modeling and Preliminary Control of a 5 DOF Upper Limb Active Exoskeleton.

DOI: 10.5220/0005984203980405

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 398-405

ISBN: 978-989-758-198-4

new exoskeleton with respect to the design require-

ment of such a device. Section 3 presents the kine-

matics of the exoskeleton, forward and reverse kine-

matic will be computed, the Jaccobian matrix will

be derived. These models will be used to develop

controller for the exoskeleton. Section 4 develops

the control setup and preliminary position and torque

control schemes of the 5 DOF exoskeleton based on a

Propotional Derivative (PD) and Propotional Integral

Derivative (PID) controllers. Finally, we will present

some results about the control loops implementation.

2 MECHANICAL DESIGN

METHODOLOGY

2.1 Design Considerations

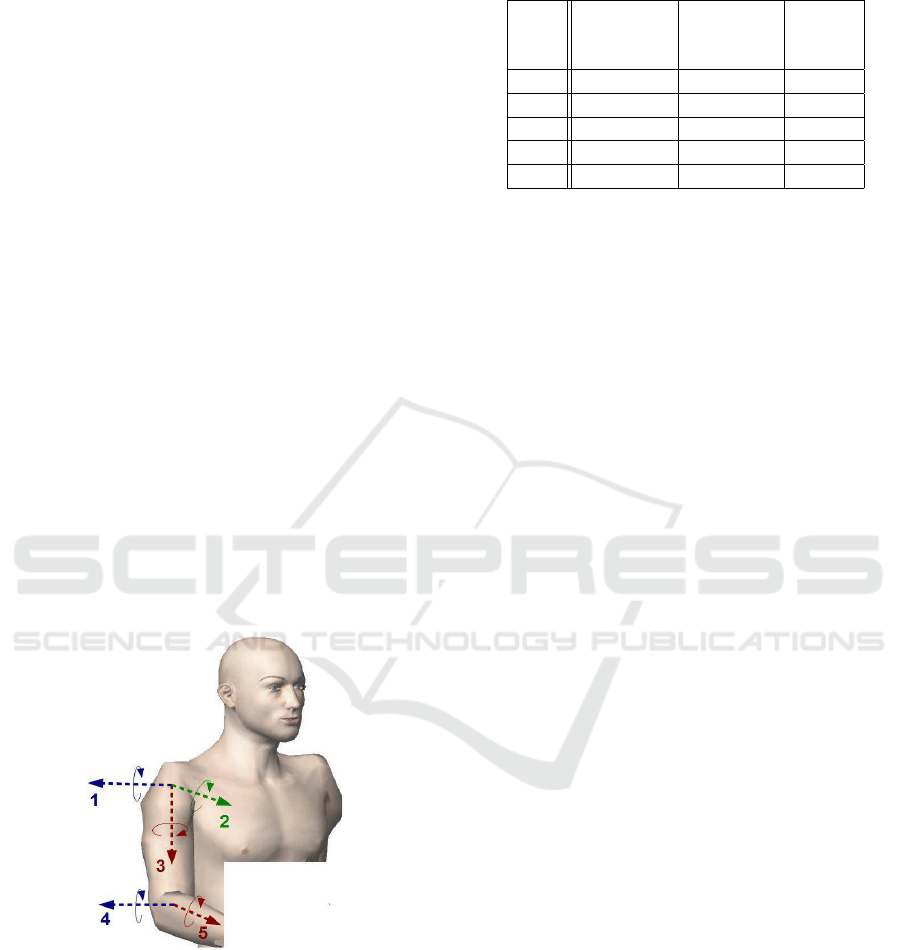
Upper limb rehabilitation devices require movement

of shoulder joint and elbow joint for both limbs. The

movement of the shoulder and elbow are contributed

to the rotation and translation of the wrist. Shoulder is

the most complex joint in the human arm i.e., move-

ment of the shoulder joint can be estimated as rotation

in single ball-and-socket joint with 3 DOFs. Elbow

has a hinge joint which can rotate with 2 DOFs as

shown in Fig. 1. The human arm torque requirements

during daily activities are presented in table 1.

Figure 1: Shoulder and Elbow rotations.

2.2 Hybrid Mechanical Structure

Design

When considering the construction of a robotic de-

vice, there is a choice between serial and parallel

mechanisms (Chen et al., 2014). The key difference

between serial mechanisms and parallel mechanisms

is in their kinematics structures. Parallel mechanisms

Table 1: Torque Requirement for each rotation (Rosen et al.,

2005).

Torque 5 % ADL

joint Human Torque Torque

max [Nm] max [Nm] [Nm]

1 115 5.75 10

2 134 6.5 10

3 60 3 3.1

4 68 3.4 3.8

5 72 3.6 3.8

are composed of, at least, two closed chains that con-

nect a moving platform to a ﬁxed base thus allow-

ing the actuator to be away from the moving plat-

form. For a relatively similar size of the linkages, a

serial mechanism presents a larger workspace volume

than a parallel mechanism. For parallel mechanism,

workspace is compromised by the constraints of all

links that connect the end-effector. For serial mech-

anism, every actuator has to exert enough torque and

power to move all distal links and overhead actuators.

However, the actuators of a parallel mechanism can

be placed on ground to support stronger payload than

a serial mechanism does. It can be made so for se-

rial mechanisms, but at the cost of complex transmis-

sion mechanisms and this is not always possible for

all the links. For parallel mechanism, the geometri-

cal errors are not accumulated, as all the branches are

connected to the end-effector. The dimension accu-

racy of each link must be high so that the position and

orientation of the end effector is more accurate than a

serial mechanism. For serial mechanism, the geomet-

rical errors are accumulated for each link. Therefore,

the end effector will have lower position accuracy.

For serial mechanism (Laycock and Day, 2003), each

chain increases the total inertia while it decreases the

total stiffness. Parallel mechanisms do not exhibit the

above problem and have a much higher stiffness (Bir-

glen et al., 2002). The disadvantage over serial mech-

anisms is that the mechanism’s elements can physi-

cally interfere. The advantages of both mechanisms

are incorporated by combining them in a hybrid con-

ﬁguration (Baser et al., 2006) that includes both par-

allel and serial linkages. By using hybrid conﬁgura-

tions, the stiffness remains relatively high and a large

workspace can be achieved.

Our design contains 5 DOF: there is 2 DOF

parallel mechanism which insures the abduc-

tion/adduction, ﬂexion/extension rotations of the

shoulder. This parallel mechanism consists in

two legs (chains), each being regarded as a serial

manipulator. The ﬁrst chain constitutes a two-axes

serial manipulator and the second chain constitutes

a three-axes serial manipulator. These two chains

Mechatronics Design, Modeling and Preliminary Control of a 5 DOF Upper Limb Active Exoskeleton

399

are coupled through a moving part that supports

a third 3 DOF serial chain. The ﬁrst DOF of this

chain ensures the lateral rotation/medial rotation of

the shoulder. The fourth and ﬁfth rotations ensure

the ﬂexion/extension and the abduction/adduction

rotations of the elbow. The design of our device

was performed and validated under the SolidWorks

software.

2.3 Actuation, Transmission and

Reduction

The actuation, the reduction and the transmission are

closely coupled and must be designed together. They

are selected according to the requirements speciﬁed in

the last subsection. The type of the incorporated actu-

ators affects the overall weight of the device. In most

cases, a good actuator should be compact and light

as well as capable of producing the necessary power

to deliver necessary forces. There are tradeoffs be-

tween power, volume and weight since actuators ca-

pable of producing large forces are generally heavier

and are larger in size than those actuators capable of

smaller forces. The dimensioning procedure of the

actuator was performed under MotionWorks plug-in

of Solidworks, by applying dynamic forces on device

end-effector and then obtaining the required actuator

torques. We select brushed Maxon DC motors with

a low inertia and low friction, which are suitable for

this kind of devices. Maxon RE40 is used for the ab-

duction/adduction, ﬂexion/extension rotations of the

shoulder and RE25 for the ﬂexion/extension and the

abduction/adduction rotations of the elbow and the

lateral rotation/medial rotation of the shoulder.

In order to provide the highest amount of ﬁdelity,

direct drive (absence of transmission of reduction) is

likely to be the best solution. However, this solu-

tion does not provide adequate forces/torques needed

for our application, which we saw earlier is criti-

cal. Among the other transmission and reduction

techniques such as the use of linkages, cables, steel

belts, shafts plus gears, this last one gives the worst

case (Hayward, 1995) since it causes high backlash

and high back-drive friction due to the gear gaps and

gear friction. Back-drive friction and backlash can be

reduced by using cable driven transmission systems.

Therefore, cable driven transmission technique (cap-

stan) was used in our design.

A solution consists of using a combined reduc-

tion (Planetary gear/capstan) in order to amplify the

torques developed by the actuators. We use plane-

tary gears reduction because it has fewer backlashes

and less friction, especially when the reduction ratio is

small (the reduction ratio are 4 for RE40 actuators and

19 for the RE25 actuators in this case). We have de-

signed capstan reduction mechanisms with a ratio of

20 for the abduction/adduction and ﬂexion/extension

rotations of the shoulder and 10 for the lateral ro-

tation/medial rotation of the shoulder and the ﬂex-

ion/extension and the abduction/adduction rotations

of the elbow. The resulting reduction ratios and the

maximal torque that could be generated for each axis

are presented in Table 2. This solution is able to pro-

vide additional torque for gravity and friction com-

pensation.

Table 2: Reduction ratio and maximal torque for each joint.

J Motor Total Resol. Max Torque

Ratio (N.m)

1 RE40 80 0.009

◦

14.5

2 RE40 80 0.009

◦

14.5

3 RE25 190 0.004

◦

5.6

4 RE25 12 0.06

◦

0.83

5 RE25 190 0.004

◦

5.6

As it was presented previousely, the exoskeleton

should include low inertia, no backlash, light weight

and negligible friction (Laycock and Day, 2003).

Therefore, a compromise has to be reached between

the various design goals. Obtaining negligible fric-

tion can be a problem, particularly when high stiffness

is required. High stiffness implies a stiff mechanical

interface which needs to be constructed from metal

which increase the friction and the overall weight of

the device. This provides a conﬂict between obtaining

high stiffness while keeping low friction (Baser et al.,

2006)(Laycock and Day, 2003). So that, the materials

used to construct such devices need to be considered

with additional costs. In our design:

• Aluminum was used in order to minimize the de-

ﬂection due to the stiffness of the linkages.

• Cable driven transmission technique was used in

order to overcome backlash deﬂection.

• Stainless steel ball bearings and high precision

manufacturing methods were used in order to

overcome joint deﬂections.

The Computer Aided Design (CAD) model of the ex-

oskeleton is shown in Figure 2 and table 3.

2.4 Stress and Deﬂection Analysis

After the completion of the preliminary mechanical

design procedure, links shape and thickness must be

optimized to satisfy the design requirements men-

tioned before, such as the reduction of the inertia of

the device and the maximization of the stiffness. For

this structure, the links stress analysis is carried out

using COSMOSXpress plug-in of Solidworks. Static

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

400

Figure 2: CAD Model of the designed exoskeleton.

Table 3: Parts designation for the CAD model.

◦

Designation N

◦

Designation

01 Motor 1 (RE40) 13 Body 2

02 Gear 14 Capstan 4

(GP42) (12:1)

03 Capstan 1 (20:1) 15 Adjustable

(20:1) link

04 Body 1 16 Body 4

05 Motor 3 17 Capstan 3

(RE25) (10:1)

06 Encoder 3 18 Body 3

(HEDS 5540)

07 Encoder 4 19 Capstan 2

(HEDS 5540) (20:1)

08 Motor 4 20 Encoder 2

(RE25) (HEDS 5540)

09 Encoder 5 21 Motor 2

(HEDS 5540) (RE40)

10 Motor 5 22 Gear

(RE25) (GP42)

11 Capstan 5 23 Fixed base

(10:1)

12 End-effector 24 Encoder 1

(HEDS 5540)

analysis of the mechanical design would be sufﬁcient

because the device will be used with low speeds. The

links shape and weights are computed for aluminum

with a Young modulus of 69000 MPa and a mass den-

sity of 2700 kg/m

as construction material. This ma-

terial is used because of its high yield strength over

weight ratio. According to the analysis results, the

shape and the thickness of the links should be mod-

iﬁed in iterations. The weight values of the motors,

reductors and links starting from the tool tip and mov-

ing to the base of the robot are used to determine the

static load on the robot links.

In Figure 3, an example of deformation and dis-

tribution of von-Mises stresses are illustrated for two

links of the manipulator. Contour diagram and max-

imum stress points are shown in the ﬁgures. Legend

on the right side of the ﬁgure shows the distribution of

contour diagram. Legend on the right hand side of the

ﬁgure shows the distribution of contour diagram. In

this analysis, deformation in the translational move-

ment direction is studied under static loading of 50 N,

which corresponds to the maximum force that shall be

applied during MIS procedures. Naturally, maximum

deﬂection occurs at the end of the links. The maxi-

mum and minimum deformation points are shown in

the ﬁgure. It has been observed that the link 1 and 3

(parts 06 and 17 in table 3) are the most critical links

since they are exposed to maximum stress in any con-

dition. The shape and thickness of the links are op-

timized according to the maximum deﬂection values

obtained from the analysis. Figure 4 represents the

manufactured exoskeleton.

Figure 3: Von-Mises Stress analysis of links 1 (left) and 3

(right).

Figure 4: Final prototype of the exoskeleton.

3 EXOSKELETON MODELING

3.1 Kinematic Modeling

Figure 5 shows the position of the frames attach-

Mechatronics Design, Modeling and Preliminary Control of a 5 DOF Upper Limb Active Exoskeleton

401

Figure 5: Kinematics of the exoskeleton.

ments. All the frames intersect at one point named ’O’

situated at the center of the moving platform that con-

nects the two parallel chains to each other, thus sim-

pliﬁes the kinematics modeling. For each chain, the

kinematics model is obtained by using the modiﬁed

method of Denavit and Hartenberg (Khalil and Dom-

bre, 1999), where

i−1

represents the rotation ma-

trix from the frame F

i−1

) to the frame

Kinematics parameters are deﬁned in tables 4

and 5, where α

represents the joint offsets, r

and L

the link lengths and θ

the joint variables. The mov-

ing platform is a body of both Chain 1 and Chain 2. In

Chain 1, it is referenced by the frame F

and in chain 2

by F

. So that, the kinematics constraints representing

the closure condition of the parallel structure formed

by Chain 1 and Chain 2 are then:

= arctan(tan(θ

)/C

) (1)

Table 4: DHM kinematics parameters of Chain 1.

j α

1 π/2 0 θ

2 π/2 0 θ

3 π/2 0 θ

4 −π/2 −L

−L

5 −π/2 L

6 −π/2 0 0 L

Table 5: DHM kinematics parameters of Chain 2.

j α

6 −π/2 0 θ

7 −π/2 0 θ

8 −π/2 0 θ

and:











= arctan2



),±

1 − (S

)



= arctan2













= arctan2













(2)

Where Ci and Si stand for cos (θ

) and sin (θ

), respec-

tively.

The angular positions of the passive joints θ

, θ

and θ

are computed based on the angular positions

of the active joints θ

and θ

. Expressions (1) and (2)

are not deﬁned for θ

= ±

and θ

= ±

. Fortu-

nately, all these conﬁgurations are outside the reach-

able workspace.

The orientation and position of the end-effector is

determined by taking the joint angles of the linkages

and using the forward kinematics calculation as fol-

lows:







0 0 0 1







Thus, the kinematic model of the exoskeleyon is de-

ﬁned as follows:











= S

(−S

+ l

) + S

(−L

+ L

) +C

((L

+ L

− L

+ S

+ L

))

+ l

))

−C

+ l

− L

+ L0))

= C

+ L

− L

) −C

+ L

))

((L

+ L

− L

+ L

)

= S

+ L

) − S

(−L

+ L

)

((L

+ L

− L

+ L2))

+ L

− L

+ L

))

(3)

where

represents the position of the end-

effector deﬁned in the frame

F and (s, n, a) its ori-

entation. We use the Euler angles (α,β ,γ ) in order to

deﬁne this orientation as follows:











β = arctan2



−s

+ s



α = arctan2(s

/cos(β),s

/cos(β))

γ = arctan2(n

/cos(β),n

/cos(β))

(4)

where :

• α deﬁnes the rotation around the Z

axis.

• β deﬁnes the rotation around the Y

axis.

• γ deﬁnes the rotation around the X

axis.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

402

and











= C

) + S

= C

− S

= C

− S

) −C

= S

) +C

= S

−C

) + S

) +C

(5)

The workspace of the exoskeleton is presented in Ta-

ble 6.

Table 6: Designed exoskeleton vs human arm workspace

comparison.

j Joint Human arm Exoskeleton

Adduction

1 /abduction -45/180

◦

-45/100

◦

(shoulder)

Extension

2 /ﬂexion -50/180

◦

-45/100

◦

(shoulder)

External

3 /internal -80/90

◦

-70/70

◦

rotation

Adduction

4 /abduction 0/200

◦

0/140

◦

(Elbow)

Extension

5 /ﬂexion 0/145

◦

0/140

◦

(Elbow)

3.2 Jaccobian Matrix

The Jacobian matrix J is one of the most important

quantities in the analysis and control of robot motion.

It arises in virtually every aspect of robotic manipu-

lation: in the planning and execution of smooth tra-

jectories, the execution of coordinated anthropomor-

phic motion, in the derivation of the dynamic equa-

tions of motion, and in the transformation of forces

and torques from the end-effector to the manipulator

joints and in the determination of singular conﬁgura-

tions.

The resulting Jaccobian matrix of the exoskeleton

is deﬁned as follows:

J =







−L

−C

−S

0 1

−S







(6)

where,











= C

(−(C

+ L

− L

+ L

)

−S

+ L

)) − S

(−S

(−(C

+ L

− L

+ L

)

−C

+ L

))

+ L

) − S

+ L

))

= (−S

−C

− L

+ L

)

= S

= C

+ L

= ((L

− L

+(−L

− S

+ S

+ (−C

(−L

+ L

+ (−C

− L

)

+ L

− S

)

= ((L

+ L

+ S

−L

+ L

+(L

− L

= (L

+ L

− L

+ L

= ((L

− L

+ (L

+ S

−S

− L

−C

(−L

+ L

+ (L

− L

)

= (−(L

+ L

)

− S

+ L

)

−C

(−L

+ L

−C

= (−L

− L

+ L

= S

−C

= (−S

−C

= −S

= (−S

−C

+ S

= −S

− S

(7)

4 ELECTRONICS INTERFACE

AND PRELIMINARY CONTROL

LOOP DESIGN

4.1 Position and Current Sensing

The angular positions of the ﬁve active joints are mea-

sured thanks to ﬁve incremental encoders type HEDS

5540 from Maxon. These encoders are placed in the

rear of the motors and provide 500 pulsations per rev-

olution of the motor axis. Thus, the position measure-

ment resolution is computed by taking into account,

the reduction ratio ((360/500)/N, while N is the re-

duction ratio). Table 2 presents the angular position

resolution of each joint. Current sensors type LTS 15-

NP are also integrated in order to measure the actua-

tor’s current. The measured current is used in order to

estimate the actuator’s torque.

Mechatronics Design, Modeling and Preliminary Control of a 5 DOF Upper Limb Active Exoskeleton

403

4.2 Electronics Interface

The control setup consists in a dSPACE DS1103 Con-

trol Board which is a versatile and powerful real-time

measurement and control board. The power stage is

designed based on two OPA541 and three OPA548

operational power ampliﬁers from Burr-Brown which

are able to provide a current about 10 for RE40 mo-

tors and 3A for RE25 motors respectively (Fig. 6).

Linear Power

Amplifier (01)

OPA541

DC Motor (02)

Maxon RE40

DC Motor (04)

Maxon RE25

Incremental Encoder

(01) HEDS 5540

Linear Power

Amplifier (03)

OPA548

Linear Power

Amplifier (04)

OPA548

Linear Power

Amplifier (05)

OPA548

DC Motor (03)

Maxon RE25

DC Motor (05)

Maxon RE25

DAC02

DAC03

DAC04

DAC05

Incremental Encoder

(02) HEDS 5540

Incremental Encoder

(03) HEDS 5540

Incremental Encoder

(04) HEDS 5540

ENC01

ENC02

ENC03

ENC04

ADC01

Current sensor (01)

Current sensor (02)

Current sensor (03)

ADC02

ADC03

ADC04

Dspase DS1103

Board

Current sensor (04)

Current sensor (05)

Incremental Encoder

(05) HEDS 5540

ENC05

ADC05

Linear Power

Amplifier (02)

OPA541

DC Motor (01)

Maxon RE40

DAC01

Figure 6: Overview of the electronics interface.

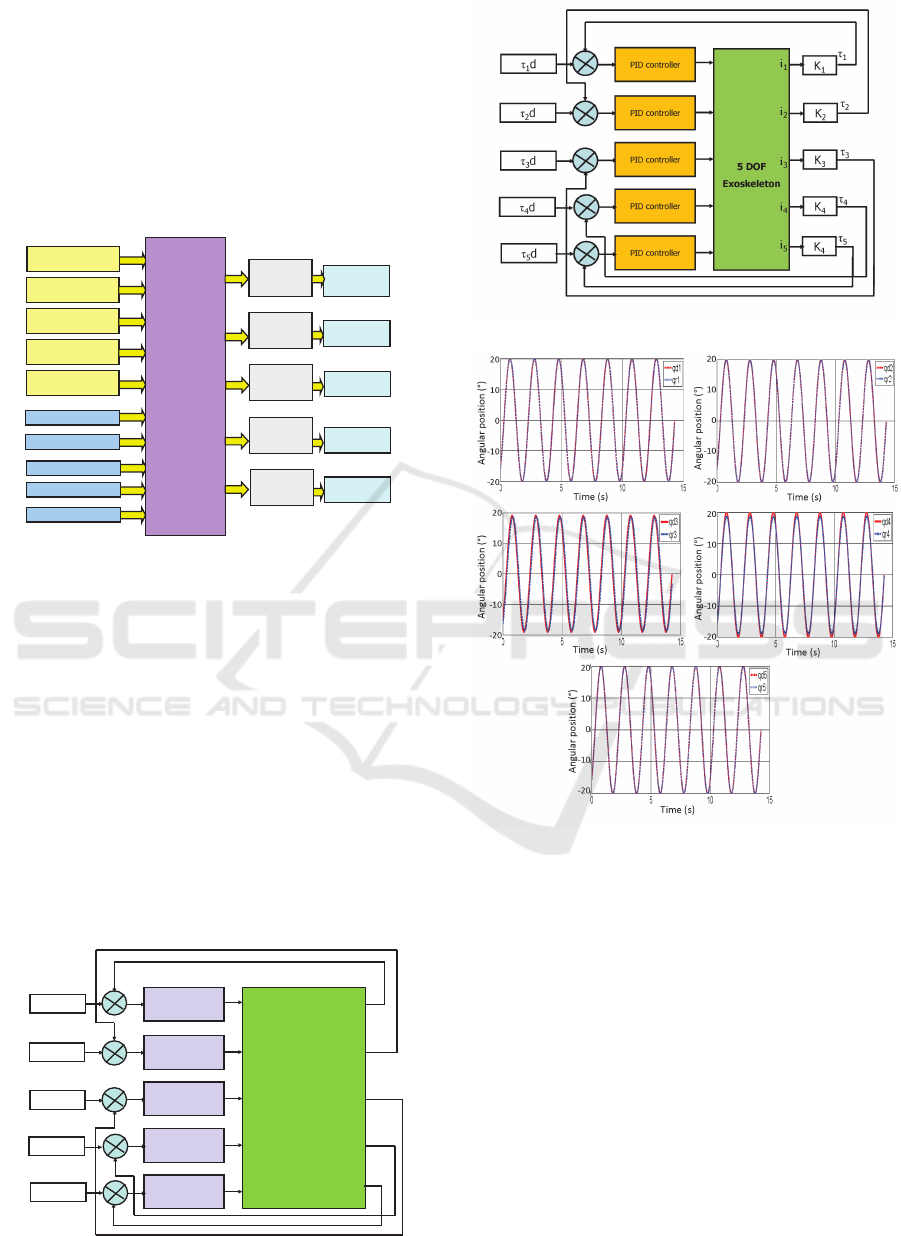
4.3 Preliminary Control Loop Design

In order to assess the model and to evaluate the per-

formances of the assembled exoskeleton, basic posi-

tion and torque control loops are implemented. We

used proportional-derivative (PD) and proportional-

derivative-intergral (PID) controllers respectively for

each joint of the exoskeleton (see Fig.7 for position

control and Fig.8 for torque control). In Fig.8, con-

stants K

(i = 1,...5) represent the torque constants of

the actuators.

These preliminary controllers have been imple-

mented successfully. Figure 9 presents an example

of the obtained results for sinusoidal position track-

ing while Fig. 10 presents an example of the obtained

PD controller

5 DOF

Exoskeleton

PD controller

Figure 7: Preliminary position control scheme.

Figure 8: Preliminary torque control scheme.

Figure 9: Articular position control example.

results for square torque tracking. These results show

that the PD controller allows improving the time re-

sponse of the system and eliminating the static error

in the position control loop in a stable way. Simi-

lar remarks are recorded for the torque controller. So

that, and since the ﬁrst instant, the resulting trajec-

tory converges faster to the desired one. These results

show the good tracking capability of the developped

exoskeleton.

5 CONCLUSION

A new exoskeleton has been designed and realized for

the upper limb rehabilitation objective. This new de-

vice takes beneﬁts from both the advantages of serial

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

404

Figure 10: Articular torque control example.

mechanisms and parallel mechanisms. It allows mov-

ing the shoulder joint around three axes and the elbow

around two axes. Kinematics of the exoskeleton has

been computed, and its capabilities have been deter-

mined and compared to the requirements. Preliminary

position and torque control loops have been imple-

mented in order to evaluate the basic performance of

the device in term of position and torque tracking. Fu-

ture works will concern a bandwidth analysis, model

based control, admittance control, and clinical evalu-

ation of the exoskeleton.

REFERENCES

Baser, O., Konukseven, E. I., and Koku, B. (2006). 7 dof

haptic device design. In EuroHaptics 2006, pages

507–512.

Birglen, L., Gosselin, C., and Pouliot, N. (2002). Shade,

a new 3-dof haptic device. IEEE Transactions on

Robotics and Automation, 18(2):166–175.

Chay, K.-H., Lee, J.-V., Chuah, Y.-D., and Chong, Y.-Z.

(2014). Upper extremity robotics exoskeleton: Appli-

cation, structure and actuation. International journal

of Biomedical Engineering and Science, 1(1):35–45.

Chen, Y., Li, G., Zhu, Y., Zhao, J., and Cai, H. (2014).

Design of a 6-dof upper limb rehabilitation exoskele-

ton with parallel actuated joints. Biomed Mater Eng.,

24(6):2527–2535.

Gopura, R. C., Kiguchi, K., and Bandara, S. V. (2011). A

brief review on upper extremity robotic exoskeleton

systems. In 6th IEEE International Conference on In-

dustrial and Information Systems, pages 346–351.

Hayward, V. (1995). Toward a seven axis haptic device.

In International Conference on Intelligent Robots and

Systems, pages 31–33, Washington, DC, USA. IEEE

Computer Society.

Jarrassee, N., Proietti, T., Crocher, V., Robertson, J., Sah-

bani, A., Morel, G., and Roby-Brami, A. (2014).

Robotic exoskeletons: A perspective for the rehabili-

tation of arm coordination in stroke patients. Frontiers

in Human Neuroscience, 8(947).

Khalil, W. and Dombre, E. (1999). Mod

elisation, identiﬁ-

cation et commande des robots. Collection robotique.

Laycock, S. D. and Day, A. M. (2003). Recent develop-

ments and applications of haptic devices. Computer

Graphics, Blackwell Publishing Ltd, 22(2):117–132.

Maciejasz, P., Eschweiler, J., Gerlach-Hahn, K., Jansen-

Troy, A., and Leonhardt, S. (2014). A survey on

robotic devices for upper limb rehabilitation. Journal

of NeuroEngineering and Rehabilitation, 11(3):1–29.

Rosen, J., Perry, J. C., Manning, N., Burns, S., and

Hannaford, B. (2005). The human arm kinemat-

ics and dynamics during daily activities-toward a 7

dof upper limb powered exoskeleton. In Advanced

Robotics, 2005. ICAR’05. Proceedings., 12th Interna-

tional Conference on, pages 532–539. IEEE.

Mechatronics Design, Modeling and Preliminary Control of a 5 DOF Upper Limb Active Exoskeleton

405