Tactile Display Design for Securing Flight and Reducing the Saturation

of Pilot’s Visual Channel

Khaled Fellah and Mohamed Guiatni

Control Laboratory, Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria

Keywords:

Tactile Feedback, Fuzzy Logic Controller (FLC), Pilot’s Visual Channel Satuation, Inverse Dynamic, Flight

Simulation, Xplane, Tactors.

Abstract:

Visual channel dominates the design of the cockpit, and auditory channel is progressively being used as well.

However, tactile displays are almost abstract in the cockpit designs. Whereas, many research proved that

several applications exist where the tactile displays may become an important or even essential choice. This is

due to the fact that the visual feedback is not suitable, not adequate, or surcharged and that the visual attention

is usually limited to a simple entity. In this paper, we propose a design of a low-cost tactile feedback system

to provide the pilot with better insight in the ﬂight path and prevent limitations during ﬂight. In the ﬁrst part

of the paper, we develop an effective control strategy based on inverse dynamic to solve the problems of use

of the low-cost tactors. The obtained results showed reduction of 48 % in settling time. The second part

describes the use of Fuzzy Logic Controllers (FLC) to compute a new form of tactile output of the translation

of a pertinent ﬂight data information and ﬂight envelope to vibrotactile feedback signals. And in the last part,

we develop a wireless (and USB) vibrotactile feedback device consisting of 16 embedded tactors controlled

with an inverse dynamic strategy via an arm Cortex M3 architecture. Pilots equipped with the developed tactile

display were capable of successfully ﬂying in a simulator. They conﬁrm that tactile feedback is an interesting

way of feeding back information about the airplane’s state, in order to give a better understanding of what the

airplane is doing during controlled ﬂight.

1 INTRODUCTION

The human vision is a very convenient channel for

processing large amounts of data because our brain

receives around 80% of all information from visual

cues (Rosenblum, 2011). However, a pilot interacts

with the modern cockpit displays through cursor con-

trol devices (CCD) or multi-function displays (MFD),

and the total quantity of information which is at the

disposal of pilot is offered mainly in a visual format

(Thomas et al., 2015). The problems which the de-

velopers of the human-machine interfaces encounter

in the modernization of the new cockpits are primar-

ily caused by the limit of the capacities of the pi-

lots to process the information related to the data of

ﬂight (Van Veen and Van Erp, 2001). In addition, the

excess of visual information channel can cause fatal

accidents if a pilot cannot analyze or perceive stim-

uli at the right time (Petit, 2013). This menace of

sensory overload makes the designers of cockpit pro-

gressively apply multimodal interfaces (Lloyd et al.,

2003). Traditionally, the auditory display is consid-

ered as an alternative or complementary to visual dis-

plays. However, the visual and auditory channels of a

pilot are sometimes strongly loaded, degraded or not

available (Van Erp and Self, 2008). Several research

tasks to integrate tactile display applications, in order

to provide countermeasures of the spatial disorienta-

tion (SD) and solutions to the threats of the sensory

and/or cognitive overload (Self et al., 2008). Appli-

cation of the touch screens in the cockpits of different

types of aircraft got much attention. In 2015, Salzer

et al. (Salzer and Oron-Gilad, 2015) designed a tac-

tile feedback system display on-thigh part in a cock-

pit to improve ﬂight safety by improving the situa-

tional awareness of helicopter pilots and reducing the

collisions probabilities. Schmidt-Skipiol (Schmidt-

Skipiol, 2015) presented a new concept of the use

of tactile feedback with Flight Envelope Protection.

Coalition Warfare Program (CWP) (Lawson and Ru-

pert, 2014) developed a Tactile Situation Awareness

System (TSAS) on-torso in UH-60 Black Hawk. The

results showed that landing performance in degraded

visual environments was signiﬁcantly improved when

ground speed and altitude were presented on a tac-

tile display (Jansen et al., 2008). Nojima et al. (No-

362

Fellah, K. and Guiatni, M.

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel.

DOI: 10.5220/0005984303620373

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 362-373

ISBN: 978-989-758-198-4

jima and Funabiki, 2005) developed a tactile display

system consisting of 6x4 pin-array tactors placed on

an aircraft control side-stick to inform a pilot about

altitude and vertical speed and increase situational

awareness during ﬂight path. VanErp et al. (Van Erp

et al., 2005) examined the possibility to present the

helicopter navigation information on a belt tactile dis-

play, including the translation of distance to vibration

rhythm and the direction to vibration location. Mc-

Grath (McGrath, 2000) used a tactile display of 12

tractors to demonstrate that it is possible to manually

ﬂy an airplane (T34-C) without visual instruments

and outside view by feeding back the pitch and the

bank angle simultaneously to the pilot. In this study,

we aim to design a vibrotactile display to provide a

current optimal state of the aircraft to the pilot and

display the warning signal about a limitation of the

ﬂight envelope, ﬂight path climb, pitch or bank angles

limitations. A new approach is adopted by exploiting

the results of the work of McGrath (McGrath, 2000)

with the use of a low cost tactors. In this study, we

aimed at ﬁnding quantitative and qualitative perfor-

mance differences while combining a low cost tactile

system with the ﬂight envelope generating an artiﬁcial

stress situation.

2 VIBROTACTILE DISPLAY

DESIGN

2.1 Vibrotactile Actuators

Devices that are used to stimulate the human skin

in embedded tactile display communication systems

must create a range of sensations which vary ac-

cording to the intensity, duration of stimulation, lo-

cus of stimulation, frequency and waveforms (Jones

and Sarter, 2008). Other important engineering con-

siderations factors generally include weight, shape,

size, power consumption, cost, durability, reliabil-

ity, availability, and wearability (Jones and Sarter,

2008). Two types of actuators are commonly used

for tactile stimulation, electrotactile and vibrotactile,

which are distinguished on the basis of the mecha-

nism used to stimulate the human skin (Jones and

Sarter, 2008). Electrotactile actuators stimulate the

human skin by passing a current through surface elec-

trodes. Vibrotactile actuators stimulate the skin by

converting electrical energy into a mechanical dis-

placement. Vibrotactile stimulation can be divided

into four broad classes, piezo-actuators, Shape mem-

ory alloy (SMA), linear resonant actuators (LRAs) or

eccentric rotating masses (ERMs) could be utilized

(Van Erp et al., 2005). Tactors type ERM actuators are

compact and lightweight, and have a larger bandwidth

than LRA actuators. Moreover, coin LRA actuators

vibrate in the axial direction (i.e. normal to the coin

surface) whereas coin type ERM actuators produce

radial vibrations (Renwick, 2008). Brown and Kaare-

soja (Brown and Kaaresoja, 2006) compared the ERM

to the C2 tactors by varying the rhythm and intensity

of the vibration. They found that the overall vibro-

tactile signal recognition of human study participants

using an ERM actuator was nearly identical to the par-

ticipants signal recognition using a C2 tactor (Choi

and Kuchenbecker, 2013). This result is promising,

as it suggests that the pager motors may provide the

same performance in terms of recognizing and iden-

tifying vibratory signals as much more expensive tac-

tors. Therefore, we have chosen the 308-102 tactors,

manufactured by Precision Microdrives. These are

ERM actuators which offer peak amplitude of 5.5G,

with a body diameter of 8mm, and they cost less than

20 $. However, this type of actuators presents a de-

lay of few hundred milliseconds (Choi and Kuchen-

becker, 2013). In order to overcome this problem, we

have developed a inverse dynamics based controller

with friction compensation.

2.2 System Design and Discussion

The developed tactile feedback system consists of 16

tactors placed in deﬁned position in the skin, and a

control device containing a FLC for the conversion of

the ﬂight data into tactile signal. Another controller

base on dynamic inverse to modify the dynamics of

the tactors to use them in the prevention from the pi-

lotes capacities degradation.

To study and analyze the developed tactile system,

a platform of tests is proposed. This tests must be

near as possible as to the real conditions. For that,

we implement the Hardware-in-the-Loop-Simulation

(HILS) including a developed tactile display system,

aircraft dynamic model and X-plane.

The model of an aircraft is implemented in Mat-

lab/ Simulink. A series of tests on X-plane environ-

ment is performed to see the behavior of the devel-

oped model in different ﬂight situations. As an ex-

periment we sent the measured geodetic latitude, lon-

gitude and altitude inputs from the model to ﬂight

control surfaces of an aircraft in the X-Plane envi-

ronment. The tactile display system recieved the cal-

culated ﬂight envelope limit, ﬂight path climb, pitch,

bank and turn rate angles and translated it into effec-

tive vibrotactile signal. Through this HIL simulation,

the tactile display system can be tested on real aircraft

minimizing risks.

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel

363

2.3 Hardware-in-the-Loop Simulation

The main components of the Design of the hardware-

in-the-loop simulation structure is :

• Aircraft Dynamics.

• Flight Simulator X-Plane application.

• Tactile display hardware and software system.

The pilot commands the aircraft surface in the X-

plane environment by introducing inputs form the

stick to the aircraft model. The ﬂight simulator X-

Plane application is used as a visualization of the air-

craft movement. Thus, the objective is to establish

the communication between aircraft model, X-Plane

and tactile display system to visualize movement of

plane and encode the ﬂight data and warning signal

into tactile signal. The aircraft model calculates po-

sition, ﬂight envelope, ﬂight path climb and turn rate

angles according to the pilot’s inputs. Tactile display

hardware system communicates with computer that

contains Aircraft dynamics block using USB commu-

nication or XBEE interface, while the communication

between Aircraft dynamics block and Flight Simula-

tor X-Plane application is the standard protocol UDP

(User Datagram Protocol).

2.4 Flight Simulation Software:

X-Plane

X-Plane offers the most realistic ﬂight model that can

be used to predict the ﬂying qualities of 30 aircraft

in the default installation with incredible accuracy.

X-Plane is not a game, but it’s an engineering tool

and has the ability to send and receive ﬂight data

via User Datagram Protocol (UDP) communication.

These parameters are sent by the Matlab/Simulink air-

craft models in the IEEE754 format. The data needed

by X-plane to visualize the movement of an aircraft

in the hardware simulation is in fact the position data

of the aircraft (longitude, latitude, altitude) and the

attitude of aircraft (roll angle, pitch angle, and yaw

angle).

The triple of states that can be sent to describe

the position of an aircraft in X-plane application are

geodetic latitude µ, the geodetic longitude λ and the

geodetic height h with respect to the ECEF-Frame and

given by equation (1).





˙µ











)

sinχ

cosγ

+(h)

)cos(µ)

)

cosχ

cosγ

+(h)

)

sinγ







(1)

Where

1 − e

sin

(µ)

1 − e

sin

(µ)

(2)

The position of a point in space is speciﬁed according

to the World Geodetic System WGS84 (Fig.1) utiliz-

ing two angles and the altitude.

Figure 1: Geodetic system WGS84.

The radius of curvature in the prime vertical Nµ

and the meridian radius of curvature Mµ are computed

from the semi-major axis length a of the reference el-

lipsoid and the ﬁrst eccentricity e, where the ﬁrst ec-

centricity e has to be calculated from the ﬂattening f :

= 2 f − f

The ﬂattening f is deﬁned as:

f =

a − b

2.5 Tactile Display System Inputs

The Results of (McGrath, 2000) showed that roll and

pitch information could be provided by tactile cues

via an array of tactors placed in belt which is incorpo-

rated into a torso harness. Which means that banking

to the left is displayed on a column of tactors on the

left side of the torso and vice versa. A display ﬂight

paths going down on the abdomen and ﬂight paths go-

ing up on the back, to have a clear distinction between

going down and up.

But in reality the pilot did not need to perceive

the pitch and bank angles during the ﬂight. On the

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

364

other hand, the turn rate and the ﬂight path climb an-

gles are two very important informations for the pi-

lot. For more details we suggestd to change the hori-

zontal feedback from feeding back the bank angle to

feeding back the turn rate angle to give a better sen-

sation of whether the aircraft was veering to the right

direction or not (which is not always directly related

to the banking angle). And the vertical feedback was

changed from feeding back the pitch angle to feed-

ing back the ﬂight-path inclination angle. This is less

complex and might be easier to understand. These

two variables take into account the aircraft’s ﬂight en-

velope and the optimal recommendation to prevent

and avoid the crash plane.

This implementation would require two columns

of tactors to display the vertical direction: one on the

abdomen and one on the back, and two columns of

tactors on each side of the torso to display the hori-

zontal ﬂight path changes.

For the acquisition of the ﬂight-path inclination

angle and the turn rate angle we use the aircraft model

implemented in Matlab/Simulink environment.

2.6 Design of the Tactile Display System

We have developed a tactile display system consisting

of 16 vibrating elements (tactors). We used 4 columns

of 4 tactors. Each tactor is placed in the box devel-

oped by a 3D printer and designed in the Institute of

Flight System Dynamics(FSD)/ Technical University

Munich of Germany (Fig.2).

Figure 2: Box of tactor.

The turn rate and the ﬂight path climb angles were

encoded using a combination of column selection.

For instance, when turn rate left, the column of tactors

on the left side of the torso was selected as the load

factor was not reached and the bank angle was not in

the boundary zone. We follow the same approach and

display ﬂight paths going down on the abdomen and

ﬂight paths going up to the back, to have a clear dis-

tinction between going down and up to avoid confu-

sion the horizon was displayed on the same side as the

ﬂight path climb angle. When the airplane was ﬂying

level (ﬂight path climb angle equals zero), the ﬂight

path climb angle and the horizon were displayed on

both sides, the abdomen and the back. Also the tactor

location was used to encode the information for turn

rate or ﬂight path climb angle. The range for the hori-

zontal feedback (turn rate) was set to [-6.0, -4.0, -2.0,

-0.7, 0.7, 2.0, 4.0, 6.0] degrees per second. For the

vertical (ﬂight path climb angle) it was set to [-7.0, -

5.0, -3.0, -0.7, 0.7, 3.0, 5.0, 7.0] degrees. We add with

these two ﬂight data, turn rate and ﬂight path climb

angle, the ﬂight envelope, pitch, ﬂight path climb and

bank angles limits to generate a warning signal wich

warns the pilot of any wrong control. For that, we im-

plemented a fuzyy logic controller block that gener-

ates the warning signal or the display of turn rate and

ﬂight path climb angles using the following logic.

As long as the limits on the ﬂight envelope, pitch,

bank or ﬂight path climb angles are not reached we

display the turn rate and the ﬂight path climb an-

gles with the recomanded frequency. If the limit of

the ﬂight path or pitch angles is reached we activate

the eight tactors on the horizontal feedback and if the

limit of the bank angle is reached we activate the other

eight tactors on the vertical feedback. The limit of the

ﬂight envelope involves the activation of all the six-

teen tactors with speciﬁc frequency.

The used ﬂight data, turn rate, ﬂight path climb,

pitch, bank angles and ﬂight envelope must be con-

verted into tactile signals ie intensity and location on

the skin by using the fuzzy logic controller (Fig.3).

Figure 3: Design of the tactile display system.

As shown in Fig.4 and Fig.5, an ARM Cortex M3

microcontroller forms the core of the Tactile Control

Unit (TCU). The modiﬁed speed controller imple-

mented on the microcontroller is used for amplitude

control, temporal rhythm generation and compensate

the static friction. Sixteen interruptions pins of the

ARM Cortex M3 are conﬁgured to read a frequency

of each tactors in the real time. All of the 16 tactors

listen to the main controller for speciﬁc commands

on the amplitude and the timing of vibration through

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel

365

the I2C bus. The spatial coordinates of a stimulus

Figure 4: Tactile controller unit schematic.

applied to the skin are accurately represented in the

central nervous system, and so it has been proposed

that spatial information about the external world may

be communicated via tactile stimulation of the skin

(Van Veen and Van Erp, 2001). In general, the abil-

ity to localize a point of vibrotactile stimulation on

the body is best when it is presented near anatomi-

cal points of reference such as the wrist, elbow, spine,

or navel (Cholewiak et al., 2004). Cholewiak et al.

(Cholewiak et al., 2004) determined the number of

sites around the waist at which participants could ac-

curately localize vibrotactile stimulation. The tactile

array comprised a belt with 12 (intertactor spacing of

72 mm), 8 (spacing of 107 mm), or 6 (spacing of 140

mm) tactors equidistantly spaced. Localization ac-

curacy averaged 74% correct with 12 tactors, and it

improved to 92% with 8 tactors and to 97% when 6

tactors were used. In our case the tactors were af-

ﬁxed to the band, with a 107 mm vertical spacing in

the torso, and spacing of 100 mm in the abdomen and

back. All communications from the fuzzy logic con-

troller or block logic are received through the IEEE

802.15.4 wireless module or USB by the ARM Cor-

tex M3. The data received are automatically used by

the modiﬁed speed controller to compensate the static

friction (Fig.5).

Figure 5: Tactile controller unit.

3 TACTILE CONTROLLER UNIT

DESIGN

3.1 Modeling, Parameters Identiﬁcation

and Open Loop Experiments on

308-102 Tactors

Tactors are modelled as eccentric rotating mass actu-

tor with an imbalanced load ﬁxed to the radial center

axe. The mathematical model of the vibration tactors

is given by (Vartholomeos and Papadopoulos, 2006):

−

− (

sign(

θ) +

θ) −

sinθ

(3)

Where K

is the tactor’s torque constant, J is the

inertia of the eccentric load mass m

, R is the tactors

ohmic resistance, r is the length between the center of

the radial axis and the center of eccentric load mass.

the voltage, V

, is the input voltage to the actuator, and

the angle θ

is the angular position of the tactor with

respect to the radial axis. The term (

sign(

) +

)

is the coulomb and viscous friction.

Parameters identiﬁcation is necessary for the sim-

ulation of a tactor dynamics and the design of the con-

troller strategies. Therefore, tactor parameters are de-

termined by recording a set of measurements. Never-

theless, an important constraint prevented from mea-

suring the angular positions by the use of the com-

mercial encoders due to the small dimensions of the

tactor. for that, an approach is adopted to overcom the

problem of measurement of the angular positions by

the implementation and design of an encoder.

The torque constant, K

is obtained by measuring

the steady state current i

through the tactor and its

steady state rotational speed ω

from the following

equation :

− Ri

) (4)

The coulomb friction reduces the torque applied by

the motor and is dependent on the direction of the ve-

locity. To obtain the coulomb friction we measure the

current i

necessary to start the tactor. The coulomb

friction coefﬁcient c is :

c = i

(5)

The viscous friction coefﬁcient b is obtained in the

steady state by :

b =

− csignω

) (6)

Then, the total inertia of the tactor, J, is given by:

J =

τK

+ Rb

(7)

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

366

Where, τ, is the time constant in the open loop re-

sponse of the equation (3). The identiﬁcation of the

different parameters of the dynamic model were de-

termined as the average of ten series of experiment.

Figure 6 shows the open loop response of rota-

tional speed in simulation and real environement for

different values of input (2.9V-4V). We observe from

the responses of angular velocity in simulation and

real environement in Fig.6 that the model of tactor is

succefully identiﬁed. However, the time constant is

about 40 ms (for more precision see Fig.11). We no-

tice that this time constant is not suitable for the tac-

tile display applications which requires stimulation of

about 50 ms. In order to minimize the time constant

of the response of tactor a rotational speed controller

is designed and implemented in the ARM Cortex M3

microcontroller.

0 1 2 3

200

400

600

800

1000

Time (s)

Speed (rad/s)

Simulation

Real

Figure 6: Speed response for diffrent voltage input in open

looop.

3.2 Speed Controller Design

In this section we are interested to develop a design

controller strategie for the tactors to minimize the

time constant of the system. The use of batteries to

achieve the autonomy, impose restriction that the volt-

age input can not exceed 5V.

To this aim, the tactor is controlled using inverse

dynamics given by:

= (K

+ Rb)ω +Rm

gr sin(ω)+cRK

−1

(8)

Where u is actuating signal incorporating in pro-

portional plus integral control:

u = K

(ω

re f

− ω) + K

(ω

re f

− ω)dt (9)

The controller is described in Fig.7. The inverse dy-

namics compensate the two non linear terms. The

, K

eliminate the permanent state error of the tac-

tor’s speed and result to a much faster response. Fig.8

shows the comparison between the open and closed

loop speed response for the desired value 700 rad/s. A

presence of overshoot is due to the closed loop zero,

and due to the limit power of the LiPo battery with

regulator (5V) while the controller requires more volt-

age (Fig.9). So, in order to overcome the problem of

overshoot we modify the strategie of controller.

Figure 7: Rotational speed controller design.

0 0.1 0.2 0.3 0.4 0.5

200

400

600

800

1000

Time (s)

Speed (rad/s)

Closed Loop

Open Loop

Figure 8: Closed and open loop simulation of speed re-

sponse.

0 0.1 0.2 0.3 0.4 0.5

3.5

4.5

Time (s)

Voltage (V)

Figure 9: Evolution of the input voltage in closed loop with

PI controller.

The modiﬁed controller speed is shown in Fig.10,

and the actuating signal u becomes:

u = −K

ω + K

(ω

re f

− ω)dt (10)

The poles of the system designed in Fig.10 are placed

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel

367

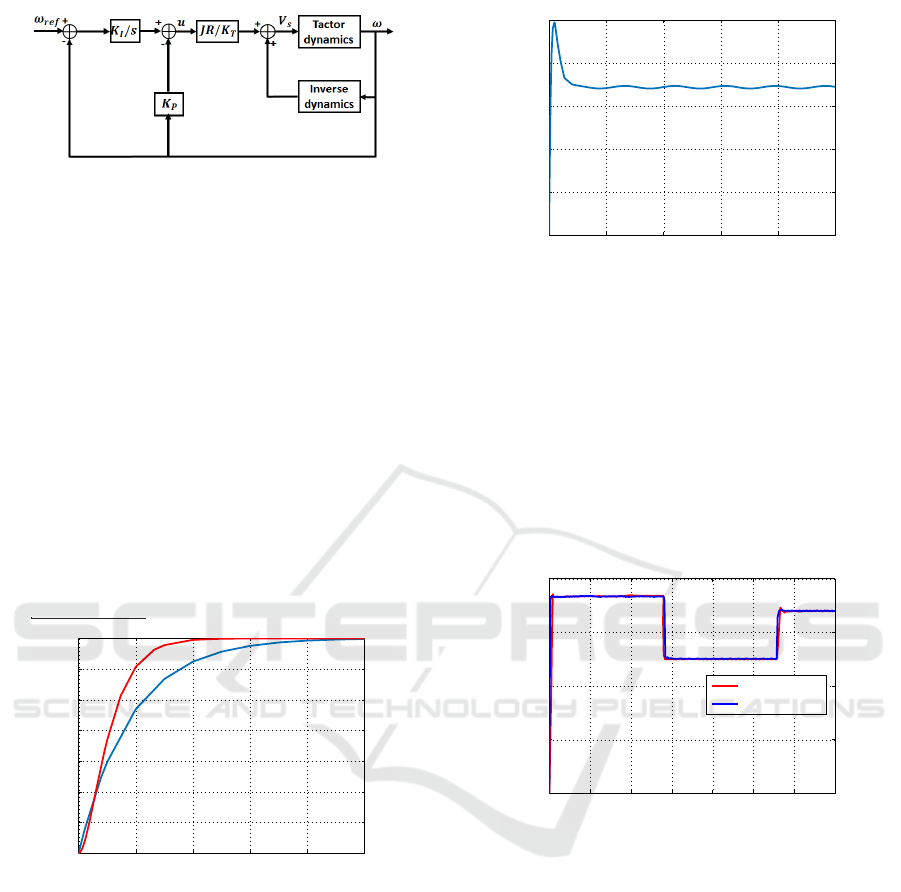
Figure 10: Modiﬁed speed controller design.

at the same point to avoid oscillations, ie the damp-

ing coefﬁcient is equal to 1, and the settling time

= 4.7ω

. Where ω

is the natural frequency. The

gain parameters of the speed controller are K

= 354,

and K

= 31343 by choosing a desired settling time

as 26.44ms under the constraint of the limit voltage

of the battery (Lipo + regulator 5v).

Figure 11 shows the response of angular speed

of closed loop of the modiﬁed speed controller (red

line) and open loop simulation (blue line) for a de-

sired speed 700 rad/s. We obtain a reduction of 48%

in settling time, ie time constant is equal to 20.8ms.

In addition, there is no overshoot in the closed loop

modiﬁed controller response. Fig.12 shows that the

input voltage in the modiﬁed controller is under 5V

and no saturation is detected during its evolution.

0 0.02 0.04 0.06 0.08 0.1

100

200

300

400

500

600

700

Time (s)

Speed (rad/s)

Figure 11: Zoomed modiﬁed speed controller and open

loop simulation of speed response.

The modiﬁed controller is implemented in the

ARM CORTEX M3 microcontroller. Eight (08) L293

quadruple half-H drivers was used to drive sixteen

tactors. Pulsed Width Modulation (PWM) with the

modiﬁed speed controller strategie were applied to

control the angular speed of the tactors. To measure

the rotational speed, a very low cost opto-reﬂective

sensor QRE1113 was used for each tactor. However,

the output signal of the opto-reﬂective sensor is ﬁltred

with a shmitt trigger HEF40106BP.

For the experimental procedure, we applied the

modiﬁed controller presented in equation 9, omitting

the term containing the angle of rotation, θ . During

0 0.1 0.2 0.3 0.4 0.5

Time (s)

Voltage (V)

Figure 12: Evolution of the input voltage in modiﬁed con-

troller.

the practice it was necessary to use the developed op-

tical encoder QRE1113 as explained in the previous

section.

Figure13 shows the response of the real and simu-

lation speed of the tactor for the closed loop with the

modiﬁed controller. We observe that the steady state

error is less than 3% and the time constant is 20.8

ms. The diagram of the developed tactile system is

0 0.5 1 1.5 2 2.5 3 3.5

200

400

600

800

Time (s)

Speed (rad/s)

Open Loop

Closed Loop

Figure 13: Real and simulation speed response of the mod-

iﬁed controller for different voltage inputs.

divided into two parts. The ﬁrst is the software unit

composed of fuzzy logic controller wich is used to

transform the ﬂight data to tactile signals. The second

part is the hardware unit which consist in reducing the

time constant to adapt the low cost tactor to the tactile

display applications and control the tactors according

the transmitted ﬂight data.

4 EXPERIMENTAL EVALUATION

4.1 Flight Data Constraints

Flight data constraints are used to check the limits of

the ﬂight envelope, pitch, bank or the ﬂight path climb

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

368

angles and activate the embedded tactile display sys-

tem in the real time.

Most operating limitations can be translated to

limits other parameters. Enforcing the speed limits

can be impossible if the pilot has full authority over

the vertical motion of an aircraft. In this case only

the throttle could be used by the ﬂight control system

for speed protection purposes. This is evidently no

sufﬁcient for an effective protection when aircraft is

in steep climb or descent. Hence, it makes sence to

translate the speed limits to the ﬂight path climb an-

gle limits. Equation ((11)) shows how the speed rate

is related to the ﬂight path climb angle.

= g(n

)

− g sinγ

(11)

The speed rate can be limited depending on the cur-

rent indicated airspeed and the limit indicated air-

speed ; as in equation (12) with a constant k (Zhang

et al., 2014).

lim

= k(V

lim

−V

) (12)

By simple rewriting of equation (12), the upper and

lower limits on the ﬂight path climb angle can be writ-

ten as in equations (13) and (14).

lim,U

= arcsin((n

)

−

k(V

lim,U

−V

)

) (13)

lim,L

= arcsin((n

)

−

k(V

lim,L

−V

)

) (14)

Where V

lim,U

is the never exceed speed V

and V

lim,L

is the stall speed V

stall

(Fisch et al., 2012). The bank

angle limitation is a function of height above terrain

(equation (15)). When the aircraft center of gravity is

at or below 2m above terrain; the wings level attitude

is imposed. At higher altitudes, the bank angle limit

linearly increases to 15m, ie., at the end of take-off or

at beginning of landing, 20

are allowed.

lim,h



0 if x ≤ 2m

h−2m

13m

if x > 2m

(15)

To prevent excessive attitudes, the following limits on

pitch and bank angle are imposed.

lim,U

= 60

lim,U

= 20

lim,L

= −10

4.2 Fuzzy Logic Controller

The architecture of the tactile display system use a

Fuzzy Logic Controllers (FLC), to controls vibration

frequency, timing and location, from which vibrotac-

tile spatiotemporal patterns can be created. One main

characteristic of a fuzzy controller is its applicabil-

ity to systems with uncertainty or even with unknown

models (Sepehri and Lawrence, 1998). This makes

a fuzzy controller ideal for dynamically reproducing

the multimodal aerodynamic display of the ﬂight data

parameters with the ﬂight envelop and the optimal de-

cision in the torso and abdomen of the pilot.

This part focuses on design of a Mamdani fuzzy

model which shall generate adequate duration, loca-

tion and frequency of each tactors based on the aero-

dynamic data (see Fig.5). The fuzzy controller was

designed to account for the different parameters those

affect the horizontal and vertical ﬂight path changes.

The stability aspect of the outer loop including the

fuzzy model is not addressed in this work and more

details about the design of fuzzy controllers can be

found in (Jantzen, 1998).

Six variables were used as input for fuzzy con-

troller those are, the ﬂight envelope limit, turn rate,

the ﬂight path climb, pitch limit, bank limit and ﬂight

path climb limit angles. The outputs of FLC are the

desired frequency and location of tactors in horizon-

tal and lateral directions. To deﬁne the outputs we

need to understand the behaviour of the skin and the

amplitudes required for frequency of stimulation and

rhythm. So, The Optimal sensitivity is achieved at

frequencies between 25 and 320 Hz for abdomen site

(Cholewiak et al., 2004). Furthermore, in most tactile

displays, people prefer that the duration of the tactile

pulses has to be between 20 and 320 ms (optimally

near 50 ms), and when the tactile display is function-

ing as a simple alert the duration has to be between

50 and 200 ms (Kaaresoja and Linjama, 2005). In our

work, we created a rhythms together so as to group

vibrotactile pulses of varying durations (Brown et al.,

2005). In which we used a duration of 50 ms with

ﬂight path climb and turn rate angles data display, a

duration of 150 ms to indicate alerts to keep the air-

craft in its ﬂight envelope. The linguistic terms of

each input variable are deﬁned as follows:

Flight Path Climb Angle: NVBG (Negative Very

Big Gamma), NBG (Negative Big Gamma), NMG

(Negative Medium Gamma), NSG (Negative Small

Gamma), ZG (Zero Gamma), PSG (Posive Small

Gamma), PMG (Posive Medium Gamma), PBG (Po-

sive Big Gamma), PVBG (Posive Very Big Gamma).

Turn Rate Angle: NVBT (Negative Very Big

Turn), NBT (Negative Very Big Turn), NMT (Neg-

ative Medium Turn), NST (Negative Small Turn), ZT

(Zero Turn), PST (Positive Small Turn), PMT (Po-

sive Medium Turn), PBG (Positive Big Turn), PVBG

(Positive Very Big Turn).

Pitch Limit: NLP (No Limit Pitch), LP (Limit

Pitch).

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel

369

Bank Limit: NLB (No Limit Bank), LB (Limit

Bank).

Flight Path Climb Angle Limit: NLG (No Limit

Gamma), LG (Limit Gamma).

Flight Envelope Limit: NLE (No Limit Enve-

lope), LE (Limit Envelope).

Once the proper inputs were created, the next

step is to create the output characteristic behavior of

the tactile signal being received by the TCU unit.

The outputs variables Vibration characteristics (Loca-

tion/Frequency/Timing) was classiﬁed as :

Vertical Tactor: VBT8 (Vertical Back Tactor 8),

VBT7 (Vertical Back Tactor 7), VBT6 (Vertical Back

Tactor 6), VBT5 (Vertical Back Tactor 5), ZVT (Zero

Vertical Tactor), VAT1 (Vertical Abdomen Tactor 1),

VAT2 (Vertical Abdomen Tactor 2), VAT3 (Vertical

Abdomen Tactor 3), VAT4 (Vertical Abdomen Tactor

5), VLT (Vertical Limit Tactors).

Side Tactor: RST8 (Right Side Tactor 8), RST7

(Right Side Tactor 7), RST6 (Right Side Tactor 6),

RST5 (Right Side Tactor 5), ZST (Zero Side Tactor),

LST1 (Left Side Tactor 1), LST2 (Left Side Tactor 2),

LST3 (Left Side Tactor 3), LST4 (Left Side Tactor 5),

SLT (Side Limit Tactors).

The next step is to create a rule base that would

govern the operation of the fuzzy controller. Proper

conditions must be created in order to implement a

system that will display the ﬂight data and secure the

ﬂight. In order to establish such a collection of fuzzy

rules, we questioned experts (pilots), using a carefully

organized questionnaire and to complete the rules ta-

ble system as shown in Table 1. The use of expert

knowledges is the most common approach to design

fuzzy controller rules and convert the ﬂight data on

tactile signals.

Figures (14), (15), (16), (17), (18),(19), (20) and

(21) show an example of simulated manoeuvres for a

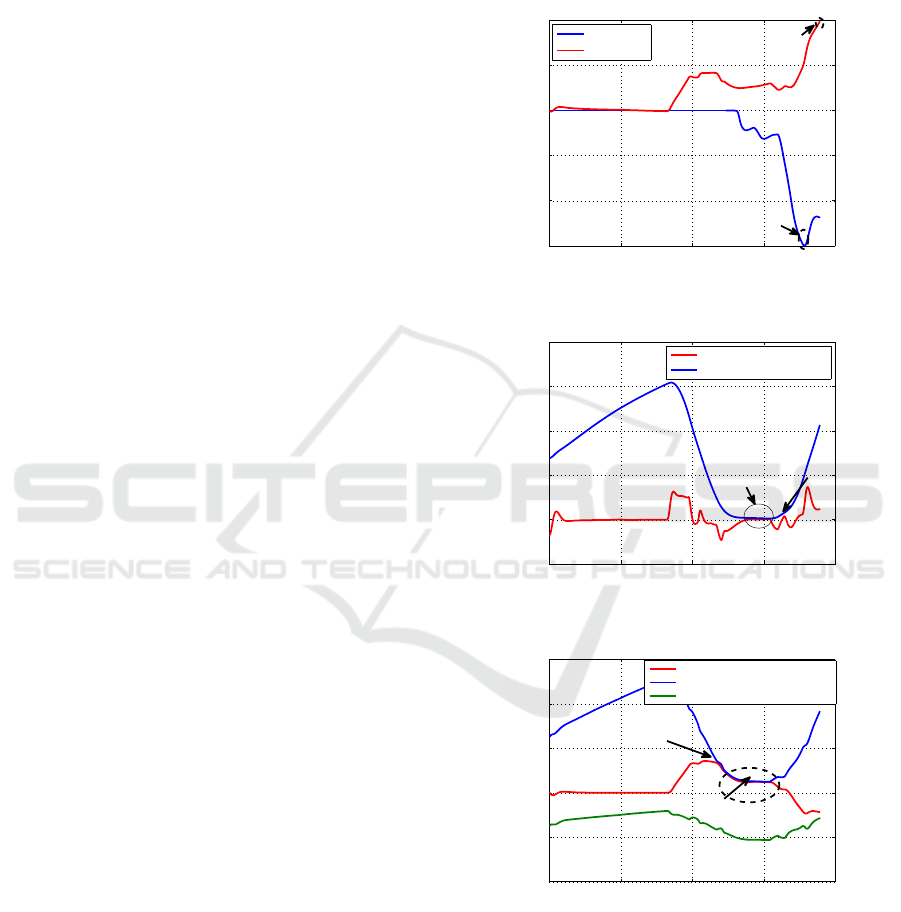
model aircraft. Fig.14 shows the evolution of the pitch

and the bank angles and Fig.15 shows the historical

time of the normal load factor and the limits of the

normal load factor according to the airspeed. Fig.16

shows the historical time of the ﬂight path climb an-

gles and its upper and lower limits while Fig.17 repre-

sents the location of each tactor in the abdomen site.

In this ﬁgure we ﬁnd the activation of the tactors T1,

T2, T3, T4 according to the value of the ﬂight path

climb angle. After 47 sec the ﬂight climb angle ap-

proach the upper limit (Fig.16) and the four tactors

are activated during this period to display the warn-

ing signal of the limit approach. This limit will cause

an approach towards the limit of the ﬂight envelope

for 14 sec (Fig.17). During this period the pilot is in-

formed of this situation by the tactile signal and tries

to avoid this approach by the action on the control

stick by decreasing the ﬂight path climb angle. These

limits will activate all the eight tactors of the horizon-

tal site (Fig.18). We notice that the tactors are acti-

vated during the ﬂight to informe the pilot about the

ﬂight path climb angle by using the tactile display.

0 20 40 60 80

−30

−20

−10

Time (s)

Amplitude(degree)

Bank angle

Pitch angle

Limit

Figure 14: Pitch and bank angles limit.

0 20 40 60 80

0.5

1.5

2.5

Time (s)

Load normal factor

Load normal factor limit

Limit

Figure 15: Load factor limit.

0 20 40 60 80

−20

−10

Time (s)

Angle (deg)

Flight Path climb angle

Flight path climb angle uper limit

Flight path climb angle lower limit

Limit

Figure 16: Flight path climb angle limit.

Figures (19) and (20) show the tactors activation

on the right and left side. In Fig.19 the tactors are

activated only in the two limit of the ﬂight envelope

(Fig. 15) and the limit of bank angle according to the

time of 70sec (Fig.14). While Fig.20 show the activa-

tion of the tactors when the pilot actuate the stick to

turn left. The limits of ﬂight envelope and bank angle

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

370

Table 1: Rule base system.

∆n

z,lim

/θ

lim

NVBG/ NBG/ NMG/ NSG/ ZG/ PSG/ PMG/ PBG/ PVBG /

γ/γ

lim

NLG NLG NLG NLG NLG NLG NLG NLG NLG

NLE/Nolimit VBT8 VBT7 VBT6 VBT5 ZVT VAT1 VAT2 VAT3 VAT4

NLE/Limit VLT VLT VLT VLT VLT VLT VLT VLT VLT

0 20 40 60 80

Time (s)

Tactors activation

Tactor 1

Tactor 2

Tactor 3

Tactor 4

Flight path climb angle

Limit1Limit2

Limit3

Figure 17: Tactors activation on the abdomen site.

0 20 40 60 80

Time (s)

Activation tactors

Tactor 5

Tactor 6

Tactor 7

Tactor 8

Flight path angle

Limit1

Limit2

Limit3

Figure 18: Tactors activation on the back site.

0 20 40 60 80

T10

T11

T12

Time (s)

Activation tactors

Tactor 9

Tactor 10

Tactor 11

Tactor 12

Turn rate

Limit1

Limit2

Limit1

Figure 19: Tactors activation on the right side site.

are respected by generating the warning signal.

Fig.21 shows the frequency of tactors on the ab-

domen site calculated from the output signal of the

fuzzy logic controller. The maximum of frequency

correspond to 320Hz and the minimum is 25 Hz.

0 20 40 60 80

T16

T15

T14

T13

Time (s)

Activation tactors

Tactor 13

Tactor 14

Tactor 15

Tactor 16

Turn rate

Limit1

Limit2

Limit3

Figure 20: Tactors activation on the left side site.

When the pilot actuat commands a positive pitch by

deﬂecting the sidestick at the time of 33sec the air-

craft climbs. This action also increase the ﬂight path

climb angle and the frequency of T1 is 320 Hz at 34

sec, T2 is 320 Hz at 36 sec, T3 is 320 Hz at 38 sec

and T5 is 270Hz at 40 sec.

0 20 40 60 80

−200

−100

100

200

300

400

Time (s)

Tactor T1(Hz)

Tactor T2 (Hz)

Tactor T3 (Hz)

Tactor T4 (Hz)

Flight path angle/30 (deg)

Figure 21: Frequency tactors on the abdomen site.

5 CONCLUSION

This paper reports a successful achievement of a new

hardware/software controller for realisation of tactile

display system used in the cockpit design. The assem-

bled prototype and the related built-in software have

been integrated successfully with a dynamic model of

an aircraft and commercial software that assure the

aircraft visualization. In order to achieve a success-

ful transformation of a ﬂight data to tactile signal fea-

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel

371

tures, we have implemented a knowledge based fuzzy

system which allows deriving the amount of vibra-

tion to be reproduced on the mechanoreceptor in the

pilot skin. The designed controller imitates the real

features of tactile display and allows the pilot’s cen-

tral nervous. Also for the ﬂight data and warning sig-

nals to control a virtual aircraft in stressed situations.

Experiments were performed in order to evaluate the

proposed control loop based on a modiﬁed speed con-

troller with a fuzzy logic controller. This idea is a step

to use the low cost tactors in the tactile display ﬁeld by

reducing the settling time in comparison to the open

loop response and delete the overshoot. our own ﬂexi-

ble tactile display can be reconﬁgured or dynamically

changed to inject different ﬂight data or simulate dif-

ferent parts of the skin.

REFERENCES

Arasan, A., Basdogan, C., and Sezgin, T. M. (2013). Hap-

tic stylus with inertial and vibro-tactile feedback. In

World Haptics Conference (WHC), 2013, pages 425–

430. IEEE.

Brown, L. M., Brewster, S. A., and Purchase, H. C. (2005).

A ﬁrst investigation into the effectiveness of tactons.

In Eurohaptics Conference, 2005 and Symposium on

Haptic Interfaces for Virtual Environment and Teleop-

erator Systems, 2005. World Haptics 2005. First Joint,

pages 167–176. IEEE.

Brown, L. M. and Kaaresoja, T. (2006). Feel who’s talking:

using tactons for mobile phone alerts. In CHI’06 ex-

tended abstracts on Human factors in computing sys-

tems, pages 604–609. ACM.

Choi, S. and Kuchenbecker, K. J. (2013). Vibrotactile dis-

play: Perception, technology, and applications. Pro-

ceedings of the IEEE, 101(9):2093–2104.

Cholewiak, R. W., Brill, J. C., and Schwab, A. (2004).

Vibrotactile localization on the abdomen: Effects

of place and space. Perception & Psychophysics,

66(6):970–987.

Cholewiak, R. W. and Collins, A. A. (2003). Vibrotactile

localization on the arm: Effects of place, space, and

age. Perception & psychophysics, 65(7):1058–1077.

Erp, V., Jan, B., Veltman, J., van Veen, H., and Oving, A.

(2003). Tactile torso display as countermeasure to re-

duce night vision goggles induced drift. Technical re-

port, DTIC Document.

Feng, G. (2006). A survey on analysis and design of model-

based fuzzy control systems. Fuzzy systems, IEEE

Transactions on, 14(5):676–697.

Fisch, F., Lenz, J., Holzapfel, F., and Sachs, G. (2012). On

the solution of bilevel optimal control problems to in-

crease the fairness in air races. Journal of Guidance,

Control, and Dynamics, 35(4):1292–1298.

Jansen, C., Wennemers, A., Vos, W., and Groen, E. (2008).

Flytact: A tactile display improves a helicopter pi-

lots landing performance in degraded visual environ-

ments. Springer.

Jantzen, J. (1998). Tuning of fuzzy pid controllers. Techni-

cal University of Denmark, report.

Jiang, T. and Li, Y. (1996). Generalized defuzziﬁcation

strategies and their parameter learning procedures.

Fuzzy Systems, IEEE Transactions on, 4(1):64–71.

Jones, L. A. and Sarter, N. B. (2008). Tactile displays:

Guidance for their design and application. Human

Factors: The Journal of the Human Factors and Er-

gonomics Society, 50(1):90–111.

Kaaresoja, T. and Linjama, J. (2005). Perception of short

tactile pulses generated by a vibration motor in a mo-

bile phone. In Eurohaptics Conference, 2005 and

Symposium on Haptic Interfaces for Virtual Environ-

ment and Teleoperator Systems, 2005. World Haptics

2005. First Joint, pages 471–472. IEEE.

Kapur, P., Jensen, M., Buxbaum, L. J., Jax, S. A., and

Kuchenbecker, K. J. (2010). Spatially distributed tac-

tile feedback for kinesthetic motion guidance. In Hap-

tics Symposium, 2010 IEEE, pages 519–526. IEEE.

Kelley, A. M., Cheung, B., Lawson, B. D., Rath, E., Chi-

asson, J., Ramiccio, J. G., and Rupert, A. H. (2013).

Efﬁcacy of directional cues from a tactile system for

target orientation in helicopter extractions over mov-

ing targets. Technical report, DTIC Document.

Lawson, B. D. and Rupert, A. H. (2014). Coalition warfare

program tactile situation awareness system for avia-

tion applications: System development. Technical re-

port, DTIC Document.

Lloyd, D. M., Merat, N., Mcglone, F., and Spence, C.

(2003). Crossmodal links between audition and touch

in covert endogenous spatial attention. Perception &

Psychophysics, 65(6):901–924.

McGrath, B. J. (2000). Tactile instrument for aviation.

Technical report, DTIC Document.

Nojima, T. and Funabiki, K. (2005). Cockpit display using

tactile sensation. In null, pages 501–502. IEEE.

Petit, G. (2013). Conception, prototypage et

evaluation dun

syst

eme pour l’exploration audio-tactile et spatiale de

pages web par des utilisateurs non-voyants. PhD the-

sis,

Ecole Polytechnique de Montr

eal.

Precup, R.-E. and Hellendoorn, H. (2011). A survey on

industrial applications of fuzzy control. Computers in

Industry, 62(3):213–226.

Renwick, K. (2008). Effectiveness of vibration-based haptic

feedback effects for 3d object manipulation.

Rosenblum, L. D. (2011). See what I’m Saying: The Ex-

traordinary Powers of Our Five Senses. WW Norton

& Company.

Sala, A., Guerra, T. M., and Babu

ska, R. (2005). Perspec-

tives of fuzzy systems and control. Fuzzy Sets and

Systems, 156(3):432–444.

Salzer, Y. and Oron-Gilad, T. (2015). Evaluation of an on-

thigh vibrotactile collision avoidance alerting compo-

nent in a simulated ﬂight mission. Human-Machine

Systems, IEEE Transactions on, 45(2):251–255.

Schmidt-Skipiol, F. J. (2015). Tactile feedback and situation

awareness.

Seiderman, A., Marcus, S. E., and Hapgood, D. (1989).

20/20 is not enough: the new world of vision. Alfred

A. Knopf.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

372

Self, B., Van Erp, J. B., Eriksson, L., and Elliott, L. (2008).

Human factors issues of tactile displays for military

environments. Tactile Displays for Orientation, Nav-

igation and Communication in Air, Sea and Land En-

vironments, pages 1–18.

Sepehri, N. and Lawrence, P. D. (1998). Fuzzy logic con-

trol of a teleoperated log loader machine. In Intelli-

gent Robots and Systems, 1998. Proceedings., 1998

IEEE/RSJ International Conference on, volume 3,

pages 1571–1577. IEEE.

Tang, F., McMahan, R. P., and Allen, T. T. (2014). Develop-

ment of a low-cost tactile sleeve for autism interven-

tion. In Haptic, Audio and Visual Environments and

Games (HAVE), 2014 IEEE International Symposium

on, pages 35–40. IEEE.

Thomas, P., Biswas, P., and Langdon, P. (2015). State-of-

the-art and future concepts for interaction in aircraft

cockpits. In Universal Access in Human-Computer

Interaction. Access to Interaction, pages 538–549.

Springer.

Van Erp, J. and Self, B. (2008). Introduction to tactile dis-

plays in military environments. Tactile Displays for

Orientation, Navigation and Communication in Air,

Sea, and Land Environments, pages 1–1.

Van Erp, J. B., Van Veen, H. A., Jansen, C., and Dobbins, T.

(2005). Waypoint navigation with a vibrotactile waist

belt. ACM Transactions on Applied Perception (TAP),

2(2):106–117.

Van Veen, H. A. and Van Erp, J. B. (2001). Tactile infor-

mation presentation in the cockpit. In Haptic Human-

Computer Interaction, pages 174–181. Springer.

van Wassenhove, V. (2009). Minding time in an amodal

representational space. Philosophical Transactions of

the Royal Society of London B: Biological Sciences,

364(1525):1815–1830.

Vartholomeos, P. and Papadopoulos, E. (2006). Analysis,

design and control of a planar micro-robot driven by

two centripetal-force actuators. In Robotics and Au-

tomation, 2006. ICRA 2006. Proceedings 2006 IEEE

International Conference on, pages 649–654. IEEE.

Wellman, P. S., Peine, W. J., Favalora, G., and Howe, R. D.

(1998). Mechanical design and control of a high-

bandwidth shape memory alloy tactile display. In Ex-

perimental robotics V, pages 56–66. Springer.

Zhang, F., Braun, S., and Holzapfel, F. (2014). Physically

integrated reference model and its aids in validation

of requirements to ﬂight control systems. In AIAA

Guidance, Navigation and Control Conference, pages

2014–0962.

Tactile Display Design for Securing Flight and Reducing the Saturation of Pilot’s Visual Channel

373