
Peaks Emergence Conditions in Free Movement Trajectories
of Linear Stable Systems
Nina A. Vunder and Anatoly V. Ushakov
ITMO University, Saint-Petersburg, Russia
Keywords: Linear System, Free Movement, Peak, Eigenvectors, Condition Number.
Abstract: The paper considers a asymptotically stable linear system with real eigenvalues of state matrix. It was found
that a peak in free movement trajectories arises. Geometric interpretation of peaks emergence was presented
through eigenspace. Quantitative estimate of the peak was obtained by using the condition number of matrix
of eigenvectors.
1 INTRODUCTION
The problem statement is to determine the
eigenvectors influence on free movement of
asymptotically stable continuous linear MIMO
system with real spectrum. It will be shown that
specific disposition of eigenvectors allows to peaking
effect (peak) emergence. It means that the norm of
state vector growths up and exceeds the norm of
initial conditions during some time and then
converges to zero. Necessary conditions of peak
emergence are the goal of research of current article.
2 GEOMETRIC
INTERPRETATION OF PEAKS
IN FREE MOVEMENT
TRAJECTORIES THROUGH
EIGENSPACE
Consider the linear system that is described as
() () ( ) ()
0
0;
=
==
t
txxtFxtx
,
(1)
where
() ()
txx ,0
are vectors of initial and current
states of the system respectively;
F
is the state
matrix with eigenvalues
ni
i
,1;0 =<
λ
,
ji
λ
λ
≠
for
ji ≠
and eigenvectors
{
}
niF
iiii
,1;: ==
ξλξξ
;
() ()
nnn
RFRkxx
×
∈∈ ;,0
.
The solution ((Andreev, 1976), (Gantmaher, 2004),
(Moler at al., 2003)) of the system (1) is
)0()( xetx
Ft
=
.
(2)
The vector
()
0x
can be decomposed into the sum of
eigenvectors
=
=
n
i
ii
x
1
)0(
ξγ
. Taking into account
properties of matrix exponential the solution (2) can
be write as follows
=
=
n
i
i
t
i
i
etx
1
)(
ξγ
λ
,.
(3)
where
ni
i
,1;1 ==
ξ
:
∗
is the Euclidean norm on
n
R .
Definition 1. The system (1) has the peak in the
case if there is a vector
() ()
10:0 =xx
such that for
some value
0>t
the solution of the system satisfies
the condition
()
1>tx
(in general case
()
ax =0
,
where
0>a
- const).
Let us formulate a statement and let us prove it by
using geometric representations.
Statement 1. Necessary conditions of peaks
emergence in free movement trajectories of the
system (1) are:
1. There is at least one pair of eigenvectors
(
)
jl
ξ
ξ
,
such that the angle between them is greater
than
2
π
in the subspace spanned by those
eigenvectors;
Vunder, N. and Ushakov, A.
Peaks Emergence Conditions in Free Movement Trajectories of Linear Stable Systems.
DOI: 10.5220/0005984605350538
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 535-538
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
535

2. There are eigenvalues
jl
λ
λ
,
associated with
eigenvectors
jl
ξ
ξ
,
such that
jl
λλ
>> .
Let us prove
of the statement 1 by geometric way.
Let consider the linear span (subspace)
{
}
jl
L
ξ
ξ
,
of
the vectors
(
)
jl
ξ
ξ
,
which dispose at an obtuse angle
(see Fig. 1).
Figure 1.
Suppose the initial condition vector
()
0x
of the
system (1) belongs to the span
()
{
}
jl
Lx
ξ
ξ
,0 ∈
and
has the unit norm
()
10 =x
. Then the vector
()
0x
can
be represented in the form
()
lljj
x
ξ
γ
ξ
γ
+=0
.
(4)
Now suppose the vector
()
0x
is a bisector of the
angle between vectors
jl
ξ
ξ
,
; then following relations
are true:
1,1, >>=
ljlj
γγγγ
.
Taking into account (3) we can write the
movement of system (1)
() ( )()
txxtx ,0=
in following
form
() ( )()
t
l
t
j
l
j
eetxxtx
λ
λ
γγ
+== ,0
.
(5)
If in (5)
jl
λλ
>> and the system (1) is stable, then
from time
03
1
≈==
−
lПl
tt
λ
following conditions
become true:
() ( )()
t
j
t
l
j
l
etxxtxe
λ
λ
γγ
≅=≅ ,0;0
and
the norm of the vector
()
tx
is
()
t
j
j
etx
λ
γ
≅ . The
statement 1 is proved.
Note 1.
It is obvious that there are no peaks in in
free movement trajectories of the system (1) if any of
following conditions holds:
1. The angle between vectors
jl
ξ
ξ
,
is equal to
2
π
for any combinations of
jl
λ
λ
,
.
2. The vector
()
0x
is a bisector of the acute angle
between vectors
jl
ξ
ξ
,
.
3. The vector
()
0x
is inside the obtuse angle
between vectors
jl
ξ
ξ
,
but not its bisector and one of
two following cases is realized:
{
}
0,1 →→
jl
γ
γ
or
{
}
1,0 →→
jl
γ
γ
for any combinations of eigenvalues
jl
λ
λ
,
.
Let’s illustrate the validity of the statement 1 on
the example 1.
Example 1. Let the state matrix
F
of the system
(1) has eigenvectors
[] [ ]
ТТ
05.09987.0;01
21
−==
ξξ
such that they
have unit norm and condition 1 of statement 1 is
fulfilled. Let the state matrix
F
has the spectrum
{} ( )
[]
{}
50;1:0λarg
21
−=−==−==
λ
λ
λ
σ
FIdetF
i
such that the condition 2 of statement 1 is fulfilled.
Using the eigenspace and the spectrum, we have
[] []
,
500
726.9781
05.00
9987.01
500
01
05.00
9987.01
0
0
1
1
21
2
1
21
1
−
−
=
=
−
−
−
−
=
=
=Λ=
−
−
−
ξξ
λ
λ
ξξ
MMF
where
M
- the matrix of eigenvectors.
Let the initial condition vector
()
[]
T
x 9997.00255.00 =
be a bisector of the angle
between
21
,
ξ
ξ
and has the unit norm
()
10 =x
.
Decompose the vector
()
0x
into eigenvectors of the
matrix
F
:
()
21
994.199935.190
ξ
ξ
+=x
. Now, we
can write the free movement (5) of the system (1) with
the state matrix
F
in the following form
() ( )() ()()
.994.199935.19
0exp,0
50
21
21
tt
tt
ee
eexFttxxtx
−−
+=
=+===
λλ
γγ
It is obvious that the component
()
t
etx
50
2
994.19
2
−
=
ξ
ξ
of the free movement is close to zero at the time
()
0599.0ln
05.0
1
2
==
=
−
ε
ελ
t . At the same time the
component
()
t
etx
−
=
1
9935.19
1
ξ
ξ
of the free
movement is equal to
()
1
0599.0
1
8311.189935.19
1
ξξ
ξ
==
−
etx
. Clearly, there is
a peak
()
tx
t
max
of the norm
()
tx
in the free
movement of the constructed two-dimensional
l
X
j
X
l
ξ
j
ξ
()
0
X
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
536
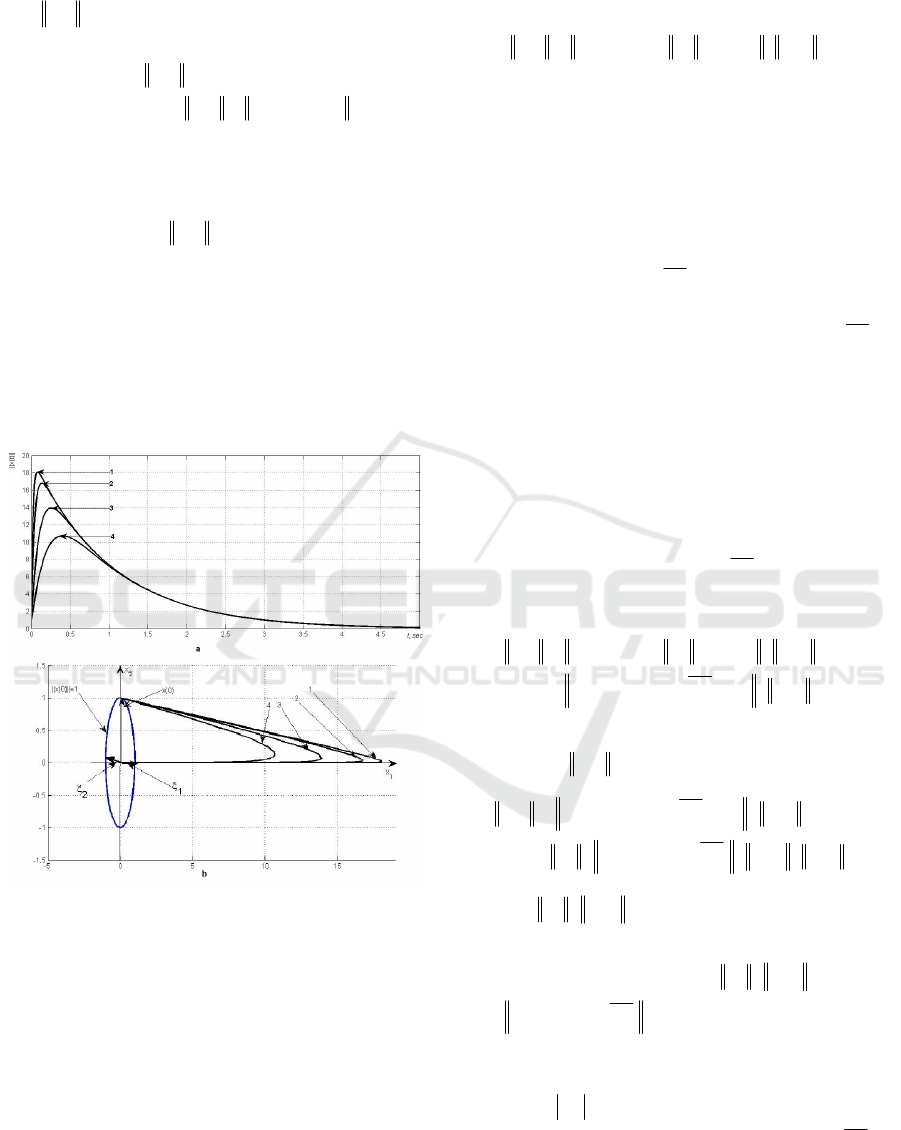
system of type (1). The peak takes on the value
()
8324.17max =tx
t
.
Let us confirm this result by observing the free
movement norm
()
tx
. It is computed using the
following formula
() ()()
0exp xFttx =
. The
obtained curve is shown on Fig. 2.a (curve 1). The
curve confirms correctness of estimation of peak of
free movement trajectories obtained through the
geometrical interpretation. Fig.2.a and fig.2.b
demonstrate norms
()
tx
of the system with same
eigenvectors but with following spectra:
{} { }
25;1
21
−=−==
λ
λ
σ
F
(curve 2),
{} { }
10;1
21
−=−==
λ
λ
σ
F
(curve 3),
{} { }
5;1
21
−=−==
λ
λ
σ
F
(curve 4).
Moreover, fig. 2.a illustrates processes in norm,
and fig. 2.b does the same in phase space spanned by
eigenvectors.
Figure 2: Example of peaks.
3 ALGEBRAIC
INTERPRETATION.
CONDITION NUMBER AS А
QUANTITATIVE ESTIMATION
OF PEAKS
Consider the solution (2) of system (1) in order to
estimate the norm of possible peaks. If in (2) we turn
to norms ((Andreev, 1976), (Gantmaher, 2004),
(Moler at al., 2003), (Lancaster at al., 1985), (Golub
at al., 1976)), we get
() ()() () ()
0exp0exp xFtxFttx ⋅≤=
.
(6)
Recall that the system (1) satisfies conditions:
{}
()()
()
≠≠=
<=−=
=
jiJm
FI
F
jii
ii
при;0
;0;0detarg
λλλ
λλλ
σ
(7)
The matrix
F
can be represented in the form
1−
Λ=
M
M
F
,
(8)
where
{
}
nirowM
i
,1; ==
ξ
is matrix composed of
eigenvectors of matrix
F
such that the following
condition is true:
iii
F
ξ
λ
ξ
=
;
{
}
nidiag
i
,1; ==Λ
λ
is
diagonal matrix of eigenvalues. It is common
knowledge ((Gantmaher, 2004), (Lancaster at al.,
1985)) that the representation (8) holds for a matrix
function
(){}
*f
of a matrix
()
*
:
() ()
1−
Λ= MMfFf
.
If the matrix function is the matrix exponential
() ( )
FtFf exp=
; then we can write
() ()
{}
.,1;
expexp
1
1
−
−
==
=Λ=
MnieMdiag
MMFt
t
i
λ
(9)
Substituting (9) in (6), we get
() ()() () ()
{}
()
.0,1;
0exp0exp
1
xMnieMdiag
xFtxFttx
t
i
⋅==
=⋅≤=
−
λ
(10)
Let us form inequality using (10) to obtain upper
estimate of
()
tx
()
{}
()
{}
()
,0,1;
0,1;
1
1
xMniediagM
xMnieMdiagtx
t
t
i
i
⋅⋅=⋅≤
≤⋅=≤
−
−
λ
λ
(11)
where
1−
⋅ MM is equal to condition number
{}
MC
((Golub, 1996), (Wilkinson, 1984, 1984),
(Zhang at al., 2014)):
{}
1−
⋅= MMMC
{}
t
t
M
i
eniediag
λ
λ
== ,1; , where
M
λ
is maximum
eigenvalue of matrix
F
and it determines stability
index
η
(Andreev, 1976) of the system (1) in the
form
M
λη
=
. The condition number
{}
MC
takes
minimal value if the matrix
{
}
nirowM
i
,1; ==
ξ
is
composed of vectors with unit norm. Then we can
write
Peaks Emergence Conditions in Free Movement Trajectories of Linear Stable Systems
537

() ()
{
}
()
0
~
xeMCtxrooftx
t
M
λ
=≤
,
(12)
where
M
~
is modified matrix of eigenvectors of
matrix
F
such that it is composed of eigenvectors
with unit norm:
()
{
}
nidiagMM
i
,1;
~
1
2
=⋅=
−
ξ
.
Example 2. Consider the system from example (1)
() () ( ) ()
0
0;
=
==
t
txxtFxtx
,
where the state matrix is
−
−
=
500
726.9781
F
; the
modified matrix of eigenvectors is
[]
−
==
05.00
9987.01
~~
~
21
ξξ
M with condition
number
{
}
MC
~
. Using (12) we get
() ()
0973.39 xetx
t−
≤
. Fig. 3 illustrates curves from
the fig. 2 (curves 1-4) and the estimate
()
{
}
()
0
~
xeMСtx
t−
≤
.
Figure 3: Quantitative estimation of peaks.
4 CONCLUSIONS
Linear asymptotically stable systems with a simple
real spectrum of state matrix were studied. Necessary
conditions for emergence of peaks in free movement
trajectories of those systems were found. It has been
established that peaks arise by certain initial
conditions in the case that the structure of
eigenvectors is close to collinear. Quantitative
estimation of peaks such as upper estimate of the state
vector norm was found through the condition number
of the modified matrix of eigenvectors.
ACKNOWLEDGEMENTS
This work was supported by the Government of the
Russian Federation (Grant 074-U01) and the Ministry
of Education and Science (Project 14. Z50.31.0031).
This work was supported by the Russian Federation
President Grant №14.Y31.16.9281-НШ.
REFERENCES
Andreev, J., N., 1976. Control of finite dimensional linear
plants, Science (in Russian).
Gantmaher, F., R., 2004. Matrix Theory, FIZMATLIT (in
Russian)
Moler, C., B., Van Loan, C., F., 2003. Nineteen Dubious
Ways to Compute the Exponential of a Matrix, Twenty-
Five Years Later. SIAM Review, Vol. 45, No. 1, pp. 3-49
Lancaster, P., Tismenetsky, M., 1985. The Theory of
Matrices, Academic Press. Orlando.
Golub, G., H., Wilkinson, J., H., 1976. ILL-conditioned
eigensystems and the computation of the Jordan
canonical form. SIAM Rev., 18, pp. 578–619.
Golub, G., H., Van Loan, C., F., 1996. Matrix
Computations, Johns Hopkins University Press.
Baltimore and London, 3
rd
Edition
Wilkinson, J., H., 1984. Sensitivity of eigenvalues. Utilitas
Mathematica. Vol. 25., pp. 5-76
Wilkinson, J., H., 1986. Sensitivity of eigenvalues II.
Utilitas Mathematica. Vol. 30., pp. 243-286.
Zhang, L., Wang, X., T., 2014. Partial eigenvalue
assignment for high order system by multi-input
control. Mechanical Systems and Signal Processing.
Vol. 42., pp. 129–136.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
538
