
Calculation of the Boundaries and Barriers of the Workspace of a
Redundant Serial-parallel Robot using the Inverse Kinematics
Adri´an Peidr´o,
´
Oscar Reinoso, Arturo Gil, Jos´e Mar´ıa Mar´ın, Luis Pay´a and Yerai Berenguer
Systems Engineering and Automation Department, Miguel Hern´andez University, 03202, Elche, Spain
Keywords:
Robot Manipulator, Redundant Robot, Workspace, Inverse Kinematics, Discretization Methods.
Abstract:
This paper presents the workspace analysis of a redundant serial-parallel robot. Due to the complexity of the
robot, the complex constraints (joint limits and no-interference between the legs of the robot), and the globally
serial structure of the robot, a discretization method based on the forward kinematics would be most appro-
priate to compute the workspace. However, this widely used method can only obtain the external boundaries
of the workspace, missing the internal barriers that hinder the motion of the robot, which may exist inside the
boundaries. To avoid missing these barriers, we use a discretization method that uses the solution of the inverse
kinematic problem of the robot. By studying the feasibility of attaining a desired position and orientation by
the different branches of the solution to the inverse kinematics, the proposed discretization method is able to
obtain both the external boundaries and the internal barriers of the workspace. Some examples are presented
to show the importance of these internal barriers in the motions of the robot inside the workspace.
1 INTRODUCTION
The workspace of a robot manipulator, which is the
set of positions and orientations that its end-effector
can reach, is very important for designing the robot
and planning its movements. There are many meth-
ods to calculate the workspace of robots, but most of
them can be classified into three main groups (Merlet,
2006): geometrical methods, singularity-based meth-
ods and discretization methods.
The geometrical methods are especially useful for
parallel robots, in which the end-effector is controlled
by two or more kinematic chains actuating in paral-
lel. These methods obtain first the workspace asso-
ciated with each kinematic chain individually. Such
individual workspaces usually are simple geometrical
objects, such as annuli (Merlet et al., 1998), spher-
ical shells (Gosselin, 1990) or tori (Liu and Wang,
2014). After obtaining the individual workspaces, the
workspace of the complete robot is obtained as the
intersection of these individual workspaces. These
methods are very fast and efficient, but they are
also limited since they are only available for specific
robots. Moreover, with these methods it may be very
difficult to take into account some restrictions in the
calculation of the workspace, such as the existence of
joint limits, or the condition that mechanical interfer-
ences between different bodies should not occur.
The singularity-based methods begin by writing
all the kinematic restrictions of the robot (including
joint limits) as a system of equations. Next, the Ja-
cobian matrix of this system with respect to all the
involved variables is derived, excluding the variables
that define the position and orientation of the end-
effector. Then, the boundaries of the workspace can
be obtained as the set of configurations of the robot
for which the mentioned Jacobian matrix is not full-
rank. These configurations that produce the rank de-
ficiency of the Jacobian matrix may be found analyti-
cally (Abdel-Malek and Yang, 2006; Abdel-Malek et
al., 2000) or numerically (Haug et al., 1996; Bohigas
et al., 2012). The main problem of the singularity-
based methods is the fact that all the constraints must
be written as equalities, which may result in too large
systems of equations. Moreover, some restrictions
cannot be modeled as equality constraints, like the
condition of no-interference between different bodies.
Finally, the discretization methods are very flexi-
ble and can easily deal with all types of constraints, al-
though they can be very computer-intensive. The dis-
cretization methods consist of discretizing the Carte-
sian (or joint) space into a regular or randomized grid
of nodes, and solving the inverse (or forward) kine-
matic problem of the robot for each node to obtain
the complete configuration of the robot (Macho et
al., 2009; Bonev and Ryu, 2001; Pisla et al., 2013;
412
Peidró, A., Reinoso, Ó., Gil, A., Marín, J., Payá, L. and Berenguer, Y.
Calculation of the Boundaries and Barriers of the Workspace of a Redundant Serial-parallel Robot using the Inverse Kinematics.
DOI: 10.5220/0005984704120420
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 412-420
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Cervantes-S´anchez et al., 2000). Then, it is checked if
the obtained configuration satisfies all the considered
constraints (e.g. joint limits or no-interference), in
which case the configuration is stored as a workspace
point. Since the forward kinematic problem is usually
easier to solve in serial robots than the inverse prob-
lem, it is more convenient to discretize the joint space
for these robots. On the contrary, the inverse kine-
matic problem is usually simpler for parallel robots
than the forward problem, therefore the Cartesian
space is usually discretized for them.
This paper presents the calculation of the
workspace of a redundant serial-parallel robot with
ten degrees of freedom, using a discretization method
and the solution of the inverse kinematic problem.
The robot is composed of some parallel mechanisms
connected in series, which grants it a globally se-
rial architecture. Both its globally serial structure
and its kinematic redundancy make its forward kine-
matic problem much simpler than its inverse kine-
matic problem. Thus, a method based on discretiz-
ing its joint space and solving the forward kinemat-
ics would be more appropriate for calculating its
workspace. Nevertheless, this method misses impor-
tant information regarding the internal structure of the
workspace, which is crucial for planning the move-
ments of the robot. For example, Figure 1a shows the
workspace that is obtained when sampling the joint
space of the robot and solving its forward kinematic
problem. This method simply generates positions for
the end-effector and “populates” the workspace with
these positions. As a result, this method only yields
the external boundaries of the workspace. However,
a more careful analysis of the workspace, as the one
presented in this paper, reveals the existence of inter-
nal barriers inside the workspace, as shown in Figure
1b. These internal barriers, which cannot be detected
when generating the workspace by using the forward
kinematics, are very important for planning the move-
ments of the robot, since they imply motion impedi-
ments.
(a) (b)
Internal barriers
Figure 1: (a) Workspace generated by discretizing the joint
space and generating positions solving the forward kine-
matic problem. This method only yields the external bound-
aries. (b) Actually, the method based on the forward kine-
matics misses existing internal barriers that hinder the mo-
tion of the robot.
In this paper, we present a discretization method to
calculate the workspace of the aforementioned serial-
parallel robot, including the internal barriers that lie
inside the external boundaries. To this end, the Carte-
sian space is discretized instead of the joint space,
and the inverse kinematic problem is solved instead
of the forward kinematics. Although the robot is re-
dundant, the different branches of the solution to its
inverse kinematic problem can be exploited to obtain
the workspace boundaries and the internal barriers,
as this paper shows. After presenting the proposed
method, some examples are used to show the impor-
tance of the internal barriers of the workspace in the
planning of the movements of the robot.
The remainder of this paper is organized as fol-
lows. Section 2 presents a ten-degrees-of-freedom
serial-parallel robot and reviews the solution to the
inverse kinematic problem of this robot. Next, Sec-
tion 3 presents a method based on the solution of
the inverse kinematics to compute the workspace of
the robot, including the barriers present inside the
workspace. Section 4 presents some examples of the
application of the proposed method to calculate dif-
ferent workspaces, and analyzes the effects of the in-
ternal barriers on the motion of the robot. Finally,
Section 5 concludes this paper.
2 INVERSE KINEMATICS OF A
SERIAL-PARALLEL ROBOT
This section reviews the solution of the inverse kine-
matic problem of the redundant serial-parallel robot
shown in Figure 2a. This robot is designed to climb
and explore 3D structures, like metallic bridges, to
inspect and maintain them. Its feet carry magnets to
adhere to the climbed structure. Figure 2b shows an
example of the robot performing a transition between
two perpendicular beams of a 3D structure.
The robot is biped, and each leg j ∈ {A, B} is
composed of two parallel mechanisms connected in
series. In each leg j, the i-th parallel mechanism
(i ∈ {1, 2}) has two linear actuators with lengths u
ij
and v
ij
(see Figure 2c). Furthermore, each leg is con-
nected to the hip H through one revolute actuated
joint, which rotates the leg an angle θ
j
with respect
to the hip. Thus, the robot has ten degrees of free-
dom. The joint coordinates associated to these ten
degrees of freedom are the lengths of the eight linear
actuators and the two rotated angles of the hip, i.e.
q = [u
1A
, v
1A
, u
2A
, v
2A
, u
1B
, v
1B
, u
2B
, v
2B
, θ
A
, θ
B
]
T
.
The geometric design of the robot depends on
four parameters, which can be seen in Figure 2: the
width b and length h of the central body of the legs,
Calculation of the Boundaries and Barriers of the Workspace of a Redundant Serial-parallel Robot using the Inverse Kinematics
413

t
Hip H
Leg A
Leg B
Foot A Foot B
ș
A
ș
B
(a) (b)
(c)
Foot j
Hip H
y
1j
ij
1j
y
2j
y
j
ij
2j
ș
j
h
2p
Foot A
Foot B
2b
u
1j
v
1j
v
2j
u
2j
Figure 2: (a) CAD model of the serial-parallel robot studied in this paper. (b) Example of the robot performing a transition
between two perpendicular beams in a 3D structure. (c) Detailed view of the kinematics of the leg j of the robot (j ∈ {A, B}).
the width p of the feet, and the separation t between
the rotations of the hip. Furthermore, in practice the
lengths of the linear actuators should be limited, i.e.
u
ij
, v
ij
∈ [ρ
0
, ρ
0
+ ∆ρ], where ρ
0
> 0 is the minimum
length of these actuators and ∆ρ > 0 is their stroke.
Thus, the parameters ρ
0
and ∆ρ will also be regarded
as design parameters of the robot.
The inverse kinematic problem of this robot was
solved in (Peidro et al., 2015), and the solution will be
summarized here since we will use it to compute the
workspace of the studied robot. The inverse kinematic
problem consists of finding the values of the joint co-
ordinates q necessary to attain a desired position and
orientation for the foot B relative to the foot A, given
by the following homogeneous transform matrix T
A
B
:
T
A
B
=
r
11
r
12
r
13
p
x
r
21
r
22
r
23
p
y
r
31
r
32
r
33
p
z
0 0 0 1
(1)
where r
ij
are the components of the rotation matrix
that defines the orientation of the foot B with respect
to the foot A and p = [p
x
, p
y
, p
z
]
T
is the position vec-
tor of the foot B relative to the foot A.
As stated above, the inverse kinematic problem
consists of calculating the vector q of the joint co-
ordinates from the relative position and orientation
between the feet of the robot, given by the matrix
T
A
B
. However, as demonstrated in (Peidro et al.,
2015), the inverse kinematic problem becomes eas-
ier by defining a set of intermediate joint coordi-
nates
˜
q = [ϕ
1A
, ϕ
2A
, ϕ
1B
, ϕ
2B
, y
1A
, y
A
, y
1B
, y
B
, θ
A
, θ
B
]
T
,
which can be solved more easily in terms of T
A
B
(the
geometrical meaning of each intermediate joint coor-
dinate is shown in Figure 2c). Then, it can be shown
that after solving
˜
q, the intermediate joint coordi-
nates unequivocally determine the joint coordinates
q. The solution for the intermediate joint coordinates
depends on the desired orientation, distinguishing two
cases (Peidro et al., 2015).
2.1 Case 1: r
2
33
6= 1
Assume that the four intermediate joint coordinates
{ϕ
1B
, y
B
, y
1A
, y
1B
} are known. In that case, it can be
shown that the remaining six intermediate joint coor-
dinates {ϕ
1A
, ϕ
2A
, ϕ
2B
, y
A
, θ
A
, θ
B
} can be calculated in
terms of {ϕ
1B
, y
B
} by performing the following oper-
ations. First, ϕ
2B
is calculated as follows:
s
B
= σ
1
r
32
q
1− r
2
33
, c
B
= σ
1
−r
31
q
1− r
2
33
(2)
ϕ
2B
= ϕ
1B
− atan2(s
B
, c
B
) (3)
where σ
1
∈ {−1, 1} and atan2(sin(ψ), cos(ψ)) is the
inverse tangent function that uses the sine and the co-
sine of an angle ψ to calculate the angle in the correct
quadrant. Next, θ
A
is calculated as follows:
s
θ
A
= −
r
31
y
B
s
ϕ
1B
+ r
32
y
B
c
ϕ
1B
+ p
z
t
(4)
c
θ
A
= σ
2
q
1− s
2
θ
A
(5)
θ
A
= atan2(s
θ
A
, c
θ
A
) (6)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
414

where σ
2
∈ {−1, 1}, s
ϕ
1B
= sin(ϕ
1B
), and c
ϕ
1B
=
cos(ϕ
1B
). Following, θ
B
can be calculated as:
s
θ
B
= r
33
s
θ
A
+ c
θ
A
(c
B
r
31
− s
B
r
32
) (7)
c
θ
B
= r
33
c
θ
A
− s
θ
A
(c
B
r
31
− s
B
r
32
) (8)
θ
B
= atan2(s
θ
B
, c
θ
B
) (9)
Finally, the remaining intermediate joint coordinates
{ϕ
1A
, ϕ
2A
, y
A
} can be calculated as follows:
s
A
= s
B
r
11
+ c
B
r
12
, c
A
= s
B
r
21
+ c
B
r
22
(10)
Ω
1
= r
11
y
B
s
ϕ
1B
+ r
12
y
B
c
ϕ
1B
+ p
x
− tc
θ
A
c
A
(11)
Ω
2
= r
21
y
B
s
ϕ
1B
+ r
22
y
B
c
ϕ
1B
+ p
y
+ tc
θ
A
s
A
(12)
y
A
=
q
Ω
2
1
+ Ω
2
2
(13)
ϕ
1A
= atan2(Ω
1
, Ω
2
) (14)
ϕ
2A
= ϕ
1A
− atan2(s
A
, c
A
) (15)
2.2 Case 2: r
2
33
= 1
In this case, we assume that the values of the five
intermediate joint coordinates {ϕ
1B
, ϕ
2B
, y
B
, y
1A
, y
1B
}
are known. Then, by defining s
B
= sin(ϕ
1B
−ϕ
2B
) and
c
B
= cos(ϕ
1B
− ϕ
2B
), we can still compute the values
of the remaining five intermediate joint coordinates
{ϕ
1A
, ϕ
2A
, y
A
, θ
A
, θ
B
} using Eqs. (4) to (15).
2.3 Feasible Regions
The solutions described in subsections 2.1 and 2.2 as-
sume that some of the intermediate joint coordinates
are known, and compute the remaining intermediate
joint coordinates in terms of the former. This is due
to the kinematic redundancy of the robot: fixing the
position and orientation of one foot with respect to
the other foot only provides six independent equations
(three for the position and three for the orientation)
to calculate ten unknown intermediate joint coordi-
nates. Thus, six independent equations only allow us
to calculate six intermediate joint coordinates in terms
of the remaining four, as described in subsection 2.1.
Moreover, when the desired orientation between the
feet satisfies r
2
33
= 1, ϕ
2B
cannot be determined from
the equations and its value must also be assumed to
be known (subsection 2.2).
According to the solutions described in the pre-
vious subsections, the solution of the inverse kine-
matic problem for a given desired position and orien-
tation is a four-dimensional set in the ten-dimensional
space of the intermediate joint coordinates (or a five-
dimensional set if the desired orientation satisfies
r
2
33
= 1). This is because the ten intermediate joint
coordinates have been solved in terms of four (or
five) of the intermediate joint coordinates [called de-
cision variables in (Peidro et al., 2015)], whose values
can be freely decided. In contrast, in non-redundant
robots the solution to the inverse kinematics is a set
of isolated points in the joint space (i.e., a zero-
dimensional set). Due to the high dimensionality of
the solution sets in this robot, it is not possible to
represent graphically the complete solutions to the in-
verse kinematics.
However, as demonstrated in (Peidro et al., 2015),
it is possible to reduce the dimensionality of these
solution sets without losing relevant information, ob-
taining an alternative and more compact representa-
tion of the solutions of the inverse kinematic problem.
This reduction of dimensionality is based on the fact
that not all the decision variables (i.e. the four or five
intermediate joint coordinates in terms of which the
remaining unknowns are calculated) are equally im-
portant to determine the posture of the robot. In fact,
it can be shown that after fixing the values of the de-
cision variables {ϕ
1B
, y
B
} (and also ϕ
2B
, if r
2
33
= 1),
the overall posture of the robot is determined, and
the remaining decision variables {y
1A
, y
1B
} only pro-
duce small internal motions of the central bodies of
the legs along the legs, which do not affect the over-
all posture of the robot. Since the overall posture of
the robot only depends on {ϕ
1B
, y
B
} (and also ϕ
2B
, if
r
2
33
= 1), we can focus only on these two (or three)
variables to analyze the solutions of the inverse kine-
matic problem, and use this information to discard the
pairs {ϕ
1B
, y
B
} that yield a forbidden posture in which
the legs of the robot interfere, for example.
Exploiting the previous idea regarding the possi-
bility of reducing the dimension of the solution sets,
(Peidro et al., 2015) developed a Monte Carlo algo-
rithm to obtain the regions R
f
of the ϕ
1B
-y
B
plane
(or the regions of the ϕ
1B
-ϕ
2B
-y
B
space, if r
2
33
= 1)
which allow the robot to attain a desired position and
orientation T
A
B
satisfying the joint limits, and they
called these regions feasible regions. Any point of
these feasible regions yields a valid solution of the
inverse kinematic problem, satisfying the condition
that the lengths of the eight linear actuators of the
robot should be between the joint limits [ρ
0
, ρ
0
+ ∆ρ].
In this paper, we will impose an additional condi-
tion to calculate the feasible regions: in order for a
pair {ϕ
1B
, y
B
} (or triplet {ϕ
1B
, ϕ
2B
, y
B
}, if r
2
33
= 1)
to belong to the feasible regions R
f
, the posture cor-
responding to that pair (or triplet) should not pro-
duce mechanical interferences between the legs of the
robot. To check this condition of no-interference be-
tween the legs, the Separating Axis Theorem will be
used (Ericson, 2004). This will be explained in Sec-
tion 4 in more detail.
Calculation of the Boundaries and Barriers of the Workspace of a Redundant Serial-parallel Robot using the Inverse Kinematics
415

According to subsection 2.1, the solution to the
inverse kinematics depends on two binary variables
σ
1
, σ
2
∈ { −1, 1} when the desired orientation satis-
fies r
2
33
6= 1. Each combination of these binary vari-
ables will yield a different feasible region R
f
, which
corresponds to a different branch of the solution to
the inverse kinematics. Thus, when r
2
33
6= 1, the so-
lution to the inverse kinematics will have four dif-
ferent branches, identified by the four possible com-
binations (σ
1
, σ
2
) of these binary variables: (1, 1),
(1, −1), (−1, 1), (−1, −1). If the desired orienta-
tion satisfies r
2
33
= 1, then according to subsection 2.2
only the binary variable σ
2
is involved in the solu-
tion of the inverse kinematics. Thus, the inverse kine-
matic problem will only have two different branches
in that case, one branch corresponding to σ
2
= 1 and
the other branch corresponding to σ
2
= −1.
3 OBTAINING THE WORKSPACE
USING THE INVERSE
KINEMATICS
In this section, we will describe how the solution to
the inverse kinematic problem, described in Section
2, can be used to obtain the workspace of the serial-
parallel robot studied in this paper, including its ex-
ternal boundaries and internal barriers.
According to the previous section, the solution to
the inverse kinematic problem of the serial-parallel
robot studied in this paper can be summarized as fol-
lows. Given a desired position and orientation be-
tween the feet of the robot, encoded by the homoge-
neous transformation matrix T
A
B
defined in Eq. (1),
the solution to the inverse kinematics depends on r
33
:
• If the desired orientation satisfies r
2
33
6= 1, then the
solution to the inverse kinematics can be repre-
sented by a feasible region R
f
in the ϕ
1B
-y
B
plane,
such that any point of this region corresponds to a
posture that allows the robot to attain the desired
position and orientation T
A
B
satisfying the joint
limits of the linear actuators and guaranteeing that
the legs of the robot do not interfere. Moreover,
there exist four different branches for the solution,
i.e. four different feasible regions R
f
correspond-
ing to the four possible combinations of the binary
variables σ
1
and σ
2
.
• If the desired orientation satisfies r
2
33
= 1, the so-
lution to the inverse kinematics can be represented
by a feasible region R
f
in the ϕ
1B
-ϕ
2B
-y
B
space,
such that any point of R
f
yields a posture that al-
lows the robot to attain the desired position and
orientation T
A
B
satisfying the joint limits of the
linear actuators and guaranteeing that the legs of
the robot do not interfere. In this case, there exist
two different branches for the solution, i.e. two
different feasible regions R
f
, one region per each
value of the binary variable σ
2
.
Once the solution to the inverse kinematics is
available (including all the branches of this solution),
the workspace boundaries and barriers can be ob-
tained using a discretization algorithm explained next.
The workspace of this robot can be defined as the
set of positions and orientations that the foot B can at-
tain with respect to the foot A. Such a workspace is a
six-dimensional set, since the position and orientation
of the foot B relative to the foot A can be represented
by three translations p = [p
x
, p
y
, p
z
]
T
and three rota-
tions r = [α, β, γ]
T
(where α, β and γ are Euler angles).
To calculate the workspace, the six-dimensional space
of the variables {p
x
, p
y
, p
z
, α, β, γ} is discretized into a
regular grid of nodes. For example, we may approx-
imate each axis of this six-dimensional space by n
d
nodes regularly distributed between two limits, which
yields an overall grid of n
6
d
nodes. Then, for each node
of this grid, the inverse kinematic problem if solved to
check if the node is attainable by each branch of the
solution of the inverse kinematics.
For each branch i of the solution to the inverse
kinematics, we create a list WS
i
of the nodes that
can be reached using that branch. After the algorithm
has checked all the nodes of the grid, the list WS
i
is
an approximation of the workspace associated to the
branch i, since it contains all the positions and orien-
tations that can be reached with that branch. Then,
the boundaries of the workspace associated to the i-th
branch can be approximated by the nodes contained in
WS
i
which have at least one unreachable neighboring
node (i.e., a neighboring node not contained in WS
i
).
After obtaining the boundaries of the workspaces as-
sociated to the different branches, the boundaries of
all the branches can be joined to obtain the bound-
aries and barriers of the complete workspace.
To determine if an arbitrary node of the grid is at-
tainable using a given branch i of the inverse kinemat-
ics, the feasible region R
f
associated to that branch is
calculated using the Monte Carlo algorithm described
in (Peidro et al., 2015). If the region R
f
is empty, then
it is considered that the node is not attainable by the i-
th branch, and the node is not included in the list WS
i
(see Figure 3). The mentioned Monte Carlo algorithm
generates the region R
f
by randomly sampling points
in the ϕ
1B
-y
B
plane (or in the ϕ
1B
-ϕ
2B
-y
B
space, if
r
2
33
= 1). If the posture generated by each randomly
sampled point satisfies the joint limits of the linear ac-
tuators, and if the legs do not interfere, then that point
is stored as a point of the feasible region R
f
. In this
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
416
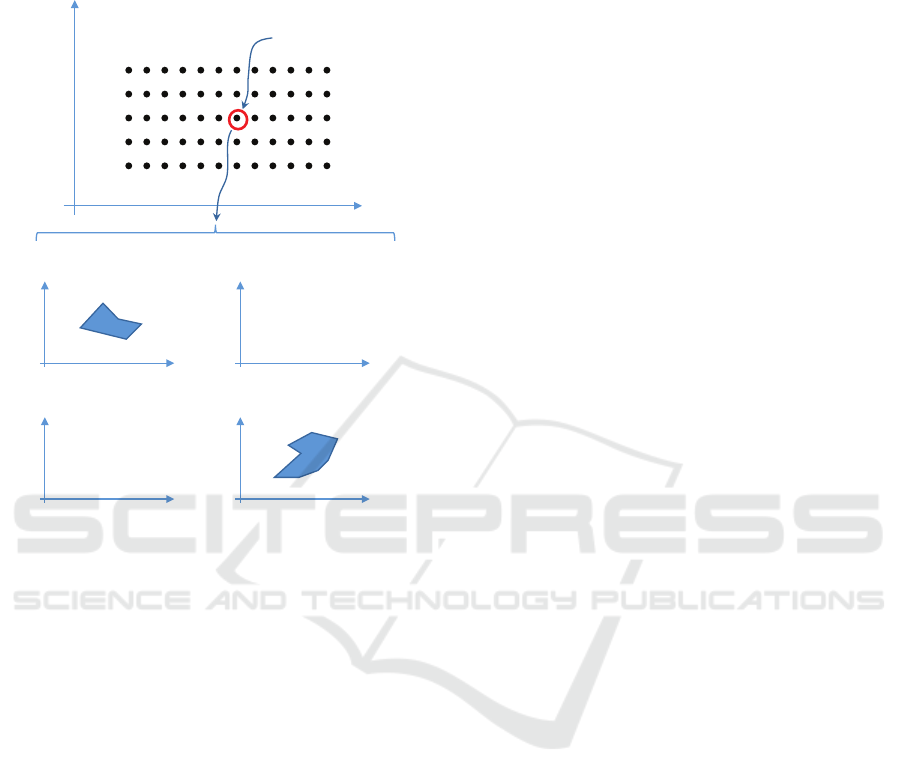
way, a discrete approximation of the region R
f
can be
obtained by sampling a large number of points in the
ϕ
1B
-y
B
plane (or in the ϕ
1B
-ϕ
2B
-y
B
space).
p
x
p
y
Node k
ij
1B
y
B
Branchı
1
ı
2
= 1
ij
1B
y
B
Branchı
1
ı
2
= -1
ij
1B
y
B
Branchı
1
= -ı
2
= 1
ij
1B
y
B
Branchı
1
= -ı
2
= -1
R
f
R
f
Figure 3: A 2D example that illustrates the process to deter-
mine whether a given node k of the potential workspace is
reachable or not. For a given node k, the feasible regions R
f
are calculated using all the branches of the solution of the
inverse kinematic problem. In this case, the node k belongs
only to the workspaces of the branches (1, 1) and (−1, −1)
since these are the only branches leading to non-empty fea-
sible regions R
f
.
Note that it is sufficient to find a single point be-
longing to R
f
to guarantee that R
f
is not empty and
classify the corresponding node of the workspace as
attainable. However, checking if R
f
is empty (and
classifying the corresponding node as unattainable by
the i-th branch of the inverse kinematics) is not that
easy, since one would need to explore exhaustively
the ϕ
1B
-y
B
plane (or the ϕ
1B
-ϕ
2B
-y
B
space) to guaran-
tee that this plane (space) does not have points satis-
fying all the constraints (i.e., to guarantee that R
f
is
empty). Since it is not feasible to perform such an
exhaustive search to check if R
f
is empty, this prob-
lem is practically solved by establishing a maximum
number n
a
of attempts to generate a point in R
f
. Then,
the aforementioned Monte Carlo algorithm begins to
randomly sample points in the ϕ
1B
-y
B
plane (or in
the ϕ
1B
-ϕ
2B
-y
B
space, if r
2
33
= 1). If it finds a point
that satisfies all the constraints (joint limits and no-
interference), the Monte Carlo algorithm stops: the
region R
f
is not empty (it contains at least one point)
and the node is classified as attainable. If, on the con-
trary, the Monte Carlo algorithm has sampled n
a
ran-
dom points and none of them satisfies the constraints,
it is considered that R
f
is empty, which means that the
corresponding node cannot be attained by the consid-
ered branch of the inverse kinematics. Obviously, this
method will be more accurate when n
a
increases, but
the computation will also take more time, so a com-
promise between precision and computational cost is
necessary.
It should be remarked that the method described
in this section to compute the workspace is very
computer-intensive if we try to discretize and com-
pute the six-dimensional workspace of the variables
{p
x
, p
y
, p
z
, α, β, γ}, since the number of nodes to
check is n
6
d
(and, for each node, the feasible regions
R
f
must be obtained for the different branches of
the inverse kinematics). Moreover, a six-dimensional
workspace cannot be represented graphically. For
these reasons, and to decrease the computational
cost, we will fix some of these six variables to ob-
tain lower-dimensional workspaces that can be repre-
sented graphically and are more easy to understand,
such as the constant-orientation workspace (i.e., the
set of positions that can be attained by the foot B with
respect to the foot A when the relative orientation be-
tween the feet is constant). The constant-orientation
workspace is very useful when planning some move-
ments which are necessary to explore a 3D structure,
such as when performing a transition between dif-
ferent beams (see Figure 2b). In the following sec-
tion, we will illustrate the algorithm described in the
present section using some examples.
4 EXAMPLES
This section presents some examples of the applica-
tion of the method described in Section 3 to compute
different workspaces of the studied robot. For the
next examples, the geometric design parameters of the
robot are: b = p = 4, h = 16, t = 15.6, ρ
0
= 19, and
∆ρ = 7.5 (all in cm). In all the examples of this sec-
tion, we will discretize the workspace into n
d
= 200
points in each axis. Moreover, we will sample a max-
imum of n
a
= 5000 random points before deciding
that the feasible region R
f
(of valid postures that yield
a given position and orientation between the feet) is
empty (n
a
was defined in Section 3). In all the exam-
ples, we will assume that the foot A is firmly attached
to the structure, and we will compute the set of posi-
tions that the foot B (which is free to move) can reach.
Calculation of the Boundaries and Barriers of the Workspace of a Redundant Serial-parallel Robot using the Inverse Kinematics
417

4.1 Example 1
In this example, we are interested in obtaining a
constant-orientation workspace, i.e. the set of attain-
able points by the foot B when the relative orienta-
tion between the feet is constant. More specifically,
we will study the workspace obtained when both feet
have the same orientation, which means that the ro-
tation submatrix of T
A
B
is the identity matrix. Fur-
thermore, we will be interested only in the intersec-
tion of such constant-orientation workspace with the
plane p
z
= 0, to study the planar motions of the robot
inside this constant-orientation workspace. Note that
the robot needs to perform motions of this type to
travel along a beam of a structure, as shown in Fig-
ure 4. The desired position and orientation will have
the following form for this example:
T
A
B
=
1 0 0 p
x
0 1 0 p
y
0 0 1 0
0 0 0 1
(16)
To apply the algorithm described in the previous
section, we will define a box B that encloses the
workspace in the p
x
-p
y
plane, and we will discretize
this box into a grid of 40000 nodes regularly dis-
tributed (200 nodes per each axis). Then, for each
node, we will solve the inverse kinematic problem us-
ing the matrix of Eq. (16) as the input, to check if each
node is attainable by the different branches of the in-
verse kinematics. The chosen box for this example
is B = {(p
x
, p
y
) : −80 cm ≤ p
x
≤ 80 cm, −50 cm ≤
p
y
≤ 50 cm}. Running the algorithm described in the
previous section for these parameters, the workspace
shown in Figure 4 is obtained. Note that, since in
this case r
2
33
= 1, according to Section 2.3 the solution
to the inverse kinematic problem in this case has two
branches: one for σ
2
= 1 and other for σ
2
= −1. The
workspaces associated to these branches are shown in
Figure 4 with different colors.
Note that this workspace is split into the compo-
nents associated with the two branches of the solu-
tion to the inverse kinematic problem. The complete
workspace (i.e. the union of the two components)
has a void around the foot A, which is necessary to
avoid the interferences between the legs. Accord-
ing to Figure 4, the robot cannot move the foot B
from one side of the workspace (e.g. the right half
the workspace, associated with the branch σ
2
= 1) to
the other side (e.g. the left half, associated with the
branch σ
2
= −1) keeping constant the orientation be-
tween the feet, since the workspaces associated with
both branches have boundaries in the middle of the
workspace, both above and below the foot A. This is
p
x
p
y
-80
80
-50
50
Beam
Branch ı
2
= -1
Branch ı
2
= 1
Foot A
Foot B
Figure 4: Planar constant-orientation workspace that pro-
vides the points at which the foot B can be placed with the
same orientation as the foot A. This constant-orientation
workspace is useful to plan movements along the direction
of the beam. The workspaces associated with the branches
σ
2
= −1 and σ
2
= 1 are represented in red and blue colors,
respectively.
illustrated in Figure 5, where the robot starts at an ini-
tial point in the workspace associated with the branch
σ
2
= 1, and tries to describe a trajectory towards the
left half of the workspace (see Figure 5a). However,
the trajectory cannot be completed because the robot
cannot cross the boundaries of the component of the
workspace in which it moves. This boundary is orig-
inated from the fact that the legs cannot interfere: as
Figure 5b shows, when the foot B is close to the men-
tioned boundary, both legs are about to intersect.
To check if the two legs interfere in all the ex-
amples of this paper, the Separating Axis Theorem is
used (Ericson, 2004). Each leg can be approximated
by the union of two cuboids (also known as rectan-
gular parallelepipeds): one cuboid encloses the foot,
and the other cuboid encloses the central body of the
leg, including the linear actuators (these cuboids are
represented in magenta in Figure 5b). Then, the two
legs will interfere if one of the cuboids of one leg in-
tersects one of the cuboids of the other leg. Since the
cuboids are convex shapes, the Separating Axis The-
orem can easily be used to check if they intersect.
4.2 Example 2
In this example, the objective is to find the planar
constant-orientation workspace defined by the follow-
ing homogeneous transformation matrix between the
feet of the robot:
T
A
B
=
0 −1 0 p
x
1 0 0 p
y
0 0 1 0
0 0 0 1
(17)
This orientation is a rotation of 90
◦
about the Z axis,
which is necessary to perform a transition between
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
418

(a)
(b)
Initial position
Final position
Trajectory
Foot A
Foot B
Central body
of the leg A
Central body of
the leg B
Figure 5: (a) A trajectory between both components of the
workspace. (b) The robot cannot reach the left component
because it cannot cross a boundary of the component in
which it moves (the right component). When approaching
the boundary, the legs are about to intersect: the foot B is
almost touching the central body of the leg A. To cross the
boundary, an interference between these two bodies would
be necessary.
two perpendicular beams in a structure, as shown in
Figures 2b and 6. Again, we are interested only in the
intersection of this constant-orientation workspace
with the plane p
z
= 0, since the motion necessary to
perform such a transition is planar.
Next, the algorithm described in Section 3 is ap-
plied, discretizing the following box B into a grid of
40000 nodes (200 nodes per axis): B = {(p
x
, p
y
) :
−40 cm ≤ p
x
≤ 80 cm, −40 cm ≤ p
y
≤ 80 cm}. The
resulting workspace is shown in Figure 6. Again,
since the desired orientation satisfies r
2
33
= 1, the
solution to the inverse kinematic problem has two
branches, one for σ
2
= 1 (shown in blue in Figure 6)
and other for σ
2
= −1 (shown in red in Figure 6).
In this case, the workspace attainable using the
branch σ
2
= −1 of the solution to the inverse kine-
matic problem is smaller than the workspace associ-
ated with the branch σ
2
= 1. Note that the workspace
associated with the branch σ
2
= −1 has two compo-
nents: a big one, which is close to the foot A in Figure
p
y
-40
-40
80
80
p
x
Foot A
Foot B
Beam 1
Beam 2
Branch ı
2
= -1
Branch ı
2
= 1
Branch ı
2
= -1
Figure 6: Planar constant-orientation workspace containing
all the points of the plane p
z
= 0 that can be reached with
the foot B rotated 90
◦
about the Z axis with respect to the
foot A.
6, and a smaller one, which is close to the beam 2 in
the same figure. Actually, the shape of the smaller
component cannot be appreciated very well in Fig-
ure 6. However, a more precise approximation of that
component can be obtained if the algorithm described
in Section 3 is executed again discretizing a smaller
box B that encloses only the area around the men-
tioned small component of the workspace, instead of
using a big box that contains all the components as
shown in Figure 6.
The posture of the robot shown in Figure 6, with
the foot B placed on the beam 2, is obtained using the
branch σ
2
= 1 of the solution to the inverse kinemat-
ics. However, according to the same figure, it would
be also possible to place the foot B on the beam 2
using the branch σ
2
= −1, since this branch yields
a small component of the workspace near the beam
2 (i.e., the small component described in the previ-
ous paragraph). This is checked in Figure 7, which
shows a posture of the robot that places the foot B at
a point of the smallest of the two workspace compo-
nents associated with the branch σ
2
= −1. As this fig-
ure shows, using the branch σ
2
= −1, the foot B can
also be effectively placed on the beam 2 with the de-
sired orientation. However, in this posture, the hip of
the robot intersects the beams, so this would not be a
feasible solution in practice. This unfeasibility can be
easily detected by the presented method if we include
the condition that no part of the robot should intersect
the obstacles of the environment, using a similar pro-
cedure to the method used to check if different legs
intersect, described in subsection 4.1.
Calculation of the Boundaries and Barriers of the Workspace of a Redundant Serial-parallel Robot using the Inverse Kinematics
419

Collisions with the
beams of the structure
Beam 2
Beam 1
Figure 7: A posture which places the foot B on the beam 2
with the desired orientation, using the branch σ
2
= −1. In
this posture, the robot collides with the structure.
5 CONCLUSIONS
This paper has presented a discretization method to
calculate the workspace of a serial-parallel redundant
robot using the solution to its inverse kinematic prob-
lem. In contrast to the methods based on the for-
ward kinematics, the proposed method is able to ob-
tain both the external boundaries and the internal bar-
riers of the workspace. Using this method, we have
analyzed the negative effects of the internal barriers
on the movements of the robot inside its workspace.
In the future, we will solve the path planning prob-
lem of this robot. We hope that the analysis presented
in this paper will be very useful to plan the move-
ments of the robot, since the presented method gener-
ates workspace maps that allow the robot to navigate
safely through its workspace, knowing the positions
at which the actuators attain the joint limits, or the
positions where the legs of the robot would collide.
ACKNOWLEDGEMENTS
This work has been supported by the Spanish Min-
istry of Education through grant FPU13/00413, by
the Spanish Ministry of Economy through project
DPI2013-41557-P, and by the Generalitat Valenciana
through project AICO/2015/021.
REFERENCES
Abdel-Malek, K., and Yang, J. (2006). Workspace bound-
aries of serial manipulators using manifold stratifica-
tion. The International Journal of Advanced Manufac-
turing Technology, Vol. 28(11), pp. 1211–1229.
Abdel-Malek, K., Yeh, H.J., and Othman, S.(2000). Interior
and exterior boundaries to the workspace of mechan-
ical manipulators. Robotics and Computer-Integrated
Manufacturing, Vol. 16(5), pp. 365–376.
Bohigas, O., Manubens, M., and Ros, L. (2012). A Com-
plete Method for Workspace Boundary Determination
on General Structure Manipulators. IEEE Transac-
tions on Robotics, Vol. 28(5), pp. 993–1006.
Bonev, I.A., and Ryu, J. (2001). A new approach to orienta-
tion workspace analysis of 6-DOF parallel manipula-
tors. Mechanism and Machine Theory, Vol. 36(1), pp.
15–28.
Cervantes-S´anchez, J.J., Hern´andez-Rodr´ıguez, J.C., and
Rend´on-S´anchez, J.G. (2000). On the workspace,
assembly configurations and singularity curves of
the RRRRR-type planar manipulator. Mechanism and
Machine Theory, Vol. 35(8), pp. 1117–1139.
Ericson, C. (2004). Real-Time Collision Detection. CRC
Press.
Gosselin, C. (1990). Determination of the Workspace of
6-DOF Parallel Manipulators. ASME Journal of Me-
chanical Design, Vol. 112(3), pp. 331–336.
Haug, E.J., Luh, C.M., Adkins, F.A., and Wang, J.Y. (1996).
Numerical Algorithms for Mapping Boundaries of
Manipulator Workspaces. ASME Journal of Mechani-
cal Design, Vol. 118(2), pp. 228–234.
Liu, X.J., and Wang, J. (2014). Parallel Kinematics. Type,
Kinematics, and Optimal Design. Springer-Verlag
Berlin Heidelberg.
Macho, E., Altuzarra, O., Amezua, E., and Hernandez, A.
(2009). Obtaining configuration space and singularity
maps for parallel manipulators. Mechanism and Ma-
chine Theory, Vol. 44(11), pp. 2110–2125.
Merlet, J.P. (1995). Determination of the orientation
workspace of parallel manipulators. Journal of Intel-
ligent and Robotic Systems, Vol. 13(2), pp. 143–160.
Merlet, J.P. (2006). Parallel Robots. Springer Netherlands.
Merlet, J.P., Gosselin, C.M., and Mouly, N. (1998).
Workspaces of planar parallel manipulators. Mecha-
nism and Machine Theory, Vol. 33(1-2), pp. 7–20.
Peidro, A., Gil, A., Marin, J.M., and Reinoso, O. (2015). In-
verse kinematic analysis of a redundant hybrid climb-
ing robot. International Journal of Advanced Robotic
Systems, 12:163, pp. 1–16.
Pisla, D., Szilaghyi, A., Vaida, C., and Plitea, N. (2013).
Kinematics and workspace modeling of a new hybrid
robot used in minimally invasive surgery. Robotics
and Computer-Integrated Manufacturing, Vol. 29(2),
pp. 463–474.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
420
