
Robust Output Control Algorithm for a Twin-Rotor Non-Linear
MIMO System
Sergey Vrazhevsky, Alexey Margun, Dmitry Bazylev, Konstantin Zimenko and Artem Kremlev
ITMO University, Kronverksky av. 49, Saint Petersburg, Russia
Keywords: Non-Linear MIMO System, Robust Control, Output Control, Consecutive Compensator, PID-Controller.
Abstract: This paper addresses to the problem of a non-linear MIMO systems control. A class of non-linear parameter
uncertain systems operating under unknown bounded disturbances is considered. It is assumed, that
mathematical model of such system can be decomposed on linear and non-linear dynamics. Proposed
control algorithm is based on the method of consecutive compensator. The only required parameter to be
known for the controller synthesis is a relative degree of linear part of plant. The effectiveness of the control
method is demonstrated experimentally using the laboratory platform named «Twin Rotor MIMO System».
The proposed method is compared with standard PID controller. Experimental results show that the
transient behaviour of the developed control algorithm provides higher accuracy and performance,
especially for the case of model parameters deviation from their nominal values.
1 INTRODUCTION
Modern technology development requires to
consider different complex mechatronic and robotic
systems as real technical objects, which are
described by systems of non-linear differential
equations, have uncertain parameters and
unaccounted dynamics in mathematical models,
operate under external and internal disturbances. For
such systems classical control methods (modal
control, PID control, etc.) are often inapplicable or
not capable to meet necessary technical
requirements. This problem is especially acute for a
class of nonlinear and multivariable systems with
sufficient couplings.
The main interest of development of advanced
control approaches satisfying these challenges is to
improve performance of such devices and extend
their application area.
This paper considers control problem for twin
rotor MIMO system (TRMS) (Feedback instruments
Ltd., 1998). There are a lot of articles proposing
different control methods applied in the area of non-
linear MIMO systems and applied to a TRMS
particularly, see (Rahideh et al, 2008).
Linear and nonlinear PID control algorithms are
analyzed in (Cajo, 2015).
Optimal controller using LQR technique is
proposed in (Pandey and Laxmi, 2015). Suboptimal
controller using iterative linearization algorithm is
proposed in (Vrazhevsky and Kremlev, 2015).
Suboptimal tracking controller using a linear
quadratic regulator (LQR) with integral action and
adaptive sliding mode controller is described in
(Phillips, 2014). Another control algorithm based
both on optimization method and on fuzzy logic
method was designed in (Allouani et al, 2012).
In (Juang et al, 2011) a fuzzy PID control
scheme with a real-valued genetic algorithm (RGA)
was proposed. A control technique based on
controller named «fuzzy-sliding and fuzzy-integral-
sliding controller» (FSFISC) is designed and
applied to the TRMS in (Tao et al, 2010). Fuzzy
controllers is a quite an intensive research area with
a set of result in non-linear MIMO systems
applications (Shi, 2014).
In (Basri et al, 2014) adaptive controller based
on on the backstepping technique was applied to
quadrotor that was described as non-linear MIMO
system.
A robust control solution is applied to a
linearizable non-linear MIMO systems in (Liu and
Söffker, 2014). It uses feedback linearization and
state feedback control with a disturbance rejection.
However, all considered solutions have a number
of disadvantages, such as complicated engineering
Vrazhevsky, S., Margun, A., Bazylev, D., Zimenko, K. and Kremlev, A.
Robust Output Control Algorithm for a Twin-Rotor Non-Linear MIMO System.
DOI: 10.5220/0005985004210427
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 421-427
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
421
realization, state vector knowledge, complicated
adjustment of control parameters. Some researches
describe modelling methods including identification
and linearization techniques, see (Nejjari et al,
2012). In (Radac et al, 2014.) iterative data-driven
algorithm for experiment-based tuning of controllers
for nonlinear systems was presented.
In this paper a robust output control method is
proposed to control the TRMS system. The control
algorithm is based on the consecutive compensator
method. Performance of proposed method is based
on its possibility to compensate a wide class of
external disturbances and save plant stability in
conditions of unaccounted internal dynamics. The
algorithm is simple to implement due to the fact, that
the only parameter required to build the controller is
a plant’s relative degree.
The paper is organized as follows. Section 2 is
devoted to a brief description of the non-linear twin
rotor MIMO system. Section 3 contains
mathematical model of TMRS bench. Designed
control algorithm is presented in Section 4. Finally,
Experimental results of the proposed control system
and its comparison with PID controller are shown in
Section 5. Finally, concluding remarks are given in
Section 6.
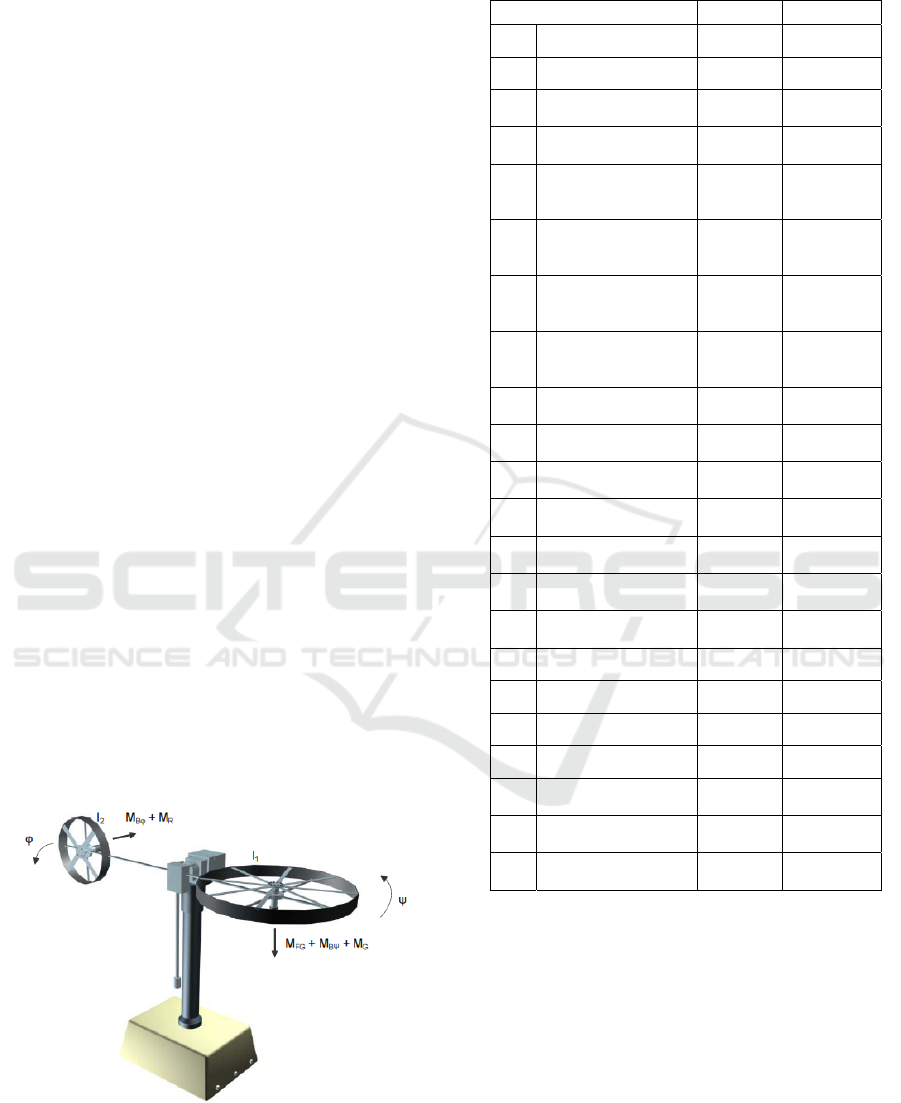
2 BENCH DESCRIPTION
Consider the non-linear twin rotor MIMO system
(TRMS) and obtain its mathematical model. TRMS
is a laboratory helicopter-like system with two
degrees of freedom and opportunity of independent
two-channel control. General view of TRMS is
shown on Fig. 1.
Figure 1: General view of Twin Rotor MIMO System.
Table 1: TRMS parameters.
Parameter description Value Units (SI)
I
1
Pitch inertia moment
6.12×10
-2
kg×m
2
I
2
Yaw inertia moment
2×10
-2
kg×m
2
M
g1
Gravity moment
coefficient
0.32
N×m
M
g2
Gravity moment
coefficient
0.48
N×m
a
1
Parameter of main
rotor static
charactetistic
1.35×10
-2
N/A
b
1
Parameter of main
rotor static
charactetistic
9.24×10
-2
N/A
a
2
Parameter of main
rotor static
charactetistic
2×10
-2
N/A
b
2
Parameter of main
rotor static
charactetistic
9×10
-2
N/A
B
1
ψ
Friction forces
moment parameter
6×10
-2
N×m×s/rad
B
2
ψ
Friction forces
moment parameter
1×10
-2
N×m×s/rad
B
1
ϕ
Friction forces
moment parameter
6×10
-3
N×m×s/rad
B
2
ϕ
Friction forces
moment parameter
1×10
-3
N×m×s/rad
K
gy
Gyroscopic forces
parameter
5×10
-2
s/rad
k
1
Main rotor gain
coefficient
1.1 N/A
k
2
Tail rotor gain
coefficient
0.8 N/A
T
11
Main rotor parameter 1.1 N/A
T
10
Main rotor parameter 1 N/A
T
21
Tail rotor parameter 1 N/A
T
20
Tail rotor parameter 1 N/A
k
c
Cross-reaction gain
coefficient
-0.2 N/A
T
p
Cross-reaction
moment parameter
2 N/A
T
0
Cross-reaction
moment parameter
3.5 N/A
Full list of its parameters is given on Table 1.
These include inertia moments, coefficients of
friction forces moment and gravity moments, cross-
reaction moment parameters, etc.
The system comprises two DC motors: one of
them provides movement in vertical plane (pitch
angle) and the other one is for motion in horizontal
plane (yaw angle). TRMS is controlled by
independent voltage levels on the armature of the
motors. The pitch and yaw angles are measurable
outputs.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
422

Maximum angles of the plant rotation are limited
by mechanical structure constraints. Input voltage
levels are limited within the [-2.5V; +2.5V].
Detailed description of the laboratory bench with
its mathematical model synthesis is given in
(Feedback Instruments, 1998).
3 TRMS MATHEMATICAL
MODEL
In this section we present mathematical model
description of the bench in form of two third-order
differential equations and in a vector-matrix form.
The TRMS works under the following forces:
DC motors torques, gravity forces, friction forces
and such coupling effects as gyroscopic moment and
cross-reaction force.
The plant can be represented as two coupled
subsystems. Given mathematical description of the
plant also include DC motor transfer functions and
friction forces moments.
Plant dynamics in vertical plane is described by
the following moment equation
,
(1)
where
ψ
is a plant pitch angle, I
1
is an inertia
moment, M
1
is a plant torque generated by the main
rotor torque
τ
1
, M
FG
is a gravity moment, M
B
ψ
is a
friction forces moment, M
G
is a gyroscopic moment.
These moments are represented as follows
sin
cos
cos
sign
(2)
DC motors dynamics approximated by first order
transfer function can be represented as
⇒
,
(3)
where
and
are
the torques generated by DC
motors,
and
are the input voltages of the
motors.
Taking into account (2) and (3), the dynamics in
vertical plane (1) can be represented as follows
,
1
1
sin
2
1
cos
sign
1
1
1
1
1
1
2
cos,
1
10
11
1
1
11
1
,
(4)
where
is a vertical angular speed of the plant.
Rewrite system (4) in the form
,
cos
sin
cos
sign
,
(5)
where
,
and
are transition coefficients,
is a function which contains all non-linear
components of the plant dynamic in vertical plane.
System (4) in vector-matrix form can be
represented as following
,
,
(6)
where
01 0
0
1
1
00
10
11
,
0
0
1
11
,
100
,
(7)
0
0
sin
0
0
cos
0
0
sign
0
0
0
0
cos,
(8)
where
is a vector-function of non-linear
components of the subsystem that related with
vertical plant dynamics.
Repeat analog calculations for plant dynamics in
horizontal plane. Moment equation is represented as
follows
,
(9)
where
ϕ
is a plant yaw angle, I
2
is an inertia
moment, M
2
is a plant torque generated by the tail
rotor torque
τ
2
, M
B
ϕ
is a friction forces moment, M
R
is a cross-reactions moment. These moments are
represented as shown
Robust Output Control Algorithm for a Twin-Rotor Non-Linear MIMO System
423

,
sign
,
.
(10)
Considering (3) and (10), the dynamics in
horizontal plane (9) can be represented as follows
,
sign
,
2
2
2
2
2
2
2
,
2
20
21
2
2
21
2
,
1
0
1
1
,
(11)
where
is a horizontal angular speed of the
system,
is a cross reaction variable.
System (11) can be represented as following:
,
2
1
1
2
sign
1
,
(12)
where
,
and
are transition coefficients,
is a function which contains all non-linear
components and cross-reactions of the plant
dynamic in vertical plane:
System (11) in vector-matrix form can be
represented as following
,
,
(13)
where
01 0
0
00
,
0
0
,
100
,
(14)
0
0
sign
0
0
0
0
,
(15)
where
is a vector-function of non-linear
components and cross-reactions of the subsystem
that related with horizontal dynamics of the plant.
As the result, TRMS mathematical model is
represented by two subsystems (5) and (12) with
couplings given as bounded external disturbances.
4 ROBUST CONTROL METHOD
In this section we propose control algorithm for
previously obtained mathematical model of TRMS.
The control law is based on consecutive
compensator (Bobtsov, A., 2002) method.
Consider multivariable control plant:
,,
,
,
,
(16)
where,1,2,1,2,
and
are linear
differential operators with dimensions
and
respectively,
∈ is an output signal,
∈
is an input signal,
,,
is a function of non-
linear components in each channel,
is a
functions of external unknown bound disturbances
in each channel,
and
are linear
differential operators of output and input couplings
respectively, / is a differential operator,
1 is a relative degree of the plant.
A reference model is described by equation:
,1,2
(17)
where
and
are linear differential
operators,
∈ is an output signal of
reference model,
∈ is a smooth bounded
reference signal.
It is necessary to provide tracking of plant’s
output for the reference model output.
Introduce decentralized consecutive compensator
control law in accordance with (Pyrkin, A., et al,
2015):
̂
,
(18)
where
is a positive number,
is a Hurwitz
polynomial with degree
1, is a complex
variable, ̂
is an estimation of tracking error
.
For error estimation the observer is used
Γ
,
̂
,
(19)
where
∈
is an observer state vector,
Γ
0
,00…
,
10…0
,
(20)
where Γ
is a Hurwitz matrix due to the choice of its
coefficients,
0 is a sufficiently large number.
In (Pyrkin, A., et al, 2015) it is proved that
control law (18) with observer (19) provides
convergence of output signal for the reference model
output with prespecified accuracy in the case of
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
424

Lipshitz function
,,. Moreover, proposed
algorithm is robust with respect to the parameter
deviations. However, nonlinear functions in (5) and
(12) are not Lipshitz function due to the presence of
the function sign∙.
In (Margun, A., and Furtat, I., 2015a) it is proved
that controller (18)-(19) provides convergence of
tracking error of MIMO system to the limited area in
the case of quantized output measurement. The
function sign∙ is Lipshitz everywhere except at the
zero point. In the paper (Margun, A., and Furtat, I.,
2015a) the control problem is solved for the system
(16) in presence of quantized output. In this case the
system is exponentially stable with respect to area
around zero caused by the quantizer step and
disturbance value. Since dynamics of quantizer
function is similar to sign∙ at zero origin we can
conclude, that system (16) is exponentially stable
with respect to area around origin. Therefore,
controller (18) and estimation algorithm (19)
provide exponentially convergence of tracking error
of TRMS to the bounded area.
5 EXPERIMENTAL RESULTS
To verify the proposed technique experimentally we
use the following parameters of the consecutive
compensator
0.5,
5
2050,
1,
1,2.
(21)
Observer parameters are taken as
Γ
01
0.01 100
,
01
,
10
,1,2.
(22)
Linear part of TRMS within parameters from
Table 1 is represented in the following form
01 0
0
6∗10
2
1.51
000,91
,
0
0
1
,
100
,
(23)
010
0
6∗10
3
4.5
001
,
0
0
0.8
,
100
,
(24)
Presented control algorithm is experimentally
tested on the TRMS and compared with PID
controller. The plant is controlled simultaneously
and independently by each degree of freedom.
Therefore, all coupling effects are taken into account
during the experiments.
Experimental results (Fig. 2 - 9) for each plant
subsystem in tracking mode and in stabilization
mode are shown in Appendix.
Several scenarios for tracking (Fig. 2 - 5) and
stabilization (Fig. 6 - 9) modes are carried out for
both control systems. PID controller tuned by TRMS
developers is tested in the same modes under the
same conditions for evaluation of proposed
controller performance.
On Fig.4 and Fig.5 it is apparent that consecutive
compensator operates more accurate than PID
controller. On Fig.6 and Fig.7 consecutive
compensator operates with comparable with PID
controller accuracy. On Fig.6 - Fig.9 plant
trajectories in stabilization mode are demonstrated.
Transient processes of the consecutive compensator
and the PID controller are quite similar.
Figure 2: Plant yaw output in tracking mode under the
consecutive compensator work.
Figure 3: Plant yaw output in tracking mode under the PID
controller work.
Figure 4: Plant pitch output in tracking mode under the
consecutive compensator work.
Robust Output Control Algorithm for a Twin-Rotor Non-Linear MIMO System
425

Figure 5: Plant pitch output in tracking mode under the
PID controller work.
Figure 6: Plant yaw output in stabilization mode under the
consecutive compensator work.
Figure 7: Plant yaw output in stabilization mode under the
PID controller work.
Figure 8: Plant pitch output in stabilization mode under
the consecutive compensator work.
Figure 9: Plant pitch output in stabilization mode under
the PID controller work.
Experimental results analysis revealed that
robust output control was successfully applied to the
chosen plant and its quality exceeds the PID
controller.
6 CONCLUSIONS
In this paper we present control algorithm for non-
linear parameter uncertain MIMO systems operating
under unknown bounded disturbances. A key
assumption for application of the control law is that
mathematical model of the system can be
decomposed on linear and non-linear dynamics.
Relative degree of the linear part of plant is the only
required parameter for the proposed controller.
Introduced robust control algorithm is applied to
the laboratory platform named «Twin Rotor MIMO
System» and provides its exponential stability with
convergence to a bounded zero origin. Non-linear
part of the TRMS that contains cross-relations of the
plant is considered as unknown bounded
disturbance. Designed control system is tested
experimentally and compared with the standard PID
controller. Several scenarios of TMRS work are held
and experiments demonstrate that proposed control
algorithm provides higher performance and accuracy
of the laboratory bench. It should be noted that
presented control algorithm is robust with respect to
parametric disturbances that is supported by
experimental results.
ACKNOWLEDGEMENTS
This work was partially financially supported by
Government of Russian Federation, Grant 074-U01.
This work was supported by the Ministry of
Education and Science of Russian Federation
(Project 14.Z50.31.0031).
The work was supported by the Russian
Federation President Grant (No. MD-6325.2016.8).
This work was supported by the Russian
Federation President Grant №14.Y31.16.9281-НШ.
REFERENCES
Allouani, F., Boukhetala, D., Boudjema, F. 2012. Particle
swarm optimization based fuzzy sliding mode
controller for the twin rotor MIMO system. In
Electrotechnical Conference (MELECON), 2012 16th
IEEE Mediterranean (pp. 1063-1066). IEEE.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
426

Basri, M. A. M., Husain, A. R., Danapalasingam, K. A.,
2014. Intelligent adaptive backstepping control for
MIMO uncertain non-linear quadrotor helicopter
systems. In transactions of the Institute of
Measurement and Control.
Bobtsov, A. A. (2002). Robust output-control for a linear
system with uncertain coefficients. Automation and
Remote Control, 63(11), 1794-1802.
Cajo, R., Agila, W., 2015. Evaluation of Algorithms for
Linear and Nonlinear PID Control for Twin Rotor
MIMO System. In Computer Aided System
Engineering (APCASE), 2015 Asia-Pacific Conference
on (pp. 214-219).IEEE.
Feedback instruments Ltd., 1998. Twin Rotor MIMO
System experiment, East Sussex, U.K.
Juang, J. G., Liu, W. K., Lin, R. W., 2011. A hybrid
intelligent controller for a twin rotor MIMO system
and its hardware implementation. In ISA transactions,
50(4), 609-619.
Liu, Y., Söffker, D., 2014. Robust control approach for
input–output linearizable nonlinear systems using
highgain disturbance observer. In International
Journal of Robust and Nonlinear Control, 24(2), 326-
339.
Margun, A., Furtat, I., 2015. Robust control of linear
MIMO systems in conditions of parametric
uncertainties, external disturbances and signal
quantization. In Methods and Models in Automation
and Robotics (MMAR), 2015 20th International
Conference on (pp. 341-346). IEEE.
Margun, A., Furtat, I., 2015. Robust control of uncertain
linear systems in conditions of output quantization. In
IFAC-PapersOnLine, 48(11), 843-847.
Nejjari, F., Rotondo, D., Puig, V., Innocenti, M. 2012.
Quasi-LPV modelling and non-linear identification of
a twin rotor system. In Control & Automation (MED),
2012 20th Mediterranean Conference on (pp. 229-
234). IEEE.
Pandey, S. K., Laxmi, V., 2015. Optimal Control of Twin
Rotor MIMO System Using LQR Technique. In
Computational Intelligence in Data Mining-Volume 1
(pp. 11-21).
Rahideh, A., Shaheed, M. H., Huijberts, H. J. C., 2008.
Dynamic modelling of a TRMS using analytical and
empirical approaches. In Control Engineering
Practice, 16(3), 241-259.
Phillips, A. E., 2014. A Study of Advanced Modern
Control Techniques Applied to a Twin Rotor MIMO
System.
Pyrkin, A. A., Bobtsov, A. A., Kolyubin, S. A., Faronov,
M. V., Borisov, O. I., Gromov, V. S., ... Nikolaev, N.
A., 2015. Simple Robust and Adaptive Tracking
Control for Mobile Robots. In IFAC-PapersOnLine,
48(11), 143-149.
Radac, M. B., Precup, R. E., Petriu, E. M., Preitl, S. 2014.
Iterative data-driven tuning of controllers for nonlinear
systems with constraints. In Industrial Electronics,
IEEE Transactions on, 61(11), 6360-6368.
Shi, W., 2014. Adaptive fuzzy control for MIMO
nonlinear systems with nonsymmetric control gain
matrix and unknown control direction. In Fuzzy
Systems, IEEE Transactions on, 22(5), 1288-1300.
Tao, C. W., Taur, J. S., Chang, Y. H., Chang, C. W. 2010.
A novel fuzzy-sliding and fuzzy-integral-sliding
controller for the twin-rotor multi-input–multi-output
system. In Fuzzy Systems, IEEE transactions on,
18(5), 893-905. IEEE.
Vrazhevsky, S., Kremlev, A., 2015. Suboptimal control
algorithm for nonlinear MIMO System. In Ultra
Modern Telecommunications and Control Systems and
Workshops (ICUMT), 2015 7th International
Congress on (pp. 20-25). IEEE.
Robust Output Control Algorithm for a Twin-Rotor Non-Linear MIMO System
427
