A Robust Approach for Improving the Accuracy of IMU based Indoor

Mobile Robot Localization

Suriya D. Murthy, Srivenkata Krishnan S, Sundarrajan G,

Kiran Kassyap S, Ragul Bhagwanth and Vidhya Balasubramanian

Department of Computer Science and Engineering, Amrita School of Engineering,

Amrita Vishwa Vidyapeetham, Amrita University, Coimbatore, India

Keywords:

Robot Localization, Indoor Localization, Sensor Fusion, Inertial Sensors, Dead Reckoning.

Abstract:

Indoor localization is a vital part of autonomous robots. Obtaining accurate indoor localization is difﬁcult in

challenging indoor environments where external infrastructures are unreliable and maps keep changing. In

such cases the robot should be able to localize using their on board sensors. IMU sensors are most suitable

due to their cost effectiveness. We propose a novel approach that aims to improve the accuracy of IMU based

robotic localization by analyzing the performance of gyroscope and encoders under different scenarios, and

integrating them by exploiting their advantages. In addition the angle computed by robots to avoid obstacles

as they navigate, is used as an additional source of orientation estimate and appropriately integrated using a

complementary ﬁlter. Our experiments that evaluated the robot over different trajectories demonstrated that

our approach improves the accuracy of localization over applicable existing techniques.

1 INTRODUCTION

Robotic indoor localization is a method in which the

position and orientation of the mobile robot is deter-

mined with respect to the indoor environment and is

an important part of any autonomous mobile robot.

Autonomous robot systems are commonly being used

during disaster response, in industries, as assistive

robots etc. In order to support the effective func-

tioning of robots in such scenarios there is a need for

accurate and efﬁcient indoor localization, navigation

and mapping methods. One of the fundamental chal-

lenges in indoor environments is localization and this

supports the other two functionalities. In this paper

our primary goal is accurate self localization of mo-

bile robots in indoor environments.

Several approaches have been designed for mo-

bile robot localization, which include infrastructure

and non-infrastructure based methods. Infrastructure

based approaches use existing WiFi or RFID installa-

tions to help localize the robot (Choi et al., 2011; Li,

2012; Zhang et al., 2014). However, the accuracy of

these approaches are environment dependent, there-

fore we need solutions that do not rely on external

infrastructure. Approaches that do not rely on infras-

This work has been funded in part by DST(India) grant

DyNo. 100/IFD/2764/2012-2013

tructure use laser range ﬁnders, on board cameras and

inertial sensors for localization of the robot (DeSouza

and Kak, 2002; Guran et al., 2014; Surmann et al.,

2003). Laser range ﬁnders have high accuracy, but

are expensive. Camera based approaches are effec-

tive in many situations, but are computationally com-

plex and perform poorly in low light conditions and

in presence of occlusions.

Cost effectiveness, practicality, and ease of use

has popularized the use of inertial sensors and digi-

tal encoders for localization purposes (Guran et al.,

2014), and are widely employed by dead reckon-

ing based approaches. While accelerometers and en-

coders have been used for distance estimates, gyro-

scopes and magnetometer sensors have been used to

estimate orientation. However the accuracy of these

sensors are affected due to accumulation of noise and

drift errors from accelerometers and gyroscopes re-

spectively. Digital encoders are affected by slippage

and other errors. To overcome these errors, map

matching techniques and sensor fusion techniques

have been proposed (Elmenreich, 2002; Xiao et al.,

2014).

In map matching, accuracy is improved by con-

sidering salient features in the map and reposition-

ing the robot based on it. Techniques like those de-

scribed in (Xiao et al., 2014) use probabilistic ap-

436

Murthy, S., S, S., G, S., S, K., Bhagwanth, R. and Balasubramanian, V.

A Robust Approach for Improving the Accuracy of IMU based Indoor Mobile Robot Localization.

DOI: 10.5220/0005986804360445

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 436-445

ISBN: 978-989-758-198-4

proaches for map matching and thereby localization.

Sensor fusion techniques can be used to combine the

data from different sensors and improve their accu-

racy. Sensor fusion can be achieved by simple ag-

gregation based approaches or by applying ﬁlters like

Kalman, extended Kalman and Complementary ﬁl-

ters (Kam et al., 1997). The current state of art in

Kalman ﬁlter based approaches use two or more dif-

ferent position and orientation estimates. The inputs

for the Kalman ﬁlter are from sensors embedded in

the robot and external features (landmarks, corridors,

walls etc.) present in the indoor environment where

the robot navigates. However accurate both sensor fu-

sion based and map matching based techniques may

be, they are ineffective when maps are incomplete and

the environment consists of dynamic obstacles. Ad-

ditionally they are computationally expensive. There-

fore a cost effective approach that does not completely

rely on a map is essential.

In this paper we propose an approach that effec-

tively combines the advantages of the encoders and

gyroscopes to improve the accuracy of localization of

the robot. While existing techniques like gyrodome-

try (Ibrahim Zunaidi and Matsui, 2006) have been de-

veloped, which use Kalman Filters for sensor fusion,

their performance is affected when accelerometers are

ineffective (as in the case of wheeled robots). Our

approach exploits the curvature of the robot’s trajec-

tory to determine when the gyroscopes and encoders

are used. This helps limit the continuous use of the

gyroscope thereby reducing drift errors. In addition

we exploit the obstacle avoidance capabilities of au-

tonomous robots to provide another source of orienta-

tion estimate. This is combined with the gyroscope’s

orientation estimate using complementary ﬁlter to im-

prove the localization accuracy.

The rest of the paper is organized as follows: Sec-

tion 2 outlines the state of art in robotic localization in

detail and positions our work with respect to it. Next

we discuss how the individual sensors are used for

distance and orientation estimate in Section 3 and ex-

plain our proposed approach in Section 4. Finally we

evaluate our approach for different scenarios (Section

5) and conclude in Section 6.

2 RELATED WORK

Many localization techniques have been developed

and implemented in robots over a period of time.

Common indoor localization methods for robots rely

on external infrastructures and sensors which are part

of the robot. Localization techniques that use RF

technologies such as RFID, WiFi and bluetooth (Choi

et al., 2011; Li, 2012; Zhang et al., 2014) rely on ad-

ditional external infrastructure such as RF antennas

and ultrasonic transceivers placed in the environment.

On the other hand, techniques that use cameras, laser

range ﬁnders or inertial sensors(DeSouza and Kak,

2002; Guran et al., 2014; Surmann et al., 2003) do

not rely on external infrastructure.

In the infrastructure based approaches, RF based

localization is one of the most prevalent techniques

and is easy to implement. In RF based methods,

the robot requires external infrastructure like anten-

nas/reference tags placed in the environment for com-

munication with the receiver carried by the robot.

RF based localization techniques can either use ﬁn-

gerprinting or non-ﬁngerprinting approaches. The

non-ﬁnger printing approaches include trilateration

method and angulation techniques(AOA) (Liu et al.,

2007). The trilateration method estimates the posi-

tion of the target with respect to the reference points

using the Received Signal Strength Indication (RSSI)

values (Easton and Cameron, 2006; Granados-Cruz

et al., 2014). This method fails to locate mobile node

in multipath dense environment. The WiFi ﬁnger-

printing technique compares the RSSI observations

made by the mobile node with a trained database

to determine the location of the moving object (Li,

2012). Deterministic approaches such as k-Nearest

Neighbors(k-NN) (Kelley, 2015), decision tree meth-

ods (Erinc, 2013) and probabilistic methods that in-

clude Bayesian, Hidden Markov Model (HMM) have

been used in ﬁngerprinting approach. In RFID based

localization, a large number of RFID tags placed in

the environment act as reference points. Hence, when

a new RFID tag enters the space, the signal strength

is compared with the reference points’ signal strength

and location of the robot is determined (Choi et al.,

2011; Zhang et al., 2014). In both RFID and WiFi ﬁn-

ger printing approaches, the collection of data set (of-

ﬂine phase) is tedious and time consuming. It also re-

quires frequent updation of ﬁngerprint maps and spe-

cial approaches are needed to reduce the cost of up-

dation (Krishnan et al., 2014).

The techniques that do not rely on infrastructure

involve the use of LIDAR (Light Detection and Rang-

ing), cameras and inertial sensors. Camera based ap-

proaches use the entire visual information or interest

points or combination of all these as input in deter-

mining the location of the robot(DeSouza and Kak,

2002). These methods are usually prone to errors due

to occlusions, changes in scale, rotation and illumina-

tion. In LIDAR based approaches, lasers have been

used to emit pulses that are reﬂected off a rotating

mirror from which time of ﬂight is determined and

used to calculate distances(Surmann et al., 2003). The

A Robust Approach for Improving the Accuracy of IMU based Indoor Mobile Robot Localization

437

main drawback here is that the laser range ﬁnders are

expensive.

Inexpensive sensors such as accelerometers, gy-

roscopes and encoders are increasingly being used

in localization. These IMU sensors are commonly

used in dead reckoning, where new state estimates are

calculated with the help of prior states(Ahn and Yu,

2007). Accelerometers and encoders have been used

to ﬁnd the distance while gyroscope and magnetome-

ter sensors have been used to determine the orienta-

tion (Guran et al., 2014). These methods do not give

accurate results because accelerometer suffers from

noise error, gyroscope suffers from static drift and

magnetometers are error-prone in places where mag-

netic interferences are high, especially in indoor en-

vironments. The encoders suffers from either system-

atic(unequal wheel dimensions and kinematic imper-

fections) or non-systematic errors(wheel slippage and

irregularities of the ﬂoor) and can be removed to a cer-

tain extent using the UMBmark test(Borenstein and

Feng, 1994). To overcome the inefﬁciencies of these

sensors we need to effectively combine the data from

multiple sensors. Sensor fusion based approaches

have been proposed to achieve this. The sensor fu-

sion in this context is the translation of different sen-

sory inputs into reliable estimates(Elmenreich, 2002).

Filters like Kalman and complementary ﬁlters have

been widely used for sensor fusion thereby improv-

ing the accuracy to some extent (Kam et al., 1997).

Map matching based techniques have also been ap-

plied (Xiao et al., 2014) that improve the accuracy of

localization accuracy using probabilistic approaches.

As mentioned in previous section, the above methods

fail when the map is not reliable and environment is

dynamic.

Therefore we need a better method that is able to

effectively localize the robot with minimum overhead

and no external infrastructure. In addition it must be

able to exploit the advantage of different sensors to

improve accuracy and without relying on maps. In

this paper we aim to achieve this using a novel deci-

sion based approach that uses the scenarios where dif-

ferent sensors work accurately. The next sections will

describe our approach for improving the localization

accuracy of indoor robots using inertial measurement

units.

3 SYSTEM OVERVIEW

Before we describe our approach we ﬁrst introduce

our robot, its system and its sensors. An image of our

robot is shown in Fig 1. Our robot is a four wheeled

autonomous light weight vehicle and has a dimension

Figure 1: Our 4-wheeled mobile robot.

of 105mm*55mm*57mm. Each of the 4 wheels has

a diameter of 110mm. The robot is equipped with

bStem (bst, 2015) single chip computer, an Arduino

micro controller, sensors and motor drivers. The en-

vironment in which the robot navigates is a partially

known environment, in which walls and corridors are

known but any furniture or moving obstacles are un-

known.

The robot is deﬁned by its pose p which is given

at time t as,

p = [x

,θ

]

where x

represents the position estimate and θ

represents the orientation estimate.

To measure the distance travelled by the robot,

two quadrature encoders associated with the stepper

motors are added to the rear wheels of the robot. It

must be noted that this is a rear wheel driven differen-

tial driven robot and speed is controlled to avoid slips

and keep the kinematic center at the middle of the rear

wheels. These encoders output the left and right ticks

(l, r), using which the distance (dist) travelled by the

robot is calculated as dist = (l + r)/2. Since we do

not use accelerometers, this is the only source of dis-

tance estimate.

The encoders also provide us with an estimate of

the robot’s orientation θ

. The tri-axial gyroscope

present in bStem provides the angular rates with re-

spect to each axis. Using the z-axis angular rate we

calculate the orientation angle θ

. Two ultrasonic and

two infrared sensors are embedded on either sides in-

front of the robot. Both the sensors return the dis-

tance between the obstacle and robot. This data serves

to provide us with an additional orientation estimate.

We use the encoders to determine the distance esti-

mate and a combination of gyroscope, encoders and

obstacle avoidance sensors for orientation estimate to

effectively determine pose. The mathematical deter-

mination of position and orientation estimate from en-

coders, gyroscope and obstacle avoidance sensors are

explained below.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

438

3.1 Position and Orientation Estimation

using Encoders

The encoders provide ticks l and r from the left and

right motors respectively. The width of the robot is

deﬁned as W . Using these, the position and orienta-

tion is calculated by applying geometric techniques

(Jensfelt, 2001). In this technique the pose is esti-

mated for the following two cases:

• Robot is taking turns.

• Robot is moving straight.

Case 1: Determination of Pose When the Robot is

Taking Turns

When the robot is taking turns, there is a difference

in the ticks between the right and left encoders. This

information is used to estimate the curvature of the

robots path (based on the previous position p

) and

hence determine the pose p. The heading direction

changes when the robot turns. The current orientation

is the heading angle which is based on the previous

orientation, and α. The new orientation estimate θ

(t)

is calculated as follows,

(t) = θ

(t −1) + α (1)

Here the angle α represents the change in heading an-

gle of the robot during traversal from previous posi-

tion to the current position. The new position estimate

(x(t), y(t)) is determined as follows:

x(t) = C

+ (R + (W /2))sin(θ

(t)) (2)

y(t) = C

+ (R + (W /2))(− cos(θ

(t))) (3)

where C(C

) is the center of the extended circle

where the arc traversed by the robot from previous

position to current position lies. Similarly, this can be

extended for the calculation of new pose when robot

turns right.

Case 2: Determination of Pose When the Bot is

Moving Straight

When the robot is moving straight, there is no change

in its orientation, and the left ticks are equal to the

value of right ticks. So, the new orientation estimate

is same as the orientation at time t − 1,

(t) = θ

(t −1) (4)

Now, the corresponding pose x(t),y(t) is calculated as

given below,

x(t) = x(t − 1) + l(cos(θ

(t))) (5)

y(t) = y(t − 1) + l(sin(θ

(t))) (6)

3.2 Orientation Estimate using

Gyroscope

Gyroscope is a sensor used to measure angular veloc-

ity. In our robot, the L3GD20 MEMS motion sensor

3-axis digital gyroscope, which is part of the bStem

provides angular velocities along three axes x,y,z re-

spectively. The sensitivity of the gyroscope is set

at 250dps, ideal for a robotic system that undergoes

heavy vibrations due to motor and chassis movement.

The goal is to calculate the orientation angle of the

robot over a period of time, which is done by integrat-

ing the angular velocity about the z-axis over a certain

time interval. In order to get reliable angle estimates

we ﬁrst calculate and eliminate the offset and noise of

our gyroscope and they are calculated as follows:

offset =

∑

i=0

ω (7)

where ω is the angular velocity at that instant of time

and N represents the number of angular velocity val-

ues taken.

noise = max(|ω

− offset|) 0 ≤ i ≤ N (8)

where ω

is the angular velocity at that instant. Noise

is calculated for all three axes. The angular velocities

which fall in the range of [−noise,noise] are ignored

and the remaining values are taken for the calculation

of orientation. The orientation angle θ

(t) at time t is

given by,

(t) = θ

(t −1) + ω

dt (9)

where dt represents the time period over which ω

can

be periodically integrated to determine the angle, in

our case this value is equal to 20ms. Using the above

(t) value we estimate the orientation and position.

The position estimate is calculated using previous po-

sition values, the newly calculated orientation value

and the distance estimate from encoders (dist) and is

determined as follows.

x(t) = x(t − 1) + dist ∗ cos(θ

(t)) (10)

y(t) = y(t − 1) + dist ∗ sin(θ

(t)) (11)

3.3 Orientation Estimate using Obstacle

Avoidance Sensors

In general orientation estimates come from the en-

coders, gyroscopes or magnetometers. Here we are

also using orientation estimates based on information

from obstacle avoidance sensors. Robots use obsta-

cle avoidance systems to avoid obstacles, and plan

their trajectory based on the distance between them

and the obstacle. At each point, while the obstacle is

A Robust Approach for Improving the Accuracy of IMU based Indoor Mobile Robot Localization

439

still in range, the autonomous robot calculate the cur-

vature angle required to safely maneuver itself. This

angle is only known when the obstacle is detected,

and it can be reasonably assumed that the robot’s ac-

tual trajectory during navigation is close to the esti-

mated trajectory determined for obstacle avoidance.

This estimated angle therefore is used by our algo-

rithm as an additional source of orientation estimate.

We explain the orientation estimation using the obsta-

cle avoidance system below.

In this paper we consider the ultrasonic and in-

frared sensors for obstacle avoidance. The sensor

speciﬁcations are given below,

1. Ultrasonic Range Finder XL-EZ3 (MB1230)

which has a range of 20cm to 760cm and a res-

olution of 1cm is used to detect obstacles present

in long range.

2. Sharp GP2Y0A41SK0F IR Distance Sensor

which has a range of 4cm to 30cm is used to de-

termine obstacles in close range.

A robot that is moving autonomously takes nav-

igational decisions based on the output from the

above sensors. An obstacle avoidance method

(Widodo Budiharto and Jazidie, 2011), is adapted to

calculate the orientation of the robot as explained be-

low. When an obstacle is detected, the two ultrasonic

sensors return the distances (d

) between the ob-

stacle and corresponding left and right sensors on the

robot. d

sa f e

, the ﬂank safety distance, is the mini-

mum distance at which robot can start to maneuver to

avoid obstacle. This value is calculated experimen-

tally based on the range of the ultrasonic sensors and

width of the robot. To determine the angle from the

distances given by ultrasonic and infrared sensors, the

following cases must be considered.

case 1: d

> d

sa f e

and d

> d

sa f e

When there

is no obstacle in front of the robot, it can continue

to move in the same direction. Hence the orientation

angle θ

(t) at time t is same as the previous angle

(t −1).

case 2: d

< d

sa f e

and d

> d

sa f e

In this case the

robot has to take a right turn in order to avoid the ob-

stacle. The closer the robot is to the obstacle the wider

it has to turn and vice versa. The ideal angle, θ

(t)

for the robot to avoid the obstacle is calculated using

the distance from left ultrasonic sensor as follows:

(t) = θ

(t −1) −

(

θu

) (12)

where k

θu

represents the collision angle constant for

the ultrasonic sensor, which is calculated based on

sa f e

and d

case 3: d

> d

sa f e

and d

< d

sa f e

When the bot

has to turn left in order to avoid obstacle, the ideal

angle is calculated using the distance from the right

ultrasonic sensor and the angle is calculated similarly,

(t) = θ

(t −1) +

(

θu

) (13)

case 4: d

< d

sa f e

and d

< d

sa f e

When the robot

is too close to the obstacle, this case comes into pic-

ture. Here, we use the distances d

, and d

returned

by the infrared sensors. The orientation is estimated

similarly. The angle calculation for right turn is given

by,

(t) = θ

(t −1) − n ∗ (

)(

θi

) (14)

Similarly, the angle calculation for left turn is given

by,

(t) = θ

(t −1) + n ∗ (

)(

θi

) (15)

where n is experimentally calculated to increase or de-

crease the rotation appropriately to avoid close obsta-

cles. k

θi

is the collision angle constant for infrared

sensors.

Finally, if the robot is too close to the obstacle and

is impossible for it to maneuver an obstacle smoothly,

i.e. if d

< d

, then the robot moves backwards by

a certain distance and checks for all the above pos-

sibilities and estimates the orientation angle. d

the maximum distance before which the robot should

start maneuvering to avoid the obstacle. This value

is calculated experimentally based on the range of the

infrared sensors and width of the robot. The region

sa f e

- d

}, is the buffer region for smooth maneu-

vering. Using the above equations, we estimate the

orientation angle based on the data from the obstacle

avoidance sensors.

Now that we have estimated the pose using the

individual sensors, the goal of our system is to im-

prove the accuracy by appropriately combining the

data from all of them.

4 CURVATURE BASED DECISION

SYSTEM

This section describes our novel approach to improv-

ing the location accuracy by fusing information from

the different sensors appropriately. In robotic local-

ization inaccuracies in orientation measure affects the

position more when compared to inaccuracies in dis-

tance measure(Borenstein and Feng, 1994). For ex-

ample, a robot with 8 inch wheel base and slip of 1/2

inch in one of the wheels results in an error of approx-

imately 3.5 degrees in orientation. So it is important

to have a highly accurate value of the orientation mea-

sure when compared to that of a distance measure.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

440

Our method assumes that the distance(l,r) measured

using the encoders is reliable, since the systematic er-

rors can be easily removed using UMBenchmark and

non-systematic errors do not affect the distance esti-

mate much, as explained in the above example. The

orientation estimate from encoders however are not

reliable since they undergo huge non-systematic er-

rors due to sudden turns and heavy slippage. Slight

deviations in distance due to non-systematic errors

results in huge deviations in orientations. The gyro-

scopes are generally accurate in estimating orienta-

tion, and is preferred over encoders. However, over

longer durations the performance degrades due to the

accumulation of drift errors. Our approach enhances

the accuracy of orientation estimation by a) reducing

the period over which the gyroscope value accumu-

lates, so that drift errors are minimized and b) fus-

ing the orientation estimates from gyroscope with ori-

entation estimates obtained to avoid obstacles as dis-

cussed in Section 3.3.

Inorder to actualize the above, the trajectory in

which the robot travels is analyzed. We identify the

part of the trajectory that is almost linear, so that ori-

entation measure from encoders can be used reliably.

In the other parts of the trajectory the gyroscope is

employed. To improve the accuracy further, the gy-

roscope data is fused with the angle estimated at the

current position by the robot to avoid obstacles. The

main steps in our approach are as follows

1. Estimation of curvature of the robot’s trajectory

2. Using the trajectory to determine the appropriate

sensor to use

3. Enhance orientation estimation accuracy using

a complementary ﬁlter to fuse orientation from

above step and obstacle avoidance system

A decision based approach is preferred to a fusion

based approach for determining the sensor to use

based on the curvature of the trajectory. Since it is

clear which sensors used perform better in different

scenarios we employ this approach.

4.1 Curvature Estimation

The robot’s trajectory is a 2D smooth plane curve.

The curvature of the past trajectory of the robot deter-

mines the sensor(s) to be used for the orientation esti-

mation at the current point. In order to ﬁnd the curva-

ture, we ﬁnd the angle between the slopes of tangents

drawn to the previous points P1(x,y) and P2(x,y) on

the trajectory. To draw the tangents we ﬁnd the center

of curvature C(C

) of the curve. We then calculate

the angle between the slopes of the tangents, which

Figure 2: Determination of slope.

gives the curvature at the point. This method is efﬁ-

cient in curvature estimation since we only store the

previous two points of the trajectory and not the com-

plete trajectory to decide on the appropriate sensors.

To ﬁnd the slope m1 of the tangent vector T at

point P1, we ﬁrst ﬁnd the slope n1 of the normal vec-

tor N at P1 passing through center of curvature C. The

slope of n1 is calculated using

n1 = (C

− P2(y))/(C

− P1(x)) (16)

The slopes m1 of the tangent vector T , which is

perpendicular to N is then calculated as the negative

of the inverse of n1; m1 = −1/n1. Similarly we cal-

culate m2, which is the slope of the tangent vector at

point P2.

Once these two slopes are calculated the degree of

curvature D

can be determined as follows

= tan

−1

((m1 − m2)/(1 + m1 ∗ m2)) (17)

This D

value helps us determine if the robot is trav-

elling in a near linear trajectory or on a curved path.

Using this we determine when to start aggregating the

gyroscope values and when to only rely on encoders.

A gyroscope controller is implemented to appropri-

ately switch between the encoders and gyroscope.

4.2 Gyroscope Controller

The gyroscope controller starts accumulating the gy-

roscope readings, and switches completely to the en-

coder based on start and stop threshold values. The

start threshold value µ1 is calculated by computing

the average of the degrees of curvature when the robot

begins to make a turn. When the robot completes a

maneuver by avoiding an obstacle and starts to follow

a linear trajectory, the average of degree of curvatures

of multiple linear paths is computed and used as the

stop threshold value µ2.

When the D

keeps increasing and goes over start

threshold value µ1, we initiate the gyroscope and use

it for orientation measure and allow it to summate as

the robot traverses the curved path. The accumulation

A Robust Approach for Improving the Accuracy of IMU based Indoor Mobile Robot Localization

441

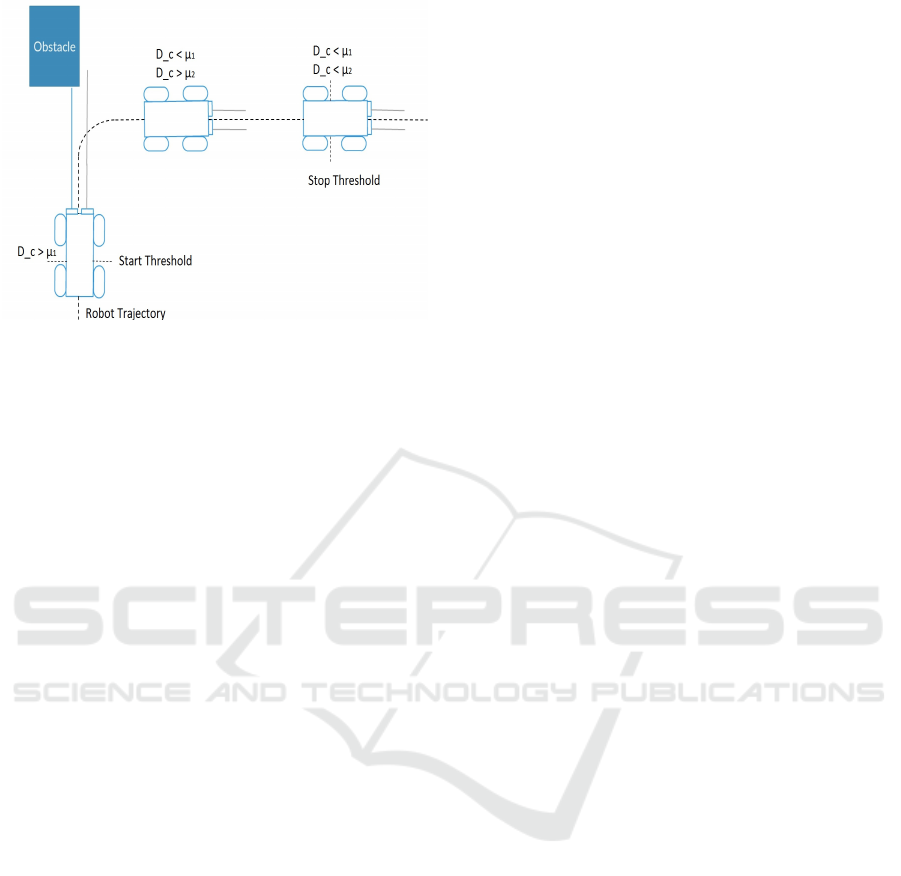
Figure 3: Determination of start and stop threshold.

of gyroscope values is stopped when the degree of

curvature becomes closer to the stop threshold value

µ2. Figure 3 shows this scenario. By doing this we

ensure that the gyroscope is not made to accumulate

continuously for a long time, thereby ensuring that

the drift errors from the gyroscopes are not a major

source of localization errors. When D

keeps decreas-

ing and becomes equal to or less than µ2, the encoders

are used for orientation estimation of the robot. Us-

ing the encoders when the D

is less than or equal to

the µ2, reduces the effect of the non systematic errors

resulting in an accurate position calculation. In order

to achieve the above the following conditions have to

be met,

1. µ2<<µ1, ensuring the left and right ticks are

equal in straight paths.

2. µ1 is given higher precedence than µ2, ensuring

gyroscope is started as soon as the robot begins to

make a turn.

In order to further increase the orientation estimate

obtained from gyroscope, it is fused with the an-

gle obtained from the obstacle avoidance sensors ex-

plained below.

4.3 Gyro-obstacle Fusion

To improve the accuracy of orientation estimates dur-

ing turns, the gyroscope values are fused with the

ideal angle estimated to avoid obstacles as explained

in Section 3.3. As discussed earlier it is our hypoth-

esis that robots tend to closely follow the trajectory

estimated to avoid obstacles. However the actual an-

gle taken by the robot to avoid the obstacle is not

controllable and hence is only known by the gyro-

scope. Therefore this estimated angle is fused with

the gyroscope angle to potentially enhance the accu-

racy. We use a complementary ﬁlter for this fusion

process since it is very easy and light to implement

making it perfect for embedded systems application

as in our case. The complementary ﬁlter is given by

the equation,

θ = αθ

+ (1 − α)θ

(18)

where θ

is the angle obtained from gyroscope, θ

angle obtained from obstacle avoidance sensors and α

is the factor which is determined experimentally.

Therefore, we get a good orientation estimate

from encoders, gyroscope and obstacle avoidance

system. This orientation is then combined with the

distance measure(l,r) from encoders to get the pose

estimate. On fusing the data by considering the ad-

vantages of individual sensors, the position is ob-

tained.

5 EXPERIMENTAL RESULTS

The previous sections discussed our approach for im-

proving the accuracy of localization by combining

data from different sensors used in our robot. In this

section we analyze the performance of this approach.

First we discuss the arena and experimental setup fol-

lowed by the metrics used for analyzing our algo-

rithm. We also discuss the methodology for obtaining

the ground truth.

The experiments are carried out in an arena of

dimensions 1710 ∗ 480cm

using a four wheeled au-

tonomous robot as shown in Figure 1. The arena is

then transformed into a grid of squares, each of area

900cm

. Obstacles are placed in different parts of the

arena. Different trajectories are considered for evalu-

ating our algorithm. In order to generate the ground

truth the grid is used to identify the points the robot

passed through. These points are plotted on a raster

map. The following algorithms are evaluated (it must

be noted that in all the techniques encoders provide

the distance estimate, and these techniques are used

for angle estimation)

1. Encoder based approach

2. Gyroscope based approach

3. Curvature based Decision Approach without in-

tegrating obstacle avoidance information (CDA-

nO)

4. Curvature based Decision Approach that uses all

three sensors (CDA-O)

To evaluate the performance of these approaches in

comparison to the ground truth we use the metrics as

discussed next.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

442

5.1 Metrics of Evaluation

The most important indicator in evaluating the per-

formance of a localization algorithm is accuracy. Ac-

curacy refers to how close the estimated trajectory as

obtained from the localization method is to the ground

truth. In order to determine the closeness, mean and

standard deviation of the Euclidean distance between

the ground truth and estimated point is calculated.

The mean Euclidean distance is the sum of Euclidean

distance at each corresponding point divided by the

total number of such corresponding points.

µ =

∑

i=0

(

((x

− x

est

)

+ (y

− y

est

)

))

(19)

) refers to the ground truth and (x

est

) is

the estimated position from the localization method

used. While the mean provides the error estimates, the

standard deviation gives an idea of how consistently

the algorithm performs.

5.2 Performance Analysis

We evaluate the above mentioned approaches over the

arena speciﬁed. The evaluation is done by making the

robot navigate along different trajectories in the arena.

We have considered three trajectories and their corre-

sponding ground truth is plotted and used for compar-

ison. Table 1 shows the mean and standard deviation

of the euclidean distance error in the corresponding

trajectories and methods used for comparison respec-

tively.

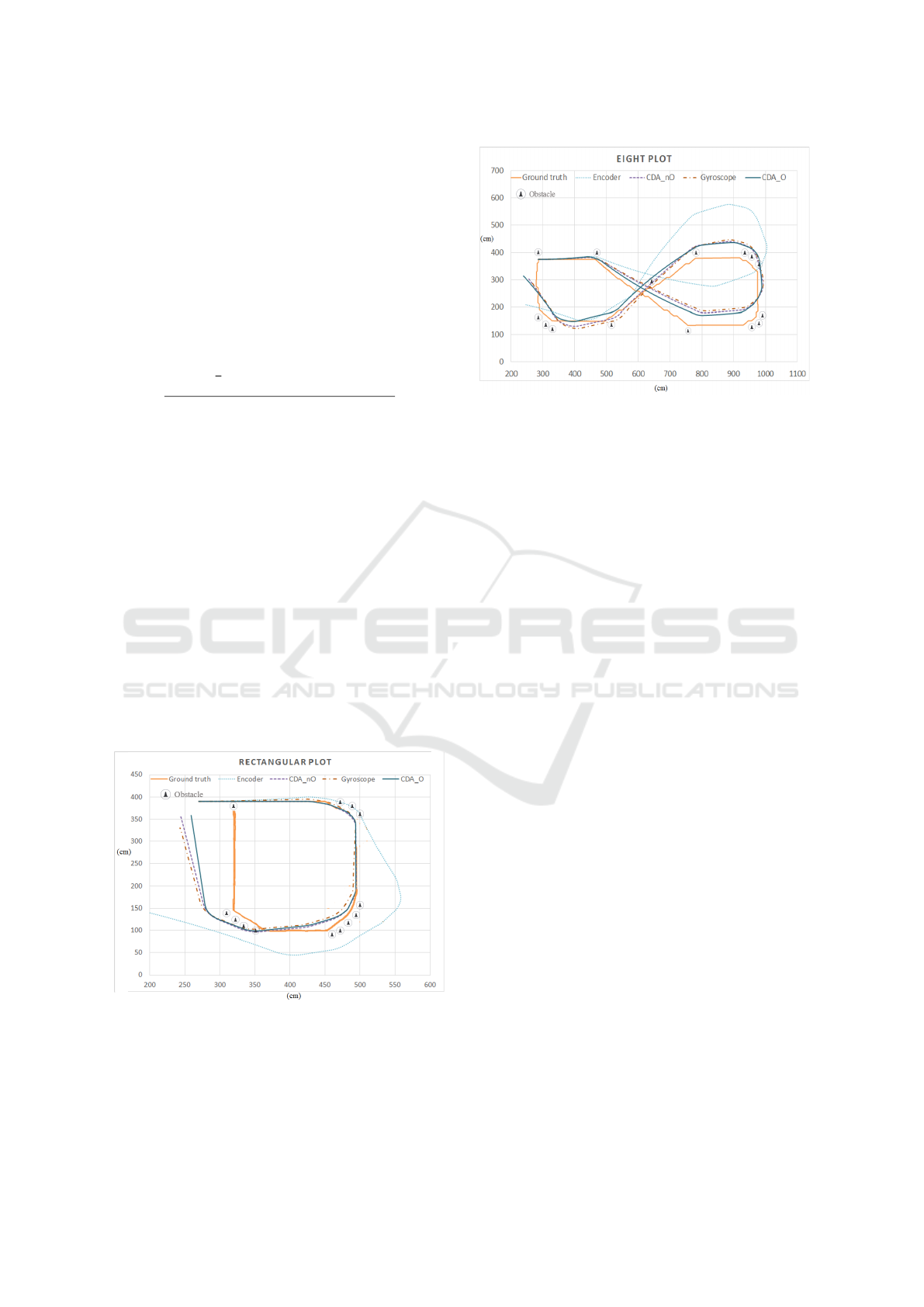
Figure 4: Performance for a Rectangular Trajectory.

5.2.1 Case 1: Rectangular Trajectory

The ﬁrst case is when the robot traversed along the pe-

riphery of the arena resulting in a rectangular trajec-

Figure 5: Performance for an Eight Shaped Trajectory.

tory. Figure 4 shows the plot of the estimated trajec-

tories for different techniques along with the ground

truth trajectory. From the ﬁgure and the table we can

see that the average error of encoder based localiza-

tion is comparatively high. This is because, in the tra-

jectory, the robot has taken sharp turns, which leads

to slips and it affects the performance of the encoder

based method. The performance of gyroscope based

localization is better than encoder because its orienta-

tion estimates are more accurate during turns, and that

dictates the accuracy of the trajectory. The curvature

based approach improves the accuracy of the localiza-

tion over the gyroscope on average. However using

the orientation estimates from the obstacle avoidance

system further improves the accuracy. This supports

our hypothesis that the robot traverses nearly close

to the estimated trajectory needed to avoid obstacles.

Additionally since the gyroscope is the only measure

of the actual angle taken by the robot in this scenario,

fusing with the estimated angles helps the estimated

trajectory come closer to the ground truth. This leads

us to the conclusion that orientation estimates during

obstacle avoidance has high accuracies and can be re-

liably used.

5.2.2 Case 2: Eight Shaped Trajectory

Figure 5 shows the output of the different localization

methods when the robot is allowed to navigate in an

eight shaped trajectory. Here we can notice that since

there are not many sharp turns, the encoder perfor-

mance improves. Here too our curvature based ap-

proaches (both with and without input from obstacle

avoidance sensors) perform the best. While the gy-

roscope plays a major role in the improvement of ac-

curacy, the nature of the trajectory limits the curva-

ture based decision approach. However we can see

that employing the input from obstacle avoidance im-

A Robust Approach for Improving the Accuracy of IMU based Indoor Mobile Robot Localization

443

Table 1: Performance analysis of different techniques for different trajectories.

Methods

implemented

Trajectory 1(Rectangular) Trajectory 2(Eight) Trajectory 3 (Random Path)

Avg Error

(cm)

Std Dev

(cm)

Avg Error

(cm)

Std Dev

(cm)

Avg Error

(cm)

Std Dev

(cm)

Encoders 121.96 79.64 89.27 51.74 333.65 191.74

Gyroscope 40.50 22.49 44.22 26.86 75.33 44.26

CDA-nO 28.64 15.96 39.50 24.91 65.38 38.96

CDA-O 20.25 12.59 34.68 24.66 20.49 12.67

Figure 6: Random plot.

proves the accuracy to a certain extent.

5.2.3 Case 3: Random Trajectory

To obtain a better idea of how well our approach for

localization works, we allowed the robot to take a

random path ﬁlled with obstacles, and this path was

much longer than the previous ones. When the path

is longer, the drift errors in the gyroscope play a role.

Figure 6 shows the plots of the estimated trajectories

for this path. We can see that here that our curva-

ture based approach that utilizes the obstacle avoid-

ance system performs exceedingly well in compari-

son to all other strategies. This is because the path

has lot of obstacles and that is well exploited here.

The gyroscope performs poorest here, since it is more

prone to drift errors here. Therefore using the curva-

ture based approach helps reduce the drift error, and

improve accuracy to a small extent. While the ’o f f set

and ’noise’ is calibrated at the beginning, we propose

to update it at regular intervals, specially when the

robot is moving straight. Overall we can see that our

approach performs consistently well in all scenarios

and gives an accuracy of around 20 to 30 cm. We

also observe that considering the curvature and fus-

ing the estimate of the orientation from the obstacle

avoidance systems with gyroscopes signiﬁcantly im-

proves accuracy. The trajectories generated by our ap-

proach are very close to the trajectory both in terms

of distance and the overall pattern, as can be seen in

the plots. The standard deviation values, specially for

the rectangular and random plots show that our ap-

proach not only provides good accuracies, but does

it consistently along the path. Additionally the over-

head of this approach is low and hence is easily im-

plementable in any autonomous robot.

6 CONCLUSIONS AND FUTURE

RESEARCH

In this paper we have described out approach for im-

proving the localization accuracy of indoor mobile

robots, which use inertial sensors for localization.

The curvature of the robot’s trajectory is analyzed to

determine when the gyroscope and encoder data are

to be used. In addition to improve the accuracy, ori-

entation estimates from obstacle avoidance systems

are fused with the gyroscope’s orientation estimates.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

444

Our experiments have shown that by using only gy-

roscopes as and when needed, and employing the ad-

ditional data from obstacle avoidance sensors, the lo-

cation accuracy is improved signiﬁcantly. It is seen

that since environments usually have obstacles, and

robots have to navigate around them, using that as

a parameter is an effective approach for localization.

Our approach provides good accuracies at a low over-

head. However when the turns are very sharp, and

acute, our approach suffers. While our approach ac-

counts for gyroscope drift errors, more work needs to

be done to reduce it further for longer distances.

REFERENCES

(2015). bstem developer kit & integrated robotics platform:

www.braincorporation.com.

Ahn, H.-S. and Yu, W. (2007). Indoor mobile robot and

pedestrian localization techniques. In Control, Au-

tomation and Systems, 2007. ICCAS’07. International

Conference on, pages 2350–2354. IEEE.

Borenstein, J. and Feng, L. (1994). Umbmark: a method for

measuring, comparing, and correcting dead-reckoning

errors in mobile robots.

Choi, B.-S., Lee, J.-W., Lee, J.-J., and Park, K.-T. (2011). A

hierarchical algorithm for indoor mobile robot local-

ization using rﬁd sensor fusion. Industrial Electronics,

IEEE Transactions on, 58(6):2226–2235.

DeSouza, G. N. and Kak, A. C. (2002). Vision for mobile

robot navigation: A survey. Pattern Analysis and Ma-

chine Intelligence, IEEE Transactions on, 24(2):237–

267.

Easton, A. and Cameron, S. (2006). A gaussian error model

for triangulation-based pose estimation using noisy

landmarks. In Robotics, Automation and Mechatron-

ics, 2006 IEEE Conference on, pages 1–6. IEEE.

Elmenreich, W. (2002). Sensor fusion in time-triggered sys-

tems.

Erinc, G. (2013). Appearance-based navigation, localiza-

tion, mapping, and map merging for heterogeneous

teams of robots.

Granados-Cruz, M., Pomarico-Franquiz, J., Shmaliy, Y. S.,

and Morales-Mendoza, L. J. (2014). Triangulation-

based indoor robot localization using extended

ﬁr/kalman ﬁltering. In Electrical Engineering, Com-

puting Science and Automatic Control (CCE), 2014

11th International Conference on, pages 1–5. IEEE.

Guran, M., Fico, T., Chovancova, A., Duchon, F., Hubinsky,

P., and Dubravsky, J. (2014). Localization of irobot

create using inertial measuring unit. In Robotics in

Alpe-Adria-Danube Region (RAAD), 2014 23rd Inter-

national Conference on, pages 1–7. IEEE.

Ibrahim Zunaidi, Norihiko Kato, Y. N. and Matsui, H.

(2006). Positioning system for 4wheel mobile robot:

Encoder, gyro and accelerometer data fusion with er-

ror model method. In CMU Journal, volume 5.

Jensfelt, P. (2001). Approaches to mobile robot localization

in indoor environments. PhD thesis, RoyalInstitute of

Technology, Stockholm, Sweden.

Kam, M., Zhu, X., and Kalata, P. (1997). Sensor fusion

for mobile robot navigation. Proceedings of the IEEE,

85(1):108–119.

Kelley, K. J. (2015). Wi-ﬁ location determination for se-

mantic locations. The Hilltop Review, 7(1):9.

Krishnan, P., Krishnakumar, S., Seshadri, R., and Bala-

subramanian, V. (2014). A robust environment adap-

tive ﬁngerprint based indoor localization system. In

In Proceedings of the 13th International Conference

on Ad Hoc Networks and Wireless (ADHOC-NOW-

2014), volume 8487, pages 360–373.

Li, J. (2012). Characterization of wlan location ﬁngerprint-

ing systems. Master’s thesis, School of Informatics,

University of Edinburgh.

Liu, H., Darabi, H., Banerjee, P., and Liu, J. (2007). Sur-

vey of wireless indoor positioning techniques and

systems. Systems, Man, and Cybernetics, Part C:

Applications and Reviews, IEEE Transactions on,

37(6):1067–1080.

Surmann, H., N

uchter, A., and Hertzberg, J. (2003). An au-

tonomous mobile robot with a 3d laser range ﬁnder for

3d exploration and digitalization of indoor environ-

ments. Robotics and Autonomous Systems, 45(3):181–

198.

Widodo Budiharto, D. P. and Jazidie, A. (2011). A robust

obstacle avoidance for service robot using bayesian

approach. International Journal of Advanced Robotic

Systems, 8:52–60.

Xiao, Z., Wen, H., Markham, A., and Trigoni, N. (2014).

Lightweight map matching for indoor localisation us-

ing conditional random ﬁelds. In Information Pro-

cessing in Sensor Networks, IPSN-14 Proceedings of

the 13th International Symposium on, pages 131–142.

Zhang, H., Chen, J. C., and Zhang, K. (2014). Rﬁd-based

localization system for mobile robot with markov

chain monte carlo. In American Society for Engineer-

ing Education (ASEE Zone 1), 2014 Zone 1 Confer-

ence of the, pages 1–6. IEEE.

A Robust Approach for Improving the Accuracy of IMU based Indoor Mobile Robot Localization

445