
Practical Application of Order-preserving Encryption in
Wide Column Stores
Tim Waage, Daniel Homann and Lena Wiese
Institute of Computer Science, Georg-August-University, Goldschmidtstraße 7, G
¨
ottingen, Germany
Keywords:
Order-preserving Encryption, NoSQL, Wide Column Stores, Apache Cassandra, Apache HBase.
Abstract:
Order-preserving encryption (OPE) produces ciphertexts that preserve the relative order of the underlying
plaintexts. Thus, it is very suitable for range queries over encrypted outsourced data, as it is a popular case
in cloud database scenarios. Unfortunately, most schemes suffer from infeasibility in practice due to require-
ments like hardly maintainable data structures or additional architectural components. While OPE is a widely
discussed topic in theory, to our knowledge only one OPE scheme received noticeable practical attention
((Boldyreva et al., 2009) for SQL-based systems in (Popa et al., 2011; Tu et al., 2013)). Therefore, our work
identifies the practical requirements for utilizing OPE in real world usage with focus on existing NoSQL cloud
database technologies. We evaluate a variety of popular schemes and propose improvements for two of them
in order to further improve their practicability. Then we assess the performance of our modifications in com-
parison to the approach of (Boldyreva et al., 2011) (which can be considered the successor of (Boldyreva et al.,
2009) by a runtime analysis in combination with two popular NoSQL wide column store databases.
1 INTRODUCTION
In Big Data applications large amounts of informa-
tion are processed by database systems. In par-
ticular, modern web services have a high demand
for availability, consistency, partition tolerance, per-
formance, and scalability, that are at best difficult
and expensive to achieve with traditional relational
databases. NoSQL databases, especially the sub-
category of wide column stores (WCSs), were de-
signed to meet those requirements. They run in dis-
tributed cloud environments as key technology behind
many popular platforms, e.g. Apache HBase behind
Facebook (Borthakur et al., 2011), Apache Cassan-
dra behind eBay or Google’s BigTable behind almost
every Google service (Chang et al., 2008). Due to
the increased amount of data being produced every
day (e.g. in social media platforms as well as by
business or research), these databases are often out-
sourced to remote and potentially untrusted servers.
Unfortunately security was not a primary concern of
their designers (Okman et al., 2011).
Encryption is a tool to protect data confidential-
ity in such untrustworthy environments, but it also
limits the options for interacting with the data that
was encrypted. Using traditional encryption methods
like AES or RSA is unfeasible, because they do not
preserve the plaintext properties, that WCSs rely on
(see section 2.2). Since a very common task in cloud
database systems is executing range queries to select
rows with consecutive row IDs, we focus on order-
preserving encryption (OPE). It preserves the order
of the row IDs and thereby allows range queries to be
executed on the encrypted data as on plaintext data.
Although OPE is an active field of research, the
practical feasibility of most schemes is insufficient.
Thus, our work makes the following contributions:
• It identifies the requirements for utilizing OPE in
NoSQL WCSs.
• Based on those criteria it evaluates the practical
feasibility of popular OPE schemes and proposes
modifications for two of them to improve it.
• It conducts a practical performance comparison
of the two proposed modifications and the pop-
ular approach of (Boldyreva et al., 2011) based
on our own implementations using the currently
most popular NoSQL WCSs
1
Apache Cassandra
(Lakshman and Malik, 2010) and Apache HBase
(Borthakur et al., 2011) as underlying platforms.
1
Solit-IT: DB-engines ranking - http://db-
engines.com/en/ranking (all URLs have been checked
on April 7th 2016.
352
Waage, T., Homann, D. and Wiese, L.
Practical Application of Order-preserving Encryption in Wide Column Stores.
DOI: 10.5220/0005991403520359
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 352-359
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 BACKGROUND
2.1 Order Preserving Encryption
Formally speaking, an order-preserving (symmetric)
encryption scheme with plaintext space D (domain)
and ciphertext space R (range) is a tuple of al-
gorithms (KGen, Enc, Dec) satisfying the following
conditions:
• The key-generation algorithm KGen outputs a
random key k.
• The encryption algorithm Enc uses k and a plain-
text p to output the ciphertext c = Enc
k
(p).
• The decryption algorithm Dec uses k and a cipher-
text c to output the plaintext p. Thus it holds:
Dec
k
(Enc
k
(p)) = p.
• The order relation of plaintexts is preserved, i.e.
p
1
≤ p
2
⇒ Enc
k
(p
1
) ≤ Enc
k
(p
2
) for all p
1
, p
2
∈
D.
(Agrawal et al., 2004) were the first to intro-
duce the notation of OPE and proposed a theoretical
scheme to address it. In database applications OPE
is a very powerful primitive, because it allows the
database system to make comparisons between the
ciphertexts that result in the same outcomes as if it
had operated on the corresponding plaintexts. Thus,
the database can still build efficient indexes on the
encrypted input for answering range queries quickly
in the same way as on plaintext data. Unfortunately
most OPE approaches define their own security no-
tion (see Table 1), which makes a comparison of their
security levels rather difficult. However, as the scope
of this paper is practical feasibility of OPE rather than
security, we refer the reader in particular to the work
of (Boldyreva et al., 2009; Boldyreva et al., 2011)
who did the first mathematical groundwork in proof-
ing OPE security.
2.2 Wide Column Stores
As surveyed for example in (Harrison, 2015) different
WCSs follow different principles in terms of architec-
ture, querying, data types, node coordination, etc. De-
spite this diversity they all use a similar data model,
which can be roughly described as follows.
WCSs can formally be considered sparse,
distributed, multidimensional maps of the form
(table, rowkey, column, timestamp) → value, for-
mally described in detail in (Chang et al., 2008).
The concept of tables, rows and columns is used
like in traditional relational (SQL-based) databases.
However, the main difference is that columns are cre-
ated for each row instead of being predefined by the
table structure. Every row has an identifier that has to
be unique for the table (commonly referred to as “row
key”). Data is maintained in lexicographic order by
that key. As WCSs are distributed systems, ranges
of such row keys serve as units of distribution. Hence
similar row keys (and thus data items that are likely to
be semantically related to each other) are always kept
physically close together, in the best case on neigh-
boring sectors of a disk, but at least on the same node
of a cluster. Thus, reads of ranges require only com-
munication of a minimal number of machines.
3 FEASIBILITY OF OPE IN WCS
3.1 Criteria
Due to the general working principles of WCSs de-
scribed in the previous section, OPE schemes have to
satisfy certain requirements. Hence we evaluate their
practical feasibility in WCS database scenarios based
on five criteria:
(I) Ciphertext (im-)mutability. The ciphertext
produced by an OPE scheme is called mutable, if it
may change as more and more input gets encrypted.
An example of this category is (Kerschbaum and
Schr
¨
opfer, 2014), described in section 3.2.2. OPE
schemes producing immutable ciphertexts avoid the
re-encryption overhead in the first place. Immutable
means once a plaintext is encrypted, the correspond-
ing ciphertext is final. An instance of this category is
(Wozniak et al., 2013), described in section 3.2.1.
As discussed in section 2.2 an encryption of the
row keys should be order-preserving to preserve the
order of the rows and thus the way data gets dis-
tributed in the cluster. The usage of a mutable OPE
for the row keys would cause row keys to change
over time and hence would result in changing the
data’s physical position inside the database (cluster),
which is prohibitively expensive (and thus, generally
not supported by WCS databases). However, muta-
ble OPE schemes should be used for the column data
itself to gain more performance, as can be observed
in section 4. Note that ciphertext mutability is often
strongly related to criterion II and V.
(II) Need for Additional Data Structures. If they
are not stateless OPE schemes require additional
data structures for storing at least their plaintext-
ciphertext-mappings. That can be done using in-
dexes, trees, dictionaries etc., either on clientside
(or at least a trusted enviroment), e.g. (Kerschbaum
Practical Application of Order-preserving Encryption in Wide Column Stores
353

and Schr
¨
opfer, 2014), or on serverside, e.g. (Popa
et al., 2013; Roche et al., 2015). Note that in par-
ticular maintaining tree structures is usually expen-
sive for (non-graph-based) database systems. Hence,
sometimes additional components on serverside are
proposed for performance reasons (see criterion III),
which makes practical implementations rather com-
plex.
(III) Need for Additional Architectural Compo-
nents. Client applications and database platforms
normally do not have built-in mechanisms for OPE.
Thus additional components are required for both
rewriting queries to make them work with the server-
side data structures (as they might have to be altered
for functioning with the OPE schemes) as well as for
performing decryption and encryption itself. Usu-
ally those components have to reside in the trusted
(clientside) environment (e.g. (Popa et al., 2011; Tu
et al., 2013)). However some OPE schemes even re-
quire components running co-located to the database
server (e.g. (Popa et al., 2013)), which cannot be con-
sidered practical due to the architectural overhead. In
particular database-as-a-service providers usually do
not support that.
(IV) Input Capabilities. The authors of all OPE
proposals that we have encountered assume only pos-
itive integer input for their schemes. This is hard to
apply to real world datasets in which we also find neg-
ative or floating point numbers. One option to deal
with negative input would be adding an offset value
to the plaintext space, that is large enough to push
every value above zero. The question is how to de-
termine this offset, when the entire plaintext space
is not known in advance. Handling floating point
data is an even bigger problem. To our knowledge
there is no technique converting floating point num-
bers to integers in an order-preserving way without
loss of precision. This rises the question whether ex-
isting OPE schemes can be modified to also work with
negative and/or floating point input. We will answer
that for the schemes we have investigated in section
3.2. However, independent from the input type, some
OPE schemes further require detailed knowledge of
all the plaintexts before encryption (e.g. (Liu and
Wang, 2012)), which is hard to realize in practical
scenarios as databases may grow unpredictably over
time. Some schemes even need to encrypt the whole
plaintext space D in advance (Wozniak et al., 2013;
Liu et al., 2014), instead of encrypting only the de-
sired values on demand. The unfeasibility of such an
approach can be illustrated easily using the follow-
ing example: let D be defined by a common Integer
datatype. Having a typical length of 32 bit, |D| would
be of size 2
32
, which means 4.3 billion items would
have to be pre-computed and stored (even if the ma-
jority is never used).
(V) Security. The first formal security analysis of
OPE (Boldyreva et al., 2009) proved that ideal se-
curity
2
with immutable ciphertexts can only be ac-
complished, if the ciphertext space size |R| is expo-
nential in the plaintext space size |D|, which is hard
to achieve in practice. OPE schemes deal with this
problem in different ways (which often has a direct
impact on the criteria II and III). Examples are mod-
ular plaintext shifting (Boldyreva et al., 2011) (easy
to implement, but only a small security enhancement)
or using fake queries to hide the query distribution
(Mavroforakis et al., 2015) (causing communication
and computation overhead). In practice ideal security
can be achieved more easily by OPE schemes pro-
ducing mutable ciphertexts, because they do not have
the requirement of a ciphertext space size being ex-
ponential in the plaintext space size. They also hide
the frequency distribution of plaintext-ciphertext as-
signments much better, being able to achieve an al-
most uniform distribution (as shown e.g. by (Woz-
niak et al., 2013)). Still, that also means dealing with
unavoidable re-encryptions of (at least parts of) the ci-
phertext, that is already stored in the database. Recent
schemes try to keep the number of such updates to a
minimum (Kerschbaum and Schr
¨
opfer, 2014) or take
the burden of reassigning ciphertexts to components
on serverside (Popa et al., 2013) to reduce at least
communication costs. An alternative approach to
avoid re-encryption in the first place is pre-encrypting
as discussed in criterion IV.
(Naveed et al., 2015) proposed two attacks on
OPE-encrypted databases. Their attacks either re-
quire the cipherspace to be small compared to the
number of encrypted values (e.g. the largest ci-
pherspace they consider has a size of 365 while the ta-
bles contain at least a few hundred rows) or the plain-
texts to deviate strongly from a uniform distribution.
If OPE is applied on reasonably chosen columns, i.e.
where the number of ciphertexts is at least an order
of magnitude smaller than the size of the cipherspace
and where the corresponding plaintexts are uniformly
distributed, OPE still provides a good level of secu-
rity.
2
Meaning “IND-OCPA”: ciphertexts reveal nothing, but
their order.
SECRYPT 2016 - International Conference on Security and Cryptography
354

3.2 Selection of Practically Feasible
OPE Schemes
For a quick overview and brief evaluation of the
schemes that we investigated based on the criteria in-
troduced in section 3.1, see Table 1. We selected the
most promising three for implementation and testing
in real world WCSs. Detailed explanations of these
schemes and our modifications to improve the practi-
cal feasibility of two of them are given in the chapters
3.2.3 - 3.2.2. For not losing scope of this paper we
do not explain the concepts of the schemes that we
ruled out. However to give an idea of why we con-
sider those OPE schemes impractical, we point out a
few of their characteristics that cannot be read from
this table.
The approaches of (Kadhem et al., 2010) and (Liu
et al., 2014) require splitting and partitioning of the
plaintext space. Hence, they have to keep track of
more metadata than most other schemes. The scheme
of (Liu and Wang, 2012) requires detailed knowledge
of the plaintext space. In particular it needs to know
the smallest distance between two input values for
adding random noise to the ciphertexts in a way that
does not corrupt the original order. Again, in prac-
tice we usually do not have this detailed information
about the plaintext in advance. Furthermore, this is a
tricky problem when encrypting floating point num-
bers, since in theory the minimum distance between
such numbers can be arbitrarily small. As mentioned
before the approach of (Popa et al., 2013) needs
an additional component running co-located to the
database server, which they call “OPE-server”. It is
responsible for performing re-encryption operations
as described in section 3.1-I. In real world scenarios
running additional applications on the same platform
as or co-located to the database server often is not pos-
sible. The approach of (Chenette et al., 2015) (calling
it order-revealing encryption) completely lacks a de-
cryption functionality. Instead it comes with a cus-
tom compare operator. Thus it is not applicable for a
database scenario, since it surely would preserve the
order of the plaintext, but their exact values would not
be recoverable.
In the following sections, we will give a brief
introduction for each of the selected OPE schemes,
identify their practical weaknesses and describe our
modifications in order to overcome them as far as pos-
sible.
3
Only rather informal security analysis provided by the
authors.
4
No security analysis provided by the authors.
Table 1: Evaluation of the practical feasibility of popular
OPE schemes regarding the criteria introduced in section
3.1, (“>” = proved by the authors to be better than...).
OPE Scheme I II III IV V
Kadhem, ’10 + −− + − ?
3
Boldyreva, ’11 + ++ + − ROPF
Liu, ’12 + −− + −− ?
4
Popa, ’13 − −− − ++ IND-OCPA
Wozniak, ’13 + − + + > IND-OCPA
Liu, ’14 + − + − ?
3
Kerschb., ’14 − − + ++ IND-OCPA
Chenette, ’15 + + + − > ROPF
3.2.1 Random Subrange Selection using
Random Uniform Sampling by (Wozniak
et al., 2013)
Description. The authors introduce three OPE
schemes, namely random offset addition (ROA), ran-
dom uniform sampling (RUS) and random subrange
selection (RSS). Since ROA is somewhat trivial and
an attacker only needs to know a single plaintext-
ciphertext-pair to break the encryption, we focus on
RSS with RUS being a sub-procedure of it.
RSS can roughly be described as follows. First
of all, randomly decide how to draw the lower and
upper bounds r
min
and r
max
of the range R, either by
choosing r
min
∈ [1, |R| − |D| + 1] and r
max
∈ [r
min
+
|D|−1, |R|] or by choosing r
max
∈ [|D|, |R|] and r
min
∈
[1, r
max
− |D| + 1]. Afterwards an order-preserving
function (OPF) from D = [1, |D|] to R = [1, r
max
−
r
min
+ 1] is sampled using an alternative OPE con-
struction scheme. We use the authors’ RUS as de-
scribed in the next paragraph. Finally add r
min
− 1 to
all ciphertexts.
RUS gets initialized with an empty OPF f and the
minimum and maximum elements of D and R as spec-
ified by RRS before. A recursive sample procedure
then randomly selects an element p ∈ [d
min
, d
max
] and
c ∈ [r
min
+ p −d
min
, r
max
+ p −d
max
]. Thus, p splits D
in a lower and a higher sub-domain and c splits R in a
lower and a higher sub-range. The pair (p, c) is added
to f and the sample procedure continues recursively
as before with the new sub-domains and sub-ranges
until D is completely covered.
Weaknesses. RSS with RUS has mainly two practi-
cal disadvantages. Firstly, it can handle only positive
numerical inputs. Secondly, it processes the whole
domain D instead of computing and returning only
the ciphertexts for actually desired plaintexts on de-
mand (an example illustrating the impracticability of
this approach was given in section 3.1-IV).
Practical Application of Order-preserving Encryption in Wide Column Stores
355

0
20000
40000
60000
80000
100000
120000
140000
160000
180000
200000
0 2000 4000 6000 8000 10000
number of samplings
number of inserted numerical values
Figure 1: Average number of samplings required in (Woz-
niak et al., 2013) with increasing dataset size.
Our Modifications. We can get rid of the first
weakness trivially by initializing the sample function
in RUS with a negative value for d
min
instead of 1.
This extends the domain D into the range of nega-
tive numbers (as far as we want). Since the algorithm
only works with random selections in intervals and
some additions and subtractions, that does not affect
its working principle. We can eliminate the second
weakness by modifying RRS and RUS in the follow-
ing way.
First of all, we define p
0
specifying the plaintext
value that we are actually aiming for in the encryp-
tion process (instead of the whole domain D). We
modify the sample procedure of RUS by adding an
extra parameter for p
0
. Now instead of always con-
tinuing recursively after a split for the lower sub-
domain [d
min
, p − 1] and the higher sub-domain [p +
1, d
max
], we only process the lower sub-domain if
p
0
∈ [d
min
, p − 1] or the higher sub-domain if p
0
∈
[p + 1, d
max
. This reduces the average number of sam-
ple function executions (in the following short: “sam-
plings”) from |R| to log
2
(|R|).
Then we modify RSS itself. Instead of always
starting with the full domain |D| (which in combi-
nation with our RUS sample function modification
would result in an inconsistent encryption anyway),
we now initialize the sample function of RUS only
with the sub-domain [d
1
, d
2
], in which d
1
is the high-
est already encrypted value smaller than p
0
and d
2
is
the smallest already encrypted value greater than p
0
.
As more and more values get encrypted, this reduces
the average number of samplings further (see Figure
1). In order to make that work for the first p
0
that
we would like to encrypt after we have determined
r
min
and r
max
in the initialization phase of RSS, we
add the minimum and maximum pairs (p
min
, c
min
) and
(p
max
, c
max
) to f by sampling c
min
from [r
min
, r
max
−1]
and c
max
from [c
min
+ 1, r
max
].
Figure 1 and 2 present an example that illustrates
0
5
10
15
20
25
30
35
40
45
50
0 2000 4000 6000 8000 10000
number of samples necessary to
compute the targeted value p'
number of inserted numerical values
Figure 2: Average number of samplings required per en-
cryption in (Wozniak et al., 2013) with increasing dataset
size.
the improvements by showing the average number of
necessary samplings for computing the ciphertexts of
10000 uniformly and randomly generated 32 bit Inte-
ger plaintext values 20 times. Instead of always hav-
ing to sample |D| = 2
32
= 4294967296 times to cover
the whole domain and then pick the 10000 (p, c) pairs
that we actually wanted, we only need 186.287 sam-
plings (= 0.004%) for those 10000 values on average.
Note that our implentation (for details see section 4)
is able to do this in less than a second. Of course
this number gets lower, if less values are supposed
to be encrypted (see Figure 1). Furthermore it can
be observed, that as more and more values have al-
ready been encrypted, the average number of neces-
sary samplings required per value decreases from the
expected log
2
(|R|) = log
2
(2
32
) = 32 for the first en-
cryption to 21 for the 10000th encryption (see Figure
2).
3.2.2 Optimal Average-complexity
Ideal-security OPE by (Kerschbaum and
Schr
¨
opfer, 2014)
Description. The OPE scheme introduced in (Ker-
schbaum and Schr
¨
opfer, 2014) can be briefly de-
scribed as follows. The OPF f is initialized with
two plaintext-ciphertext-pairs, namely (−1, −1) and
(|D|, |R|). New pairs (p, c) are always inserted be-
tween (p
n
, c
n
) and (p
n+1
, c
n+1
) with p
n
≤ p < p
n+1
and c = c
n
+ d
c
n+1
−c
n
2
e. If p = p
n
, the value was al-
ready encrypted. If c
n+1
−c
n
= 1 there is no gap large
enough to accommodate the new ciphertext c. In this
case a re-encryption procedure is executed: From all
the sorted and distinct plaintexts p
1
...p
m
that have al-
ready been encrypted, start over like described above
with p = p
b
m
2
c+1
and continue recursively with the in-
terval p
1
...p
b
m
2
c
if m > 1 and p
b
m
2
c+2
...p
m
if m > 2.
SECRYPT 2016 - International Conference on Security and Cryptography
356
Practical Weaknesses. This scheme comes with
a couple of weaknesses. The most obvious one
is its re-encryption phase, because in practice that
means reading all already encrypted values from the
database, re-encrypt them and finally write them back
into the database. In order to keep the occurrences
of those re-encryptions as rare as possible, the cipher-
text space should be chosen large enough. Having a
plaintext space of length n bit the authors recommend
a ciphertext space of size λn bits, with a theoretical
safe upper bound of λ = 6.31107, but they also show
in their practical experiments that λ = 3 (sometimes
even λ = 2) is already sufficient for most datasets.
Another practical weakness of this scheme is the fact,
that the insertion order matters. The best case is when
all elements of a perfectly balanced binary search tree
are inserted in pre-order traversal order. The average
case is a uniform input distribution. The worst case is
inserting pre-sorted values, which should be avoided
at all (see section 4). Last but not least the scheme
cannot handle negative input by the authors’ defini-
tion. Even though this scheme comes with all these
practical weaknesses, we chose it because it works
with very simple computations, that do not even in-
volve randomness. Thus it is very promising in terms
of speed.
Our Modifications. Since we cannot avoid the re-
encrytion phase other than by defining the range large
enough and we also might not have any influence
on the insertion order of the plaintexts later on, the
only modification we can apply is initializing f with
(−|D|, −|R|) and (|D|, |D|
λ
), instead of (−1, −1) and
(|D|, |R|). Similar to our modification for (Wozniak
et al., 2013) this extends the domain to also cover
negative input. To make sure this does not increase
the number of necessary re-balancings, we adjusted
the ciphertext space as recommended by the authors.
3.2.3 mOPE by (Boldyreva et al., 2011)
Description. mOPE is an extension of (Boldyreva
et al., 2009). It is based on the fact that any order-
preserving function from {1...M} to {1...N} can be
represented by a combination of M out of N ordered
items. Thus, ciphertexts can be computed by sam-
pling values according to the hypergeometric distribu-
tion. mOPE adds a secret modular shift to the encryp-
tion in the following way: if DEC
OPE
and ENC
OPE
are the decryption and encryption function of the stan-
dard Boldyreva OPE (Boldyreva et al., 2009), then
ENC
mOPE
(x) = ENC(x + m) (where m is a secret
offset) and DEC
mOPE
(x) = DEC
OPE
(x)−m mod |D|
(where |D| is the size of the plaintext space).
Practical Weaknesses. The core element of this al-
gorithm is sampling from the hypergeometric distri-
bution, which is computationally expensive and re-
quires the input to be a positive Integer. However,
we still consider (Boldyreva et al., 2011) to be an in-
teresting candidate for practical usage because to our
knowledge, it is the only OPE scheme that does not
require maintaining a state. That makes it easy to
implement the algorithm for client server scenarios.
Furthermore, since to our knowledge its predeces-
sor (Boldyreva et al., 2009) is the only OPE scheme
of practical relevance so far (implemented in (Popa
et al., 2011; Tu et al., 2013)), it is interesting to com-
pare it to the other OPE schemes.
4 IMPLEMENTATION AND
EXPERIMENTS
Since disk access and memory management in WCSs
are performed at column family level, we imple-
mented the indexes of (Wozniak et al., 2013; Ker-
schbaum and Schr
¨
opfer, 2014) in the same way. For
our experiments we inserted up to 20000 uniformly
distributed and randomly created 32-bit Integer val-
ues into Cassandra and HBase using the three OPE
schemes as described in section 3.2.1 - 3.2.3. While
for (Boldyreva et al., 2011; Wozniak et al., 2013) the
order of insertion does not matter, for (Kerschbaum
and Schr
¨
opfer, 2014) we tested the three cases as de-
scribed in section 3.2.2. We used local installations to
avoid network effects, as we wanted to measure the
computation time of the schemes in combination with
the insertion speed of the databases. All implementa-
tions were done in Java 8. We ran our experiments on
an Intel Core i7-4600U CPU @ 2.10GHz, 8GB RAM,
a Samsung PM851 256GB SSD using Ubuntu 15.04.
0
2
4
6
8
10
12
2000 4000 6000 8000 10000 12000 14000 16000 18000 20000
time [s]
number of inserted numeric values
unencrypted
Boldyreva11
Wozniak13
Kerschb14 (best)
Kerschb14 (average)
Kerschb14 (worst)
Figure 3: Time needed for encryption with increasing data
set size in Apache Cassandra.
Practical Application of Order-preserving Encryption in Wide Column Stores
357

0
2
4
6
8
10
12
14
16
2000 4000 6000 8000 10000 12000 14000 16000 18000 20000
time [s]
number of inserted numeric values
unencrypted
Boldyreva11
Wozniak13
Kerschb14 (best)
Kerschb14 (average)
Kerschb14 (worst)
Figure 4: Time needed for encryption with increasing data
set size in Apache HBase.
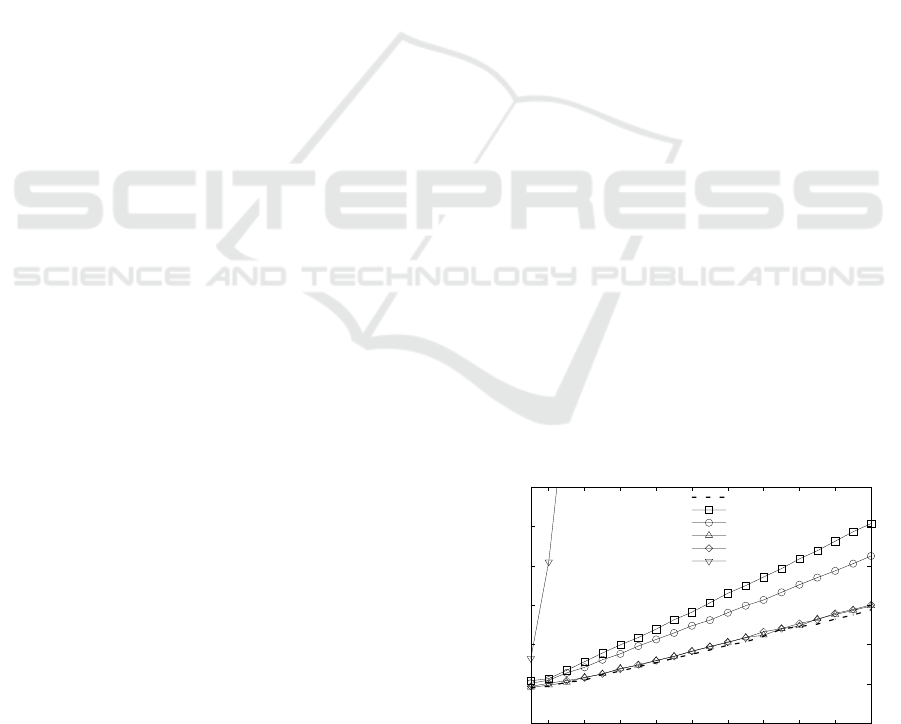
Figure 3 and 4 present the results, showing the av-
erage of ten measurements. Even though they have an
index to maintain the approaches of (Wozniak et al.,
2013; Kerschbaum and Schr
¨
opfer, 2014) are gener-
ally faster than the stateless scheme of (Boldyreva
et al., 2011). The only exception is using (Ker-
schbaum and Schr
¨
opfer, 2014) with pre-sorted input,
which is prohibitively slow and should be avoided.
The best combination of OPE scheme and WCS is
(Kerschbaum and Schr
¨
opfer, 2014) in its best and av-
erage case with Cassandra, where the encryption step
causes a performance loss of only 3%.
Cassandra is generally ca. 40% faster than HBase,
mainly because (Wozniak et al., 2013; Kerschbaum
and Schr
¨
opfer, 2014) are so fast that the database sys-
tem’s mere insertion time requires a significant share
in the overall process of encrypting and inserting.
With Cassandra being optimized for writes it takes ad-
vantage of this. An exception is the worst case usage
of (Kerschbaum and Schr
¨
opfer, 2014), where because
of the re-balancing phases not only writing but also
reading performance matters. In this case HBase is
always 12-15% faster than Cassandra, which seems
to reflect the fact, that while Cassandra is optimized
for writes, HBase is optimized for reads.
Because decrypting is very simple, we do not
elaborate on it in the same level of detail as we did
for encrypting. In (Wozniak et al., 2013) and (Ker-
schbaum and Schr
¨
opfer, 2014) it is just a lookup in the
index which takes less than 1 ms. (Boldyreva et al.,
2011) is computational more expensive, since it has
no index to use. Hence it requires up to 5 ms for de-
cryption.
5 DISCUSSION
The results show that OPE can be used in WCSs ef-
ficiently. However, when choosing an OPE scheme
it makes sense to think about the future use of the
database. If speed matters and there is a low probabil-
ity of pre-sorted inputs, the scheme of (Kerschbaum
and Schr
¨
opfer, 2014) is advisable. If an index should
be avoided and ciphertexts are required to be im-
mutable (Boldyreva et al., 2011) is the way to go.
(Wozniak et al., 2013) is a compromise between both.
It delivers immutable ciphertext almost as fast as
(Kerschbaum and Schr
¨
opfer, 2014) for every input,
but it requires an index.
Of course in the practical application a combina-
tion of the different OPE schemes is most promis-
ing. Row keys should be encrypted with the OPE
of (Boldyreva et al., 2011) or (Wozniak et al., 2013)
Regular, unordered columns can be encrypted with
the scheme of (Kerschbaum and Schr
¨
opfer, 2014).
For regular columns with ordered data the algorithm
of (Wozniak et al., 2013) is the best choice.
6 RELATED WORK
So far there is not much work using OPE with real
world technologies besides the work that we already
mentioned throughout the paper. The most popu-
lar example surely is “CryptDB” (Popa et al., 2011)
utilizing the immutable scheme of (Boldyreva et al.,
2009), tweaked by operating with a binary search tree
and caching in the background. Another system for
executing queries over encrypted data is “Monomi”
(Tu et al., 2013), also using (Boldyreva et al., 2009)
for OPE. Both approaches are designed for working
with SQL-based systems.
7 CONCLUSION AND FUTURE
WORK
We discussed how OPE can be used in NoSQL
WCSs and quantified the performance of three OPE
schemes on the two currently most popular platforms.
Since we have already done the same for a couple
of schemes for searchable encryption (Waage et al.,
2015), our next goal is to build a seamless integrating
proxy client similar to “CryptDB” for executing more
sophisticated queries on encrypted WCS databases.
Furthermore we plan support for Apache Accumulo.
SECRYPT 2016 - International Conference on Security and Cryptography
358

ACKNOWLEDGEMENT
This work was funded by the DFG under grant num-
ber WI 4086/2-1.
REFERENCES
Agrawal, R., Kiernan, J., Srikant, R., and Xu, Y. (2004).
Order preserving encryption for numeric data. In Pro-
ceedings of the 2004 ACM SIGMOD International
Conference on Management of Data, pages 563–574.
ACM.
Boldyreva, A., Chenette, N., Lee, Y., and O’Neill, A.
(2009). Order-preserving symmetric encryption. In
Advances in Cryptology-EUROCRYPT 2009, pages
224–241. Springer.
Boldyreva, A., Chenette, N., and O’Neill, A. (2011). Order-
preserving encryption revisited: Improved security
analysis and alternative solutions. In Advances in
Cryptology–CRYPTO 2011, pages 578–595. Springer.
Borthakur, D., Gray, J., Sarma, J. S., Muthukkaruppan,
K., Spiegelberg, N., Kuang, H., Ranganathan, K.,
Molkov, D., and Menon, A. (2011). Apache hadoop
goes realtime at facebook. In Proceedings of the SIG-
MOD International Conference on Management of
Data, pages 1071–1080. ACM.
Chang, F., Dean, J., Ghemawat, S., Hsieh, W. C., Wal-
lach, D. A., Burrows, M., Chandra, T., and Fikes, A.
(2008). Bigtable: A distributed storage system for
structured data. ACM Transactions on Computer Sys-
tems (TOCS), 26(2):4.
Chenette, N., Lewi, K., Weis, S. A., and Wu, D. J. (2015).
Practical order-revealing encryption with limited leak-
age.
Harrison, G. (2015). Database survey. In Next Generation
Databases, pages 217–228. Springer.
Kadhem, H., Amagasa, T., and Kitagawa, H. (2010).
Mv-opes: Multivalued-order preserving encryption
scheme: A novel scheme for encrypting integer value
to many different values. IEICE TRANSACTIONS on
Information and Systems, 93(9):2520–2533.
Kerschbaum, F. and Schr
¨
opfer, A. (2014). Optimal average-
complexity ideal-security order-preserving encryp-
tion. In Proceedings of the 2014 ACM SIGSAC Con-
ference on Computer and Communications Security,
pages 275–286. ACM.
Lakshman, A. and Malik, P. (2010). Cassandra: a decen-
tralized structured storage system. ACM SIGOPS Op-
erating Systems Review, 44(2):35–40.
Liu, D. and Wang, S. (2012). Programmable order-
preserving secure index for encrypted database query
in service cloud environments. In Cloud Computing
(CLOUD), 2012 IEEE 5th International Conference
on, pages 502–509. IEEE.
Liu, Z., Chen, X., Yang, J., Jia, C., and You, I. (2014). New
order preserving encryption model for outsourced
databases in cloud environments. Journal of Network
and Computer Applications.
Mavroforakis, C., Chenette, N., O’Neill, A., Kollios, G.,
and Canetti, R. (2015). Modular order-preserving en-
cryption, revisited. In Proceedings of the 2015 ACM
SIGMOD International Conference on Management
of Data, pages 763–777. ACM.
Naveed, M., Kamara, S., and Wright, C. V. (2015).
Inference attacks on property-preserving encrypted
databases. In Proceedings of the 22nd ACM SIGSAC
Conference on Computer and Communications Secu-
rity, pages 644–655. ACM.
Okman, L., Gal-Oz, N., Gonen, Y., Gudes, E., and
Abramov, J. (2011). Security issues in nosql
databases. In Trust, Security and Privacy in Com-
puting and Communications, 2011 IEEE 10th Inter-
national Conference on, pages 541–547. IEEE.
Popa, R. A., Li, F. H., and Zeldovich, N. (2013). An ideal-
security protocol for order-preserving encoding. In
IEEE Symposium on Security and Privacy, pages 463–
477.
Popa, R. A., Redfield, C., Zeldovich, N., and Balakrish-
nan, H. (2011). Cryptdb: protecting confidentiality
with encrypted query processing. In Proceedings of
the 23rd ACM Symposium on Operating Systems Prin-
ciples, pages 85–100. ACM.
Roche, D., Apon, D., Choi, S. G., and Yerukhimov, A.
(2015). Pope: Partial order-preserving encoding.
Technical report, Cryptology ePrint Arch. 2015/1106.
Tu, S., Kaashoek, M. F., Madden, S., and Zeldovich, N.
(2013). Processing analytical queries over encrypted
data. In Proceedings of the VLDB Endowment, vol-
ume 6, pages 289–300. VLDB Endowment.
Waage, T., Jhajj, R. S., and Wiese, L. (2015). Searchable
encryption in apache cassandra. In Proceedings of the
8th Symposium on Foundations and Practice of Secu-
rity (FPS). Springer.
Wozniak, S., Rossberg, M., Grau, S., Alshawish, A., and
Schaefer, G. (2013). Beyond the ideal object: to-
wards disclosure-resilient order-preserving encryption
schemes. In Proceedings of the 2013 ACM workshop
on Cloud computing security, pages 89–100. ACM.
Practical Application of Order-preserving Encryption in Wide Column Stores
359
