Enhancing Operation Security using Secret Sharing

Mohsen Ahmadvand

, Antoine Scemama

, Mart

ın Ochoa

and Alexander Pretschner

Technische Universit

at M

unchen, M

unchen, Germany

Brainloop, M

unchen, Germany

Singapore University of Technology and Design, Singapore, Singapore

Keywords:

Secret Sharing, Master Key Security, Threshold Based Schemes, Generalized Access Structure.

Abstract:

Storing highly conﬁdential data and carrying out security-related operations are crucial to many systems. Start-

ing from an industrial use case we propose a generic architecture based on secret sharing which address critical

operation authorization. By comparing and benchmarking different scheme from the literature we analyze the

different trade-offs (security, functionality, performance) which can be achieved. Finally by providing an open

source .NET implementation of several secret sharing schemes, this paper aims to rise awareness regarding

the capabilities of such algorithms to increase security in industrial setting.

1 INTRODUCTION

Storing highly conﬁdential and sensitive data, such

as encryption keys, is a challenging task. Under-

standably, any accidental or other incidental disclo-

sure of these classiﬁed data could be catastrophic.

However, counting on a single copy of a secret in-

creases the risk of losing data in case of failure. On

the other hand, preserving multiple copies of a secret

increases resilience to failures, while it downgrades

security, because it widens the attack surface and thus

increases the probability of secret exposure. Conse-

quently, there is a trade-off between resilience to fail-

ure and preserving conﬁdentiality.

One way to address this problem is to use secret

sharing (Shamir, 1979; Benaloh and Leichter, 1990;

Blakley et al., 1979; Schoenmakers, 1999; Feldman,

1987). This technique offers redundancy by splitting

the secret in a way that each share on its own carries

no information about the actual secret. At the same

time, certain authorized sets of these copies would,

together, reveal the secret. This approach makes the

secret recoverable when confronting disasters, while

at the same time, it does not increase the risk of secret

leakage. Compared to the classic approach in which a

single mistake causes secret exposure, this technique

can tolerate multiple breaches.

Likewise, there exist security-related operations

that are so critical for a system, that resemble the sit-

uation of highly conﬁdential data. Such operations

inevitably require redundancy (multiple users could

carry them out) and security (guarantees that no mis-

use could occur). For instance, altering the system

wide security policies should be considered as a crit-

ical operation. In this case, overly trusting multi-

ple users (say admins) to perform such operations in-

creases the risk of insider attacks. At the same time,

paranoid settings such as only enabling a single super

trusted user to perform highly critical operations may

result in availability issues.

Therefore, one way to deal with the authoriza-

tion of security-related operations is to require the

agreement of multiple users (similar to the four eyes

principle) before the operations can be carried out.

Such setting lowers the likelihood of misuse by sin-

gle users, and increases the availability of the system.

Problem: In this paper, we conduct a case study

that is inspired by Brainloop, a secure cloud storage

provider for document collaboration. For their com-

mercial solution, they use symmetric encryption with

different keys for each client. In addition to that, their

cloud storage offers document processing and collab-

oration features. Thus, their servers need to access all

encryption keys on demand. However, these keys are

encrypted with another key, known as the master key

(a 256 bit AES key).

On the one hand, loss or damage of the master key

is disastrous, since it leaves all clients with no possi-

bility to recover their data. On the other hand, Brain-

loop considers altering the master key and changing

hardware conﬁguration as critical operations, which

are only permitted after agreement of all the trusted

446

Ahmadvand, M., Scemama, A., Ochoa, M. and Pretschner, A.

Enhancing Operation Security using Secret Sharing.

DOI: 10.5220/0005992104460451

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 446-451

ISBN: 978-989-758-196-0

parties. It means that if such incidents occur, the sys-

tem stops functioning until the parties approve the

changes. Therefore, it is desired to let an authentic

subgroup of trusted parties to approve the legitimacy

of a critical operation. This subgroup could be for in-

stance any k persons out of all n participants or even

an arbitrary subset of the trusted parties, e.g. a well-

deﬁned subset, such as (party

and party

) or (party

and party

). Brainloop’s use case clearly resembles

the secret sharing scenario.

Proposed Solution: Our proposed solution com-

bines these two separate requirements via the use of

secret sharing. The core idea is to set an authentica-

tion framework, based on a token shared among sev-

eral trust parties via secret sharing. A critical opera-

tion is authorized if the trust parties are authenticated

in this framework, i.e. if the system is able to re-

construct the token from the shares sent by the trust

parties. Additionally this token consists in the most

valuable information which is best protected against

malicious admin (either in or out of the system) and

for which there is redundancy need. This way we

achieve: a) redundancy of the most secret data, with-

out enlarging the attack surface and b) in order for a

malicious admin to run a critical operation, he would

have to obtain ﬁrst the most secret data, which is ei-

ther not in the system or in the most secure place

(e.g. secured by means of orthogonal technology such

as trusted computing (Garﬁnkel et al., 2003; Santos

et al., 2009; Neisse et al., 2011)).

Implementing our Approach: Having distribu-

tively secure shares and ﬂexibility in deﬁning security

parameters makes secret sharing a potentially good

solution for Brainloop’s problem. However, the effec-

tiveness and applicability of various schemes to real-

istic use cases (i.e., Brainloop) are vague. Similarly,

the trade offs between security features and perfor-

mance with real world parameters (when number of

parties increase) have not been thoroughly studied in

practice. Therefore, as part of our contribution, we

explore the most prominent schemes from the litera-

ture, study their applicability to our use case and dis-

cuss the trade offs, as a guideline for future applica-

tions.

Additionally, we provide an open source imple-

mentation for the selected schemes, in order to foster

the adaptability of our solution. For instance, standard

libraries of two popular software development frame-

works (Microsoft .Net version 4.5 and Java version

8.0) have not implemented secret sharing schemes,

which make it difﬁcult for practitioners to adopt them

or experiment with them.

We use our library to evaluate performance of

various different schemes with reasonable parameters

for an authorization system. These implementations

serve as guideline to practitioners to choose an ac-

ceptable security vs. performance trade off. Summa-

rizing:

Contributions: a) Starting from an industrial use

case, we propose an architecture, based on secret

sharing as a building block, for enforcing multi-user

agreement as well as secret data redundancy b) we

study the applicability of the most prominent schemes

in the secret sharing research: (Shamir, 1979), Gener-

alized Access Structure (Benaloh and Leichter, 1990)

and (Schoenmakers, 1999) to our critical operation

authorization system (i.e Brainloop) c) we study the

efﬁciency of these schemes with real world parame-

ters d) we provide an open source implementation for

the aforementioned secret sharing schemes.

Organization: The rest of the paper is organized

as follows: Preliminaries on secret sharing in Sec-

tion 2 are discussed. Then we describe details of our

authorization system and present benchmarks in Sec-

tion 3. In Section 4 we review Brainloop’s case study

and apply our authorization system to it. Later, we

discuss in Section 5 our benchmark results and shed

light on applicability of the implemented schemes in

real world problems . We review related works in Sec-

tion 6. Lastly, we conclude in Section 7.

2 PRELIMINARIES

Secret sharing is a technique in which a dealer se-

curely divides a secret among a group of players (par-

ticipants). Later, the secret can only be reconstructed

if an authentic subset of participants agree on provid-

ing their possessed shares, otherwise it remains un-

computable. Since the seminal work of Shamir and

Blakley (Blakley et al., 1979), many secret sharing

schemes were designed. Based on the main feature,

we roughly categorize secret sharing schemes into

three subcategories.

Threshold Schemes. This group of schemes di-

vides a secret among n parties, and enables k, 0 < k ≤

n, of them to compute the secret. Also, they are the

most optimal in terms of execution time and (short)

share length. For instance, (Shamir, 1979) is a thresh-

old scheme. Nevertheless, these schemes are not so

ﬂexible in terms of handling more complex use cases.

Generalized Access Structures. These schemes

allow for full customization in determining authen-

tic sets. For example, one can take into account par-

ties’ roles and/or department in the share distribution

and secret reconstruction. A particular business use-

case may require shares from at least one member of

department

and one member of department

to re-

Enhancing Operation Security using Secret Sharing

447

cover the secret. Hence, they are ﬂexible enough to

handle all complex business requirements. (Benaloh

and Leichter, 1990) is a scheme that realizes general-

ized access structures.

Veriﬁable Schemes. Beside typical sharing and

reconstruction operations, these schemes provide a

mathematical guarantee that the shares are consis-

tent. In exact words, players and the dealer can verify

the integrity of the shares on demand. For example,

(Feldman, 1987; Schoenmakers, 1999) are samples of

veriﬁable schemes.

In this paper, we opt for the secret sharing

schemes which we view as the most prominent within

each category. Shamir as a candidate for thresh-

old schemes, Benaloh-Leichter for generalized ac-

cess structure and ﬁnally Schoenmakers as veriﬁable

secret sharing scheme. These schemes are selected

for further implementation and performance analy-

sis. Due to space constraints, we refer the reader to

(Shamir, 1979; Benaloh and Leichter, 1990; Schoen-

makers, 1999) for the schemes’ details.

3 IMPLEMENTATION AND

BENCHMARKS

Employing secret sharing schemes in the industrial

context requires mindful identiﬁcation of certain un-

avoidable trade-offs. In other words, we need to thor-

oughly ﬁnd out the efﬁciency compromises one has

to make for a particular security (integrity check, en-

cryption and collusion) or functional (threshold vs.

non-threshold) feature. This also supports our case

study by shedding light on the performance differ-

ences.

To the best of our knowledge, there is no pub-

licly available implementation for most of the se-

cret sharing schemes discussed previously in mod-

ern programming languages such as Java and .NET.

Not only does this make difﬁcult to decide whether

certain trade-offs are acceptable in practice (although

there are some published benchmarks in the litera-

ture (DSouza et al., 2011) and complexity-theoretical

bounds are known (Beimel, 2011)), but ultimately, it

makes it very hard for practitioners to actually inte-

grate secret sharing into their solutions, since they

would have to implement the algorithms themselves.

This is a daunting task, since it requires a non-trivial

cryptography background and additional cost and ef-

fort. Therefore, as a ﬁrst contribution, and in order

to derive concrete performance bounds, we imple-

mented

∗

Shamir, Benaloh-Leichter and Schoenmak-

∗

available at (Ahmadvand, 2015)

ers in .NET

†

(which is the standard used by Brain-

loop).

3.1 Benchmarks

To choose the appropriate scheme for our case study,

runtime performance plays an important role. As

mentioned earlier complexity-theoretical bounds for

the practitioner are helpful but insufﬁcient. Plus we

need concrete implementations (for system integra-

tion) which to the best of our knowledge for some

schemes are not publicly available. Therefore, we im-

plemented all three reviewed schemes and performed

benchmarks on a Windows 7 computer with the fol-

lowing conﬁguration: Intel core i5 processor and 8

GB memory. The key sizes of 128, 256 and 512

bits were used in the experiment of the Shamir and

Benaloh-Leichter scheme. For Schoenmakers, since

the scheme security relies on the difﬁculty of the dis-

crete logarithm problem, we evaluated our implemen-

tation with 1024 and 2048 bit ﬁelds, which are known

to be secure to handle 128 bit and 256 bit keys (BSI,

2015).

The main operations Share Generation, Secret Re-

construction and Share Veriﬁcation (only for Schoen-

makers) operations have undergone experiments for

the keys sized 128, 256 bits. Each operation is iterated

100 times to ﬁnd a reliable performance. To ﬁlter out

random prime generation noises from our evaluation,

we generate 1000 prime numbers per each ﬁeld size,

later, at the execution time, we randomly choose an

element from the prepared list. We show mean aver-

age diagrams for various key sizes. The performance

results are depicted in Figures 1 to 3.

4 Brainloop CASE STUDY

Background. Brainloop provides a secure SaaS

storage and collaboration platform. Data are stored

encrypted with an AES key speciﬁc to each client.

In order for the system to provide collaborative fea-

tures, those AES keys are stored in a DB, encrypted

with another AES key known as the master key. This

master key is the most important key. It ensures (di-

rectly and indirectly) the security of all user data. So

on the one hand, it is very important not to lose it,

on the other hand no malicious person (including a

malicious administrator) should have access to it. To

prevent its loss (due to defective hardware) the master

key is split into chunks and distributed to various trust

†

to accelerate our implementation we are using the (C lan-

guage) NTL library which is an open source number theory

library (Shoup, 2016).

SECRYPT 2016 - International Conference on Security and Cryptography

448

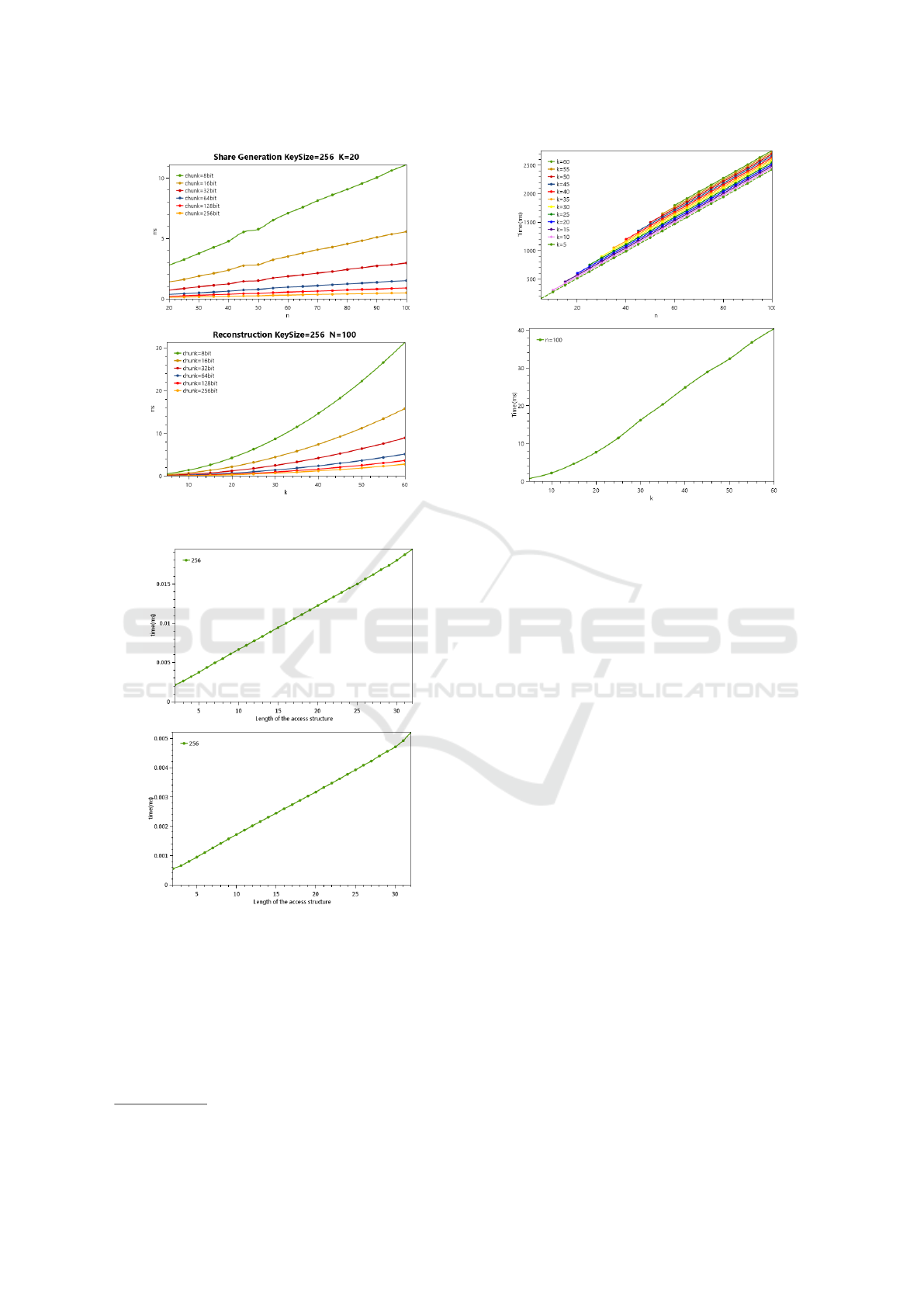
Figure 1: Shamir benchmark results for share generation

and secret reconstruction for a 256 bit key.

Figure 2: Benaloh-Leichter generation and reconstruction

benchmark results for a 256 bit secret.

parties a.k.a VIPs

∗

. The ownership of the master key

chunks is also used within system workﬂows in which

VIPs must agree on before starting critical operations.

The importance of these operations prohibits admin-

istrators from starting them.

The ﬁrst critical operation which requires VIPs’

agreement is changing the master key, since any cryp-

∗

C-level people of Brainloop

Figure 3: Schoenmakers benchmark results for share gener-

ation and secret reconstruction in a 2048 bit ﬁeld.

tographic key should be periodically rotated. Once

the master key is changed it needs to be re-distributed

to selected VIPs and of course administrators should

not be able to control this action (and to which indi-

viduals the key parts are sent). The other critical oper-

ation is when hardware needs to be changed. In order

to prevent a malicious hardware replacement, a hard-

ware ﬁngerprint is stored (encrypted) in the system

and regularly checked. If a ﬁngerprint mismatch hap-

pens there are two possibilities: either the hardware is

broken and needs to be changed, or a malicious per-

son tried to changed it. When a mismatch occurs the

system turns into a ”failed state” and the VIPs need to

“agree” in order to reset the system back to the ”nor-

mal state”.

For these two critical operations, the VIPs agree in

that they upload (securely) their key parts to the sys-

tem. The system accepts this “agreement” if it is able

to reconstruct the master key from the different key

parts. This architecture relates the most valuable data

with the ability to start the most critical operations,

however it has two drawbacks: on the one hand, the

VIPs get to know a part of the master key, so if 2 out 3

VIPs were malicious they could collude and recover

2/3 of the master key, which lets the last third open

to brute-force. On the other hand, all the VIPs must

be present to start a critical operation, this is not con-

venient at all considering that a hardware failure can

happen any time and the system needs to be recovered

as soon as possible.

Solution. By using secret sharing in this context

it is possible to improve both the overall security and

Enhancing Operation Security using Secret Sharing

449

ﬂexibility of the system. Indeed, by giving shares (us-

ing secret sharing) and not parts of the master key, the

VIP can still perform the agreement process, but with-

out knowing a part of the key. Moreover, they do not

need all to be present and upload the key parts in case

of critical operations.

Note that the master key is meant to be accessible

by the server at any time. This may raise the concern

about its security when confronting malicious host ad-

ministrators. We believe this protection (against an

admin) is an orthogonal problem that requires a set

of security policy enforcements at various levels, in-

cluding operation, infrastructure and software (Haldar

et al., 2004; Garﬁnkel et al., 2003; Neisse et al., 2011;

Rocha and Correia, 2011; Santos et al., 2009; Chou,

2013; Rocha et al., 2013). Therefore, the rogue in-

sider threat is excluded from our case study.

Following this study, the solution was implemented in

Brainloop product.

5 DISCUSSION

Our benchmark results indicate that the collusion-

prevention security feature alone does not have

performance drawbacks. However, handling non-

threshold use cases using Benaloh-Leichter grows ex-

ponentially in the number of parties in the worst

case. Furthermore, supporting share integrity veriﬁ-

ability along with encryption, which is offered by the

Schoenmakers algorithm, slowed the runtime execu-

tion into the order of seconds with upper bound of 25

seconds when n = 100 and k = 60. Thus, for a given

context, one should decide upon a set of trade-offs at

scheme selection phase.

Although in principle all three considered

schemes are suitable to solve the master key sharing

problem, it is not obvious which one would precisely

yield the best trade-off between efﬁciency, security

and functionality. For this reason, it is crucial to ﬁrst

deﬁne the relevant factors, then have a reliable set of

benchmarks and salient features per schema as docu-

mented in the previous subsections.

We have identiﬁed the three following aspects,

that in our experience generalize to several similar

scenarios and thus constitute another contribution of

this work: authorized subsets, integrity check and

scheme efﬁciency. In the following, we study these

features in the context of our use case.

Authorized Subsets. First we need to identify

which secret sharing category (according to our cat-

egorization in section 2) can address our secret recov-

ery scenario. Trusted parties need to deﬁne the recov-

ery policy by answering: ”Which parties are needed

to recover the secret and under which conditions?”.

We conducted a set of interviews at Brainloop with

the operation and security teams, along with man-

agers, to answer this question. It turned out that a

subgroup of a certain size of trusted parties should be

able to recover the secret. Similarly, the main concern

after preventing a collusion attack is to cope with fail-

ures and disasters such as share loss. If one party is

not available or has lost her share, still an authentic set

of the players can recover the secret. Subsequently,

threshold schemes such as Shamir or Schoenmakers

seem to be appropriate in this case. On the other

hand, deﬁning a complex set of users like in Benaloh-

Leichter was not a desired functionality.

Share’s Integrity Check. Some schemes lack

veriﬁability of the shares’ integrity, thus it is neces-

sary to understand the importance of the veriﬁability

in our use case. Here we question: ”In what cases

does the scheme security beneﬁt from the share’s in-

tegrity checks?”. In Brainloop setting, since the mas-

ter key is available on the server inside the secure

storage, receiving tampered shares for secret recon-

struction will automatically result in rejection of the

shares. Thus, an extra integrity check is unnecessary.

Efﬁciency. Algorithm runtime complexity, usage

frequency and integration costs are also playing an

important role in scheme selection for industrial use

cases. Our goal is to ﬁnd the cheapest integration

cost with the best performance. As a matter of fact,

Shamir’s scheme does not require further infrastruc-

tural supports such as PKI as opposed to Schoenmak-

ers’ scheme. Therefore, it is low cost and easy to in-

tegrate to the ongoing production system.

6 RELATED WORKS

Complexity-theoretical bounds of different secret

sharing schemes are surveyed by (Beimel, 2011).

Also, applications of secret sharing as a primitive has

been explored by many individual researchers for var-

ious sort of problems. (Hadavi et al., 2015) proposes

a policy enforcement mechanism for outsourced data

to untrusted servers using Shamir secret sharing and

Chinese remainder theorem. Their protocol enforces

access policies by spreading the over multiple servers.

More on the multiparty computation ground, (Bog-

danov et al., 2008) developed a secure multiparty

computation framework based on additive secret shar-

ing scheme. In addition to that, they actually pro-

totyped a secure solution for Estonia tax fraud de-

tection process based on their framework (Bogdanov

et al., 2015). In our case study we are given a situ-

ation that can leverage secret sharing security guar-

SECRYPT 2016 - International Conference on Security and Cryptography

450

antees. Since a secret is used to authorize security-

related operations, we use secret sharing as a medium

to grant actions when dealing with critical operations

on a server.

7 CONCLUSION

Secret sharing can be used to solve challenging key-

management issues (DSouza et al., 2011). However,

due to a lack of public implementations and unclear

functionality, efﬁciency and security trade-offs, it has

not found its way into industrial use cases.

Based on the example of Brainloop

∗

we showed a

concrete and generic architecture, using secret shar-

ing, which securely perform critical operations as

well as secret key redundancy.

We highlighted the different criteria that need to

be taken into account for the secret sharing algo-

rithm selection. To help selection we also carried

out benchmarks over an open source .NET imple-

mentation (Ahmadvand, 2015) of three of the most

prominent secret sharing schemes from the literature:

Shamir, Benaloh-Leichter and Schoenmakers.

As part of future work, we would consider com-

bining both custom access structure (non-threshold)

and share integrity veriﬁcation. For this purpose,

Schoenmakers scheme can be modiﬁed to handle gen-

eralized access structures. Besides, it would be inter-

esting to measure Schoenmakers’ performance when

elliptic curves are used.

REFERENCES

Ahmadvand, M. (2015). Secret sharing library. Available at

https://github.com/mr-ma/secret-sharing.

Beimel, A. (2011). Secret-sharing schemes: a survey. In

Coding and cryptology, pages 11–46. Springer.

Benaloh, J. and Leichter, J. (1990). Generalized secret shar-

ing and monotone functions. In Proceedings on Ad-

vances in cryptology, pages 27–35. Springer-Verlag

New York, Inc.

Blakley, G. R. et al. (1979). Safeguarding cryptographic

keys. In Proceedings of the national computer confer-

ence, volume 48, pages 313–317.

Bogdanov, D., J

oemets, M., Siim, S., and Vaht, M. (2015).

How the estonian tax and customs board evaluated a

tax fraud detection system based on secure multi-party

computation. In Financial Cryptography and Data Se-

curity, pages 227–234. Springer.

∗

As a consequence of our study, the improved agreement

protocol has been integrated into the Brainloop system.

Bogdanov, D., Laur, S., and Willemson, J. (2008). Share-

mind: A framework for fast privacy-preserving com-

putations. In Computer Security-ESORICS 2008,

pages 192–206. Springer.

BSI (2015). Algorithms for qualiﬁed electronic signatures.

Available at http://www.bundesnetzagentur.de/.

Chou, T.-S. (2013). Security threats on cloud computing

vulnerabilities. International Journal of Computer

Science & Information Technology, 5(3):79–88.

DSouza, R., Jao, D., Mironov, I., and Pandey, O.

(2011). Publicly veriﬁable secret sharing for cloud-

based key management. In Progress in Cryptology–

INDOCRYPT 2011, pages 290–309. Springer.

Feldman, P. (1987). A practical scheme for non-interactive

veriﬁable secret sharing. In Foundations of Computer

Science, 1987., 28th Annual Symposium on, pages

427–438. IEEE.

Garﬁnkel, T., Pfaff, B., Chow, J., Rosenblum, M., and

Boneh, D. (2003). Terra: A virtual machine-based

platform for trusted computing. In ACM SIGOPS Op-

erating Systems Review, pages 193–206. ACM.

Hadavi, M. A., Jalili, R., and Karimi, L. (2015). Ac-

cess control aware data retrieval for secret sharing

based database outsourcing. Distributed and Parallel

Databases, pages 1–30.

Haldar, V., Chandra, D., and Franz, M. (2004). Semantic re-

mote attestation: a virtual machine directed approach

to trusted computing. In USENIX Virtual Machine Re-

search and Technology Symposium, volume 2004.

Neisse, R., Holling, D., and Pretschner, A. (2011). Imple-

menting trust in cloud infrastructures. In Proceedings

of the 2011 11th IEEE/ACM International Symposium

on Cluster, Cloud and Grid Computing, pages 524–

533. IEEE Computer Society.

Rocha, F. and Correia, M. (2011). Lucy in the sky without

diamonds: Stealing conﬁdential data in the cloud. In

Dependable Systems and Networks Workshops (DSN-

W), 2011 IEEE/IFIP 41st International Conference

on, pages 129–134. IEEE.

Rocha, F., Gross, T., and Van Moorsel, A. (2013). Defense-

in-depth against malicious insiders in the cloud. In

Cloud Engineering (IC2E), 2013 IEEE International

Conference on, pages 88–97. IEEE.

Santos, N., Gummadi, K. P., and Rodrigues, R. (2009). To-

wards trusted cloud computing. In Proceedings of the

2009 conference on Hot topics in cloud computing,

pages 3–3. San Diego, California.

Schoenmakers, B. (1999). A simple publicly veriﬁable se-

cret sharing scheme and its application to electronic

voting. In Advances in CryptologyCRYPTO99, pages

148–164. Springer.

Shamir, A. (1979). How to share a secret. Communications

of the ACM, 22(11):612–613.

Shoup, V. (2016). Number theory library.

http://www.shoup.net/ntl/.

Enhancing Operation Security using Secret Sharing

451