
Computations on Private Sets and their Application to Biometric based
Authentication Systems
∗
Wojciech Wodo, Lucjan Hanzlik and Kamil Kluczniak
Department of Computer Science, Wroclaw University of Technology, Wybrzeze Wyspianskiego 27, Wroclaw, Poland
Keywords:
Biometric Template, Cancelable Biometrics, Intersection Cardinality, Private Sets, Security, Impersonation,
Whitelist, Anonimity, Bloom Filter.
Abstract:
In this paper we investigate the concept of cancelable biometrics and propose a new scheme for user autho-
risation providing anonymity based on privacy-preserving computations on sets. We define a problem called
(t,n)-Threshold Subset Problem and apply it to a biometric-based security system. Our solution implements
biometric template protection based on one-way transformations and Bloom filters. Users authentication data
is stored in form of a whitelist and the authorisation process is based on a zero-knowledge proof approach.
Using oblivious polynomial evaluation (OPE) a legitimate user is able to recreate a secret polynomial and
answer the challenge send by a verifier. We assume that biometric data can be acquired and digitized to the
form of a vector representation.
1 INTRODUCTION
Security systems have been developing rapidly these
days, we process and transfer more and more data
and we would like to protect this data in a proper
way. Simultaneously we would like to keep our pri-
vacy and anonymity on a high level. Unlike common
solutions based on cryptographic protocols, biome-
try offers a new way of securing data. It gives us
unusual binding between data and it’s owner, based
on unique features of the individual (physical or be-
havioural). These features are highly distinguishable
and constant over time. That uniqueness raises a se-
curity threat - attempt of stealing the biometric data
and impersonation trials. This is a reason why bio-
metric data should be treated with great responsibility
and highly protected. In simple words biometry itself
may be viewed as a key.
Usage of biometry in security systems allows to
replace passwords or physical keys. In this scenario
it is impossible to lose or forget your credential, it is
very ergonomic and a promising use case. Unfortu-
nately, depending on chosen biometrics, system accu-
racy may vary significantly. This raises issues of im-
personation and forgery. This is the reason why biom-
etry should be very carefully tailored to the system re-
quirements and desired level of trust. Some biometric
∗
This research was supported by National Research
Center grant PRELUDIUM no 2014/15/N/ST6/04375
features are hard to enrol or need complex equipment
or even could cause feeling of discomfort for users
during the verification process. Every biometric sys-
tem has to be equipped in alternative way of operat-
ing, because of an exclusion factor. There is always
a fraction of users, which is unable to use particular
biometry (e.g. 4% of population does not have fin-
gerprints for various reasons (Prabhakar, 2001)). All
concerns mentioned above should be taken into con-
sideration while designing a system based on biome-
try.
Motivation and Contribution
Most popular systems opt to store the user’s biomet-
ric data on some data carrier, instead of keeping a
database. Such a database of biometric features is
an attractive target for identity thefts and other cy-
ber criminals. What is more, in some cases such a
database is even prohibited by law. To solve some of
the problems, different methods are applied to create
so called biometric templates from which the original
raw biometric data cannot be reconstructed. However,
in such a case a similar problem remains, this tem-
plates can be used to impersonate a user in a different
system.
This problem is solved by the popular match-on-
card technology (Bringer et al., 2009). User’s receive
a smart card that store the biometric features of the
card owner and which can be used to verify if a given
input matches the data stored on the card. This tech-
452
Wodo, W., Hanzlik, L. and Kluczniak, K.
Computations on Private Sets and their Application to Biometric based Authentication Systems.
DOI: 10.5220/0005992204520457
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 452-457
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

nology heavily relies on the hardware security of the
smart card, as it responses to the verifying system
whether the biometric data matches.
It is easy to see that it is not easy to design a fully
secure biometric system. On one hand, keeping a
database of users biometric features creates possible
security and legal risks. On the other hand, relying
on the user’s device may lead to attacks where a user
accesses the system without valid credentials.
In this paper we try to solve the problem from
a different angle. We propose a biometric system
in which the server (or verifier) stores some sort of
whitelist and checks whether the biometric data pro-
vided by the user is on the whitelist.
Instead of storing raw data or templates, the
whitelist stored by the server is in form of a bloom fil-
ter. This not only makes it impossible to reconstruct
the biometric data but mixes data of several users into
one data structure. Thus, this whitelist works as kind
of anonymity set.
In order to proof that the data provided by the user
are on the whitelist, the user and the server engage a
two-party protocol. We first present a general version
of a problem solved by this protocol. Let’s introduce
a problem called (t, n)-Threshold Subset Problem, in
which one party with a private set S
P
must convince
an other party with private set S
V
, that there exists
a subset U
P
⊆ S
P
, such that U
P
⊆ S
V
and t ≤ |U
P
|.
Then, we present how to use a protocol that solves this
problem to create a whitelist based biometric system.
The work presented in this paper is a work-in-
progress. Thus, most of the results are presented in
an informal way, e.g. description of problem, security
analysis. A more formal approach to the problem will
be presented in the full paper.
Related Work
Privacy-preserving set operations have been exten-
sively studied. One of the most popular problems is
the set intersection problem (Cristofaro and Tsudik,
2009) and its cardinality version (Cristofaro et al.,
2011). In those problems, user want to compute the
intersection (or respectively its cardinality) based on
private sets. The main property is that beside the so-
lution to the problem, no other information should
leak. In (Kissner and Song, 2005) the authors pro-
pose a generic solution to several set operations. In
particular, they propose a solution to the subset proto-
col, which is closely related to the problem considered
in this paper. The above mentioned approaches have
their application in biometric based security system as
well, in (Socek et al., 2007) authors proposed a new
scheme for securing biometric templates based on set
intersection similarity measure approach. The author
of (Sarier, 2015) integrate the private set intersection
cardinality protocol and a suitable helper data system
for biometrics in minutia-based security system.
2 (T,N)-THRESHOLD SUBSET
PROBLEM
In this paper we focus on a new problem, which we
call the (t,n)-Threshold Subset Problem. The prob-
lem can be stated as follows. Two users, one called
Prover and one called Verifier, posses private sets of
values S
P
and S
V
, where the Prover’s set has at most
n elements i.e. |S
P
| ≤ n. Users try to answer the ques-
tion whether there exists a subset U
P
⊆ S
P
, such that
U
P
⊆ S
V
and t ≤ |U
P
|. In particular, the Prover tries to
convince the Verifier that it knows such a subset U
P
.
Due to space reasons we do not include a formal
syntax that is common for cryptographic schemes but
use a rather informal description of the protocol per-
formed by users. The more formal version will be
given in the full paper.
We begin by recalling some facts about bloom fil-
ters and oblivious polynomial evaluation schemes.
2.1 Bloom Filter
Bloom filters are space-efficient probabilistic data
structures that can be used to test whether an element
is a member of a set.
Empty filters are just bit arrays of m zeros (where
m is a parameter). To add an element to the set, one
feeds it to each of k hash functions (that map elements
to one of the m array positions) and sets the bits at all
these positions to 1. On the other hand, to verify if an
element is in the set, one feeds it to each of the k hash
functions and if any of the bits at these positions is 0,
then the element is not in the set. On the other hand,
if all positions are set to 1, then it is highly proba-
ble (depending on parameters (k,m) and the number
of elements inserted) that the element is in the set.
For more information we refer the reader to (Bloom,
1970).
2.2 Oblivious Polynomial Evaluation
Oblivious polynomial evaluation (OPE) is a two party
protocol initially introduced by Naor and Pinkas
(Naor and Pinkas, 1999). The protocol involves a
sender, whose secret input is a polynomial P with co-
efficients in a large field F
q
, and a receiver, whose
secret input is a value α. Informally, from an OPE
protocol we require that at the end the receiver learns
P(α) and the sender learns nothing. We leave a more
formal description to the full paper. We will use
Computations on Private Sets and their Application to Biometric based Authentication Systems
453

S
OPE
(P) and R
OPE
(α) to denote the execution of re-
spectively the sender and receiver part of the protocol.
2.3 Lagrange Polynomial Interpolation
In this paper we will use the well-known Lagrange
polynomial interpolation. We will use the procedure
P(x) = Lag(M) to denote the procedure that computes
the interpolation polynomial P of points in set M, i.e.
∀
(x,y)∈M
P(x) = y.
Let M = {(x
0
,y
0
),.. .,(x
n
,y
n
)} be the set of n + 1
points on the polynomial P of degree n, where no two
x
i
are the same. The procedure Lag(M) outputs the
polynomial P(x) =
∑
n
i=0
y
i
l
i
(x), where we define
l
i
(x) =
∏
j∈{0,...,n}, j6=i
x − x
j
x
i
− x
j
.
Notice that l
i
(x
j
) = 1 if i = j and l
i
(x
j
) = 0 for all j ∈
{0,.. .,n}, j 6= i. What is more, there exists only one
polynomial P of degree n for which ∀
i∈{0,...,n}
P(x
i
) =
y
i
.
2.4 Efficient Solution for the Problem
We now describe our solution to the Threshold Sub-
set Problem. Let S
P
denote the set of elements of
the Prover and S
V
the set of elements of the Verifier.
Moreover, let (t, n) denote the thresholds defined in
the problem and λ a security parameter. Now both
parties perform the following steps:
1. the Verifier chooses a random value k ←
$
{|S
V
|,.. .,2 ·|S
V
|}, computes ` = f (t,k,λ) (where
f is some function that we define in the security
analysis), chooses a large prime ` < q and sends k
and q to the Prover,
2. the Prover computes the parameter ` = f (t,k, λ), ,
3. each party uses its set S
i
to create a (1,`) bloom
filter B
i
, where by o
i
we will denote the number
of 1’s in B
i
, for i ∈ {P,V },
4. the Verifier chooses a random challenge c ←
$
F
q
and chooses a random polynomial P of degree t −
1, such that P(0) = c,
5. the Verifier chooses a random polynomial W, such
that W (x) = P(x) for all x, where the x-th bit in fil-
ter B
V
is set and W (x) ←
$
F
q
for some other points
x,
6. both parties perform n-times the OPE protocol,
where the Verifier executes the S
OPE
(W ) algo-
rithm and the Prover executes the R
OPE
(α) algo-
rithm for α = j, where the j-th bit is set in B
P
,
7. the Prover reconstructs polynomial P and sends
c
0
= P(0) to the Verifier,
8. the Verifier accepts if c
0
= c.
Details of our protocol are depicted in Figure 1.
Remark. The above description is generic and al-
lows to use sets of different type. However, for some
applications it may be more efficient for the Verifier
to compute the Bloom filter B
V
and parameters q,k,`
once. Of course, this only concerns systems in which
we add data to the set, as one cannot delete elements
from a Bloom filter.
2.5 Security Analysis
Here we present an informal security analysis of our
solution. First we show that if t < |S
V
|, then the Ver-
ifier cannot distinguish which subset of S
V
was used
by the Prover. Secondly we show that without know-
ing t elements of S
V
it is hard to compute c
0
, such that
the Verifier accepts.
Privacy of Prover’s Subset. We first note that if
t = |S
V
|, then there exists only one subset of S
V
of
size t. In such a case the Verifier knows that S
P
= S
V
.
Thus, we only consider cases where t < |S
V
|. We will
show that an honest-but-curious Verifier learns no in-
formation about the Prover’s subset U
P
.
To see this, first notice that the Verifier encodes
the challenge c into polynomial P. This polynomial
is then encoded into polynomial W . In order to re-
construct P, the Prover must evaluate W at points for
which B
V
is set, i.e. know an element of S
V
. However,
since the Prover and the Verifier use oblivious poly-
nomial evaluation of W , the Verifier does not know
which elements of S
V
are known to the Prover. This
concludes this informal analysis.
Verification of Prover’s Knowledge. We will now
compute the probability that the Prover computes a
value c
0
that will be accepted by the Verifier. First no-
tice that the fraction of ones in the bloom filter is at
most
|S
V
|
`
. Thus, the probability that the Prover ran-
domly guesses t positions with the bit set in B
V
is at
most
|S
V
|
`
t
. In order to minimize the probability of
cheating we define function f as follows:
f (t,k,λ) =
t
p
k
t
· 2
λ
.
It follows that for such a function f the probability
|S
V
|
`
t
=
|S
V
|
t
k
t
· 2
λ
≤
k
t
k
t
· 2
λ
=
1
2
λ
,
depends on the security parameter λ.
SECRYPT 2016 - International Conference on Security and Cryptography
454

Prover: Verifier:
private set S
P
private set S
V
threshold (t,n) threshold (t,n)
security parameter λ security parameter λ
• choose k ←
$
{|S
V
|,.. .,2 · |S
V
|}
• compute ` = f (t,k, λ)
• choose large prime q, such that ` < q
k,q
←−
• compute ` = f (t,k, λ)
• generate (1,`) Bloom filter B
P
from set S
P
• generate (1,`) Bloom filter B
V
from set S
V
• choose c,x
1
,.. .,x
t−1
,y
1
,.. .,y
t−1
←
$
F
q
• P(x) ← Lag((0,c),(x
1
,y
1
),.. .,(x
t−1
,y
t−1
))
• denote by x
P
1
,.. .,x
P
|S
P
|
the values for which filter B
P
is set • denote by x
V
1
,.. .,x
V
|S
V
|
the values for which filter B
V
is set
• choose x
V
|s
V
|+1
,.. .,x
V
2·|S
V
|
,y
V
|S
V
|+1
,.. .,y
V
2·|S
V
|
←
$
F
q
• W (x) ← Lag((x
V
1
,P(x
V
1
)),.. .,(x
V
|S
V
|
,P(x
V
|S
V
|
)),.. .
(x
V
|S
V
|+1
,y
V
|S
V
|+1
),.. .,(x
V
2·|S
V
|
,y
V
2·|S
V
|
))
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . n-times OPE Protocol . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
• for i ∈ {1,.. .,n} execute R
OPE
(x
P
i
) receiving y
P
i
• execute S
OPE
(W ) n times
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
• P
0
(x) ← Lag((x
P
1
,y
P
1
),.. .,(x
P
t
,y
P
t
))
• c
0
= P
0
(0)
c
0
−→
• abort if c
0
6= c
Figure 1: Description of Our Protocol.
2.6 Efficiency
We will now discuss the efficiency of our solution. In
particular, we will focus on communication complex-
ity. We also give a proposal on how to choose the sys-
tem parameters for several security levels λ and upper
bound on size of S
V
, see Figure 2.
It is easy to see that the communication complex-
ity of our protocol is dominated by the OPE protocol
executed n times. However, in our protocol we use
OPE in a black box way and the actual complexity
depends on the used OPE instantiation. Note that the
values k,q, c
0
are all smaller than or equal to q. Thus,
the overall communicational complexity of our proto-
col is n times the cost of using OPE and 3 times the
size of q.
3 BIOMETRIC SYSTEM
3.1 Related Work
Biometric systems have been studied extensively. The
authors of (Labati et al., 2012) give a broad overview
of existing biometric techniques and systems. The au-
thors of (Barni et al., 2010a) propose a biometric sys-
tem based on homomorphic encryption. This scenario
is a bit different that the one compared in this paper,
i.e. in our system the server knows whether the user’s
biometric template is in the server’s database. In
(Barni et al., 2010b) the author’s describe the imple-
mentation of a homomorphic encryption based bio-
metric system.
3.2 Biometric Templates
Biometric features are unique for individuals and are
mutually correlated with them, so that it is almost im-
possible to change them over the time. That is the
reason they have to be treated with great carefulness
and protected in a proper way. The most important is-
sue, when working with biometrics is that, biometric
data should not be stored and exposed anywhere.
The concept of cancelable biometrics (Lee and
Kim, 2010) is essential in biometric systems. It de-
fines that one can generate multiple biometric iden-
tities from one acquired biometric data. In practice
it means that if one user identity is compromised, it
should be withdrawn and, based on the same biomet-
ric data, one can generate a new one. The whole pro-
cedure needs some extra external data e.g. password
or PIN.
A biometric identity is generated from raw bio-
metric data, which are digitalized and transformed in
a one way manner in order to protect them against re-
trieving the original data. We call such a biometric
identity, biometric template.
Computations on Private Sets and their Application to Biometric based Authentication Systems
455
Security Level Upper bound on |S
V
| - k
∗
Size of B
V
(in bits) - ` Size of q (in bits)
80 2
20
2
20+80/t
1248
80 2
30
2
30+80/t
1248
128 2
20
2
20+128/t
3248
128 2
30
2
30+128/t
3248
∗
2
20
∼ 1 million and 2
30
∼ 1 billion
Figure 2: System Parameters for Our (t, n) Protocol.
Figure 3: General scheme of our solution implemented in biometric security system.
In our considerations we assume that biometric
data of the user can be represented by a vector. It
is a reasonable approach and, according to the paper
(Sutcu et al., 2007), it is possible to use SVD (Sin-
gular Value Decomposition) for storing face features
or quantized minutia amount vectors for fingerprints.
Such a representation of the biometric data is usable
in the context of generic solutions. In fact, our sys-
tem works with any type of biometrics that can be
represented as a vector of values. In particular, iris
templates represented as binary strings.
Following the authors (Sutcu et al., 2007) there
are three main types of protection for biometric tem-
plates:
• robust hash functions, where small changes in a
biometric sample would yield the same hash value
(special property)
• similarity preserving and hard to invert transfor-
mations, where similarity of biometric samples
would be preserved through the transformation
(possibility of comparison)
• security sketch - a cryptographic primitive, such
that given a noisy biometric sample, the original
one can be recovered with help of some additional
information (i.e. sketch), which makes it possible
to use biometric in the same way as passwords
3.3 Embedding Biometrics into the
Threshold Decisional Subsection
Problem
In the previous part of the paper we presented a proto-
col for solving (t,n)-Threshold Subset Problem. We
would like to apply our approach to a biometric-based
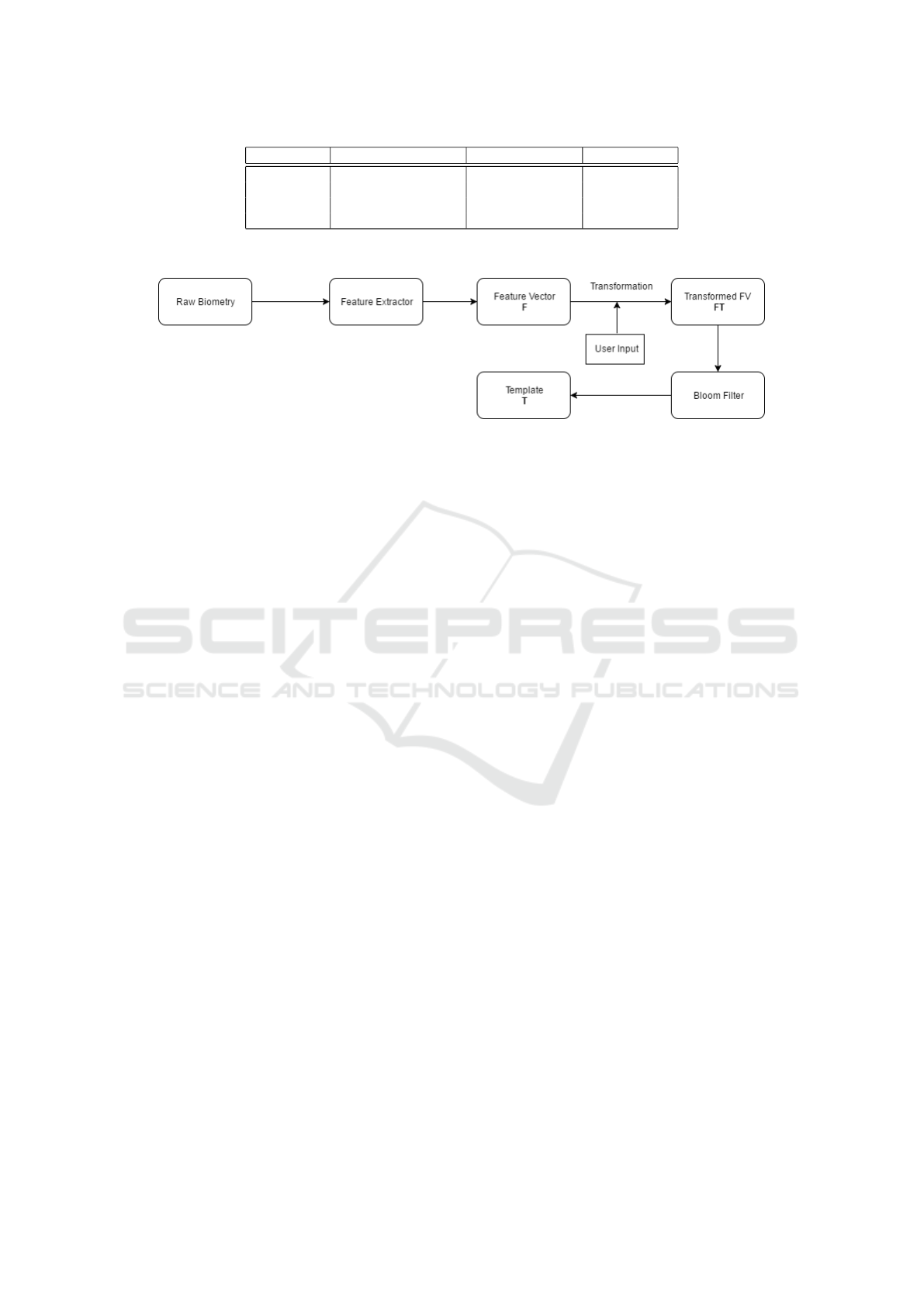
security system. At Figure 3 we visualize a diagram
of the data flow of the system.
The system consists of two phases - enrolment
and verification, both processes are similar to each
other. The only difference is that the user template
created during the interaction is saved on the verifier’s
whitelist (in the first case) or compared against stored
records (in the latter case). Below, some properties of
the system are presented and discussed.
We assume that for any kind of chosen biometric
data, there is a Feature Extractor such that we obtain
a Feature Vector F = (e
1
,e
2
,.. .,e
n
). In some cases
one F may be similar to each other (e.g. in case of
fingerprints - the number of minutia is limited). Thus,
we use a transformation function to obfuscate the vec-
tor, simultaneously we preserve the discriminativness
of the sample (cancelability property). We cannot use
a randomization matrix, because one error in the vec-
tor influences the final result. Thus, we have to ob-
fuscate each value from the vector independently by
using multiplication by a randomization scalar.
The process of conversion analog data to digital
form is liable for noises and errors of quantization.
Thus, the result of the Feature Extractor may be
loaded with discrepancies in comparison to the pat-
tern vector. User Input: H(PIN
U
i
) - hash value from
user PIN, used as a seed for pseudorandom number
generator in the Transformation phase for obfusca-
tion. In effect we obtained a Transformed Feature
Vector FT . This vector FT is used as the input to the
protocol, i.e. values from FT are input to the bloom
filter, creating a so called the temporary user template
T . This template has the cancelability property in
terms of biometric identity. In the next step (depend-
ing on phase: enrolment or verification), we save T
on the verifier whitelist (by simply adding bloom fil-
ters) or run the authorization procedure by executing
the (t,n)-Threshold Subset Protocol.
SECRYPT 2016 - International Conference on Security and Cryptography
456

4 CONCLUSIONS
In this paper we informally defined a new two party
computation on private sets. We also proposed a
fairly efficient work-in-progress protocol that solves
it. Moreover, we describe how to apply the protocol
to biometric based authentication systems and solve
some existing problems, e.g. reliance on the hard-
ware used by the system user. Future work involves a
formal model of the (t, n)-Threshold Subset Problem,
sound security proofs in this model and test imple-
mentation of the solution.
REFERENCES
Barni, M., Bianchi, T., Catalano, D., Di Raimondo, M.,
Donida Labati, R., Failla, P., Fiore, D., Lazzeretti, R.,
Piuri, V., Scotti, F., and Piva, A. (2010a). Privacy-
preserving Fingercode Authentication. In Proceed-
ings of the 12th ACM Workshop on Multimedia and
Security, MM&Sec ’10, pages 231–240, New
York, NY, USA. ACM.
Barni, M., Bianchi, T., Catalano, D., Raimondo, M. D., La-
bati, R. D., Failla, P., Fiore, D., Lazzeretti, R., Pi-
uri, V., Piva, A., and Scotti, F. (2010b). A privacy-
compliant fingerprint recognition system based on ho-
momorphic encryption and Fingercode templates. In
Biometrics: Theory Applications and Systems (BTAS),
2010 Fourth IEEE International Conference on, pages
1–7.
Bloom, B. H. (1970). Space/time trade-offs in hash cod-
ing with allowable errors. Commun. ACM, 13(7):422–
426.
Bringer, J., Chabanne, H., Kevenaar, T. A. M., and Kin-
darji, B. (2009). Extending Match-on-card to Local
Biometric Identification. In Proceedings of the 2009
Joint COST 2101 and 2102 International Conference
on Biometric ID Management and Multimodal Com-
munication, BioID MultiComm’09, pages 178–186,
Berlin, Heidelberg. Springer-Verlag.
Cristofaro, E. D., Gasti, P., and Tsudik, G. (2011). Fast
and private computation of cardinality of set intersec-
tion and union. Cryptology ePrint Archive, Report
2011/141. http://eprint.iacr.org/.
Cristofaro, E. D. and Tsudik, G. (2009). Practical private set
intersection protocols with linear computational and
bandwidth complexity. Cryptology ePrint Archive,
Report 2009/491. http://eprint.iacr.org/.
Kissner, L. and Song, D. (2005). Advances in Cryptology
– CRYPTO 2005: 25th Annual International Cryp-
tology Conference, Santa Barbara, California, USA,
August 14-18, 2005. Proceedings, chapter Privacy-
Preserving Set Operations, pages 241–257. Springer
Berlin Heidelberg, Berlin, Heidelberg.
Labati, R. D., Piuri, V., and Scotti, F. (2012). E-Business
and Telecommunications: International Joint Confer-
ence, ICETE 2011, Seville, Spain, July 18-21, 2011,
Revised Selected Papers, chapter Biometric Privacy
Protection: Guidelines and Technologies, pages 3–19.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Lee, C. and Kim, J. (2010). Cancelable fingerprint tem-
plates using minutiae-based bit-strings. J. Network
and Computer Applications, 33(3):236–246.
Naor, M. and Pinkas, B. (1999). Oblivious transfer and
polynomial evaluation. In Proceedings of the Thirty-
first Annual ACM Symposium on Theory of Comput-
ing, STOC ’99, pages 245–254, New York, NY, USA.
ACM.
Prabhakar, S. (2001). Fingerprint Classification and Match-
ing Using a Filterbank. PhD thesis, Michigan State
University, Computer Science & Engineering. 259
pages.
Sarier, N. D. (2015). Information Security Theory and Prac-
tice: 9th IFIP WG 11.2 International Conference,
WISTP 2015, Heraklion, Crete, Greece, August 24-
25, 2015. Proceedings, chapter Private Minutia-Based
Fingerprint Matching, pages 52–67. Springer Interna-
tional Publishing, Cham.
Socek, D., Culibrk, D., and Bozovic, V. (2007). Practical
secure biometrics using set intersection as a similar-
ity measure. In SECRYPT 2007, Proceedings of the
International Conference on Security and Cryptogra-
phy, Barcelona, Spain, July 28-13, 2007, pages 25–32.
Sutcu, Y., Li, Q., and Memon, N. (2007). Secure biomet-
ric templates from fingerprint-face features. In Com-
puter Vision and Pattern Recognition, 2007. CVPR
’07. IEEE Conference on, pages 1–6.
Computations on Private Sets and their Application to Biometric based Authentication Systems
457
