Design and Numerical Characterization of a First Stage of a High
Capacity Multistage Centrifugal Pump
Nicolas La Roche-Carrier, Guyh Dituba Ngoma and Walid Ghie
University of Quebec in Abitibi-Témiscamingue, School of Engineering’s Department,
445, Boulevard de l’Université Rouyn-Noranda, Quebec, J9X 5E4, Canada
Keywords: Multistage Centrifugal Pump, Impeller, Diffuser, ANSYS-CFX, Modeling and Simulation.
Abstract: In this paper, a numerical characterization of a first stage of a high capacity multistage centrifugal pump was
performed for very high flow rates. A particular emphasis was placed on the diffuser design procedure. For
this purpose, the equations of the continuity and the Navier-Stokes accounting for the boundary conditions
were used by mean of ANSYS-CFX code to describe and to simulate the complex liquid flow in the multistage
centrifugal pump. In order to identify the key parameters of the diffuser that can improve the pump stage
performances, the effects of the inlet height of the diffuser vanes, the number of the diffuser vanes, the number
of the diffuser return vanes, and the gap between the impeller and the diffuser on the pump stage head, brake
horsepower and efficiency were analyzed. The validation of the developed model of a first pump stage was
done comparing results of numerical simulations and experimental results obtained from a pump
manufacturer.
1 INTRODUCTION
Multistage centrifugal pumps are widely used in
industrial and mining enterprises. They are composed
of several stages. These last are constituted of an
impeller, a diffuser and a casing. The diffuser is
generally provided of the return vanes except the
diffuser of the last pump stage. The impeller and the
diffuser are the most important components of a
multistage centrifugal pump. The performances of
multistage pumps are depended to both components.
The impeller must be designed to obtain a high head
with an optimum efficiency, while the diffuser is
designed to maximizer the pressure gain in the
diffuser vanes and to minimize the pressure drop in
the return vanes. Therefore, the relevant parameters
of the impeller and the diffuser including the return
vane must be determined with high precision in the
planning, the design and the optimization phases in
design and off-design conditions. This is to achieve
better multistage centrifugal pump performances
accounting for the three-dimensional and turbulent
liquid flow in multistage centrifugal pumps. Many
experimental and numerical studies have been
conducted on multistage centrifugal pumps (Qihua Z.
et al, 2013; La Roche-Carrier N. et al., 2013; Qihua
Z. et al, 2012, and Miyano M. et al., 2008).Thorough
analysis of previous works shows that there are
several diffuser types. The design procedure of
diffusers are not well detailed, while the design
procedure for the impeller is well documented. The
diffuser design depends on the experience of the
designer and the information available. Moreover,
analysis of previous studies clearly revealed that the
research results obtained are specific to the design
parameters and configuration of components in
multistage centrifugal pumps, and thus cannot always
be generalized. Therefore, in the present work, the
goal is to enhance the design and the performances of
multistage centrifugal pumps using rigorously the
design procedure described in (Gülich, J. F., 2010) to
model the diffuser including return vanes, as shown
in Fig. 1. This diffuser must be allowed a higher
pressure gain to the level of the diffuser vanes and a
lower pressure lost in diffuser return vanes. To
identify adequately diffuser parameters that could be
enhance the performances of a first stage of a
multistage centrifugal pump, a numerical
investigation was conducted using ANSYS-CFX
code (Ansys inc., 2015). This was done considering
the three-dimensional turbulent liquid flow through a
first stage of a multistage centrifugal pump account
for various flow conditions and diffuser key
Roche-Carrier, N., Ngoma, G. and Ghie, W.
Design and Numerical Characterization of a First Stage of a High Capacity Multistage Centrifugal Pump.
DOI: 10.5220/0005995102830290
In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 283-290
ISBN: 978-989-758-199-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
283

parameters including the inlet height of the diffuser
vanes, the number of the diffuser vanes, the number
of the diffuser return vanes, and the gap between the
impeller and the diffuser. Upon applying the
equations of the continuity and the Navier-Stokes, the
liquid flow velocity and the liquid pressure
distributions in a stage of a multistage centrifugal
pump were determined, while accounting for
boundary conditions and considering a constant
rotating speed for the impeller. The pump stage
performances were represented as a function of the
flow rate in each case study.
Figure 1: Modeled first stage of a multistage centrifugal
pump.
2 GOVERNING EQUATIONS
The used fluid domains of the first stage obtained
from Fig. 1 for the governing equations for liquid
flow are shown in Fig. 2.
a) Impeller b) Diffuser
c) Stage: combined impeller and diffuser
Figure 2: Fluid domains of the first pump stage.
The following assumptions were made to describe
the governing equations for liquid flow: (i) a steady
state, three-dimensional and turbulence flow using
the k-ε model was assumed; (ii) it was an
incompressible liquid; (iii) it was a Newtonian liquid;
and (iv) the liquid’s thermophysical properties were
constant with the temperature.
To account for these assumptions, the theoretical
analysis of the liquid flow through the first pump
stage was based on the equations of the continuity and
the Navier-Stokes (Ansys inc., 2015). For the three-
dimensional liquid flow through these components of
a first pump stage as shown in Fig. 2, the equations of
the continuity are expressed by:
0V.
vel
=∇

(1)
where
()()()()
z,y,xw,z,y,xv,z,y,xuVV
velvel

=
is the liquid
flow velocity vector.
Using the coordinate system, Eq. 1 can be
rewritten as:
0
z
w
y
v
x
u
=
∂
∂
+
∂
∂
+
∂
∂
(2)
and the equations of the Navier–Stokes are given by:
B))V(V.(
p)VV.(
T
velveleff
velvel
+∇+∇∇μ+
−∇=⊗∇ρ



(3)
where p is the pressure, ρ is the density, μ
eff
is the
effective viscosity accounting for turbulence, ⊗ is a
tensor product and B is the source term. For flows in
an impeller rotating at a constant speed ω, the source
term can be written as follows:
()
(
)
rxxVx2B
vel



ωω+ωρ−=
(4)
where
r

is the location vector,
vel
Vx2


ω
is the
centripetal acceleration and
()
rxx

ωω
is the Coriolis
acceleration.
B is zero for the flow in the stationary components
like the diffuser. Using the coordinate system, Eq. 3
can be rewritten as:
z
2
2
2
2
2
2
eff
y
2
2
2
2
2
2
eff
x
2
2
2
2
2
2
eff
B
z
p
z
w
y
w
x
w
z
w
w
y
w
v
x
w
u
B
y
p
z
v
y
v
x
v
z
v
w
y
v
v
x
v
u
B
x
p
z
u
y
u
x
u
z
u
w
y
u
v
x
u
u
+
∂
∂
−








∂
∂
+
∂
∂
+
∂
∂
μ=








∂
∂
+
∂
∂
+
∂
∂
ρ
+
∂
∂
−








∂
∂
+
∂
∂
+
∂
∂
μ=








∂
∂
+
∂
∂
+
∂
∂
ρ
+
∂
∂
−








∂
∂
+
∂
∂
+
∂
∂
μ=








∂
∂
+
∂
∂
+
∂
∂
ρ
(5)
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
284

where
0B
)u2r(B
)v2r(B
z
zy
2
zy
zx
2
zx
=
ω−ωρ=
ω+ωρ=
(6)
Furthermore, μ
eff
is defined as
teff
μ+μ=μ
, where
μ is the dynamic viscosity and μ
t
is the turbulence
viscosity.
Since the k-ε turbulence model is used in this
work because convergence is better than with other
turbulence models, μ
t
is linked to turbulence kinetic
energy k and dissipation ε.
To solve equations 2 and 5 numerically while
accounting for the boundary conditions and
turbulence model k-ε, the computational fluid
dynamics ANSYS-CFX code, based on the finite
volume method, was used to obtain the liquid flow
velocity and pressure distributions. According to the
boundary conditions, they were formulated as
follows: the static pressure provided was given at the
stage inlet, while the flow rate provided was specified
at the stage outlet. The frozen rotor condition was
used for the impeller-diffuser interface. A no-slip
condition was set for the flow at the wall boundaries.
The performance parameters of the first pump
stage are described as follows:
The pump stage head is given by H = (p
to
– p
ti
) / ρg,
where p
ti
is the total pressure at the pump stage
inlet and p
to
the total pressure at the pump stage outlet.
Furthermore, the hydraulic power of the pump
stage is formulated as P
h
= ρQgH, where Q is the
flow rate.
In addition, the brake horsepower of the pump
stage is given by P
s
= Tω, T is the impeller torque.
From the hydraulic power and the brake
horsepower, the efficiency of the pump stage can be
written as
η = P
h
/ P
s
.
3 DESIGN PROCEDURE OF THE
DIFFUSER
The diffuser including the return vanes were designed
in this work according to the book of Gülich (Gülich,
J. F., 2010) with respect of the design conditions for
first pump stage such as the head, the flow rate and
the rotating speed. Fig. 3 shows the geometrical main
parameters of the considered diffuser.
Figure 3: Design parameters of a diffuser including of
return vanes (Gülich, J. F., 2010).
3.1 Design of the Diffuser Vanes
The inlet height of the diffuser vanes b
3
is calculated
using the following equation:
()
23
b1.3 to1.05b ⋅=
(7)
where b
2
is the impeller outlet height.
The inlet angle of the diffuser vane α
3b
can be
defined by:

3
3b3
±α=α
(8)
where








=α
−
3u
3m
1
3
V
V
tan
, V
u3
is the tangential
component of absolute velocity of diffuser inlet, and
V
m3
is the meridional component of absolute velocity
at diffuser inlet.
V
m3
is given by:
33
3
3m
bD
Q
V
⋅⋅π
τ⋅
=
(9)
where τ
3
is the blade blockage factor (supposed to be
1) and D
3
is the diffuser inlet diameter
Additionally, V
u3
can be expressed as:








⋅=
3
2
2u3u
D
D
VV
(10)
Design and Numerical Characterization of a First Stage of a High Capacity Multistage Centrifugal Pump
285

where V
u2
is the tangential component of absolute
velocity at impeller outlet. It is given by:
2
u1m1
2h
2
u
U
VU
U
gH
V +
η
=
(11)
Moreover, the vane number of the diffuser Z
Le
is
chosen as a function of the blade number of the
impeller Z
b
according to Tab. 1.
Table 1: Number of blades required for the diffuser (Gülich,
J. F., 2010).
Z
b
5 6 7
Z
Le
7 8 12 10 9 10 11 12 (15)
Furthermore, the diffuser inlet wide is formulated as














−














⋅






⋅⋅
⋅








⋅= 1
Z
2
D
Vb
Q
exp
2
D
fa
Le
2
u23
3
3a3
(12)
where f
a3
is the correction factor. Its value is between
1.1 and 1.3.
The diffuser vane inlet thickness can be expressed as:
()
23
D015.0à01.0e ⋅=
(13)
Additionally, the diffuser outlet diameter is given by:
()
(
)
2q4
Dn01.015.1à05.1D ⋅⋅+=
(14)
where n
q
is the specific speed.
The diffuser opening angle ϑ
b
is expressed as:
()








−⋅
=ϑ
−
−
43
34
1
b
L
aa5.0
tan
(15)
where L
3-4
is the length of the vane passage of diffuser
and a
4
is the diffuser outlet wide.
Furthermore, the outlet height of the diffuser vane
is given by:
()()
43b34
Ltanbb
−
⋅ϑ+=
(16)
3.2 Design of the Diffuser Return
Vanes
The number of return vanes Z
R
is chosen with respect
to the relationship
LeR
ZZ ≤
in order to allow the
liquid flow to defect sufficiently in the return vane
passages. The thickness of the diffuser return vanes
e
6
is estimated based on the experience of the
designer. Moreover, the inlet height of the diffuser
return vanes b
5
is supposed to be equal to the outlet
height of the diffuser return vanes b
6
. It can be
formulated as follows:
6m6
65
VD
Q
bb
⋅⋅π
==
(17)
where D
6
is the diameter at the diffuser return vane
outlet, by hypothesis, it is equal to the diameter at the
inlet of the impeller D
1
, and V
m6
is the meridional
velocity at the return vanes outlet. It is given by:
()
1m6m
V9.0à85.0V ⋅=
(18)
Furthermore, the flow angle at the diffuser return
vane inlet is expressed as:








=α
−
5u
5m
1
5
V
V
tan
(19)
Where
55
5
m
bD
Q
V
⋅⋅π
=
(20)








⋅=
5
4
4u5u
D
D
VV
(21)








⋅=
4
3
3u4u
D
D
VV
(22)
In addition, the flow angle at the outlet of the return
vanes α
6b
is formulated as:
°±α=α 5
6
b
6
(23)
where the outflow angle is supposed to be α
6
= 90°.
4 RESULTS AND DISCUSSION
The working liquid water was used for all simulation
runs in this study. It was considered to have the
following reference values at 25 °C: dynamic
viscosity of 8.899 x 10
-4
Pas and density of 997 kg/m³.
The main reference data for the impeller, the diffuser
and diffuser return vanes are given in Tabs. 1-3
respectively.
To identify the parameters of the first stage of a
multistage centrifugal pump that were influenced
their performances, five key parameters were selected
taking account to the diffuser including the return
vanes: a) diffuser inlet height (31,75 mm; 41,98 mm;
50,8 mm), b) number of diffuser Vanes (9, 10,11), c)
number of diffuser return vanes (7, 8, 9), and d) gap
between the impeller and the diffuser (75%; 81.25%;
87.5%; 93.75%; 100% of the impeller outlet
diameter).
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
286

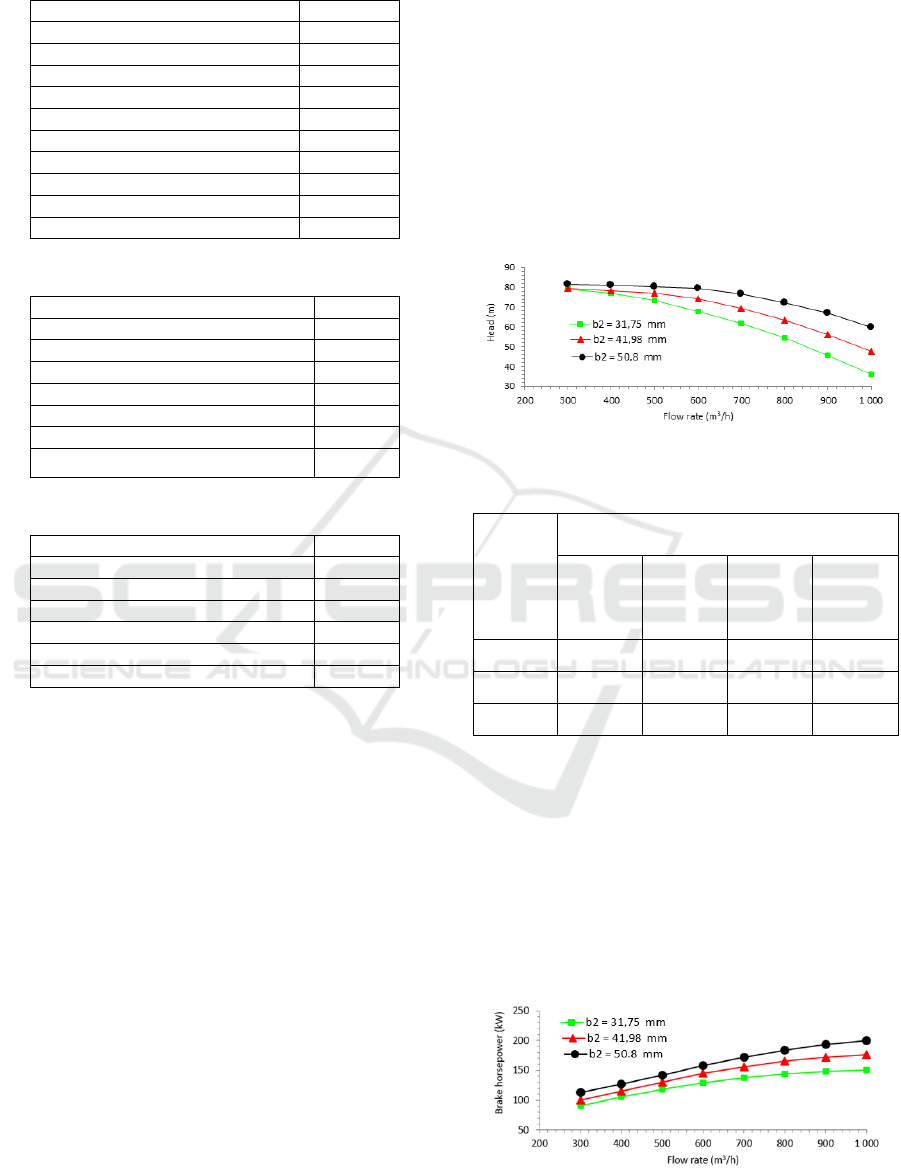
Table 2: Impeller.
Inner diameter [mm] 195
Outer diameter [mm] 406
Number of blades 6
Blade inlet angle [Degree] 18
Blade outlet angle [Degree] 22.5
Blade thickness [mm] 7.94
Blade inlet height [mm] 56
Blade outlet height [mm] 41.98
Number of blades 6
Hub diameter 84.84
Rotating speed [rpm] 1750
Table 3: Diffuser.
Inner diameter [mm] 407.016
Outer diameter [mm] 572.42
Number of vanes 11
Vane inlet angle [Degree] 10
Inlet height of flow passage [mm] 41.98
Outlet height of flow passage [mm] 75.39
Inlet width of flow passage [mm] 18.71
Vane thickness [mm] 6
Table 4: Diffuser return vanes.
Inner diameter [mm] 459
Outer diameter [mm] 194.95
Number of return vanes 8
Inlet angle [Degree] 21
Outlet angle [Degree] 95
Outlet height of flow passage [mm] 14.14
Thickness [mm] 6.35
Mesh-independent solution tests have been carried
out with highest accuracy using different numbers of
mesh elements in each case study.
4.1 Effect of the Inlet Height of
Diffuser Vanes
To investigate the effect that the inlet height of the
diffuser vanes has on the pump stage performances,
the vane inlet height of 31.75 mm, 41.98 mm and 50.8
mm were selected supposing that the outlet height of
the impeller blade was equal to the inlet height of the
diffuser vane, while other parameters were keep
constant. Fig. 4 shows the pump head as a function of
the flow rate with the inlet height of the diffuser vanes
as parameter. From this figure, it is to assess that the
pump head increases with increasing inlet height of
the diffuser vanes. By fixed the flow rate, this can be
explained by the fact that the meridional velocity at
the outlet of the impeller decreases with increasing
outlet height of the impeller blades that is equal to the
inlet height of the diffuser vanes. The liquid pressure
drops in the impeller, and the diffuser decreases with
increasing inlet height of the diffuser vanes. This
leads to the increase of the static pressure in the first
pump stage. Moreover, Tab. 5 indicates the pressure
difference for 700 m³/h in the impeller, the diffuser,
and the diffuser return vane passages. There, it can be
observed that the pressure gain in diffuser increases
with increasing inlet height of the diffuser, and the
pressure loss in the diffuser return vane passages
decreases, while the impeller head rises. The total
pressure difference is highest for a diffuser inlet vane
height of the 50.8 mm.
Figure 4: Pump stage head versus flow rate.
Table 5: Distribution of pressure difference for 700 m³/h.
Inlet
height
of the
diffuser
vane
[mm]
Pressure difference ∆p [Pa]
Impeller Diffuser Diffuser
return
vane
passages
∆p
total
31.75 574 849 98 063 -71 039 601 874
41.98 631 536 119 480 -74 264 676 752
50.80 682 690 136 546 -70 367 748 869
Moreover, the corresponding curves of the pump
stage brake horsepower as a function of the flow rate
are shown in Fig. 5, illustrating that the brake
horsepower increases with increasing inlet height of
the diffuser vanes. This can be explained by the fact
that the brake horsepower increases relative to the
outlet height of the impeller blade and the inlet height
of the diffuser vane due to the requested increase in
pump shaft torque relative to the increased diffuser
vane height and impeller blade height.
Figure 5: Brake horsepower versus flow rate.
Design and Numerical Characterization of a First Stage of a High Capacity Multistage Centrifugal Pump
287

Furthermore, the curves representing pump stage
efficiency as a function of the flow rate is represented
in Fig. 6, where it is observed that the efficiency for
the inlet height of the diffuser vane of 50.8 mm is the
lowest for the flow rate below of 700 m³/h, while it is
the highest for the flow rate above 700 m³/h.
Figure 6: Pump stage efficiency versus flow rate.
4.2 Effect of the Number of the
Diffuser Vanes
Three diffuser vanes numbers (9, 10 and 11) were
selected to analyze it effect on the pump stage head,
brake horsepower, and efficiency, while other
parameters were kept constant. Fig. 7 shows the head
as a function of the flow rate. There, it can be seen
that the head is only slightly affected by the number
of the diffuser vanes.
Figure 7: Pump stage head versus flow rate.
Additionally, the corresponding curves of the brake
horse power as a function of the flow rate is shown in
Fig. 8, there it can be seen the variation in the number
of the diffuser vanes don't nearly affect the brake
horsepower.
Figure 8: Brake horsepower versus flow rate.
Furthermore, Fig. 9 represents the efficiency as a
function of the flow rate. From this figure, it is
observed that the highest efficiency was obtained for
the diffuser vane number of 11 for a flow rate higher
than 480 m³/h.
Figure 9: Pump stage efficiency versus flow rate.
Moreover, Tab. 6 indicates the distribution of the
pressure difference in the impeller, the diffuser, and
the diffuser return vane passages for a flow rate of 700
m³/h. From this table, it is observed that the increase
of the diffuser vane number leads to the decrease of
the impeller head, while the pressure gain in the
diffuser rises and the pressure loss in the diffuser
return vane passages decreases. But, globally, the
head of the pump stage is not nearly influenced by the
variation of the diffuser vane number.
Table 6: Distribution of pressure difference for 700 m³/h.
Pressure difference ∆p [ Pa]
Diffuser
vane
number
Impeller Diffuser Diffuser
return
vane
passages
∆p
total
9 649 275 97 114 -78 487 667 902
10 636 433 108 425 -76 866 667 991
11 631 536 119 480 -74 264 676 752
4.3 Effect of the Number of Diffuser
Return Vanes
To examine the effect of the number of diffuser return
vanes on the performances of the pump stage, three
diffuser models with 7, 8 and 9 return vanes were
selected, while other parameters were kept constant.
Figs. 10-12 show that the variation in the number of
diffuser return vanes don't nearly influence the head,
brake horsepower and the efficiency of pump stage,
in spite of a light increase of the head and the
efficiency of the diffuser with 9 return vanes.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
288

Figure 10: Pump stage head versus flow rate.
Figure 11: Brake horsepower versus flow rate.
Figure 12: Pump stage efficiency versus flow rate.
4.4 Effect of Gap between the Impeller
and the Diffuser
To investigate the effect of the gap between the
impeller and the diffuser on the performances of the
pump stage, the impeller outer diameter values of
406.4 mm (impeller diameter ratio: 100 %), 381mm
(impeller diameter ratio: 93.75 %), 355.6 mm
(impeller diameter ratio: 87.5 %), 330.2 mm (impeller
diameter ratio: 81.25 %) and 304.8 mm (impeller
diameter ratio: 75 %) were selected when keeping
other parameters constant. Fig. 13 shows the head of
the pump stage as a function of the impeller diameter
ratio for the flows rates of 500 m
3
/h, 700 m
3
/h and 900
m
3
/h. From this figure, it can be seen that the pump
stage head increases with decreasing gap between the
impeller and the diffuser. This can be explained by
the fact that the pressure difference between the
impeller outlet and inlet decreases with increasing
impeller diameter ratio maintaining the diffuser inner
diameter constant.
Figure 13: Pump head versus flow rate.
Furthermore, Fig. 14 shows that the brake horsepower
increases with decreasing gap between the impeller
and the diffuser due to the requested augmented
impeller shaft torque relative to the size of the
impeller diameter keeping the diffuser inner diameter
constant. Additionally, the corresponding efficiency
curves as a function of the flow rate presented in Fig.
15 indicate that the level of the flow rate and the
impeller diameter ration have an impact on achieving
a better efficient.
Figure 14: Brake horsepower versus flow rate.
Figure 15: Efficiency versus impeller diameter ratio.
4.5 Model Comparison
The developed model of a first stage of a multistage
centrifugal pump using the design procedure
described in (Gülich, J. F., 2010) was validated
comparing the numerical simulation results with the
experimental results obtained from a pump
manufacturier (Technosub Inc.). Fig. 16 show that the
numerical curves are in good agreement with the
experimental curves.
Design and Numerical Characterization of a First Stage of a High Capacity Multistage Centrifugal Pump
289

Figure 16: Results comparison.
5 CONCLUSION
In this study, the design procedure described in
"Gülich, J. F., 2010" for the diffuser including the
return vanes was used to model a diffuser in order to
identify the diffuser parameters that improve the
pump stage performances. To this effect, a complex
liquid flow model in a pump stage was developed to
analyze the effects of the inlet height of the diffuser
vanes, the number of the diffuser vanes, the number
of the diffuser return vanes, and the gap between the
impeller and the diffuser on the pump stage head,
brake horsepower and efficiency. The achieved
results for considered value ranges reveal, among
others, that the diffuser height strongly influences the
pump stage performances. The variations in the
number of the diffuser vanes and of the diffuser return
vanes slightly affect the pump stage performances.
Moreover, the gap between the impeller and the
diffuser affects the pump stage performances
dependently of the impeller diameter ratio. The
comparison of numerical simulation results from the
developed model with experimental results obtained
from a pump manufacturer shows good harmony.
ACKNOWLEDGMENTS
The authors are grateful to the company Technosub
inc. (pump manufacturer) in Rouyn-Noranda,
Quebec, Canada.
REFERENCES
Gülich, J. F., 2010. Centrifugal Pumps, second Edition,
Springer.
Qihua Z., Weidong S., Yan X., Xiongfa G., Chuan W.,
Weigang L., and Dongqi M. 2013. A New Proposed
Return Guide Vane for Compact Multistage Centrifugal
Pumps. International Journal of Rotating Machinery,
Volume 2013, Article ID 683713, 11 pages.
La Roche-Carrier N., Dituba Ngoma G., and Ghie W.,
2013. Numerical investigation of a first stage of a
multistage centrifugal pump: impeller, diffuser with
return vanes, and casing. ISRN Mechanical
Engineering, Volume 2013, Article ID 578072, 15
pages.
Qihua Z., Yan X., Weidong S., Weigang L., Ling Z. 2012.
Research and development on the Hydraulic Design
System of The Guide Vanes of Multistage Centrifugal
Pumps. Applied Mechanics and Materials.
Miyano M., Kanemoto T., Kawashima D., Wada A., Hara
T., Sakoda K., 2008. Return Vane Installed in
Multistage Centrifugal Pump. International Journal of
Fluid Machinery and Systems, Vol. 1, No. 1.
Ansys inc. 2015. ANSYS-CFX (CFX Introduction, CFX
Reference Guide, CFX Tutorials, CFX-Pre User's
Guide, CFX-Solver Manager User's Guide, CFX-
Solver Modeling Guide, CFX-Solver Theory Guide),
release 16.2, USA.
Technosub Inc., www.technosub.net.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
290