Material Behavior Simulation of 42CrMo4 Steel
Marina Franulovic, Robert Basan and Kristina Markovic
Faculty of Engineering, University of Rijeka, Vukovarska 58, 51000 Rijeka, Croatia
Keywords: Material Behaviour, Material Parameters Identification.
Abstract: It is becoming increasingly important to make possible constitutive modelling and simulation of material
behaviour for the prediction of possible failures in material. This can allow to the optimization of design of
highly loaded engineering components. In order to achieve that goal, material parameters should be
accurately determined for the chosen material model. The major step in material parameters identification is
material behaviour simulation. The procedure of material behaviour simulation is based on the results of the
fatigue testing on the materials’ samples. The paper presents the procedures required for the material
behaviour simulation of 42CrMo4 steel, starting from the fatigue testing, through numerical procedures
related to complex material model, which results in material parameters identification, to the validation of
described procedures by comparison of the simulated and real materials response in cyclic loading
conditions.
1 INTRODUCTION
The optimal engineering design consists of the
knowledge on the loading applied on the
components, together with the knowledge on
material behaviour in different loading conditions.
Although many researchers prefer to use simple
material models to take into account the material
fatigue and its influence on materials’ life-time, the
development of ever more complex material models
makes possible description of material behaviour
even in different phases of its’ loading cycles. With
the usage of complex material models, it is possible
to take into account wide range of phenomena that
occur in the materials’ structure and influence the
material behaviour through its’ life cycles. These
complex material models are usually highly non-
linear and they consist of large number of unknown
material parameters, which have to be identified on
the basis of fatigue testing results.
The main goal in material parameters
identification is to use stress-strain data, recorded
through loading cycles of materials’ specimen life
and on the basis of developed procedures define
optimal set of parameters which describe the
material behaviour as accurately as possible. The
validation of both the procedures of parameter
identification and the identified parameters’ set is
possible by the simulation of material behaviour in
different loading conditions and its’ comparison to
the real material behaviour, acquired through fatigue
testing results.
The material behaviour analysis in the low-cycle
fatigue conditions is performed on the specimens
produced out of the 42CrMo4 steel, which tend to
experience both kinematic and isotropic softening
behaviour. These phenomena can be described well
by the Chaboche’s material model (Chaboche, 2008,
Lamaitre and Chaboche, 1990). Although it proved
to be very efficient in the description of material
behaviour in different operating conditions of the
components, the simple parameters’ identification
processes proved to be very unreliable and time-
consuming, because of the material model’s
nonlinearity and large amount of data that have to be
taken into account. Therefore, the development of
evolutionary algorithms, specifically genetic
algorithm, is chosen to overcome these difficulties.
It is known to be well-used in similar problems
(Furukawa and Yagawa, 1997).
Genetic algorithm for the material parameters
identification is proven to be insensitive to the
possible errors in measured data, it has large
probability to achieve global optima and to converge
to the accurate results in very short time. It also
works well with the large number of data and with
the highly non-linear systems (Franulovic et al.,
2009, Mahmoudi et al., 2011). In order to make
possible for the genetic algorithm to work optimal in
any given conditions, it’s operators should be
Franulovic, M., Basan, R. and Markovic, K.
Material Behavior Simulation of 42CrMo4 Steel.
DOI: 10.5220/0005995402910296
In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 291-296
ISBN: 978-989-758-199-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
291

developed, together with the proper objective
function.
2 MATERIAL PARAMETERS
IDENTIFICATION
The parameter identification system consists of set
of defined procedures which enable accurate
description of material characteristics possible.
These procedures are divided into two main parts.
The first part consists of prescribed tasks that
include material model definition, fatigue testing and
numerical procedures definition. The second part
includes controls that have to be performed in
different phases of derived tasks in order to ensure
an accurate solution of the parameter identification
process. These controls relate to tests accuracy,
irregularities in data sets, stress-strain hystereses
comparison, evolution of parameters, but also to
numerical procedures convergence. Although these
procedures can be applied to a wide range of
material models, they are mainly developed for
advanced ones because all the tasks that have to be
performed to identify their material parameters take
much time to gain satisfactory results.
2.1 Material Model
Considered material model is a rate-independent
version of the model, suitable to describe material
behaviour in low-cycle fatigue regime, proposed by
Chaboche (Chaboche, 2008), as a three-
decompositioned Armstrong- Fredericks model for
the back-stress tensor X
ij
:
pXCX dd)3/2(d
ij
p
ijij
 
, (1)



n
XX
1i
(n)
ijij
dd
, n = 3. (2)
Values C and γ are material parameters, dɛ
ij
is
increment of plastic strain and dp is increment of
accumulated plastic strain. The model is also
appropriate to simulate the Bauschinger effect with
kinematic and isotropic hardening/softening of the
material. Isotropic hardening takes into account the
cyclic evolution of the yield region in the strain-
controlled conditions. It is expressed by:

d)(d RRbR 

, (3)
where R represents isotropic hardening, R
∞
is the
boundary of the isotropic hardening, b is the isotropic
hardening rate and dλ is plastic multiplicator.
The constitutive equations are based on linear
isotropic elasticity, while multiaxial plasticity
criteria is described by well-known von Mises yield
criterion (Chaboche, 2008, Lemaitre, 1996) with
associated flow rule. This material model for
kinematic and isotropic hardening description of
material behaviour is consequently defined by the
set of nonlinear equations with 11 unknown material
parameters included, which have to be identified to
make possible simulation of material behaviour.
While one parameter is usually assumed, the rest 10
depend on the results of stress-strain relationship in
real material behaviour, recorded through fatigue
testing procedure.
2.2 Fatigue Testing
The fatigue testing was performed in the strain-
controlled conditions, according to standard testing
procedure (E606 – 92, 1992). The testing specimen
were produced out of steel 42CrMo4 in tempered
state. During testing, detailed stress-strain response
was recorded through cycles, until the fracture of
specimen in two parts. The materials response
served later for the material behaviour simulation.
The measuring system was set in following
conditions: strain rate of 1,5% s
-1
was held constant
for the duration of each test. The tests were
performed at the temperature of 20 °C. The strain
amplitude for symmetric cyclic testing were
maintained at 0,9%, 1,2% and 1,8% respectively.
The results showed that material experiences
isotropic and kinematic softening with emphasized
Bauschinger effect phenomenon (Bari and Hasan,
2000, Bari and Hassan, 2002). Prior to these fatigue
testing, the monotonic tests were performed by using
the same specimens made of the same materials. In
these tests, the load was applied and increased until
the specimen fracture to record the stress-strain
response of the material.
2.3 Numerical Procedures
In order to identify material parameters of highly
nonlinear material models and thus make possible
material behaviour simulation, genetic algorithm is
planned to be used. The procedure of genetic
algorithm for parameter identification in its basic
form could be relatively simple, but in that form is
not suitable for the particular problem. Namely, in
this case the large amount of experimentally
obtained data influence the possibility of
convergence to accurate results. In order to
overcome this problem, specific genetic operators
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
292

should be developed and finite element analysis
should be used to make possible simulation of
material behaviour and consequently calibration of
material parameters. The numerical procedure for
the parameter identification is shown in Figure 1.
Figure 1: Parameter identification system.
Material parameters E
stat
(Modulus of elasticity)
and

0y
(Yield stress) are obtained from the
monotonic stress-strain curve by linear regression,
while kinematic hardening/softening parameters
)3()2()1(
,,

XXX
,
)3()2()1(
,, 
and isotropic hardening /
softening parameters R

and b are part of the
algorithm’s numerical procedures, which include
simulation of material behaviour.
The accuracy of the results can be ensured
through several controls (Franulovic et. al., 2009),
such as: experimental tests accuracy control,
accuracy of preliminary parameters identification
through the phases (kinematic hardening and
isotropic hardening behaviour) and comparison of
simulated and real material behaviour during
parameters calibration procedure.
The high non-linearity of the system is included
in the hardening parameters’ set identification, so
the genetic algorithm for hardening parameters
identification holds the greatest responsibility for
this system to give satisfactory material behaviour
simulation.
2.4 Genetic Algorithm
In order to apply the genetic algorithm for parameter
identification, inverse analysis is applied (Tarantola,
2005, Hernandez et al., 2012). Inverse analysis
consists of defining search methods of unknown
material parameters by observing material sample’s
response to a probing signal. Proposed procedure
consists of three main parts (Figure 2). The system
characterization means that material parameters
which can fully characterize the system should be
defined. The second part is forward modelling. In
this part mechanical principles and physical laws
required to enable the prediction of the system
behaviour have to be defined. The third part is
backward or inverse modelling. In this part the
actual measurement results, the stress - strain data
obtained from fatigue tests affect the values of
model parameters in order to characterize the system
as accurately as possible.
Figure 2: Inverse analysis for parameter identification.
The system characterization for the presented
problem is based on the chosen material model
definition and includes hardening material
parameters. Forward modelling, based on
mechanical principles of material behaviour, is
defined in two domains. The first one


i
a;
ˆ




(4)
a
i
= [
)3()2()1()3()2()1(
,,,,, 

XXX
] A
(5)
is generated for the identification of kinematic
hardening parameters a
i
, based on Eqs (1,2), by
following relation:



































2
tanh
2
tanh
2
tanh
2
p
3)3(
p
2)2(
p
1)1(







X
X
XkR
(6)
Material Behavior Simulation of 42CrMo4 Steel
293

The second one

bN
NN
;,
ˆ
maxmax
  (7)
b  B (8)
is for isotropic hardening parameter
determination b, following relation:






N
b
p
1
max
S
max
1
max
N
max
2-
/1ln





(9)
where σ
max
is maximal stress in specific loading
cycle (1-first cycle, S-stable cycle, N- Nth cycle).
Parameter R

is calculated as the difference
between initial yield stress and yield stress in stable
cycle and therefore isn’t part of the genetic
algorithm calculation procedure.
Domains A and B are predefined for each
procedure in order to improve genetic algorithms’
calculation performance. The objective functions in
backward modelling for each procedure are based on
least squares method with w
ij
as the weighting factor
(Fedele et al., 2005.). Procedure for domain A is
performed on all data of j tests with different
measuring protocols that are executed for one
material.





m
j
m
i
j
i
j
iijA
j
awf
11
2
**
;
ˆ

;
2
*
1









j
i
ij
w

(10)
Procedure for domain B is performed for each
test separately and then average values of the
parameters are determined for each material.

2
* * *
max max
1
ˆ
,;
m
NN
Bii ii
i
fw Nb 





;
2
*
max
1




i
N
i
w

(11)
The asterisk refers to experimental data (stresses and
strains).
In order to accomplish as fast and as accurate
solution as possible, the genetic algorithm creates a
population of solutions and applies genetic
operators, such as scaling, selection, mutation and
crossover to evolve the solutions in order to find the
best ones. They influence the initial population
through phases in order to converge to the final
population (Figure 3).
The best individuals have low fitness value and
the possibility of their selection is high, but genetic
algorithm procedure is developed to take into
account also the genetic material of the individuals
with lower fitness value, but with the lower
expectancy of selection.
Figure 3: Genetic algorithm operators.
The 4-tournament selection mechanism is chosen
to select individuals which are going to be a part of
the mating pool. For the crossover the intermediate
recombination is used in this case (Pohlheim, 1999).
In order to achieve low fitness value in short time,
both domain procedures have specific crossover
technique, which means different dispersion and
solution controls, as shown in Figure 4.
Figure 4: Crossover operator procedure.
In each generation, the parent who contributes its
variable to the child is chosen randomly with equal
probability. There is, however, possibility to select
two identical parents. If that is the case, one parent is
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
294

mutating with the 25% ratio. The child’s value can
be calculated through one, two or three stages,
depending upon performed genetic algorithm’s
control points. Mutation procedures of the proposed
genetic algorithm in both domains have the same
mutation routine. Within this procedure each
variable is changing, while the mutation ratio is
decreasing through generations. The mutation
procedure is shown in Figure 5.
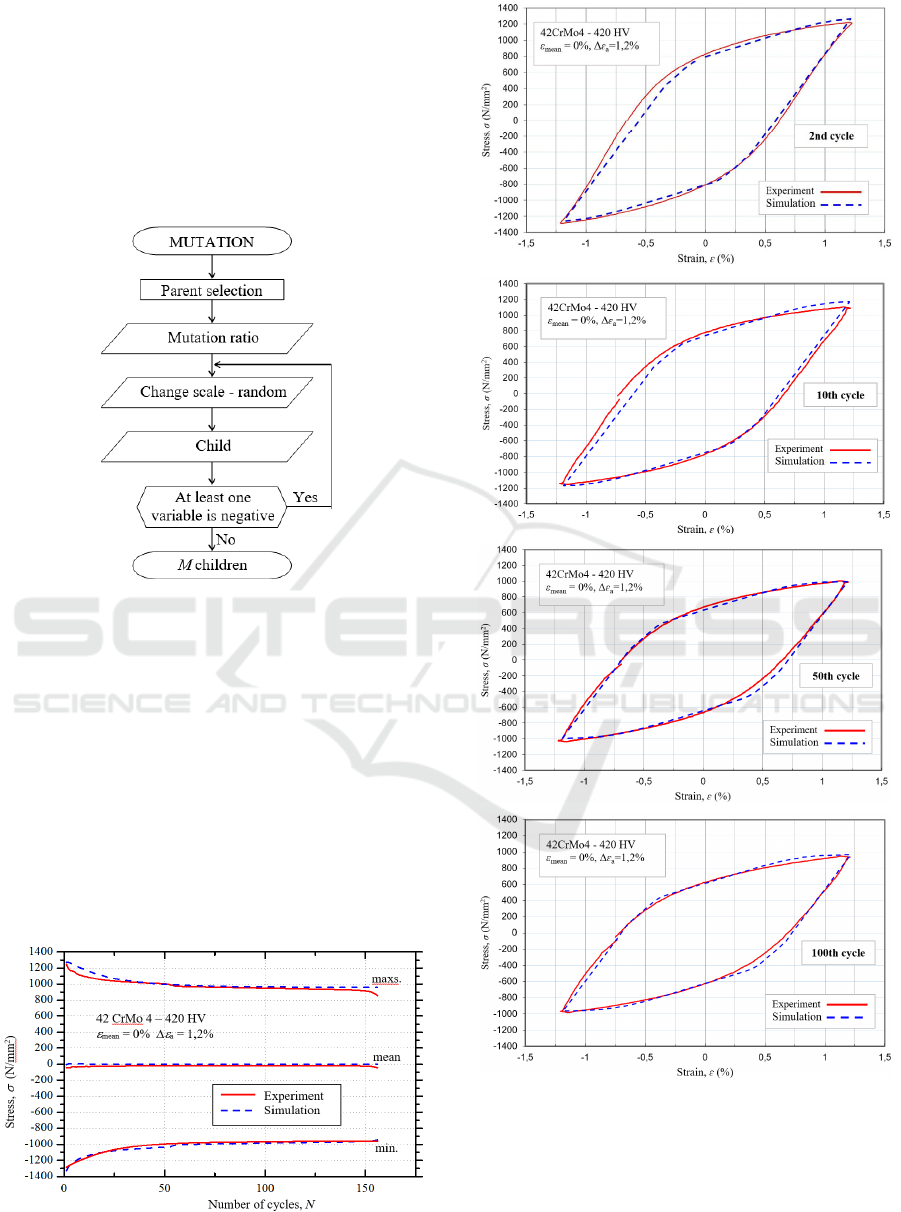
Figure 5: Mutation operator procedure.
3 MATERIAL BEHAVIOR
SIMULATION
The validation of material behaviour simulation and
thus accuracy of obtained material parameters is
performed as comparison of numerical models’ and
real materials’ response under cyclic loading, as
shown in Figures 6 and 7. The maximum, minimum
and mean stresses through cycles for both simulated
and real material’s response have the same tendency
through materials life (Figure 6).
Figure 6: Stress – Number of cycles curves.
Figure 7: Stress – Strain relationships for 2
nd
, 10
th
, 50
th
and
100
th
loading cycle.
In the presented example of the stress-strain
relationship (Figure 7), the second, tenth, fiftieth and
the hundredth cycles are simulated and compared to
the real material behaviour. The simulation of the
Material Behavior Simulation of 42CrMo4 Steel
295

material behaviour shows very good results in
comparison to the real material behaviour and thus
validate the proposed material parameters
identification procedure.
4 CONCLUSIONS
The design and optimization of mechanical
structures depend largely on accurate modelling of
material behaviour. If large number of phenomena
that occur in the material in hard operating
conditions need to be described, advanced material
models are necessary to be used. Since these models
are quite complex, their parameter identification
process is also challenging. The genetic algorithm
proved to be a good choice for this task. In order for
it to be effective, its’ operators have to be
specifically developed for the task. The simulation
of material behaviour, together with the usage of
developed optimization procedures are crucial to
validate the process and also acquire set of results
which are as accurate as possible. The presented
procedure for material parameter identification,
which is validated by the simulation of material
behaviour and its’ comparison to the real material
behaviour of 42CrMo4 steel, can be further used for
the description of material behaviour of other
metallic, but also different innovative materials. The
research on the material behaviour of new materials
can enhance mechanical engineering design of
components and bring new findings in this area.
ACKNOWLEDGEMENTS
This work has been supported in part by Croatian
Science Foundation under the project number IP-
2014-09-4982 and also by the University of Rijeka
under the projects number (13.09.1.2.09) and
(13.09.2.2.18).
REFERENCES
Bari, S., Hassan, T., 2000. Anatomy of Coupled
Constitutive Models for Racheting Simulation, Int. J.
Plasticity 16, 381-409.
Bari, S., Hassan, T., 2002. An advancement in cyclic
plasticity modeling for multiaxial ratcheting
simulation, Int. J. Plasticity 18, 873-894.
Chaboche, J. L., 2008. A review of some plasticity and
viscoplasticity constitutive theories, Int. J. Plasticity
24-10, 1642-1693.
E606 – 92, 1992., reapproved 1998., Standard Practice for
Strain – Controlled Fatigue Testing, ASTM
International standard.
Fedele, R., Filippini, M., Maier, G., 20085. Constitutive
model for railway wheel steel through tension-torsion
tests, Comp. Struct. 83.
Feng X. T., Yang, C., 2001., Genetic evolution of
nonlinear material constitutive models, Computer
Methods in Applied Mechanics and Engineering 190.
Franulović, M., Basan, R., Kunc, R., Prebil, I., 2010.
Automation of LCF material model parameters'
identification, Comp. Mater. Sci. 48-3, 529-536.
Franulović, M., Basan, R., Prebil, I., 2009. Genetic
algorithm in material model parameters' identification
for low-cycle fatigue, Comp. Mater. Sci. 45-2, 505-
510.
Furukawa, T., Yagawa, G., 1997. Inelastic Constitutive
Parameter Identification using an Evolutionary
Algorithm with Continuous Individuals, Int. J. Numer.
Meth. Eng. 40-6, 1071-1090.
Hernandez C., MaranonA., Ashcroft I. A., Casas-
Rodriguez J.P., 2012. Inverse methods for the
mechanical characterization of materials at high strain
rates, EPJ Web of Conferences 26, 04022.
Lemaitre, J., 1996., A Course on Damage Mechanics,
Springer.
Lemaitre, J., Chaboche, J. L., 1990. Mechanics of Solid
Materials, Cambridge University Press, 1990.
Mahmoudi, A. H., Pezeshki-Najafabadi, S. M., Badnava,
H., 2011. Parameter determination of Chaboche
kinematic hardening model using a multi objective
Genetic Algorithm, Comp. Mater. Sci. 50-3, 1114-
1122.
Pohlheim, H., 1999., Evolutionary Algorithms: Overview,
Methods and Operators, Technical report.
Tarantola, A., 2005. Inverse Problem Theory and Methods
for Model Parameter Estimation, Siam.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
296