Secret Sharing Scheme and Key Sharing Scheme Suitable for

Clustered Sensor Networks

Shinichi Goto

, Keiichi Iwamura

, Yuji Suga

and Kitahiro Kaneda

Department of Electrical Engineering, Tokyo University of Science, 6-3-1 Niijuku, Katsushika-ku, Tokyo, Japan

Internet Initiative Japan, 2-10-2 Fujimi, Chiyoda-ku, Tokyo, Japan

Institute of Document Analysis and Knowledge Science, Osaka Prefecture University, 1-1 Naka-ku, Sakai, Osaka, Japan

Keywords: Sensor Network, Key Sharing, Secret Sharing Scheme, Node Analysis, Storage Capacity Reduction.

Abstract: A clustered sensor network collects two or more nodes and makes a cluster from them. Generally a cluster

head (CH) has all the encryption keys of the nodes in a cluster and performs encrypted communication.

However, this type of network has a problem in that the keys are revealed if the CH is analyzed every time

after key sharing. Moreover, when all the nodes are set to CH, another problem arises, which is the need for

large storage for holding the keys of all the nodes in a cluster. In this paper, we propose the first key sharing

scheme that carries out key sharing with the CH and each node in a cluster and that realizes information

theoretical security using a secret sharing scheme, even if the CH is analyzed except for the time of

encryption communication. Next, we propose the second key sharing scheme in which additional storage for

the CH for saving the keys of all the nodes in a cluster is not needed. In order to realize it, the secret sharing

scheme is improved and the security is evaluated. In addition, we present the third key sharing scheme in

which none of the keys are revealed at all even if CH or all the child nodes are analyzed.

1 INTRODUCTION

Wireless sensor networks are known as ad hoc

networks that consist only of sensor nodes

connectable by radio. Generally, the sensor nodes

send various data such as the temperature, humidity,

etc., to a base station (BS) directly or indirectly

through multi-hop routing. Sensor networks can be

used for various purposes, from military to

noncommercial uses, and are expected to become

the next-generation communication infrastructure.

However, sensor nodes are not tamper resistant

and do not have high computational resources owing

to cost factors. Therefore, it is difficult to perform

complicated calculations like public key encryption.

Additionally, since the memory capacity of a sensor

node is small, the amount of data it can hold is

limited. Moreover, sensor nodes have a low-capacity

battery. Therefore, efficient energy consumption is

an important consideration point. In addition, since

sensor nodes are often placed outdoors to monitor

the information in the field, an attacker can easily

steal and analyze the nodes to obtain sensitive

information. In contrast, a BS is generally managed

securely and has enough electrical power and

computational resources.

The main research on sensor networks is how to

decrease the energy consumption of sensor nodes,

and there are many results on efficient energy

consumption. One of these is LEACH (Low Energy

Adaptive Clustering Hierarchy) (Heinzelman et al.,

2000), which has been proposed as a clustered

sensor network. A clustered sensor network makes a

group of nodes called a cluster and sets one of these

nodes as the cluster head (CH). The nodes in each

cluster send the sensing data to the CH. The CH then

forwards the data to the BS. What LEACH does is to

change the CHs in turn so that the clusters are

independently composed without the need for a BS.

In LEACH, when all the nodes are periodically set

to CH, the deviation of the energy consumption of

all the nodes is equalized, allowing the life of the

network to be extended.

However, the original LEACH protocol did not

consider the issue of security. Thus, some new

LEACH protocols that realize security using

common key encryption, such as SecLEACH

(Oliveira et al., 2007), MS-LEACH (Qiang et al.,

2009), etc., were proposed.

172

Goto, S., Iwamura, K., Suga, Y. and Kaneda, K.

Secret Sharing Scheme and Key Sharing Scheme Suitable for Clustered Sensor Networks.

DOI: 10.5220/0005999601720180

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 6: WINSYS, pages 172-180

ISBN: 978-989-758-196-0

However, almost all of the key sharing schemes

in a clustered sensor network have the same

problem: since the CH has the encryption keys of all

the nodes in the cluster to perform encrypted

communication, if the CH is analyzed, these

encryption keys are revealed. Moreover, when all

the nodes are set to the CH like in LEACH, another

problem arises, which is the need for big storage to

hold the keys of all the nodes in the cluster.

On the other hand, some key sharing schemes

use (k,n) secret sharing scheme. The secret sharing

scheme makes n shares from a secret, and the secret

can be restored from k (k

≦

n) shares. In the key

sharing scheme, when CH does not have any keys, it

restores the encryption key by receiving shares from

k neighboring nodes (Bertier et al., 2010). However

in these schemes, the encryption key is leaked either

by the analysis of k neighboring nodes or k

communication paths, both of which are smaller

than the total number of child nodes. Therefore,

some schemes, e.g., that proposed in (Yiying et al.,

2013) use a public key cryptosystem to hide the

shares. However, because of the computational

complexity of a public key cryptosystem, the energy

consumption of a node is very large.

In this paper, we propose the following three

kind of key sharing schemes using secret sharing

schemes.

(1) The first scheme realizes that, even if the nodes

including the CH are analyzed, the CH does not

at all reveal the key between the nodes that are

not analyzed. This means that this scheme

realizes information theoretical security on key

analysis.

(2) The second scheme is a key sharing scheme in

which the CH does not need to save the keys or

the shares on all the nodes in a cluster, but

manages only its own key. Realization of this

scheme requires the secret sharing scheme to be

improved. This scheme achieves computational

security.

(3) The third scheme is a key sharing scheme that

does not leak the key at all even if CH or all of

the child nodes are analyzed. This scheme can

either select information theoretical security or

computational security.

The first scheme is recommended if the user

wants to focus on information theoretical security

against CH analysis and if the storage capacity of the

nodes is sufficient to hold the keys. The second

scheme is recommended for Internet of Things (IoT)

device that requires fewer calculation and memory

resources. The third scheme is suitable for group key

sharing which is used as a common key within a

cluster.

The remainder of this paper is organized as

follows: In Section II, we explain LEACH and

discuss existing research studies on LEACH with

security. Section III describes the first scheme using

an existing secret sharing scheme. Section IV

describes the improved secret sharing scheme and

the second scheme. Section V presents the third

scheme and its variations. Finally, in Section VI, we

describe the performance evaluation.

2 EXISTING RESEARCH

STUDIES

2.1 Leach

LEACH is a protocol that selects a node that, in turn,

becomes the CH and averages the energy

consumption of all nodes to extend the life of

clustered sensor networks.

LEACH has two communication phases: a setup

phase and a steady-state phase. In the setup phase,

LEACH uses a random number to choose a CH in a

cluster. The chosen node then broadcasts a message

that it has become the CH. The nodes choose the

nearest CH and send a message that they have

become child nodes. The CH then sends a time

division multiple access (TDMA) schedule for the

steady-state phase to the child nodes. In the steady-

state phase, the nodes send the sensing data to the

CH according to the TDMA schedule. The CH

compresses the data received from multiple child

nodes and transmits the combined data to the BS.

2.2 SecLEACH

In SecLEACH, an administrator sets some element

keys to each node before use at random from a key

pool, which is a set of element keys. Each element

key has a key ID. SecLEACH performs key sharing

in the setup phase as follows:

1. The CH announces the key IDs to the child

nodes.

2. Each child node selects a key ID(s) that is (are)

common to the CH.

3. Each child node transmits the common key ID(s)

to the CH.

4. Each child node and the CH generate and save

the common key, which was generated by the

common element key(s).

Secret Sharing Scheme and Key Sharing Scheme Suitable for Clustered Sensor Networks

173

SecLEACH can determine a common key by

knowing only the ID of the element keys. However,

SecLEACH has some problems. First, the key

sharing between the CH and a node is probabilistic

because there is not necessarily a common element

key. If a child node does not have a common key,

the node cannot communicate with the CH. Second,

if an attacker steals and analyzes nodes, the keys of

the other nodes may be analyzed. That is,

SecLEACH is weak to node analysis. If the number

of element keys that are saved is increased, analysis

will become difficult and the problem of requiring

more memory for the element keys arises.

In addition, all the keys of the nodes in a cluster

are revealed if the CH is analyzed every time after

key sharing.

2.3 MS-LEACH

MS-LEACH uses the Localized Encryption and

Authentication Protocol (LEAP) to obtain a common

key.

All the nodes have a function to generate

pseudo-random number. The procedure for

obtaining a common key is as follows:

1. An administrator makes an initial key K and sets

it to all nodes. A child node u makes a master

key Ku = E

(u). E

(u) is a pseudo-random

function that uses as input K and node ID u.

2. The CH and a child node transmit their own ID

to each other.

3. A child node u makes a common key K

(ch) using the pseudo-random function, with

Ku and the CH ID as input.

4. The CH makes the master key Ku using the

pseudo-random function, with K and a child

node’s ID as input. After that, the CH makes a

common key K

= E

(ch) using the master key

Ku and its own ID.

5. All the nodes delete the initial key K after

making a common key.

When MS-LEACH is used, the CH can share the

keys with all nodes certainly. In MS-LEACH, even

if an attacker steals and analyzes a node after the

deletion of the initial key, the other links remain

secure. However, all common keys are leaked if an

attacker obtains an initial key K, since MS-LEACH

generates the entire key from the initial key. In

addition, MS-LEACH does not realize information

theoretical security since it makes the common key

using a pseudo-random function.

All the keys of the nodes in a cluster are revealed

if the CH is analyzed every time after key sharing.

2.4 SSKM: Secret Sharing-based Key

Management

To keep secure channel for delivering shares, SSKM

(Yiying et al., 2013) adopt the discrete logarithm in

the finite field and DDH difficulty assumption.

Therefore, this scheme requires a large amount of

communication and computational complexity,

because the discrete logarithm is calculated on a

large finite field.

This scheme shares one cluster key (group key)

between all the nodes.

[Initial phase]

Assume that there are −1 clusters, and each

cluster has a cluster head and n (n ≥ k) member

nodes. In this phase, BS sets the parameters for key

sharing.

1. BS chooses two big primes 1 and 1; let  =

21 + 1 and  = 21 + 1,  = ; it is

computationally intractable to solve the factor 

without , . Meanwhile, BS selects a generator

 ( ∈[

1/2

,]) and another prime  ( > ).

And then, BS broadcasts the three triple (, ,

) to sensors in the network.

2. BS randomly and uniformly chooses a

polynomial () of (k − 1)-degree for each

cluster as follows:

() =  + 



+







+⋯+







3. BS independently selects a session key 

from

GF() in the finite field  and hides the session

key with secret 

, namely Z

[Cluster key management]

1. CH chooses xch randomly which relatively

primes with p-1 and q-1, and CH sends it to BS.

Then, BS counts out y

=

xch

and sends (ID

) to sensor node in cluster; meanwhile,

sensor node picks xi randomly which relatively

primes with p-1 and q-1, computes yi=

mod

N, and then sends (IDi, yi) to the BS. The BS

ensures that if IDi

≠

IDj, there should be no

yi=yj; otherwise it reselects until success.

Furthermore, the BS utilizes CH's ID

and

members' IDi (i=1,...,k) to count out the share

(ID

) and f

(IDi), respectively.

2. The CH selects a group of users  = {ID1,…,

IDk}, while BS unicasts (ID

, f

(ID

)･(yi)

xch

mod N) to sensor node in the cluster and

sends (IDi, f

(IDi)･(y

)

mod ) to CH.

3. BS sends Z

not to leak the K

[Secret recovery]

WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

174

Depending on the received information from BS,

public generator, node’s private key , and CH’s

own key 

, cluster head and members can obtain

their share through the following formulas:

)(

)()(

)(

)()(

iCH

chiCH

CHCH

iCHCH

IDf

yIDf

IDf

yIDf

⋅

3 FIRST SCHEME

3.1 A Fast Secret Sharing Scheme

using XOR

Shamir’s secret sharing scheme is a typical scheme.

However, since this scheme needs a polynomial

operation, it is complicated to process in a sensor

node. Therefore, we selected a fast secret sharing

scheme (Kurihara et al., 2008) using just an

exclusive OR (XOR) operation. This scheme has

minimal processing requirements and information

theoretical security. The details of this scheme are

omitted owing to page restrictions.

3.2 Application to LEACH

Existing key sharing schemes (Bertier et al., 2010)

distributes n shares to n nodes and collects any k (k

≦

n) out of n to recover the encryption key.

Therefore, the key is analyzed if k communication

paths are eavesdropped. In contrast, since the

proposed scheme sets threshold k to be larger than

the number of target child nodes, the key does not

leak even if all communication paths from the child

nodes are eavesdropped. Only the targeting node

that performs encryption communication holds the

multiple shares or the key itself to realize the key

recovery.

First, we put the following assumptions:

 A cluster contains m + 1 nodes whose IDs are

named ID

, ID

, …, ID

, and ID

m+1

. The

number of child nodes is m and CH is 1.

 Each node stores its own ID, the unique key K

and the link key L

in advance. K

is different for

each node. L

is used as a common key for the

encrypted communication between the CH and a

node. L

is independently selected from uniform

random number.

 The BS knows the aforementioned information

about all nodes, and communication using the

unique key K

between the BS and each node is

secure.

The proposed scheme can be applied independently

to every cluster or CH even if there are two or more

clusters or CHs. Our schemes are performed in the

setup phase after selecting the CH. In the first

scheme, we set k=2. Since each child node performs

a one-to-one key sharing with the CH, the number of

the targeting child node is 1 for one key. We can

select (n,k)=(3,2) and a child node that has W

and

without storing the link key, but the following is

easier.

In our schemes, although BS sends encrypted

shares to each child node directly to keep the

explanation simple, the shares can be sent via CH.

Since CH does not know each unique key, CH

cannot decrypt it. The first scheme is performed as

follows:

[Distribution]

1. The CH transmits the IDs of the child nodes in

the cluster to the BS.

2. The BS sets n=k=2 and performs the secret

sharing scheme in 3.1 for each link key L

as a

secret information independently, and it

generates two shares, W

and W

3. The BS encrypts W

(i=1,…,m) with the unique

key of the CH and sends them to the CH. The

CH decrypts W

(i=1,…,m) and saves them in

association with ID

4. The BS encrypts W

with each unique key of ID

and sends it to ID

. Each ID

decrypts W

and

saves it.

[Key sharing and encrypted communication]

1. ID

sends the following information to CH. E

)

is encrypted data of the sensing data f

using the

link key L

(ID

, W

, E

))

2. The CH restores the link key L

from W

and W

3. The CH obtains the sensing data f

by decrypting

) using L

4. The CH deletes the link key L

3.3 Security Assessment

(1) Security Against CH Analysis

The CH has only one share on one key. Therefore,

since k=2, no link key is revealed even if the CH is

analyzed except for the time of encryption

communication. This scheme has information

theoretical security based on the secret sharing

scheme in 3.1. Since key sharing between the CH

Secret Sharing Scheme and Key Sharing Scheme Suitable for Clustered Sensor Networks

175

and each node is independently set, even if two or

more CHs are analyzed, the security does not change.

However, at the time of encryption communication,

since CH restores the link key to communicate with

a child node, the link key is revealed. However, a

key sharing scheme equal to an attack that combines

CH analysis and information to CH to generate a key,

does not exist as far as the authors know. In addition,

since the CH in other schemes contains all the keys

of the child nodes, all these keys are leaked every

time the CH is analyzed.

(2) Security Against Child Node Analysis

Each child node has its own link key L

. Therefore,

the link key is leaked if a child node is analyzed.

However, L

is set independently, which means that

the link keys of the other nodes are not revealed at

all; thus, this scheme realizes information theoretical

security also in regard to child node analysis. In

contrast, as described previously, when many child

nodes are analyzed in SecLEACH, or when a child

node is analyzed before eliminating the initial key in

MS-LEACH, the other link keys are revealed.

(3) Security Against CH and Child Node Analysis

The first scheme has the same security as the child

node analysis, even if both the CH and child nodes

are analyzed. This is because each link key L

is set

up independently, and the number of shares that the

CH has is one for one key.

(4) Security Against Eavesdropping on

Communication Paths

Although W

is sent as it is in the key sharing and

encrypted communication phase, since W

does not

appear in the communication path, information

theoretical security is realized. SecLEACH also

realizes information theoretical security since it

sends only the key ID, whereas MS-LEACH realizes

computational security.

4 SECOND SCHEME

In the first scheme, the CH needs to save all the

shares of the child nodes. Therefore, we propose the

second scheme in which the CH does not need to

save these shares, but only manages its own key.

However, the second scheme cannot be realized by

applying the secret sharing scheme in 3.1 as it is.

Therefore, we apply asymmetric reduction

(Takahashi et al., 2014) to the scheme in 3.1.

Asymmetric reduction reduces the shares of each

server non-uniformly, in contrast to the ramp

scheme, which reduces the shares in each server

uniformly. In other words, the asymmetric secret

sharing scheme can set the shares on the server up to

k-1 to 0 (it manages only a key). The asymmetric

reduction in (Takahashi et al., 2014) was applied to

Shamir’s secret sharing scheme and has been proven

to have computational security, which depends on

the security of the pseudo-random number used.

Therefore, we show the asymmetric secret sharing

scheme of 3.1 as follows.

4.1 Asymmetric Secret Sharing Scheme

using XOR

In the following scheme, secret information S has an

ID named IS, and the size of the secret key is (n-1)d

bits. ‘⨁’ is XOR, and ‘||’ is the connection of the bit

sequence.

[Distribution]

1. The dealer arbitrarily selects t (1

≦

k-1)

servers in n servers and calls them key servers.

The ID of the key servers is i (1

≦

t). The

dealer and the key server have a pseudo-

random number generator.

2. The dealer sets key

to each key server i.

3. The dealer generates a pseudo-random number

qi=E

keyi

(IS) of (n-1)d bits from the ID of S using

the key

of each server, and it is considered as the

share of the key server.

4. The dealer divides 



for every d bits and makes



(

,

)

(0 ≤  ≤  − 2). He divides S for every d

bits and makes partially secret information items

(



,



,…,



). We assume 



=0.





=

(,)

||

(,)

|| … ||

(,)

=



||



|| … ||



, 



∈







5. The dealer assumes the following n(k-1)-1

random numbers.





,





,⋯,





,





,⋯,





,





,⋯,





,⋯,





6. The dealer generates (k-1)n-(n-1)t-1 random

numbers and arbitrarily assigns them to the

aforementioned 

∙



7. The dealer calculates the remaining (n-1)t

random numbers of 

∙



from



(

,

)

,⋯,

(

,

)

,⋯,

(

,

)

such that the

following equation is realized:



(

,

)

=



⨁⊕







∙





(1≤≤,0≤≤−2)

8. The dealer generates the partial shares as follows

using the assigned and calculated 

∙





(,)

=



⨁⊕







∙





WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

176

(t+1≤≤−1,0≤≤−2)

9. The dealer generates the remaining shares 



connecting each partial share and distributes 



to the server except (1 ≤  ≤ ) . The server

stores the shares. We call the server data server.





=

(,)

||

(,)

|| … ||

(,)

(



∈



0,1



(



)



)

[Restoration]

When we restore S, we select k servers from n servers

and send the ID of S to the servers. When we select a

key server i, the server generates and sends the share





=



(IS). When we select a data server, the

server sends the stored share. S is restored by the

same restoration process as in 3.1 using these k shares.

4.2 Application to LEACH

The second scheme has the same premise as the first

scheme except that CH has a pseudo-random

number generator.

[Distribution]

1. The CH transmits the IDs of the child nodes in

the cluster to the BS.

2. The BS sets n=k=2, t=1, and performs the secret

sharing scheme shown in 4.1 for each link key L

as the secret information independently, and it

then generates two shares, W

and W

. Here, the

CH is selected as the key server. Thus, W

=



and W

=Wi in 4.1. IS is the ID of each node.

3. The BS encrypts W

with each unique key of ID

and sends it to ID

(i = 1, ···, m). Each ID

decrypts W

and saves it.

[Key sharing and encrypted communication]

1. ID

sends the following information to CH. E

)

is the sensing data f

that was encrypted using the

link key L

(ID

, W

, E

))

2. The CH generates W

using the pseudo-random

number generator from ID

and key

, and

restores L

from W

and W

3. The CH obtains the sensing data f

by decrypting

) using L

4. The CH deletes the link key L

4.3 Security Assessment

The scheme in 4.1 has computational security,

depending on the used pseudo-random number, but

the proof is omitted because of page restrictions. The

security of the second scheme is shown as follows:

4.3.1 Security against CH Analysis

When the CH is analyzed, a key for generating the

shares 



will be revealed. This is equivalent to the

case in which all the shares in CH are revealed in the

first scheme. In the second scheme, since each link

key is independently set up as in the first scheme, no

link key is revealed from just one share. This means

that the second scheme has information theoretical

security similar to the first scheme on CH analysis.

4.3.2 Security against Child Node Analysis

The link key of a child node is also revealed in the

second scheme. In this scheme, W

= 



and

⨁



. When the node ID

is analyzed, 



known from W

and L

. If the pseudo-random

numbers that are used are vulnerable, 



may be

obtained from some 



. However, even in such a case,

if W

in node ID

is not obtained, L

is not revealed,

since the analysis of 



= W

does not contain L

. That

is, the key of a node that is not analyzed is not

revealed at all, even if many child nodes may be

analyzed, and the second scheme has information

theoretical security also on child node analysis.

4.3.3 Security against CH and Child Node

Analysis

The second scheme as well as the first scheme has the

same security as far as child node analysis is concerned.

4.3.4 Security against Eavesdropping on

Communication Paths

In the key sharing and encrypted communication

phase, W

is sent as it is from a child node. If 



known because of the vulnerability of the pseudo-

random numbers, L

may be revealed, since W

contains L

. Therefore, in this case, it is accepted that

this scheme depends on the computational security

of the pseudo-random numbers that were used.

5 THIRD SCHEME AND ITS

VARIATIONS

5.1 Application to LEACH

The third scheme has the same premise as the first

scheme except that each node does not have a link

key. In this scheme, it is assumed that threshold

k=m+1 and m>1. This means even if all the  child

Secret Sharing Scheme and Key Sharing Scheme Suitable for Clustered Sensor Networks

177

nodes are analyzed, none of the keys are revealed at

all. In addition, we assume that nodes up to u (0≤

≤−2) may be unable to communicate.

[Distribution]

1. CH informs the IDs of the child nodes in the

cluster to BS.

2. BS decides each link key L

for node ID

(i=1, ･･･,m), sets n=m+u+2 and k=m+1, and

performs the secret sharing scheme in 3.1 for

each Li as the secret information independently,

and BS generates n shares W

(j=1,･･･,n) for

each ID

3. BS encrypts the W

(i=1, ･･･,m) with each

unique key of ID

and send them to ID

whereupon ID

decrypts and saves them.

4. BS encrypts the W

i,m+1

～

i,m+u+2

(i=1, ･･･,m)

with the unique key of CH and sends it to CH.

[Key sharing and encrypted communication]

1. When ID

sends the sensing data f

to CH, ID

broadcasts its own ID to all nodes.

2. CH and nodes ID

except ID

broadcasts a share

. CH sends shares until m when the distributed

shares are less than m form W

i,m+3

～

i,m+u+2.

3. ID

restores the link key L

from the distributed m

shares and the share which only ID

has. ID

sends E

), which is encrypted sensing data f

with the link key L

4. CH restores the link key L

from the distributed

m shares and the remaining share W

i,m+2

which is

only contained by CH.

5. CH gets the sensing data f

by decrypting E

)

using L

6. After communication, CH and ID

delete the link

key.

If this scheme selects the secret sharing scheme

in 4.1 instead of that of 3.1, and all child node are set

as key server (t=m), none of the child nodes would

have any share; instead, they would simply be

managing a key.

We show a variation suitable for group key

sharing. It changes the following portions of the

third scheme.

[Distribution]

2. BS decides a group key L for a cluster, sets

n=m+u+2 and k=m+2, and performs the secret

sharing scheme in 3.1 for L as the secret

information, and BS generates n shares W

(j=1,･･･,n).

3. BS encrypts each W

(i=1,･･･,m) and W

m+2

with

each unique key of ID

and send them to ID

decrypts and saves them.

4. BS encrypts the W

m+1

～

m+u+2

with unique key

of CH and send them to CH.

[Key sharing]

2. All nodes including CH broadcasts a share of

those other than W

m+2

. CH sends shares until

m+1 when the distributed shares are fewer than

m+1 from W

m+3

～

m+u+2

3. All nodes including CH restores the link key L

from the distributed m+1 shares and W

m+2

This variation is named the third dash scheme.

This scheme can also select the secret sharing

scheme in 4.1 instead of that of 3.1

5.2 Security Assessment

5.2.1 Security against CH Analysis

In the third and dash schemes, CH has u+2 (0≤≤

−2) shares on one key. Therefore, none of the

link keys are revealed even if CH is analyzed. These

schemes have information theoretical security based

on the secret sharing scheme in 3.1. Since key

sharing between CH and each node occurs

independently, even if two or more CH(s) are

analyzed, the security does not change.

5.2.2 Security against Child Node Analysis

In the third scheme, each child node has one share

on one key, the number of child nodes is , and

k=m+1. Thus, none of the link keys are leaked if all

the child nodes are analyzed.

In the dash scheme, each child node has one

share W

for every node and a common share W

m+2

and k=m+2. Thus, any link key is not leaked if all

the child nodes are analysed since the known share

is m+1.

5.2.3 Security against CH and Child Node

Analysis

The third scheme has robustness against analysis of

CH and −u−2 nodes, since CH has u+2 shares.

The dash scheme has robustness against analysis

of CH and −u−1 nodes.

WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

178

5.2.4 Security against Eavesdropping on

Communication Path

Since the number of shares on communication path

is less than threshold k, information theoretical

security is realized in the third and dash schemes.

6 PERFORMANCE

EVALUATION

We consider the case in which the number of child

nodes is m and CH is 1 within a cluster. For simplicity,

the length of each ID and each key is denoted by L,

and the length of the sensing information is expressed

by H. It is presupposed that one node communicates c

times in one round. We evaluate the case in which all

the child nodes share a key with the CH and one child

node carries out encryption communication with the

CH. In this case, the CH has already known the ID of

all the child nodes, and the child node has already

known the ID of the CH. In this evaluation, the BS is

not a candidate for evaluation since it has enough

electric power and computational resources; we thus

evaluate only the CH and a child node. We compared

SecLEACH and MS-LEACH with our schemes in the

key sharing phase (“Distribution” in our schemes) and

communication phase (“Key sharing and encrypted

communication” in our schemes). We do not include

SSKM in 2.4 in the comparison, since SSKM is

clearly inefficient compared with other schemes.

6.1 Evaluation of the Communication

Traffic

In SecLEACH, the number of keys that a node has is

set to a, and the average number of keys that is in

agreement with CH is set to b. From the viewpoint

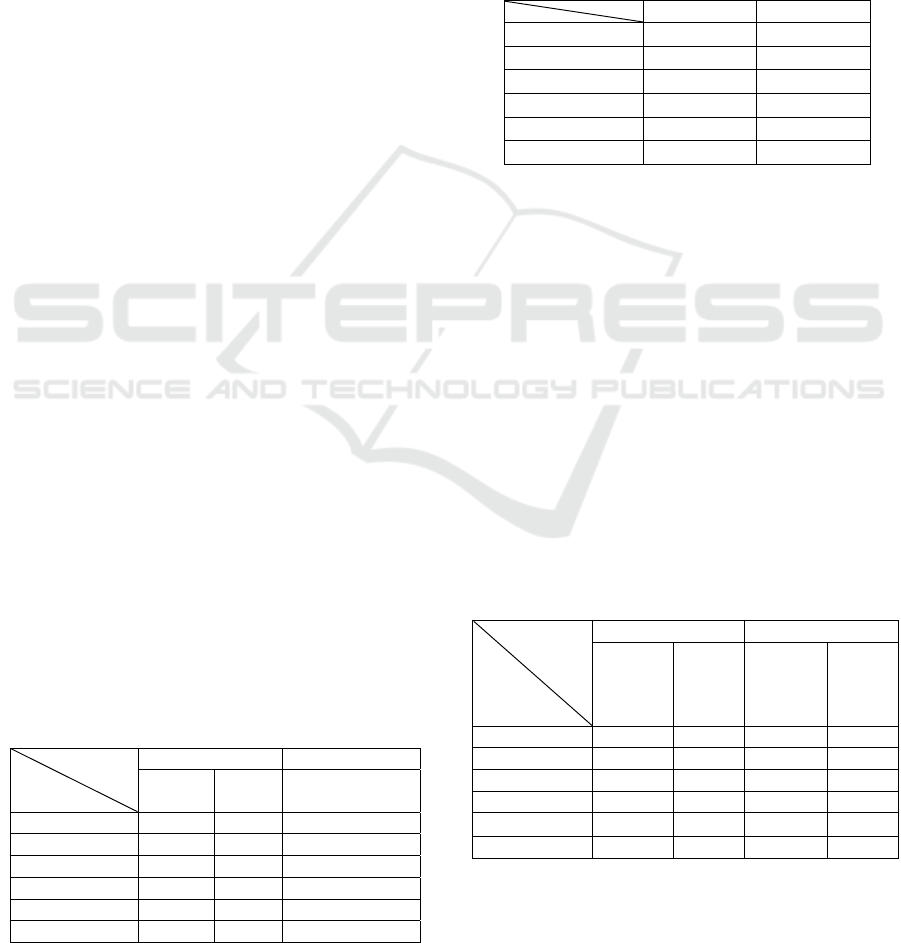
of communication traffic, MS-LEACH is the best. If

a>m and b>c, the first and second schemes are

better than SecLEACH. Although the third scheme

is worst, if H is larger than

mL enough, H becomes

dominant, and the difference becomes small.

Table 1: Comparison of data traffic.

Key sharing Communication

Child

node

Child node

SecLEACH aL bL c(L+H)

MS-LEACH 0 0 c(L+H)

1-st scheme mL 0 c(2L+H)

2-nd scheme mL 0 c(2L+H)

3-rd scheme mL 0 c{(m+1)L+H}

3-rd’ scheme mL 0 (m+1)L+cH

6.2 Evaluation of the Memory Capacity

In LEACH, since all the nodes turn into CH, the

memory size of the largest one serves as the amount

of memory of all the nodes. The CH, except in the

second and third dash scheme, stores the pair of IDs

of child nodes and the keys, in addition to the

memory capacity. Therefore, the second scheme is

the best, and the second and third dash schemes do

not need additional memory depending on the

number of nodes.

Table 2: Comparison of the amount of memory.

Child node CH

SecLEACH 2aL 2aL+2mL

MS-LEACH 2L 2L+2mL

1-st scheme 4L 4L+2mL

2-nd scheme 4L 4L

3-rd scheme 2(1+m)L (2+3m)L

3-rd’ scheme 4L (4+u)L

6.3 Evaluation of Computational

Complexity

We counted the number of times of encryption and

decryption since their computational complexity is

larger than that of the other operations. Therefore,

the computational complexity of the comparison of

the key ID in SecLEACH and of the XOR operation

in our schemes was set to 0.

From the viewpoint of the computational

complexity, SecLEACH is the best. The amount of

calculation of MS-LEACH is larger than that of the

first scheme and the third dash scheme, and if c<2m,

it is larger than that of the second scheme, although

the second scheme adds the c encryption of the ID in

order to make a share.

Table 3: Comparison of calculation.

Key sharing Communication

Child

node

Sum

child

node

SecLEACH 0 0 cH cH

MS-LEACH 2mL 2L cH cH

1-st scheme mL L cH cH

2-nd scheme 0 L c(L+H) cH

3-rd scheme 2mL ml cH cH

3-rd’ scheme (2+u)L 2L cH cH

Secret Sharing Scheme and Key Sharing Scheme Suitable for Clustered Sensor Networks

179

7 CONCLUSIONS

We proposed three key sharing schemes. The user

can choose either of them according to the intended

usage.

REFERENCES

Heinzelman, W.R., Chandrakasan, A., Balakrishnan, H.,

2000. Energy-Efficient Communication Protocol for

Wireless Microsensor Networks, Proceedings of the

33rd Hawaii International Conference on System

Sciences, January 4-7.

Oliveira, L.B., Ferreira, A., Vilaça, M.A., Wong, H.C.,

Bern, M., Dahab, R., Loureiro, A.A., 2007.

SecLEACH—On the Security of Clustered Sensor

Networks, Signal Processing. Vol. 87, No. 12, pp.

2882-2895.

Qiang, T., Bingwen, W., Zhicheng, D., 2009. MS-LEACH:

A Routing Protocol Combining Multi-hop

Transmissions and Single-hop Transmissions, Pacific-

Asia Conference on Circuits, Communications and

Systems, pp. 107-110.

Bertier, M., Mostefaoui, A., Tédan, G., 2010. Low-Cost

Secret Sharing in Sensor Networks, Proceedings of the

IEEE 12th International Symposium on High

Assurance Systems Engineering (HASE'10), pp. 1–9,

November.

Yiying, Z., Chunying, W., Jinping, C., Xiangzhen, L.,

2013. A Secret Sharing-Based Key Management in

Hierarchical Wireless Sensor Network, International

Journal of Distributed Sensor Networks Volume 2013.

Kurihara, J., Kiyomoto, S., Fukushima, K., Tanaka, T.,

2008. On a Fast (k,n)-Threshold Secret Sharing

Scheme, IEICE Transactions on Fundamentals of

Electronics, Communications and Computer Sciences,

Vol. E91-A, No. 9, pp. 2365-2378, Sep.

Takahashi, S., Kang, H., Iwamura, K, 2014. Asymmetric

Secret Sharing Scheme Suitable for Cloud Systems,

2014 IEEE 11th Consumer Communications and

Networking Conference (CCNC), pp. 798-804，Las

Vegas, Jan.

WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

180