Efﬁcient Proxy Signature Scheme from Pairings

Francesco Buccafurri

, Rajeev Anand Sahu

and Vishal Saraswat

DIIES, University of Reggio Calabria, Reggio Calabria, Italy

C. R. Rao Advanced Institute of Mathematics Statistics and Computer Science, Hyderabad, India

Keywords:

Identity-based Cryptography, Digital Signature, Bilinear Pairing, Proxy Signature, Delegation of Signing

Rights.

Abstract:

A proxy signature enables an entity to transfer its signing rights to another entity, called the proxy signer,

without actually sharing its signing key. Most of the proxy signatures in literature have been designed using

bilinear pairing on the elliptic curve group with the aim of providing either the property of being identity-based

or efﬁciency or security. But almost all of these schemes do not provide all these three desirable properties to-

gether and most of the identity-based proxy signature (IBPS) schemes are either too inefﬁcient or their security

is based on non-standard assumptions to have practical signiﬁcance. In this paper, we propose an efﬁcient and

provably secure identity-based proxy signature scheme from bilinear pairing based on a standard assumption,

the hardness of the computational Difﬁe-Hellman problem. The proposed scheme is secure against existential

forgery on adaptive chosen-message and adaptive chosen-ID attack in the random oracle model. Moreover, we

do an efﬁciency analysis and show that our scheme is signiﬁcantly more efﬁcient in the view of computation

and operation time than the existing similar schemes.

1 INTRODUCTION

We live in a digital era in which communications

and transactions are mostly online and it is crucial to

have efﬁcient and usable tools to verify the authen-

ticity and integrity of exchanged information. Digi-

tal signature is a cryptographic primitive which facil-

itates the above desired properties and guarantees the

sender’s non-repudiation. In many ﬁelds, including

e-government and e-commerce, there may be many

situations in which the signatory entity itself is un-

able to apply the signature and needs to delegate its

rights to another entity. For example, the CEO of a

company may wish to authorize the chief ﬁnancial of-

ﬁcer (CFO) or the chief operating ofﬁcer (COO) to

sign certain messages on his behalf during a certain

period of his absence. A proxy signature scheme en-

ables a signer (entity) O, called the original signer,

also called the designator or delegator, to delegate its

signing rights (without transferring the private key) to

another entity P , called the proxy signer, to produce,

on the delegator’s behalf, signatures that can be veri-

ﬁed by the receiver R under the delegator O

s public

key. In other words, whenever a receiver entity ver-

iﬁes a proxy signature, it veriﬁes the signature itself

along with original signer delegation.

1.1 Related Work

The idea of proxy signature was introduced in (Gasser

et al., 1989), but the ﬁrst formal construction was pre-

sented in (Mambo et al., 1996) in 1996. The formal

model of security for the proxy signature was struc-

tured by (Boldyreva et al., 2012). (Schuldt et al.,

2008) strengthened the security model for proxy sig-

natures in more formal way and have also extended it

on the identity-based setting.

Since then, many proxy signature schemes have

been proposed in the identity-based setting using bi-

linear pairings. (Xu et al., 2005) formalized the no-

tion of security for identity-based proxy signature

schemes based on the work of (Boldyreva et al., 2012)

and (Malkin et al., 2004). However, (Wu et al., 2007)

showed that the model deﬁned in (Xu et al., 2005)

does not capture the deﬁnitions of adaptive chosen-

message and chosen-identity attack in identity based

system and proposed a new scheme. (Wang, 2008)

showed that the schemes given in (Xu et al., 2005) are

vulnerable to proxy key exposure attack.

1.2 Our Contribution

We propose an efﬁcient and provable secure identity-

Buccafurri, F., Sahu, R. and Saraswat, V.

Efﬁcient Proxy Signature Scheme from Pairings.

DOI: 10.5220/0005999804710476

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 471-476

ISBN: 978-989-758-196-0

471

based proxy signature (IBPS) scheme suitable for

real-life applications. The construction of our scheme

is motivated by the identity based signature of (Choon

and Cheon, 2003) which is secure against existential

forgery on adaptive chosen-message and given-ID at-

tack in the random oracle model. We do a non-trivial

transformation to their scheme to construct a proxy

signature which is secure against existential forgery

on adaptive chosen-message and adaptive chosen-ID

attack in the random oracle model. Our scheme fol-

lows a delegation by warrant approach and is secure

under the computational Difﬁe-Hellman assumption.

Since the last decade most of the works on

proxy signature have been carried out with some ex-

tensions viz. multi-proxy signature, proxy multi-

signature, multi proxy multi- signature (Cao and Cao,

2009a; Cao and Cao, 2009b; Sahu and Padhye,

2015). Considering them for one-to-one delegation,

these schemes may be seen as simple proxy signa-

ture schemes. Some recent basic proxy signature

scemes (Singh and Verma, 2012; Asaar et al., 2014)

have been proposed with an additional property of

message recovery, in which the message need not to

be sent with signature and can be recovered from the

signature by one more additional step after veriﬁca-

tion. In this paper, we show that even these schemes

are less efﬁcent than our proposed scheme. Due to

the page limitation, though we do not compare our

scheme with the schemes with multi-delegation here,

it can be easily seen that our scheme is more efﬁ-

cient than these schemes when those are used for sin-

gle delegation. Our scheme beats even one of the

most recent one-to-one delegation scheme (Sarde and

Banerjee, 2015) by more than 25% in computation

time. Moreover, the scheme is up to 39% more efﬁ-

cient in the view of computation and operation time

than the existing proxy signature schemes (Xu et al.,

2005; Chow et al., 2005; Wu et al., 2007; Wang, 2008;

Singh and Verma, 2012; Asaar et al., 2014; Sarde and

Banerjee, 2015).

Most of the new primitives of proxy signature as

multi-proxy signature, proxy multi-signature, multi-

proxy multi signature, proxy blind signature, thresh-

old proxy signature etc. use a simple proxy signature

as a building block. Hence, the construction of an

efﬁcient and provable secure proxy signature scheme

is desired. Almost all the proxy signature schemes

from bilinear pairings deﬁned on the elliptic curve

group are either inefﬁcient or they have some secu-

rity issues. As a consequence, the new primitives us-

ing these schemes as building blocks also have the

same issues and, in fact, these issues are magniﬁed

depending on the nature of the construction. Thus

our efﬁcient and provably secure identity-based proxy

signature scheme would be very useful as a concrete

scheme to be further used to construct efﬁcient exten-

sions of proxy signature scheme.

1.3 Outline of the Paper

The rest of this paper is organized as follows. In

Section 2, we introduce some related mathematical

deﬁnitions, problems and assumptions. In Section 3,

we present the formal deﬁnition of an identity-based

proxy signature scheme and formal security model

for it. Our proposed identity-based proxy signature

scheme is presented in Section 4. In Section 6 we an-

alyze the security of our scheme and in Section 7 we

do an efﬁciency comparison with the state-of-art. Fi-

nally, in Section 8 we draw a conclusion of our work.

2 PRELIMINARIES

In this section, we introduce some relevant deﬁni-

tions, mathematical problems and assumptions.

2.1 Notations

We denote by y ← A(x) the operation of running a

randomized or deterministic algorithm A(x) and stor-

ing the output to the variable y. If X is a set, then

← X denotes the operation of choosing an element

v of X according to the uniform random distribution

on X. We say that a given function f : N → [0,1] is

negligible in n if f (n) < 1/p(n) for any polynomial p

for sufﬁciently large n. For a group G and g ∈ G, we

write G = hgi if g is a generator of G.

Deﬁnition 1 (Bilinear Map). Let G

be an additive

cyclic group with generator P and G

be a multi-

plicative cyclic group with generator g. Let both the

groups are of the same prime order q. Then, a map

e : G

× G

→ G

satisfying the following properties,

is called a cryptographic bilinear map:

1. Bilinearity: For all a,b ∈ Z

∗

, e(aP, bP) = e(P,P)

or equivalently, for all Q,R,S ∈ G

, e(Q + R,S) =

e(Q,S)e(R, S) and e(Q,R + S) = e(Q,R)e(Q,S).

2. Non-Degeneracy: There exists Q,R ∈ G

such that

e(Q,R) 6= 1. Note that, since G

and G

are groups

of prime order, this condition is equivalent to the

condition e(P,P) 6= 1, which again is equivalent to

the condition that e(P,P) is a generator of G

3. Computability: There exists an efﬁcient algorithm

to compute e(Q,R) ∈ G

, for any Q,R ∈ G

Deﬁnition 2 (Computational Difﬁe-Hellman Prob-

lem). Let G

be a cyclic group with generator P.

SECRYPT 2016 - International Conference on Security and Cryptography

472

1. Let a,b ∈ Z

∗

be randomly chosen and kept secret.

Given P,aP, bP ∈ G

, the computational Difﬁe-

Hellman problem (CDHP) is to compute abP ∈

2. The (t, ε)-CDH assumption holds in G

if there is

no algorithm which takes at most t running time

and can solve CDHP with at least a non-negligible

advantage ε.

3 IBPS SCHEME AND ITS

SECURITY

In this section, we give the formal deﬁnition and the

security model for an identity-based proxy signature

(IBPS) scheme. Here onwards we mean by IBPS an

identity-based proxy signature.

3.1 Deﬁnition of IBPS Scheme

In an IBPS scheme, an original signer delegates its

signing rights to a proxy agent to make a signature on

its behalf, where the public keys of the original and

proxy signers can be computed from their identities

by anyone and their private keys are generated using

their corresponding identities by a trusted authority,

the private key generator (PKG). Let O be the original

signer with identity ID

and P be the proxy signer

with identity ID

. Precisely, an IBPS scheme consists

of the following algorithms:

Params ← Setup(1

): For a security parameter 1

input, the PKG runs this algorithm and generates the

public parameters params of the system and a mas-

ter secret.

) ← KeyGen(ID): With this private key

generation algorithm, the PKG outputs the private

key S

for a given identity ID.

) ← ProxyKeyGen(w,S

): This is a pro-

tocol between the original signer and the proxy

signer during which they agree on the warrant w,

which includes some speciﬁc information regarding

the message as restrictions on the message, time of

delegation, identity of original and proxy signer, pe-

riod of validity, etc. After the successful interaction,

the proxy signer P outputs its proxy signing key, d

(σ

) ← ProxySignature(m,w,d

): This random-

ized algorithm outputs an IBPS σ

on a message m

satsfying a warrant w.

(0/1) ← Veriﬁcation(m,w,σ

): This

deterministic algorithm outputs 1 if the signature

is a valid IBPS on the message m by the proxy

signer on behalf of the original signer and outputs 0

otherwise.

3.2 Security Model for IBPS Scheme

In this model, an adversary A tries to forge the proxy

signature working against a user, either against the

original signer say O or against the proxy signer say

P . The adversary A can access polynomial num-

ber of hash queries, extraction queries, delegation

queries, proxy key generation queries and proxy sig-

nature queries. Consider that the response to each

query is provided to A by using the random oracle.

The goal of adversary A is to produce one of the fol-

lowing forgeries:

1. An IBPS σ

for a message m on behalf of the orig-

inal signer, where user P

is the proxy signer, such

that either the original signer never designate user

, or m was not submitted to the proxy signing

oracle.

2. An IBPS σ

for a message m by the proxy signer

on behalf of the user O

, where user O

plays the

role of original signer, and the proxy signer was

never designated by the user O

Deﬁnition 3. An IBPS scheme is said to be existen-

tial unforgeable against adaptive chosen-message and

adaptive chosen-ID attack if no probabilistic polyno-

mial time adversary A has a non-negligible advantage

against the challenger C in the following game:

1. Setup: The challenger C runs the setup algorithm

and provides the public parameters params to the

adversary A.

2. Hash queries: On hash query of adversary A ,

challenger C responds through random oracle and

maintains lists say L

and L

for the hash

queries.

3. Extraction queries: On key extraction query by A

for an identity ID, C provides the corresponding

private key S

to A.

4. Delegation queries: A produces a warrant w

and receives its corresponding delegation value T

from C .

5. Proxy key generation queries: A produces a valid

warrant w

with respect to an adaptively chosen

identity ID and receives its corresponding proxy

signing key d

from C .

6. Proxy signature queries: A produces a message

, a valid warrant w

corresponding to the mes-

sage m

and identity ID and receives from C an

IBPS σ

on the adaptively chosen message.

After the series of queries, A outputs a new IBPS σ

∗

on the message m

∗

under a warrant w

∗

for identities

and ID

, where – A has not requested the pri-

vate key for at least one of the identities ID

and ID

in extraction queries; A did not request a delegation

query on warrant w

∗

and identity ID

; A did not re-

quest a proxy key generation query including warrant

Efﬁcient Proxy Signature Scheme from Pairings

473

∗

and identity ID

; A never requests a proxy signa-

ture query on message m

∗

with warrant w

∗

and iden-

tities ID

. The adversary A wins the above game if it

is able to provide a validity proof of the new IBPS σ

∗

on message m

∗

under the warrant w

∗

Deﬁnition 4. An adversary A

(t,q

,2,ε)-breaks an 2-user

IBPS scheme by adaptive chosen-message and adap-

tive chosen-ID attack, if A wins the above game with

probability ε within time t and makes at most q

queries, q

extraction queries, q

delegation queries, q

proxy key generation queries

and q

proxy signature queries.

Deﬁnition 5. An IBPS scheme is

(t,q

,2,ε)-secure against

adaptive chosen-message and adaptive chosen-ID

attack, if no probabilistic polynomial time adversary

can (t,q

,2,ε)-break it.

4 PROPOSED SCHEME

In this section, we present our IBPS scheme. As de-

ﬁned in Section 3, our scheme consists of the follow-

ing phases: Setup, KeyGen, ProxyKeyGen, ProxySig-

nature, and Veriﬁcation.

Setup. In the setup phase, the private key generator

(PKG), on input security parameter 1

, generates the

system’s master secret key s and the system’s public

parameters

params = (λ,G

,q,e,H

,P, Pub),

where G

is an additive cyclic group of prime order q

with generator P; G

is a multiplicative cyclic group

of prime order q with generator g; e : G

×G

→ G

a bilinear map as deﬁned in Section 2; H

: {0,1}

∗

→

and H

: {0,1}

∗

× G

→ Z

∗

are two cryptograph-

ically secure hash functions, and Pub = sP ∈ G

system’s public key.

KeyGen. Given an identity ID, the PKG returns the

public and private keys for ID as follows:

• public key: Q

:= H

(ID) ∈ G

; and

• private Key: S

:= sQ

∈ G

Thus, the original signer O has its private key

while anyone can compute the corresponding

public key Q

. Similarly, for the proxy signer P ,

the public key is Q

and corresponding private key

is S

ProxyKeyGen.

Make Warrant: In this phase, the original signer O

delegates its signing capability to the proxy signer

through a signed warrant w. The warrant w includes

the identity of original signer O, the identity of the

proxy signer P , the time of delegation, the period of

validity, the nature of messages that can be signed,

etc.

Sub Proxy Generation: The original signer O ran-

domly chooses x

∈ Z

∗

and computes

• S

= x

∈ G

• h

= H

(w, S

) ∈ Z

∗

, and

• T

= (x

+ h

∈ G

and appends to the war-

rant w,

Finally, the original signer O sends D = (w,S

)

to the proxy signer through a secure channel, with

as a delegation value.

Sub Proxy Veriﬁcation: The proxy signer P , ac-

cepts the delegation value T

on warrant w, if the

equality

e(T

,P) = e(S

+ h

,Pub)

holds. Otherwise, it asks for a new delegation value

or terminate the protocol.

Proxy Key Generation: After receiving the (cor-

rect) delegation value, the proxy signer P generates

its proxy signing key as

= T

+ h

ProxySignature. To generate the proxy signature on

a message m, on behalf of the original signer O, the

proxy signer P does the following:

• randomly selects y ∈ Z

∗

• computes U

= y · Pub ∈ G

• h

= H

(m,U

) ∈ Z

∗

• and V

= (y + h

The proxy signature generated by the proxy signer

P on the message m, on behalf of the original signer

O is σ

= (S

Veriﬁcation. Receiving a proxy signature σ

(w, S

) and message m, the veriﬁer proceeds

as follows:

1. Checks the validity of message m with respect to

the warrant w. Continue, if it is a valid one. Re-

jects otherwise.

2. Checks the authorization of the proxy signer by the

original signer. Stop the veriﬁcation, if the proxy

signer is not authorized by the warrant. Continue

otherwise.

3. Finally, accepts the proxy signature if the equality

e(V

,P) = e(S

+ h

+ Q

),U

+ h

Pub)

holds.

SECRYPT 2016 - International Conference on Security and Cryptography

474

5 PROOF OF CORRECTNESS

The correctness of veriﬁcation of our scheme holds as

follows:

e(S

+ h

+ Q

),U

+ h

Pub)

= e(x

+ h

,yPub + h

Pub)

= e((x

+ h

,(y + h

)Pub)

= e((x

+ h

,(y + h

)P)

= e(T

+ h

,(y + h

)P)

= e(d

,(y + h

)P)

= e((y + h

,P)

= e(V

,P)

6 PROOF OF SECURITY

In this section, we give the theorem which proves of

the security of our scheme against existential forgery

on adaptive chosen-message and adaptive chosen-

identity attack in the random oracle model. In the full

paper, we will use the rewinding technique and the

forking lemma (Pointcheval and Stern, 2000) to prove

this theorem.

Theorem 6. If there exists an adversary

A(t,q

, 2,ε) which breaks

the proposed IBPS scheme in time t with suc-

cess probability ε, then there exists an adversary

B(t

,ε

) which solves CDHP with success probability

at least ε

≥

(1−1/q)M

+2q

+3q

ε in time at most

≥ t + (q

+ q

+ 2q

+ q

+ 2q

+ 4)C

where

denotes the maximum time taken for scalar

multiplication in G

and M is a maximum value as

deﬁned in the proof.

Let, for a security parameter 1

, the adversary B

is challenged to solve the CDHP for hq,G

,P, sP,bPi

where G

is an additive cyclic group of prime or-

der q with generator P and s,b ∈ Z

∗

. The goal of

B is to solve CDHP by computing sbP ∈ G

using

A, the adversary who claims to forge our proposed

IBPS scheme. B simulates the security game with A

as described in section 3, and solves an instance of

CDHP, using the values A requires to forge the pro-

posed signature. The probability of success and time

have been calculated as given in the above theorem, in

the full version we will describe the complete analysis

we have done, with all the required steps.

7 EFFICIENCY COMPARISON

In this section, we compare the efﬁciency of our IBPS

scheme with the existing popular IBPS schemes (Xu

et al., 2005), (Chow et al., 2005), (Wu et al., 2007)

and (Wang, 2008), and with the recently proposed

IBPS schemes (Singh and Verma, 2012; Asaar et al.,

2014; Sarde and Banerjee, 2015) and show that our

scheme is more efﬁcient in the sense of computa-

tion and operation time than these existing schemes.

As few of the recently proposed proxy signature

schemes (Singh and Verma, 2012; Asaar et al., 2014)

provide the message recovery property, we do not

count the computation for the message recovery dur-

ing the comparison. To evaluate the total opera-

tion time in the efﬁciency comparison tables, we use

the method from (Cao et al., 2010; He et al., 2011).

We note that the OT for one pairing computation

is 20.04ms, for one map-to-point hash function it is

3.04ms, for one modular exponentiation it is 5.31ms,

for one scalar multiplication it is 6.38ms and for one

general hash function it is < 0.001ms. For example,

during the proxy key generation phase of our scheme,

each proxy signer computes 2 pairings (P), 0 map-

to-point hash (H), 0 modular-exponentiation (E), and

4 scalar multiplications (S), hence the total operation

time can be calculated as: 2 × 20.04 + 0 ×3.04 +0 ×

5.31 +4 ×6.38 = 65.60ms. The OT for each phase of

all the schemes has been computed similarly.

From the efﬁciency comparison tables, it is clear

that our scheme is computationally more efﬁcient

than the existing popular and recent identity-based

proxy signature schemes. In particular, our scheme

is 39%, 19%, 33%, 22%, 26%, 20%, 28% and 25%

more efﬁcient than the schemes given in (Xu et al.,

2005), (Chow et al., 2005), (Wu et al., 2007), (Wang,

2008), (Singh and Verma, 2012), (Asaar et al., 2014)

and (Sarde and Banerjee, 2015) respectively.

8 CONCLUSION AND FUTURE

WORK

We have proposed an efﬁcient and provably secure

identity-based proxy signature scheme from bilinear

pairing based on the hardness of the computational

Difﬁe-Hellman problem. In the full version of this

paper, we will provide a full security analysis of our

scheme. Our scheme is useful for the application in

various real world scenareo including those discussed

in Section 1. In the fullversion we will envisage a few

more suitable applications for practical implementa-

tion of our scheme.

Efﬁcient Proxy Signature Scheme from Pairings

475

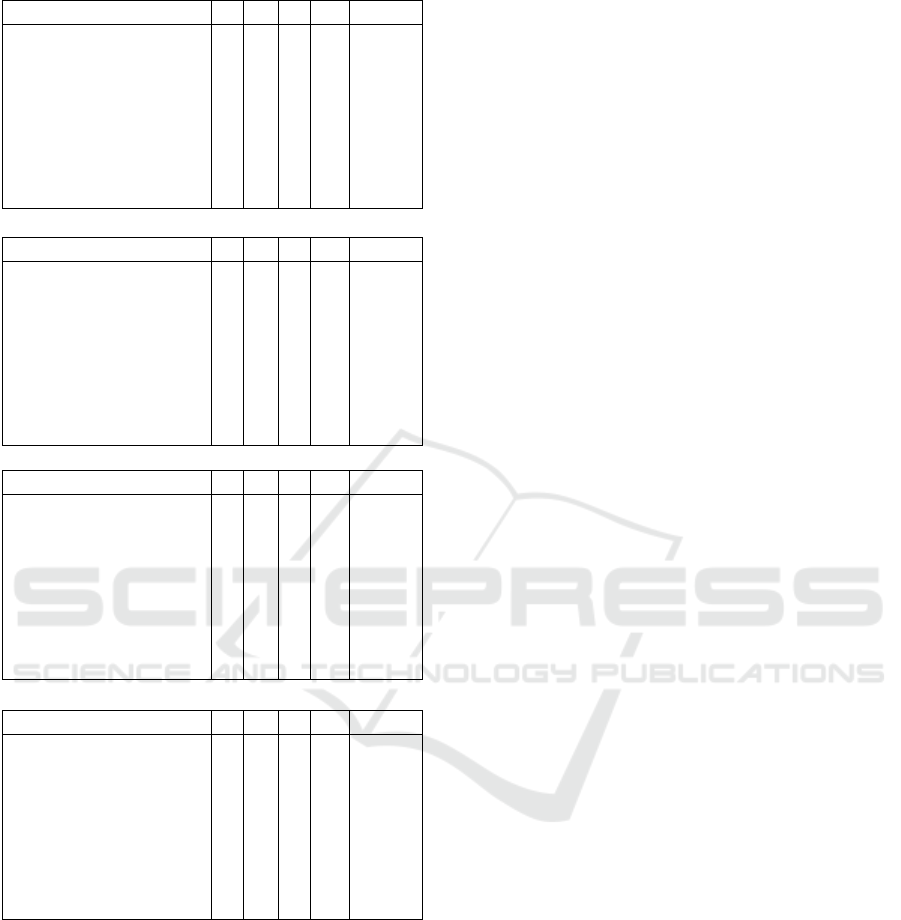
Proxy key generation

Scheme P H E SM OT (ms)

(Xu et al., 2005) 3 3 0 3 88.38

(Chow et al., 2005) 3 1 0 3 82.30

(Wu et al., 2007) 0 1 0 2 15.80

(Wang, 2008) 3 1 0 2 77.92

(Singh and Verma, 2012) 3 1 2 3 92.92

(Asaar et al., 2014) 3 2 2 0 76.82

(Sarde and Banerjee, 2015) 4 1 2 4 119.26

Our scheme 2 0 0 4 65.60

Proxy signature generation

Scheme P H E SM OT (ms)

(Xu et al., 2005) 0 1 0 2 15. 80

(Chow et al., 2005) 0 1 0 2 15. 80

(Wu et al., 2007) 0 3 0 6 47.40

(Wang, 2008) 0 1 0 2 15.80

(Singh and Verma, 2012) 1 0 1 1 31.73

(Asaar et al., 2014) 1 0 1 0 35.71

(Sarde and Banerjee, 2015) 0 0 0 2 12.76

Our scheme 0 0 0 2 12.76

Veriﬁcation

Scheme P H E SM OT (ms)

(Xu et al., 2005) 5 4 1 0 117.66

(Chow et al., 2005) 3 1 0 1 69.54

(Wu et al., 2007) 5 4 0 0 112.36

(Wang, 2008) 4 4 0 0 92.32

(Singh and Verma, 2012) 2 0 1 0 45.39

(Asaar et al., 2014) 3 2 2 0 76.82

(Sarde and Banerjee, 2015) 2 0 1 1 51.77

Our scheme 2 2 0 2 58.92

Overall operation time

Scheme P H E SM OT (ms)

(Xu et al., 2005) 8 8 1 5 221.84

(Chow et al., 2005) 6 3 0 6 167.64

(Wu et al., 2007) 5 8 0 8 175.56

(Wang, 2008) 7 6 0 4 186.04

(Singh and Verma, 2012) 6 1 4 4 170.04

(Asaar et al., 2014) 7 4 5 0 189.35

(Sarde and Banerjee, 2015) 6 1 3 7 183.79

Our scheme 4 2 0 8 137.28

REFERENCES

Asaar, M. R., Salmasizadeh, M., and Susilo, W. (2014). A

short id-based proxy signature scheme. International

Journal of Communication Systems.

Boldyreva, A., Palacio, A., and Warinschi, B. (2012). Se-

cure proxy signature schemes for delegation of sign-

ing rights. Journal of Cryptology, 25(1):57–115.

Cao, F. and Cao, Z. (2009a). A secure identity-based multi-

proxy signature scheme. Computers & Electrical En-

gineering, 35(1):86–95.

Cao, F. and Cao, Z. (2009b). A secure identity-based

proxy multi-signature scheme. Information Sciences,

179(3):292–302.

Cao, X., Kou, W., and Du, X. (2010). A pairing-free

identity-based authenticated key agreement protocol

with minimal message exchanges. Information Sci-

ences, 180(15):2895–2903.

Choon, J. C. and Cheon, J. H. (2003). An identity-based

signature from gap difﬁe-hellman groups. In PKC,

pages 18–30.

Chow, S. S., Lui, R. W., Hui, L. C., and Yiu, S.-M. (2005).

Identity based delegation network. In Progress in

Cryptology–Mycrypt 2005, pages 99–115. Springer.

Gasser, M., Goldstein, A., Kaufman, C., and Lampson, B.

(1989). The digital distributed system security archi-

tecture. In NCSC, pages 305–319.

He, D., Chen, J., and Hu, J. (2011). An id-based proxy

signature schemes without bilinear pairings. Ann.

Telecommun., 66(11-12):657–662.

Malkin, T., Obana, S., and Yung, M. (2004). The hierar-

chy of key evolving signatures and a characterization

of proxy signatures. In EuroCrypt, volume 3027 of

LNCS, pages 306–322.

Mambo, M., Usuda, K., and Okamoto, E. (1996). Proxy

signatures: Delegation of the power to sign messages.

IEICE transactions on fundamentals of electronics,

communications and computer sciences, 79(9):1338–

1354.

Pointcheval, D. and Stern, J. (2000). Security arguments

for digital signatures and blind signatures. Journal of

cryptology, 13(3):361–396.

Sahu, R. A. and Padhye, S. (2015). Identity-based multi-

proxy multi-signature scheme provably secure in ran-

dom oracle model. Trans. Emerging Telecommunica-

tions Technologies, 26(4):547–558.

Sarde, P. and Banerjee, A. (2015). A secure id-based proxy

signature scheme from bilinear pairings. International

Journal of Computer Applications, 124(9).

Schuldt, J. C. N., Matsuura, K., and Paterson, K. G. (2008).

Proxy signatures secure against proxy key exposure.

In PKC, volume 4939 of LNCS, pages 141–161.

Singh, H. and Verma, G. K. (2012). Id-based proxy sig-

nature scheme with message recovery. J. Syst. Softw.,

85(1):209–214.

Wang, B. (2008). A new identity based proxy signature

scheme. IACR Cryptology ePrint Archive, 2008:323.

Wu, W., Mu, Y., Susilo, W., Seberry, J., and Huang, X.

(2007). Identity-based proxy signature from pairings.

In Autonomic and Trusted Computing, pages 22–31.

Xu, J., Zhang, Z., and Feng, D. (2005). Id-based proxy

signature using bilinear pairings. In Parallel and

Distributed Processing and Applications-ISPA 2005

Workshops, pages 359–367.

SECRYPT 2016 - International Conference on Security and Cryptography

476