Refinement of UML2.0 Sequence Diagrams for Distributed Systems
Fatma Dhaou
1
, Ines Mouakher
1
, Christian Attiogb
´
e
2
and Khaled Bsaies
1
1
LIPAH, Faculty of Sciences of Tunis, Tunis, Tunisia
2
LINA UMR 6241, University of Nantes, Nantes, France
Keywords:
UML2.0 Sequence Diagrams, Refinement Relation, Sequence Diagrams Refinement, Event-B.
Abstract:
Refinement process applied to UML2.0 Sequence Diagrams (SD) is adopted to deal with the complexity of
modeling distributed systems. The various steps leading to the checking of the refinement of SDs theoretically
as well as practically are explained. A refinement relation possessing the necessary properties, is formalized;
its implementation in the Event-B method is proposed in order to check the correctness of the refinement of
SDs, and to verify some safety, liveness properties and the termination of the new introduced events.
1 INTRODUCTION
Context. The UML2.0 sequence diagrams (SD) are
widely used by designers thanks to their intuitiveness,
the ease of graphical representation, and their high ex-
pressivity, allowing to model complex behaviour of
systems. Refinement process is a privileged approach
adopted by researchers to manage complexity. SDs
must be refined correctly, this requires the formaliza-
tion of refinement relation supporting an incremental
development. Since the semi formality of SD didn’t
allow such a verification, the coupling of a formal
and tooled method supporting this process is recom-
mended.
Motivation. The notion of refinement was well
studied, in several works, for the labeled transition
systems (LTS), and more generally for the modal tran-
sition systems (MTS) (Fischbein et al., 2006). How-
ever, few works are interested in the refinement of
UML2.0 SDs, which are more and more used. In-
tuitively, refinement of SD consists either in substi-
tuting a lifeline by new lifelines and/or detailing the
internal behaviour of a lifeline by adding new sub-
lifelines and eventually new events. We outline two
aspects for the SD: the structural aspect (lifelines,
messages, events, CF) and the semantic aspect that
is its traces. Mainly, the existing approaches that deal
with refinement of SDs focus on one aspect and im-
pose a restrictive hypothesis for the other aspect: i)
most of them use a refinement relation which does
not support explicitly the introduction of new events
in the refined SD; these later are then hidden in order
to verify the refinement relation, which can lead to
some errors of modeling that might not be detected;
ii) other approaches ignore or didn’t deal correctly
with the guards of combined fragments (ALT, OPT,
LOOP), in the formalization of the considered refine-
ment relation that they consider; iii) most of the exist-
ing approaches did not propose efficient tools for the
checking of refinement relation; iv) to our knowledge,
all the approaches are based on trace semantics, and
the verification of the refinement relation requires the
computation of traces of SD pairs. This can lead to
combinatorial explosion of number of traces to gen-
erate. Moreover, they are based on rules of standard
semantics (Object Management Group, 2009) for the
derivation of traces, that are not suitable for SD mod-
eling distributed systems, since they take no account
of the independence of components of distributed sys-
tems.
In our approach, SDs are equipped with an oper-
ational semantics based on causal semantics (Dhaou
et al., 2015), which in turn are based on partial orders
theory; this is suitable for distributed systems, permits
to formalize the refinement relation straightforwardly
and facilitates its verification.
The verification of the approach is absolutely nec-
essary. The choice of a formal method that supports
the refinement process (Schneider, Steve and Tre-
harne, Helen and Wehrheim, Heike, 2012), and which
offers the verification of data as well as the verifica-
tion of traces is primordial.
310
Dhaou, F., Mouakher, I., Attiogbé, C. and Bsaies, K.
Refinement of UML2.0 Sequence Diagrams for Distributed Systems.
DOI: 10.5220/0006005403100318
In Proceedings of the 11th International Joint Conference on Software Technologies (ICSOFT 2016) - Volume 1: ICSOFT-EA, pages 310-318
ISBN: 978-989-758-194-6
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Contribution. The contribution of our work is
manifold: we proposed an approach that deals
with refinement of SDs, while preserving required
behaviours and deals correctly with guards. We
formalize a refinement relation favourable to an
incremental development, it is based on existing
ones that are already defined on guarded LTS.
Finally, we propose a generic implementation with
Event-B/Rodin-ProB, for checking of correctness of
refinement relation.
Organization. The remainder of the article is struc-
tured as follows. In Section 2, we present a case study
that is used to illustrate our approach. In Section 3 we
first present an overview of the operational semantics
of UML2.0 SD, then we formalize our refinement re-
lation. Section 5 is devoted to the implementation of
our approach in Event-B, we provided an overview on
the methodology that allows us to verify the refine-
ment between two SDs. Before concluding in Section
7, we present some related works in Section 6.
2 CASE STUDY
Through the following case study, we show a con-
crete example of an incremental development of be-
haviour of a distributed system. We model the inter-
actions in a restaurant with UML2.0 SD (depicted in
Fig. 1). The restaurant system has independent and
distributed components: the Client, the Head Waiter,
the Kitchen and the Barkeeper. The Client orders
meal and drink to the Head Waiter. This latter trans-
mits the orders respectively to the Kitchen and to the
Barkeeper. Once the orders are ready, the kitchen
and the Barkeeper solicit the Head Waiter to serve
it. Then, the Head Waiter brings the bill. For bill
payment, the Client has several alternatives: he can
pay by cash, by card or by cheque. Once the bill
was paid, the Head Waiter delivers a receipt to the
Client. A possible refinement is depicted in Fig. 2.
The abstract lifeline Head Waiter is substituted by
the new lifelines Waiter1 and Waiter2. The events
of Head Waiter are distributed between Waiter1 and
Waiter2. The lifeline Kitchen delegates the task of
preparation of meal to the new lifeline Cook, which
in turn, once the meal is ready, alerts the Kitchen at
most 3 times. For simplicity, all the abstract events
keep their same name in the refined SD.
3 SET THEORY NOTATIONS AND
DEFINITIONS
This section introduces some necessary rudiments on
UML2.0 SD as well as a part of the set theory no-
tation that we use. The table 1 provides a summary
of set theory notations. We consider a sub-set of SD
containing sequential combined fragment CF.
alt
[type=1]
[type=2]
[type=3]
order_meal
tr_order_meal
prepared_meal
serve_meal
order_drink
tr_order_drink
prepared_drink
serve_drink
bring_bill
pay_cash
pay_card
pay_cheque
issue_a_receipt
Kitchen
Client
H_Waiter
Bar_K
Figure 1: Interactions in a restaurant (SD1).
alt
[type=1]
[type=2 & m >=20]
[type=3 & m >=20]
loop
[0,3]
order_meal
tr_order_meal
delegate
alert
prepared_meal
serve_meal
order_drink
tr_order_drink
prepared_drink
serve_drink
bring_bill
pay_cash
pay_card
pay_cheque
issue_a_receipt
Kitchen
Client
Waiter1
Cook
Bar_k
Waiter2
Figure 2: A refinement of SD1 (SD2).
Table 1: Notations.
Symbols Definition Symbols Definition
C− Domain subtraction 7 Partial injection
 anti domain restriction  Total injection
 range restriction 7 Partial surjection
→ total function →→ Total surjection
→ Bijective function C− Relational overriding
7→ Partial function ran(E) range of a set E
The formal definition of a SD is as follows:
Definition 1 (Sequence Diagram). A
sequence diagram is a tuple SD :
hO, M, EV T, E s, E r, FCT s, FCT r, FCT o, F, <
Caus
i
where:
• O, M, EV T are respectively a finite and non-empty
set of lifelines, messages and events. We consider
Refinement of UML2.0 Sequence Diagrams for Distributed Systems
311

asynchronous messages, the set M is well formed
if every message is identified by a pair of events:
a sent event and a received event.
• E s, E r denote respectively the set of sent events
and the set of received events,
• FCT
s, FCT r are two bijective functions that asso-
ciate respectively for each message a sent event
and a received event,
• FCT o is total surjective function that associates
for each event one lifeline representing the trans-
mitter or the receiver,
• F =< F
1
, F
2
, ..., F
k
> is the sequence of k combined frag-
ments (ALT, OPT; LOOP),
• <
Caus
denotes the partial order relationship which
is non-reflexive.
The definitions of ALT, OPT, LOOP CF depend on
guard, that is a predicate on variables, or can be a tem-
poral constraint.
Definition 2 (Conditional combined frag-
ment (ALT, OPT)). A conditional com-
bined fragment F is a sequence of couples
F =< (guard
1
, OP
1
), (guard
2
, OP
2
), ..., (guard
j
, OP
l
) > where:
guard
i
is the constraint which guards the i
th
operand;
OP
i
is the set of events covered by the i
th
operand.
Definition 3 (Combined fragment (LOOP)). A com-
bined fragment F is a quadruple F = hguard, min, max, OPi
where guard is the constraint which guards the loop
operand, min is the minimum number of iteration,
max is the maximum number of iteration and OP is
the set of events covered by a LOOP CF.
4 REFINEMENT OF SEQUENCE
DIAGRAM
In this section, we present the formalization of the re-
finement relation, and we enunciate the rules that gov-
ern a correct refinement between SD.
4.1 Operational Semantics of Sequence
Diagram
Refinement based on trace semantics requires a metic-
ulous work that consists in generating of all possible
traces of SD, then in their categorization into required
and possible traces (Lu and Kim., 2011) and (øys-
tein Haugen et al., 2005); where possible traces corre-
spond to all possible combinations of SD events, that
are obtained by rules of derivation of traces of the
considered semantics, and required traces are those
that must be preserved when refining the SD. More-
over, these semantics are based on rules of standard
semantics that are not suitable for SD that model
distributed systems. The refinement of guard is not
treated correctly. These drawbacks explain our orien-
tation for defining refinement relation based on oper-
ational semantics that we defined on a previous work
(Dhaou et al., 2015). (Dhaou et al., 2015).
The operational semantics that we proposed, is
useful for the formalization of refinement relation. In-
deed, an operational semantics is concretely given as
a guarded transition system. Besides refinement re-
lation is already well defined on transition system as
a simulation relation. This advantage is exploited to
express our refinement relation in Subsection 4.2. In
addition, in our operational semantics, guards are sup-
ported intuitively. Our proposed operational seman-
tics is different from existing approaches because it is
based on the semantics for the scenario-based lecture
named causal semantics; that is based on rules taking
account of the independence of the objects involved to
interaction, in a given distributed system. Intuitively,
these rules are defined by the set of traces with some
properties which can be summarized as follows: i) the
events of the same lifeline are not necessarily ordered;
ii) two successive events emitted by the same lifeline
are ordered. In certain case of distributed systems, if
they are addressed to the same lifeline, their recep-
tions are ordered; iii) the reception of an event by a
lifeline causes the emission of the event that is suc-
cessive to it. These obvious rules was extended, in
our previous work (Dhaou et al., 2015), to support
SD with the most popular combined fragments (ALT,
OPT, LOOP). Contrarily to the standard semantics, the
computation of traces, in our work, for SD with com-
bined fragment is made without flattening them.
According to this semantics a trace is a sequence
of event occurrences and it may be finite or infinite.
We consider only the finite traces by excluding in-
finite loop. A trace depicts the history of message-
exchange corresponding to executions of the system.
Since, we deal with interleaving semantics, two en-
abled events to be executed may not occur at exactly
the same time. We allow the same event to occur only
once in the same trace, and N times in the LOOP CF.
Definition 4 (Trace). Let EV T be the set of events
in a sequence diagram SD. A trace of SD is a finite
sequence: < e
1
, e
2
, e
3
, e
4
, ..., e
n
> where e
i
∈ EV T .
The operational semantics of a SD is the traces of
events. It is given as a guarded transition system, that
allows to take account of guard
Sem(SD) = hS, S
0
, 4i
where S is the set of possible states of the SD, S
0
is
the initial state, 4 the transition relation.
ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications
312

State. Each state of a SD is expressed with two
variables (state, current instance) such that, the first
one expresses the states of all events of SD, and the
second one expresses the lifeline of the current event.
The variable state is a function
State : EV T → {−1, 0, 1, N}
where 1 and N express that the event is not yet exe-
cuted, and must be executed respectively 1 or N times;
0 and −1 express that the event is respectively con-
sumed or ignored. Initially all the events are not yet
executed (1 or N). The initial state S
0
of SD is when
any event is not yet executed (1 or N). The final state
of SD is when all events are occurred or ignored.
Transition Relation. The events of the guarded
transition system correspond to the events of the con-
sidered SD and some fictitious events. Consequently,
the transition system has two rules such that the first
rule deals with the execution of a single event; and the
second rule handles the fictitious events. The intro-
duction of the fictitious events is necessary to allow
a high flexibility in defining execution strategies for
ALT, OPT and LOOP CF. We define the following set
of fictitious events: evt
f ic
= { f ic
alt
, f ic
opt
, f ic
loop
}.
By disregarding fictitious events, the set of traces of
SD is the same as the set of traces of its correspondent
operational semantics. For each category of event we
define a rule for the guarded transition system. For
instance, for an event e in SD, we associate the fol-
lowing transition:
p
[Guard]e
→ q
de f
≡ ((p, [g] e, q) ∈ 4 ∧ g)
An event e is enabled in state p only when its trigger
conditions hold. The triggers conditions of an event
e consist in: verifying the execution of its preceding
events, it is not yet executed and its guard is true. Af-
ter its execution, its state is decreased and the current
lifeline is updated.
4.2 Formalization of the SD Refinement
Relation
The existing approaches focus on one aspect of refine-
ment by imposing restrictive hypothesis for the other
aspect, this can be constraining. In our work, we tried
to benefit of the advantages of the existing approaches
for proposing an approach that takes account of both
aspect of refinement (structural and semantic) by re-
laxing some hypothesis.
We consider SD with distinct alphabets. We
define a refinement relation with respect to an explicit
mapping between the abstract and refined labels
(lifelines, events). It permits the introduction of new
events and lifelines, and guaranties the preservation
of required behaviours. In addition, the refinement
relation supports intuitively guard since it is defined
as a simulation between guarded LTS (Leuschel,
Michael and Butler, Michael, 2005).
The verification of the correctness of the refine-
ment requires the satisfaction of the rules of the
refinement that must be defined beforehand, and
formalized in the refinement relation.
In the following, we explain the refinement of SD
that we consider, and we give the rules of a correct
refinement that are marked with the symbol (Ri). The
rules are dependents. Structural refinement concerns
the refinement of labels (lifelines, messages) of the
abstract SD.
R1. The events of substituted lifelines must be
inherent by the new substituted lifelines.
R2. The lifelines which are not refined have to keep
the same events.
R3. New events, if they exist, must be exchanged
only between new lifelines.
Indeed, each lifeline can be substituted by new
lifelines or its internal behaviour can be detailed by
adding new sub-lifelines (child lifelines). For the
first case of lifeline refinement, it is obvious that
the abstract events must be distributed between new
lifelines (R1), and the not-refined lifelines must keep
its abstract events (R2). Evidently, the new lifelines
can exchange between them new events (R3).
R4. By remaining in the same level, a behaviour of a
given lifeline can be detailed. Its sub-lifelines must
exchanged exclusively messages with it .
In the second case of lifeline refinement, the internal
behaviour of the refined lifeline (parent lifeline) is
not visible by the other lifelines. Hence, the child
lifelines must exchange exclusively new events with
their parent lifeline (R4), and the parent lifeline keep
the same abstract events (R2).
R5. The new events must terminate.
In order to make verification of refinement relation.
The new events are considered as silent events (τ
events).
Our approach supports semantic refinement by the
reduction of abstract possible traces in the refined
SD. This is achieved by the following methods:
i) changing the order of appearance of some abstract
messages in the refined SD. This is allowed by our
semantics since the events are not ordered along
lifelines. For example, in the refined SD of Fig.2,
the message order drink is moved after the message
serve meal.
ii) reduction of non-determinism for guarded CF:
this is done by strengthening the guards with sup-
plementary conditions (C). For instance, in the
Refinement of UML2.0 Sequence Diagrams for Distributed Systems
313

refined SD of Fig.2, the guards of the second and the
third operand of ALT CF are strengthened such that
guard2 becomes (type = 2 ∧ m >= 20) and guard3
becomes (type = 3 ∧ m >= 20); where m denotes
the amount bill. iii) adding some CF like STRICT or
ASSERT to cover some abstract events in the refined
SD;
R6. All the events of SD1 must be present in SD2 up
to a renaming.
To preserve branches of ALT CF, the rule R6 must be
applied. Indeed, by applying one method among them
we must ensure that each refined trace must have its
counterpart in the abstract SD, by disregarding new
events. Some approaches, proposed the suppression
of some branches of ALT CF (Kruger, 2000) in
order to eliminate non-determinism. However, the
non-determinism offered by branches of alt reflects
choices and must be kept during refinement. But it
can be reduced by strengthening guards.
We consider two sequence diagrams SD1 and SD2 such
that: SDi = hO
i
, M
i
, EV T
i
, E
i
s, E
i
r, FCT
i
s, FCT
i
r, FCT
i
o, F
i
, <
Caus
i
i,
and their operational semantics Sem(SD
i
) = hS
i
, S
0
i
, 4
i
i with
i ∈ {1, 2}.
Structural Refinement. The preliminary step of
the refinement checking is the definition of the map-
ping relation between the considered SDs; this re-
quires the software designer’s intervention. A map-
ping relation between SD1 and SD2 is defined as a
mapping between their lifelines and their messages.
A lifeline O can be either substituted by lifelines, or
its internal behaviour can be detailed by adding new
sub-lifeline(s). Hence, a mapping relation must be
defined between the abstract lifeline and refined life-
lines. Each abstract lifeline must be linked to one or
more lifelines, that can be either not refined lifelines
or new lifelines (substituent or child lifelines).
Definition 5 (Lifeline mapping).
We define the function, lifeline mapping χ, that is a
partial surjective function: χ : O
2
7 O
1
.
All the abstract messages must be present in the re-
fined SD, and the refined SD may contain new mes-
sages.
Definition 6 (Message mapping).
We define the function ρ, ρ : M
2
7→ M
1
, which is a
partial bijection, such that its domain is the set of the
refined messages, and its codomain is the set of the
abstract messages.
For simplicity, we overload the partial bijection ρ as
follows to support events.
ρ :











EV T
2
7→ EV T
1
{(e, e
0
)|e ∈ E s
2
∧ e
0
∈ E s
1
∧
e
0
= FCT s
1
(ρ(FCT s
−1
2
(e)))}∪
{(e, e
0
)|e ∈ E r
2
∧ e
0
∈ E r
1
∧
e
0
= FCT r
1
(ρ(FCT r
−1
2
(e)))}
We introduce a new set New M
2
, and New EV T
2
such that New M
2
= M
2
\ ρ
−1
(M
1
and New EV T
2
=
EV T
2
\ρ
−1
(EV T
1
) to identify respectively the new in-
troduced messages and new events in refined diagram.
Proposition 1. (Does SD2 v
χ
SD1?)
Let SD1 and SD2 be two sequence diagrams in SD.
We define two functions χ and ρ. SD2 is a structural
refinement of SD1 with respect to χ and ρ, denoted
SD2 v
χ,ρ
SD1, if the following conditions hold:
• the abstract messages in the SD2 are mapped to
its correspondents in the SD1 by means of the
function χ: M
1
⊆ ρ(M
2
);
• the abstract lifelines must keep all their abstract
events, and the substitute lifelines inherit the ab-
stract events in SD2:
FCT o
1
= ρ
−1
;(EV T
1
 FCT o
2
);χ
• the new messages exchanged between new life-
lines in the SD2 are linked to the same abstract
lifeline:
(New M
2
)  FCT s
2
;FCT o
2
;χ =
(New M
2
)  FCT r
2
;FCT o
2
;χ
Each item of Prop.1 refers to one or more rules de-
fined above. The first one references R6; the second
one deals with R2, R1 and the third one refers to R3.
This relation is in accordance with Event-B refine-
ment relation. Indeed, we support a refinement re-
lation based on alphabet translation, that requires an
explicit mapping between labels of SD pairs. New
events in refined SD are considered as silent and re-
placed by τ transitions. We introduce the mapping re-
lation between operational semantics pairs associated
to SD pairs.
Semantic Refinement. The refinement relation is
defined as a simulation on operational semantics. Two
models may be compared only if they have the same
alphabet. Therefore, the new events are considered as
silent and replaced by τ transitions.
Definition 7 (States mapping).
Let Sem(SD1) and Sem(SD2) be two operational se-
mantics associated to SD pairs. The mapping rela-
tion R between pairs operational semantics consists
in linking their respective states S
i
with respect to
both functions χ and ρ. S
i
depends on values of the
two variables current instance i and state i; where
i ∈ {1, 2}
ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications
314

• each refined lifeline must be mapped with an ab-
stract one:
current instance 1 = χ(current instance 2)
• by disregarding new introduced events, each ab-
stract event, in the refined SD, must be mapped to
its correspondent in the abstract SD:
(New EV T
2
) C− state 2 = ρ; state.
Proposition 2. (Does SD2 v
R
SD1?)
Let SD1 and SD2 be two sequence diagrams such
that SD2 is a structural refinement of SD1 (SD2 v
χ,ρ
SD1), and Sem(SD
i
) = hS
i
, s
0
i
, 4i their operational
semantics. Moreover, the new events of SD2 must ter-
minate. SD2 is refinement of SD1 with respect to a
map relation R(ρ, χ) denoted SD2 v
R
SD1 if the fol-
lowing conditions hold:
• Initial states are linked : (s
0
1
, s
0
2
) ∈ R
• For each execution of an event e in SD2 which
refines an abstract event e ∈ ρ
−1
(M1), there exists
an execution of ρ(e) in SD1 that is relied to it, with
strengthening of guard, in case of an event whose
its execution depends on guard:
(∀e ∈ ρ
−1
(M
1
)) (∀p ∈ S1) (∀q ∈ S2) (∀q
0
∈ S2)
[(q, p) ∈ R ∧ q
[g]e
→
2
q
0
⇒ (∃p
0
∈ S1)[p
[g
0
]ρ(e)
−→
1
p
0
∧ g ⇒ g
0
∧ (q
0
, p
0
) ∈ R]]
• New events didn’t change the state of abstract SD.
(∀e ∈ New EV T
2
) (∀p ∈ S
1
) (∀q ∈ S
2
) (∀q
0
∈ S
2
)
[(p, q) ∈ R ∧ q
e
−→
2
q
0
⇒ (q
0
, p) ∈ R]
Properties Preserved by Refinement Relation. As
consequence of the Prop.2, we have a trace refine-
ment (Leuschel, Michael and Butler, Michael, 2005),
by disregarding new introduced events in SD2, where
the required behaviours are preserved. The refinement
relation allows the extension of traces, by distinguish-
ing between the observable and the non-observable
events.
It is reflexive, since we have SD1 v
R
SD1 that al-
ways holds. It is transitive, since SD
2
v
R
SD1 and
SD3 v
Q
SD2 implies SD3 v
R;Q
SD1. Finally it is sub-
stitutive because it supports the renaming of abstract
labels in the refined SD.
5 IMPLEMENTATION OF
REFINEMENT RELATION IN
EVENT-B
Our semantics is encoded in Event B (RODIN, 2007),
in such way that proving the consistency (PO) of B
models establishes the correctness of the refinement.
For correctness analysis purpose, SD pairs to be
checked are translated into Event-B specifications;
these specifications are updated with the defined rules
and analyzed with theorem prover Rodin, as well as
checking model ProB. The choice of Event-B method
is justified thanks to several advantages offered by
it. Firstly, the existing similarities between both for-
malisms (Dhaou et al., 2015) provide an immedi-
ate translation of both SD formal definition, that is
based on set theory and predicate logic, and its op-
erational semantics, into Event-B specification. Sec-
ondly, Event-B refinement relation supports naturally
the introduction of new events as well as the ver-
ification of their termination. Moreover, contrarily
to the most refinement relations that require an im-
plicit mapping between labels of SD pairs, Event-B
refinement relation is based on alphabet translation
which requires an explicit mapping between labels of
SD pairs. Hence, errors of modeling are easily de-
tected when the invariant is broken. Finally, Event-
B has a powerful tool that allows the verification of
the correctness of refinement SD. An Event-B spec-
ification is composed by a B-machine and a context.
Event-B machine is mainly made of four elements: a
name, a list of named predicates, the invariants, and
the events. The context referenced by a B-machine is
made of: a name, a list of distinct carrier sets, a list of
constants and a list of named properties.
5.1 Translation of SD into Event-B
Specification
Let SD : hO, M, EV T, E s, E r, FCT s, FCT r, FCT o, F, < Causi and
its operational semantics Sem(SD) = hS, S
0
, 4i. Firstly, we
translate SD formal definition into contexts; to allevi-
ate B specification and facilitate its proofs, we define
two contexts such that: i) in the first context CT X XP,
the concrete values the SD configuration (lifelines,
messages, events) are expressed by sets and constants;
ii) in the second context CT X X that EX T ENDS the
first one, properties that express that the considered
SD is well-formed are marked as theorems. Secondly,
the operational semantics of SD, Sem(SD), is trans-
lated into Event-B machine such that: i) the State is
translated into two variables: state, which is a total bi-
jective function that expresses the state of each event,
and current instance, which expresses the transmitter
or the receiver of the current event; ii) each transition
that belongs to 4 is represented by an event of Event-
B machine.
5.2 Checking of the Correctness of
Refinement between Two SD
Once we translate independently pairs SD into B-spe
Refinement of UML2.0 Sequence Diagrams for Distributed Systems
315

ecifications, we express the mapping relations, de-
fined in Subsection 4.2 that should be proved stati-
cally, for some of them, and dynamically for the other
ones. We add two new contexts CT X 2P and CT X 2,
such that in CT X 2P we express the concrete map-
ping between pairs SD; and in CT X 2 we express
the rules of structural refinement, in Subsection 4.2,
that are marked as theorems to be proved. Tab. 3
depicts the expression of some structural refinement
rules. For instance, R3 is expressed by axiom8, R2
and R1 are expressed by axiom9 and the lifeline map-
ping is expressed by axiom10. The refined machine
is updated by adding the gluing invariant Tab.2 that
expresses the state mapping.
Table 2: Gluing invariant.
inv1: current instance = FCT INSTANCES(current instance r)
inv2: New EV T C−state r = state
Table 3: Some theorems of CTX2.
axm8: ran(New EV T  R FCT o = New INSTANCES
axm9: A FCT o = ((A EV T  R FCT o); FCT INSTANCES)
axm10 :FCT INSTANCES ∈ R INSATANCES → A INSTANCES
Table 4: The event E order drink.
E order drink: not extended extraordinary
REFINES
grd1: ∀EE.((EE ∈ EV T 2 ∧ EE ∈ [Caus2 ∼ [E order drink])) ⇒
(state 2(EE) < state 2(R alert)))
WHERE
grd2: state 2(E order drink) >= 1
THEN
act1: state 2(E order drink) := state 2(E order drink) − 1
act2: current instance 2 = FCT o(E order drink)
END
Concerning the events of the refined machine, we
refund all the abstract events, which corresponds to
message mapping, in addition to the new introduced
events. In Tab. 4, we present an event of the refined
machine: E order drink).
Verification of the Termination of the New Intro-
duced Events. The new events which are intro-
duced in the refined model must not take indefinitely
the control. Event-B method allows to verify this
property. This is done by the definition of an expres-
sion called variant. By demonstrating that the exe-
cution of each new event decreases the variant that
must never goes below zero. Since a variant can-
not be decreased indefinitely, this allows us to prove
that a new event cannot take control forever. As ex-
ample of new event we have E alert. Its status is
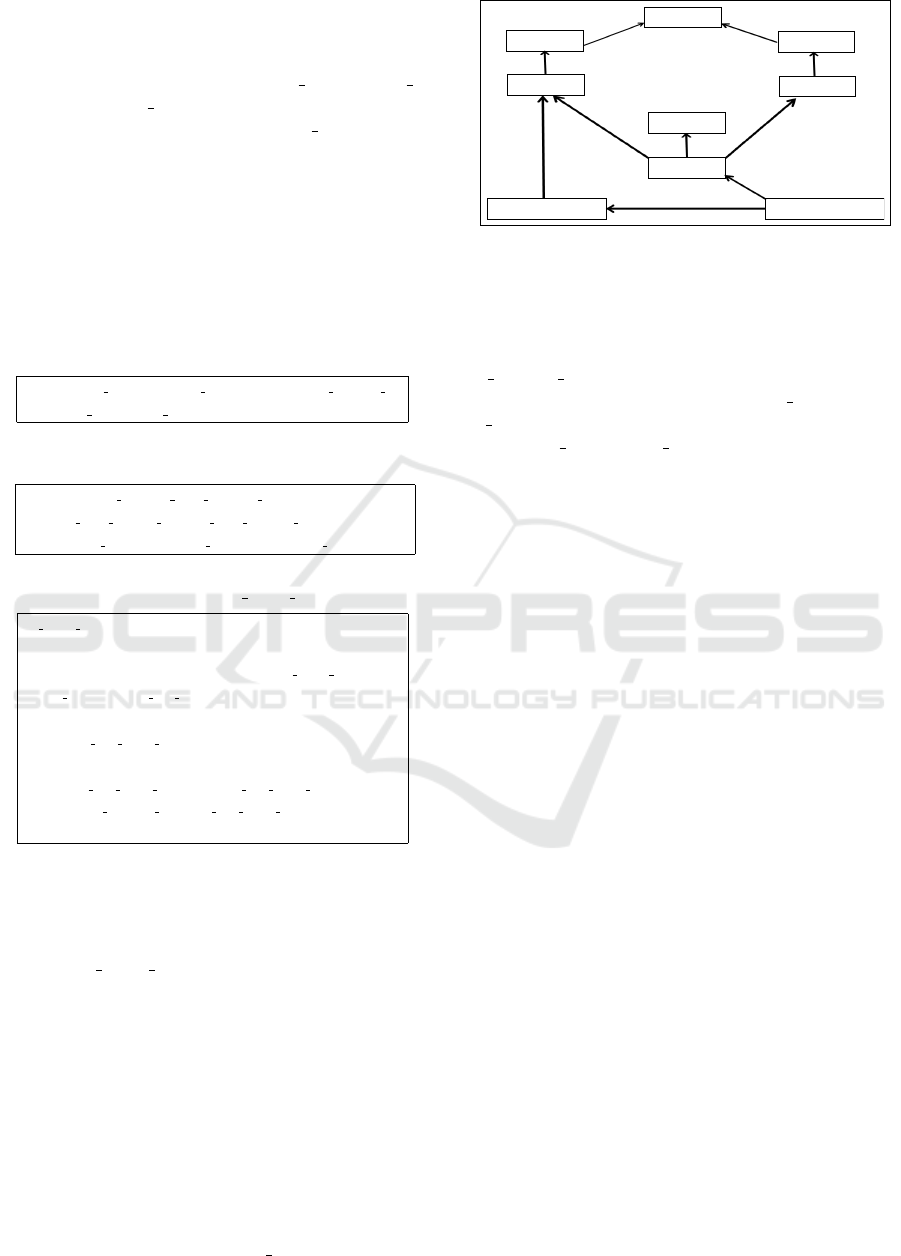
CTXAP
CTX
CTXRP
CTXR
CTX2P
CTX2
CTXA
MACHINE A
MACHINE R
EXTENDS
EXTENDS
EXTENDS
EXTENDS
EXTENDS
EXTENDS
EXTENDS
SEES
REFINES
SEES
Figure 3: The generic architecture of the implementation
process.
set to convergent, which means that for each execu-
tion of this event, the variant is decreased. In the
case study, we have new events, on the one hand
E alert, R alert which can be repeated at maximum
3 times, on the other hand we have E delegate and
R delegate. We define for them the following vari-
ant: ((New event  state r) {1}) ∧N. By proving the
termination of new events, the rule R5 Sec. 4 is sat-
isfied. When all proof obligations of B-specification
are proved, we have a correct structural and semantics
refinement.
The verification of refinement relation of SD pairs
is based on systematic rules of translation. The case
study is totally implemented in Event-B on the ba-
sis of the generic architecture Fig. 3. The refinement
is proved correct; through POs that were either au-
tomatically proved for some of them, or interactively
proved for others ones.
6 RELATED WORKS
Mainly, existing approaches for building behavioural
models of distributed systems by refinement are of
two categories: the first one is based on formal frame-
works, like Input/Output Automata (Peter M. Musial,
2012), the second one is based on scenarios like MSC,
MTS, SD (Kruger, 2000). Despite the rigour of the
approaches of the first category, they remain very hard
which repress their use by engineers. The approaches
of the second category are attractive and intuitive. Our
approach belongs to this category of works.
Two important aspects must be considered for re-
finement SD: i) structural aspect that includes the dif-
ferent features of the SD (lifelines, messages, events,
CF...); ii) semantic aspect that concerns traces. The
existing approaches focus on one aspect by imposing
strict hypothesis for the other aspects.
In (Ohlhoff, 2006), the authors treated the refine-
ment of SD by defining strict rules of a correct struc-
tural refinement of SD that are impractical for de-
ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications
316

signer. The majority of the existing approaches, (Har-
ald, 2003), (Lu and Kim., 2011), (øystein Haugen
et al., 2005), of the second category, required the com-
putation of positive and negative traces sets, but they
are based on rules of standard semantics. Hence, they
do not permit the computation of all possible traces
for SD that models a distributed system. i.e they are
not suitable for such system. In addition, they did
not distinguish between mandatory and possible be-
haviours which can lead to the loss of some manda-
tory behaviours when refining SD; they also ignore
guard conditions. Our approach is more appropriate
and safe for distributed systems, because, it is based
on an operational semantics permitting to avoid the
shortcomings of trace semantics that are related to
the factorial complexity of the computation of traces.
In (øystein Haugen et al., 2005), the authors define
new operator XALT (not yet standardized by OMG)
that permits to express mandatory choices. When re-
fining SD, their approach permitted the loss of alter-
natives expressed by ALT CF when they didn’t permit
the loss of any alternative expressed by XALT opera-
tor. They defined three types of refinement: i) supple-
menting that consists in categorizing inconclusive be-
haviours as either positive or negative; ii) narrowing
that consists to reduce possible behaviours; iii) de-
tailing that permits to increase the granularity of se-
quence diagram. In the work of (Lu and Kim., 2011),
required behaviours are expressed by ALT CF; the au-
thors defined a new semantics by extending the def-
inition of trace by including the guard condition as
an essential element. This extension is mainly made
in order to preserve ALT branches when the SD is re-
fined. In our point of view, this definition is not intu-
itive because the guard is systematically lost when a
trace is generated.
With our operational semantics (Dhaou et al.,
2015), guards are supported intuitively by preserv-
ing the standard definition of trace. Although, in
their works (Lu and Kim., 2011), (øystein Haugen
et al., 2005), the authors claimed that their approach
supports, in addition to the semantic refinement, the
structural one, in the formalized refinement relation,
new labels are hidden without making any prelimi-
nary verification. This leads to many inconsistencies
that can not be detected. For instance, in case of hori-
zontal refinement, two child lifelines of distinct parent
lifelines can exchange new events which is prohibited.
In our refinement relation an explicit mapping be-
tween abstract and refined labels is defined and per-
mits to avoid such inconsistencies.
7 CONCLUSION
This work deals with refinement of SDs that, espe-
cially, model behaviours of distributed systems. To
overcome the limitations of existing approaches, our
proposed approach has the following advantages:
• it considers both structural and semantic refine-
ments of SD: i) by defining clearly rules that gov-
ern a correct structural refinement guiding the de-
signer; ii) by proposing an intuitive and coherent
method for the formalization of refinement rela-
tion. This latter possesses the necessary proper-
ties favorable to an incremental development like
transitivity; it permits the addition of new labels in
the refined SD. It is substitutive since it supports
the renaming of labels; which is a desired prop-
erty in case of reuse of SD and their instantiation,
• it permits to reduce the set of possible abstract
traces in the refined SD, while the required ones,
expressed by ALT CF, are preserved,
• we deal correctly with the guards (of ALT, OPT
and LOOP CF) as well as their refinement,
• our approach is not linked with a target formal-
ism chosen for the implementation. The imple-
mentation processing in Event-B for correction of
refinement relation is generic.
We are extending our proposal to consider SD
with some CF that are particularly important for dis-
tributed systems like parallel operator and co-regions,
as well as time features and nested CF.
REFERENCES
Dhaou, F., Mouakher, I., Attiogb
´
e, C., and Bsaies, K.
(2015). Extending Causal Semantics of UML2.0 Se-
quence Diagram for Distributed Systems. ICSOFT-EA
2015 - Proceedings of the 10th International Confer-
ence on Software Engineering and Applications, Col-
mar, Alsace, France, pages 339–347.
Fischbein, D., Uchitel, S., and Braberman, V. (2006). A
Foundation for Behavioural Conformance in Software
Product Line Architectures. pages 39–48.
Harald, S. (2003). Semantics of Interactions in UML 2.0.
In HCC, pages 129–136.
Kruger, I. H. (2000). Distributed System Design with Mes-
sage Sequence Charts.
Leuschel, Michael and Butler, Michael (2005). Automatic
Refinement Checking for B. In Lau, Kung-Kiu and
Banach, Richard, editor, Formal Methods and Soft-
ware Engineering, volume 3785 of Lecture Notes in
Computer Science, pages 345–359. Springer Berlin /
Heidelberg.
Lu, L. and Kim., D.-K. (2011). Required Behavior of
Sequence Diagrams: Semantics and Refinement. In
Refinement of UML2.0 Sequence Diagrams for Distributed Systems
317

16th IEEE International Conference on Engineering
of Complex Computer Systems (ICECCS), pages 127–
136.
Object Management Group (2009). OMG Unified Model-
ing Language (OMG UML), Superstructure Version
2.2.
Ohlhoff, A. (2006). Consistent Refinement of Sequence
Diagrams in the UML2.0. PhD thesis, Christian-
Albrechts-Universitat zu Kiel, Department of Com-
puter Science Real -time Embedded System Group.
øystein Haugen, Husa, K. E., Runde, R. K., and STAIRS
(2005). Towards Formal Design with Sequence Dia-
grams. In Software and System Modeling, volume 4,
pages 355–357. John Wiley & Sons, Inc.
Peter M. Musial (2012). Using Timed Input/Output Au-
tomata for Implementing Distributed Systems.
RODIN, P. I.-. (2007). Rigorous Open Development Envi-
ronment for Complex Systems. In RODIN Deliverable
D28 Report on Assessment of Tools and Methods.
Schneider, Steve and Treharne, Helen and Wehrheim, Heike
(2012). The behavioural semantics of Event-B refine-
ment. Formal Aspects of Computing, 26(2):251–280.
ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications
318