A Matheuristics for the Single-period Lot Scheduling with Component

Availability Constraints in a Partially Closed

Manufacturing/Remanufacturing System

Davide Giglio and Massimo Paolucci

DIBRIS, University of Genova, Via Opera Pia, 13, 16145, Genova, Italy

Keywords:

Remanufacturing, Production Scheduling, Mixed-integer Programming Modelling, Matheuristics.

Abstract:

An integrated manufacturing/remanufacturing system is considered in this paper with the aim of scheduling

the operations of the manufacturing plant. The system is partially closed in the sense that the raw materials,

necessary for assembling the ﬁnal products, can be obtained both from an internal remanufacturing plant

(which disassembles returned products) and from external suppliers. The manufacturing system is modelled

as a ﬂexible ﬂow shop whose stages represent the different assembly phases leading to the ﬁnal products.

In this paper, an original event-based mixed integer programming (MIP) formulation is presented, whose

objective consists of minimizing, as primary objective, the weighted number of tardy jobs and, as secondary

ones, the ﬁxed and variable purchase costs of raw materials possibly acquired from external suppliers. Due to

the complexity of the problem, the MIP formulation can be used to solve only small instances. For this reason,

a matheuristics is proposed, which consists of three interoperating mathematical programming models: the

ﬁrst model assigns the jobs to the machines; the second model sequences the jobs on the machines; the third

model deﬁnes the external supplies, taking into account the component availability constraints. A preliminary

computational analysis shows the effectiveness of the proposed algorithm.

1 INTRODUCTION

In recent years the research community has increas-

ingly dedicated efforts in dealing with environmen-

tal issues. Among these, the ones relevant to sup-

ply chains, speciﬁcally reverse logistics, represent the

overall framework for the work presented in this pa-

per. Classical supply chain research focuses on the

management and optimization of the ﬂow of mate-

rials and products within a network connecting sup-

pliers, producers, distributors and customers so that

the product demand can be satisﬁed in the right times,

quantities and locations by optimizing the use of the

available resources and the operational costs. To ac-

count for environmental aspects, this structure has

been extended by incorporating reverse ﬂows of ﬁn-

ished products at their end-of-life that are returned by

customers (Fleischmann et al., 2001; Shah, 2005).

Therefore, reverse logistics includes all the logistic

activities allowing to transform the used products,

discarded and then returned by customers, into new

products to be delivered in the market.

Several classes of reverse logistics are distin-

guished according to the way used to recover the re-

turned products (Thierry et al., 1995), i.e., reuse, re-

cycling, and remanufacturing. In reuse, the returned

product (e.g., a pallet) is directly used after some

cleaning or reprocessing; recycling does not maintain

the product but aims at recovering the materials com-

posing it (e.g., plastic); remanufacturing denotes the

industrial process through which the returned prod-

ucts are restored to like-new condition: products are

ﬁrst disassembled, then usable parts are cleaned, re-

furbished and stored into parts inventory; ﬁnally, the

new ﬁnished products are reassembled using the re-

stored parts and possibly new parts (Lund, 1998). In

this way, the need for new materials is diminished, so

increasing the environmentalsustainability of the pro-

duction processes and in general improving the sur-

vivability of companies with respect to the new envi-

ronmental regulations and the environmental aware-

ness of the market.

In this paper the problem of deﬁning the

production schedule in an integrated manufactur-

ing/remanufacturing system is considered. In partic-

ular, the focus is on optimizing the scheduling of the

orders (jobs) in the manufacturing facility taking into

account the constraints due to the use of shared com-

110

Giglio, D. and Paolucci, M.

A Matheuristics for the Single-per iod Lot Scheduling with Component Availability Constraints in a Partially Closed Manufacturing/Remanufacturing System.

DOI: 10.5220/0006005501100120

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 110-120

ISBN: 978-989-758-198-4

ponents that are produced by the remanufacturing fa-

cility and made available through a component stor-

age. The main scheduling objective consists in mini-

mizing the number of orders completed after the due

date, weighted according to the priority of the orders.

In addition, as secondary objective, the possible ac-

quisitions of lots of new components from external

suppliers must be optimized. Indeed, the replenish-

ment plan for the shared components from the reman-

ufacturing facility is assumed given and additional

new components that may be needed should be or-

dered to the external suppliers. Such further supplies

should be needed as late as possible to increase the

possibility of receiving the new components on time,

and they should consist of lots as large as possible to

reduce the ﬁxed costs of supplies.

In the literature the presence of component avail-

ability constraints is considered in both resource-

constrained project scheduling (RCPS) and machine

scheduling, even if few papers can be found in the

latter case. Among them, in (Grigoriev et al., 2005)

the complexity of single machine scheduling with raw

material constraints with the objective of minimizing

the number of tardy jobs or the makespan is analyzed,

stating that some variants of this problem are strongly

NP-hard even with unit processing times, although

polynomially-solvable cases exist. Several types of

mathematical programming models are introduced in

the literature for scheduling problems with compo-

nent availability constraints. The case of assem-

bly scheduling is considered in (Kolisch and Hess,

2000) and (Kolisch, 2000) where RCPS-based mixed-

integer programming (MIP) models, which use time-

indexed variables, are proposed. In general the MIP

models provided in the literature differ for the kind

of time representations, as analysed in (Pinto and

Grossmann, 1995), (Li et al., 2010), and (Mouret

et al., 2011). In particular, in (Li et al., 2010)

three main classes of models are distinguished, i.e.,

slot-based, event-based and sequence-based. Among

them, event-based MIP models have been recently de-

ﬁned to solve RCPS problems (Zapata et al., 2008;

Kon´e et al., 2011; Artigues et al., 2013).

This paper is organized as follows. After hav-

ing formally deﬁned the considered scheduling prob-

lem, in Section 2 an original event-based MIP model

is proposed for its solution. Due to the problem

complexity, this formulation can solve only small in-

stances within acceptable computation times. There-

fore, in Section 3 a matheuristics, which exploits

three interoperating mathematical programmingmod-

els, based on both event-based and sequence-based

MIP formulations, is proposed: the ﬁrst sequence-

based model assigns the jobs to the machines; the

second sequence-based model identiﬁes the overall

priority order among the jobs; the third event-based

model deﬁnes the external supplies, taking into ac-

count the component availability constraints. In Sec-

tion 5 a preliminary computational analysis showing

the effectiveness of the proposed algorithm is reported

and, ﬁnally, conclusions are drawn in Section 6.

2 THE SCHEDULING PROBLEM

An integrated manufacturing/remanufacturing

(“man/reman”) system is considered, in which ﬁnal

products are produced in a manufacturing plant by

assembling raw components supplied both by an

internal remanufacturing facility (which disassem-

bles returned products) and by external suppliers.

A representation of such class of systems is given

in Figure 1. The manufacturing system is modelled

as a ﬂexible ﬂow shop whose stages represent the

different assembly phases which lead to the ﬁnal

products. Let M

be the k-th machine at stage s, with

s ∈ {1, ...,S} and k ∈ {1, ...,N

}, being S the num-

ber of stages and N

the number of parallel machines

which are present at stage s. The remanufacturing

system consists of a disassembling subsystem which

extracts the components to be recovered from the

returned products, and of a refurbishing subsystem

which processes the components bringing them back

to an as-good-as-new state. The disassembling sub-

system is modelled as a ﬂow shop of N

machines,

whereas the refurbishing subsystem consists of a set

of N

parallel machines which perform operations.

Let M

be the k-th machine in the ﬂow-shop of the

disassembling subsystem, with k ∈ {1,..., N

}, and

be the k-th parallel machine in the refurbishing

subsystem, with k ∈ {1,... , N

In this paper, the scheduling of manufacturing ac-

tivities is considered, assuming that the disassembling

and refurbishing operations in the remanufacturing

plant have been already suitably planned and sched-

uled. For this reason, the ﬂow of raw components

from the remanufacturing system to the manufactur-

ing system is assumed given, both for what concerns

times and quantities.

The manufacturing system has to produce a set

of orders that are due at the end of the considered

planning horizon, conventionally set to [0,T], being T

the optimization horizon for the scheduling problem.

This corresponds to process a set of jobs, consisting

of operations that transform raw components into ﬁ-

nal products, and to adopt a common due-date model,

since all the jobs should be completed before the end

of the planning period.

A Matheuristics for the Single-period Lot Scheduling with Component Availability Constraints in a Partially Closed

Manufacturing/Remanufacturing System

111

CUSTOMERS

NEW RAW COMPONENTS

PURCHASE

RETURNS DISASSEMBLY

FLOW SHOP

PRODUCTS ASSEMBLY

FLEXIBLE FLOW SHOP

stage 1 stage 2 stage S

PARALLEL

MACHINES

PARALLEL

MACHINES

PARALLEL

MACHINES

RETURNS

RECOVERED

COMPONENTS

RAW

COMPONENTS

FINAL

PRODUCTS

COMPONENTS

REFURBISHMENT

PARALLEL MACHINES

REMANUFACTURING

SYSTEM

MANUFACTURING

SYSTEM

Figure 1: The integrated manufacturing/remanufacturing (“man/reman”) system.

Let J be the set of jobs and let i, j be two indexes

used to denote a job. A job i, i ∈ J, is character-

ized by the lot size L

and by a priority coefﬁcient

(weight) which, in this paper, is assumed to be a

fractional number proportional to the size of the lot,

that is,W

= L

∑

j∈J

. The processing of a job con-

sists of operations (one per stage) which consume raw

components in order to assemble the lot of ﬁnal prod-

ucts. Let R be the set of raw components and let:

• Q

isr

, with i ∈ J, s ∈ {1,... , S}, r ∈ R, be the num-

ber of raw components of type r which are re-

quired to execute job i at stage s; Q

isr

is deﬁned

as L

· Q

isr

, being Q

isr

the (given) number of com-

ponents r that are required to produce one unit of

job i at stage s (unitary component requirement);

• P

isk

, with i ∈ J, s ∈ {1,. . .,S}, k ∈ {1,... ,N

}, is

the processing time of job i at stage s when as-

signed to machine k; P

isk

is deﬁned as L

· P

isk

, be-

ing P

isk

the (given) time to produce one unit of

job i on machine k at stage s (unitary processing

time).

The remanufacturing plant carries out some dis-

assembling and refurbishing operations aimed at re-

covering raw components from returned products. As

previously discussed, the activities of the remanufac-

turing system are independently planned and sched-

uled. Therefore, it is here assumed that the arrival

times of raw components from the remanufacturing

plant are known in advance. Let H be the planned

number of arrivals of lots of raw components, and let:

• D

, with h ∈ {1,... ,H}, be the time instant of the

h-th arrival (from the remanufacturing system) of

lots of raw components;

• M

, with r ∈ R, h ∈ {1,... ,H}, be the number of

raw components of type r for the h-th arrival.

Raw components are stored in inventories, one per

each kind of components; the value I

, with r ∈ R, de-

notes the initial inventory of raw components of type

r. It is worth observing that such inventories contain

both components recovered by the internal remanu-

facturing plant and the ones acquired from external

suppliers when the recovered components are not suf-

ﬁcient to satisfy the production requirements of the

manufacturing plant.

The considered scheduling problem has the ob-

jective of minimizing the sum of the following cost

terms:

1. weighted number of tardy jobs;

2. variable purchase costs;

3. ﬁxed purchase costs.

The second cost term is weighted by the unitary cost

of raw materials and also by a coefﬁcient which is in-

versely proportional to the time instant at which the

supply is needed. This is justiﬁed by the fact that the

possible acquisitions of new components from exter-

nal suppliers are better planned if such components

are needed as late as possible in the planning period

[0,T]); in this way, indeed, the additional supply or-

ders have a greater chance of being delivered on time

since they are issued at the beginning of the planning

period. The third cost term is proportional to the num-

ber of orders from the external suppliers and it is jus-

tiﬁed by the convenience of grouping the acquisition

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

112

of the different kinds of raw components. The ﬁrst

cost term is the primary objective and therefore it is

weighted by a parameter, denoted as G, whose value

is chosen “sufﬁciently large” to give to this term a

lexicographic priority with respect to the other terms.

In addition, the second and the third term are respec-

tively weighted by coefﬁcients h

, r ∈ R, and H: the

former represents the cost of a unit of raw material

of type r purchased from external suppliers, whereas

the latter represents the ﬁxed cost to be paid for any

distinct purchase of raw materials from external sup-

pliers.

Such a problem can be modelled as a mixed inte-

ger mathematical programming problem as described

in the following subsection.

2.1 The Mathematical Programming

Formulation

The system under concern can be viewed as a

discrete-event system whose state changes at some

discrete instants (of the continuous-time axis) corre-

sponding to the beginning of operations of jobs on

the various machines of the ﬂexible ﬂow shop. In this

regard, the state is basically represented by the list

of jobs that have started their execution (one list per

each stage of the system), and by the inventory level

for each class of raw materials; the system state is up-

dated at each of the discrete instants, by adding the

job that starts its processing (at a certain stage) to the

list of started jobs, and by updating the inventory lev-

els according to the number of raw materials required

by the starting job, the size of the lots of refurbished

raw components that are possibly provided by the re-

manufacturingplant, and the amount of new raw com-

ponents that are purchased from the external suppliers

if necessary. Thus, a continuous-time event-based ap-

proach is here proposed to solve the scheduling prob-

lem. The number of events is N = S· |J|, being |J| the

number of jobs to be processed in the ﬂow shop.

The decision variables are the following:

• s

∈ R, s

≥ 0, with i ∈ J, s ∈ {1,.. .,S}, repre-

sents the start time of job i at stage s;

• x

ijsk

∈ {0,1}, with i, j ∈ J, i 6= j, s ∈ {1,..., S},

k ∈ {1,... ,N

}, is a binary sequencing variable

such that x

ijsk

= 1 if both job i and job j are pro-

cessed at stage s by machine k and job i is se-

quenced before job j, namely

ijsk



1, if i, j assigned to k and s

< s

0, otherwise

(1)

• w

isk

∈ {0,1}, with i ∈ J, s ∈ {1,... , S}, k ∈

{1,. . .,N

}, is a binary assignment variable such

that w

isk

= 1 if job i is processed by machine k at

stage s;

• u

∈ {0,1}, with i ∈ J, is a binary variable such

that u

= 1 if job i completes after its due date

(tardy job), namely



1, if s

∑

k=1

iSk

> T

0, otherwise

(2)

• y

ise

∈ {0, 1}, with i ∈ J, s ∈ {1,...,S}, e ∈

{1,. . .,N}, is a binary variable associating events

with jobs; y

ise

= 1 if the processing of job i at

stage s starts in correspondence of event e;

• t

∈ R, t

≥ 0, with e ∈ {1, ...,N}, represents the

time of occurrence of event e;

• z

∈ {0,1}, with h ∈ {1, . ..,H} , e ∈ {1,... ,N},

is a binary variable such that z

= 1 if the time

of occurrence of event e does not precede the h-th

arrival of raw components from the remanufactur-

ing system, namely



1, if t

≥ D

0, otherwise

(3)

• a

∈ R, a

≥ 0, with r ∈ R, e ∈ {1,..., N}, repre-

sents the number of new raw components of type

r, purchased from the external suppliers, arriving

at instant t

(since needed to execution of the job

associated with event e);

• α

∈ {0,1}, with e ∈ {1,... ,N}, is a binary vari-

able such that α

= 1 if any new component from

the external suppliers arrives at instant t

, namely



1, if

∑

r∈R

> 0

0, otherwise

(4)

• i

∈ R, i

≥ 0, with r ∈ R, e ∈ {1,... , N}, rep-

resents the number of raw components of type r

in the inventory after the occurrence of event e at

instant t

(inventory level).

The mathematical programming model is the fol-

lowing.

min



∑

i∈J

∑

e=1

(N − e)

∑

r∈R

+ H

∑

e=1



(5)

subject to:

≤ Vα

, ∀r ∈ R, ∀e ∈ {1,...,N} (6)

∑

k=1

iSk

− Bu

≤ T , ∀i ∈ J (7)

A Matheuristics for the Single-period Lot Scheduling with Component Availability Constraints in a Partially Closed

Manufacturing/Remanufacturing System

113

≥ s

i(s−1)

(s−1)

∑

k=1

i(s−1)k

∀i ∈ J, ∀s ∈ {2,..., S} (8)

≥ s

+ P

isk

− B(1− x

ijsk

) ,

∀i, j ∈ J , i 6= j, ∀s ∈ {1, ..., S},

∀k ∈ {1,. . .,N

} (9)

∑

k=1

isk

= 1 , ∀i ∈ J, ∀s ∈ {1,...,S} (10)

2(x

ijsk

+ x

jisk

) ≤ w

isk

+ w

jsk

∀i, j ∈ J , i 6= j, ∀s ∈ {1, ..., S},

∀k ∈ {1,. . .,N

} (11)

ijsk

+ x

jisk

≥ w

isk

+ w

jsk

− 1 ,

∀i, j ∈ J , i 6= j, ∀s ∈ {1, ..., S},

∀k ∈ {1,. . .,N

} (12)

∑

e=1

ise

= 1 , ∀i ∈ J, ∀s ∈ {1,..., S} (13)

∑

i∈J

∑

s=1

ise

= 1 , ∀e ∈ {1, . ..,N} (14)

≥ t

− B(1− y

ise

) ,

∀i ∈ J , ∀s = 1,... , S, ∀e ∈ {1,... , N} (15)

≥ s

− B(1− y

ise

) ,

∀i ∈ J , ∀s = 1,... , S, ∀e ∈ {1,... , N} (16)

≥ D

− B(1− z

) ,

∀h ∈ {1,..., H} , ∀e ∈ {1,.. . ,N} (17)

≤ D

+ Bz

∀h ∈ {1,..., H} , ∀e ∈ {1,.. . ,N} (18)

≥ z

h(e−1)

∀h ∈ {1,..., H} , ∀e ∈ {2,.. . ,N} (19)

≥ t

e−1

, ∀e ∈ { 2,..., N} (20)

= I

∑

h=1

∑

f=1

−

∑

f=1

∑

i∈J

∑

s=1

isr

isf

∀r ∈ R, ∀e ∈ {1,. ..,N} (21)

The ﬁrst term of the objective function (5) corre-

sponds to the weighted number of tardy jobs; the sec-

ond term is the acquisition cost from external suppli-

ers of new components, where the multiplier N− e pe-

nalizes the acquisitions needed early in the planning

period; the third term is the ﬁxed acquisition cost. The

coefﬁcient G is ﬁxed much greater than parameters h

r ∈ R, and H such that the weighted number of tardy

jobs is the primary objective. Constraints (6) allow

determining the number of purchases from the exter-

nal suppliers, whereas constraints (7) establish which

jobs are tardy. Constraints (8) impose that the start

time of any job i at a stage s must be greater than

the sum of the start time and the processing time of

job i at the previous stage. Constraints (9) deﬁne the

sequence of the jobs on the machines at each stage;

given two distinct jobs i and j, if i precedes j on

machine k at stage s then x

ijsk

= 1 and (9) becomes

≥ s

+ P

isk

, imposing that job j starts after the

completion of job i; otherwise, if x

ijsk

= 0, the rel-

evant constraint is always satisﬁed. Constraints (10)

guarantee that each job at each stage is assigned to

one and only one machine. The joint role of con-

straints (11) and (12) is that of forcing a sequence or-

der among pairs of jobs that are assigned to the same

machine; indeed, if two jobs i and j are both assigned

to machine k, the variables w

isk

and w

jsk

are equal to

1 and the constraints (11) and (12) are equivalent to

ijsk

+ x

jisk

= 1, then either “i precedes j” or “j pre-

cedes i” and machine k. Constraints (13) and (14)

state that only one event can be associated with the

start time of a job and viceversa. Constraints (15)

and (16) associate the timee of occurrence of the

events with the start times of the jobs (when y

ise

= 1

such constraints reduce to t

= s

). Similarly, con-

straints (17) and (18), together with (19), associate the

arrivals of components from the remanufacturing sys-

tems to events. Constraints (20) impose the time se-

quencing of events and ﬁnally, constraints (21) com-

pute the inventory levels for the components in corre-

spondence of each event.

3 THE PROPOSED

MATHEURISTICS

The MIP model presented in the previous section can

be used to solve the considered class of problems

only in the case of small instances. This problem

indeed is NP-hard since it generalizes the problem

of minimizing the number of tardy jobs on parallel

machines proved to be NP-hard in (Garey and John-

son, 1990). For this reason, in this paper an heuris-

tic algorithm to solve the problem even in the case of

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

114

STEP 1STEP 2STEP 3

PSfrag

Goal

Objective (min)

Fixed variables

Solution (main)

Job assignment

Makespan

none

isk

, ∀i ∈ J, ∀s ∈ {1, .. ., S} , and ∀k ∈ {1, .. ., N

}

Job sequencing

Weighted number of tardy jobs

isk

, ∀i ∈ J, ∀s ∈ {1, .. ., S} , and ∀k ∈ {1, .. ., N

}

ijsk

, ∀i, j ∈ J, ∀ s ∈ {1,. .. ,S}, and ∀k ∈ {1,. .. ,N

}

Components acquisition

Weighted number of tardy jobs and (variable and ﬁxed) purchase costs

isk

and y

ise

, ∀i ∈ J, ∀ s ∈ {1,...,S}, ∀k ∈ {1,...,N

}, and ∀e ∈ N

, ∀r ∈ R and ∀e ∈ {1,. .. ,N}

Figure 2: The structure of the proposed matheuristics.

medium and large instances is proposed. In partic-

ular, a matheuristic algorithm based on a decompo-

sition heuristics implemented through the interoper-

ation of different mathematical programming models

is introduced in the following.

The basic idea is to decompose the problem de-

cisions in a series of sub-problems. First of all, the

decisions on the assignment of the jobs to the avail-

able machines are separated from the ones relevant

to the sequencing of the jobs on the machines; sec-

ondly, the timing decisions are taken considering the

component availability constraints only after having

assigned and scheduled the jobs at the various stages

of the ﬂexible ﬂow shop. Such an approach appears

promising having adopted a common due-date model

and being the manufacturing/remanufacturing system

partially closed. As a matter of fact, a strategy for

minimizing the number of tardy jobs in case of a com-

mon due-date can be that of balancing the utiliza-

tion of the machines through a suitable job assign-

ment and then scheduling the jobs trying to minimize

the makespan. Moreover, since it is assumed always

possible to acquire the needed additional new compo-

nents from the external suppliers and being the penal-

ization of such additional supplies a secondary objec-

tive, then it is reasonable to consider the component

availability constraints only in the ﬁnal timing sub-

problem.

More speciﬁcally, the proposed matheuristics con-

sists of three steps:

1. the jobs are assigned to the machines at each stage

of the ﬂexible ﬂow shop with the objectiveof min-

imizing the makespan; this problem is solved in

a short computation time by a very simple MIP

model, presented in Section 3.1, which assigns the

jobs on the basis of their processing times P

isk

; the

solution of this step is used to ﬁx the values of

the binary assignment variables, i.e., w

isk

, ∀ i ∈ J,

∀s ∈ {1,..., S}, and ∀k ∈ {1,...,N

};

2. the jobs are scheduled on the machines, at each

stage of the ﬂexible ﬂow shop, without consid-

ering the component availability constraints; to

this end a simpliﬁed version of the MIP model

shown in Section 2.1, as reported in section 3.2,

is considered: since the component availability

constraints are not taken into account, only the

weighted number of tardy jobs is minimized and

constraints (6) and (13)÷(21) become not nec-

essary; in addition, w

isk

are no longer decision

variables since they are ﬁxed to the values ob-

tained by step 1; the solution of such a model

provides the values of the binary sequencing vari-

ables, i.e., x

ijsk

, ∀i, j ∈ J, ∀s ∈ {1,..., S}, and

∀k ∈ {1,. . .,N

};

3. the possible additional component acquisitions

from the external suppliers are determined on the

basis of the component availability constraints; at

this step the MIP model presented in section 2.1

is solved, having ﬁxed the values of the binary as-

signment variables w

isk

, ∀i ∈ J, ∀s ∈ {1,.. . ,S},

and ∀k ∈ {1,. . .,N

}, obtained at step 1 and also

the values of the variables y

ise

, ∀i ∈ J, ∀s ∈

{1,. . .,S}, and ∀e ∈ {1, ...,N}, computed accord-

ing to the overall order among all the job oper-

ations determined by the values of the start time

variables s

, ∀i ∈ J, ∀s ∈ {1,... ,S}, found at step

Such an approach, which is depicted in Figure 2, does

not guarantee to ﬁnd an optimal solution; however,

the preliminary experiments discussed in Section 5

show that the proposed heuristics is able to ﬁnd in

minutes solutions better than the ones yielded by the

MIP solver in one hour.

A Matheuristics for the Single-period Lot Scheduling with Component Availability Constraints in a Partially Closed

Manufacturing/Remanufacturing System

115

3.1 The Model for Step 1

The MIP model used at the ﬁrst step of the proposed

matheuristics to determine the assignment of the job

operations to the machines for each stage of the ﬂexi-

ble ﬂow shop is the following.

min C

max

(22)

subject to:

max

≥ c

∀s ∈ {1,..., S} , ∀ k ∈ {1,.. .,N

} (23)

∑

i∈J

isk

∀s ∈ {1,..., S} , ∀ k ∈ {1,.. .,N

} (24)

∑

k=1

isk

= 1 , ∀i ∈ J, ∀s ∈ {1,...,S} (25)

In this model, C

max

denotes the makespan, whereas

∈ R, c

≥ 0, with s ∈ {1,... , S}, k ∈ {1,... , N

is a decision variable representing the completion

time of the last operation on machine k at stage s.

The objective function (22) corresponds to the min-

imization of the makespan, which is deﬁned through

constraints (23). Constraints (24) compute, for each

stage of the ﬂexible ﬂow shop, the sum of the pro-

cessing times of all operations assigned to a certain

machine, i.e., the completion time of the last opera-

tion on such machine. Finally, constraints (25) im-

pose that each job is assigned, at each stage, to one

and only one machine.

3.2 The Model for Step 2

The MIP model exploited at the second step for se-

quencing the operations of jobs on the machines, at

each stage of the ﬂexible ﬂow shop, disregarding the

componentavailability constraints, is illustrated in the

following.

min



∑

i∈J



(26)

subject to (7)÷(12).

The objective function (26) minimizes the

weighted number of tardy jobs. This model cor-

responds to a relaxation of the MIP model in Sec-

tion 2.1, where only the variables relevant to sequenc-

ing decisions are used, having ﬁxed the assignment

variables and neglecting the ones used to model the

component availability constraints that link the job

operations to the events.

3.3 The Model for Step 3

The MIP model introduced in section 2.1 is employed

at the last step of the matheuristics to determines both

the timing of the job operations and the acquisitions

from external suppliers of the different types of com-

ponents possibly needed to process the job operations,

on the basis of the availability and the usage of the

different components.

As previously pointed out, this model is solved at

step 3 having ﬁxed the variables w

isk

and y

ise

accord-

ing to the solutions obtained at steps 1 and 2, respec-

tively. In particular, the values of the variables y

ise

are

determined ﬁrst sorting the values of the N variables

in non decreasing order (ties are broken arbitrar-

ily) and then assigning the events e ∈ {1, . ..N} to the

job operations identiﬁed by the pairs (i,s) according

to the obtained order. Finally, if an event e is assigned

to the job operation (i,s), then it is ﬁxed y

ise

= 1, oth-

erwise y

ise

= 0.

4 EXAMPLE

A small instance of the scheduling problem is con-

sidered in this section with the aim of showing the

application of the proposed matheuristics.

Let the manufacturing system consists of three

stages (S = 3) and two machines per stage (N

= 2

∀s ∈ {1,...,S}). The system processes two types of

raw components (R = {1,2}) and the remanufactur-

ing plant provides two lots of refurbished “as-good-

as-new” raw components (H = 2); the lot sizes M

and the arrival times D

are reported in table 1 (which

also includes the initial inventoryof rawcomponents).

Five jobs J

,... ,J

must be carried out by the

manufacturing system. Values Q

isr

and P

isk

, repre-

senting respectively the number of raw components r

required to execute job i at stage s and the process-

ing time of job i when processed by machine M

stage s, are reported in tables 2 and 3. Moreover, the

weights of jobs in the cost function are W

= 0.169,

= 0.262, W

= 0.123, W

= 0.2, and W

= 0.246.

Finally, the common due-date for all jobs is T = 25.

This small instance of the problem has been

solved through the proposed matheuristics. At the

ﬁrst step, jobs are assigned to machines in all the

stages of the ﬂexible ﬂow shop; the solution of this

step is reported in table 4. In the second step, jobs are

sequenced on the assigned machines without taking

into account the component availability constraints;

the solution of this step is reported in table 5.

In the second step of the matheuristics, the event

assignment is also performed, that is, the assignment

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

116

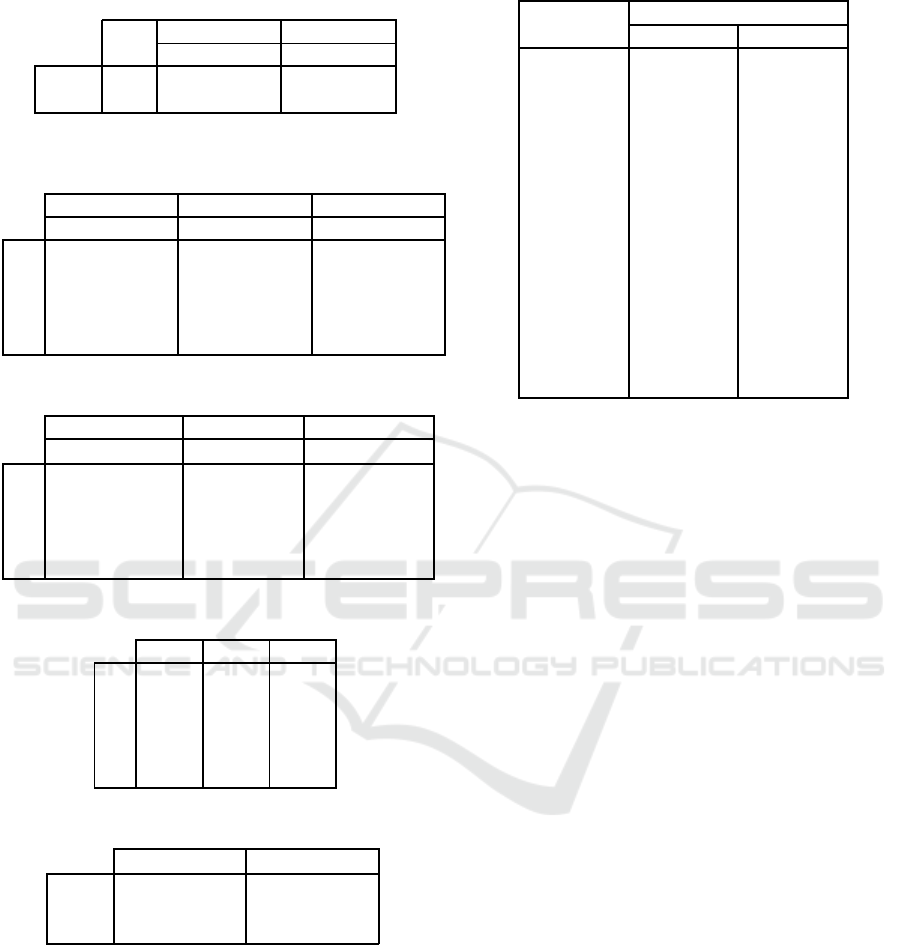
Table 1: Example – Lots of refurbished raw components

and M

) and initial inventory levels (I

h = 1 h = 2

r = 1 500

17.92

221

4.99

160

r = 2 200 195 106

Table 2: Example – Number of raw components that are

required to execute jobs (Q

isr

s = 1 s = 2 s = 3

r = 1 r = 2 r = 1 r = 2 r = 1 r = 2

88 66 77 99 55 55

51 68 153 68 17 51

56 64 48 56 32 24

91 91 117 52 65 52

16 128 112 32 64 80

Table 3: Example – Processing times of jobs (P

isk

s = 1 s = 2 s = 3

1,1

2,1

1,2

2,2

1,3

2,3

4.35 10.04 6.03 7.33 2.85 5.99

11.66 5.52 9.98 6.35 9.89 6.24

5.24 5.82 7.41 6.96 5.72 3.13

10.44 7.9 4.19 9.11 8.26 11.24

14.09 10.17 5.03 8.03 15.1 11.47

Table 4: Example – Solution of step 1: job assignment.

s = 1 s = 2 s = 3

1,1

1,2

1,3

2,1

2,2

2,3

2,1

2,2

1,3

2,1

1,2

1,3

1,1

1,2

2,3

Table 5: Example – Solution of step 2: job sequencing.

1,s

2,s

s = 1 J

→ J

s = 2 J

→ J

s = 3 J

→ J

of job operations to the ordinal numbers of the event

from 1 to 15 (in general, from 1 to S· |J|) according

to the job operation start times. Such an association

“(event #, job start)”, which is reported in table 6, is

obviously made in accordance with the job sequenc-

ing shown in table 5. The solution of step 2 is also

represented by the Gantt chart illustrated in ﬁgure 3.

The solution in ﬁgure 3 can be not feasible with

respect to the component availability constraints. At

step 3, such constraints are actually considered; how-

ever, in order to speed up the determination of the op-

Table 6: Example – Solution of step 2: event assignment.

Event #

Associated job start

job stage

2 J

3 J

4 J

5 J

6 J

9 J

10 J

11 J

12 J

13 J

timal solution, the assignment/sequencing of the jobs

and the assignments of the events to the job opera-

tions are ﬁxed to the values provided by the ﬁrst two

steps of the matheuristics. Therefore, the solution of

step 3, which is illustrated through the Gantt chart

in ﬁgure 4, is very similar to the one obtained after

step 2; however, it is easy to notice that some opera-

tions are delayed to satisfy the component availabil-

ity constraints. In addition, such delays are also due

to the fact that, when new raw components must be

purchased from the external suppliers to satisfy the

component availability constraints, it is convenient to

delay the purchase as much as possible.

In conclusion, the Gantt chart illustrated in ﬁg-

ure 4 represents the ﬁnal solution of the proposed

matheuristics.

5 COMPUTATIONAL

EXPERIMENTS

The performances of the proposed matheuristics were

evaluated considering a set of 25 problem instances

that were randomly generated. Instances from #1 to

#10 are relevant to a ﬂow-shop of 3 stages, includ-

ing 3, 2, and 3 machines for the instances #1-5 and

4, 3, and 4 machines for the instances #6-10. The

number of jobs is 10 for the instances #1-5 and 20 for

the instances #6-10. The instances from #11 to #25

are relevant to a ﬂow-shop of 4 stages, including 4, 3,

4, and 3 machines for all instances; in this case, the

number of jobs is 30 for the instances #11-15, 60 for

the instances #16-20, and 90 for the instances #21-

25. According to such characteristics the considered

A Matheuristics for the Single-period Lot Scheduling with Component Availability Constraints in a Partially Closed

Manufacturing/Remanufacturing System

117

STAGE 1STAGE 2STAGE 3

1,1

2,1

1,2

2,2

1,3

2,3

0 10

due date

Figure 3: Gantt chart of the solution after step 2.

STAGE 1STAGE 2STAGE 3

1,1

2,1

1,2

2,2

1,3

2,3

0 10

due date

Figure 4: Gantt chart of the solution after step 3 (ﬁnal solution of the matheuristics).

Table 7: Comparison between Cplex and the proposed matheuristics.

Instance Njobs Nstages

Cplex matheuristics

Comparison

Opt CPUOpt Obj NumTard CPU

1 10 3 92.20 38.6 96.10 9 1.3 +4.2%

2 10 3 99.90 2.7 99.90 10 2.9 0.0%

3 10 3 90.20 61.9 100.20 10 2.0 +11.1%

4 10 3 91.30 762.6 95.60 9 2.9 +4.7%

5 10 3 88.00 345.6 94.40 9 3.8 +7.3%

6 20 3 83.40 3600.1 51.90 10 47.1 −37.8%

7 20 3 79.40 3604.3 40.80 8 43.1 −48.6%

8 20 3 69.80 3600.9 40.00 8 114.3 −42.7%

9 20 3 86.16 3600.4 51.81 10 8.3 −39.9%

10 20 3 91.13 3600.4 45.88 8 11.9 −49.7%

11 30 4 100.87 3601.6 48.79 14 306.9 −51.6%

12 30 4 102.30 3600.9 48.15 11 312.7 −52.9%

13 30 4 94.61 3600.8 52.06 13 308.6 −45.0%

14 30 4 110.20 3599.7 60.72 13 305.7 −44.9%

15 30 4 92.35 3600.6 37.50 8 308.3 −59.4%

16 60 4 152.56 3603.2 95.82 29 607.7 −37.2%

17 60 4 145.46 3603.3 84.48 22 608.2 −41.9%

18 60 4 150.03 3604.6 89.78 27 556.5 −40.2%

19 60 4 145.12 3604.5 85.11 26 559.6 −41.4%

20 60 4 157.49 3603.9 92.53 23 608.9 −41.2%

21 90 4 – 3614.0 169.57 51 627.5 –

22 90 4 – 3614.1 148.80 42 631.9 –

23 90 4 – 3625.6 154.03 45 631.2 –

24 90 4 – 3623.4 136.47 34 631.4 –

25 90 4 – 3623.3 172.11 48 633.5 –

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

118

Table 8: Values obtained in each step of the proposed matheuristics.

Instance Njobs Nstages

step 1 step 2 step 3

Cmax CPU WNTJ CPU OverallObj CPU

1 10 3 33.15 0.7 96.10 0.5 96.10 0.0

2 10 3 43.18 1.7 99.90 0.7 99.90 0.5

3 10 3 31.41 0.9 100.20 0.5 100.20 0.7

4 10 3 40.93 0.7 95.60 0.7 95.60 1.5

5 10 3 35.66 2.1 94.40 0.9 94.40 0.7

6 20 3 39.14 0.4 51.90 46.1 51.90 0.6

7 20 3 37.57 0.5 40.80 42.0 40.80 0.6

8 20 3 35.14 0.5 40.00 113.1 40.00 0.7

9 20 3 40.18 0.3 51.60 7.8 51.81 0.2

10 20 3 35.22 0.5 45.00 10.7 45.88 0.6

11 30 4 60.85 2.6 46.90 300.5 48.79 3.8

12 30 4 52.85 3.0 39.70 300.2 48.15 9.4

13 30 4 58.77 2.1 49.40 300.6 52.06 5.9

14 30 4 62.43 1.4 53.50 300.1 60.72 4.2

15 30 4 45.60 0.9 33.40 300.5 37.50 6.9

16 60 4 105.93 1.6 48.40 300.6 95.82 305.6

17 60 4 109.33 2.4 41.80 300.4 84.48 305.5

18 60 4 108.80 1.5 44.40 300.3 89.78 254.7

19 60 4 111.27 2.5 44.80 300.5 85.11 256.6

20 60 4 98.34 3.9 40.10 300.8 92.53 304.2

21 90 4 166.33 1.2 57.30 300.6 169.57 325.8

22 90 4 170.70 8.7 46.70 300.6 148.80 322.6

23 90 4 170.84 5.1 50.90 300.3 154.03 325.8

24 90 4 156.82 5.0 40.00 300.3 136.47 326.1

25 90 4 165.91 4.9 52.10 300.4 172.11 328.2

instances require to schedule a number of operations

ranging from 30 to 360. In addition, the MIP model

of Section 2.1 needs 2,074 variables (1,830 binary)

and 4,560 constraints for the smallest instances and

247,414 variables (244,530 binary) and 602,820 con-

straints for the largest ones.

The IBM ILOG Cplex 12.6.2 MIP Solver was

used to solve the MIP model presented in section 2.1

imposing a time limit of 1 hour. The solver was able

to optimally solve only the instances #1-5, whereas

it reached the time limit for the instances #6-20, and

it did not ﬁnd any feasible solution for the instances

#21-25. The results obtained with Cplex are reported

in the columns 4-5 of Table 7.

The three MIP models which constitute the

matheuristics were also implemented with the solver

Cplex 12.6.2. In this case, a time limit of 5 min-

utes was imposed for solving each step. The re-

sults obtained with the proposed heuristic approach

are reported in the columns 6-9 of Table 7. As it

can be noted in this table, the instances #1-5 in the

ﬁrst group were optimally solved by Cplex, whereas

the matheuristics obtained the optimal solution for

instance #2 only; however, for the other four in-

stances in the ﬁrst group the matheuristics found a

slightly larger value (with an average percentage de-

viation, given by the ratio (matheuristics

result −

solver

result)/solver result, of 6.8%). Differently,

the matheuristics found for the instances #6-20 very

better solutions than the ones provided by Cplex in

1 hour. As it can be observed in Table 7, for the

instances #6-20 the matheuristics produced solutions

whose overall average percentage deviation from the

ones yielded by Cplex is −45.0%. No comparison is

possible for the instances #21-25 since the MIP solver

was unable to ﬁnd a feasible solution in 1 hour. For

what concern the computational burden of the pro-

posed approach, it is worth noting that the solution of

the MIP model at step 2 reached the 5 minutes time

limit for the instances #11-25, whereas the solution of

the MIP model at step 3 reached the same time limit

for the instances #16-25. The details about the solu-

tions provided at each step of the matheuristics and

the corresponding CPU times are reported in Table 8

(note that the CPU times reported for the step 3 for

some of the instances #16-25 are greater than 5 min-

utes as they include also the time needed to generate

the MIP model).

A Matheuristics for the Single-period Lot Scheduling with Component Availability Constraints in a Partially Closed

Manufacturing/Remanufacturing System

119

On the basis of these results, it can be concluded

that the proposed approachcan be an effectivemethod

to ﬁnd, in an acceptable short time, good solutions for

the problem under concern.

6 CONCLUSIONS

In this work, an original matheuristics is proposed to

solve a scheduling problem in an integrated manufac-

turing/remanufacturingsystem. The matheuristics de-

composes the decisions related to the assignment of

the jobs to the machines, the sequencing of the jobs

on the machines, and the determination of the addi-

tional acquisitions from external suppliers of needed

components into three separate (but interoperating)

mathematical programming models. In this way, it

is possible to obtain, in short computation times, so-

lutions to medium-large instances of the problem that

are much better than the ones yielded within one hour

of computation by solving the complete MIP model.

Besides, an event-based formulation is proposed for

the considered problem as it is suitable to represent

the discrete-event dynamic of the system under con-

cern and the interactions among the remanufacturing

plant, the external suppliers and the manufacturing

system.

The presented experimental analysis, based on 25

randomly generated instances of the problem of dif-

ferent sizes, points out the effectiveness of the pro-

posed algorithm when few minutes are available to

generate a solution. A more extensive tests will be

performed in the next developments of this research.

For what concerns future research directions, cur-

rent activities on this topic are mainly related to the

scheduling of disassembling and refurbishing activ-

ities in the remanufacturing system, taking into ac-

count uncertainties which naturally characterize the

return of ﬁnished products. In addition, a next step

of this research will consider the problem of planning

the remanufacturing and manufacturing activities in

an integrated way, so deﬁning also the schedule of the

remanufacturing system to better match the compo-

nent requirements issued by the manufacturing sys-

tem to satisfy the customer demand.

REFERENCES

Artigues, C., Brucker, P., Knust, S., Kon´e, O., Lopez, P., and

Mongeau, M. (2013). A note on “event-based {MILP}

models for resource-constrained project scheduling

problems”. Computers & Operations Research,

40(4):1060–1063.

Fleischmann, M., Beullens, P., Bloemhof-Ruwaard, J. M.,

and Van Wassenhove, L. N. (2001). The impact of

product recovery on logistics network design. Produc-

tion and Operations Management, 10(2):156–173.

Garey, M. R. and Johnson, D. S. (1990). Computers

and Intractability; A Guide to the Theory of NP-

Completeness. W. H. Freeman & Co., New York, NY,

USA.

Grigoriev, A., Holthuijsen, M., and van de Klundert, J.

(2005). Basic scheduling problems with raw ma-

terial constraints. Naval Research Logistics (NRL),

52(6):527–535.

Kolisch, R. (2000). Integrated scheduling, assembly area-

and part-assignment for large-scale, make-to-order as-

semblies. International Journal of Production Eco-

nomics, 64(1–3):127 – 141.

Kolisch, R. and Hess, K. (2000). Efﬁcient methods for

scheduling make-to-order assemblies under resource,

assembly area and part availability constraints. Inter-

national Journal of Production Research, 38(1):207–

228.

Kon´e, O., Artigues, C., Lopez, P., and Mongeau, M. (2011).

Event-based {MILP} models forresource-constrained

project scheduling problems. Computers & Opera-

tions Research, 38(1):3–13.

Li, J., Susarla, N., Karimi, I. A., Shaik, M. A., and Floudas,

C. A. (2010). An analysis of some unit-speciﬁc

event-based models for the short-term scheduling of

noncontinuous processes. Industrial & Engineering

Chemistry Research, 49(2):633–647.

Lund, R. (1998). Remanufacturing: An american resource.

In Proceedings og the Fifth International Congress for

Environmentally Conscious Design and Manufcatur-

ing. Rochester Institute of Technology, Rochester, NY.

Mouret, S., Grossmann, I. E., and Pestiaux, P. (2011). Time

representations and mathematical models for process

scheduling problems. Computers and Chemical Engi-

neering, 35(6):1038 – 1063.

Pinto, J. M. and Grossmann, I.E. (1995). A continuous time

mixed integer linear programming model for short

term scheduling of multistage batch plants. Indus-

trial & Engineering Chemistry Research, 34(9):3037–

3051.

Shah, N. (2005). Process industry supply chains: Advances

and challenges. Computers and Chemical Engineer-

ing, 29:1225–1235.

Thierry, M., Salomon, M., Van Nunen, J., and Van Wassen-

hove, L. N. (1995). Strategie issues in product re-

covery management. California Management Review,

37(2):114–135.

Zapata, J. C., Hodge, B. M., and Reklaitis, G. V. (2008).

The multimode resource constrained multiproject

scheduling problem: Alternative formulations. AIChE

Journal, 54(8):2101–2119.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

120