Practical Multi-pattern Matching Approach for Fast and Scalable Log

Abstraction

Daniel Tovar

nák

Masaryk University, Faculty of Informatics, Botanická 68a, 602 00 Brno, Czech Republic

Keywords:

Log Processing, Pattern Matching, Log Abstraction, Big Data.

Abstract:

Log abstraction, i.e. the separation of static and dynamic part of log message, is becoming an indispensable

task when processing logs generated by large enterprise systems and networks. In practice, the log message

types are described via regex matching patterns that are in turn used to actually facilitate the abstraction process.

Although the area of multi-regex matching is well studied, there is a lack of suitable practical implementations

available for common programming languages. In this paper we present an alternative approach to multi-pattern

matching for the purposes of log abstraction that is based on a trie-like data structure we refer to as regex trie.

REtrie is easy to implement and the real world experiments show its scalability and good performance even for

thousands of matching patterns.

1 INTRODUCTION

Computer logs are typically generated in the form of

formatted strings with the most important information

represented as a free-form message in natural language.

Akin to many similar cases in the domain of string pro-

cessing, regular expressions (REs) are typically used

to extract useful information from log messages. Com-

mon methods used by log analysis practitioners range

from ad-hoc analysis using grep tool to writing com-

plex proprietary scripts, and more recently, standalone

applications, for example Logstash

. Formally speak-

ing, the transformation of log messages into structured

representation suitable for further analysis and pro-

cessing is referred to as log abstraction (Nagappan and

Vouk, 2010) or message type transformation (Makanju

et al., 2012). Simply put, the goal of log abstraction is

the separation of static and dynamic part of log mes-

sage. Static part is referred to as the message type,

whilst dynamic part is represented by a set of parame-

ters.

Listing 1 represents the approach we use in our

work to describe matching patterns (i.e. message

types) that are consequently used to transform log

messages into structured representation. Our goal was

to develop a simple syntax and data format (YAML-

based) that could be used to describe pattern sets with

large number of corresponding message types in a con-

https://www.elastic.co/products/logstash

venient way. The

regexes

key contains a list of regular

expression shortcuts we refer to as tokens. The tokens

are essentially used as wildcards. Each token is deﬁned

by its name, data type and the actual regular expression

it is supposed to match. The

patterns

key contains a

list of hierarchically grouped matching patterns that

correspond to the message types. The patterns cannot

contain any regular expressions, only uniquely named

references to tokens, e.g.

%{IP:server_ip}

, that rep-

resent variable parameters. Note, that no nesting of

either tokens or patterns is allowed.

regexes: # sometimes refered to as tokens

INT : [integer, ’[0-9]+’]

STR : [string, ’[!-~]+’]

patterns: # patterns describe the message types

user:

session : ’User %{STR:name} logged %{STR:dir}’

created : ’User id %{INT:id} created’

service:

crashed : ’Service %{STR:service} crashed’

started : ’%{STR:service} took %{INT:time}

milliseconds to start’

Listing 1: Matching patterns representing message types.

A common naïve approach to the actual pattern

matching is to iterate the pattern set until a match

is found. Considering, that our largest pattern set

for Apache Hadoop logs is currently composed of

more than 3500 matching patterns, this can quickly be-

come a serious bottleneck in the log processing chain.

Tovar

nák, D.

Practical Multi-pattern Matching Approach for Fast and Scalable Log Abstraction.

DOI: 10.5220/0006006603190329

In Proceedings of the 11th International Joint Conference on Software Technologies (ICSOFT 2016) - Volume 1: ICSOFT-EA, pages 319-329

ISBN: 978-989-758-194-6

319

Note, that a large infrastructure is able generate up to

100,000 logs per second (Chuvakin et al., 2012).

Although multi-regex matching is an extensively

studied area, e.g. in networking domain, usable prac-

tical implementations and libraries for common pro-

gramming languages and general purpose processor ar-

chitectures are seriously lacking. In this paper we pro-

pose an alternative approach for multi-pattern match-

ing based on trie data structure that is very easy to im-

plement, scales well with respect to number of match-

ing patterns, and exhibits very respectable real-world

performance.

The rest of this paper is structured as follows. Sec-

tion 2 provides background for the problem at hand.

Section 3 presents our approach for practical multi-

pattern matching. Section 4 evaluates the proposed

approach. Section 5 discusses the results. Section 6

presents limited amount of related work, and Section 7

concludes the paper.

2 BACKGROUND

In computer science the term of multi-pattern match-

ing traditionally refers to the goal of ﬁnding all oc-

currences of the given set of keywords in the input

text, e.g. as addressed by Aho-Corasic algorithm (Aho

and Corasick, 1975). However, in the context of log

abstraction the goal is to exactly match a single pattern

from a set of patterns (message type) against the whole

input (log message) and return the captured matching

groups that correspond to the dynamic part of log mes-

sage. Naïve approach, still widely used in practice,

is to iterate the set of matching patterns until the ﬁrst

match is found. Therefore, in the worst-case scenario

the whole set must be iterated in order to match the

last pattern. This also obviously applies to situation

when no matching patterns can be found. For hundreds

of matching patterns this quickly becomes a serious

limiting factor with respect to performance. With re-

gard to this fact it is important to note that our work

is focused on results applicable to general purpose

processor architectures based on (possibly distributed)

COTS multi-core CPUs, or virtualized hardware (i.e.

not massively parallel architectures).

A slightly modiﬁed generalization of the above-

mentioned problem is the problem of multi-regex

matching, i.e. ﬁnding all the patterns of the given

set of regexes that match the input text. Note, that ﬁnd-

ing the exact boundaries of the matches, i.e. capturing

the matching groups, is an additional problem (Cox,

2010). Formally speaking, every regular expression

can be transformed into a corresponding ﬁnite automa-

ton that can be used to recognize the input. By using

Thompson’s algorithm an equivalent nondeterminis-

tic ﬁnite automaton (NFA) can be constructed which

can be in turn converted into a deterministic ﬁnite au-

tomaton (DFA) via power-set construction (Hopcroft

J.E. Motwani R.Ullman J.D., 2001). Similarly, given

a set of regular expressions an equivalent NFA, and

subsequently DFA, can be constructed using the same

method.

In general, NFAs are compact in the terms of stor-

age space and number of states, however, the pro-

cessing complexity is typically high since possibly

many concurrent active states must be considered for

each input character (all states in the worst-case). For

performance-critical applications NFAs are typically

transformed into DFAs since they exhibit constant pro-

cessing complexity for each input character. Yet, with

the growing set of regular expressions the space re-

quirements can grow exponentially – a problem known

as state explosion. Thus, for some large regex pattern

sets a practical implementation of DFA-matching can

be infeasible due to memory limits. This conundrum

still attracts a great deal of research in many domains,

e.g. genomics, biology, and network intrusion detec-

tion. For example, in the networking domain, two

large groups of approaches can be identiﬁed utilizing

either NFA parallelization (e.g. on FPGAs), or DFA

compression techniques (e.g. regex grouping, alterna-

tive representation, hybrid construction, and transition

compression) (Wang et al., 2014).

However, in the terms of practical multi-regex

matching implementations suitable for log abstraction

the situation is unsatisfactory to say the least. This can

be due to the fact that, apart from a relative complexity

and individual limitations of the optimization tech-

niques (NFA/DFA), with the combination of vague

implementation details provided by the researchers,

the amount of implementation work needed to build a

fast full-ﬂedged matching library is likely to be great.

For example, pure DFA-based approaches are unable

to capture matching groups – additional NFA-based

matching is needed, increasing the complexity of the

matching engine (Cox, 2010).

To the best of our knowledge, Google’s RE2 (Cox,

2007), (Cox, 2010), is the only available matching

library (C++, Linux only) that supports multi-regex

matching. RE2 aims to eliminate a traditional back-

tracking algorithm and uses so-called lazy DFA in or-

der to limit the state explosion – the regex is simulated

via NFA, and DFA states are built only as needed,

caching them for later use. The implementation of

multi-regex matching returns a vector of matching pat-

tern ids, since it is possible that multiple regexes match

the input (a likely situation as we will discuss below).

Therefore, additional logic is needed to select the best

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

320

matching pattern. Subsequently, the selected pattern

must be executed once more over the input in order to

capture the matching groups.

3 REGEX TRIE

To address the above-mentioned facts, we have fo-

cused on addressing the problem from a different di-

rection – what if we wanted to avoid the complexity

of multi-regex matching altogether by leveraging the

speciﬁc goals of log abstraction and characteristics

of the matching patterns created for this purpose? In

the following paragraphs we will discuss an elegant

matching algorithm that is able to practically eliminate

the need for multi-regex matching, whilst imposing

only minimal limitations on the way the matching pat-

terns can be created. The basic idea of our approach is

based on three important observations.

Patterns can be viewed as keys in an abstract data

structure where the input is used to query the struc-

ture for key membership.

The number of tokens present in a pattern is rel-

atively limited when compared to the number of

static characters.

Set of patterns can be represented as a tree with

two types of nodes – characters and tokens.

c f

r o

Figure 1: Trie containing three strings – car, foo, and for.

Trie (preﬁx tree, radix tree) is a tree-like data struc-

ture used for storing strings. Alongside with hash

table, trie is one of the fastest data structures for string

retrieval when implemented properly. To paraphrase

Heinz et al. (Heinz et al., 2002) trie can be concisely

described as follows. A node in a standard trie is an

array of pointers, one for each letter in the alphabet,

with an additional pointer for the empty string. A leaf

is a record concerning a particular string. A string

is found in a trie by using the letters of the string to

determine which pointers to follow. For example, if the

alphabet is the letters from ’a’ to ’z’, the ﬁrst pointer

in the root corresponds to the letter ’a’; the node

indicated by this pointer is for all strings beginning

with an "a–". In node

, the pointer corresponding to

the letter ’c’ is followed for all strings beginning with

an "ac–" and so on; the pointer corresponding to the

empty string in node

is for the record concerning

the single-letter string "a". Search in a trie is fast,

requiring only a single pointer traversal for each letter

in the query string. That is, the search cost is bounded

by the length of the query string.

Figure 2: Trie containing three abstract strings representing

matching patterns.

For illustration purposes, let

•

denote a special

character, which represents some regex token in a

pattern as seen in Listing 1, and also let denote

a non-printable space. Such patterns are clearly equiv-

alent to strings of characters and can be stored in a

standard trie. Figure 2 depicts a simple pattern set rep-

resented as a trie consisting of three short patterns

%{STRING:ip}

Id %{INT:id}

, and

true

. A basic version

of our algorithm that slightly modiﬁes a standard trie

and imposes some limitations on the matching patterns

can be described as follows:

is a pattern sufﬁx starting immediately after

some token

then token

is not allowed to match

any preﬁx of

(including other tokens). For ex-

ample, for deﬁned token

ANY : [string, ’.

’]

the

pattern

%{ANY:any} foo bar

is not allowed since the

token would consume the rest of the pattern.

In addition to the alphabet pointers and an empty

string pointer in a trie node, let us introduce a

special token pointer

•

which can be followed

only if the corresponding token matches some

preﬁx of the input. However, an important con-

dition must be met – the alphabet pointers and

the special pointer

•

are not allowed to coexist

in a single node. This means that either alpha-

bet pointers must be empty, or the special pointer

must be empty. For example, if patterns

Service

crond crashed

and

Service %{STRING:svc} started

Practical Multi-pattern Matching Approach for Fast and Scalable Log Abstraction

321

were to be inserted into the modiﬁed trie it would

result into a conﬂict in a node that represents the

preﬁx "Service –".

When searching, the character-by-character traver-

sal of input is identical to the standard trie search

algorithm using an alphabet array of pointers and

empty string pointer. However, when a token

pointer is encountered it is followed only after

the token is successfully matched against the un-

traversed input (provided there is any input left).

The matched portion of the input is saved and the

algorithm continues normally with the unmatched

portion of the input.

When the algorithm cannot follow any pointer

from the current node it reports a non-match for

the given input. In the opposite case, the key was

found and the associated record is retrieved. The

associated record can, for example, hold the name

of the pattern, and the types and names of the to-

kens which can be then combined with the matched

portions of the input – thus, capturing the matching

groups.

The basic algorithm on the modiﬁed trie works thanks

to the ﬁrst two limitations on matching patterns. The

ﬁrst rule assures that even after the token pointer con-

sumes a portion of the input, the algorithm can con-

tinue its traversal on a path corresponding to sufﬁx

The second rule assures that there is no ambiguity as to

what pointer should be followed next by the algorithm

in the search process.

The ﬁrst rule is of key importance to our trie-based

approach, and it somewhat limits the way the match-

ing patterns can be created. However, we argue that

due to the nature of patterns used for log abstraction

this limitation can be viewed as marginal. The second

rule, on the other hand, can be seen as much more pro-

hibitive. Consider a pattern set in Listing 1. It is appar-

ent that the ﬁrst two matching patterns

user.session

and

user.created

clearly represent distinct message

types, yet their insertion into the modiﬁed trie would

result into a conﬂict in a node corresponding to preﬁx

"User –". In addition, the

service.start

pattern essen-

tially prohibits insertion of any other pattern starting

with a character.

In an extended version of the algorithm the second

rule can be eliminated by deﬁning priorities among

alphabet and token pointers and the use of backtrack-

ing. Such an extended version not only allows for a

given trie node to contain both alphabet pointers and a

single special token pointer, but multiple token point-

ers as well. The principle for achieving this is simple

– the alphabet pointers have the highest priority and

they are always traversed ﬁrst. If there are no pointers

available for the input character, special token pointers

are iterated in the order of their priority until a match

is found. This is done for each node in a recursive

and backtracking manner. In general, the priorities of

tokens can be determined by different ways, e.g. by

explicit deﬁnition, by their lexicographical order, or

by the order in which they are deﬁned in the pattern

set description ﬁle.

Provided the tokens are represented by regular ex-

pressions that can be matched in linear time, and there

are no nodes containing both alpha and token point-

ers, the search over the regex trie can be performed

in linear time with respect to input length, irrespec-

tive of the number of patterns – an equivalent of a

standard trie and also a processing complexity DFAs

are known for. This is somewhat natural, since trie

can be viewed as a special case of DFA (Lucchesi and

Kowaltowski, 1993). However, similarly to majority

of standard regex libraries, the use of backtracking can

theoretically lead to exponential worst-case time com-

plexity if a "malicious" pattern set is carefully crafted.

Yet, as we will demonstrate later via experimental eval-

uation, typical pattern sets used for log abstraction do

not exhibit this behavior.

From the point of view of practical implementa-

tion there is, however, a more pressing issue – tries

are fast, but if implemented naïvely, they are space

inefﬁcient. The size of a standard trie is determined

by the size of its nodes multiplied by their number.

In practice, the alphabet pointers are implemented as

arrays of size

r = 2

where

is the number of bits

used to traverse the trie in each step –

is sometimes

also referred to as radix. For

H = 1

the trie can be

viewed as a binary tree and the number of bit compar-

isons grow accordingly, therefore

H = 8

is commonly

used, traversing the trie byte-by-byte, or character-

by-character for ASCII strings. Note, that randomly

distributed strings represented as a trie tend to form

long node chains, i.e. each node in the path has only

single child, which is rather wasteful for an array of

size

= 256

. In addition, the pointer arrays quickly

grow very sparse with the increasing distance from the

trie root.

Fortunately, there are well-known techniques that

are able to signiﬁcantly reduce the amount of trie nodes

and also fairly reduce the size of array pointers. First

commonly used technique is generally known as trie

compression and it is used to limit the number of trie

nodes. First proposed by (Morrison, 1968) for bi-

nary tries (

H = 1

) the optimization eliminates chains

of nodes by omitting trie nodes that has only a sin-

gle child. The resulting trie includes only nodes that

branch on some signiﬁcant bit. Whilst slightly in-

creasing the implementation complexity of the trie, it

considerably reduces the number of its nodes and from

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

322

a certain perspective also the number of bit compar-

isons. Morrison referred to the resulting compressed

trie as to PATRICIA tree. Further compression can

be achieved by using

H > 1

, preferably

H = 8

, which

inherently reduces the height of the trie.

When inserting into a compressed trie, new node

is created only if it needs to distinguish between two

(

H = 1

) or more (

H > 1

) children (we consider the

stored value to be a child). Inner trie nodes essentially

represent common preﬁxes of their children. When

searching, the number of comparisons is reduced, since

only branching positions are compared. However, it

must be ensured, that the comparisons are not out of

bounds, i.e. the preﬁx the node represents cannot be

longer than the rest of the searched input. Addition-

ally, since only signiﬁcant (branching) positions are

compared a ﬁnal comparison is needed in order to

assure the stored key/string is indeed equal to the in-

put. Alternatively, this veriﬁcation can be performed

on-the-ﬂy with each node traversal, i.e. the pointer is

still determined only by the signiﬁcant position, yet

it is followed only if the corresponding node preﬁx is

also a preﬁx of the input. This option is preferable in

the case of our approach since the reconstruction of

the found key from the regex-matched portions of the

input would be too cumbersome.

car fo

r o

Figure 3: Compressed trie containing three strings – car, foo,

and for.

Second group of optimizations aims to reduce the

size of the nodes themselves, especially the structures

that represent the child pointers. The general goal is

to avoid sparse data structures by adaptively changing

the size and representation of the nodes with respect to

the number of children. For example, in (Heinz et al.,

2002) the authors describe burst tries that limit the

number of sparse nodes by grouping suitable sub-tries

into binary search trees. But since in our approach

we mix alphabet pointers with token pointers in nodes

this optimization is not very suitable. In (Leis et al.,

2013) an Adaptive Radix Tree is presented that uses

path compression described above with the addition

of adaptive nodes. ART uses four different types of

pointer structures, based on the number of stored chil-

dren. The nodes use different levels of indirection in

order to reduce their size. Note, that generally speak-

ing, similar approaches are most efﬁcient when imple-

mented in languages supporting pointers and pointer

arithmetic. On the other hand, this optimization is

very suitable in the context of our approach, therefore,

depending on the used implementation language, any

technique based on indirection that will reduce sparse

pointer structures will do.

Service˽

User˽id:˽

%{INT}

˽logged˽

%{STRING }

˽started

in out

Figure 4: Regex trie example.

Up to now we have presented only a sketch of

our approach based on a modiﬁed trie with alphabet

and token pointers priorities for backtracking search.

After the addition of path compression and node size

reduction we can ﬁnally present an exact description

of our approach/data structure we refer to as regex trie.

The pseudo-codes of the corresponding algorithms

can be found in the appendix of this paper. Algorithm 1

describes the abstract data types used in Algorithm 2

and Algorithm 3 for regex trie insertion. Algorithm 4

is used for search over this data structure. Similarly to

many others, the deletion algorithm is not considered

here since for our purposes, rebuilding the updated

trie from scratch is sufﬁcient. However, for pattern

sets that are changing very frequently this may not

be the case and the deletion should be implemented

– it closely follows the recursive deletion procedure

for standard trie. Finally, Algorithm 5 shows the way

regex trie can be utilized for abstraction of logs into a

structured representation. For each pattern in a pattern

set, its name and name of its tokens is stored as value

in the regex trie. In the case of a match, the returned

value is combined with the matched portions of the

input log message and a map representing its structured

representation is returned.

4 EVALUATION

We have performed a series of experiments based on

two real-world pattern sets and partially generated data

sets in order to evaluate practical implementation of the

presented data structure and the related multi-pattern

Practical Multi-pattern Matching Approach for Fast and Scalable Log Abstraction

323

matching approach. First, we have aimed to evaluate

scalability of the regex trie and naïve approach with re-

spect to the number of patterns. We have also included

multi-regex matching to serve as a control. Second im-

portant goal was to determine processing throughput

with the growing number of CPU cores since our main

aim is parallel processing.

The base data set

used in our experiments con-

sists of 100 million lines of syslog’s auth/authpriv facil-

ity (i.e. auth.log) generated by a multi-purpose cluster

over the period of one month. The average velocity this

data set was generated with can be therefore estimated

to a surprisingly low number of 39 logs/second.

The base pattern set

consists of 22 reasonably

complicated matching patterns fully covering the data

set

. Listing 2 shows the pattern set

includ-

ing the exact number of messages for each message

type (message type cardinality) present in

in order

to assure reasonable repeatability of the experiments

without disclosing the whole, rather sensitive, data set.

corresponds to a pattern set consisting of ﬁrst

existing message types. To assure equal selectivity

of each corresponding message pattern we have gen-

erated data sets

and

consisting

of 1.1 million messages each.

corresponds to a

data set where

is the number of present message

types with cardinality

1100000

with the messages shuf-

ﬂed randomly several times. Data sets

are directly

based on D

— only the messages with message type

cardinality lower than

1100000

were duplicated in order

to reach the desired cardinality.

Second pattern set

is based on Apache Hadoop

pattern set consisting of more than 3500 patterns we

have discovered using source code analysis. In the

original pattern set the patterns are divided into 8 in-

dividual groups for maintainability purposes. For ex-

ample the HDFS group alone consists of more than

1700 patterns. However, for experimental purposes

the pattern set

always consists of all the patterns

merged into a single group up to the size of 3500. Sim-

ilarly to the previous case, data set

corresponds

to a data set of size 1.1 million with

message types

each having cardinality

1100000

. The data sets were

generated randomly from the corresponding message

types.

We have implemented both the naïve and the regex

trie approach in Erlang language in order to be directly

comparable. We use Erlang OTP platform extensively

in our work since we focus on parallel and distributed

processing on many-core CPUs thus rendering Erlang

a very reasonable choice in our eyes. Additionally,

when using HiPE (high-performance) compiler, suit-

able portions of the Erlang code are translated into

native code potentially resulting in better performance.

As already pointed out, in naïve approach the pat-

tern set is iterated until a match is found or an empty

match is returned. The patterns have the form of valid

regular expressions with named matching groups. The

implementation was rather straightforward since Er-

lang includes traditional regex matching functionality

with group matching.

Similarly, we have developed a prototypical imple-

mentation of regex trie matching described above in

detail. The patterns are deﬁned in the format shown

in Listing 1 and Listing 2. The implementation tra-

verses the input byte-by-byte (

H = 8

) resulting in radix

r = 256

. In order to reduce the size of the trie nodes

we use pointer structure with one level of indirection,

i.e. two nested arrays of size 16.

To serve as a control, a simple multi-regex match-

ing prototype based on already discussed Google’s

RE2 library was developed in C++ language. The

patterns have the form of valid regular expressions

with named matching groups. As already revealed,

the multi-regex functionality of RE2 returns vector

of pattern ids that match the given input, thus, addi-

tional matching step to extract the matching groups

is needed. In our implementation the ﬁrst matching

pattern is always picked for the extraction, therefore,

proper ordering of the patterns is critical. Note, that

this implementation serves as a control, it is not meant

to be directly compared. With C++ being generally

faster than garbage collected Erlang, we have expected

the multi-regex matching to be faster as well, yet ex-

hibiting very similar behavior in the terms of scalabil-

ity. Remember that in best case, the theoretical time

complexity of regex trie corresponds to the one of

DFA.

Given a particular pattern set, the task of each im-

plementation was to abstract each matching log line in

the corresponding data set, i.e. to convert it to struc-

tured representation. The tests were performed on a

server machine with Intel

Xeon

CPU E5-2650 v2

@ 2.60GHz with 64GB RAM. When not stated other-

wise, the tests were performed on a single core. The

single measured value was the duration in seconds

(with milliseconds precision) needed to process the

whole data set whilst not including the output phase

and normalizing the input phase. Each individual com-

bination of data set, pattern set and implementation

was executed 10 times with best and worst results dis-

carded. The ﬁrst series of experiments were executed

over the data set/pattern set pairs

, P

)

in order

to evaluate the scalability of the implementations for

small pattern sets. We have also aimed to validate the

hypothesis that for a certain number of patterns the

naïve approach would begin to perform worse than

the regex trie since the cost of iteration would be too

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

324

regexes:

INT : [integer, ’[0-9]+’]

S1 : [string, ’[!-~]+’]

S2 : [string, ’[-./_a-zA-Z0-9]+’]

ANY : [string, ’[^\n\r]+’]

patterns:

auth:

p01 : ’Failed %{S1:method} for invalid user %{S1:user} from %{S1:ip} port %{INT:port} ssh2’ # 3468121

p02 : ’Failed %{S1:method} for %{S1:user} from %{S1:ip} port %{INT:port} ssh2’ # 6832536

p03 : ’Accepted %{S1:method} for %{S1:user} from %{S1:ip} port %{INT:port} ssh2’ # 4536585

p04 : ’Did not receive identification string from %{S1:host}’ # 15398

p05 : ’last message repeated %{INT:count} times’ # 29221

p06 : ’Invalid user %{S1:user} from %{S1:ip}’ # 3465382

p07 : ’Received disconnect from %{S2:ip}: 11: %{ANY:reason}’ # 1751038

p08 : ’reverse mapping checking getaddrinfo for %{S1:host} [%{S2:ip}] failed - POSSIBLE BREAK-IN

ATTEMPT!’ # 872869

p09 : ’Address %{S2:ip} maps to %{S2:host}, but this does not map back to the address - POSSIBLE BREAK-

IN ATTEMPT!’ # 68139

p10 : ’pam_unix(%{S2:p1}:%{S2:p2}): check pass; user unknown’ # 3465791

p11 : ’pam_unix(%{S2:p1}:%{S2:p2}): authentication %{S2:variable2}; logname= uid=0 euid=0 tty=ssh ruser

= rhost=%{S1:rhost} ’ # 3463858

p12 : ’pam_unix(%{S2:p1}:%{S2:p2}): authentication %{S2:variable2}; logname= uid=0 euid=0 tty=ssh ruser

= rhost=%{S1:rhost} user=%{S1:user}’ # 6785737

p13 : ’pam_unix(%{S2:p1}:%{S2:p2}): session %{S1:operation} for user %{S1:user}’ # 30870038

p14 : ’pam_unix(%{S2:p1}:%{S2:p2}): session %{S1:operation} for user %{S1:user} by (uid=%{INT:uid})’ #

30871428

p15 : ’pam_unix(%{S2:p1}:%{S2:p2}): account %{S1:account} has expired (account expired)’ # 646

p16 : ’PAM service(sshd) ignoring max retries; %{INT:variable1} > %{INT:variable2}’ # 13833

p17 : ’PAM %{INT:more} more authentication %{S2:failure}; logname= uid=0 euid=0 tty=ssh ruser= rhost=%{

S1:rhost} ’ # 1420

p18 : ’PAM %{INT:more} more authentication %{S2:failure}; logname= uid=0 euid=0 tty=ssh ruser= rhost=%{

S1:rhost} user=%{S1:user}’ # 45204

p19 : ’Authorized to %{S2:user}, krb5 principal %{S1:principal} (krb5_kuserok)’ # 376475

p20 : ’pam_krb5(%{S2:p1}:%{S2:p2}): user %{S1:user} authenticated as %{S1:principal}’ # 937

p21 : ’pam_krb5(%{S2:p1}:%{S2:p2}): authentication failure; logname=%{S1:logname} uid=0 euid=0 tty=ssh

ruser= rhost=%{S1:rhost}’ # 1782027

p22 : ’Authentication tried for %{S1:user} with correct key but not from a permitted host (host=%{S2:

host}, ip=%{S2:ip}).’ # 1283317

Listing 2: Pattern set P

high. The use of (

) pairs is important since

the selectivity of 100% needed to be maintained for

each pattern set

(i.e. 100% messages in the data set

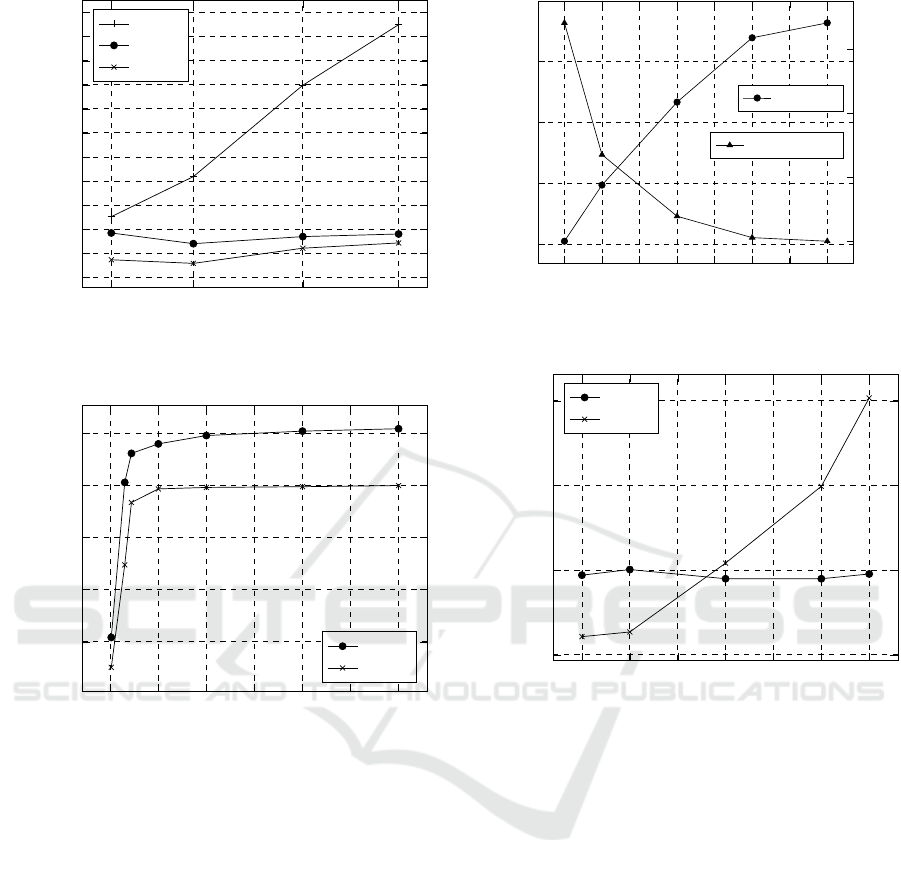
had to be matched by the given pattern set). Figure 5

depicts the running times for X = {1, 7, 15, 22}. Both

REtrie and RE2-based implementations scale well for

small pattern sets exhibiting only a marginal growth

with RE2 performing better overall as expected. Yet,

since RE2 exhibits somewhat steeper growth, the dif-

ference stops at 13.28% for

. The slight jitter is

a result of a fact that not every pattern has the same

length and also the number of regex tokens varies. The

results also show that even for a single pattern the

regex trie implementation exhibits better performance

than naïve iteration-based approach. The real problem,

however, relates to the scalability (or its lack) of the

naïve approach – the running time grows rapidly with

the number of patterns. This growth would be even

more profound for pattern sets with lower selectivity,

since in the case of absence of matching pattern (no-

match) the whole pattern set must be always iterated.

This behavior is strongly in contrast with the one of

REtrie and RE2, which fail fast. When no matching

pattern can be found, both implementations possibly

fail fast and return nomatch. In the best case scenario

this fail can occur already at the ﬁrst input character.

In the second series of experiments we have fo-

cused on data set

in order to evaluate the behavior

of the REtrie with different pattern sets selectivity.

When the number of needed patterns exceeded the size

of the base auth pattern set

, we have appended pat-

terns from the base Apache Hadoop pattern set

300

order to achieve the desired size. This way, we were

able to create artiﬁcial pattern sets up to

300

. Results

in Figure 6 shows that as the number of matching pat-

terns grows from 1 to 22, increasingly larger portion

Practical Multi-pattern Matching Approach for Fast and Scalable Log Abstraction

325

1 7

Number of patterns in pattern set P

[x]

Running time for data set D

[seconds]

Naïve

REtrie

RE2

Figure 5: Performance of multi-pattern matching implemen-

tations for (D

, P

) pairs.

100

150

200

250

300

1.5

2.5

Number of patterns in pattern set P

[x]

Running time for data set D

[seconds]

REtrie

RE2

Figure 6: Performance of multi-pattern matching implemen-

tations for (D

, P

) pairs.

of the data set

must be fully matched (i.e. the pat-

tern set selectivity increases). Therefore, the overall

time needed to match the data set increases accord-

ingly. However, for larger pattern sets

–

300

the

selectivity remains the same (100%) therefore the run-

ning times remain essentially constant. Very similar

behavior of RE2-based implementation is apparent.

Third series of experiments was designed to eval-

uate the scalability of the regex trie implementation

with respect to multiple processor cores and to deter-

mine the theoretical throughput for real-world data

set and pattern set. In this case the experiments were

performed on a base data set

with pattern set

in order to achieve real-world distribution of the mes-

sage types. The parallel processes shared single (im-

mutable) regex trie structure and the input was par-

allelized as much as possible. Figure 7 shows that

the processing performance indeed grows with the

number of used CPU cores. It can be seen that for 2

1 2 3 4

5 6

7 8

100

150

200

Number of CPU cores

Running time for data set D

[seconds]

Relative speed-up

Running time

Speed-up

Figure 7: Multi-core performance of REtrie for real-world

data set D

and pattern set P

500

1,000

1,500

2,000

2,500

3,000

3,500

2.5

3.5

Number of patterns in pattern set R

[x]

Running time for data set H

[seconds]

REtrie

RE2

Figure 8: Multi-pattern matching performance for large pat-

tern sets on (H

, R

) pairs.

cores almost ideal 2-fold speedup is achieved. With

the increasing number of cores the speed-up slowly

decreases. At 8 cores the data set with 100 million

lines was processed in 52.543 seconds thus yielding

theoretical throughput of 1,903,203 lines per second.

In the last series of experiments we have aimed to

determine the effects of large pattern sets on REtrie

performance. We have measured the running times

for Apache Hadoop data set-pattern set pairs

, R

)

with

X = {500, 1000, 2000, 3000, 3500}

. For pattern

sets larger than 400, RE2 reached its default memory

limit for DFAs and needed to be increased accord-

ingly. The memory cap can be declared at run-time for

each set of regexes and controls how much memory

can be used to hold the compiled form of the regexes

and the corresponding cached DFA graphs. Figure 8

shows that whilst REtrie implementation scales very

well even for large pattern sets RE2-based implementa-

tion starts to slow down. For more than 2000 patterns

REtrie implementation even starts to outperform the

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

326

multi-regex implementation. Even after careful pro-

ﬁling we did not ﬁnd any malicious/wrongly-formed

pattern(s) that would seem to cause this slowdown.

A possible explanation for this slowdown can be the

large size of the resulting state machine combined with

the combination of lazy DFA approach. However, we

are not RE2 engineers and we were not able to further

analyze this behavior.

5 DISCUSSION

The results showed that the performance of regex trie

scaled well with respect to the number of patterns as

well as number of CPU cores. The overall single-core

performance for small pattern sets was relatively close

to the multi-regex matching implemented in C++ on

top of RE2 library.

Surprisingly enough, for very large pattern sets

the Erlang regex trie implementation outperformed the

implementation of multi-regex matching based on RE2.

It must be noted that RE2 served only as a control for

our experiments and any deﬁnitive conclusions would

be premature. On the other hand the tested pattern set

was fairly standard not containing any patterns that

would seem to cause this slowdown. This must be

revisited in the future. For multiple cores the Erlang

implementation exhibited decent speed-up stopping

at overall throughput of more than 1.9 million log

lines per second on 8 cores, which we deem to be an

outstanding result, considering the task.

Note, that by using

cloc

tool we have determined

that the RE2 library is based on approximately 30000

lines of code whilst the Erlang implementation of regex

trie has 300 lines of code following the algorithms at

the end of this paper very closely. Nevertheless, the

algorithms can be easily implemented in any modern

programming language with traditional regular expres-

sion matching support, and this is one of the goals we

have aimed for.

6 RELATED WORK

The authors of (Azodi et al., 2013b) use regular expres-

sions with named capturing groups (matching rules) to

be able to read logs from different sources and convert

them into normalized format. In order to speed up

the process of ﬁnding the correct regex for a given

log, the authors utilise a priority queue with frequently

matched regexes at the top of the queue. In their later

works the authors use knowledge base approach in

order to improve the matching performance by limit-

ing the number of possible matching rules. In (Azodi

et al., 2013a), similarity search is used to ﬁnd the ap-

propriate matching rule, and in (Jaeger et al., 2015)

the rules are organized in a hierarchical manner based

on static indicators (e.g. the name of the application

that generated the logs).

To the best of our knowledge, syslog-ng

is in the

terms of available open-source log processing software

the only one to support multi-pattern matching. The

matching is, similarly to our case, based on radix tree,

yet we were unable to determine the exact approach/al-

gorithm used. For example, when trying to test it, we

were unable to describe some of our pattern sets, and

in addition, the matching seems to be greedy, not exact,

i.e. the used algorithm matched also longer inputs that

it was supposed to. This, in some cases, resulted in

false-negative (non-)matches. Additionally, the order-

ing of patterns seems to inﬂuence the output, which

is quite undesirable considering the pattern sets can

consist of thousands of patterns.

7 CONCLUSION

In this paper we have presented a multi-pattern match-

ing approach for log abstraction based on a trie-like

data structure we refer to as regex trie. We have pre-

sented related algorithms that are very easy to imple-

ment, scale well with respect to number of match-

ing patterns, and exhibit respectable real-world per-

formance for our Erlang implementation. The results

have shown that on a fairly standard commodity hard-

ware it is possible to abstract hundreds of thousands

of logs per second.

In our future work we would like to focus on utiliz-

ing REtrie for general log processing and normaliza-

tion. In particular we would like to focus on many-core

distributed deployments in order to push the log ab-

straction performance even further. Our second goal is

related to the discovery and deﬁnition of pattern sets

and normalization logic for a base set of logs generated

by general-purpose servers, e.g. standard Linux-based

machines.

REFERENCES

Aho, A. V. and Corasick, M. J. (1975). Efﬁcient string match-

ing: an aid to bibliographic search. Communications

of the ACM, 18(6):333–340.

Azodi, A., Jaeger, D., Cheng, F., and Meinel, C. (2013a).

A new approach to building a multi-tier direct access

knowledgebase for IDS/SIEM systems. Proceedings -

https://syslog-ng.org

Practical Multi-pattern Matching Approach for Fast and Scalable Log Abstraction

327

2013 IEEE 11th International Conference on Depend-

able, Autonomic and Secure Computing, DASC 2013.

Azodi, A., Jaeger, D., Cheng, F., and Meinel, C. (2013b).

Pushing the limits in event normalisation to improve

attack detection in IDS/SIEM systems. Proceedings

- 2013 International Conference on Advanced Cloud

and Big Data, CBD 2013, pages 69–76.

Chuvakin, A., Schmidt, K., and Phillips, C. (2012). Log-

ging and log management: the authoritative guide to

understanding the concepts surrounding logging and

log management. Newnes.

Cox, R. (2007). Regular expression matching can be simple

and fast (but is slow in java, perl, php, python, ruby).

URL: http://swtch.com/˜rsc/regexp/regexp1.

Cox, R. (2010). Regular expression matching in the wild.

URL: http://swtch.com/˜ rsc/regexp/regexp3.html.

Heinz, S., Zobel, J., and Williams, H. E. (2002). Burst tries:

a fast, efﬁcient data structure for string keys. ACM

Transactions on Information Systems, 20(2):192–223.

Hopcroft J.E. Motwani R.Ullman J.D. (2001). Introduction

to automata theory, languages, and computation-.

Jaeger, D., Azodi, A., Cheng, F., and Meinel, C. (2015). Nor-

malizing Security Events with a Hierarchical Knowl-

edge Base, volume 9311 of Lecture Notes in Computer

Science. Springer International Publishing, Cham.

Leis, V., Kemper, A., and Neumann, T. (2013). The adap-

tive radix tree: ARTful indexing for main-memory

databases. In 2013 IEEE 29th International Confer-

ence on Data Engineering (ICDE), pages 38–49. IEEE.

Lucchesi, C. L. and Kowaltowski, T. (1993). Applications of

ﬁnite automata representing large vocabularies. Softw.

Pract. Exper., 23(1):15–30.

Makanju, A., Zincir-Heywood, A. N., and Milios, E. E.

(2012). A lightweight algorithm for message type ex-

traction in system application logs. IEEE Transactions

on Knowledge and Data Engineering, 24(11).

Morrison, D. R. (1968). PATRICIA—Practical Algorithm To

Retrieve Information Coded in Alphanumeric. Journal

of the ACM, 15(4):514–534.

Nagappan, M. and Vouk, M. a. (2010). Abstracting log

lines to log event types for mining software system

logs. 2010 7th IEEE Working Conference on Mining

Software Repositories (MSR 2010), pages 114–117.

Wang, K., Fu, Z., Hu, X., and Li, J. (2014). Practical regu-

lar expression matching free of scalability and perfor-

mance barriers. Computer Communications, 54.

APPENDIX

Algorithm 1: Regex Trie Types.

1: def TRIENODE(label)

2: label String ← label

3: al phas AdaptiveArray ← []

4: tokens PrioritySet ← {}

5: terminator Value ← ∅

6: def TOKENPOINTER(priority, regex)

7: priority Integer ← priority

8: regex Regex ← regex

9: child TRIENODE ← ∅

Algorithm 2: Regex Trie Insert – PART 1/2.

Input:

single matching

pattern

, associated

value

to be

stored, TRIENODE root or an empty node

Require: pattern

must be a list of chunks; chunk is either

string chain or token

Output:

TRIENODE root

node

representing recursively

built trie

1: function INSERT(pattern, value,node)

2: if node = ∅ then

3: node ← new TRIENODE(M)  root node

4: chunk, rest ← pattern  get next pattern chunk

5: if chunk = ∅ then

6: node.terminator ← value

7: else if isToken?(chunk) then

8: if node.tokens{chunk.priority} = ∅ then

9: n ← new TRIENODE(chunk.regex)

10: t p ←

new TOKEN-

POINTER(chunk. priority, chunk.regex)

11: t p.child ← INSERT(rest, value, n)

12: else

13: t p ← node.tokens{chunk.priority}

14: t p.child ← INSERT(rest, value, t p.child)

15: node.tokens  t p

16: else

17: c ← chunk[0]

18: if node.al phas[c] = ∅ then

19: n ← new TRIENODE(chunk)

20: node.al phas[c] ← INSERT(rest, value, n)

21: else

22: n ← node.alphas[c]

23: node.al phas[c] ←

IN-

SERTCHAIN(chunk, rest, value, n)

24: return node

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

328

Algorithm 3: Regex Trie Insert – PART 2/2.

1: function INSERTCHAIN(chain, pattern, value, node)

2: lcp ← longestCommonPreﬁx(node.label, chain)

3: if lcp = node.label then  the label is preﬁx of the

chain

4: n ← node

5: else

6: n ← new TRIENODE(lcp)

7: c1 ← stripPreﬁx(lcp, node.label)

8: node.label ← c1

9: n.al phas[c1[0]] ← node

10: if lcp = chain then

the chain is preﬁx of the label

11: return INSERT(pattern, value, n)

12: else

13: rest ← [stripPreﬁx(lcp, chain) | pattern] 

append to start

14: return INSERT(rest, value, n)

Algorithm 4: Regex Trie Search.

Input: inputstr

ing, TRIENODE root

node

, empty array

[]

for token captures

Output:

associated

value

and token

captures

, or nonmatch

∅

1: function SEARCH(inputstr, node, captures)

2: if inputstr = ∅ then

3: value ← node.terminator

4: if value = ∅ then

5: return ∅

6: else

7: return (value,captures)

8: x ← SEARCHPREFIX(inputstr, node, captures)

9: if x = ∅ then

10: for t p in node.tokens do

11: x ←

SEARCHREGEX(

inputstr, t p, captures

)

12: if x 6= ∅ then

13: break

14: return x

15: function SEARCHPREFIX(inputstr, node, captures)

16: c ← inputstr[0]

17: if node.al phas[c] = ∅ then

18: return ∅

19: else

20: child ← node.al phas[c]

21: label ← child.label

22: if not isPreﬁx?(label, inputstr) then

23: return ∅

24: else

25: tail ← stripN(len(label), inputstr)

26: return SEARCH(tail, child, captures)

27: function SEARCHREGEX(inputstr,t p, captures)

28: match ← matchRegex(t p.regex, inputstr)

29: if match = ∅ then

30: return ∅

31: else

32: captures ← [captures + match.matched]

33: tail ← stripN(match.length, inputstr)

34: return SEARCH(tail,t p.child, captures)

Algorithm 5: Log Abstraction Using Regex Trie.

Input: message

to be matched,

trie

containing all patterns

from a given pattern set

Require:

the value associated with each pattern must be a

tuple (pat_name,tok_names)

Output: pat_name

and captured tokens map

<tok_names → capures>, or nonmatch ∅

1: function ABSTRACTMESSAGE(message,trie)

2: result ← SEARCH(message,trie, [])

3: if result 6= ∅ then

4: ((pat_name,tok_names), captures) ← result

5: return

(

pat_name

mapFromList(zip(tok_names, captures))

6: else

7: return ∅

Practical Multi-pattern Matching Approach for Fast and Scalable Log Abstraction

329