MILP-based Approach for Optimal Implementation of Reconﬁgurable

Real-time Systems

Wafa Lakhdhar

, Rania Mzid

2,3

, Mohamed Khalgui

1,5

and Nicolas Treves

LISI Lab INSAT, University of Carthage, INSAT Centre Urbain Nord BP 676, Tunis, Tunisia

ISI, University Tunis-El Manar, 2 Rue Abourraihan Al Bayrouni, Ariana, Tunisia

CES Lab ENIS, University of Sfax, B.P:w.3, Sfax, Tunisia

CEDRIC Lab, CNAM, 292 rue Saint-Martin, Paris, France

SystemsControl Lab, Xidian University, August Bebel Str 70, Halle, China

Keywords:

Embedded System, Reconﬁgurable Architecture, Real-time Scheduling, Linear Programming, Posix-based

Implementation.

Abstract:

This paper deals with the design and implementation of reconﬁgurable uniprocessor real-time embedded sys-

tems. A reconﬁguration is a run-time operation allowing the addition-removal of real-time tasks or the update

of their parameters. The system is implemented then by different sets of tasks such that only one is executed at

a particular time after a corresponding reconﬁguration scenario according to user requirements. The problem

is to optimize the system code while meeting all related real-time constraints and avoiding any redundancy

between the implementation sets. Based on the Linear Programming (MILP), we propose a multi-objective

optimization technique allowing the minimization of the number of tasks and their response times. An opti-

mal reconﬁgurable POSIX-based code of the system is manually generated as an output of this technique. We

apply the paper’s contribution to the study of the performance evaluation.

1 INTRODUCTION

A real-time system is any system which has to re-

spond to externally generated input stimuli within a

ﬁnite and speciﬁed delay (Burns and Wellings, 2009).

The development of real-time systems is not a triv-

ial task because a failure can be critical for the safety

of human beings (Cottet and Grolleau, 2005). The

researchers are moving today toward proposing tech-

niques for programming concurrent reconﬁgurable

real-time systems.

To provide design-time guarantees on timing con-

straints, different scheduling methodologies can be

used, such as Rate Monotonic (RM) which is a

scheduling algorithm which was deﬁned by Liu and

Layland (Liu and Layland, 1973) where the prior-

ity of tasks is inversely proportional to their peri-

ods. The authors of (Bouaziz et al., 2015) provide

a method to drive the designer by producing a set of

design solutions based on RM scheduling algorithm.

In (Mehiaoui et al., 2013; Wo

zniak, ), the authors

are interested in the optimization of deployment tech-

niques from functional and platform models of real-

time systems by using mixed integer linear program-

ming (MILP). An MILP formulation is easily exten-

sible, re-targetable to a different optimization metric

and can easily accommodate additional constraints or

legacy components (Mehiaoui et al., 2013). There are

many programming languages designed for the devel-

opment of real-time systems such as POSIX (Portable

Operating System Interface) (Lewine, 1991). The

POSIX standard promotes portability of applications

across different operating system platforms. The au-

thors (Obenland, 2000) use POSIX in the develop-

ment of software for real-time and embedded sys-

tems.

The synthesis of a valid and optimal implementation

model consists in building the set of tasks implement-

ing the applicative functions while meeting all related

real-time constraints. The reconﬁguration at the im-

plementation level consists in adding/removing tasks

or modifying their timing parameters to go from one

implementation to another, which may require an ad-

ditional time for reconﬁguration. So that, the resulting

implementation model should avoid redundancy be-

tween the different implementations to minimize the

possible overhead.

In this paper, we present an approach toward an op-

330

Lakhdhar, W., Mzid, R., Khalgui, M. and Treves, N.

MILP-based Approach for Optimal Implementation of Reconﬁgurable Real-time Systems.

DOI: 10.5220/0006006703300335

In Proceedings of the 11th International Joint Conference on Software Technologies (ICSOFT 2016) - Volume 1: ICSOFT-EA, pages 330-335

ISBN: 978-989-758-194-6

timal implementation of reconﬁgurable uniprocessor

real-time systems. The proposed approach aims to au-

tomatically produce a valid and optimal task model

from a given speciﬁcation. The task model consists of

a set of tasks implementing the applicative functions

that we assume independent and periodic. We assume

also that assigning priorities to tasks is performed us-

ing rate monotonic algorithm RM (Klein et al., 1993).

The paper is organized as follows. Section 2 gives

an overview on related works. Section 3 provides the

formalisation of approach. Section 4 explains in de-

tails the proposed approach to obtain a valid and op-

timal implementation model from the user speciﬁca-

tion. Section 5 illustrates the approach on the chosen

case study and evaluates its efﬁciency. Finally, we

summarize our work and discuss the future work in

Section 6.

2 RELATED WORKS

In this section, we present the related works that deal

with real-time systems and reconﬁgurable architec-

tures.

In the literature, many approaches have been car-

ried out in the area of schedulability analysis for meet-

ing real-time requirements. Pillai and Shin (Pillai

and Shin, 2001) propose an optimal algorithm for

computing the minimal speed that can make a task

set schedulable. Concerning the system model and

the optimization objectives, the proposed approach is

closely related to the research works in (Bertout et al.,

2014; Bouaziz et al., 2015; Mehiaoui et al., 2013). In

(Bertout et al., 2014), the authors propose a technique

to minimize the number of tasks in a real-time system

while satisfying timing constraints. The approach in

(Bouaziz et al., 2015) aims both to reduce the num-

ber of preemptions for minimizing timing overheads

and to maximize the laxity of tasks in order to im-

prove the schedulability of the design model. There

are also related approaches which generate complete

real-time systems. In (Pillai and Shin, 2012), the au-

thors deliver an approach called TASTE to enable the

generation of a complete real-time distributed system.

The authors in (Pagetti et al., 2011) provide a frame-

work that allows designers to automatically generate

by the Prelude language, a set of real-time tasks that

can be executed on a uniprocessor architecture.

Nowadays, many research works have been pro-

posed to develop reconﬁgurable systems. The authors

in (Gharsellaoui et al., 2012) propose an approach that

deals with reconﬁgurable systems to be implemented

with different tasks under deadline constraints accord-

ing to user requirements. In (Krichen et al., 2010),

the authors aim to provide an automated development

process from modeling to implementation for the dy-

namic software part of reconﬁgurable systems.

There are many programming languages designed

for the development of real-time systems. Among

the most used real-time languages, we cite real-time

java (RT-java) which aims to support the program-

ming of real-time codes from different directions used

by other software development platforms. POSIX

(Portable Operating System Interface) is a standard

written in terms of the C programming language.

(Lewine, 1991). This standard facilitates the applica-

tion portability that is why we adopt it as a target lan-

guage to implement a reconﬁgurable real-time system

in the current paper.

The main contributions of this paper are four-fold.

The ﬁrst part consists in ensuring the respect of tim-

ing properties before the effective implementation of

the real-time system (i.e. at the design level). Sec-

ond, we are interested in the reconﬁguration of real-

time systems where the addition and removal of tasks

are applied at run-time. Third, we propose a multi-

optimization metric. Indeed, the proposed approach

aims to minimize the reconﬁguration time by avoid-

ing a redundancy between the different implementa-

tions from one side. From the other side, it aims to

minimize the response times of the real-time tasks in

order to maintain the performance of the system. The

fourth part, this work automatically generates a com-

plete reconﬁgurable real-time system from the spec-

iﬁcation level by using the programming language

POSIX. None of the existing works is solving all the

four problems together.

3 SYSTEM FORMALIZATION

In this section, we present a formal description of a re-

conﬁgurable uniprocessor system. We present in ad-

dition real-time prerequisites required to introduce the

paper’s contribution.

It is assumed in this work that a reconﬁgurable

real time system Sys is deﬁned as a set of implemen-

tations: S ys = {imp

,imp

...imp

}. We denote by

Sys(t) the implementation deﬁning the system at a

particular time t (i.e. Sys(t) = imp

). An implemen-

tation imp

is composed of n tasks that we assume in-

dependent and periodic (i.e. imp

= {τ

,τ

...τ

}).

Each task τ

executes a set of applicative functions

= {F

...F

}. A function F

is character-

ized by static parameters F

= (T

) where T

f i

the activation period of the function F

and C

f i

is an

estimation of its worst case execution time WCET.

Note that these parameters are considered as inputs

MILP-based Approach for Optimal Implementation of Reconﬁgurable Real-time Systems

331

to the proposed approach and must be speciﬁed by

the user. Each task τ

is characterized by a set of real-

time parameters (r

) : its release time r

we assume that r

= 0, its activation period T

which

is deducted from the activation periods of the func-

tions implemented by this task, its capacity or worst

case execution time C

which is equal to the sum of

the WCETs of the functions executed by this task, its

deadline D

we assume that D

= T

, the priority P

, we

assume that P

= 1/T

since we adopt the Rate Mono-

tonic priority assignment(RM).

Let U be the processor utilization factor deﬁned by:

U =

∑

i=1

. We perform Rate-Monotonic (RM) re-

sponse time analysis based on the computation of an

upper bound of the response time Rep

of the different

tasks constituting the task model. This analysis aims

to verify whether these tasks complete their computa-

tions within the time limit speciﬁed by the real-time

application i.e. the deadline (Rep

≤ D

)(Klein et al.,

1993). The reconﬁguration scenario corresponds to

adding/removing tasks or modifying timing param-

eters. Thus, we introduce the reconﬁguration time

recon f

which refers to the time required to jump from

one implementation to another according to user re-

quirements (i.e. reconﬁguration conditions). This pa-

rameter is deﬁned as follow:

recon f

= A ∗ T

delete

+ B ∗ T

creat

Where A is the number of deleted tasks, B is the

number of created tasks, T

delete

is the spent time to

delete a task and T

creat

is the spent time to create a

task. We assume that the blanking time T

delete

and

creation time T

creat

of all the tasks are equals for a

considered platform (i.e. T

delete

= T

creat

). We denote

by T

cost

the spent time to create a task or to delete it

(i.e. T

delete

= T

creat

= T

cost

). Thus, the reconﬁguration

time is given as follow:

recon f

= (A + B) ∗ T

cost

4 PROPOSED APPROACH

In this section, we present an overview on our ap-

proach and detail the structure of different modules

involved in this work. We deliver an approach which

automatically converts a high-level speciﬁcation of

a reconﬁgurable real-time system into an executable

running on POSIX platform. Figure 1 shows the pro-

cess of the proposed approach. As entry, the designer

provides the speciﬁcation model which deﬁnes the

reconﬁguration conditions, the applicative functions

that must be executed under a considered condition

and the temporal parameters of each function. This

model presents the input of the task generator step

which aims to produce an initial task model. Then,

Figure 1: Process overview.

the optimization step receives the generated model

and proposes a valid and optimal task model. This

model is ﬁnally converted into an executable program

running under POSIX.

4.1 Task Generator

The ﬁrst step consists in generating the initial task

model. This stage considers the speciﬁcation model

as an input and aims to generate the initial task model

which deﬁnes a possible implementation of the con-

sidered system. For each reconﬁguration condition,

this step generates an implementation and associates

its appropriate functions. Then, for each generated

implementation, it regroups the functions having the

same period T

f i

to be executed by one task τ

. Since

we assume that the release time r

= 0 and P

= 1/T

the task τ

is characterized only by (T

) where

the period T

corresponds to the period of the grouped

functions, C

is the sum of WCETs of the grouped

functions and the deadline D

of each task is equal to

the corresponding period T

. Let us note that for the

generation of this model, the optimization and real-

time feasibility concerns are not considered.

4.2 Task Model Optimization

This phase aims to produce a feasible and optimal im-

plementation of the reconﬁgurable real-time system

from the initial task model.

In order to avoid redundancy between the sets of im-

plementation and reduce the number of tasks, this

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

332

phase aims to merge the tasks belonging to differ-

ent implementations but implementing the same func-

tions and/or having the same periods. To implement

properly the problem by taking into consideration the

different constraints, we propose a MILP formulation

of our problem. So we should deﬁne the objective

function and the required constraints for parameters

and variables.

Deﬁnitions. Let m be the number of tasks in the ini-

tial model, let N be the number of tasks in the new

task model, let s be the starting time which corre-

sponds to effective starting time of each task. We de-

note by InitTask the initial task model which is a three

column matrix where the ﬁrst column presents the pe-

riod T

of task, the second one presents their WCETs

and the third column is their deadline D

. NewTask

is the resulting task model after merging the different

tasks (i.e. optimized task model).

Objective Function.

Maximize

∑

i, j∈{1,m}

Merge

i j

−

∑

i, j∈{1,m}

Rep

i j

(1)

This expression deﬁnes the objective function of our

problem. Merge denotes a boolean variable used

to mention whether two tasks τ

and τ

are merged.

More in detail, Merge

i j

is equal to 1 if task t

∈ imp

and task t

∈ imp

are merged. The expression(1)

aims to maximize the number of merged tasks and

minimize the sum of response times of the different

tasks constituting the task model. In order to limit non

meaningful merging situations, we deﬁne in addition

the following constraints:

Merging Situation Constraints.

The constraints (2) and (3) introduce the merging con-

dition such as tow the tasks τ

∈ imp

and τ

∈ imp

will be merged if they have the same period.

∀i, j ∈ {1 .. .m} et i 6= j,

i f (InitTask[i,1] − InitTask[k, 1]) = 0 then Merge

i j

= 1

(2)

∀i, j ∈ {1 .. .m} et i 6= j,

i f (InitTask[i,1] − InitTask[k, 1]) 6= 0 then Merge

i j

= 0

(3)

The constraint (4) means that we have to maximize

the number of merged tasks and thus minimize the

number of tasks used in the task model. Indeed, this

equation serves as a bound for the objective function

(i.e. the number of merging operations).

N = m − (

∑

i, j∈{1...m}

Merge

i j

)/2 (4)

Real-time Constraints.

NewTask is a three column matrix where the ﬁrst col-

umn presents the periods of the new tasks computed

by the constraint (5). The second column presents the

WCETs of the tasks computed by the constraint (6)

and the last column is the deadline presented by the

constraint (7)

∀k ∈ {1 .. .N},∀i ∈ {1 ... N} : NewTask[k, 1] = InitTask[i, 1]

(5)

NewTask[i,2] = (InitTask[i,2]+InitTask[ j,2])Merge[i, j]+

(1 − Merge[i, j])InitTask[i,2] (6)

∀i ∈ {1 . . . N},NewTask[i,3] = NewTask[i,1] (7)

The constraint (8) veriﬁes whether the new model

meets the timing constraints.

U =

∑

i=1

NewTask[i,2]

NewTask[i,1]

≤

∑

i=1

N(2

− 1) (8)

Constraint (9) ensures that the response times Rep

the different tasks in the optimized model are lower

or equal than their deadlines:

∀i ∈ {1 . . . N}Rep

≤ NewTask[i,3] (9)

Constraint (10) gives the computation formula of the

response time Rep

of task τ

Rep

= s[i] + NewTask[i,2] (10)

The response time Rep

of a task τ

is deﬁned as the

sum of its start time and its execution time.

∀i ∈ {1 . . . N}s[i] − s[ j] >= NewTask[ j,2] (11)

∀i ∈ {1 . . . N}s[ j] − s[i] >= NewTask[i,2] (12)

To ensure a single executed task at any time, we

should have either

s[i] − s[ j] − NewTask[ j,2] >= 0 or s[ j] − s[i] −

NewTask[i,2] >= 0, for every pair of tasks t

and t

∀i ∈ {1 . . . N}s[i] <= r[i] (13)

The task model generated by the linear program will

be interpreted by the code generator in order to gen-

erate a running program in POSIX.

4.3 Code Generator

The last step of our approach consists in building

the executable application from the optimized task

model. We manually generate a POSIX code on the

basis of transformation rules. For each task in the op-

timized task model, the code generator implements a

POSIX thread by using pthread. In addition, this step

produces the controller code of the reconﬁgurable

real-time system, which allow moving from imple-

mentation to another, following well-deﬁned condi-

tions (i.e. user requirements).

MILP-based Approach for Optimal Implementation of Reconﬁgurable Real-time Systems

333

5 CASE STUDY

In this section, we illustrate the proposed approach

through a case study. The considered case study con-

sists in a Global Positioning System (GPS). Firstly,

we present the GPS speciﬁcation. Then we apply

the proposed approach to an automatic construction

of a feasible and optimal implementation of a recon-

ﬁgurable real-time system.

5.1 GPS Presentation

The global positioning system (GPS) is used to deﬁne

the position of an object on a plan or a map using the

information provided via radio signals by the associ-

ated satellites.

To show the applicability of our approach, we con-

sider in this paper a simpliﬁed version of this system.

For clarity, several features of the system (GPS) were

omitted. Therefore, we only deﬁne two modes of op-

eration:

Insecure Mode:

This mode is deﬁned by seven functions:

(i) F

: Co ntrolBase used to synchronize the satel-

lite clock,

(ii) F

: GpsSatellite used to send radio signals (ana-

logue) terminal,

(iii) F

: Position used to receive the satellite signal,

(iv) F

: Receiver used to convert the analogue signal

into a digital signal,

(v) F

: Decoder used to decode the digital informa-

tion and separate the information of calculating

the distance from time information,

(vi) F

: TreatmentUnit used to calculate the distance

of the satellite and determine position.

(vii) F

: Encoder used for encoding information of

time and position.

Secure Mode:

The secure mode is deﬁned by eight functions.

Compared with the insecure mode, we have replaced

the function Position by Position Secure function

noted F

and we added AccessController function F

to ensure the secure reception of radio signals.

5.2 GPS Initial Task Model

The second step consists in generating the implemen-

tations and their tasks from the speciﬁcation model by

applying the Algorithm. We obtain two possible im-

plementations of the GPS which refer respectively to

the two execution modes already speciﬁed.

5.3 GPS Optimized Task Model

The third step corresponds to the generation of the

optimized task model from the initial one. A tabular

description of the task model generated by this phase

is given in Table 1.

We can see from Tables 1, this model satisﬁes the

Table 1: Tabular description of the optimized task model of

the GPS.

Execution mode Task T

Rep

Function

(ms) (ms) (ms) (ms)

100 50 100 80 F

200 40 200 200 F

Insecure Mode

300 140 300 280

400 100 400 360 F

500 60 500 450 F

100 60 100 50 F

200 40 200 200 F

300 140 300 280

Secure Mode

400 100 400 360 F

500 60 500 450 F

600 50 600 500 F

timing constraints of the GPS system since the re-

sponse times Rep

of the different tasks are lower than

their deadlines D

5.4 Performance Evaluation

We denote by T

recon f

initial

the reconﬁguration time in

the initial task model of the GPS and T

recon f

Current

the

reconﬁguration time in the optimized task one. These

parameters are given as follow:

recon f

initial

= 5 ∗ T

delete

+ 6 ∗ T

creat

= 11 ∗ T

cost

recon f

Current

= 1 ∗ T

delete

+ 2 ∗ T

creat

= 3 ∗ T

cost

We note that the proposed approach allows to re-

duce the reconﬁguration time and thus improves the

overall performance of the reconﬁgurable real-time

system (GPS). It minimizes also the sum of the re-

sponse times of the all considered tasks such as

Rep

initial

= 3010 ms and after optimization it becomes

Rep

optimized

= 1920 ms . In addition, we have ran-

domly generated instances with 5 to 40 tasks. We

compare the reconﬁguration time and the sum of re-

sponse times after optimization with the initial corre-

sponding parameters. The numerical results are de-

picted in ﬁgures 2 and 3:

These ﬁgures show that the optimization of the re-

conﬁguration and response times are clearer and more

important for large scale reconﬁgurable real-time sys-

tems.

6 CONCLUSION

In this paper, we have proposed an approach to sup-

port the development of reconﬁgurable real-time sys-

ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications

334

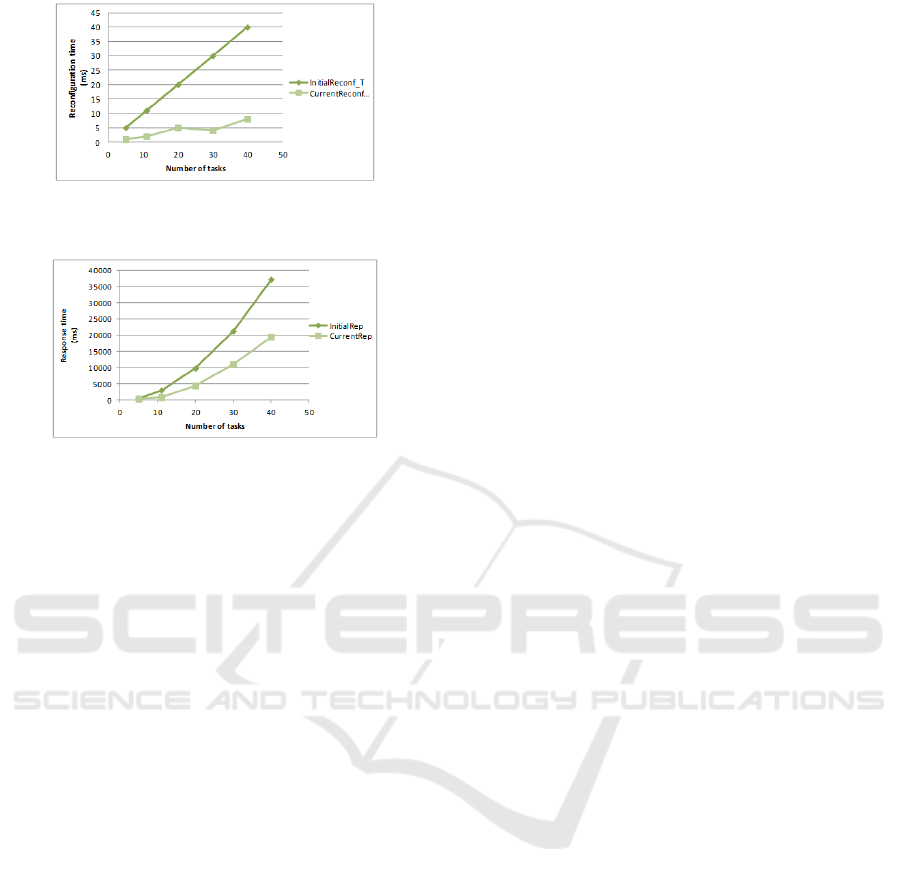
Figure 2: Comparison between Current reconﬁguration

time and initial one.

Figure 3: Comparison between Current response time and

initial one.

tems. This approach consists in deﬁning the speci-

ﬁcation such as reconﬁgurable conditions, functions

and temporal constraints, then it generates an initial

task model. After that, a MILP integral formulation

is provided to compute the optimal solution for min-

imizing redundancy. Finally, the proposed approach

generates a POSIX-based program describing the re-

conﬁgurable real-time system. We have evaluated the

performance of the three-step approach. The numeri-

cal results show that the integer programming model

allows to minimize the reconﬁguration time and re-

sponse times.

As a future work, we aim to extend our approach by

considering multiprocessor systems and other opti-

mization metrics. So that we expect to evaluate scal-

ability of the proposed method with an industrial ex-

ample.

REFERENCES

Bertout, A., Forget, J., and Olejnik, R. (2014). Minimiz-

ing a real-time task set through task clustering. In

Proceedings of the 22nd International Conference on

Real-Time Networks and Systems, Versailles, France,

page 23. ACM.

Bouaziz, R., Lemarchand, L., Singhoff, F., Zalila, B.,

and Jmaiel, M. (2015). Architecture exploration of

real-time systems based on multi-objective optimiza-

tion. In Proceedings of the 20nd International Confer-

ence on Engineering of Complex Computer Systems

(ICECCS), Gold Coast, QLD, pages 1–10. IEEE.

Burns, A. and Wellings, A. (2009). Real-Time Systems and

Programming Languages: Ada, Real-Time Java and

C/Real-Time POSIX. Addison-Wesley Educational

Publishers Inc, USA, 4nd edition.

Cottet, F. and Grolleau, E. (2005). Systmes Temps R

eel de

Contr

ole-Commande. Dunod, Paris.

Gharsellaoui, H., Gharbi, A., Khalgui, M., and Ahmed, S.

(2012). Feasible automatic reconﬁgurations of real-

time os tasks. Handbook of Research on Industrial

Informatics and Manufacturing Intelligence: Innova-

tions and Solutions: Innovations and Solutions.

Klein, M., Ralya, T., Pollak, B., Obenza, R., and Harbour,

M. G. (1993). Analyzing complex systems. In Pro-

ceedings of Real-Time Analysis, US, pages 535–578.

Springer.

Krichen, F., Hamid, B., Zalila, B., and Coulette, B. (2010).

Designing dynamic reconﬁguration for distributed

real time embedded systems. In Proceedings of

10th Annual International Conference on New Tech-

nologies of Distributed Systems (NOTERE), Tozeur,

Tunisia, pages 249–254. IEEE.

Lewine, D. (1991). POSIX programmers guide. O’Reilly

Media, Inc., USA.

Liu, C. and Layland, J. (1973). Scheduling algorithms for

multiprogramming in a hard-real-time environment.

Journal of the ACM (JACM), 20(1):46–61.

Mehiaoui, A., Wozniak, E., Tucci-Piergiovanni, S.,

Mraidha, C., Natale, M. D., Zeng, H., Babau, J.,

Lemarchand, L., and Gerard, S. (2013). A two-step

optimization technique for functions placement, par-

titioning, and priority assignment in distributed sys-

tems. ACM SIGPLAN Notices, 48(5):121–132.

Obenland, K. M. (2000). The use of posix in real-time sys-

tems, assessing its effectiveness and performance. The

MITRE Corporation.

Pagetti, C., Forget, J., Boniol, F., Cordovilla, M., and

Lesens, D. (2011). Multi-task implementation of

multi-periodic synchronous programs. Discrete event

dynamic systems, pages 307–338.

Pillai, P. and Shin, K. (2001). Real-time dynamic voltage

scaling for low-power embedded operating systems.

In Proceedings of the 13th Euromicro Conference on

Real-Time Systems, USA, pages 59–66. ACM.

Pillai, P. and Shin, K. (2012). Taste-an open-source tool-

chain for embedded system and software develop-

ment. In Proceedings of the Embedded Real Time

Software and Systems Conference (ERTS), Toulouse,

France.

zniak, E. Model-based Synthesis of Distributed Real-

time Automotive Architectures. PhD thesis, Universit

Paris Sud-Paris XI.

MILP-based Approach for Optimal Implementation of Reconﬁgurable Real-time Systems

335