Human Tracking in Occlusion based on Reappearance Event Estimation

Hassan M. Nemati, Saeed Gholami Shahbandi and Bj

orn

Astrand

School of Information Technology, Halmstad University, Halmsatd, Sweden

Keywords:

Detection and Tracking Moving Objects, Extended Kalman Filter, Human Tracking, Occlusion, Intelligent

Vehicles, Mobile Robots.

Abstract:

Relying on the commonsense knowledge that the trajectory of any physical entity in the spatio-temporal do-

main is continuous, we propose a heuristic data association technique. The technique is used in conjunction

with an Extended Kalman Filter (EKF) for human tracking under occlusion. Our method is capable of tracking

moving objects, maintain their state hypothesis even in the period of occlusion, and associate the target reap-

peared from occlusion with the existing hypothesis. The technique relies on the estimation of the reappearance

event both in time and location, accompanied with an alert signal that would enable more intelligent behavior

(e.g. in path planning). We implemented the proposed method, and evaluated its performance with real-world

data. The result validates the expected capabilities, even in case of tracking multiple humans simultaneously.

1 INTRODUCTION

An autonomous mobile robot is not only expected to

self-localize and navigate through the environment,

but also perceive and understand the dynamic of its

surrounding to avoid collisions. Becoming aware

of moving objects is a contributing factor to this

objective. From this perspective, object detection and

tracking is a crucial requirement for a safe operation,

especially in environments where humans and robots

share the work space. In the context of intelligent

vehicles, human detection and tracking is an im-

portant concern for automation safety. Examples

of such context are self-driving cars in cities and

auto-guided lift trucks in warehouses (see ﬁgure 1.)

The challenge is often referred to as Detection and

Tracking Moving Objects (DTMO), which also

contributes to the performance of SLAM algorithms

(Wang and Thorpe, 2002).

Related Works: Various techniques and algo-

rithms have been proposed for movement and human

detection using different types of sensors. Some ap-

proaches are based on 2D and 3D laser scanners (Cas-

tro et al., 2004), (Xavier et al., 2005), (Arras et al.,

2007), (Nemati and

Astrand, 2014), (Lovas and Barsi,

2015), visual sensors and cameras (Papageorgiou and

Poggio, 2000), (Dalal and Triggs, 2005), (Tuzel et al.,

2007), (Schiele et al., 2009), (Zitouni et al., 2015), or

a combination of both laser scanners and visual sen-

sors (Zivkovic and Krose, 2007), (Arras and Mozos,

2009), (Linder and Arras, 2016).

The accuracy, robustness, and metric result of

range scanner sensors makes them more suitable, and

consequently the favorable choice. The number of

employed sensors varies depending on the approach.

For instance (Mozos et al., 2010) uses three laser

scanners in different heights to detect human’s legs,

torso, and the head. Carballo et al. in (Carballo et al.,

2009) employ a double layered laser scanner to de-

tect legs and torso. In these approaches, the pose of

the tracked object (what we call “target”) is estimated

after ﬁtting a model to the measurements of the sen-

sors. While using multiple sensors improves the per-

formance of system, it comes with a trade off on the

cost and maintenance of more sensors.

For many task such as path planning and obsta-

cle avoidance, detection of the objects alone does not

sufﬁce. Such tasks require the ability to track the mo-

tion and predict the future state of the moving objects.

In order to reliably track a moving object’s motion,

one must tackle different challenges, such as non de-

terministic motion model and occlusion. Under such

circumstances, using a probabilistic framework is cru-

cial (Schulz et al., 2001).

The human tracking problem can be reduced to a

search task and formulated as an optimization prob-

lem. Accordingly, the human tracking problem could

be considered as a deterministic or a stochastic prob-

lem. In case of the deterministic methods, the track-

ing results are often obtained by optimizing an ob-

jective function based on distance, similarity or clas-

Nemati, H., Shahbandi, S. and Åstrand, B.

Human Tracking in Occlusion based on Reappearance Event Estimation.

DOI: 10.5220/0006006805050512

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 505-512

ISBN: 978-989-758-198-4

505

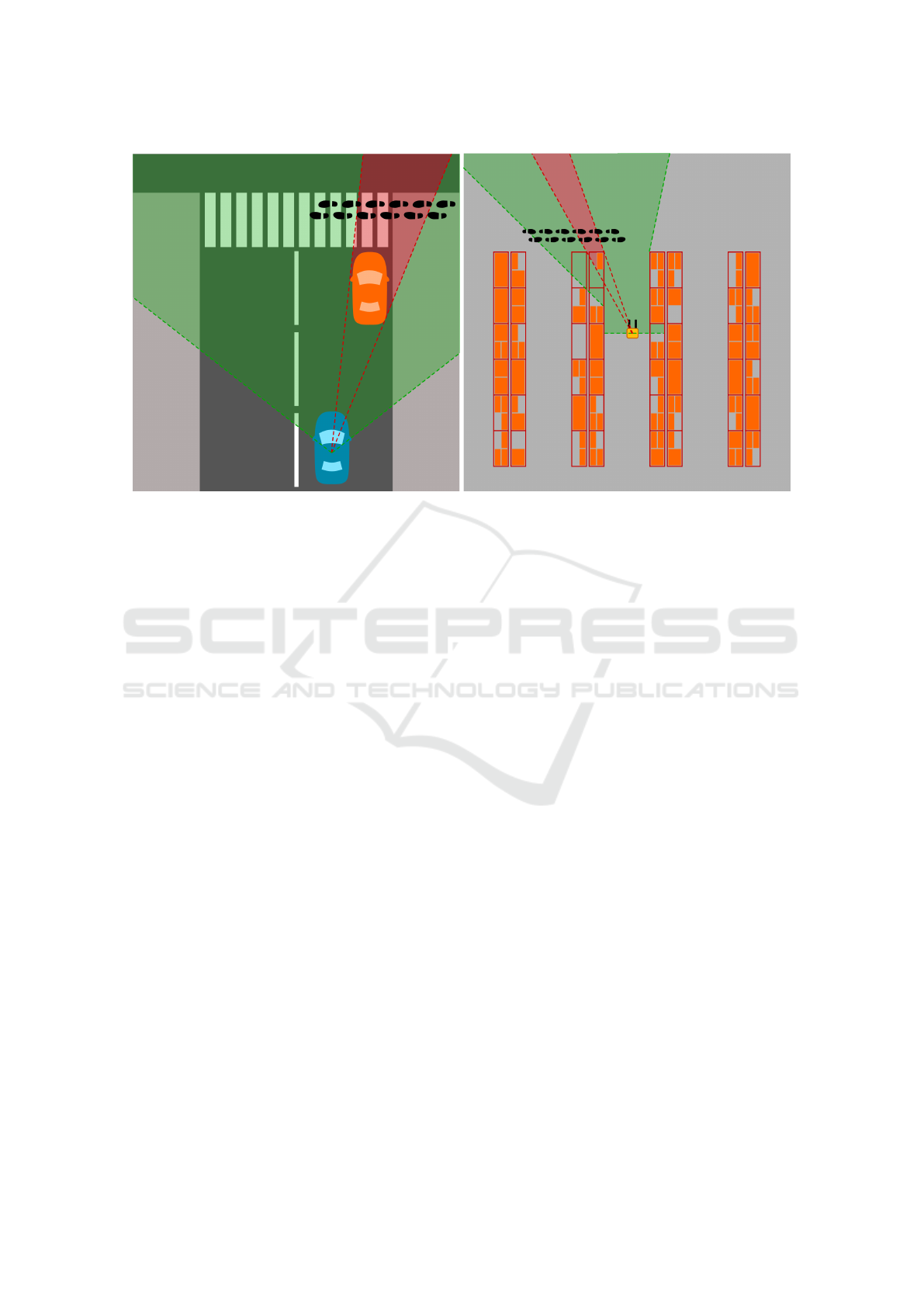
(a) occlusion in an urban scenario

(b) occlusion in a warehouse scenario

Figure 1: Two examples where the target (tracked object) disappears momentarily.

siﬁcation measures. The Kanade-Lucas-Tomasi al-

gorithm (Lucas et al., 1981), the mean-shift track-

ing algorithm (Comaniciu et al., 2003), Kalman Filter

(Fod et al., 2002), (Castro et al., 2004), (Xavier et al.,

2005), (Le Roux, 1960), and Extended Kalman Fil-

ter (EKF) (Grewal and Andrews, ), (Kalman, 1960),

(Welch and Bishop, 2004), (Kmiotek and Ruichek,

2008), (Rebai et al., 2009) are some examples of

deterministic methods. Stochastic methods on the

other hand usually optimize the objective function by

considering observations over multiple scans using a

Bayesian rule. It improves robustness over determin-

istic methods. The condensation algorithm (Isard and

Blake, 1998) and Particle Filters (PF) (Schulz et al.,

2001), (Thrun et al., 2005), (Almeida et al., 2005),

(Br

aunl, 2008), (Arras and Mozos, 2009) are some

examples of stochastic approaches.

Observability of the target has often been an

underlying assumption in the formulation of human

tracking problem. Few has taken into account the

problem of partially occluded targets (Arras et al.,

2008), (Leigh et al., 2015), but not the problem

of fully occluded target. Figure 1 demonstrates

two scenarios where the target disappears and

might reappear again from behind the obstacle. In

these examples the target momentarily becomes

hidden from the laser scanner due to obstacles in

between. If the autonomous vehicle (what we call

“agent”) is not capable of maintaining the hypoth-

esis associated with the to-be occluded target, the

probable reappearance event might surprise the agent.

Our Approach: In this paper we propose a novel

approach for human (“target”) tracking under occlu-

sion. Our heuristic method relies on the common-

sense knowledge that the trajectory of any physical

entity in the spatio-temporal domain is continuous.

Detecting occluded regions caused by stationary ob-

jects, the method is enabled to associate an upcom-

ing occlusion event to a target. The time and location

of the reappearance event is estimated according to

the last observed velocity and direction of the target,

and the relative location between the agent, occluding

obstacle and the target. Awareness of the upcoming

occlusion event provides a probabilistic insight to the

future state of the target, improving the data associa-

tion between observation of the reappeared target and

the agent’s hypothesis of target’s state. Our approach

enables the agent to detect the occlusion event, and

the upcoming reappearance event more reliably, and

consequently would improve decisions towards safe

operation, on adaptive path planning to avoid colli-

sion.

In the rest of this paper, we review the architec-

ture of a DTMO system in section 2. This section also

contains a full description of our proposed method in

details, along with its integration with an EKF algo-

rithm. The performance of our proposal is evaluated

in section 3 through a series of real-world experiments

with different setups. In the last section, we conclude

the paper by reviewing the advantages and limitations

of our method, and presenting our plans for future

works.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

506

2 APPROACH

A general DTMO system for human detection and

tracking procedure is composed of several sequen-

tial steps: i) segmentation of objects; ii) modeling

of the objects; iii) human detection; iv) pose estima-

tion; and v) associating a hypothesis to each target’s

state and tracking the hypothesis . The ﬁrst step is

the segmentation of the sensor’s measurement into a

set of objects based on the connectivity of data points

(Castro et al., 2004), (Xavier et al., 2005), (Preme-

bida and Nunes, 2005). Segmentation step is followed

by modeling each distinct object with a geometrical

model of line or circle. In order to identify potential

targets (i.e. humans) we take two criteria into con-

sideration. i) size; and ii) motion . The length of

the lines, or diameter of the circles denote the size of

the objects. Small objects with a length less than an

empirical threshold (50

) are classiﬁed as potential

targets (i.e. humans leg). If two legs are close enough

to each other (less than 40

), they are grouped into a

single target. The position of the human body is then

calculated based on the mean value of center of grav-

ity of each leg. Additionally, we consider the motion

of the potential targets to distinguish between station-

ary and moving objects. Motion of each object is esti-

mated over consecutive frames of measurement. As-

sociating a hypothesis with target’s state, and tracking

the hypothesis through observation, makes it possible

to predict the next position of the target and conse-

quently to alleviate the consequence of occlusion.

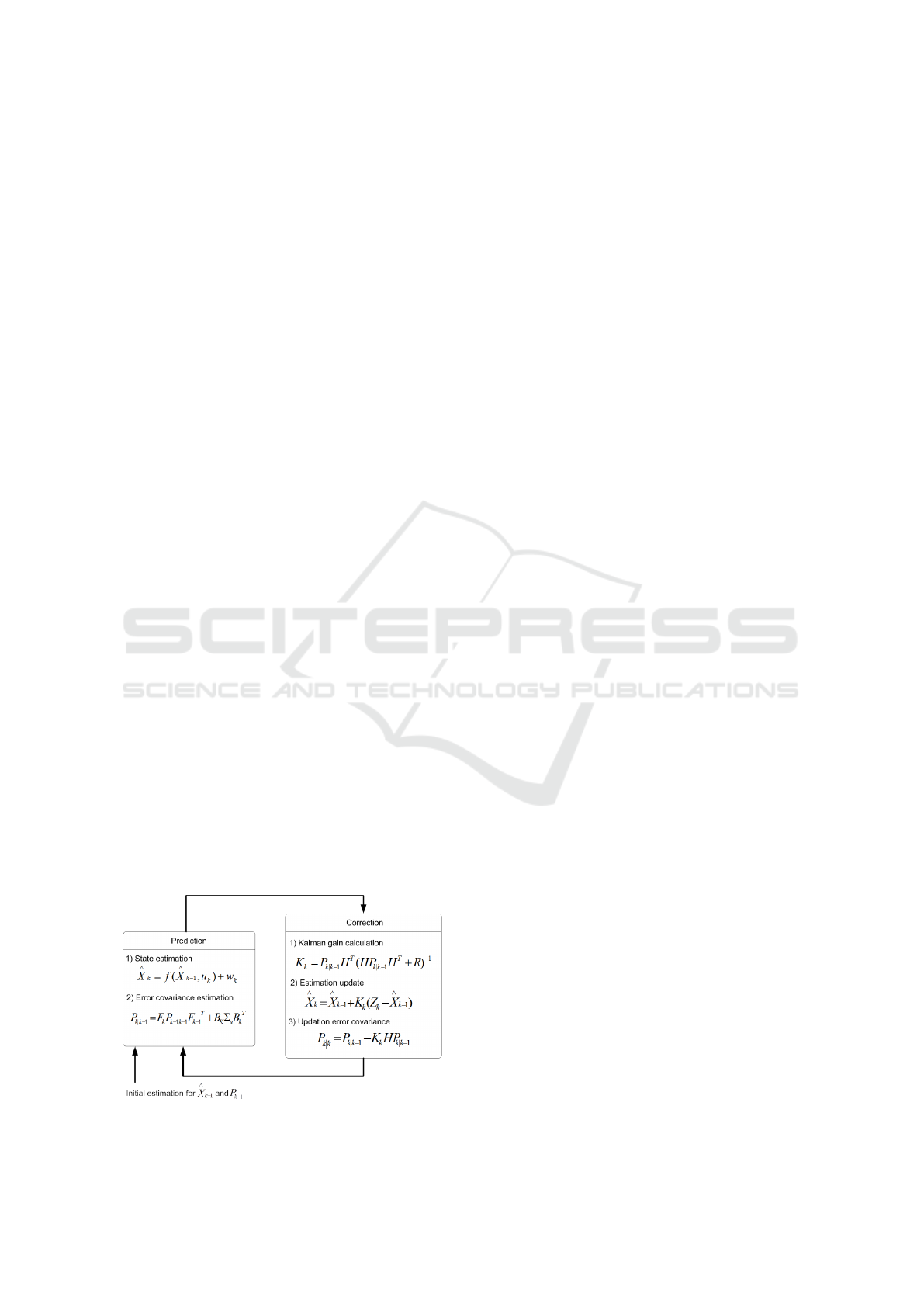
The most common approach for tracking problem

is Kalman ﬁlter, and in nonlinear situations EKF. The

general procedure of EKF tracking is illustrated in

Figure 2. EKF procedure starts by associating each

target with one single modal hypothesis of the state

of that target. In other words, the hypothesis is the

agent’s “belief” of the target’s state. The state in-

cludes the pose and velocity of the target. Each hy-

pothesis contains an uncertainty denoted by a covari-

ance matrix. The uncertainty indicates how much the

Figure 2: Extended Kalman Filter.

agent is sure of the target’s state. Based on the mo-

tion model and the hypothesis, EKF predicts the next

state of the target. The EKF updates the hypothesis

with new sensor measurments /or/ observations, and

consequently decreases the uncertainty.

2.1 Hypothesis Tracking in Occlusion

The challenge rises when the agent can not observe

the target (loses visibility) and therefore is unable to

update its hypothesis. Increase of uncertainty over the

iterations of prediction stage without updating cycles

is the consequence of the occlusion (see ﬁgure 3b).

The increased in uncertainty makes it impossible for

the agent to recover its hypothesis even after the reap-

pearance of the target. That is to say, the agent would

not be able to associate the new observations of the

reappeared target with the existing, but highly uncer-

tain hypothesis. More importantly the agent would

become less aware of the target’s location as the time

passes.

Here we propose an approach to maintain the

hypothesis associated with occluded target, so that

the agent would become aware of the upcoming

reappearance event. The novelty in this work is a

heuristic assumption that our method relies on, and

it is based on the continuity of target’s trajectory

in the spatio-temporal domain. In this case, if an

object becomes invisible by an observer, it is out of

sight or occluded, but does not mean it disappeared

to “nowhere”. By formulating the occlusion event

and its consequences in terms of observations,, our

approach enables the agent to detect the occlusion

event, and consequently handle the upcoming reap-

pearance event more reliably.

Occluded Region: Every stationary object is

counted as an obstacle which can cause an occluded

region. Each occluded region is bounded by the

causing obstacle, the lines of sight from the agent,

and the range of sensor (see ﬁgure 3a). Note that

in the result section, we only highlight the potential

candidate among all the occluded regions where the

target is about to hide in that region.

Hypothesis Tracking: The tracking algorithm

is modiﬁed to update the hidden target’s state (i.e.

pose = (x, y, θ)) based on the last observed direction

and velocity of the target. Instead of expanding the

uncertainty region associated with the state of the

hidden target in every direction (default in EKF),

the modiﬁed updating procedure would increase the

uncertainty along the line of sight (see ﬁgures 3b

and 3c). The imposed restriction on the uncertainty

Human Tracking in Occlusion based on Reappearance Event Estimation

507

(a) occlusion and events

(b) default prediction

Figure 3: In this illustration we present an occlusion scenario in detail. Figure 3a show the relative locations of the agent,

target and the occluding obstacle. The concepts of “occluded region” and “lines of sight” are also described. Figure 3b and

3c represent the difference between the default hypothesis tracking of the EKF and our proposed method.

update improves the agent’s ability to associate the

target at reappearance with its existing hypothesis.

This in turn provides the agent with more knowledge

of its surrounding (i.e. occluded targets) that would

improve decisions on path planning, and obstacle

avoidance if required. In addition, the modiﬁcation

does not demand any extra computation.

Bounding Hypothesis Location: We pose a con-

straint over the estimated position of the occluded tar-

get. The bound to this constraint is the estimated reap-

pearance location on the line of sight (see ﬁgure 3a).

This is also motivated by the continuity of the target’s

trajectory in spatio-temporal domain. In other words,

the target is not expected to appear anywhere far from

the line of sight. We do not address the possibility of

drastic changes of the motion model (i.e velocity and

trajectory) in this paper.

In this case the covariance matrix R (in the cor-

rection phase of EKF) is modiﬁed to R

based on the

bounding hypothesis and is expanded on the line of

sight (see ﬁgure 3a) according to the following for-

mulas.

= Rot(θ) ·





Rot(θ) =



cos(θ) −sin(θ)

sin(θ) cos(θ)



θ = arctan(

obstacle

− y

agent

obstacle

− x

agent

)

, where σ

= λ · σ

, λ > 1 and varies depending on

the distance between the agent and the target.

Hypothesis Rejection: when should the agent

reject the hypothesis associated with a hidden target?

We consider two criteria to reject a hypothesis:

i) when the agent moves and the estimated trajectory

of the target in the occluded region becomes visible;

and ii) an upper bound in time (t

), relative to the

estimated occlusion period (see ﬁgure 4). The hy-

pothesis rejection time is dependent on the estimation

of reappearance event. The estimated reappearance

event in turn is adaptive to the relative pose of the

agent and the obstacle. Consequently, we can assume

that the ﬁrst criterion for rejecting the hypothesis will

be included in the second criterion.

Alert Signal: Furthermore, for a more reliable

behavior, we estimate the location and the time of

reappearance event for the hidden target. This esti-

mation is associated with an alert signal which warns

the agent of the reappearance event beforehand. The

signal is deﬁned as:

Alert

(t) =











−t

< t < t

1 t

< t < t

0 otherwise

3 EXPERIMENTS AND RESULTS

To evaluate the performance of our proposed ap-

proach, several experiments with multiple moving

objects in different situations are performed. Even

though the experiments are done from a stationary

agent’s sensor perspective, the proposed method of

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

508

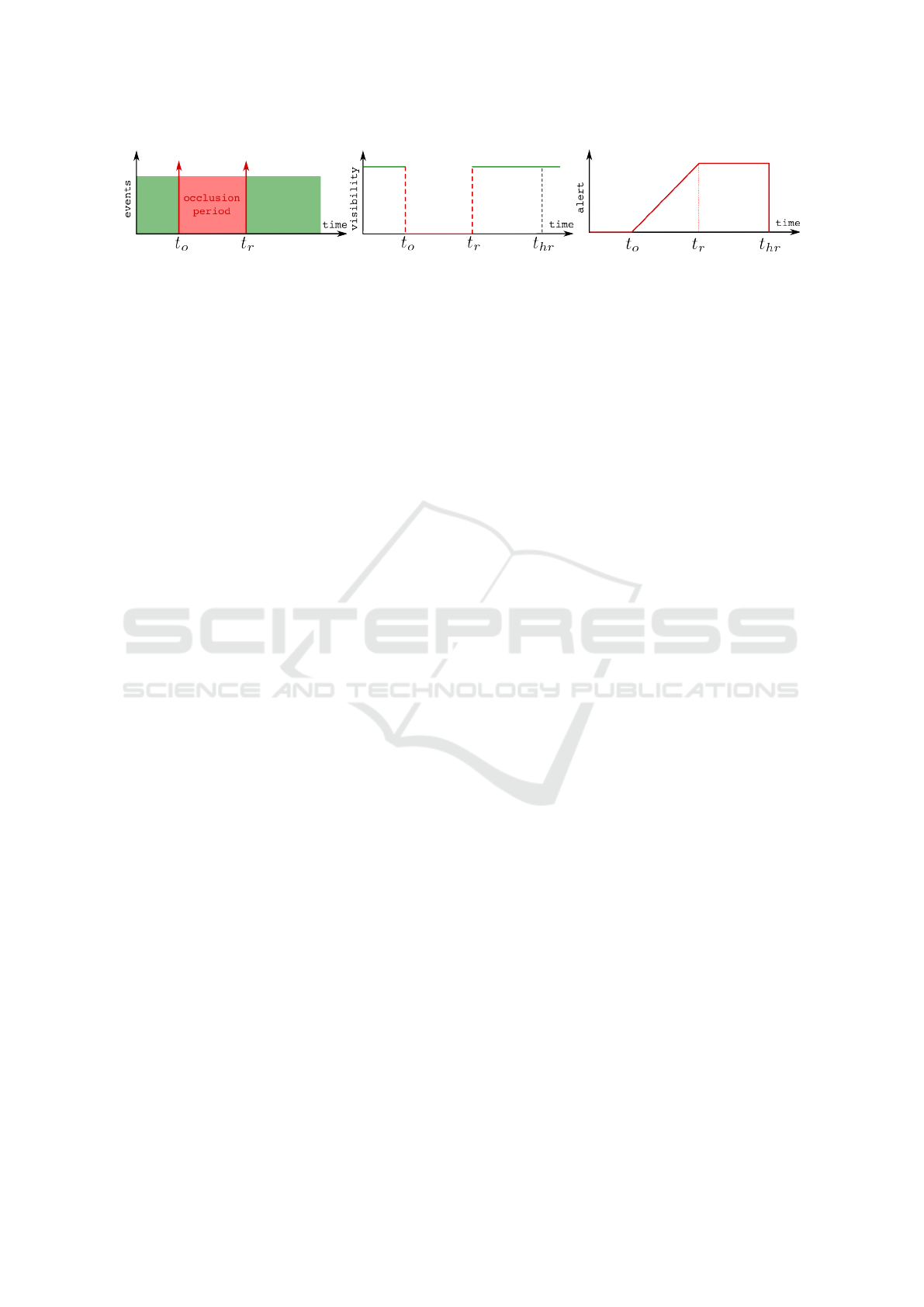
(a) events of interest

(b) visibility of the target

Figure 4: A temporal analysis of the occlusion scenario is provided in this ﬁgure. In (a) two events of occlusion and reap-

pearance are presented by upward arrows. t

is the time of occlusion, t

is the estimated time of reappearance, and t

is the

time of hypothesis rejection. (b) shows the visibility of the target from the agents point of view with respect to time. And (c)

illustrates the proposed “alert signal” that could be used for a cautious behavior planning of the autonomous vehicle.

this paper is intended to be employed by mobile

agents. The conversion between the two cases could

be simply done by the conversion of observations

from an ego-centric to world-centric reference frame.

The experiments have been done at Halmstad Univer-

sity Laboratory. The laser scanner (SICK S300) is

mounted at the height about 30

above the ground

and two obstacles are placed in the sensor’s ﬁeld of

view.

In the ﬁrst experiment, a person is moving in the

sensor’s ﬁeld of view and walking behind an obstacle.

Two examples of applying our approach in this setup

are shown in ﬁgure 5a and ﬁgure 5b.

In the second setup two people are moving in the

ﬁeld. In the case of having multiple targets, one target

might be occluded by the other target. Such occlusion

is known as partially occluded situation in the track-

ing and detection domain. Therefore, in these exper-

iments the target might become hidden partly (by the

other target) or fully (by an obstacle) from the laser

scanner. Figures 5c and 5d show successful track-

ing results applying our approach under these circum-

stances.

In the next experiment, a more complex situation

is investigated, where multiple people are walking in

the sensor’s ﬁeld of view. Figure 5e shows an exam-

ple of three people walking in the environment. The

results verify how efﬁcient our approach can handle

human tracking in occlusion situation.

Last experiment is devoted to one of the most

challenging situation in which two targets are ap-

proaching to each other, and the meeting point is

hidden behind an obstacle. In fact they are passing

each other while they are hidden by an obstacle,

so the sensor does not receive any measurement to

update its hypotheses. The question is whether the

approach can correctly continue tracking the targets

after reappearing, and be able to associate them with

the correct hypothesis. The result shows in ﬁgure 5f

and veriﬁes that both targets are correctly tracked as

they reappear from behind the obstacle.

In the classic EKF tracking, when the target is hid-

den for a certain time, the uncertainty area of the oc-

cluded target will be increased at each scan. This will

result in a drastic drop of certainty before the target

reappears from behind the obstacle, and consequently

it is nearly impossible for the system to recover. In

addition, any change in the targets velocity would re-

sult in a mismatch between the targets location and

the hypothesis. In such cases even if the uncertainty

is not too high, the association would fail due to the

mismatch between target’s real location and the hy-

pothesis.

Our proposed approach would not fall into the

same pitfall since the hypothesis will not be expanded

like classical EKF. Instead the hypothesis is adjusted,

with an increased uncertainty but only in the direction

of the sensor’s line of sight. Furthermore according to

the aforementioned heuristic (trajectory continuity in

the spatio-temporal domain), the location of the hy-

pothesis is adjust to where the object is estimated to

reappear. This improves the ability of the intelligent

vehicle to associate the person at reappearance with

its existing hypothesis.

4 CONCLUSION

In an environment shared between humans and au-

tonomous vehicles, detection and tracking of moving

objects is one of the most crucial requirements for

safe path planning (i.e. collision avoidance). This

challenge becomes more of a concern when a moving

object hides momentarily behind an obstacle. We

tackled this problem by proposing a novel approach in

maintaining hypotheses in occlusion. Our approach

detects the occlusion event, predicts the reappearance

event both in time and location. Relying on these

information, the agent is enabled to maintain the state

hypothesis of the occluded target. Consequently the

agent becomes aware of the upcoming reappearance

and can take appropriate action to avoid hazards. The

performance of the approach is evaluated through a

series of real-world experiments. The experiments

Human Tracking in Occlusion based on Reappearance Event Estimation

509

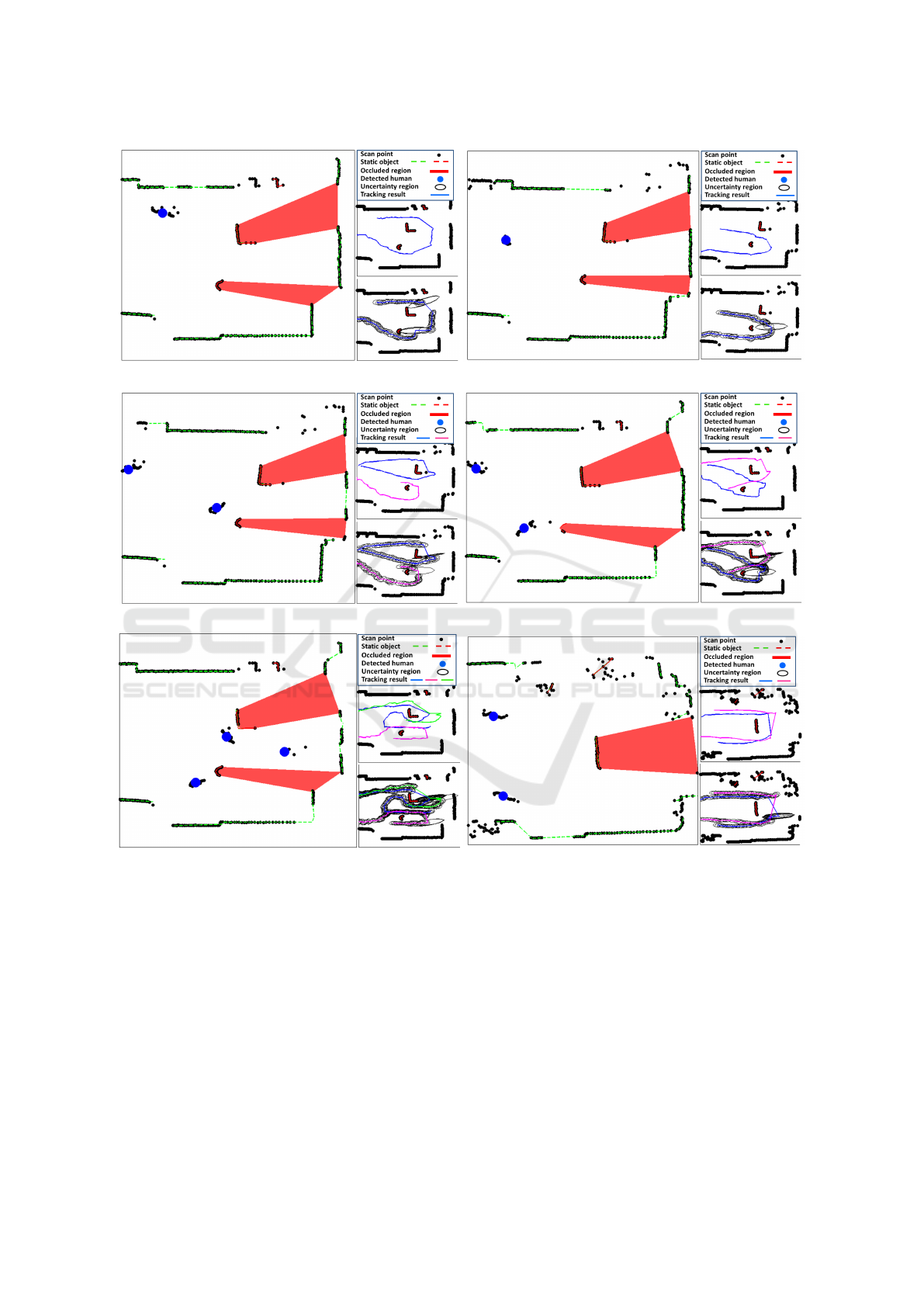
(a) One moving human and two obstacles

(b) One moving human and two obstacles

(d) Two moving humans and two obstacles

(e) Multiple moving humans and two obstacles

(f) Two moving humans and one obstacle

Figure 5: In each sub-ﬁgure, the laser scanner’s ﬁeld of view with the result of object segmentation and modeling are shown

in the left hand side (single bigger image) The tracking results based on the proposed method are shown in the right hand plots

in a column of two plots, the bottom one also shows the uncertainties associated with hypotheses. Black dots are the scan

point, dash red and green lines are static objects, red area is the occluded region, blue circle is the estimated human position,

black ellipse are the uncertainty regions for each scan, and the blue, cyan, and green lines are the tracking results.

vary in environment conﬁguration, number of targets

and their trajectories. Our proposed approach can

handle human tracking in occlusion situation in a

more efﬁcient way compared to classical EKF. It does

not require additional computational power, which

makes it faster than PF, specially in crowded envi-

ronment with multiple targets. Due to the conﬁned

space of the common robotic labs, our experimental

result could not reﬂect the ability to tackle the

problem in case of a moving agent. Nevertheless

our proposed approach can be used by moving

agents, using a conversion of observation from the

ego-centric to world-centric frame of reference.

A video compilation of the results is available at

https://www.youtube.com/watch?v=16TyoN-LxzA.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

510

Prospective: In the future works we plan to im-

prove our target tracking systems from different per-

spective. We plan to employ more advanced tech-

niques in estimating the trajectory of the hidden tar-

get, instead of the straight line trajectory assumption.

In addition we will integrate a mutation based trajec-

tory bifurcation to expand the hypothesis over a trel-

lis to account for the possible radical changes in the

trajectory of the target. Furthermore we plan to im-

plement a more comprehensive system, composed of

different sensory modalities, so that the data associa-

tion could beneﬁt from visual cues. The continuation

of this work will be evaluated over more experimental

results, that we plan to carry out in a real warehouse

environment.

REFERENCES

Almeida, A., Almeida, J., and Ara

ujo, R. (2005). Real-

time tracking of multiple moving objects using par-

ticle ﬁlters and probabilistic data association. AU-

TOMATIKA:

casopis za automatiku, mjerenje, elek-

troniku, ra

cunarstvo i komunikacije, 46(1-2):39–48.

Arras, K. O., Grzonka, S., Luber, M., and Burgard, W.

(2008). Efﬁcient people tracking in laser range data

using a multi-hypothesis leg-tracker with adaptive oc-

clusion probabilities. In Robotics and Automation,

2008. ICRA 2008. IEEE International Conference on,

pages 1710–1715. IEEE.

Arras, K. O. and Mozos, O. M. (2009). People detection

and tracking.

Arras, K. O., Mozos,

O. M., and Burgard, W. (2007). Us-

ing boosted features for the detection of people in

2D range data. In Robotics and Automation, 2007

IEEE International Conference on, pages 3402–3407.

IEEE.

aunl, T. (2008). Embedded robotics: mobile robot design

and applications with embedded systems. Springer

Science & Business Media.

Carballo, A., Ohya, A., and Yuta, S. (2009). Multiple peo-

ple detection from a mobile robot using double lay-

ered laser range ﬁnders. In ICRA Workshop.

Castro, D., Nunes, U., and Ruano, A. (2004). Feature ex-

traction for moving objects tracking system in indoor

environments. In Proc. 5th IFAC/euron Symposium on

Intelligent Autonomous Vehicles. Citeseer.

Comaniciu, D., Ramesh, V., and Meer, P. (2003). Kernel-

based object tracking. Pattern Analysis and Machine

Intelligence, IEEE Transactions on, 25(5):564–577.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In Computer Vision and

Pattern Recognition, 2005. CVPR 2005. IEEE Com-

puter Society Conference on, volume 1, pages 886–

893. IEEE.

Fod, A., Howard, A., and Mataric, M. J. (2002). A

laser-based people tracker. In Robotics and Automa-

tion, 2002. Proceedings. ICRA’02. IEEE International

Conference on, volume 3, pages 3024–3029. IEEE.

Grewal, M. S. and Andrews, A. P. Kalman ﬁltering: theory

and practice, 1993.

Isard, M. and Blake, A. (1998). Condensationconditional

density propagation for visual tracking. International

journal of computer vision, 29(1):5–28.

Kalman, R. E. (1960). A new approach to linear ﬁltering

and prediction problems. Journal of basic Engineer-

ing, 82(1):35–45.

Kmiotek, P. and Ruichek, Y. (2008). Representing and

tracking of dynamics objects using oriented bound-

ing box and extended kalman ﬁlter. In Intelligent

Transportation Systems, 2008. ITSC 2008. 11th Inter-

national IEEE Conference on, pages 322–328. IEEE.

Le Roux, J. (1960). An introduction to kalman ﬁltering:

Probabilistic and deterministic approaches. ASME J.

Basic Engineering, 82:34–45.

Leigh, A., Pineau, J., Olmedo, N., and Zhang, H. (2015).

Person tracking and following with 2D laser scanners.

In Robotics and Automation (ICRA), 2015 IEEE Inter-

national Conference on, pages 726–733. IEEE.

Linder, T. and Arras, K. O. (2016). People detection, track-

ing and visualization using ROS on a mobile service

robot. In Robot Operating System (ROS), pages 187–

213. Springer.

Lovas, T. and Barsi, A. (2015). Pedestrian detection by pro-

ﬁle laser scanning. In Models and Technologies for

Intelligent Transportation Systems (MT-ITS), 2015 In-

ternational Conference on, pages 408–412. IEEE.

Lucas, B. D., Kanade, T., et al. (1981). An iterative image

registration technique with an application to stereo vi-

sion. In IJCAI, volume 81, pages 674–679.

Mozos, O. M., Kurazume, R., and Hasegawa, T. (2010).

Multi-part people detection using 2D range data. In-

ternational Journal of Social Robotics, 2(1):31–40.

Nemati, H. and

Astrand, B. (2014). Tracking of people

in paper mill warehouse using laser range sensor. In

Modelling Symposium (EMS), 2014 European, pages

52–57. IEEE.

Papageorgiou, C. and Poggio, T. (2000). A trainable system

for object detection. International Journal of Com-

puter Vision, 38(1):15–33.

Premebida, C. and Nunes, U. (2005). Segmentation and ge-

ometric primitives extraction from 2D laser range data

for mobile robot applications. Robotica, 2005:17–25.

Rebai, K., Benabderrahmane, A., Azouaoui, O., and

Ouadah, N. (2009). Moving obstacles detection

and tracking with laser range ﬁnder. In Advanced

Robotics, 2009. ICAR 2009. International Conference

on, pages 1–6. IEEE.

Schiele, B., Andriluka, M., Majer, N., Roth, S., and Wojek,

C. (2009). Visual people detection: Different mod-

els, comparison and discussion. In IEEE International

Conference on Robotics and Automation.

Schulz, D., Burgard, W., Fox, D., and Cremers, A. B.

(2001). Tracking multiple moving targets with a mo-

bile robot using particle ﬁlters and statistical data as-

sociation. In Robotics and Automation, 2001. Pro-

Human Tracking in Occlusion based on Reappearance Event Estimation

511

ceedings 2001 ICRA. IEEE International Conference

on, volume 2, pages 1665–1670. IEEE.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic

robotics. MIT press.

Tuzel, O., Porikli, F., and Meer, P. (2007). Human de-

tection via classiﬁcation on riemannian manifolds.

In Computer Vision and Pattern Recognition, 2007.

CVPR’07. IEEE Conference on, pages 1–8. IEEE.

Wang, C.-C. and Thorpe, C. (2002). Simultaneous localiza-

tion and mapping with detection and tracking of mov-

ing objects. In Robotics and Automation, 2002. Pro-

ceedings. ICRA’02. IEEE International Conference

on, volume 3, pages 2918–2924. IEEE.

Welch, G. and Bishop, G. (2004). An introduction to the

kalman ﬁlter. university of north carolina at chapel

hill, department of computer science. Technical re-

port, TR 95-041.

Xavier, J., Pacheco, M., Castro, D., Ruano, A., and Nunes,

U. (2005). Fast line, arc/circle and leg detection from

laser scan data in a player driver. In Robotics and Au-

tomation, 2005. ICRA 2005. Proceedings of the 2005

IEEE International Conference on, pages 3930–3935.

IEEE.

Zitouni, M. S., Dias, J., Al-Mualla, M., and Bhaskar, H.

(2015). Hierarchical crowd detection and represen-

tation for big data analytics in visual surveillance. In

Systems, Man, and Cybernetics (SMC), 2015 IEEE In-

ternational Conference on, pages 1827–1832. IEEE.

Zivkovic, Z. and Krose, B. (2007). Part based people de-

tection using 2D range data and images. In Intelligent

Robots and Systems, 2007. IROS 2007. IEEE/RSJ In-

ternational Conference on, pages 214–219. IEEE.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

512