Functional Evaluation of the Solid Model Creation

using 3D Direct Drawing System

Kaoru Mitsuhashi

, Hiroshi Hashimoto

and Yasuhiro Ohyama

Department of Mechanical Engineering, School of Engineering, Tokyo University of Technology, Hachioji, Tokyo, Japan

Master Program of Innovation for Design and Engineering, Advanced Institute of Industrial Technology, Tokyo, Japan

Keywords: 3D Direct Drawing, ARToolKit, Solid Model, Projective Method, Taguchi Method.

Abstract: 3D model of computer is usually created using 3D CAD software, but 3D direct drawing method is still

developing the research. In this paper, we suggest and construct the 3D direct drawing system with ARToolKit

and develop the required creating methods and tools. The method is the creating solid algorithm using

projective methods. The algorithm is the converting multiple surfaces into a solid. After that, the functionality

of the methods and tools are evaluated using the Taguchi method (quality engineering). In addition, we

investigate the optimal condition of the creating methods and tools required for modeling.

1 INTRODUCTION

Recently, most of products have been designed via 3D

CAD models. In order to get a good appearance, the

products developed for the consumers have many

solid models. Then, the requirement for developing

solid models is increasing, and these solid models are

designed using 3D CAD software. 3D CAD software,

which are CATIA

, SolidWorks

, Rhinoceros

etc., is used for creating 3D solid models. A mouse

and a keyboard are key components for using the

software. However, creating 3D solid models needs

special skill and training. Intuitive 3D modeling

based on conceptual design is very difficult.

On the other hand, 3D direct modeling methods

without using 3D CAD software have been proposed,

in order to carry out 3D modeling easily. According

to haptic devices, the space to draw is decided in

advance to give a kinesthetic sense (Keefe, Zeleznik,

Laidlaw, 2007), or an existing model is deformed by

cutting and modifications (Chen, Yan, Lian, 2005),

(Akgunduz, Yu, 2004). However, the 3D model

cannot be created intuitively. In addition, it takes a

long time to form as a conceptual model. In contrast,

3D direct drawing researches have also been done.

They involve drawing/creating using a sensor

(Wesche, Seidel, 2001), (Bruno, Luchi, Muzzupappa,

2002) or camera (Cheok, Chuen, Eng, 2002).

However, they are not efficient system, because their

equipment is complicated and needs a large space.

The conceptual design modeling is difficult without

haptic sense. Therefore, they are neither popular nor

innovative.

In previous papers, the algorithm to create a

polygonal model and a curved surface model is

suggested and investigated (Mitsuhashi, Yoshida,

etc.…, 2014). However, we have never researched the

3D solid model, because creating method of solid

model is various. The conventional method is B-Reps

(Boundary representation) method or CGS

(Constructive Solid Geometry) method (Llamas,

Kim, etc.…, 2003). They make the 3D model rapidly,

but are difficult to operate only visual sensation and

too many commands.

In this paper, we construct the method for creating

a solid model in a 3D direct drawing system, so as to

create a 3D solid model easily. Then, the algorithm to

create a solid model is suggested. The algorithm is a

projective method, which is used as a third angle

projective method in mechanical design. Some

conventional methods used for surface drawing are

employed in 3D drawing, and the functionality of

these methods is evaluated by the Taguchi method

(quality engineering) to search for the most effective

method (Roy, 1990), (Yokoyama, 1988). In

particular, the function of creating methods or tools in

3D direct drawing is evaluated, and the optimal

method for drawing curved surfaces is proposed.

Mitsuhashi, K., Hashimoto, H. and Ohyama, Y.

Functional Evaluation of the Solid Model Creation using 3D Direct Drawing System.

DOI: 10.5220/0006007005130521

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 513-521

ISBN: 978-989-758-198-4

513

2 3D DIRECT DRAWING

SYSTEM WITH ARTOOLKIT

Many kinds of 3D direct drawing systems exist, but

no popular drawing system exists, because they are

expensive, difficult to operate, and require a large

space. In contrast, 3D drawing using AR (Augmented

Reality) with markers can be used to display 3D

models easily. Therefore, we use ARToolKit in the

3D drawing system. ARToolKit is a programming

library for C/C++ language to support AR

implementation. It is an open source, and the source

code is available easily. It has many functions, such

as the recognition of marker detection and patterns,

measurement of the position and posture of the

marker, and composition display of the photographic

image and the 3D CG model.

Figure 1 shows the schematic and the photograph

of the 3D drawing system with ARToolKit. An

operator carries the pen-type marker for carrying out

commands in the arranged marker for determining

space, equipping a Head Mount Display (HMD), and

controlling a web camera. The web camera measures

the distance between a marker for command and

space, and reads the contents of the marker command.

It has a resolution of 640×840 pixels. After measuring

the distance and reading the command, points, lines,

and surfaces (only when lines are created) can be

output from the pen’s nib and displayed by the HMD

in the drawing space. Display of objects, such as

points, lines, and surfaces, is carried out via the

Figure 1: 3D direct drawing system with ARToolKit.

OpenGL library. Two light sources are set above the

drawing space. The objective color can be selected

from red, green, and blue. It should be noted that

points or lines are always output only by indication of

the marker. However, the operator cannot have yet

drawn concept shapes using only virtual reality and

graphic software. Then, the button switch having an

ON/OFF function is equipped on the fingertip of the

pen. This function enables the operator to control the

output of points or lines. Furthermore, the operator

moves unexpectedly in many cases, which causes the

arm, head, or body of the operator to swing. For this

reason, a drawing speed of 1.0 - 10.0 mm/s is adopted.

Thus, the creation of unexpected points or lines can

be prevented. The contents of the AR command

markers determine of the color of the object, the

output of a point or line, creation of a surface, and

movement or elimination of a point or line. Space

markers are set at the bottom of the wall in drawing

space. The area of the large marker is 50mm×50mm,

whereas that of the small marker is 20mm×20 mm.

After the web camera has detected the position and

direction of space markers and command markers,

the drawing object is displayed from the fixed space

markers.

3 METHOD AND TOOL FOR

CREATING SOLID

Many kinds of 3D drawing methods exist, but none

of them is effective. Then, we constructed and

investigated the methods and tools with ARToolKit.

We explain an example of these methods in the

following sections.

3.1 Command Marker Pen

For drawing points, lines, and surfaces in the drawing

space, it is necessary to use the 3D direct drawing

tools. In this paper, we use the AR marker in a manner

similar to that in a previous study. AR markers enable

operators to give more commands than a point

marker. Furthermore, we can control the drawing

time by the use of an ON/OFF draw switch equipped

on the fingertip. It is difficult to say which type of AR

marker pen is the most effective because of their

various applications. Hence, we developed three

kinds of the command marker pen in this study in

Figure 2. The first is the large marker pen (in Figure

2(a)). It is generally called the AR marker rod in

ARToolKit. The second is a small marker that has

reduced weight and that divides the command

Marker pen

HMD with

web camera

Marker space

Measure

Display

Line with trace

(a) Scheme

(b) Situation from outer

Operator

Measure

Drawing object

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

514

function and the drawing output (in Figure 2(b))

(Cheok, Chuen, Eng, 2002). The third is a small

marker equipped on the fingertip similar to the one

used in a previous study (in Figure 2(c)). We

investigate which pen is useful.

3.2 Drawing Space

When 3D direct drawing is performed with

ARToolKit, it is necessary to prepare the fixed

marker space. Generally, it is said that a good result

is obtained as many established markers are set in the

entire drawing space. However, the computational

complexity is enormous, and it is difficult to set the

space because of the presence of obstacles. Then, we

prepared three kinds of drawing spaces, which are

shown in Figure 3. The first is a plane drawing space

(only XY plane), similar to the one used in a previous

Figure 3: Drawing space.

study (in Figure 3(a)) (Cheok, Chuen, Eng, 2002).

The second space consists of two right-angled planes

(XY plane and XZ plane) so as to observe the top and

bottom direction (in Figure 3(b)). The third space

consists of three planes where the XZ plane is bent to

form an angle of 120 degrees in order to widen the

angle of the space (Figure 3(c)). We investigate which

drawing space is useful.

3.3 Polygonal Surface Drawing

We should create the some polygonal surfaces to

create a solid model. The creating method of

polygonal surface is shown in Figure 4. First, line

segments (or point clouds) are drawn by detecting the

position of one hand using Kinect. Then, all the

drawing points are projected to the one plane using

the Least squares methods. Second, the center point

is calculated from all the points, and the most distant

point is elected from the center point (Mitsuhashi,

Yoshida, etc.…, 2014). It is a 1st vertex of polygonal

surface. In a square, the segment between the center

and 1st vertex is rotated 90 degree counterclockwise

towards the normal vector of the one plane. In a

triangle, the angle is 120 degrees. In a n-polygonal,

the angle is 360/n degree. Polygonal surface is created

by connecting among the neighbor vertexes.

3.4 Design Support Tool

PC software can create a straight line or rectangular

or square, but freehand drawing in 3D space is

difficult for them. Then, we suggest the design

support tools. Figure 5 shows the straight edge ruler,

Figure 6 shows the absorption plane ruler. Both rulers

are made of acrylic material with AR marker, because

acrylic material prevents the rulers from disappearing

drawing space markers. The straight edge ruler in

Figure 5 can draw the straight line or segment,

because the drawing points are absorbed on the ruler.

The absorption plane ruler can draw the segment or

face on one plane, it has the same function. It is a

necessary tool, because a plane drawing in 3D space

is difficult. Therefore, we can create the segment and

the face (polygonal surface, circle, etc.…) easily.

Figure 4: Drawing method of Polygonal surface.

AR marker

Switch

AR marker

(a) Large marker type

(b) Small marker type

Figure 2: Drawing pen.

(a) One plane

(b) Two planes (right-angled)

(wide-angled)

AR marker

AR marker pen

Center

Polygonal surface

Convert

Functional Evaluation of the Solid Model Creation using 3D Direct Drawing System

515

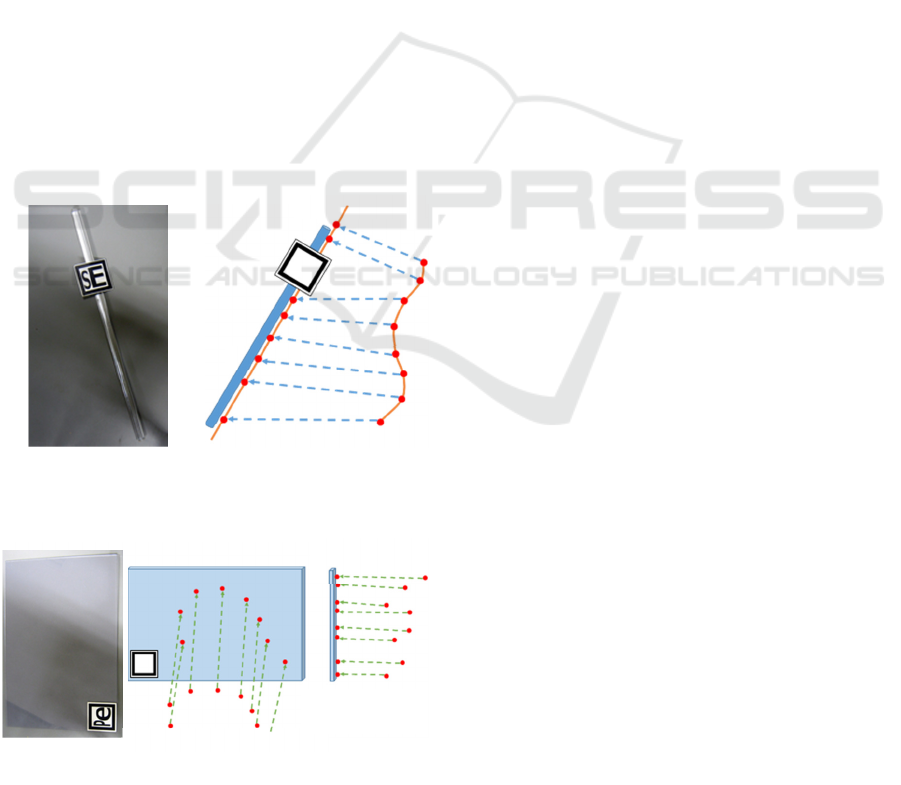
Then, we investigate the effects of design support

tools.

4 SUGGESTIONS OF

ALGORITHM FOR CREATING

SOLID

4.1 Solid Creating Method

Drawing a point, segment, and surface in gesture is

easy, but solid is difficult. Because human

recognition and image 2D objects, can’t image 3D

objects in detail. The conventional 3D modeling

method is B-Reps (Boundary representation) method

or CGS (Constructive Solid Geometry) method

(Akgunduz, Yu, 2004), (Llamas, Kim, etc.…, 2003).

B-Reps method transforms many closed points to

segment, many closed segments to surface, many

closed surfaces to solid. It has the information about

the position and vector of vertex, edge, and face. It is

easy to create a complicated shape, but it must close

all the face. Therefore, we must draw many surfaces

with great difficulty. We are pained to draw and close

many surfaces and can’t create the solid well in

Figure 6: Absorption plane ruler for 3D space.

previous papers (Mitsuhashi, 2012). On the other

hand, CSG method gives the primitive objects that are

cuboid (cube), cylinder, cone, pyramid, and spheroid

(sphere). And the primitive objects are assembled into

the complicated shape using Boolean operations.

CSG method has the information about the primitive

shape, position, size, combination. The information

has simple tree structure. So we can use the function

Redo or Undo easily. However, the complicated

shape takes many Boolean operations, that is difficult,

painful, and not intuitive. Because we create or draw

lots of the 2D models in 3D modeling. In addition,

CSG method can’t deform the solid model intuitively.

So we suggest an algorithm to create solid model

using the projective method. It is already introduced

at MasterCAM

, Solidworks

. When two or more

of polygon surface are created, they can be converted

to a solid. However, it has never used in 3D real

space. So we suggest an algorithm to create solid

model using the projective method in 3D real space.

4.2 Solid Creating Projective Method

in 3D Real Space

We construct the program using the projective

method in 3D real space, in order to create solid

model. Figure 7 shows the schematic diagram of a

projective method in 3D real space. Solid model is

projected and created from front, side, and top surface

in Figure 7. Thin lines are prism edges. The scheme

is that two or more of polygonal surfaces are drawn at

first, after that they are converted as a section of prism,

and an infinitely long prism is created. Then, the

scheme (program) finds the intersection of all prisms,

it calculates the boolean logical product (AND

operation), and the intersect solid model is created.

These algorithms are calculated by OpenCSG and

OpenSCAD library. Creating solid data is converted

to STL (Stereo Lithography) file or OFF (Object File

Format) file.

Figure 8 shows the solid made by the projective

method in 3D real space. When a polygonal surface

is created, prism edges are the role of the guide from

Figure 8. The solid is displayed by many polygonal

surfaces using OpenGL and ARToolKit. The operator

can decide the position of solid with watching the

guide.

(a) All over view

(b) Scheme

Absorb

Real drawing trajectory

Output line

Figure 5: Straight edge ruler for 3D space.

Absorption to plane

Real drawing trajectory

Absorption

to plane

Real drawing

trajectory

(a) All over view

(b) Scheme

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

516

Figure 8: Situation of projection method.

4.3 Creating Algorithm for

Cube/Cuboid and Pyramid

The algorithm of creating a solid is to convert

multiple polygon surfaces using the projective

method from the preceding section. Figure 9 shows

the creating algorithm for cube or cuboid. The

operator can use single hand or double hands or both,

in creating a polygonal surface using Kinect, but can’t

create multiple surfaces at the same time. If two or

more of rectangular surface is drawn, a cube/cuboid

is created. Therefore, the operator can create the solid

like gesture experiment results. Figure 10 shows the

creating algorithm for a quadrangular pyramid. If two

or more of triangle surface is drawn, a quadrangular

is created. Then, triangular pyramid is the same

algorithm. On the other hand, the same algorithm

enables to create a sphere or spheroid theoretically,

but the operator must create the infinite circle or

curved surface. A polyhedron like sphere/spheroid

can be created, it is not sphere/spheroid. So the

creating algorithm for sphere/spheroid is in future

work.

Figure 10: Creating algorithm of pyramid.

5 FUNCTIONAL EVALUATION

OF 3D DRAWING USING THE

TAGUCHI METHOD

There is extremely little research on the evaluation of

the functionality of 3D direct drawing methods and

tools. Evaluating the constructed methods and tools

requires a large number of experiments. We

investigate the functional evaluation of the drawing

methods and tools via experiments using Taguchi’s

L18 orthogonal array in this paper (Roy, 1990),

(Yokoyama, 1988).

Solid

Prism

Polygonal surface

Polygonal

surface

Figure 7: Solid creature projection method in 3D space.

Polygonal surface

Solid

1. Draw surface

2. Make prism

(infinite depth/height)

2. Make prism

(infinite depth/height)

3. Solid creation

Figure 9: Creating algorithm of cuboid/cube.

1. Draw surface 1. Draw surface

2. Make prism

(infinite depth/height)

2. Make prism

(infinite depth/height)

3. Solid creation

Functional Evaluation of the Solid Model Creation using 3D Direct Drawing System

517

Figure 12: Change the volume sample model.

5.1 Experiment

We evaluate the shape of the solid model. The use of

any of the three methods should yield the required

model. We adopted a combination solid model of the

pyramid and the cube, which is usual to create with

3D-CAD software. Because a large number of models

must be evaluated, as stable solid models cannot be

drawn repeatedly, it is difficult to evaluate shape error

by using static characteristics. Thus, we adopt

dynamic characteristics, not static characteristics.

Figure 11 (a) shows an example of the solid model.

The bounding box is 50mm wide, 50mm deep and

93mm high. The change in the edge of the solid model

in the bounding box is considered as the signal factor.

The volume is output when the edge is changed.

Figure 12 shows the shape when the edge is changed.

The relations of the edge M' and the volume y' are (a)

=50mm, y'

=160833mm

, (b) M'

=63mm,

=321667mm

, and (c) M'

=72mm,

=482500mm

. Then, we calculate the proportional

Figure 13: Creating solid model.

reference point expression based on 50mm height.

Proportion relations of y=βM

are obtained as results.

The operator traces the preparation guide of the solid

model. Figure 13 shows an example of the creating

process.

5.2 Determination of Control and Noise

Factors in the L18 Orthogonal

Array Experiment

Seven control factors of the three levels and one

control factor of two levels are set, for the experiment,

to evaluate the functionality of the drawing methods

and tools. The control factors are type of input

method for the drawing tool, type of drawing space,

and support tool. The other factors are the edit

function of the drawing point, the guide character, the

3D display function, the change section size of the

pyramid, and the number of the necessary faces

(a) Default (b) Two times (c) Three times

(a) Perspective

(b) Top view

Height

Depth

Width

Figure 11: Sample model (cube + pyramid).

Polygonal surface

Solid

(a) Using the rulers

(b) Useless the rulers

Polygonal surface

Solid

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

518

(surfaces) for projective method. The edit methods

involve the removing or moving function, which

changes a polygonal surface shape. The display

function of the guide character is CG model, real

model, and nothing. The number of necessary faces

in the solid model is 2 or 3. The noise factor indicates

the change in the shape caused by the operator, and

its effect was examined with the help of two 30-years-

old men (noise factor: N

, N

). Tables 1-3 list the

control factors, the results of the L18 orthogonal array

experiment, and the relation of the output to the signal

factor and the noise factors, respectively. Here, the

third level of the control factor E and F are assumed

as a dummy level because this factor has only two

parameters.

5.3 SN Ratio

After an experiment is carried out, we must evaluate

the SN (signal-to-noise) ratio

. The SN ratio

is an

index for expressing the stability of the noise level.

Therefore, SN ratio η were calculated in this study.

The expressions of

[dB] are as follows.



−

log10

(1)

Here, S

is the promotional variation, S

is the

error variation, V

is the error variance, and V

is the

noise variance. The expressions are as follows.

















jii

(2)

()

41132

−

−−×



(3)

()

132

2,1,

−×

+−



iii

SyyM

(4)

Then, the optimum control factor is decided by

, wh

ich is remarkably high.

Table 1: Control factors (*: Current condition).

Table 2: L18 orthogonal array experiment.

Table 3: Relation of outputs to signal factors

and noise factors.

5.4 Results and Repeatability

Table 4 shows the averages of SN ration according to

the level of all the control factors. Figure. 14 shows

the graphs of their factorial effects. We selected the

optimum levels where the SN ratio is remarkably

high. In other words, we give priority to the difference

in the SN ratio only when a change in the SN ratio

made a slight difference. Therefore, it was found that

the factors affecting the SN ratio are the number of

faces, the drawing space, the display of guide model,

and the editing function. If there are too less faces, a

No. A B C D E F G H

1 11111111

2 11222222

3 11332'2'33

4 12112233

5 12222'2'11

6 12331122

7 131212'23

8 13232131

9 13312'212

1021132'221

11212112'32

1221322113

1322122'132

1422231213

15223122'21

16231322'12

1723212'123

1823321231

1st level 2nd level 3rd level

A: Face 2 pieces* 3 pieces -

B: Pen type Large Small Fingertip*

C: Space 1 plane* 2 planes 3 planes

D: Edit Translate Erase Nothing*

E: Edge ruler With Without* -

F: Plane ruler With Without* -

G: Guide Display Real CG Notihing*

H: Section size 1 time* 2 times 3 times

Functional Evaluation of the Solid Model Creation using 3D Direct Drawing System

519

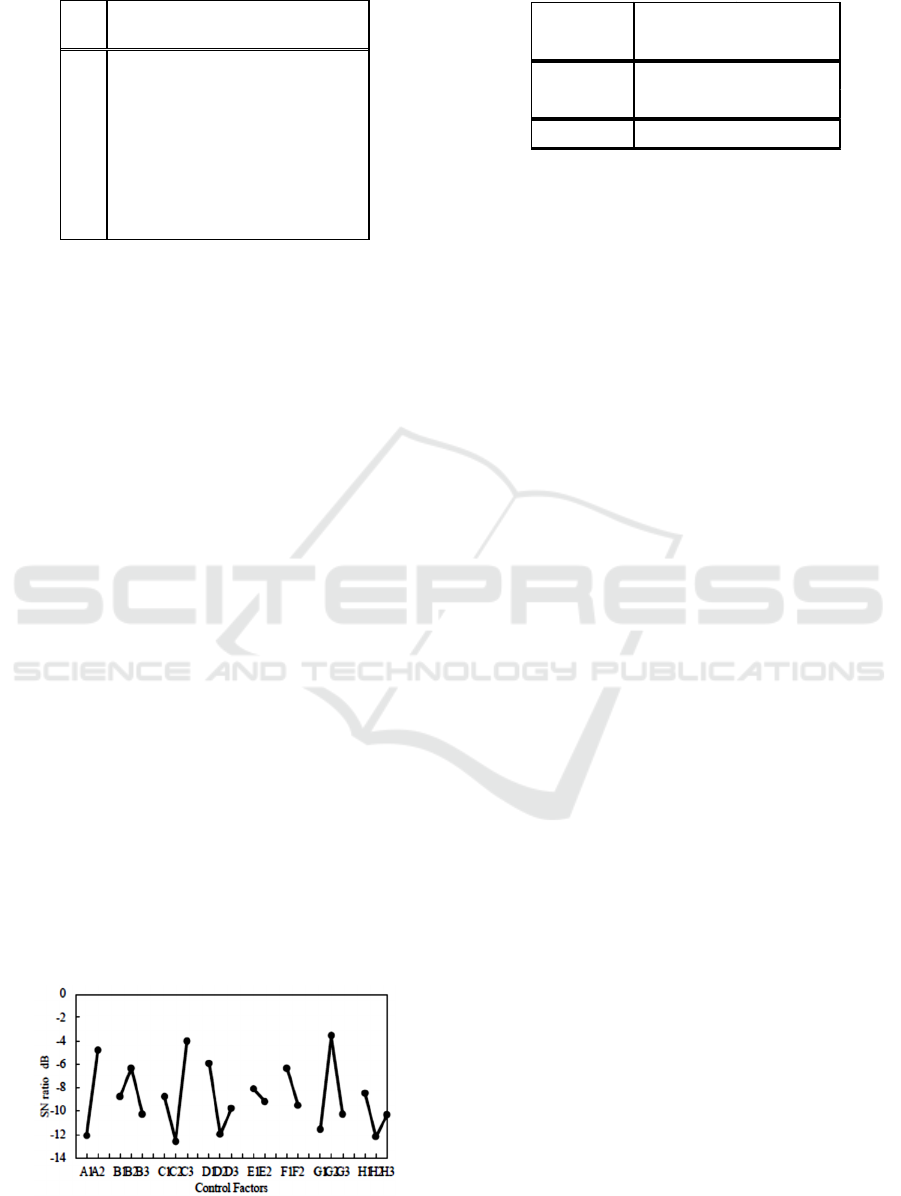
Table 4: Average of SN ratio at all control factors level.

shape can be wrinkled and be different from the

conceptual shape; however, the change in the shape

decreases if there are too many faces. With respect to

the guide model displayed, it is difficult to determine

a position if the guide model cannot display. With

respect to the editing function, the SN ratio of the

point translate function is the best, because it is

believed that the unintentional removal point occurs.

In terms of the drawing space, the SN ratio of the 120

°wide model is the best, because the range of vision

is spread out. Determining the optimum method for

drawing a solid model becomes the future problem.

Other factors have little influence on the modeling.

Therefore, the optimum condition for drawing solid

models is assumed as A

It is necessary to check the repeatability of this

optimum condition, in addition to determining the

current condition. The condition is assumed as

from conventional research.

Experiments under the two conditions were carried

out for validation. Table 5 lists the results of the

confirmation experiment and the estimation of the SN

ratio. Here, the estimation is carried out using the

averages, according to the level of all control factors.

From the results, it was found that the optimum

condition showed a higher SN ratio than the current

condition. Therefore, the repeatability of this

optimum condition was confirmed. However, further

research on the few kinds of drawing tool proposed,

re-investigation of the method for the drawing

another solid model.

Figure 14: SN ratio of factorial effects.

Table 5: Confirmation experiments.

6 CONCLUSIONS

In this paper, we construct the method for creating a

solid model in a 3D direct drawing system, so as to

create a 3D solid model easily. Then, the algorithm to

create a solid model is suggested. The algorithm is a

projective method. After that, the functionality of the

methods, tools, and factors in 3D drawing is

evaluated using the Taguchi method (quality

engineering). In this result, we find that the effective

control factors are the number of faces, the drawing

space, the display of guide model, and the editing

function. Furthermore, in order to investigate the

repeatability of this optimum condition, the

supporting experiment was performed for

verification. Further work can be focused on the kinds

of drawing tool proposed, re-investigation of the

method of drawing another solid model.

ACKNOWLEDGEMENTS

This work was in part supported by JST RISTEX

Service Science, Solutions and Foundation Integrated

Research Program.

REFERENCES

Daniel F. Keefe, Robert C. Zeleznik, and David H. Laidlaw,

Drawing on Air: Input Techniques for Controlled 3D

Line Illustration, IEEE Transactions on Visualization

and Computer Graphics, Vol. 13, No. 5, 2007

Yonghua Chen, Zhengyi Yang, and Lili Lian, On the

Development of a Haptic System for Rapid Product

Development, Computer-Aided Design, Vol.37, No.5,

pp. 559-569, 2005

Ali Akgunduz and Hang Yu, Two-Step 3-Dimensional

Sketching Tool for New Product Development,

Proceedings of the 2004 Winter Simulation Conference,

pp.1728-1733, 2004

Gerold Wesche, and Hans-Peter Seidel, FreeDrawer – A

Free-Form Sketching System on the Responsive

Workbench, VRST’01, November, pp. 15-17, 2001

123

A -12.11 -4.78

B -8.75 -6.34 -10.25

C -8.75 -12.59 -4.00

D -5.93 -11.97 -9.77

E -8.09 -9.16 -9.16

F -9.50 -6.34 -6.34

G -11.57 -3.52 -10.25

H -8.45 -12.20 -10.30

SN ratio [dB]

Estimate Confirm

Current -1.96 -7.29

Optimum -0.24 -0.70

Gain 1.72 6.60

SN ratio [dB]

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

520

F. Bruno, M. L. Luchi, M. Muzzupappa, and S. Rizzuti, A

Virtual Reality Desktop ConFigureuration for Freeform

Surface Sketching, In Proceedings of XIV Congreso

Internacional de Ingeniería Gráfica, ed. F. F. Salazar

and A. A. Badiola de Miguel, Santander, Spain, 2002

Adrian David Cheok, Neo Weng Chuen Edmund, and Ang

Wee Eng, Inexpensive Non-Sensor Based Augmented

Reality Modeling of Curves and Surfaces in Physical

Space, Proceedings of the International Symposium on

Mixed and Augmented Reality (ISMAR

’

02) ISMAR

2002, 2002

Ranjit Roy, A Primer on the Taguchi Method, Society of

Manufacturing Engineers, 1990

Y. Yokoyama, Quality Engineering Lecture 4:

Experimental Design for Quality Designs, Japanese

Standards Association, 1988

Kaoru MITSUHASHI, Functional Evaluation of the

Curved Surface Created by 3D Direct Drawing, The

2nd IFToMM (International Federation for the

Promotion of Mechanism and Machine Science) Asian

Conference on Mechanism and Machine Science 2012,

November7-10，Tokyo，Japan, 2012.

Kaoru MITSUHASHI, Ikuo YOSHIDA, Jin-Hua SHE,

Yasuhiro OHYAMA, “Suggestion of 3D Direct

Drawing Method by Microsoft Kinect”, 15th

International Conference on Precision Engineering

(ICPE2014), July23-25, Kanazawa, Japan, 2014

Ignacio Llamas, ByungMoon Kim, Joshua Gargus, Jarek

Rossignac, and Christopher D. Shaw: Twister: a space-

warp operator for the two-handed editing of 3D shapes.

ACM Trans. Graph. 22(3), 2003, pp.663-668

Functional Evaluation of the Solid Model Creation using 3D Direct Drawing System

521