
Steerable Filters for Rotation Invariant Salient Feature Points Applied to
Monocular SLAM
Youn`es Raoui and El Houssine Bouyakhf
LIMIARF, Physics department, Faculty of Sciences, Mohammed V University, Rabat, Morocco
Keywords:
Steerable Filters, Repeatability, Color, Detector Descriptor, SLAM, Mapping.
Abstract:
In this paper, wepropose a new detector descriptor for the visual salient points and use it for a monocular visual
Simultaneous Localization and Mapping (visualSLAM) application. Because in SLAM, the landmarks should
be indexed with distinctive features, we aim to build a detector descriptor insuring the invariance to the rotation
and the scale. First, the detector starts filtering an image with a steerable filter set, extracts Harris corners from
the convolved image, next it clusters these corners, then it calculates a resulting set of feature points. We show
that the repeatability of the detector is higher that other detectors like SIFT, SURF, CENSURE and BRISC.
In addition, we implement the descriptor using color attributes. We represent the color at the location of each
feature point with a pyramid characterized with many levels of quantization, and we calculate the entropy at
each level. We make a simulation of Visual SLAM with known correspondences using these features to prove
their efficiency in the localization and the map management of the robot.
1 INTRODUCTION
The extraction of salient feature points is an impor-
tant step in many robot navigation tasks. Visual fea-
ture points are used in visual Simultaneous Local-
ization and Mapping in order to compare the map’s
landmarks. The computation of such salient points
is made with a detector descriptor quantifying locally
the content of the image. In one hand, the detector
computes the visual corners and the more they are in-
dependent of the scale and the orientation the more
they are useful in SLAM. In the other hand, the de-
scriptor gives a measurement of the appearance at the
patch around a corner (Harris and Stephens, 1988).
In visual Simultaneous Localization and Map-
ping(Visual SLAM), the feature points are used for
data association making a relationship between the
robot’s observation and the landmark of the map.
In such operation, the feature points have to be re-
peatable and stable against the extreme viewpoint
changes. Also the descriptor is used during the map
management and it needs to be invariant to the scale
variations and the rotation so that the robot recognizes
a familiar scene. We apply this technique in visual
SLAM for the map computation , the management
and the localization of the robot. In this paper, we
propose a new detector descriptor adapted to the vi-
sual SLAM a mobile robot equipped with a monoc-
ular camera. We conceive the detector with the cal-
culation of Harris feature points from many filtered
images received from steerable filters through tuning
their characteristic scales and orientations. The de-
scriptor is an algorithm having several applications
such as object recognition and categorization and vi-
sual features matching. In our method we describe the
color attribute through representing it in many levels
of quantization, and we compute the entropy of each
row. The paper is organized as following : we start
by related works, then in the computer vision part, we
present our method for the design of the detector de-
scriptor, and we give some test results. In the SLAM
part, we present generally the problem of monocular
SLAM, then we describe the method we use to apply
our detector descriptor in the mapping.
2 RELATED WORKS
The Harris detector is an old technique of extraction
of feature points, but it still efficient since the second
moment matrix operator is computed quickly. The
SIFT uses difference of Gaussians to construct a scale
space, but without considering the orientation inside
the pyramid including the features. In addition, the
SURF detector computes the orientation in many lev-
Raoui Y. and Bouyakhf E.
Steerable Filters for Rotation Invariant Salient Feature Points Applied to Monocular SLAM.
DOI: 10.5220/0006007205670572
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016), pages 567-572
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
567

els of the Gaussian scale space but when changing the
viewpoint the features are not so stable if the robot
turns with a high angle. Furthermore, the descrip-
tor of SIFT is of size 128 which is a very high num-
ber making slow the matching process necessary in
the map management of a robot. It is for this rea-
son that SURF (Bay et al., 2008) outperforms SIFT
in the time computation, because it uses the Haar
wavelets to represent each of the visual patches in
the location-frequencyspace, while SIFT uses the Ga-
bor filter. The BRISC detector descriptor (Leuteneg-
ger et al., 2011) is newer than the previous ones in-
suring a stability against view changes by applying a
sampling pattern rotated by an angle around the key-
points. In (McCann and Lowe, 2014), a new method
called spatial local coding (SLC) is designed to con-
struct a model with a Hough transform approxima-
tion. It uses a cascade of thresholds followed by gra-
dient descent to localize accurately the features. Such
a technique is a categorizationmethod useful for robot
navigation based on scene understanding by recog-
nizing objects such as in the the SLAM++ method
developed in (Salas-Moreno et al., 2013). Besides,
many of the feature points in the literature are used
in SLAM. In the seminal work of Lowe and Se (Se
et al., 2002), the SIFT keypoints were used to calcu-
late the robot’s map equipped with a Triclops sterio-
vision system, and using the Extended Kalman Fil-
ter (EKF), the robot’s pose is updated. The work
of Davison (Davison et al., 2007) is considered one
of the most important in visual SLAM running at 30
Hz. It uses the detection operator of Shi and Tomasi
and updates the corner’s position and the robot’s po-
sition with EKF. The use of such features is for their
high repeatability in resolving problems when poten-
tially extreme camera motions happen (Mikolajczyk
and Schmid, 2005). An interesting work on real time
SLAM is developed in (Roussillon et al., 2012) where
an open source software of real time SLAM was de-
veloped, and it is adaptable to many types of robots,
sensors and observation models.
3 THE VISUAL DETECTOR
DESCRIPTOR
3.1 The Steerable Filter
Steerable filters (Freeman and Adelson, 1991) are ap-
plied to a template image and convolved with a set
of deformed kernels so that we analyze it with many
scales and orientations, but we can use this approxi-
mation only if the kernel is compact (see fig. 2). We
chose the the orientation θ dependent kernel F
θ
is ap-
proximated with F
[n]
θ
defined with :
F
[n]
θ
=
n
∑
i=1
σ
i
a
i
(x)b
i
(θ) (1)
Where σ
i
, a
i
(x), b
i
(θ) are defined as following : Let
us have h given with :
h(θ) = F
θ
(x)
¯
F
θ
′
=0
(x)dx (2)
ˆ
h(v) = F (h(θ)) (3)
Such as F is the Fourier transform.
σ
i
=
ˆ
h(υ
i
)
1
2
(4)
b
i
(θ) = exp
j2πυ
i
θ
dθ (5)
a
i
(x) = σ
−1
i
F
θ
(x)exp
j2πυ
i
θ
dθ (6)
Furthermore, for multiscale analysis of a template im-
age, we apply the following kernel dependent of the
scale σ:
F
σ
(x) = σ
1
2
F(σx) (7)
Where σ ∈ (0,∞).
3.2 The Detector Design
Let us have a template image I(x,y) captured with a
monocular camera fixed on the robot’s head. We con-
volve I(x,y) with a family of kernels of the steerable
filter.
I
σθ
(x,y) = I(x,y) ∗ F
σ
(x) ∗ F
[n]
θ
(8)
Or
I
σθ
(x,y) = I(x,y) ∗ F
σ
(x) ∗ f
θ
(x,y) (9)
I
σθ
(x,y) = I(x,y) ∗ F
σ
(x) ∗
M
∑
j=1
k
j
(θ) f(θ
j
)(x,y) (10)
In addition, we apply the Harris detector whose prin-
ciple is the following :
• Computation of the second moment matrix ex-
pressed with:
A
σθ
=
∑
p,q
ω(p,q)
I
2
σθ,x
(x) I
σθ,x
I
σθ,y
(x)
I
σθ,x
I
σθ,y
(x) I
2
σθ,y
(x)
(11)
Where I
σθ,x
, I
σθ,y
are the respective derivatives of
I
σθ
(x) in the x and y directions at the point (x,y),
and p,q are the values of the weighting function
given by :
w(p,q) = g(x,y, σ) =
1
2πσ
2
e
−(x
2
+y
2
)
2σ
2
(12)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
568

• Finding the coordinates of the corners: By defini-
tion, the corners are the image pixels which inten-
sities change largely at the x and y directions. We
compute the cornerness measure provided by :
R = det(A
σθ
)− αtrace
2
(A
σθ
) = λ
1
λ
2
− α(λ
1
+λ
2
)
(13)
Where α = 0.4 In addition, fixing the threshold s,
depending on the number of the corners we want
to get, returns us the coordinates of the feature
points characterized by the values of λ
1
and λ
2
higher than s.
• Clustering the feature points Provided that we
have obtained after applying the steerable filter
n*m*l feature points (respectively the number of
the features extracted by the Harris detector, the
number of scales and the number of the orienta-
tions of the steerable filter), we propose to cluster
this large set of features to get n cluster, like inside
an unfiltered image, for increasing the speed of the
matching. We fix the number of the clusters equal
to the number of the feature points in a single im-
age to improve the speed of the computation. It is
because of its simplicity and its quick time com-
putation that we choose the Kmean algorithm for
the clustering. Once we apply it, we get N clus-
ters containing m*l points. Next, we compute the
mean of each cluster, and we show thanks to the
repeatability computation, that the features are in-
variant to the viewpoint changes(see 1, algorithm
1), and figures 4 and 5.
Figure 1: The process of clustering the feature points and
computing their mean to represent the final set of the cor-
ners.
3.3 The Descriptor Design
The descriptor we compute is invariant to the level of
quantization characterizing the image. We note that
each image can be coded in a number of the color
quantization levels so as we describe the appearance.
We choose to describe with the color attribute because
the more the descriptor is invariant the more it is good
for visual landmarks matching.
We start by constructing a square of size 20*20
pixels around each of the corners, then we construct a
pyramid of this rectangle using the level of quantiza-
tion starting from 16 colors to 256 colors with a step
Figure 2: (a) Odd-phase analyzing filters, oriented at
0
◦
,45
◦
,90
◦
,135
◦
.(b-d) Steerable, bandpass coefficients in a
multi-scale pyramid representation of low pass filtered im-
age.
Algorithm 1: Detector.
1: procedure DETECTOR(image)
2: filteredImage← image.steerableFilter(s,o)
⊲ s is the scale and o is the orientation
for each: i ∈ filteredImage
3: featurePoints(i) ← filteredImage.harris()
4: clusterCorner ← f eaturePoints.kmean()
for each: c ∈ clusterCorner
5: cornerMean(c) ← clusterCorner.mean()
6: image.return
result()
7: end procedure
of 2
n
, n=4 to 8. Then for each of the levels of the
pyramid we compute the entropy measuring the vari-
ance of the appearance inside each level. Then final
descriptor is of size 5 for each feature point (see algo-
rithm and fig. 3), and the less the number of entries
per descriptor is, the faster computation becomes. We
coose 5 entries because we have 5 level of quantiza-
tion, and up to this number, the image is blurred.
Algorithm 2: Descriptor.
1: procedure DESCRIPTOR(featurePoint) ⊲ The
coordinates of the corner
2: patch ← featurePoint.put
window(20,20) ⊲
20,20, respectively the width and the height of the
window
3: colormap ← [16,32, 64,128, 256]
for each: c ∈ colormap
4: local
patch(c) ← patch.quantize(c)
5: S = local
patch(c).compute entropy()
6: featurePoint.return result()
7: end procedure
3.4 Detector Descriptor Evaluation
To evaluate our detector descriptor, we use many im-
ages being taken under several view points and scales,
because we would like to use them in the construction
of the robot map, and they will be used in SLAM to
Steerable Filters for Rotation Invariant Salient Feature Points Applied to Monocular SLAM
569

Figure 3: A scheme of the construction of the descriptor. A
squared window is put around the feature point, the values
are computed at different levels of computation.
update the robot pose. The best way to evaluate a de-
tector is to compute the repeatability score given with
this formula (Mikolajczyk and Schmid, 2005).
R =
Number of correct matches
Number of the extracted feature points
(14)
Provided that we describe two images of the same
view, the higher the repeatability score the better the
detector which prove that the feature points are sta-
ble against the viewpoints and are partially invariant
to the scale.
3.5 Figures
The figures 4 and 5 show respectively changes in the
repeatability per the view angle of our detector and
most used in the literature. in the figure 4, we can
clearly see that the repeatability drops steadily from
the viewangle 20
◦
to 40
◦
. From the viewangle 40
◦
to 80
◦
it drops drastically. In the viewangle 40
◦
, the
repeatability of our detector is 90%. However in view
angle 50
◦
, it dropped to 72%. In the figure 5, we find
when applying the BRISC detector a repeatability of
60% for a viewangle 40
◦
, but for 50
◦
, the repeatability
is 38%. However when we apply SURF, the value
Figure 4: The repeatability score of our detector.
Figure 5: The repeatability score of the detectors AGAST,
BRISC, CENSURE, ORB, SURF, SIFT and FAST.
of the repeatability related to the angle 40
◦
is 56%
and related to the angle 50
◦
nears 28%. Overall, we
can clearly see that the repeatability of our detector is
better than the repeatability of the detectors AGAST,
BRISC, CENSURE, ORB, SURF, SIFT and FAST.
4 MONOCULAR SLAM USING
THE NEW DETECTOR
DESCRIPTOR
In the Simultaneous Localization and Mapping
(SLAM), we estimate the pose X of the robot and of
the map m simultaneously having the motion model
u and the observation z. In our application, we will
only consider the case of SLAM with known corre-
spondences. In other words we assume that the re-
lationship between the features and the landmarks is
known at each step of the algorithm. The problem of
SLAM is to estimate the following belief:
P(X,m/z,u) (15)
Additionally, the full PDF of the robot’s pose and the
map is expressed with a single multivariate Gaussian.
Bel(X,m) = N (
x
v
x
i
,
P
xx
P
xy
1
P
xy
2
..0..0
P
y
1
x
P
y
1
y
1
P
y
1
y
2
..0..0
P
y
2
x
P
y
2
y
1
P
y
2
y
2
..0..0
0 0 0..0..0
0 0 0..0..0
)
(16)
where x
v
are the coordinates of the robot in the world
frame, and x
i
=(xk
i
,yk
i
) are the coordinates of the vi-
sual landmarks. P is the covariance matrix of size
3+2*n, n is the number of the visual landmarks. Be-
sides, compute only the error on the robot pose with-
out considering the error on the landmarks. Explicitly,
the camera pose is composed as following:
x
v
= (r
W
,q
WR
,v
w
,ω
R
) (17)
Where r
W
is a 3D position of the robot, q is an ori-
entation quaternion, v
W
is a velocity vector, and ω
R
is
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
570

an angular velocity relative to a fixed frame (Davison
et al., 2007). Furthermore, the robot’s motion model
is given with :
f
v
=
r
w
new
q
WR
new
v
W
new
ω
W
new
=
r
w
+ (v
w
+V
w
)δ
t
q
WR
∗ q((ω
W
+ Ω
W
))δ
t
v
W
+V
W
ω
W
+ Ω
W
(18)
v
w
+V
w
δ
t
denotes the quaternion trivially defined by
the angle-axis rotation vector (ω
W
+ Ω
W
)δ(t).
4.1 Map Construction
The map is composed of 2D landmarks (X,Z) com-
puted from the robot’s observation of the visual
points. The feature points should be repeatable and
the description should be distinctive to finding a good
match. With this SLAM simulation we will use our
visual feature points, having the advantage of being
highly repeatable.
When the robot observes a landmark on the map, we
use the pinhole model to compute the 2D coordinates
in the camera frame (see VisualSLAM algorithm).
The relationship between the features and the land-
marks is given with the following equation:
u = KR
t
(P− t) ∈ R (19)
We transcribe the coordinates in the image frame: K is
the intrinsic matrix of the camera, P is the landmark
pose (X,Y,Z) in the 3D space, (R,t) is the homoge-
neous transformation from the world frame to the im-
age frame. We must compute the feature coordinates
from the landmark’s position so that we match it with
the new extracted feature point, because we do ver-
ify whether any feature has been seen before or not,
ensuring there is no redundancy in the robots map.
4.2 Landmark Computation
The camera acquires at each time an image, and ex-
tracts the feature points (fig. 6) and their descriptors
with our detector. By inversing equation 18, the robot
computes the landmark position.
4.3 EKF Filtering
he (X,Z) coordinates of the corners of each landmark
will be used during the EKF update of the robot pose,
so we have to ignore the y landmark’s coordinate (see
fig. 7, 8). Essentially, the observation model is given
with :
z(k/k − 1) = h( ˆx(k/k − 1)) (20)
The difference between the prediction and the true ob-
servation used by EKF improves the robot’s and the
map’s state. This process is called the data associa-
tion (See Algorithm 3).
Algorithm 3: VisualSLAM.
1: procedure VISUALSLAM(
˜
X
t−1
,
˜
∑
t−1
,u
t−1
,map
t−1
) ⊲
The coordinates of the corner
2: [
ˆ
X
t
,
ˆ
∑
t
] ← motion(X
t−1
,
˜
∑
t−1
,u
t−1
)
3: [FP
i
,Descriptor
i
] ← detectorDescriptor(
ˆ
X
t
)
for each: l ∈ map
t−1
4: [FP
l
i
,descriptor
l
i
] ← cameraPiholeModel(l)
5: L ← matching(FP
i
,Descriptor
i
,FP
l
i
,descriptor
l
i
)
6: map
t
← L
for each: i ∈ map
t
7: L
i
← map
i
8: ˆz
i
← h(L
i
,
ˆ
X
i
) ⊲ h is the observation model
9: z
i
←
p
((x
t
− L(1)
i
)
2
+ (y
t
− L(2)
i
)
2
)
atan(
y
t
−L(2)
i
x
t
−L(1)
i
) − θ
t
!
⊲
(x
t
,y
t
,θ
t
) are the ground truth
10: H
i
t
=
d
2
h
drφ
⊲ r his the range and φ is the bearing
11: K
i
t
←
¯
∑
t
H
iT
t
(H
i
t
¯
∑
t
H
iT
t
+ Q
t
)
−1
⊲ Q is the error
affecting the motion model)
12:
¯
X
t
←
¯
X
t
+ K
i
t
(z
i
−
ˆ
z
i
)
13:
¯
∑
t
← (I − K
i
t
H
i
t
)
¯
∑
t
⊲ r I is an identity matrix
14:
˜
X
t
←
¯
X
t
15:
˜
∑
t
←
¯
∑
t
16: return
˜
X
t
,
˜
∑
t
17: end procedure
4.4 Figures
Figure 6 shows 2 images of the same scene where
we extracted salient feature points. For each of the
feature points (indexes) we stored a descriptor vec-
tor. In the figure 7 and 8 we present a simulation of
robot localization in a rectangular environment of size
100cm*120cm. In the figure 7, we showed the evolu-
tion of the predicted position of the robot. The blue
disk represents the position of the robot given in the
equation 16. We can clearly see that the ellipse of
the uncertainty rose sharply when the robot moved.
By the end of the simulation, the error reached 10cm.
However, when we used our feature points as the ob-
Figure 6: (left) A scene captured by the robot where fea-
ture points are extracted.(right) The same scene from an-
other viewpoint extracted and feature points extracted.
Steerable Filters for Rotation Invariant Salient Feature Points Applied to Monocular SLAM
571
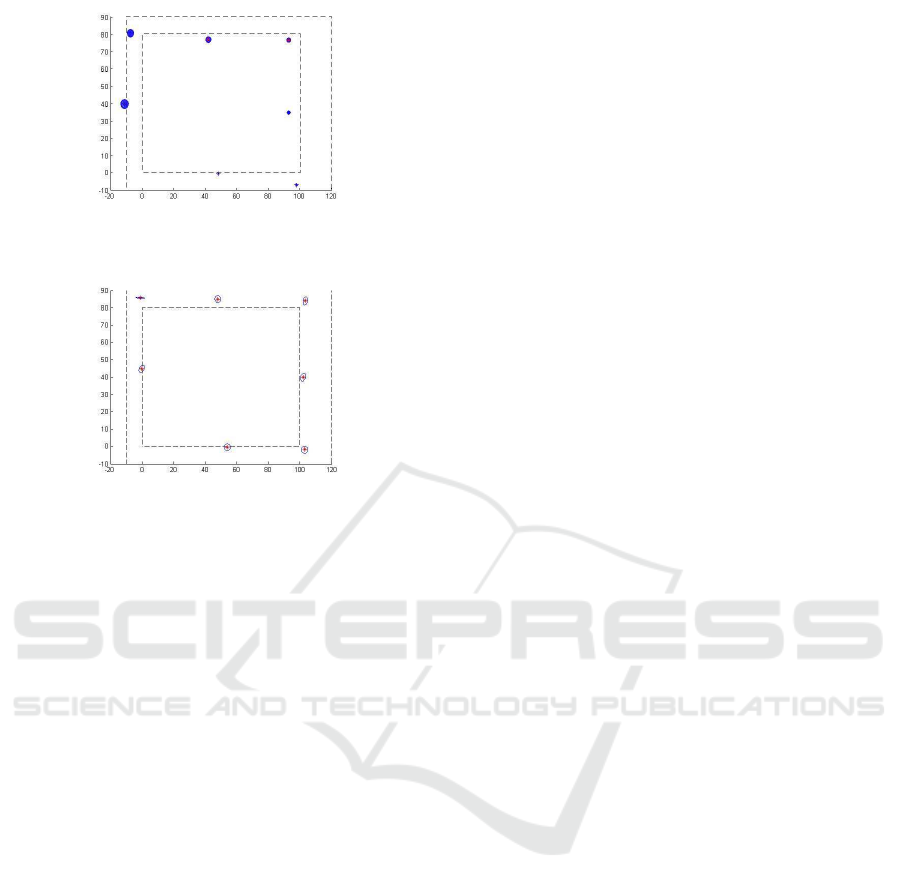
Figure 7: The predicted positions of the robot represented
with blue disks representing the uncertainty.
Figure 8: The estimated positions of the robot represented
with red points with the ellipse uncertainty with a blue cir-
cle.
servations of the Extended Kalman Filter, the radius
of the ellipse of uncertainty dropped drastically. It is
about 4 cm. Overall, we can clearly see that the use
of our visual feature points decreased the error during
the localization of the robot.
5 CONCLUSIONS
In summary, in this paper we have presented a new
detector descriptor for the extraction of salient visual
features. It has a good repeatability, so the robot
can manage better the visual landmarks during the
SLAM. We aim in the future to make the detector
more robust to the scale changes by convolving the
image with scale spaces before the extraction of sta-
ble corners. Furthermore,we aim doing more experi-
ments on the hardware for testing the algorithms and
comparing them to other SLAM ones. It is also im-
portant to focus on extracting salient feature points
having low dimensions and describing the essence of
the image to improve the frequency of the SLAM run-
ning on the hardware.
REFERENCES
Bay, H., Ess, A., Tuytelaars, T., and Van Gool, L. (2008).
Speeded-up robust features (surf). Comput. Vis. Image
Underst., 110(3):346–359.
Davison, A. J., Reid, I. D., Molton, N. D., and Stasse,
O. (2007). MonoSLAM: Real-time single camera
SLAM. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 26(6):1052–1067.
Freeman, W. T. and Adelson, E. H. (1991). The design
and use of steerable filters. IEEE Trans. Pattern Anal.
Mach. Intell., 13(9):891–906.
Harris, C. and Stephens, M. (1988). A combined corner
and edge detector. In In Proc. of Fourth Alvey Vision
Conference, pages 147–151.
Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).
Brisk: Binary robust invariant scalable keypoints. In
Proceedings of the 2011 International Conference on
Computer Vision, ICCV ’11, pages 2548–2555, Wash-
ington, DC, USA. IEEE Computer Society.
McCann, S. and Lowe, D. G. (2014). Efficient detection
for spatially local coding. In Computer Vision - ACCV
2014 Workshops - Singapore, Singapore, November 1-
2, 2014, Revised Selected Papers, Part I, pages 615–
629.
Mikolajczyk, K. and Schmid, C. (2005). A performance
evaluation of local descriptors. IEEE Trans. Pattern
Anal. Mach. Intell., 27(10):1615–1630.
Rosten, E. and Drummond, T. (2006). Machine learning for
high-speed corner detection. In Proceedings of the 9th
European Conference on Computer Vision - Volume
Part I, ECCV’06, pages 430–443, Berlin, Heidelberg.
Springer-Verlag.
Roussillon, C., Gonzalez, A., Sol, J., Codol, J.-M.,
Mansard, N., Lacroix, S., and Devy, M. (2012). Rt-
slam: A generic and real-time visual slam implemen-
tation. cite arxiv:1201.5450Comment: 10 pages.
Salas-Moreno, R. F., Newcombe, R. A., Strasdat, H., Kelly,
P. H., and Davison, A. J. (2013). Slam++: Simulta-
neous localisation and mapping at the level of objects.
In The IEEE Conference on Computer Vision and Pat-
tern Recognition (CVPR).
Se, S., Lowe, D. G., and Little, J. J. (2002). Mobile
robot localization and mapping with uncertainty using
scale-invariant visual landmarks. I. J. Robotic Res.,
21(8):735–760.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
572
