
HPC Mobile Platform for Solving Oil Recovery Problem
Т. S. Imankulov, D. Zh. Akhmed-Zaki, B. S. Daribayev and O. N. Turar
al-Farabi Kazakh National University, al-Farabi ave., 71, Almaty, Kazakhstan
Keywords: CUDA, Kepler, NVidia Tegra K1, Mobile Computing, Oil Recovery, EOR.
Abstract: The paper describes applying of mobile computational tools to numerical solving of full value industrial
problems. As an example, we used surfactant/polymer flooding problem with thermal effects. The problem
solved by using different graphics processing units including the GPUs of mobile devices. Parallel
implementation of numerical algorithm was launched on the following devices: NVidia GeForce 770, NVidia
Tesla K20 and mobile GPU NVidia Tegra K1. We developed mobile application implementing the algorithm.
The application was tested and compared with desktop GPUs of same microarchitecture. Results of the tests
shows that calculation on the mobile devices gives the same computation efficiency as desktop GPU with
average characteristics.
1 INTRODUCTION
Using mobile devices in computation of physical
simulations are not yet common. However, the large
number of hardware demanding applications on
mobile devices proves that these devices have
sufficient computing power.
Implementation of some grid systems’ nodes as
mobile devices, for example, considered in (Ketan,
2013; Phan, 2002). A clear example of such system
developed up to industrial scales is BOINC
(boinc.berkeley.edu). Nevertheless, such systems do
not consider heterogeneity of mobile processors. In
such applications only CPU kernel of the processor is
used.
However, GPUs of mobile devices are quite
suitable for resource intensive computations. They
are widely used for image recognition problems
(Singhal, 2010; Wang, 2013). Also, (Cheng, 2011)
gives an idea of general-purpose computation on
mobile graphics processors.
High performance parallel computing using
CUDA has been attracting many researchers in
various disciplines, including computational fluid
dynamics (Tolke,2008; Micikevicius; Thibault, 2009;
Kelly, 2013). This work presents applying and testing
mobile GPU for simulation of surfactant/polymer
flooding (SPF) process, which is taken as an example
of complex industrial problem. Polymer/surfactant
flooding is one of the effective chemical enhanced oil
recovery (EOR) methods. Polymer increases
viscosity of a water thereby improving the mobility
ratio and increasing the recovery efficiency. Primary
benefit of polymer flooding is to improve sweep
efficiency and acceleration of oil production (Lake,
1983; Sorbie, 1991). Surfactant flooding method
involves addition of surface-active agents or
surfactants to the injected water. Surfactants reduces
the interfacial tension between oil and water within
reservoir, reduce the residual oil saturation and
improve displacement efficiency (Babalyan, 1983).
For test analysis results of mobile GPU
computation were compared with two PC NVidia
GPUs on Kepler microarchitecture. The reason of the
technology selection is that available at the moment
computational mobile GPU NVidia Tegra K1 is also
has this microarchitecture. First GPU used for
comparison is one of the most forward computational
processors NVidia Tesla K20 and the second one is
common GPU NVidia GeForce 770 with average
features and performance.
Mobile application implementing described
simulation is presented at the end of the paper after
tests and analysis. Further, it may be developed for
computing any continuous media simulations and
also using the mobile GPU as nodes of large
heterogeneous distributed systems.
This paper is structured as follows. In section 2,
we consider the mathematical model of SPF problem
and implementation of numerical solution. In section
3, we discuss parallel algorithm for solving SPF
problem using CUDA and calculation time tests on
different devices.
Imankulov, T., Akhmed-Zaki, D., Daribayev, B. and Turar, O.
HPC Mobile Platform for Solving Oil Recovery Problem.
DOI: 10.5220/0006007505950598
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 595-598
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
595

2 MATHEMATICAL MODEL OF
SPF AND ITS NUMERICAL
SOLUTION
The mathematical model of two-phase flow in porous
media has following assumptions:
- incompressible flow;
- gravitational forces and capillary effects is
neglected;
- two-phase flow (water, oil) obeys Darcy’s law.
Mass conservation equations and velocities for
each phase can be written as follows:
+
(
)
=
(1)
+
(
)
=
(2)
+
=1
=−
(
)
∇, = ,
(3)
where – porosity,
,
–water and oil saturations,
,
- source or sink,
,
– velocity of the water
and oil phases,
(
)
,
– relative permeability and
viscosity for phase i,
–permeability tensor.
Polymer, surfactant, salt and heat transport
equations are given by (Babalyan, 1983):
+
+
=
∇
(4)
(
+
)
+
+
(
+
)
=
(
∇
+
∇
)
(5)
(
)
+
(
)
=0
(6)
(
1−
)
+
(
+
)
+
(
)
+
(
)
=
(
1−
)
+(
+
)∇
(7)
where
,
– polymer and salt concentrations in
aqueous phase,
,
–surfactant concentration in
water and oleic phases,
,
– polymer and
surfactant adsorption functions,
,
,
–
polymer and surfactant diffusion coefficients,
,
,
– specific heat of water, oil and rock,
,
,
– density of water, oil and rock,
,
,
–
coefficients of thermal conductivity.
Initial conditions:
|
=
,
=
,
|
=
,
|
=
,
|
=
,
(8)
|
=
=
,
=
,
Boundary conditions:
= 0;
= 0;
=0;
=0;
=0;
=0;
(9)
We used the following viscosity dependence on
injected reagent concentrations and temperature:
(Flory-Huggins, 1953):
=
1 + (
+
+
+
)
−
( −
)
(10)
=
1 −
( −
)
(11)
where
,
,
,
,
,
,
– constants.
−
initial viscosity of oelic phase,
−reservoir
temperature. The imbibition relative permeability
curve for water/oil flow is given by
(
)
=
.
;
(
)
=(1−
)
.
The adsorbed concentration of polymer is a
function of polymer concentration, given by:
=
1+
where −Langmuir constant.
The numerical formulation of equations (1)-(9)
based on finite difference method and explicit
scheme. The explicit schemes are naturally
parallelizable using the GPUs. Numerical realization
and results of numerical experiments was proposed
by the authors in (Danaev, 2015; Ahmed-Zaki, 2015).
3 TESTING RESULTS OF
PARALLEL ALGORITHM
USING CUDA TECHNOLOGY
For testing of the SPF problem we used devices with
NVIDIA Tesla K20, GeForce GTX 770 and Tegra K1
video cards with Kepler microarchitecture
(www.nvidia.com). For further testing, we compared
the characteristics of the devices. All characteristics
affect the performance of programs calculation
(Table 1).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
596
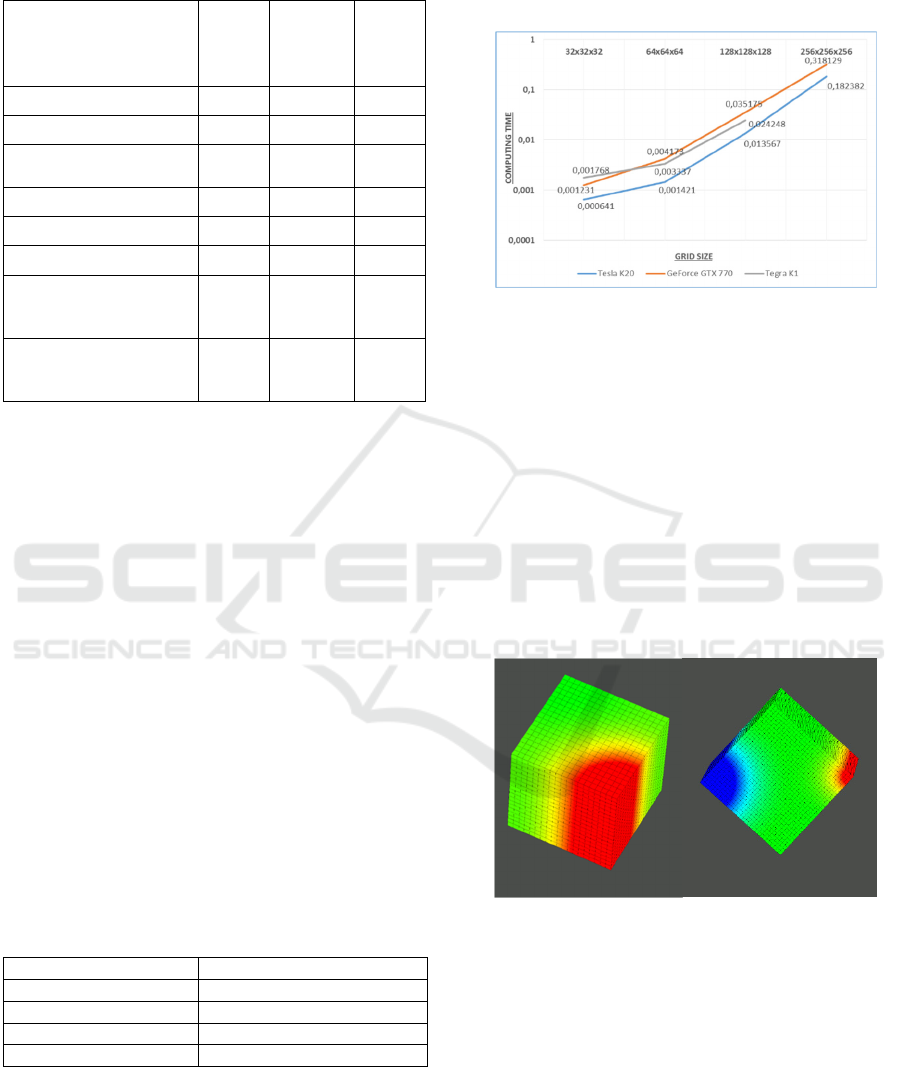
Table 1: Description of the NVIDIA Kepler architecture
video cards.
T
esla
K
20
GK110
GeForce
GTX 770
GK104
T
egra
K
1
GK20A
Cores 2496 1536 192
Clock Speed [MHz] 732 1046 950
Memory bandwidth
[GB/s]
208 224 17
Memory (max) [GB] 5 2 1
TDP(Watt) 225 230 10
Compute Capability 3.5 3.0 3.0
Theoretical
performance single
(GFLOPS)
3524 3213 365
Theoretical
performance double
(GFLOPS)
1175 134 290
Let NX, NY and NZ to be respectively a number
of nodes in the x, y, and z directions of the
computational domain. Three-dimensional area with
size NX x NY x NZ will be presented as one-
dimensional array of size NX x NY x NZ on CPU
side. One-dimensional representation of data in
global memory is also used on the GPU. Data
distribution in the device memory is performed once
at the beginning of calculation. On GPU data stored
in the shared memory of processor kernel.
Computational threads of each block copies data from
global memory to the shared memory. The
calculation is performed in the threads using that data.
Thereafter, the calculation results are written back
into the global memory before finishing the kernel
function. To obtain the benefit of using shared
memory arithmetic operations in the core must be
complex enough to compensate the cost of copying
the data. One way to achieve this is to increase size of
the block. Working with the shared memory we must
consider that it has restriction of 16 Kbytes.
Table 2: Memory required for array initialization.
Grid size Required memory (Gb)
32x32x32 ~0.005
64x64x64 ~0.042
128x128x128 ~0.344
256x256x256 ~2.750
In the numerical algorithm of the solution, each
computational node needed 176B memory space. So
implementing memory allocation to whole grid
required particular amount of free space (Table 2).
Tegra K1 could not launch program computing the
problem on 256x256x256 grid. It can be explained by
the fact that the RAM of used mobile device is only
1GB and initialization arrays did not fit to it.
Figure 1: Program calculation time on different devices.
Tests show that Tegra K1 graphic card computes
on the same level with other tested ones. For example,
on a 64x64x64 grid the mobile device performs the
calculation faster than the GeForce GTX 770. In this
case, we cannot find an excuse of architecture
difference, since the microarchitecture of processors
are the same. It can also be explained by the fact that
algorithm minimizes addressing to global memory.
As we can see in Table 1 memory bandwidth is a
weak point of Tegra K1 and we are reducing its usage
as much as possible. Tesla K20 has three times lesser
calculation time since its characteristics significantly
exceeds the remaining cards (figure 1).
Figure 2: Distribution of water saturation and pressure.
The results of parallel computational experiments
conducted on the tablet presented on figures 2-3.
Including OpenGL visualization it forms mobile
application that can be used to calculate main
technological parameters of oil recovery.
HPC Mobile Platform for Solving Oil Recovery Problem
597
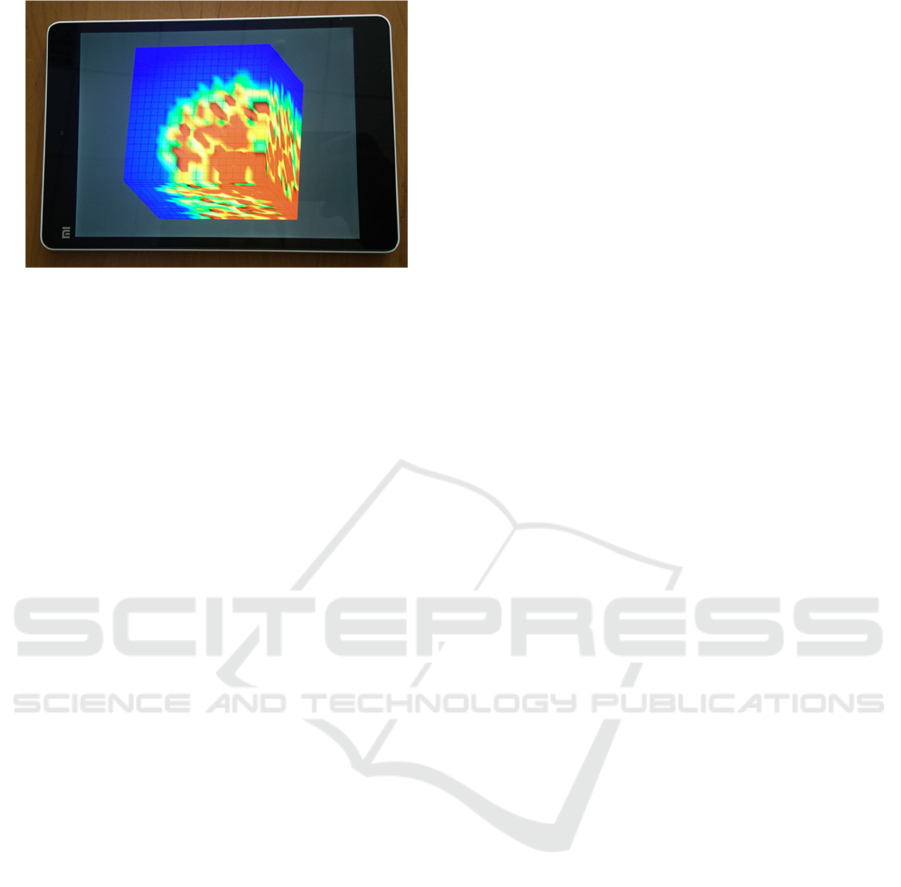
Figure 3: Demonstration of the mobile application results.
4 CONCLUSIONS
The paper describes usability of mobile devices to
GPGPU calculation of industrial scale problem. As
the problem we took a mathematical model of oil
displacement process by polymer/surfactant
injection. We presented the problem as an example of
complex industrial simulation. The problem was
solved by explicit numerical method because it well
suits to GPGPU parallelization.
The main steps of the numerical algorithm are
implemented with separate CUDA kernel functions
by using shared memory. The reason is that mobile
device graphics card has an architecture that is
adverse to only global memory algorithms. This is
due to the fact that device has combined CPU and
GPU RAM.
By testing calculation time of the program on
different grids, we will notice that the mobile device
with the Tegra K1 video card, not much inferior to
device with the Tesla K20 video card and practically
equal to GeForce GTX 770. This suggests that the
complex hydrodynamic problems can run wherever
there is a mobile device with a video card that
supports CUDA technology.
Engineers can use presented mobile application
for planning and analyze of oil recovery on real oil
fields. Our future work will focus on the use of
graphics cards power to calculate programs at a time
on several mobile devices. We also plan to expand
our code for heterogeneous computing.
REFERENCES
Ahmed-Zaki D.Zh., Mukhambetzhanov S.T.,
Imankulov T.S., 2015. Design of i-Fields System
Component: Computer Model of Oil-Recovery by
Polymer Flooding. Proceedings of the 12th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO 2015), Volume 2
Colmar, Alsace, France. pp. 510-517.
Babalyan G.A., Levy B.I., Tumasyan A.B.,
Khalimov E.M., 1983. Oilfield development using
surfactants. Nedra, Moscow.
Cheng K.T., Wang Y.C., 2011. Using mobile GPU for
general-purpose computing - a case study of face
recognition on smartphones. VLSI Design, Automation
and Test (VLSI-DAT), 2011 International Symposium.
pp. 1–4.
Danaev N.T., Mukhambetzhanov S.T, Ahmed-Zaki D.Z,
Imankulov T.S., 2015. Mathematical modeling of oil
recovery by polymer/surfactant flooding.
Communications in computer and information science.
Vol. 549, pp. 1-12.
Flory, P.J., 1953. Principles of polymer chemistry. Cornell
University Press.
Ketan B. Parmar, Nalinbhai N. Jani, Pranav S. Shrivastav,
Mitesh H. Patel, 2013. Mobile Grid Computing: Facts
or Fantasy? International journal of multidisciplinary
sciences and engineering, Vol. 4, No. 1.
Kelly J.M., Divo E.A., Kassab A.J., 2013. A GPU-
accelerated meshless method for two-phase
incompressible fluid flows. WIT Transactions on
Modelling and Simulation, Vol 54, WIT Press.
www.witpress.com.
Lake, L.W., 1989. Enhanced oil recovery. Prentice Hall
Inc, New Jersey.
Micikevicius, P.: 3D fnite difference computation on GPUs
using CUDA. GPGPU-2:Proceedings of 2nd
Workshop on General Purpose Processing on Graphics
Processing Units.
NVIDIA Kepler Compute Architecture -
www.nvidia.com/object/nvidia-kepler.html.
Open-source software for volunteer computing BOINC
http://boinc.berkeley.edu/
Phan T., Huang L., Dulan C., 2002. Challenge: Integrating
Mobile Wireless Devices into the Computational Grid.
ACM MOBICOM.
Singhal N., Park I. K., Cho S., 2010. Implementation and
optimization of image processing algorithms on
handheld GPU. Image Processing (ICIP), 17th IEEE
International Conference. pp. 4481–4484.
Sorbie, K.S., 1991. Polymer improved oil recovery. CRC
Press, Boca Raton.
Thibault, J.C., Senocak, I., 2009. CUDA implementation of
a Navier-Stokes solver on multi-GPU desktop
platforms for incompressible flows. 47th AIAA
Aerospace Sciences Meeting. Orlanda, FL. Paper
No:AIAA-2009-758.
Tolke, J., Krafczyk, M., 2008. TeraFLOP computing on a
desktop PC with GPUs for 3D CFD. International
Journal of Computational Fluid Dynamics 22(7), 443–
456.
Wang G., Xiong Y., Yun J., Cavallaro J.R., 2013.
Accelerating computer vision algorithms using
OpenCL framework on the mobile GPU - a case study.
IEEE International Conference on Acoustics, Speech,
and Signal Processing (ICASSP).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
598
