Fuzzy Modeling and Control for Intention Recognition in Human-robot

Systems

Rainer Palm, Ravi Chadalavada and Achim J. Lilienthal

AASS, Dept. of Technology

Orebro University SE-70182

Orebro, Sweden

Keywords:

Fuzzy Control, Fuzzy Modeling, Human-robot Interaction, Human Intentions.

Abstract:

The recognition of human intentions from trajectories in the framework of human-robot interaction is a chal-

lenging ﬁeld of research. In this paper some control problems of the human-robot interaction and their inten-

tions to compete or cooperate in shared work spaces are addressed and the time schedule of the information

ﬂow is discussed. The expected human movements relative to the robot are summarized in a so-called ”com-

pass dial” from which fuzzy control rules for the robot’s reactions are derived. To avoid collisions between

robot and human very early the computation of collision times at predicted human-robot intersections is dis-

cussed and a switching controller for collision avoidance is proposed. In the context of the recognition of

human intentions to move to certain goals, pedestrian tracks are modeled by fuzzy clustering, lanes preferred

by human agents are identiﬁed, and the identiﬁcation of degrees of membership of a pedestrian track to spe-

ciﬁc lanes are discussed. Computations based on simulated and experimental data show the applicability of

the methods presented.

1 INTRODUCTION

Dealing with interactions of humans and autonomous

robots in common working areas is a challenging re-

search ﬁeld with regard to system stability and per-

formance and to human safety. Research results on

planning of mobile robot tasks, learning of repeated

situations, navigation and obstacle avoidance have

been published by (Mataric, 1990; Firl, 2014; Khatib,

1985; Palm and Bouguerra, 2013). When human

agents and robots share the same workspace, both of

them have to adapt their behavior, to either support

their cooperation, or to enable them to do their own

task separately. In this connection it is difﬁcult to

predict the behavior, motions and goals of a human

agent. Even more it is important to predict the hu-

man behavior for a limited time horizon with a cer-

tain probability to enable the robot to perform ade-

quate reactions. One class of solutions to this prob-

lem is the building of models of the human behav-

ior by clustering methods (Mataric, 1990; F. Sadri

and Xaﬁ, 2012; R. Palm and Kadmiry, 2009). Fur-

ther research activities focus on Bayesian networks

(Tahboub, 2006; Han and Pereira, 2013), Hidden

Markov Models (HMM) (M. Bennewitz and Thrun,

2005), Fuzzy logic or Fuzzy Cognitive Maps and re-

inforcement learning (Tahboub, 2006; A. Ciaramella

and Straccia, 2010). Heinze addresses human in-

tentions from the ontological point of view (Heinze,

2004). Another aspect is the (automatic) recognition

of human intentions to aim at a certain goal. Some

research on intention recognition describes human-

robot interaction scenarios and the ”philosophical and

technical background for intention recognition” (Tah-

boub, 2006). Further research deals with ”Intention

Recognition in Human-RobotCollaborativeSystems”

(Aarno, 2007; Krauthausen, 2012), human-robot mo-

tions initiated by human intentions (T. Fraichard

and Reignier, 2014), and socially inspired planning

(J.V. Gomez and Garrido, 2013). In practice, the iden-

tiﬁcation of a human intention needs to predict the di-

rection of motion, the average velocity and parts of

the future trajectory. In this connection, Bruce et al

address a planned human-robot rendezvous at an in-

tersection zone (J. Bruce and Vaughan, 2015). Satake

et al (Satake et al., 2009) describe a social robot, that

approaches a human agent in a way that is acceptable

for humans. Further research on human intentions to-

gether with trajectory recognition and planning is pre-

sented by (A.F.Johansson, 2009; Chadalavada et al.,

2015). The modeling of pedestrian trajectories using

Gaussian processes is shown in (T. Ellis and Reid,

2009). In (Makris and Ellis, 2010) fuzzy methods,

probabilistic methods and HMM approaches for mod-

Palm, R., Chadalavada, R. and Lilienthal, A.

Fuzzy Modeling and Control for Intention Recognition in Human-robot Systems.

DOI: 10.5220/0006015400670074

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 67-74

ISBN: 978-989-758-201-1

eling of human trajectories are compared. In addition

to the recent research mentioned above and as an ex-

tension of our work described in (R. Palm and Lilien-

thal, 2016), this paper concentrates on the recognition

of human intentions to move along certain trajecto-

ries. The method is based on observations of early

trajectory parts, plus a subsequent extrapolation. The

here discussed control principles of interaction be-

tween human and robot mainly deal with trajectory

planning and external sensor feedback on a higher

level of the control hierarchy. Furthermore, the time

schedule of the information ﬂow and the kinematic re-

lationship of a human-robot system in motion is con-

sidered. The observation of the human agent by the

robot supplies motion data that are Kalman-ﬁltered to

cope with uncertainties and noise. This leads to an es-

timation of the velocity vector of the human relative to

the robot which is depicted in a ”compass dial”. From

this, a set of fuzzy rules is extracted that results in a

possible reaction of the robot either to prevent a col-

lision or enable a cooperation. Our case is somehow

different from the usual case of avoidance of moving

obstacles due to the uncertainty to predict human in-

tentions. A special issue is the case of unchanged di-

rections of a motion both of the human and the robot

that should be distinguished from a common obstacle

avoidance methods (Khatib, 1985). This is tackled by

a switching robot controller that computes the time

for possible collisions at the intersections. According

to this knowledge the controller changes the robot’s

speed which helps to prevent collisions at intersec-

tion of the planned paths. Due to uncertainties in the

observations and to measurement noise the intersec-

tion points are extended to intersection areas which

must not be entered at the same time neither by the

human nor by the robot. Since this operation com-

prises only the ﬁrst part of the human motion the sub-

sequent extrapolations are updated at each time step

in order to avoid larger errors. Another essential issue

is the identiﬁcation of lanes from trajectories usually

preferred by human agents in an open area or at a fac-

tory work ﬂoor. This is motivated by the need for an

early reaction of the robot to the human’s intention to

walk, and to plan either a collision avoidance or a co-

operation action. In this paper we concentrate on the

fuzzy modeling of pedestrian tracks, the identiﬁcation

of lanes preferred by the human agents, and the iden-

tiﬁcation of a membership of a pedestrian track (or

parts of it) to a speciﬁc lane.

The paper is organized as follows. In Section 2

we address the interaction between human and robot

from the control structure point of view and the time

schedule of the information ﬂow. Section 3 deals with

the kinematic and geometric relations between human

and robot. A ”compass dial” with the relative veloci-

ties and the corresponding fuzzy rules is presented in

Sect. 4. Section 5 deals with avoidance strategies at

intersections. Section 6 addresses the fuzzy modeling

of sets (bundles) of pedestrian tracks and the identiﬁ-

cation of the membership of a single track to a certain

lane. Section 7 presents results based on simulations

and experimental data, and Sect. 8 ends with a dis-

cussion and conclusions.

2 INTERACTION BETWEEN

HUMAN AND ROBOT

In a shared working environment, human and robot

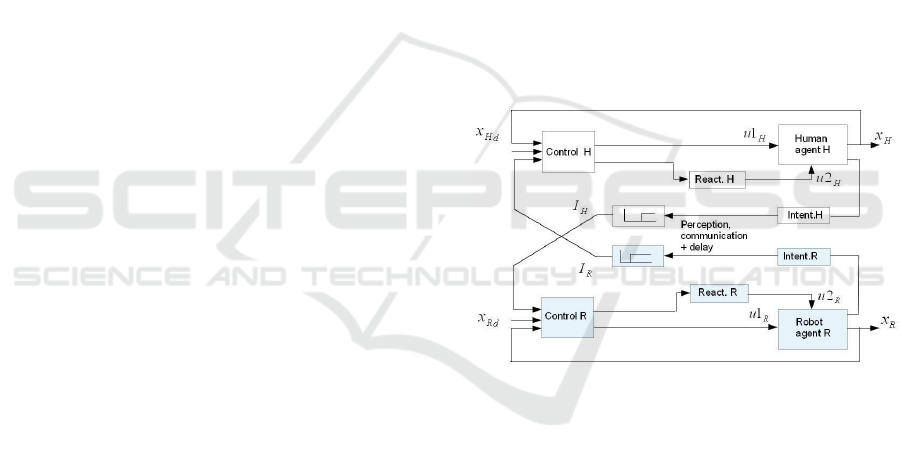
are constituted by a common control system shown in

Fig. 1. Both human and robot are driven by their in-

dividual goals (desired trajectories) x

and x

. Ac-

tions and reactions are represented by desired states

) and x

). From the interaction of the two

agents we obtain observable states x

) and x

Figure 1: Human-robot interaction, control scheme.

Intentions I

and I

are signals (e.g. information

about parts of trajectories) transmitted to/observed by

the other agent. The dynamic equations can formally

be written as

˙x

= f

,u1

,u2

); ˙x

= f

,u1

,u2

)

= g1

);u1

= g1

)

= g2

);u2

= g2

)

= h

);I

= h

) (1)

The 1-st two lines of (1) denote the individual dy-

namics of human and robot, where the next two lines

denote the ’crosswise’ inﬂuence of intention and reac-

tion between human and robot. The functions in (1)

are highly nonlinear hybrid functions with continuous

and switching attributes. A good example for model-

ing human-robot dynamics can be found in (P. Leica

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

and Carelli, 2015). Recall here that the control prob-

lems discussed here deal with the higher control level

of external sensory and trajectory generation. Fur-

thermore the feasibility of the desired trajectory x

and its possible variations should be guaranteed be-

cause of the nonholonomic kinematics of the robot.

In our case, intentions are functions of desired and

actual states. The robot controllers g1

and g2

can

be designed based on the knowledge about the system

dynamics (R.-E.Precup and Preitl, 2009) whereas the

human controllers g1

and g2

, which have been in-

troduced due to formal reasons, cannot be designed in

the same way. The same is true for the formal descrip-

tion f

of the human behavior which is usually only a

rough approximation of the reality. Since a modeling

especially of the human’s behavior is quite difﬁcult,

the modeling of both the robot and the human by TS

fuzzy models from motion data is worth mentioning.

In this case each of the nonlinear functions of (1) split

up into n local functions like

∑

i=1

) · f

,u1

,u2

) (2)

∑

i=1

) · f

,u1

,u2

)

where w

are membership functions. Let furthermore

the robot controllers u1

,u2

either be designed as

weighted combinations of local controllers

∑

i=1

) · g1

) (3)

∑

i=1

) · g2

)

or as Mamdani expert rules formulated in Sect. 4.

On the other hand, human controllers u1

,u2

are

also expressed as Mamdani expert rules which are the

counterparts of the robot expert rules. A switching

robot controller for collision avoidance is presented

in Sec. 5. An intention may become observable in

an early part of the human trajectory x

|k = 1...m)

where m is the time horizon on the basis of which

the robot should recognize the human’s intention to

move. This information is sent to the robot with a de-

lay T

. After that the robot starts its intention recog-

nition and starts to plan/compute a corresponding re-

action x

). The intention to react is realized as

a part of the trajectory of the robot x

|k = j...n)

where (n − j) is the corresponding time horizon on

the basis of which the human tries to recognize the

robot’s intention to move. Then this intention is trans-

mitted to the human.

The sampling time of the whole process is T

tot

Robot and human can control the mutual cooperation

only if T

tot

meets certain requirements regarding the

time constants of the system. There are two time con-

stants involved, the time constant τ

of the human and

the time constant τ

of the robot. Let the total process

time constant be the sum of the two

tot

= τ

+ τ

(4)

A rule of the thumb says that the sample time T

tot

should be 5...30 times shorter than the largest time

constant of the process ((Ed.), 1995).

3 KINEMATIC RELATIONS OF

HUMAN AGENTS AND

MOBILE ROBOTS IN A

COMMON WORKSPACE

The analysis of the mutual observations between

human and robot requires the formulation of rela-

tive positions/orientations and velocities in the lo-

cal coordinate systems C

(human) and C

(robot)

and the global coordinate system C

(basis). First,

let us assume a sufﬁcient knowledge of the posi-

tions/orientations of robot and human both in their lo-

cal systems C

, C

and in the basis system C

. The

relation between two coordinate systems C

and C

is then deﬁned by the transformation Figure 2 shows

the kinematic relations between the coordinate sys-

tems C

, C

, and C

: T

between human and ba-

sis, T

between robot and basis, T

between human

and robot. The orientation, of human and robot are

chosen so that the y axis is pointing in the direction

of motion. Next an additional coordinate system C

is deﬁned whose y-axis points from the center of C

to the center of C

. This coordinate system is nec-

essary for the formulation of the heading angle from

human to robot. The distance between C

(and C

)

andC

is denoted by d

. In the following we assume

parts of the intended trajectory x

) of the human

to be measurable by the robot from which the velocity

Figure 2: Transformations between frames.

Fuzzy Modeling and Control for Intention Recognition in Human-robot Systems

˙x

), the orientation angle φ

) and the trans-

formation matrix T

) can be estimated. Since the

robot is assumed to know its own trajectory x

)

and the transformation matrix T

) we can compute

the transformation matrix: T

) = T

) · T

Then we measure the distance d

between C

and

, and the relative angle α

between the line C

– C

and the y-axis of C

. Finally we compute the

heading angle φ

= π − (α

+ φ

R) between C

and C

which is necessary for the qualitative relation

between human and robot. Now we have all informa-

tion to formulate a set of qualitative fuzzy rules for

human-robot interactions.

4 FUZZY RULES FOR

HUMAN-ROBOT

INTERACTIONS

In the center of C

a so-called compass dial

is introduced that expresses the qualitative rela-

tionship of the human intentions seen from the

robot. These comprise 8 human motions rela-

tive to the robot: ’APP=approach’, ’AVR=avoid

right’, ’MOR=move right’, ’RER=recede right’,

’REC=recede’, ’REL=recede left’, ’MOL=move

left’, ’AVL=avoid left’.

Figure 3: Compass dial for human actions.

To identify the trajectory of the human relative to

the robot it is enough to know the heading angle φ

and the relative velocity ∆v = |˙x

− ˙x

| = |˙x

Since ∆v is an invariant it becomes clear that it can be

computed in each arbitrary coordinate system. Ones

the heading angle φ

is computed one can deter-

mine a qualitative relation between human and robot

according to the compass dial in Fig. 3. A fuzzy la-

bel is attached to each motion direction of the human

agent. A crisp heading angle φ

is fuzziﬁed with re-

Figure 4: Fuzzy sets for human motions.

spect to the corresponding fuzzy sets for ’approach’,

’avoid right’ etc (see Fig. 4). From α

, φ

, ∆v and

the distances |∆x| = |x

| the response of the robot to

the human’s intention is computed in an early state of

the human action. However, because of the uncer-

tain nature of the data (system/measurement noise)

one obtains estimates of positions and velocities by

an appropriate Kalman ﬁlter. Noise on velocity and

measurement are ﬁltered out leading to a smooth tra-

jectory (or part of trajectory) from which the velocity

vector is estimated. The variables to be processed are

, φ

, the distance |∆x| = |x

|, and the relative

velocities |∆v|. For |x

| and |∆v| fuzzy sets ’Small’,

’Medium’, and ’Large’ of Gaussian type are deﬁned

and appropriate fuzzy rules are formulated

IF α

= A

= P

AND

|∆x| = DX

AND |∆v| = DV

(5)

THEN ACT

rob

ACT

rob

: φ

rob

= PH

AND |v|

rob

= VR

i - rule number

- relative angle between C

and C

- fuzzy set for the relative angle

- heading angle between C

and C

- fuzzy set for the heading angle

|∆x| - distance between C

and C

- fuzzy set for the distance

|∆v| - relative velocity between C

and C

- fuzzy set for the relative velocity

rob

- steering angle of robot

- fuzzy set for the steering angle

|v|

rob

- desired velocity of the vehicle

- fuzzy set for the desired velocity

However, not every combination makes sense. There-

fore ”pruning” of the set of rules and intelligent hier-

archization can solve this problem. A simple set of

rules for α

> 0 to avoid a collision between human

and robot contains only the heading angle φ

and

the steering angle φ

rob

like:

IF φ

= APP THEN φ

rob

= TR (6)

where TR=turn right, TL=turn left, MS=move

straight ahead, MSSD=move straight ahead/slow

down.

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

5 SWITCHING CONTROLLER

FOR COLLISION AVOIDANCE

5.1 Early Observation of Trajectories

From measured robot/human positions taken at an

early point in time Kalman ﬁltered sequences of robot

and human positions x

) and x

) are gained

from which the velocities v

and v

are estimated.

Then the distance d

between C

and C

and the

relative angle α

are measured and the angle φ

computed.

Despite of existent trafﬁc rules a collision be-

tween human agent and robot may occur especially

in the cases AVR,MOR,RER or AVL,MOL,REL of

the compass dial. Therefore at a certain distance the

robot controller switches from the ’normal mode’ to

a ’prediction mode’ to compute an ’area of intersec-

tion’ and the time to reach it. After having reached

this area the controller switches back to the ’normal

mode’ keeping its latest velocity constant.

5.2 Uncertainty in Measurements

Uncertainties in measurements and unexpected

changes in directions and velocities lead to deviations

in the calculations of possible crossing points. From

simulations and experiments circular areas of possi-

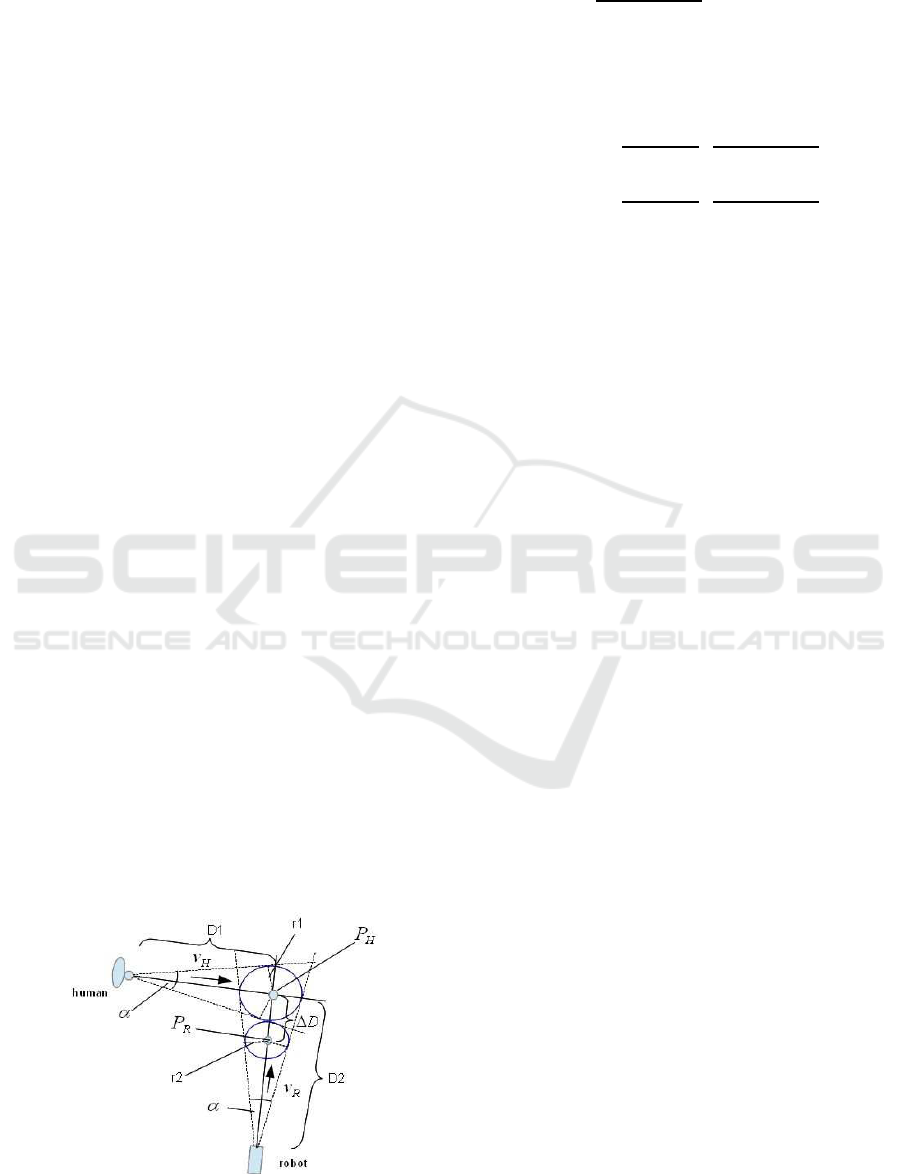
ble collisions can be designed. Figure 5 shows the

relations for the ”1 human - 1 robot” case. Let P

the crossing point of human and robot and α the an-

gle of uncertainty for both human and robot at a spe-

ciﬁc time t

. A circle with the radius r

= D

· sinα/2

describes the uncertainty area A

of the human to

be avoided by the robot. On the other hand, the

robot has its own circular uncertainty area A

that

should not overlap with A

. Let the distance between

robot and crossing point be ∆D then the radius of A

is r

= (D

− ∆D) · sinα/2. From the requirement

∩A

0 we obtain ∆D ≥ r

. For ∆D = r

Figure 5: Crossing areas.

we obtain

sinα/2

(1+ sinα/2)

− r

) (7)

and ﬁnally the velocity v

for the robot to reach the

distance point P

in the time t

that the human would

need to get to P

(see (8 a))

a : v

opt

− r

)

(1+ sinα/2)

(8)

b : v

opt

+ r

)

(1− sinα/2)

(8 a) is valid for the case when the human passes the

crossing point before the robot. To be on the safe side

one should require v

≤ v

opt

. For the case when the

human passes the crossing point after the robot we get

(8 b)

with v

≥ v

opt

6 INTENTION RECOGNITION

BASED ON LEARNING OF

PEDESTRIAN LANES

6.1 Fuzzy Modeling of Lanes

A good option to identify/recognize human intention

to aim at a speciﬁc goal is to learn from experience.

The framework of ”programming by demonstration”

focusses on the recognition of human grasp pattern

by fuzzy time clustering and modeling (R. Palm and

Kadmiry, 2009). Likewise for the intention recogni-

tion it is a matter of pattern recognition, when a model

is used that has been built on the basis of recorded

pedestrian trajectories. For this purpose we used the

”Edinburgh Informatics Forum Pedestrian Database”

which consists of a large set of walking trajectories

that has been measured over a period of months (edi,

2010) (see Fig. 6). The idea is to identify lanes that

people normally use in a speciﬁc working area. In our

case the models are built by fuzzy time clustering as

follows:

1. From the whole set of data select 12 trajectories

and divide them into 3 ”bundels”.

2. Make a clustering of each trajectory separately

with c = 10 time clusters C

i,k,l

∈ R

k-number of set; l-number of trajectory in the set; i -

number of time cluster

3. Compute the mean values of the time clusters in

each set: C

k,i

= 1/m

∑

l=1

i,k,l

- number of trajectories in set k. C

i,k

= (c

)

i,k,l

are the x, y coordinates of the i-th cluster centers in the

Fuzzy Modeling and Control for Intention Recognition in Human-robot Systems

k-th set. The connections of C

i,k

i = 1...c represent ﬁ-

nally the lanes k = 1...3. Fig.7 shows the results for

all 3 sets.

Figure 6: Edinburgh pedestrian data.

Figure 7: Lanes 1...3, average trajectories.

6.2 Recognition of Intentions to Follow

Certain Lanes

In order to recognize the intention of a human agent to

aim at a certain goal, the membership of his trajectory

(or part of it) to one of the lanes is to be computed.

The membership of a point x = (x,y)

to a cluster

center C

i,k

is here deﬁned by

i,k

∑

j=1

(

i,k

j,k

)

proj

−1

(9)

where d

i,k

= (x−x

i,k

)

(x−x

i,k

), x

i,k

- i-th cluster cen-

ter in the k-th lane, m

proj

> 1 - fuzziness parameter

(Runkler and Palm, 1996). The algorithm works as

follows:

1. Compute the closest distances d

min

= min

(|x−

j,k

|) to the cluster centers C

j,k

(j = 1...c,k = 1...m

)

2. Compare the membership functions w

min

and se-

lect the lane with the highest membership:

min

)

max

= max(w

min

), k = 1...m

max

= argmax(w

min

However, only one data point is obviously not sufﬁ-

cient for intention recognition. Therefore moving av-

erages ( ¯w

min

)

max

over a predeﬁned number of time

steps n are computed

( ¯w

min

)

max

) =

n−1

∑

i=0

min

)

max

− i) (10)

With this the inﬂuence of noise is further reduced and

the degree of membership of a human trajectory to a

particular lane is reliably identiﬁed.

7 SIMULATION RESULTS

7.1 Collision Avoidance at Intersections

In the 1st simulation the ”1 human - 1 robot” case

is considered where the estimations of the crossing

points are made during motion. This experiment is

a combination of real human walking data from the

Edinburgh Data and a simulated robot. At each time

point the crossing points of the two tangents along the

velocity vectors are computed and the robot velocity

will be adjusted according to eq.(8 a). Figure 8 shows

the plot before the crossing point and Fig. 9 shows

the time schedule before and after the crossing point.

In the case of stationarity the velocity is limited at a

−2 0 2 4 6 8 10 12 14

−2

tangents

robot

human

crossing point

distance point

y, m

x, m

Figure 8: Motion before crossing, case 1.

0 10 20 30 40 50 60 70 80 90 100

DHR2ed, m

0 10 20 30 40 50 60 70 80 90 100

DR2Hed, m

0 10 20 30 40 50 60 70 80 90 100

0.5

1.5

t, 10s

vR2, m/s

0 10 20 30 40 50 60 70 80 90 100

vH, m/s

t, 0.1s

human

velocity, robot

distance to intersection, human

distance to intersection, robot

velocity

Figure 9: Time schedule before and after crossing, case 1.

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

predeﬁned distance between robot and actual crossing

point in order to prevent from too high robot veloci-

ties. Fig. 9 shows that after 3s the robot has reached a

velocity that guarantees the human to pass the cross-

ing point 1.5 second before the robot. Case 2 (eq.(8

b)) is shown in Figs. 10 and 11. Here the robot passes

the intersection before the human with a time differ-

ence of 2.5 seconds.

−2 0 2 4 6 8 10 12 14

−2

human

robot

crossing point

distance point

tangents

y, m

x, m

Figure 10: Motion before crossing, case 2.

0 10 20 30 40 50 60 70 80 90 100

DHR2ed,m

0 10 20 30 40 50 60 70 80 90 100

DR2Hed,m

0 10 20 30 40 50 60 70 80 90 100

1.5

t, 10s

vR2, m/s

0 10 20 30 40 50 60 70 80 90 100

t, 10s

vH, m/s

human

robot

human

Distance to intersection

velocity

Figure 11: Time schedule before and after crossing, case 2.

7.2 Recognition of Lanes While

Tracking

From 11 trajectories of the Edinburgh-data 3 differ-

ent lanes were identiﬁed beeing used in both direc-

tions with different velocities. Lanes 1, 2, and 3 are

modeled off line on the basis of 4, 5, and 2 trajec-

tories, respectively. The modeling results are repre-

sentative trajectories/paths of bundles of similar tra-

jectories. In our example, 3 from 20 test trajectories

(tracks) were selected from the Edinburgh-data which

have not been used for modeling but whose entry/exit

areas coincide with those of the modeled lanes (see

Fig. 12). During motion the degrees of membership

(see Fig. 13) for each track are computed accord-

ing to (9) and (10) with a moving average about 10

time steps. Here, from the membership degrees in

Figs.14-16 one can see, that from only a few samples

the membership of a track to a lane can be recognized.

0 2 4 6 8 10 12 14 16

lane 1

lane 2

track 1

track 2

track 3

lane 3

Figure 12: Lanes 1-3, test tracks.

0 1 2 3 4 5 6 7 8 9 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

cluster centers

lane 1

lane 2

lane 3

Figure 13: Membership

functions.

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

time step i

w(i)

lane 1

lane 2

lane 3

Figure 14: Memberships

track 1.

8 CONCLUSIONS

The problem of the recognition of human intentions

is part of a control task for human-robot interaction

and cooperation. A prominent role plays the pre-

diction of human motions to plan corresponding on

line reactions and maneuvers. The time schedule for

the information exchange and the kinematic relations

have been discussed, a general scheme of regarding

fuzzy control rules for the human-robot interaction

is presented and collision avoidance and optimization

strategies are discussed. Another method to recognize

intentions is the fuzzy modeling of pedestrian tracks,

the identiﬁcation of lanes preferred by human agents,

and the identiﬁcation of a membership of a pedestrian

track to a speciﬁc lane. Examples with both simu-

lated and real data show the applicability of the meth-

ods presented, whereas - because of the lack of space

- we conﬁned ourself to the switching controller and

the recognition of lanes.

ACKNOWLEDGEMENT

This research work has been supported by the AIR-

Fuzzy Modeling and Control for Intention Recognition in Human-robot Systems

0 10 20 30 40 50 60 70 80 90

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

time step i

w(i)

lane 2

lane 3

lane 1

Figure 15: Memberships

track 2.

0 5 10 15 20 25 30 35 40

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

time step i

w(i)

lane 3

lane 2

lane 1

Figure 16: Memberships

track 3.

project, Action and Intention Recognition in Human

Interaction with Autonomous Systems.

REFERENCES

(2010). Edinburgh informatics forum pedestrian

database. http://homepages.inf.ed.ac.uk/rbf/

FORUMTRACKING/.

A. Ciaramella, M.G.C.A.Cimino, F. M. and Straccia, U.

(2010). Combining fuzzy logic and semantic web

to enable situation-awareness in service recommenda-

tion. Database and Expert Systems Applications, Lec-

ture Notes in Computer Science., Volume 6261:31–45.

Aarno, D. (2007). Intention recognition in human machine

collaborative systems. Licentiate Thesis Stockholm,

Sweden., pages 1–104.

A.F.Johansson (2009). Data driven modeling of pedestrian

crowds. Doctoral Thesis., pages 1–185.

Chadalavada, R. T., Andreasson, H., Krug, R., and Lilien-

thal, A. J. (2015). That’s on my mind! robot to human

intention communication through on-board projection

on shared ﬂoor space. European Conference on Mo-

bile Robots (ECMR).

(Ed.), W. L. (1995). The control handbook. page 316.

F. Sadri, W. W. and Xaﬁ, A. (2012). Intention recognition

with clustering. Ambient Intelligence., Lecture Notes

in Computer Science, 7683:379–384.

Firl, J. (2014). Probabilistic maneuver recognition in trafﬁc

scenarios. Doctoral dissertation, KIT Karlsruhe,.

Han, T. A. and Pereira, L. (2013). State of the art of

intention recognition. AI Communications., Volume

26:237–246.

Heinze, C. (2004). Modelling intention recognition for in-

telligent agent systems. Research Report, Air Opera-

tions Division.

J. Bruce, J. W. and Vaughan, R. (2015). Human-robot ren-

dezvous by co-operative trajectory signals. pages 1–2.

J.V. Gomez, N. M. and Garrido, S. (2013). Social path plan-

ning: Generic human-robot interaction framework for

robotic navigation tasks. Workshop of the IEEE/RSJ

Intern. Conf. on Int. Rob. and Syst. (IROS’13).

Khatib, O. (1985). Real-time 0bstacle avoidance for ma-

nipulators and mobile robots. IEEE Int. Conf. On

Robotics and Automation,St. Loius,Missouri, 1985,

page 500505.

Krauthausen, P. (2012). Learning dynamic systems for in-

tention recognition in human-robot-cooperation. Doc-

toral dissertation, University report, Karlsruhe.

M. Bennewitz, W. Burgard, G. C. and Thrun, S. (2005).

Learning motion patterns of people for compliant

robot motion. The International Journal of Robotics

Research., vol. 24 no. 1:31–48.

Makris, D. and Ellis, T. (2010). Spatial and probabilistic

modelling of pedestrian behaviour. In Proc. ICRA,

page 39603965. IEEE.

Mataric, M. (1990). A distributed model for mobile robot

environment-learning and navigation. Technical Re-

port., pages 1–139.

P. Leica, M.Toibero, F. R. and Carelli, R. (2015). Switched

control to robot-human bilateral interaction for guid-

ing people. Journal of Intelligent and Robotic Sys-

tems,DORDRECHT. Argentina. 77. 1., pages 73–93.

Palm, R. and Bouguerra, A. (2013). Particle swarm opti-

mization of potential ﬁelds for obstacle avoidance. In

Proceeding of RARM 2013, Istanbul, Turkey. Volume:

Scient. coop. Intern. Conf. in elect. and electr. eng.

R.-E.Precup, M. T. and Preitl, S. (2009). Fuzzy logic con-

trol system stability analysis based on lyapunov’s di-

rect method. In International Journal of Computers,

Communications and Control,vol. 4, no. 4, pages 415–

426.

R. Palm, B. I. and Kadmiry, B. (2009). Recognition of

human grasps by time-clustering and fuzzy model-

ing. Robotics and Autonomous Systems, Vol. 57, No.

5.:484–495.

R. Palm, R. C. and Lilienthal, A. (2016). Recognition of

human-robot motion intentions by trajectory observa-

tion. In 9th Intern. Conf. on Human System Interac-

tion, HSI2016. IEEE.

Runkler, T. and Palm, R. (1996). Identiﬁcation of nonlinear

system using regular fuzzy c-elliptotype clustering. In

Proc. FUZZIEEE 96, pages 1026–1030. IEEE.

Satake, S., Kanda, T., Glas, D. F., Imai, M., Ishiguro, H.,

and Hagita, N. (2009). How to approach humans?-

strategies for social robots to initiate interaction. 13th

Intern. Symp. on Experimental Robotics, pages 109–

116.

T. Ellis, E. S. and Reid, I. (2009). Modelling pedes-

trian trajectory patterns with gaussian processes. In

2009 IEEE 12th International Conference on Com-

puter Vision, Workshops (ICCV Workshops), pages

1229–1234. IEEE.

T. Fraichard, R. P. and Reignier, P. (2014). Human-robot

motion: Taking attention into account . Research Re-

port, RR-8487.

Tahboub, K. A. (2006). Intelligent human-machine interac-

tion based on dynamic bayesian networks probabilis-

tic intention recognition. Journal of Intelligent and

Robotic Systems., Volume 45, Issue 1:31–52.

Takagi, T. and Sugeno, M. (1985). Identiﬁcation of sys-

tems and its applications to modeling and control.

IEEE Trans. on Syst., Man, and Cyb., Vol. SMC-15.

No.1:116–132.

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications