A Convolution Model for Heart Rate Prediction
in Physical Exercise
Melanie Ludwig
1
, Harald G. Grohganz
2
and Alexander Asteroth
1
1
Computer Science Department, Bonn-Rhein-Sieg University o.A.S., Grantham-Allee 20, 53757 Sankt Augustin, Germany
2
Blue Square Group e.V., Bonn, Germany
Keywords:
Predictive Models, Heart Rate Prediction, Training Optimization.
Abstract:
During exercise, heart rate has proven to be a good measure in planning workouts. It is not only simple to
measure but also well understood and has been used for many years for workout planning. To use heart rate to
control physical exercise, a model which predicts future heart rate dependent on a given strain can be utilized.
In this paper, we present a mathematical model based on convolution for predicting the heart rate response
to strain with four physiologically explainable parameters. This model is based on the general idea of the
Fitness-Fatigue model for performance analysis, but is revised here for heart rate analysis. Comparisons show
that the Convolution model can compete with other known heart rate models. Furthermore, this new model
can be improved by reducing the number of parameters. The remaining parameter seems to be a promising
indicator of the actual subject’s fitness.
1 INTRODUCTION
Exercising has a proven therapeutic effect on the car-
diovascular system. To avoid overstrain, determin-
ing an optimal training dose is crucial. In general,
heart rate prediction based on physical activity can
be a useful tool in properly controlling and moni-
toring the strain that a smart training device imposes
on a subject during exercise (Achten and Jeukendrup,
2003). Hence, accurately predicting heart rate from
work load information is an essential part in models
used for training control since too much and wrong
exercising can do more harm than good.
If an accurate prediction shows a heart rate too
high or an unexpected increase or decrease of the
heart rate, workload can be reduced or improved in
adequate time. Ignoring the limits of the physical ca-
pabilities will risks overtraining and will not only nul-
lify the effect of the exercise but also reduce the sub-
ject’s motivation (Lehmann et al., 1993; Smith, 2003).
Any physical mobilization and training activity for a
human subject must therefore be highly sensitive to
the subject’s physical capabilities and actual physical
condition in order to be effective. This means that
a trainer or therapist that plans the workout must be
able to understand and predict with reasonable ac-
curacy how the subject’s cardiovascular system will
respond to a certain exercise strain, e.g., by measur-
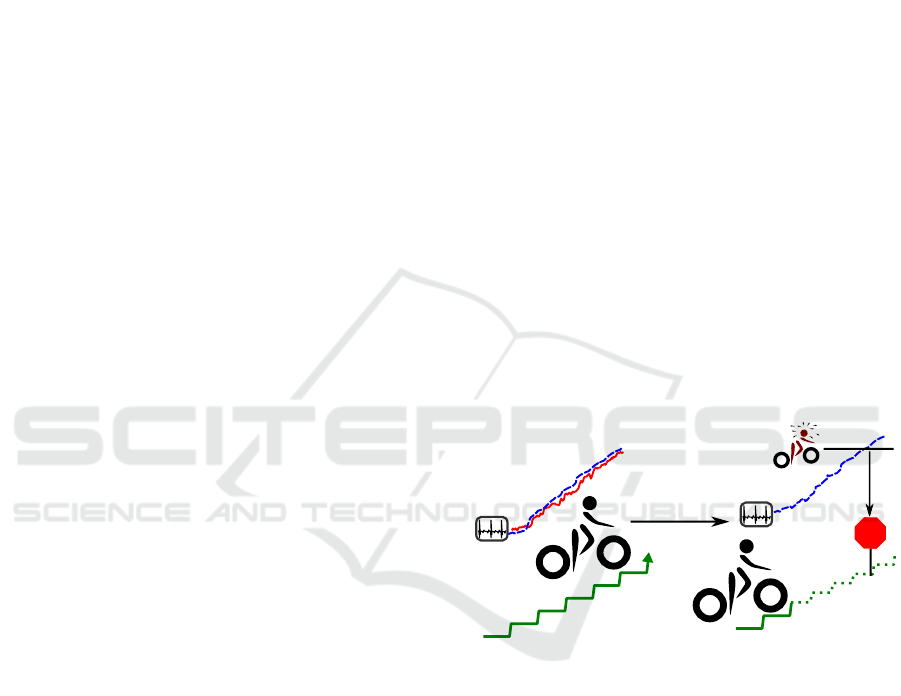
Fitting
Prediction
STOP
Model,
individual
parameter set
Figure 1: Overview of the fitting and prediction process. On
the left-hand side, a heart rate model is fitted according to
the measured heart rate of a subject and performed strain.
With these individualized parameters, the model can then
be used to predict heart rate for a given workload before the
work commences and prevent exhaustion (right-hand side).
ing and monitoring the subject’s heart rate (Borresen
and Lambert, 2008). Reliable prediction requires a
model that establishes a functional relation between
the strain to which the subject is exposed over time
and the response of the cardiovascular system, as il-
lustrated in Figure 1.
Suitable models depends on a preliminary fitting
process where model specific parameters are adapted
to the subject in order to fit a simulated heart rate
to the measured heart rate based on some performed
strain. After the fitting, the model can then be used
to predict heart rate for a whole training session. This
Ludwig, M., Grohganz, H. and Asteroth, A.
A Convolution Model for Heart Rate Prediction in Physical Exercise.
DOI: 10.5220/0006030901570164
In Proceedings of the 4th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2016), pages 157-164
ISBN: 978-989-758-205-9
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
157

prediction could be helpful in planning the training
beforehand since any crossing of the personal perfor-
mance limit can be predetermined.
However, these models are often mathematical
models with a number of parameters that can rarely
be explained physiologically. Furthermore, a large
number of parameters can lead to problems with com-
puting time, error handling, and prediction instability.
The paper presents a mathematical heart rate model
where all four parameters have a physiological mean-
ing. During the experiments, the number of parame-
ters could be reduced down to one degree of freedom,
leading to much more stability and a very fast compu-
tation.
The structure of the paper is as follows: In Sec-
tion 2, the process of heart rate prediction is explained
in general, followed by a brief overview of usual heart
rate prediction models. In this context, the new Con-
volution model is presented in Section 3. In Section 4,
data material and executed experiments are explained,
followed by the presentation, evaluation and discus-
sion of results. The paper is completed by a con-
clusion and an outline for future experiments in Sec-
tion 5.
2 HEART RATE PREDICTION
DURING EXERCISE
Usually, the human body does not adapt to strain im-
mediately. The reaction is delayed, so heart rate in-
creases after a certain time of physical activity, and re-
generation in relaxation is also delayed which results
in hysteresis. The adaption rate of these processes
depends greatly on the specific person, and modeling
requires individual adaptation. Each suitable model
should therefore have at least one parameter that can
account for this individual component.
In general, many heart rate models M can be con-
sidered as functions mapping all parameters
~
α re-
quired by the model, and a strain curve u to a pre-
diction of a heart rate curve y:
M : P × R
∗
−→ R
∗
,
where P is the parameter set, and both input (i.e.,
strain curve) as well as output (i.e., heart rate curve)
are real time series, denoted by R
∗
:=
S
n∈N
R
n
. The
data can be assumed as an equidistant, discrete time
series. The estimated heart rate at point of time t is
labeled by y(t) = M (
~
α,u), where
~
α ∈ P is the pa-
rameter setting and u = u
1
,...,u
t
∈ (R
+
)
∗
serves as
the model input. In the conducted experiments, u is
defined as a sequence of positive values and given
by the considered workload. An additional constraint
in computing y(t) is added: only elements u(s) with
s ≤ t are allowed to enable real-time applications. In
some models, the measured heart rate up to the actual
point in time serves as an additional model input.
Within the last ten years, a variety of models for
heart rate prediction have been discussed. Some typi-
cal mathematical concepts are systems of differential
equations or variants of a Hammerstein model. While
(Cheng et al., 2007) introduce a nonlinear state-space
model to predict the heart rate behavior of a subject
based on the running velocity on a treadmill, (Par-
adiso et al., 2013) use the same model to regulate the
heart rate using a cyclic ergometer. Both models in-
clude nonlinear components to simulate changes in
the organism due to long term exercise. The fuzzy
Takagi-Sugeno model by (Mohammad et al., 2011)
deals with 12 parameters and is commonly used for
optimizing physical activity for elderly non-trained
people. During cycling exercises it is used to con-
trol the power system which can regulate the amount
of strain and hereby control the heart rate. Further
model-based systems exist for both, running (Su et al.,
2007; Su et al., 2010; Koenig et al., 2009) and cycling
(Leitner et al., 2014; Le et al., 2008) on different train-
ing devices.
A linear time invariant (LTI) model from (Baig
et al., 2010) can be used for this topic as well, but
it is presented in literature explicitly for a single-step
prediction. This means, only the next heart beat is
predicted using preceding measurements of its spe-
cific workload. To use it for a whole session predic-
tion, the heart rate must be estimated iteratively and
a beforehand predicted heart rate must be used. The
original model and its adjustment have four parame-
ters to scale previously measured or predicted values
of heart rate and strain.
Even fitness trackers or smartphone apps support
their users with heart rate information and are usu-
ally able to inform the user about, e.g., an increasing
heart rate. Exemplary, (Sumida et al., 2013) presents
a method to estimate heart rate with a smartphone
based on walking speed and acceleration. Here as
well, heart rate is simulated on demand during the ex-
ercise.
So the most common applications for these mod-
els are automatic control systems, especially for
treadmills or cycle ergometers. During this kind of
exercise, a quick system response to actual heart rate
is necessary but in this case it is not necessary to sim-
ulate or predict a whole training session in advance.
Usually, only some seconds up to a few minutes are
predicted.
Nevertheless, planning a training as a whole in ad-
vance might be important when doing outdoor activ-
icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support
158

ities where the subject has to deal with the actual en-
vironmental setting. In this case, knowing the limit
beforehand is crucial if overtraining is to be avoided.
The workload can then be optimized for a planned
route, similar to the prediction of a velocity protocol
in running as presented in (Brzostowski et al., 2013).
The Convolution model presented here is able to pre-
dict a whole training session beforehand.
3 THE CONVOLUTION MODEL
APPROACH
For the related task of predicting a measure for fit-
ness in general, the Fitness-Fatigue model (Calvert
et al., 1976) has been widely used since its first de-
scription in the early seventies. This model works
with convolution to compute the actual prediction by
using not only the last input value but also all previ-
ous input values in decreasing intensity. This method
means that the shorter the time span between an in-
put value and the current point in time, the stronger
its influence on the computation of the currently com-
puted output value. Its great advantage is therefore a
weighted consideration of past strain with a slight ef-
fect on actual physiological response, performance in
general or heart rate in particular. Because of the de-
layed reaction of human body to any strain, a model
based on convolution seems to be promising for pre-
dicting the heart rate response to strain as well.
Here, elements from the estimated heart rate se-
quence y at time t follows:
y(t) = a
2
·
1
a
1
(u ∗ e
−•/a
1
)(t)
a
4
+ a
3
.
In contrast to the original Fitness-Fatigue model,
the proposed model uses four parameters to improve
adapting a strain value to a predicted heart rate. As
our experiments show, these parameters allow this ap-
proach to successfully predict a heart rate curve from
a strain curve. This parametrization is not simply a
mathematical trick; each of these parameters has a di-
rect physiological origin and meaning:
a
1
: memory parameter used for convolution. This pa-
rameter describes the effect of former strain on
actual heart rate, i.e., how much influence does
previous strain have.
a
2
: impact parameter used as a multiplicative fac-
tor. This parameter explains the impact of rising
strain on heart rate (e.g., proportional or dispro-
portional), i.e., it illustrates how strong the reac-
tion to strain becomes and how steeply heart rate
increases over time.
a
3
: level parameter used as an additive constant to lift
the predicted heart rate up to a suitable level. Ev-
ery subject has a specific resting heart rate, from
which heart rate under strain ascends.
a
4
: slope parameter used as exponent. This allows a
non-linear reaction of the heart rate to increasing
strain near the personal performance limit. Hence
this parameter can be used to refine the conceptu-
ally related impact parameter.
Our experiments show that the number of parame-
ters can be reduced. A linkage was found between the
memory and the impact parameter using a polynomial
of the second degree, a
1
= x
1
+ x
2
· a
2
+ x
3
· a
2
2
, with
suitable values for x
i
. Additionally, level and slope
parameter a
3
and a
4
could be predefined, so that the
arising model has only one degree of freedom left by
use of a
2
.
4 EXPERIMENTS
In this paper, the terms fitting and prediction (instead
of training set and test set following machine learning
phrases) are used. Nevertheless, fitting describes the
direct fit of parameters to given data, while prediction
makes use of these identified parameters without any
changes and applies them to different given data of
the same subject. A training in this context always
refers to physical exercise, and a test or protocol test
refers to standardized protocol exercise tests realized
by a cycle ergometer.
The data used was obtained by two male vol-
unteers doing a standardized test every two to four
weeks during an approximate seven month period —
a third one started later, so his total period was two
months. The sports of the three volunteers is cycling
and their tests were performed on the cycle ergome-
ter “Cyclus 2” (RBM elektronik-automation GmbH,
Germany). The protocols followed a step-size proto-
col: starting with 50 W, increased by 25 W every 3
minutes. The test protocol were examined until ter-
mination by exhaustion. 17 tests were collected alto-
gether.
In general, heart rate models are fitted to a vary-
ing number of training sessions for one and the same
person using Levenberg-Marquardt as suggested by
(Busso et al., 1997). The individualized model can
then be used to predict further sessions.
Session prediction is used for predicting a whole
time series, i.e., to predict the heart rate curve for a
given strain over a certain time, which usually is a
whole training session. Especially for planning such a
training session, it is important to assess the behavior
A Convolution Model for Heart Rate Prediction in Physical Exercise
159

of the heart rate to a given workload at a given time
(Ludwig et al., 2015).
For measuring the quality and accuracy, the root-
mean-square error (RMSE) is considered.
To prove the competitiveness of the Convolution
model in relation to existing heart rate models, a spe-
cial type of a cross-validation, namely past only cross-
validation, is invented and performed:
In real usage, only past training sessions will be
available for fitting. Unlike the common leave-one-
out cross-validation (Refaeilzadeh et al., 2009), only
training series up to one point of the past are used for
fitting and heart rate is predicted for all training ses-
sions in the future compared to the specified point in
time. We call this a past only cross-validation, which
is conducted for model comparison.
The Convolution model is evaluated here in com-
parison to the Takagi-Sugeno model (without feed-
back model control) and the adjusted LTI model,
which have showed best results in previous studies on
analytical non-machine learning models only (Lud-
wig et al., 2015). Additionally, a simple polynomial
model is used as baseline: As described in (Ludwig
et al., 2015) and (F
¨
uller et al., 2015), a polynomial
model is suitable as a baseline scaling function for
mapping any kind of input data (such as workload) to
any kind of output data (such as heart rate). We use
this baseline function to determine the fitting-quality
without any physiological modeling.
In earlier experiments, the Convolution model was
computed for some other data sets, e.g., in running,
where it could compete with published models. But
these data sets are not comparable for this investiga-
tion and therefore not considered in this paper.
While data sets are available for three persons with
4, 5, and 8 training sessions and a fitting was com-
puted over at least two training sessions, the number
of possible experiments results in 30, with respect to
the time line. Exemplary for the subject with 5 train-
ing sessions, the fitting on the first two training ses-
sions results in 3 data sets for prediction, fitting on
the first three training sessions results in 2 prediction
sets and fitting on all but the last training session leads
to another prediction experiment.
To analyze possible dependencies and restrictions,
several experiments are conducted for reducing the
amount of parameters in the Convolution model step
by step and dependent on the results.
4.1 Results
Competitiveness in General. To prove that the Con-
volution model can compete with other analytical
models, a past only cross-validation was performed
5
10
15
20
25
30
RMSE: prediction
error in bpm
Conv.
Conv.
(1 p.)
TS
LTI
Polyn.
Figure 2: Median RMSE and standard deviation for heart
rate prediction of two variations of the Convolution model,
Takagi-Sugeno model, LTI and Polynomial model. Outliers
are marked by crosses.
with 30 experiments as stated before. As a result, me-
dian RMSE and standard deviation are illustrated in
Figure 2 for two variations of the Convolution model,
and the remaining three literature models, Takagi-
Sugeno model, LTI and Polynomial model. Outliers
are marked with crosses. The Convolution model with
one parameter (Conv. (1p)) is explained explicitly
in the next paragraph. This comparison shows how
the Convolution model gains the smallest median er-
ror and smallest deviation. Furthermore, it achieves
some of the smallest errors overall. Beyond the Con-
volution model, Takagi-Sugeno yields better results
than LTI and the baseline Polynomial model, which
confirms results by (F
¨
uller et al., 2015). Neverthe-
less, it is conspicuous that the Takagi-Sugeno model
produces some large outliers with errors of above
25 bpm.
Parameter Reduction and Further Competitive-
ness. Multiple experiments were performed to reduce
the number of necessary parameters within the Con-
volution model. First of all, each single parameter
was set to an appropriate value while the remaining
three parameters were left arbitrary. Since some fit-
ting data appears to show that the current effect of us-
ing bygone strain seems to correlate with the impact
of the actual effects of strain, the slope parameter and
the impact parameter are bound together using a poly-
nomial – once with a degree of two, once with a de-
gree of five. The parameters for both were computed
using a fit curve to data MATLAB function. Addition-
ally, the setting of different experiments is combined.
Table 1 shows median, standard deviation and mean
value over all 30 experiments for the following nine
different settings. Here, experiment number 0 serves
as a baseline, where the past only cross-validation is
executed with all 4 parameters. Experiments 1 −8 are
described hereafter and lead to the following findings:
1. Exponential slope parameter is fixed to a
4
= 0.9:
icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support
160

Table 1: Median, standard deviation and mean in different
experiments for reducing the parameters of the Convolution
model.
No. exp. Median STD Mean
0 9.25 2.29 8.95
1 9.24 2.28 9.96
2 6.12 2.65 6.82
3 9.34 2.50 9.11
4 9.26 2.29 8.95
5 9.75 2.36 9.09
6 9.26 2.26 9.03
7 6.91 2.58 7.31
8 6.31 2.56 7.08
The exponential parameter can be set to 0.9 for
all subjects without increasing the median error.
Compared to the baseline experiment, this degree
of freedom does not appear to be necessary and
a
4
can be fixed without any substantial loss of ac-
curacy, except for some cases, as the higher mean
error implies.
2. The level parameter a
3
is set to a precalculated
resting heart rate for each subject individually:
The prediction seems to be much more stable if
the resting heart rate is fixed. This experiment
yields the smallest errors over all performed ex-
periments.
3. The memory parameter a
1
has been shown to
range between 1.8 and 2.2, so it is set to a
1
= 2:
Since the error is increased compared to the base-
line, this setting has to be improved by combina-
tion with other experiment settings or some differ-
ent approach.
4. The impact parameter a
2
has been shown to al-
ternate in an area around 0.002 and is therefore
set to this value, so a
2
= 0.002: The fixed impact
parameter yields similar results compared to the
baseline experiment. It seems to be that this de-
gree of freedom is not a necessity.
5. Since a further look at a
1
and a
2
indicates a de-
pendency, a linkage with a polynomial of the sec-
ond degree is examined: This linking results in
slightly higher errors compared to the baseline ex-
periment.
6. A dependency of memory parameter a
1
and im-
pact parameter a
2
with a polynomial of the fifth
degree is examined: Likewise, linking leads to
slightly higher errors compared to the baseline ex-
periment.
7. Settings of experiments 1 and 2 were combined,
so a
3
and a
4
are predefined as stated before: This
fixation results in errors not quite as small as in ex-
Dataset number
Method
5 10 15 20 25 30
TS
C
C1p
10
20
30
Figure 3: Heat map for the Takagi-Sugeno model (TS), the
Convolution model (C), and the Convolution model with
one parameter (C1p) for all 30 training session experiments.
Lower RMSE values are colored lighter, higher errors are
colored black.
periment 2, but it might be reasonably comparable
and is much better than the baseline experiment.
8. Settings of experiments 1, 2 and 5 combined, i.e.,
a
3
and a
4
are fixed and the polynomial of the sec-
ond degree is applied additionally: Compared to
experiment 7, an improvement with smaller errors
can be assessed. Except for fixing only the level
parameter, this experiment gains the smallest er-
rors.
Since the 8
th
experiment yields the best combina-
tion of small errors and few parameters, an enhanced
Convolution model is built that has only one degree
of freedom using the impact parameter a
2
, denoted
by α. Here, the additive level parameter is fixed to
the individual resting heart rate for each person, the
exponential slope parameter is set to 0.9, and the cor-
responding polynomial of the second degree is given
as a
1
= 2.06 + 158.8 · a
2
− 36750 · a
2
2
.
As stated before, Figure 2 illustrates prediction ac-
curacies for the considered literature models and the
two Convolution model approaches. The model la-
beled “Conv. (1p)” is the Convolution model from
experiment number 8. It can be seen that the me-
dian value for this one parameter Convolution model
is lowest, and even the best outliers with smallest er-
rors could be reached using this model approach. As
stated before, the four parameter Convolution model
can easily compete with Takagi-Sugeno model, as
shown by its lower median error and its lower error
regarding outliers.
Figure 3 compares errors for the three models for
every single training session. The color bar visual-
izes the RMSE while white is used for very small
errors and a black coloring is used for RMSE val-
ues of 25 bpm and above. In most of the 30 exper-
iments, smaller errors are generated by one of the
Convolution model approaches than by the Takagi-
Sugeno model. There are only few distinct identifi-
able counterexamples, such as the predicted data sets
with number 21 and 25. In contrast, some data set pre-
dictions show huge errors using the Takagi-Sugeno
model, while both Convolution model approaches can
A Convolution Model for Heart Rate Prediction in Physical Exercise
161

(a1)
0 5 10 15 20 25 30 35
50
100
150
200
Model: Takagi−Sugeno, Prediction
time [min]
heart rate [bpm]
0 5 10 15 20 25 30 35
0
100
200
300
power [watt]
measured heart rate
simulated heart rate
workload
(b1)
0 10 20 30 40
60
80
100
120
140
160
180
200
Model: Takagi−Sugeno, Prediction
time [min]
heart rate [bpm]
0 10 20 30 40
0
50
100
150
200
250
300
350
power [watt]
measured heart rate
simulated heart rate
workload
(a2)
0 5 10 15 20 25 30 35
50
100
150
200
Model: Convolution, Prediction
time [min]
heart rate [bpm]
0 5 10 15 20 25 30 35
0
100
200
300
power [watt]
measured heart rate
simulated heart rate
workload
(b2)
0 10 20 30 40
60
80
100
120
140
160
180
200
Model: Convolution, Prediction
time [min]
heart rate [bpm]
0 10 20 30 40
0
50
100
150
200
250
300
350
power [watt]
measured heart rate
simulated heart rate
workload
(a3)
0 5 10 15 20 25 30 35
50
100
150
200
Model: Convolution (1 parameter), Prediction
time [min]
heart rate [bpm]
0 5 10 15 20 25 30 35
0
100
200
300
power [watt]
measured heart rate
simulated heart rate
workload
(b3)
0 10 20 30 40
60
80
100
120
140
160
180
200
Model: Convolution (1 parameter), Prediction
time [min]
heart rate [bpm]
0 10 20 30 40
0
50
100
150
200
250
300
350
power [watt]
measured heart rate
simulated heart rate
workload
Figure 4: Three typical heart rate prediction examples for label (1) Takagi-Sugeno model, (2) Convolution model, (3) Convo-
lution model with one parameter. Sets a and b illustrated two different experiments, but the same predicted training session
each for all three models.
deal with the same prediction setting, with numbers 7,
9, 10, 22, 23 and 24 leading the way.
As an example, prediction 21 and 22 are visual-
ized in Figure 4, where strain is given in watt and
measured heart rate is plotted against predicted heart
rate for better comparison of model accuracies. Here,
each column shows figures computed with these three
models but using the same data set. The figures in
the first row are predictions executed from Takagi-
Sugeno, the second row illustrates predictions using
the four parameter Convolution model, and the last
row presents prediction results from the one param-
eter Convolution model approach. While set a illus-
trates an example (no. 22) where the error of Takagi-
Sugeno model is huge, in comparison to Convolution
model approaches, which can both deal with this set-
ting, set b illustrates an example (no. 21) where the
error of all three models is in a similar range, but
the one parameter Convolution model performs a bit
worse than the others.
icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support
162
4.2 Evaluation and Discussion
Comparison of the Convolution model against known
analytical models has shown that the Convolution
model yields a comparable or even better accuracy.
The Convolution model with one parameter seems to
bring further enhancement. The experiments show
that restrictions to the parameter area can actually im-
prove prediction accuracy. At least, it seems to be rea-
sonable to set the level parameter a
3
to an individual
resting heart rate value. Since the error in experiment
number 8 is only slightly higher than the error in ex-
periment number 2, the advantages of one parameter
instead of three should be considered: computation is
much faster, fitting is more stable and risks of local
minima are reduced because of the reduced complex-
ity. Since the linkage of a
1
and a
2
using a polyno-
mial of the fifth degree yields slightly smaller errors
compared to using the presented polynomial of the
second degree, this linkage combined with the other
two parameter specifications might be a valid option,
too. But since the average deviation is comparably
small, we decided to uphold the model as simple as
reasonable possible. Therefore we preferred this one
parameter model against the other possibilities.
Given, however, that the training zone for aero-
bic and anaerobic training are approximately 15 to
20 bpm wide (10% of the maximum heart rate), such
a prediction accuracy would not be sufficient. For a
detailed training plan, an accuracy of 5% of the max-
imum heart rate is desired—which can be achieved
using the Convolution model, which yields an error
of around 9 bpm (approach with four parameters) or
7 bpm (approach with one parameter).
In some cases, especially the first minutes of train-
ing show huge deviation between the measured and
the predicted heart rate values. By neglecting first
minutes of a prediction, the accuracy can be im-
proved. But since this is the case for all models, we ig-
nored this potential improvement and took these first
stages into account without exception.
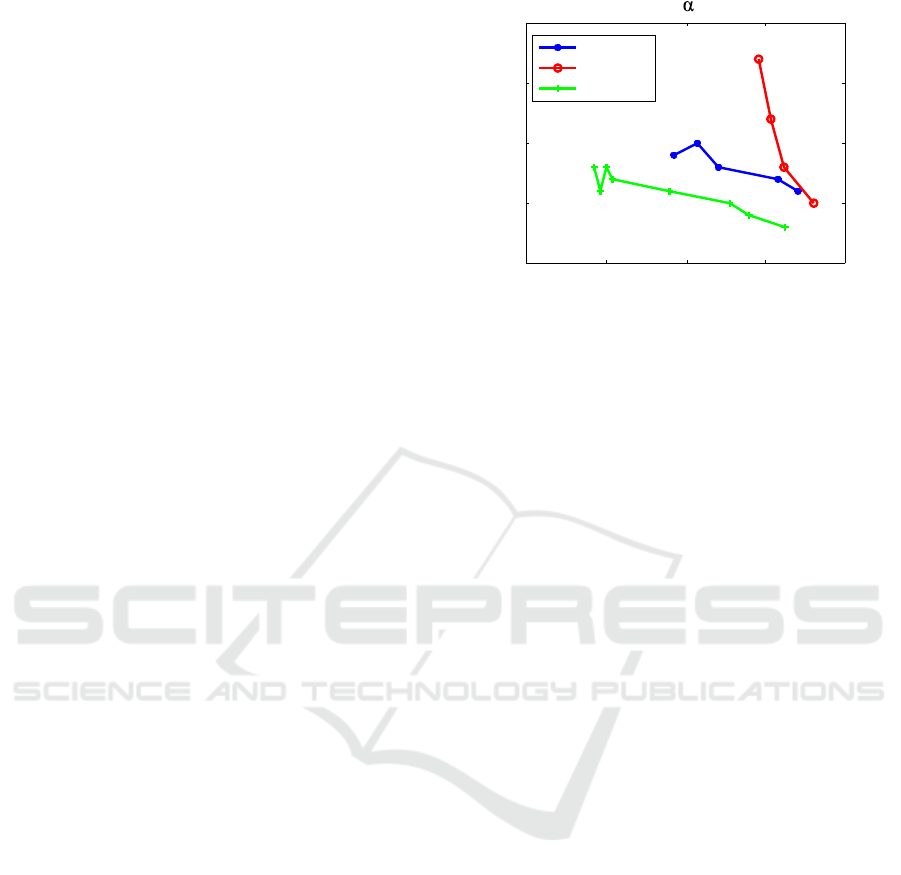
The Convolution model with only one parameter
not only yields good prediction results but also al-
lowed the changes in this remaining parameter for
each subject over time to be observed. In doing so,
the remaining parameter seems to correspond to the
fitness process itself. Figure 5 shows that—apart from
some peaks in the beginning for two subjects—the
value of this parameter decreases while the subject’s
training program continues. Since the subjects re-
ported that they had trained regularly during the ex-
periment period, the measured behavior might explain
their increased fitness. This assumption is based on a
few data only, hence the results will need to be vali-
Jul 2014 Oct 2014 Jan 2015 Apr 2015 Jul 2015
1.5
2
2.5
3
3.5
x 10
- 3
subject 1
subject 2
subject 3
Parameter over time
Figure 5: The remaining parameter over time for all three
subjects.
dated using more and larger data sets. At the moment,
the remaining parameter as fitness indicator can only
be taken as a conceptual idea that needs further inves-
tigation.
Regarding other than cycling sports, first experi-
ments in running were conducted: Using data of one
male athlete, six exercises performed on a treadmill
were performed. Predicting the heart rate in these
running data results in a median RMSE of 10.68 ±
6.37 bpm using the Takagi-Sugeno model and in a
median RMSE of 6.49 ± 2.35 bpm using the Convo-
lution model with four parameters, indicating that the
Convolution model is applicable to other sports than
cycling as well.
5 CONCLUSION AND FUTURE
WORK
This work presented a new model for heart rate pre-
diction. First of all, a comparison to other heart rate
models was performed. It has been shown that the
Convolution model can fairly compete with other an-
alytical models for predicting the heart rate a whole
training session in advance. Moreover, reducing the
number of arbitrary parameters leads to even smaller
errors and more stability. First experiments on the re-
maining parameter lead us to the assumption that this
parameter might indicate the actual fitness condition
of a subject.
An important next step will be to analyze the use-
fulness of this model in simulating outdoor workouts.
Many cyclists have their well-known training routes
or plan their ride in advance. Therefore, a previous
simulation based on strain according to GPS profiles
might be beneficial in training planning.
Additionally, the usefulness of the Convolution
model should be investigated for other sports compre-
A Convolution Model for Heart Rate Prediction in Physical Exercise
163

hensively, such as cycling on other protocols, cycling
without any protocol, running with or without proto-
col, and others.
Furthermore, experiments using a larger data set
with more subjects have to show if a correlation be-
tween changes in fitness and in the remaining Con-
volution model parameter α can be consistently ob-
served.
ACKNOWLEDGEMENT
This work was supported by a funding of the state
North Rhine-Westphalia, Germany.
REFERENCES
Achten, J. and Jeukendrup, A. E. (2003). Heart rate moni-
toring. Sports medicine, 33(7):517–538.
Baig, D.-e.-Z., Su, H., Cheng, T. M., Savkin, A. V., Su,
S. W., and Celler, B. G. (2010). Modeling of human
heart rate response during walking, cycling and row-
ing. In Engineering in Medicine and Biology Soci-
ety (EMBC), 2010 Annual International Conference
of the IEEE, pages 2553–2556. IEEE.
Borresen, J. and Lambert, M. I. (2008). Autonomic con-
trol of heart rate during and after exercise. Sports
medicine, 38(8):633–646.
Brzostowski, K., Drapala, J., and Swiatek, J. (2013). Data-
driven models for ehealth applications. International
Journal of Computer Science and Artificial Intelli-
gence, 3(1):1–9.
Busso, T., Denis, C., Bonnefoy, R., Geyssant, A., and La-
cour, J.-R. (1997). Modeling of adaptations to phys-
ical training by using a recursive least squares algo-
rithm. Journal of applied physiology, 82(5):1685–
1693.
Calvert, T. W., Banister, E. W., Savage, M. V., and Bach, T.
(1976). A systems model of the effects of training on
physical performance. IEEE Transactions on Systems,
Man and Cybernetics, 6(2):94–102.
Cheng, T. M., Savkin, A. V., Celler, B. G., Wang, L., and
Su, S. W. (2007). A nonlinear dynamic model for
heart rate response to treadmill walking exercise. In
29th Annual International Conference of the IEEE En-
gineering in Medicine and Biology Society (EMBS),
pages 2988–2991. IEEE.
F
¨
uller, M., Meenakshi Sundaram, A., Ludwig, M., Aster-
oth, A., and Prassler, E. (2015). Modeling and pre-
dicting the human heart rate during running exercise.
In Information and Communication Technologies for
Ageing Well and e-Health, volume 578, pages 106–
125. Springer International Publishing.
Koenig, A., Somaini, L., and Pulfer, M. (2009). Model-
based heart rate prediction during lokomat walking.
Engineering in Medicine and Biology Society, 2009.
EMBC 2009. Annual International Conference of the
IEEE.
Le, A., Jaitner, T., Tobias, F., and Litz, L. (2008). A dy-
namic heart rate prediction model for training opti-
mization in cycling (p83). In The Engineering of Sport
7, pages 425–433. Springer.
Lehmann, M., Foster, C., and Keul, J. (1993). Overtrain-
ing in endurance athletes: a brief review. Medicine &
Science in Sports & Exercise.
Leitner, T., Kirchsteiger, H., Trogmann, H., and del Re, L.
(2014). Model based control of human heart rate on
a bicycle ergometer. In Control Conference (ECC),
2014 European, pages 1516–1521. IEEE.
Ludwig, M., Sundaram, A. M., F
¨
uller, M., Asteroth, A.,
and Prassler, E. (2015). On modeling the cardiovascu-
lar system and predicting the human heart rate under
strain. In Proceedings of the 1st International Confer-
ence on Information and Communication Technolo-
gies for Ageing Well and e-Health (ICT4AgingWell),
pages 106 – 117.
Mohammad, S., Guerra, T. M., Grobois, J. M., and Hec-
quet, B. (2011). Heart rate control during cycling exer-
cise using takagi-sugeno models. In 18th IFAC World
Congress, Milano (Italy), pages 12783–12788.
Paradiso, M., Pietrosanti, S., Scalzi, S., Tomei, P., and Ver-
relli, C. M. (2013). Experimental heart rate regulation
in cycle-ergometer exercises. IEEE Transactions on
Biomedical Engineering, 60(1):135–139.
Refaeilzadeh, P., Tang, L., and Liu, H. (2009). Cross-
validation. In Encyclopedia of database systems,
pages 532–538. Springer.
Smith, L. L. (2003). Overtraining, excessive exercise, and
altered immunity. Sports Medicine, 33(5):347–364.
Su, S. W., Huang, S., Wang, L., Celler, B. G., Savkin, A. V.,
Guo, Y., and Cheng, T. M. (2010). Optimizing heart
rate regulation for safe exercise. Annals of biomedical
engineering, 38(3):758–768.
Su, S. W., Wang, L., Celler, B. G., Savkin, A. V., and Guo,
Y. (2007). Identification and control for heart rate reg-
ulation during treadmill exercise. IEEE Transactions
on Biomedical Engineering, 54(7):1238–1246.
Sumida, M., Mizumoto, T., and Yasumoto, K. (2013). Esti-
mating heart rate variation during walking with smart-
phone. In Proceedings of the 2013 ACM international
joint conference on Pervasive and ubiquitous comput-
ing, pages 245–254. ACM.
icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support
164
