
Multiobjective Adaptive Wind Driven Optimization
Zikri Bayraktar
1
and Muge Komurcu
2
1
Schlumberger-Doll Research Center, 1 Hampshire Street, Cambridge, U.S.A.
2
Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, U.S.A.
Keywords: Multiobjective Adaptive Wind Driven Optimization, Covariance Matrix Adaptation Evolutionary Strategy,
Numerical Optimization, Wind Driven Optimization, WDO, AWDO, MO-AWDO, Pareto, Nondominated
Sorting.
Abstract: In this work, we introduce a new nature-inspired multiobjective numerical optimization algorithm where
Pareto dominance is incorporated into Adaptive Wind Driven Optimization for handling multiobjective
optimization problems and named as Multiobjective Adaptive Wind Driven Optimization (MO-AWDO)
method. This new approach utilizes an external repository of air parcels to record the non-dominated Pareto-
fronts found at each iteration via the fast non-dominated sorting algorithm, which are then utilized in the
velocity update equation of the AWDO for the next iteration. The performance of the MO-AWDO is tested
on five different numerical test functions with two objectives and results indicate that the MO-AWDO offers
a very competitive approach compared to well-known methods in the published literature even performing
better than NSGA-II for ZDT4 test function.
1 INTRODUCTION
Evolutionary algorithms (EA) and nature-inspired
optimization methods like Genetic Algorithms (GA),
Particle Swarm Optimization (PSO), Ant Colony
Optimization (ACO), etc. were successfully utilized
since their introduction to the literature as single
objective optimization algorithms. To handle multi-
objective functions, variants of these algorithms were
proposed and they were shown to be very effective
(Deb, 2002; Zitzler, 2000; Coello, 2004; Coello,
2007). The primary goal of these multi-objective
optimization algorithms is to identify the Pareto-
optimal front solutions as diversely as possible. To
achieve this, different methods were proposed such as
archiving the solutions over iterations, preserving
elitism, implementing crowding distance, utilizing
adaptive grids, introducing new operators into
existing methods or hybridization of multiple EAs
and many others.
In this work, we are introducing a new population
based multi-objective optimization method, where
Pareto dominance is incorporated into the Adaptive
Wind Driven Optimization. At each iteration Pareto-
fronts are identified using the fast non-dominated
sorting algorithm and stored in an external
population. At each iteration, each particle utilizes
one of the randomly selected members of the external
repository to update its velocity vector and then the
position of the particle is updated accordingly. Such
an external population provides a diverse set of
solutions on the non-dominated Pareto-front that the
rest of the population can utilize to follow and to
update their location on the search domain.
The rest of this paper is structured as follows. The
second section introduces the Wind Driven
Optimization (WDO) (Bayraktar, 2010) algorithm
and discusses the update equations. The third section
describes the Adaptive WDO (AWDO) technique
(Bayraktar, 2015) and the fourth section describes the
newly introduced multiobjective AWDO algorithm
(MO-AWDO) in detail. The fifth section
demonstrates the efficient implementation of the MO-
AWDO on five numerical benchmark functions.
Conclusions and recommendations for future work
are presented in the last two sections.
2 WIND DRIVEN
OPTIMIZATION
The Wind Driven Optimization (WDO) algorithm
was first introduced in (Bayraktar, 2010) as an
efficient population-based and nature-inspired global
Bayraktar, Z. and Komurcu, M.
Multiobjective Adaptive Wind Driven Optimization.
DOI: 10.5220/0006031801150120
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 115-120
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
115

optimization algorithm. The WDO is inspired by the
motion of wind in atmosphere and is derived from the
atmospheric dynamics equations in hydrostatic
equilibrium (Bayraktar, 2013). The movement of
wind, or in other words, the movement of an
infinitesimally small air parcel in wind, can be
explained via Euler description, where one can derive
the position and velocity of the air parcel from various
forces that are exerted on the air parcel by utilizing
Newton’s second law of motion. While the WDO
algorithm tries to stay true to the real physical
equations, certain assumptions and simplifications
are made to achieve an efficient numerical
optimization algorithm mapped to a search space with
N-dimensions. Details of the WDO can be found in
(Bayraktar, 2013), hence we will only briefly describe
the position and velocity update equations below:
(1)
where u
n
is the updated velocity for next iteration
and, u
c
is the velocity at the current iteration. The x
c
term represents the current position of the air parcel
in the search space and x
max
represents the best
position found so far during the search. u
c
otherd
is
velocity at another dimension affecting the velocity
update in dimension, d. Air parcels are ranked by their
pressure value, i.e. cost function value, among
themselves, where i represents the rank of the air
parcels within the population. Let us call this ranking
as the population ranking. Low-pressure value, i.e.
low cost, indicates a good solution and high-pressure
value indicates a bad solution. Other terms in
equation 1 are the inherent coefficients of the
classical WDO algorithm and are preset by the user,
which allow users to tune them if needed (Bayraktar,
2013). These terms are friction coefficient, α,
gravitational constant, g, Coriolis constant, c, to
represent the rotation of the Earth, universal gas
constant, R, and temperature, T, which can be
combined into single coefficient term of RT. Air
parcels’ position is bounded within the range of [-1,
1] before the position vector is linearly scaled to the
upper and lower bounds of the optimization problem.
Updated velocity is limited to a value of V
max
= + |0.5|,
if it becomes larger than the V
max
.
After the new velocity, u
n
, is computed the position
is updated by the position update equations:
(2)
where x
n
is the updated position of an air parcel, that
is the sum of the current position vector, x
c
, and
updated velocity, u
n
, with the assumption that time
step is set to unity, Δt = 1. Using equations 1 and 2,
the position of the air parcel changes at each iteration
on the search domain. The WDO algorithm
terminates either when a predetermined level of
pressure value is achieved or when the maximum
number of iterations is exhausted.
3 ADAPTIVE WIND DRIVEN
OPTIMIZATION
The inherent terms of the velocity update equations in
the classical WDO, namely, α, g, c, and RT, must be
determined by the user, which provides the flexibility
to tune the algorithm performance per optimization
problem at hand. A numerical study is conducted in
(Bayraktar, 2013) to recommend the best value
ranges for these terms. However, such flexibility
brings a challenge to novice users and selecting the
most appropriate values for the inherent terms
becomes a burden. To eliminate algorithms
dependency on user input, Adaptive Wind Driven
Optimization (AWDO) algorithm was introduced in
(Bayraktar, 2015).
The AWDO utilizes an existing optimization
algorithm, namely, Covariance Matrix Adaptation
Evolutionary Strategy (CMAES) as a block-box
solver to select the inherent terms. At each iteration,
pressure values are calculated for each parcel by the
WDO and these values are passed on to CMAES as
cost values so that CMAES can choose a new set of
values for the inherent terms, α, g, c, and RT, based
on the cost from the WDO. This creates a four-
dimensional optimization problem for CMAES with
the same population size as the WDO, and CMAES
does not make any cost function calls since it utilizes
the pressure values computed by the WDO. Because
the inherent terms are chosen adaptively by CMAES,
there is no need to preset them at initialization
removing the burden on user and creating a parameter
free adaptive wind driven optimization method.
4 MULTIOBJECTIVE
ADAPTIVE WIND DRIVEN
OPTIMIZATION ALGORITHM
The cost function of WDO (or AWDO) was
originally designed for single objectives while one
can also optimize multiobjective problems through
implementing a weighted sum cost function
(Komurcu, 2011; Bayraktar 2011). However, instead
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
116
of a weighted sum of multiple objectives, one can aim
to find the Pareto-optimal solutions, which are the
best solutions to the problem but are not better than
each other. Multiobjective evolutionary algorithms
have shown to be effective in finding multiple Pareto-
optimal solutions in one single run since they utilize
large populations (Deb, 2001; Fonseca, 1993; Zitzler,
1998). Similarly, we introduce a new population-
based multiobjective optimization method for
AWDO utilizing fast-nondominated sorting method
(Deb, 2002) to identify Pareto-front solutions and an
external population to archive the non-dominated
fronts. We will refer to this method as Multiobjective
Adaptive Wind Driven Optimization (MO-AWDO).
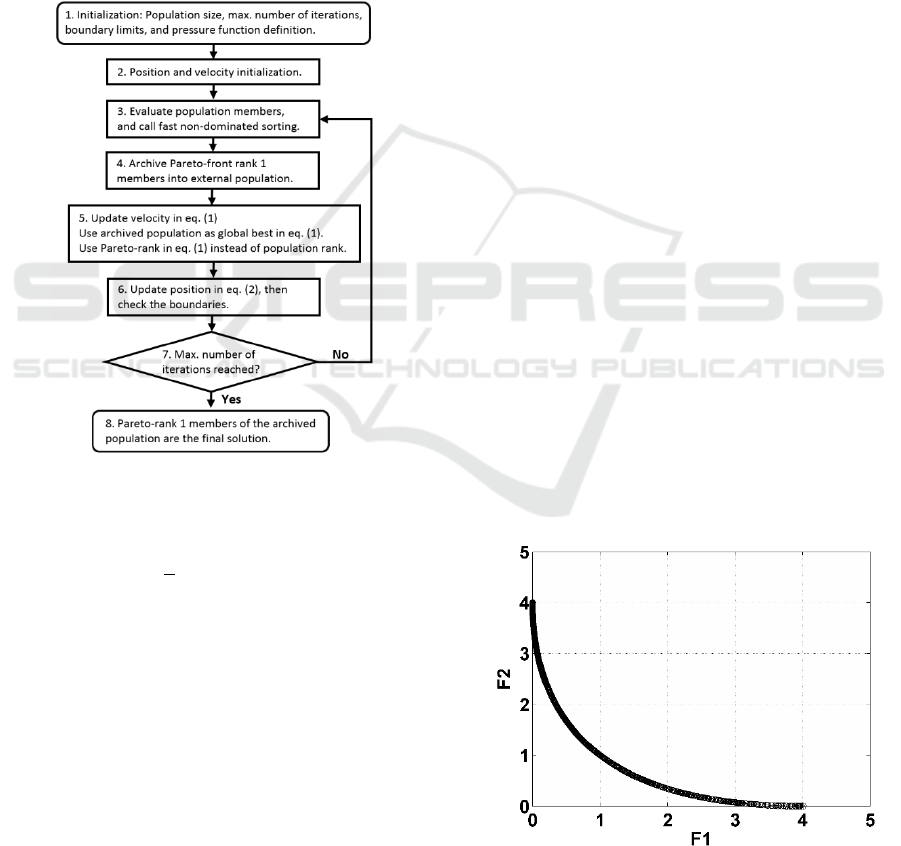
Figure 1: Flowchart of the Multiobjective Adaptive Wind
Driven Optimization Algorithm (MO-AWDO).
In MO-AWDO method, the maximum velocity is
bounded by V
max
= + |0.5| but chosen adaptively by
the AWDO in addition to the four inherent terms
mentioned in the previous section. The MO-AWDO
flowchart is shown in Figure 1, where the algorithm
starts with randomly initializing the position and
velocity vectors. Then, at each iteration, pressure
functions are evaluated for each member in the
population. Based on the two cost functions per
multiobjective problem, the fast non-dominated
sorting algorithm determines the Pareto-fronts among
the current population members, i.e. each member is
assigned a Pareto-front number based on the sorting.
This Pareto-front rank information for each parcel is
used in equation 1 in place of i. At each iteration,
members with Pareto-front rank one are added to the
external population archive and then the archived
population also goes through the fast non-dominated
sorting. The members of the archived population with
Pareto-front rank one then become the ones selected
for the x
max
in equation 1, simply because they
represent the global best solutions found so far with
the non-dominated Pareto-fronts. Once velocity is
updated with the modifications described above, then
the position is updated as shown in equation 2. Next,
boundaries are checked along with the termination
criterion. If the termination criterion is met, the
algorithm terminates with results of Pareto-front rank
one of the archived population as final best results.
5 NUMERICAL RESULTS
In this section, we describe and utilize five test
functions to demonstrate the performance of the MO-
AWDO algorithm. These standard numerical
functions are selected from published literature (Deb,
2002; Zitzler, 2000; Coello, 2004) and many others
can be found in the literature. We picked five
representative functions with different dimensions
and properties to be tested here. All of these five
problems have two objective functions and only
Kita’s function comes with constraints. All cases
were run with a population size of 100 air parcels for
maximum number of 250 iterations totaling a
maximum of 25,000 function evaluations as in (Deb,
2002) to compare.
5.1 Schaffer’s Function
The Schaffer’s function is a convex problem and it is
the simplest out of all problems presented here, such
that the number of decision variables is only n=1. The
variable bounds are set to be within [-10
3
, 10
3
], where
Figure 2: Pareto front produced by MO-AWDO for the
Schaffer’s Function shown with circles. The true Pareto
front is shown as a continuous line.
Multiobjective Adaptive Wind Driven Optimization
117

the optimal solutions are within the range of x
2]. The two cost
function are:
F
1
(
x
)=x
2
, and
F
2
(
x
)=(x-2)
2
(3)
Figure 2 shows the results of the MO-AWDO
from the archived Pareto population at the end of the
maximum number of iterations. The true Pareto front
for the Schaffer’s function is illustrated with a
continuous line on the same figure as well.
5.2 Kita’s Function
The Kita’s function is a constrained multi-objective
function with number of decision variables of n=2.
The variable bounds are limited to be within [0, 7].
The two cost functions to be maximized are shown
below along with constraints:
F
1
(
x
1
, x
2
1
2
+x
2
and
F
2
(
x
1
, x
2
) = (x
1
/2) +x
2
+1.
(4)
subject to
Figure 3: Pareto front produced by MO-AWDO for the
Kita’s Function shown with circles. The true Pareto front is
shown as a continuous line.
Since MO-AWDO is designed to minimize the
pressure (i.e. cost function), we simply took the
negative of the pressure for the Kita’s function to be
minimized. Constraints are handled at pressure
computation so that if any of the three constraints are
violated, the pressure is penalized by setting it to be a
very large value, i.e. 1e-5. Such high pressure
encourages the particles to stay away from the
constraints and converge on the Pareto front.
Figure 3 shows the results of the MO-AWDO
from the archived Pareto population at the end of the
last iteration. The true Pareto front for the Kita’s
function is illustrated with a continuous line on the
same figure along with the results.
5.3 Kursawe’s Function
The Kursawe’s function is a nonconvex multi-
objective function with number of decision variables
of n=3. The variable bounds are set to be within
[-5, 5]. The two cost functions to be minimized are:
(5)
Figure 4 shows the results of the MO-AWDO
from the archived Pareto population at the end of the
maximum number of iterations. The true Pareto front
for the Kursawe’s function is illustrated with a
continuous line on the same figure along with the
results. The MO-AWDO converges to the true Pareto
front finding diverse solutions including the extreme
points.
Figures 4: Pareto front produced by MO-AWDO for the
Kursawe’s Function shown with circles. The true Pareto
front is shown as a continuous line.
5.4 ZDT1 Function
The ZDT1 function is a convex multi-objective
function with number of decision variables of n=30.
The variables are bounded within [0, 1] and the two
cost functions to be minimized are:
(6)
where,
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
118
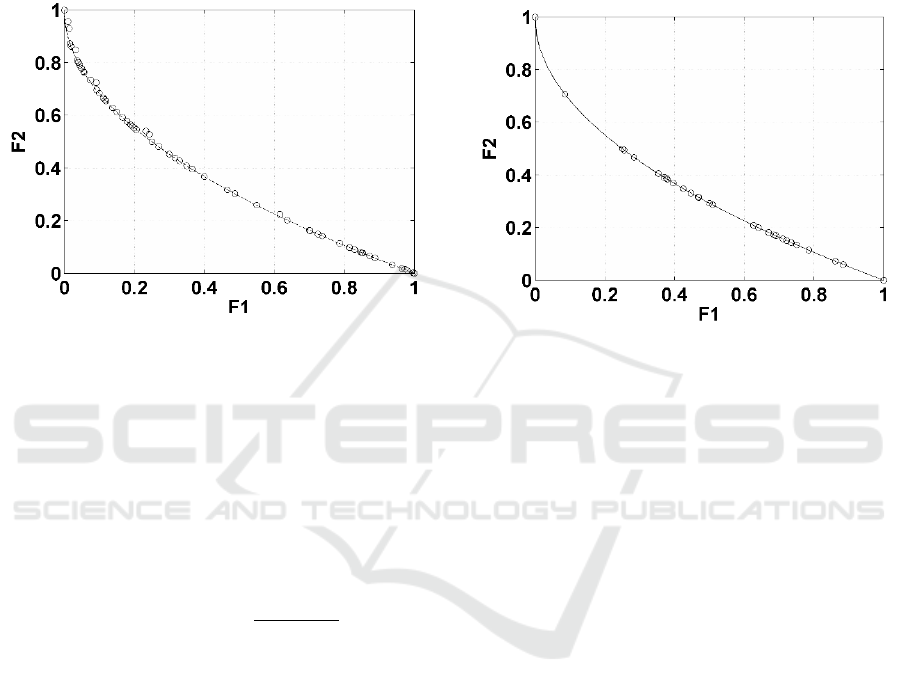
Figure 5 shows the results of the MO-AWDO
from the archived Pareto population at the end of the
maximum number of iterations. The true Pareto front
for the ZDT1 function is illustrated with a continuous
line on the same figure along with the results. The
MO-AWDO converges to the true Pareto front
finding diverse solutions including the extreme
points.
Figure 5: Pareto front produced by MO-AWDO for the
ZDT1 Function shown with circles. The true Pareto front is
shown as a continuous line.
5.5 ZDT4 Function
The ZDT4 function is a nonconvex multi-objective
function with number of decision variables of n=10.
The variable bounds are x
1
[0, 1], and x
i
-5, 5] for
The two cost functions to be minimized are:
(7)
where,
The ZDT4 function has 21
9
different local Pareto-
optimal fronts (Zitzler, 2000), and only one of them
is the global Pareto-optimal front. This challenging
problem has been studied in (Deb, 2002) and they
demonstrated that NSGA-II, and other MO-
algorithms compared in their paper needed a
population of 500 members ran for 250 iterations to
be able find the global Pareto-optimal front. On the
other hand, MO-AWDO can easily find the global
Pareto-optimal front with a population of 100 air
parcels within 100 iterations as shown in Figure 6,
providing 10x speed up in convergence.
Figure 6 shows the results of the MO-AWDO
from the archived Pareto population at the end of the
maximum of 100 iterations using only 100 members.
The true global Pareto-optimal front for the ZDT4
function is shown with a continuous line on the same
figure. The MO-AWDO converges to the true Pareto
front finding diverse solutions including the extreme
points.
Figure 6: Pareto front produced by MO-AWDO for the
ZDT4 Function shown with circles. The true global Pareto-
optimal front is shown as a continuous line.
6 CONCLUSIONS
In this work, we introduced the Multiobjective
Adaptive Wind Driven Optimization (MO-AWDO)
algorithm and successfully demonstrated its efficient
performance on five different numerical multi-
objective benchmark functions with different
dimensions and properties from published literature.
The MO-AWDO combines the fast non-dominated
sorting method with the Adaptive Wind Driven
Optimization to identify the Pareto-fronts at each
iteration and archives them in an external population.
At each iteration, randomly selected archived non-
dominated Pareto-optimal solutions are utilized as the
global best solutions in the velocity update equation
of the AWDO, providing elitism while preserving
diverse non-dominated Pareto-fronts. Successful
demonstration of the MO-AWDO shows that it can
outperform well-known multi-objective algorithms
like NSGA-II on difficult problems like ZDT4.
7 FUTURE WORK
As future work, we aim to improve how the MO-
AWDO handles the archived population in terms of
size and diversity so that it can record the most
Multiobjective Adaptive Wind Driven Optimization
119

diverse Pareto-fronts with minimum number of
members reducing memory requirements as iterations
progresses. Also, extension of MO-AWDO to handle
many-objective functions are also planned as future
work.
REFERENCES
Deb, K., Pratap A., Agarwal, S., Meyarivan, T., 2002. A
fast and elitist multiobjective genetic algorithm:
NSGA-II. In IEEE Transactions on Evolutionary
Computation.
Zitzler, E., Deb, K., Thiele, L., 2000. Comparison of
multiobjective evolutionary algorithms: emprical
results. Evolutionary Computation.
Coello, C. A. C., Pulido, G. T., Lechuga M. S., 2004.
Handling multiple objectives with particle swarm
optimization. IEEE Transactions on Evolutionary
Computation.
Coello, C. A. C., Lamont, G. B., Van Veldhuizen, D. A.,
2007. Evolutionary Algorithm for Solving Multi-
Objective Problems. Springer, 2
nd
Edition.
Bayraktar, Z., Komurcu, M., Werner, D. H., 2010, Wind
driven optimization (WDO): a novel nature-inspired
optimization algorithm and its application to
electromagnetics. IEEE International Symposium on
Antennas and Propagation and USNC/URSI National
Radio Science Meeting.
Bayraktar, Z., Komurcu, M., 2015. Adaptive wind driven
optimization. 9th EAI International Conference on Bio-
Inspired Information and Communications
Technologies.
Bayraktar, Z., Komurcu, M., Bossard, J. A., Werner, D. H.,
2013. The wind driven optimization technique and its
application in electromagnetics. IEEE Transactions on
Antennas and Propagation.
Bayraktar, Z., Komurcu, M., Jiang, Z., Werner, D. H.,
Werner, P. L., 2011. Stub-loaded inverted-F antenna
synthesis via wind driven optimization. IEEE
International Symposium on Antennas and Propagation
and USNC/URSI National Radio Science Meeting.
Bayraktar, Z., Turpin, J. P., Werner, D. H., 2011. Nature-
inspired optimization of high-impedance metasurfaces
with ultra-small interwoven unit cells. IEEE Antennas
and Wireless Propagation Letters.
Deb, K., 2001. Multiobjective Optimization Using
Evolutionary Algorithms. Wiley. Chichester U.K.
Fonseca, C. M., Flemming, P. J., 1993. Genetic algorithm
for multiobjective optimization: Formulation,
discussion and generalization. Fifth International
Conference on Genetic Algorithms.
Zitzler, E., Thiele, L., 1998. Multiobjective optimization
using evolutionary algorithms-A comparative case
study. Springer-Verlag, Berlin.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
120
