Enhanced Genetic Algorithm for Mobile Robot Path Planning in

Static and Dynamic Environment

Hanan Alsouly and Hachemi Bennaceur

Computer Science Department, Al-lmam Muhammad Ibn Saud Islamic University, Riyadh, Saudi Arabia

Keywords: Genetic Algorithm, Path Planning, Mobile Robot, Dynamic Environment, Static Environment.

Abstract: Path planning is an important component for a mobile robot to be able to do its job in different types of

environments. Furthermore, determining the safest and shortest path from the start location to a desired

destination, intelligently and in quickly, is a major challenge, especially in a dynamic environment.

Therefore, various optimisation methods are recommended to solve the problem, one of these being a

genetic algorithm (GA). This paper investigates the capabilities of GA for solving the path planning

problem for mobile robots in static and dynamic environments. First, it studies the different GA approaches.

Then, it carefully designs a new GA with intelligent crossover to optimise the search process in static and

dynamic environments. It also conducts a comprehensive statistical evaluation of the proposed GA approach

in terms of solution quality and execution time, comparing it against the well-known A* algorithm and

MGA in a static scenario, and against the Improved GA in a dynamic scenario. The simulation results show

that the proposed GA is able to find an optimal or near optimal solution with fast execution time compared

to the three other algorithms, especially in large problems.

1 INTRODUCTION

The robotics field has received a great deal of

attention from many people beside those in research

and industrial communities (Elshamli et al., 2004).

The wide variety of robotics applications is a natural

motivator for people to study this area and

contribute to it. Building sophisticated and

intelligent robots that can change the world is the

aim of everyone working in the field. The building

of intelligent robots began with basic intelligence,

models which could only move around and perform

a small set of tasks. Today, these robots outperform

humans in various kinds of tasks in terms of

efficiency and accuracy (Tiwari et al., 2012).

However, there remain several challenges to

building a complete intelligent robot. One of these

challenges is intelligently determining its fastest and

safest route to its destination. This is what is known

as the path planning problem (Elshamli et al., 2004).

The path planning problem addresses two types of

environment, static and dynamic (Miao, 2009). The

environment is called static when its information

cannot change during the robot planning and

navigation. On other hand, if the environment does

change while the robot is deliberating, then it is

called dynamic environment (Russell and Norvig,

2002). The changes may occur at the goal position,

obstacle location, or entering a new obstacle (Tiwari

et al., 2012). Path planning is an important

component for a mobile robot to be able to perform

assigned tasks in different types of environments.

The robot path planning problem is not an easy task

to solve because it has a number of issues that may

affect the efficiency of the path planning algorithm

(Tiwari et al., 2012; Chaari et al., 2012):

completeness, computational time, optimality of the

path, the path smoothness and energy consumption.

In this paper, we would like to deal with the

issue of how these robots might intelligently plan

their path in a static and dynamic environment by

using genetic algorithm. We chose to study this

problem because the current solutions suffer from

several drawbacks, among them high computation

expense, inflexibility in responding to changes in the

environment or to different optimisation goals.

Genetic algorithm was chosen because its efficiency

has been proven in many optimisation and static

path planning problems. In this paper, we study the

use of genetic algorithm in that problem.

Furthermore, we suggest a new algorithm that not

only focus on the optimality of the path but also

Alsouly, H. and Bennaceur, H.

Enhanced Genetic Algorithm for Mobile Robot Path Planning in Static and Dynamic Environment.

DOI: 10.5220/0006033401210131

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 121-131

ISBN: 978-989-758-201-1

121

reduce the real-time execution for large problems, as

this is a critical criterion in mobile robots path

planning. The new algorithm is enhanced by

designing a new intelligent crossover and a set of

mutations. In addition, we test the new algorithm

and conduct a comparison study between some of

existing solutions.

The remaining parts of this paper are organised

as follows: section 2 reviews related works. Section

3 introduces our algorithm and explains its

components, while section 4 presents a comparative

study between the algorithms, evaluates

performance, reports results and discusses them.

Finally, section 5 concludes with a summary of

contributions and makes suggestions for future

research work.

2 RELATED WORK

Genetic algorithm (GA) is one of the heuristic

search algorithms. The heuristic search algorithms

do not guarantee to find a solution, but when they

do, they do it so much faster than classic search

algorithms (Masehian and Sedighizadeh, 2007). GA

proposed in 1975 by John Holland at the University

of Michigan. It is used to generate useful solutions

to optimisation, search problems and machine

learning (Hussein et al., 2012). GA belongs to the

evolutionary algorithms, which generate solutions

by using inspired techniques from natural evolution,

such as inheritance, mutation, selection, and

crossover (Reshamwala and Vinchurkar, 2013). Due

to the robustness and effectiveness of GA in several

optimisation problems, various studies have been

done to use GA in robot path planning problems.

(Elshamli et al., 2004) proposed a GA planner that

can solve the robot path planning problem in a

dynamic environment that may presents new

obstacles. To model the search space, they used

polygonal representation. The proposed algorithm

uses a variable length of chromosome and generates

random feasible initial population. For the crossover,

the algorithm uses a random one-point crossover,

whereas the mutation operation changes a node

value randomly. To solve the dynamic aspect, the

authors used four techniques, the best being Memory

and Random Immigrants. In addition, this algorithm

takes into consideration path smoothness. It has

many operations besides the basic ones, such as

Repair, Shortcut and Smooth operators.

Consequently, it takes a long time to find an optimal

or near optimal path. Therefore, (Koryakovskiy et

al., 2009) suggested eliminating the use of Repair,

Shortcut and Smooth operators, and using 3-point

interpolation by Bezier curves instead to generate

smooth paths in the initial population. The suggested

method reduces the time in finding the target path.

However, the proposed method works only in a

well-known environment with static and new

obstacles.

On other hand, (Mahjoubi et al., 2006) also used

polygonal representation for the obstacles as a

search space to make the search faster. To evaluate

the individual, the algorithm uses a fitness function

that depends on the path’s total length and penalty

factor for collision parts. This algorithm uses three

types of mutation operators: delete, insert and

change node mutation operators. This method

supports well-known environment with moving

obstacle only. (Zou et al., 2012) also suggested

improving the environment modelling by using a

grid size-adjustment technique, which can zoom-in

and zoom-out from the grid map to provide an

accurate and fast search map. Furthermore, the

authors used a nonlinear fitness function to improve

the convergence and operational efficiency of the

algorithm. In addition, (Shi and Cui, 2010) have

used a new modelling method to speed up the

execution of searching. The new method projects the

two dimensional data to one dimensional data,

which helps to reduce the size of the search space

and the size of the chromosomes. Their fitness

function depends on the path length, path security

and path smoothness. The suggested method can be

used to solve the problem in an unknown dynamic

environment.

(Zhao and Gu, 2013) devised a different idea to

solve the problem. They suggested using a two-layer

GA mechanism. In this method, each layer has

different fitness functions. The first layer is

responsible for static obstacles avoidance, while the

second layer is responsible for dynamic obstacles

avoidance. Beside of that, a new operation known as

Delete operation is used to delete the redundant bits

in the individual and the bits between them. (Yun et

al., 2011) provide an algorithm that avoids acute

obstacles in the dynamic environment. The provided

solution prevents the robot from being trapped in an

acute ‘U’ or ‘V’ shaped obstacle. In addition, this

solution handles static, dynamic and new obstacles.

When new obstacles are detected, the algorithm re-

plans the path from the current position.

Furthermore, (Zhu et al., 2015) invented a helpful

new idea for global path planning and well-known

environment. In their solution, the path is

represented as a sequence of straight-line segments,

which connect the obstacles’ vertices that are

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

122

bypassed by the path. The method limits the search

space in the space of obstacles. Furthermore, after

each crossover and mutation, the path refinement

function is applied to the child chromosomes to

correct the collide parts and enhance the quality of

the paths.

This paper in addition to proposing a new GA

and using a new environment representation method,

it is different from these works in that it evaluates

the performance of the GA on semi-large-size maps

starting from 100*100 up to 500*500.

3 DYNAMIC GENETIC

ALGORITHM

The aim of our paper is to find a practical approach

to solve a path planning problem in a dynamic

environment by using GA. To achieve that, we have

designed a new GA planner that depends on a grid-

based map to represent the environment with

polygonal representation for the obstacles. The

following subsections describes the environment

representation and the new planner.

3.1 Environment Representation

In our work, we have selected a grid-based map to

represent the environment with polygonal

representation for the obstacles. By this means, we

could cover the environment completely and update

it easily. Beside of that, polygonal representation

helps to reduce the use of the memory, to produce

smoother paths, and we can use efficient and simple

geometric algorithms (O'Rourke, 1998) (Sunday,

2012) to check the feasibility of the paths and reduce

the computational complexity.

3.1.1 Grid Representation

The used grid map represents the environment in a

2D way by dividing it into equal square cells, as

shown in figure 1. Each cell has a coordinate

number. We assume the environment is rectangular

and its boundary is static. In addition, the mobile

robot can move from one cell to another free cell in

a straight line if the line between them does not

collide with any obstacle.

3.1.2 Obstacles Representation

We assume the obstacles are polygons, and they are

represented by the ordered list of its vertices. Each

vertex represents cell coordination on the grid map.

Obstacle segments are constructed by connecting

these vertices, starting with the first vertex and

ending with connecting the last vertex to the first

one. For example, the first obstacle in figure 1 is

represented as [(1,4), (4,4), (4,6), (2,6)].

3.1.3 Solution Encoding

The paths encoding is one of the most important

issues for GA, because the encoding may affect GA

performance and memory performance. Since the

paths may have variable lengths and line segments,

we have chose to use a variable size solution

encoding. The solution is represented by a

chromosome. The chromosome consists of a

sequence of ordered positions that represent the line

segments, starting from the initial point and ending

at the goal point. Euclidean distance is used to count

the path cost. This method has been used to reduce

the size of the memory and to help making smooth

paths. Figure 1 shows an example of a feasible path.

The path is encoded as [(2,1), (9,1), (11,3)], the

initial cell is (2,1), the goal cell is (11,3) and the cost

of the path is=



29



11





911



13



= 9.83.

Figure 1: Grid representation.

3.2 Genetic Algorithm Designing

To design efficient GA, we need to take care in

designing all of its parameters and operators,

because they affect the performance of a GA and

they are interrelated. In the following subsections,

we will describe how we designed these important

parameters and operators.

3.2.1 Initial Population

Generating an initial population is the first step in

the functioning of a GA. Each member of this

population encodes a possible solution to the

problem or may lead to finding the solution. In our

Enhanced Genetic Algorithm for Mobile Robot Path Planning in Static and Dynamic Environment

123

algorithm, part of initial population is generated

completely randomly. The number of cells in any

random given path is assigned randomly. In

addition, the cells’ coordinates are generated

randomly, but they must be feasible cells (outside

occupied space). The generated paths may contain

feasible and infeasible segments (intersect with

obstacles). The second part of the initial population

is generated by one-point crossover. We have used

these approaches in generating the initial population

to get a diverse population with paths of various

quality in fast time and ensure that some paths

intersected with others to help performing the

intelligent crossover in later stage.

3.2.2 Fitness Function

The value of the fitness function determines the path

cost of a chromosome. Therefore, all problem

objectives must be considered. In this paper, our

objective is to generate the shortest possible path in

acceptable time. Therefore, the same objective has

been used in the definition of the fitness function as

with the method used by (Mahjoubi et al., 2006).

This fitness function calculates the Euclidean

distance between successive points of each

chromosome and adds the results to each other. This

represents the length of each feasible chromosome.

However, the fitness of a chromosome with

collisions should be higher than the worst feasible

chromosome. The cost for path p with n cells is

defined by:

















,

















∗

(1)

where C(p) is the calculated cost for path p, D(A, B)

is the Euclidean distance between point A and point

B, L( p) is the total length of the collided parts in

path p, Pi is the i

point in the corresponding

sequence of path p (i=1, 2…, n), and M is the

penalty factor.

3.2.3 Selection Operators

The selection operator selects the best individuals

from the population to spawn a new generation of

the population. In this paper, we used two selection

operators. Elitist selection is used to move the best

individuals in the current generation to the next

generation without any change. The elitist selection

is used to avoid losing the best paths because of the

genetic operator’s randomness (Al-Ajlan et al.,

2013). In addition, the tournament selection is used

to select a group of individuals from the population

randomly. These individuals are ranked according to

their relative fitness, and the fittest individuals is

selected to produce the next generation. The

tournament selection is used because it gives each

individual a chance to be selected even the infeasible

paths, as a result, the diversity of the population

increases (Elshamli et al., 2004).

3.2.4 Crossover Operators

The crossover operator is primarily responsible for

improving the generations to obtain the best paths.

The improvement is achieved by recombining two or

more individuals called parents to generate better

solutions called offspring. In this paper, we proposed

a new crossover operator called intelligent

crossover. Figure 2 illustrates the intelligent

crossover. As shown in the figure, the intelligent

crossover is performed at the beginning by taking

the same start node to the offspring and then

comparing the next nodes from the two parents. The

comparison depends on two conditions:

a. Whether the line segment between the

selected node and the next node is feasible or

infeasible. The feasible line is preferred.

b. If the two lines have the same status, then the

Euclidean distance between those nodes and

the goal node will be calculated. The node that

has shorter distance will be selected as the

next node for the offspring.

After that, intelligent crossover looks for the

selected node value in the two parents; if it exists in

the two parents, then the operator performs the

comparison between the next two nodes to the

selected node to select the best one. Otherwise,

when the selected node is located in one parent only;

the next node is selected directly from that parent.

The operation continues in this way until it finds the

goal node. There are two issues with this method:

the first occurs when we compare two nodes that

have the same status and Euclidean distance. To

handle this issue, intelligent crossover will choose

the next node from the first parent. The second issue

occurs when we have two parents that do not share

any nodes; thus, the result will be exactly same as

one of the parents. To overcome the second issue,

we performed one-point crossover during the

generation of the initial population as described in

section 3.2.1, in addition to trying to select two

parents that have at least one common node, other

than start and goal nodes. Algorithm 1 presents the

intelligent crossover operator.

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

124

Figure 2: Intelligent crossover operator.

3.2.5 Mutation Operators

The mutation operator is primarily responsible for

giving GA the required diversity to explore the

entire solution space and prevent the population

from being stuck in a local optimum. In this paper,

we use five types of mutation operators:

a. Add Node: selects a random feasible cell

from the environment and adds it to the path

in a random index.

b. Delete Node: selects a random node from the

path and deletes it.

c. Change Node: selects a random node from

the path and exchanges its value with a

random feasible cell from the environment.

d. Shorten the Path: reduces unreasonable

curves in the path by deleting the intermediate

nodes between the nodes that have feasible

line segments.

e. Correct the Path: enhances the infeasible

path by correcting all infeasible parts, in

addition, it removes any duplicate nodes in the

path. To correct infeasible parts, the operator

uses the best first search algorithm (BFS)

based on Euclidean distance heuristic. BFS is

a simple heuristic search algorithm (Dudek

and Jenkin, 2010). We use it to help building

suboptimal path in fast time.

The mutation chooses one of these operators

randomly each time to generate new offspring.

Figure 3 shows an example for each operator, add

node, delete node, change node and shorten

operators are applied on parent 1, while correct

operator are applied on parent 2. The examples has

been taken from the represented map in figure 2.

3.2.6 Control Parameters

GA requires the various values of algorithm’s

parameters to be set, namely, population size,

crossover probability, mutation probability, and

stopping condition. These parameters have a great

impact on the performance and efficiency of the

algorithm; they affect the quality of the solution and

Enhanced Genetic Algorithm for Mobile Robot Path Planning in Static and Dynamic Environment

125

the search time.

a. Population Size: Research has indicated that

if the population size is too small, GA might

fail to reach a high-quality solution. On the

other hand, a large population size increases

the computational time of the GA (Al-Ajlan et

al., 2013). After performing some experiments

on the population size starting from 15 to 80,

the population size is set to 40, which can be

consider large enough to cover the

environment in which we work without

adding too much computational overhead.

b. Stopping Condition: After performing some

experiments on the stopping condition starting

from 50 to 200 iterations, the stopping criteria

of our GA are defined by 100 generations. We

chose this method to reduce the computational

time of the algorithm and give it enough time

to find the optimal solution.

c. Crossover and Mutation Probabilities: A

high crossover probability leads to the

generation of new individuals faster and

explores more solutions, but also it may leads

to disrupt the good solutions. Whereas, a high

mutation probability increases the diversity of

the population but risks the individuals

jumping over a solution to which they were

close and transforms the GA into a random

search. However, having excessively low

probabilities lead to solutions that become

stuck in local optima. Typically, the crossover

probability should range from 0.7 to 0.9,

whereas the mutation probability should range

from 0.01 to 0.1 (Al-Ajlan et al., 2013),

(Asteroth and Hagg, 2015). We will conduct

experiments to test different probability

values.

Figure 3: Examples on mutation operators.

3.3 Handling Dynamic Aspect

At the beginning, our GA tries to find the best path

based on the available static information. Then,

when change is detected, the GA seeks to manage

the dynamicity of the environment by using Memory

with Random Immigrants technique (MRI). This

technique has been selected because of its ability to

maintain population diversity, which is the key to

successful GA implementation for dynamic

problems and exploits useful information from

Algorithm 1: Intelligent Crossover Operator.

INPUT: chromosomes: parent1 and parent2, and node: goal

OUTPUT: new chromosome: child

BEGIN

child [1] = parent1[1]

n = 1

while (goal not reached)

x1 = find child [n] in parent1 and return the next node

x2 = find child [n] in parent2 and return the next node

if (x1 == null)

child [n+1] = x2

else

if (x2 == null)

child [n+1] = x1

else

f1= is(child [n], x1) line intersects with obstacles?

f2= is(child [n], x2) line intersects with obstacles?

if (f1 == false and f2 == true)

child [n+1] = x2

else

if (f1 == true and f2 == false)

child [n+1] = x1

else

d1=calculate Euclidean distance(child [n], x1)

+ calculate Euclidean distance(x1, goal)

d2=calculate Euclidean distance(child [n], x2)

+ calculate Euclidean distance(x2, goal)

if (d1 <= d2)

child [n+1] = x1

else

child [n+1] = x2

end if

n = n+1

end loop

END

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

126

previous phases (Elshamli et al., 2004). The memory

part is responsible for storing useful information

from the environment to be reused later in a new

environment. For every generation, we select the

best individuals from the population and add them to

the memory rather than the worst ones. Then, we use

all of its content to replace the worst individuals in

the population when the environment changed. The

random immigrant technique is a simple method to

address the convergence issue (Yang, 2008). It

maintains the diversity level of the population

through substituting a percentage of individuals in

the current population with new random ones when

the environment changed. Algorithm 2 shows how

the GA generates the new population based on the

MRI.

Algorithm 2: Memory with Random Immigrants.

INPUT: population p[], memory m[], start, goal,

and the number of random immigrants r

OUTPUT: new population g[]

BEGIN

edit start and goal nodes in all the paths in m[]

copy all the paths from m[] to g[]

generate r new random paths and add them to g[]

edit start and goal nodes in all the paths in p[]

copy (p[].size – r – m[].size) paths from p[] to g[]

END

4 PERFORMANCE

EVALUATION

At the beginning, we will test the algorithm with

different Crossover and Mutation probabilities to

study the effect of these two parameters on our GA.

Then, the static version of the algorithm will be

compared to A* (Tiwari et al., 2012), because it is

widely used in solving path planning problems due

to its optimality and completeness. In addition, it

will be compared to another efficient static GA

(Alajlan et al., 2016), (MGA). For dynamic

environments, we will compare the re-planning

method and the MRI to see the effect of using the

memory, as well as comparing the algorithm with

(Zhao and Gu, 2013) algorithm, (improved GA).

4.1 Experiment Setup

To test and evaluate the performance of our GA path

planner in different size environments, we designed

an object-oriented simulation model. We

implemented it by using C++ programming

language, and compiled it under Linux OS; Ubuntu

14.04 LTS. All the runs were conducted on a Dell

Venue 11i Pro device, which has an Intel Core i5

processor running at 1.6 GHz with 8 GB of RAM

and 104 GB of Disk.

In order to obtain a good analysis of the

algorithm, a set of benchmarks must be defined. The

benchmark set is composed of both simple and

difficult ones. The set consists of four different size

maps and different complexities (i.e. obstacle ratio).

The benchmarks were selected from (Sturtevant,

2012) and (Al-Ajlan et al., 2013). Figure 4 shows

the selected benchmarks. The dynamic environments

are simulated by introducing new obstacles during

the search process. Since the GA is a stochastic

technique, like all other metaheuristic techniques,

conclusions cannot be drawn from a single run. All

the results are based on the following: for each

configuration, ten runs are performed for the same

configuration. The best, average and worst cost, and

the average CPU time are registered for these runs.

4.2 Impact of GA Parameters

The aim of this section is to explore the impact of

mutation probability, crossover probability and the

proposed intelligent crossover operation on the GA

path planner. In order to do that, Map #2 was used.

4.2.1 Crossover Operator Impact

Table 1 demonstrates how Intelligent Crossover and

One-Point Crossover have impacted path cost and

CPU time. In order to calculate this, the generation

number was set to 100, population size to 40,

mutation probability to 0.01, and crossover

probability to 0.9. As can be clearly seen the two

types of crossover have different impacts on the

measured outcomes, where the Intelligent crossover

can find better path in much less time compared to

One-Point crossover.

Table 1: Crossover type impact.

Crossover

Type

Best

Path

Worst

Path

Average

Path

Average

Time

Intelligent

Crossover

71.562 102.123 86.1851 8.6251

One-Point

Crossover

72.198 164.201 110.126 14.4016

4.2.2 Crossover Probability

The impacts of the crossover probability (Intelligent

Crossover) on path cost and CPU time are shown in

Table 2. In order to calculate this, the generation

Enhanced Genetic Algorithm for Mobile Robot Path Planning in Static and Dynamic Environment

127

Figure 4: Benchmarks.

number was set to 100, population size to 40,

mutation probability to 0.01, and crossover

probability range from 0.5 to 1.0.

We can see that in table 2 increasing crossover

probability improves the average path cost but

equally increases execution time. Based on these

results, the most efficient crossover probability is

within the range of 0.7-0.9.

Table 2: Crossover probability impact.

Crossover

Probability

Best

Path

Worst

Path

Average

Path

Average

Time

0.5 69.044 146.474 94.52451 6.306106

0.6 71.428 148.066 99.11437 6.854905

0.7 70.201 130.608 97.18876 7.013214

0.8 72.639 110.968 88.08952 7.04423

0.9 71.562 121.339 86.18512 8.625075

1.0 74.062 180.799 125.0532 8.774862

4.2.3 Mutation Probability

The impact of mutation probability on path cost and

CPU time are shown in Table 3. In order to calculate

this, the generation number was set to 100,

population size to 40, crossover probability to 0.9

using Intelligent Crossover and mutation probability

range from 0.01 to 0.5. With an increase in mutation

probability, the average path cost improved but the

execution time increased alongside it. Therefore, the

most efficient mutation probability in terms of costs

and time is between 0.2-0.3.

Table 3: Mutation probability impact.

Mutation

Probability

Best

Path

Worst

Path

Average

Path

Average

Time

0.01 71.562 121.339 86.18512 8.625075

0.1 70.316 102.771 79.97139 7.377394

0.2 68.634 80.7936 73.47892 7.220681

0.3 69.170 73.2536 71.03801 7.987558

0.4 68.922 74.4373 70.88054 8.710724

0.5 68.719 70.7892 69.73331 8.77626

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

128

4.3 Performance Evaluation in Static

Environments

This section presents an evaluation of the

performance of the GA path planner in a static

environment focusing on path length as an indicator

of solution quality and execution time as an

indicator of the speed of the algorithm. This

performance is compared to A* and MGA. The GA

parameters, which produced the best results in the

previous section, were selected for all four

benchmarks: population size = 40, crossover

probability = 0.75, mutation probability = 0.3 and

number of iterations = 100. The start point is placed

at the topmost point on the left side, while goal point

is placed at the bottommost point on the right side in

order to increase the distance between them.

The results of all the four benchmarks for our

GA, A* and MGA can be seen in Table 4. For our

GA, we presented the best, worst and average path

costs and CPU times. For A* and MGA, as they

have similar results for all runs (best, worst and

average costs are all equal); we present only the

average path cost and the average CPU time.

Table 4 shows that our GA is able to find an

optimal or near optimal path, but as the complexity

and size of benchmarks is increased the gap between

the GA, A* and MGA also increases. In the last

benchmark, A* is better than GA 1.46 times. A*

finds the optimal path every time, but GA is an

incomplete method so it is not possible to be sure

that the GA and MGA paths are optimal. However,

as Table 4 shows, our GA was able on occasion to

find the shortest paths. This is because a grid-based

map used to represent the environment with

polygonal representation for the obstacles. This

approach means that the robot can move in any

direction with fewer detours than they are allowed in

the regular grid representation used by A* and

MGA, where robots can move in just eight

directions.

On other hand, the time gap between our GA and

A* and MGA decreases when the size of the

benchmarks increase. In large maps, GA

outperformed A* and MGA in terms of execution

time. For example, in the last benchmark, GA is

faster than A* 3.9 times. This is because our GA

uses random paths in the initial population and then

fix them later with the crossover and mutation

operators. This keeps the times low in most cases.

A* is a greedy approach, while MGA uses the

greedy approach to generate the initial population.

Both expands nodes exponentially with the depth of

the solution, which takes time during large

problems. In fact, MGA failed to complete the final

benchmark after 10 hours of trying, and overall it

took longer time to solve large problems.

4.4 Performance Evaluation in

Dynamic Environments

Here we tested the algorithms by using the first two

benchmarks. Again, the start and goal points were

chosen in the top left and bottom right cells. To

create a dynamic environment, user-defined

obstacles were introduced during each run in such a

way that they affect the best path produced in the

static mode.

4.4.1 Re-planning Vs Memory with Random

Immigrants

Two techniques were used to manage the dynamic

obstacles, MRI and re-planning. These were

compared in order to study the effect of using the

memory when the environment changes. The same

GA parameters that produced the best average

values were used for each technique: population size

= 40, crossover probability = 0.75, mutation

probability = 0.3, and number of iterations = 100.

Table 5 demonstrates that the MRI technique is

more efficient than re-planning from the start

because the MRI uses promising potential solutions

to improve the new path. The re-planning method

also had a longer execution time because it

generated more random paths that need to be fixed,

and this consume much more time.

Table 4: Results of GA, A* and MGA for four static benchmarks.

Benchmark

A* MGA

Best Path Worst Path Average Path Average Time

Average Path Average Time Average Path Average Time

1 130.265 135.246 133.0312 7.903324

131.865 1.72329 131.865 0.95037

2 264.734 294.393 275.2191 9.216908

269.061 77.59117 269.061 11.07575

3 263.331 297.479 281.0732 13.40991

270.819 62.12198 290 23.12085

4 857.16 1178.8 1035.997 918.0374

805.919 3579.913 Failed

Enhanced Genetic Algorithm for Mobile Robot Path Planning in Static and Dynamic Environment

129

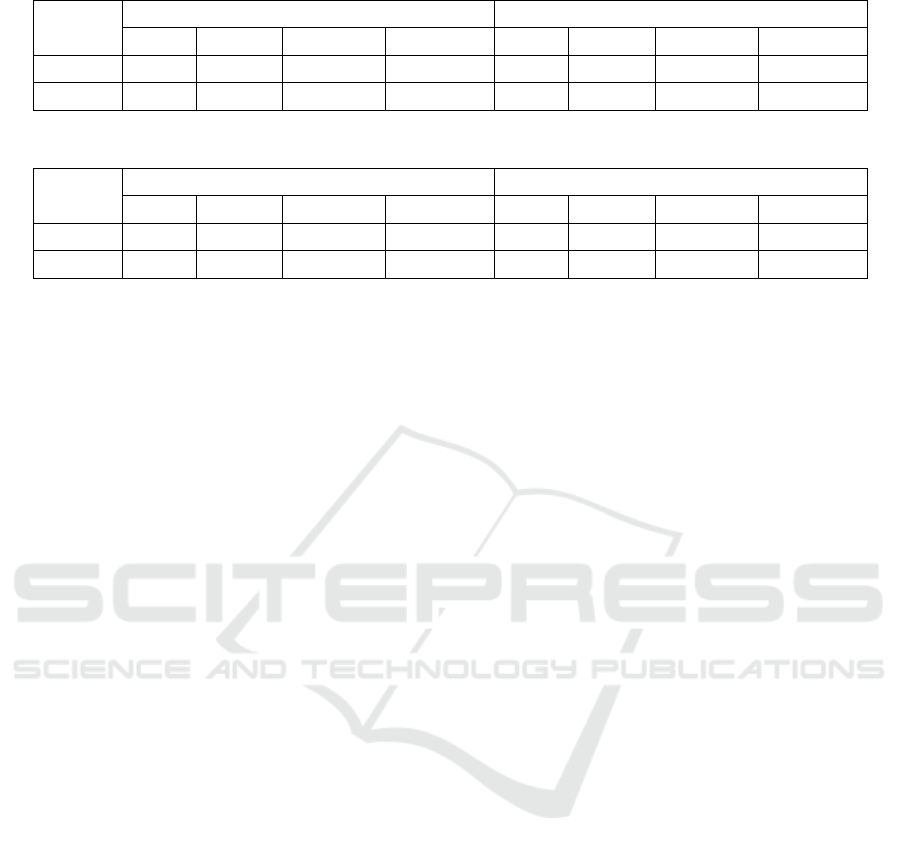
Table 5: Results of MRI and re-planning techniques in dynamic environments.

Benchmark

GA (MRI)

GA (Re-planning)

Best Path Worst Path Average Path Average Time

Best Path

Worst Path Average Path

Average Time

1 142.107 148.899 144.6106 17.59538

143.069 186.14 148.8587 17.68738

2 267.143 311.728 288.8071 29.18556

272.45 309.196 296.01564 34.66139

Table 6: Results of MRI and Improved GA in dynamic environments.

Benchmark

GA (MRI)

Improved GA

Best Path Worst Path Average Path Average Time

Best Path

Worst Path Average Path

Average Time

1 142.107 148.899 144.6106 17.59538

150.409 171.498 158.6494 26.7439

2 267.143 311.728 288.8071 29.18556

271.647 300.694 281.0783 139.4874

4.4.2 Comparison in Dynamic Environment

This section presents a comparative study between

our GA and the improved GA (Zhao and Gu, 2013)

in dynamic environments. They are assessed in

terms of solution quality, measured as path length,

and algorithm speed, measured as execution time.

The results of the evaluation are shown in Table

6. Both GAs were able to find optimal or near

optimal paths, although it is not guaranteed that

these are optimal because GA is not a complete

method. In our GA, the path cost was on average

slightly better than in the improved GA as a result of

the various mutation and crossover operations, and

as Table 6 shows, our GA found slightly shorter

paths. Again, this is a result of using the grid-based

map representation with polygonal obstacle

representation. For the same reason, our GA also

had consistently much better execution times than

the improved GA. Our representation is better since

the sizes of individuals are much smaller than the

size of individuals of the classical grid

representation. Therefore, the GA operations could

be performed efficiently.

5 CONCLUSIONS

Path planning is the process of deciding how to

move from one point to another one with respect to

the objectives of the problem. It is a fundamental

problem to mobile robots. In this paper, we

addressed the problem of path planning for mobile

robots in static and dynamic environment. Our

motivation was the need of finding the best path

within acceptable time, and studying the impact of

using a genetic algorithm in solving the problem.

This paper introduced a GA approach for solving

mobile robot path planning problems in static and

dynamic environments. The planner uses a grid-

based map with polygonal representation for the

environment as the knowledge base. The developed

GA planner uses variable-length chromosomes for

the path encoding to reduce the memory usage. Part

of the initial population is generated completely

randomly, while the second part is generated by one-

point crossover to get a diverse population with

paths of various quality in fast time and ensure that

some paths intersected with others to help

performing the intelligent crossover in later stage.

The fitness function is used to integrate the

objectives of the problem. Our GA uses two

selection operators: Elitist Selection and Tournament

Selection. In addition, the algorithm uses a new

crossover operator called Intelligent Crossover,

whereas, for mutation operation, five types of

mutation operators have been used. Furthermore, our

GA manages the dynamicity of the environment by

using Memory with Random Immigrants technique.

The GA was implemented by using C++

programming language and tested with four

benchmarks. We studied the impact of the crossover

operator, mutation and crossover probabilities, in

addition to MRI and re-planning techniques. We

also compared its performance in a static

environment against the A* algorithm and MGA

(Alajlan et al., 2016), as well as compared the

performance in a dynamic environment against

Improved GA (Zhao and Gu, 2013). It has been

shown that our algorithm is able to generate an

optimal or near optimal solution with fast execution

time compared to the three algorithms, especially in

large problems. In fact, we can accept some gaps to

optimality for enhancing the computational

expenses, since in real robotics applications; it does

not disadvantage to find paths with slightly taller

lengths, if they can be found much faster.

For future work, we intend to enhance the GA to

manage more dynamicity aspects, such as avoiding

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

130

moving obstacles and tracking moving goals. In

addition to improve the GA parameters.

REFERENCES

Alajlan, M. et al., 2016. Global Robot Path Planning

Using GA for Lagre Grid Maps: Modelling,

Performance and Experimntation. in press.

Al-Ajlan, M. et al., 2013. Global Path Planning for

Mobile Robots in Large-Scale Grid Environments

using Genetic Algorithms. Sousse, Tunisia, s.n., pp. 1-

Asteroth, A. and Hagg, A., 2015. How to Successfully

Apply Genetic Algorithms in Practice: Representation

and Parametrization. Madrid, Spain, s.n., pp. 1-6.

Chaari, I. et al., 2012. smartPATH: A hybrid ACO-GA

Algorithm for Robot Path Planning. Brisbane,

Australia: IEEE Congress on Evolutionary

Computation.

Dudek, G. and Jenkin, M., 2010. Computational

Principles of Mobile Robotics. s.l.:Cambridge

University Press.

Elshamli, A., Abdullah, H. and Areibi, S., 2004. Mobile

Robots Path Planning Optimization in Static and

Dynamic Environments. Canda: Master thesis, The

University of Guelph.

Hussein, A. et al., 2012. Metaheuristic Optimization

Approach to Mobile Robot Path Planning. Cairo,

Egypt, s.n., pp. 1-6.

Koryakovskiy, I., Hoai, N. X. and Lee, K. M., 2009. A

Genetic Algorithm with Local Map for Path Planning

in Dynamic Environments. Montreal, Canada, s.n., pp.

1859-1860.

Mahjoubi, H., Bahrami, F. and Lucas, C., 2006. Path

Planning in an Environment with Static and Dynamic

Obstacles Using Genetic Algorithm: A Simplified

Search Space Approach. Vancouver, Canada, s.n., pp.

2483-2489.

Masehian, E. and Sedighizadeh, D., 2007. Classic and

Heuristic Approaches in Robot Motion Planning – A

Chronological Review. International Journal of

Mechanical, Industrial Science and Engineering, 1(5),

pp. 13-18.

Miao, H., 2009. Robot path Planning in Dynamic

Environments Using A Simulated Annealing Based

Approach. Brisbane, Australia: Master thesis,

Queensland University of Technology.

O'Rourke, J., 1998. Computational Geometry in C. Second

ed. New York, USA: Cambridge University Press.

Reshamwala, A. and Vinchurkar, D. P., 2013. Robot Path

Planning using An Ant Colony Optimization

Approach: A Survey. International Journal of

Advanced Research in Artificial Intelligence, 2(3).

Russell, S. and Norvig, P., 2002. Artificial Intelligence: A

Modern Approach (2nd Edition). s.l.:Prentice Hall.

Shi, P. and Cui, Y., 2010. Dynamic Path Planning for

Mobile Robot Based on Genetic Algorithm in

Unknown Environment. Xuzhou, China, s.n., pp. 4325-

4329.

Sturtevant, N., 2012. Benchmarks for Grid-Based

Pathfinding. Transactions on Computational

Intelligence and AI in Games, 4(2), pp. 144-148.

Sunday, D., 2012. Inclusion of a Point in a Polygon.

[Online]

Available at: http://geomalgorithms.com/a03-

_inclusion.html

[Accessed 11 March 2015].

Tiwari, R., Shukla, A. and Kala, R., 2012. Intelligent

Planning for Mobile Robot Algorithmic Approaches.

s.l.:IGI Global.

Yang, S., 2008. Genetic Algorithms with Memory- and

Elitism-Based Immigrants in Dynamic Environments.

Evolutionary Computation, Fall, 16(3), pp. 385-416.

Yun, S. C., Parasuraman, S. and Ganapathy, V., 2011.

Dynamic Path Planning Algorithm in Mobile Robot

Navigation. Langkawi, Malaysia, s.n., pp. 364-369.

Zhao, Y. and Gu, J., 2013. Robot Path Planning Based on

Improved Genetic Algorithm. Shenzhen, China, s.n.,

pp. 2515-2522.

Zhu, Z., Wang, F., He, S. and Sun, Y., 2015. Global Path

Planning of Mobile Robots Using A Memetic

Algorithm. International Journal of Systems Science,

46(11), pp. 1982-1993.

Zou, X., Ge, B. and Sun, P., 2012. Improved Genetic

Algorithm for Dynamic Path Planning. International

Journal of Information and Computer Science, May,

1(2), pp. 16-20.

Enhanced Genetic Algorithm for Mobile Robot Path Planning in Static and Dynamic Environment

131