Classiﬁcation Confusion within NEFCLASS Caused by Feature Value

Skewness in Multi-dimensional Datasets

Jamileh Youseﬁ

and Andrew Hamilton-Wright

1,2

School of Computer Science (SOCS), University of Guelph, Guelph, Ontario, Canada

Department of Mathematics and Computer Science, Mount Allison University, Sackville, NB, Canada

Keywords:

Fuzzy, Discretization, Neurofuzzy, Classiﬁcation, Skewness, NEFCLASS.

Abstract:

This paper presents a model for the treatment of skewness effects on the accuracy of the NEFCLASS classiﬁer

by changing the embedded discretization method within the classiﬁer. NEFCLASS is a common example of the

construction of a neuro-fuzzy system. The popular NEFCLASS classiﬁer exhibits surprising behaviour when

the feature values of the training and testing data sets exhibit signiﬁcant skew. As skewed feature values are

commonly observed in biological data sets, this is a topic that is of interest in terms of the applicability of such

a classiﬁer to these types of problems. From this study it is clear that the effect of skewness on classiﬁcation

accuracy is signiﬁcant, and that this must be considered in work dealing with skewed data distributions. We

compared accuracy of NEFCLASS classiﬁer with two modiﬁed versions of NEFCLASS embedded with MME

and CAIM discretization methods. From this study it is found the CAIM and MME discretization methods

results in greater improvements in the classiﬁcation accuracy of NEFCLASS as compared to using the original

EQUAL-WIDTH technique NEFCLASS uses by default.

1 INTRODUCTION

Data distributions in machine learning, when they are

discussed at all, are generally expected to have a sym-

metric distribution, with a central tendency, if not ac-

tually being normally distributed. When the feature

values of data are skewed, however, issues arise hav-

ing to do with the relative scarcity of sample values in

the tails of the distribution relative to the abundance

of data near the median.

Several studies (Chittineni and Bhogapathi, 2012;

Liu et al., 2008; Mansoori et al., 2007; Tang and Chiu,

2004; Au et al., 2006; Peker, 2011; Changyong et al.,

2014; Qiang and Guillermo, 2015) have examined the

question of transforming the data when incorporat-

ing the distribution of input data into the classiﬁca-

tion system in order to more closely approximate nor-

mally distributed data. Very few studies (Mansoori

et al., 2007; Liu et al., 2008; Zadkarami and Rowhani,

2010; Hubert and Van der Veeken, 2010) addressed

these issues while focusing on some alternative to a

data transformation approach.

Data transformation is a common preprocessing

step to treat the skewness and improve dataset nor-

mality. However, in the biological and biomedical

domain, data transformation interferes with the trans-

parency of the decision making process, and can lead

to the exclusion of important information from the de-

cision making process, and affect the system’s ability

to correctly classify the case. Therefore, rather than

transformation of the data to achieve a more normally

distributed input, in this paper we directly investigate

and report the NEFCLASS classiﬁer’s behaviour when

dealing with distribution of data with skewed feature

values.

The choice of discretization technique is known

to be one of the important factors that might af-

fect the classiﬁcation accuracy of a classiﬁer. NEF-

CLASS classiﬁers use an EQUAL-WIDTH discretiza-

tion method to divide the observed range of continu-

ous values for a given feature into equally sized fuzzy

intervals, overlapping by half of the interval width.

EQUAL-WIDTH discretization does not take the class

information into account, which, as we show here, re-

sults in a lower classiﬁcation accuracy for NEFCLASS

classiﬁer than other techniques, especially when the

feature values of the training and testing data sets ex-

hibit signiﬁcant skew. Dealing with skewness without

performing a transformation will provide greater clar-

ity in interpretation, and by extension better classiﬁ-

cation transparency, as the projection incurred by the

transformation does not need to be taken into account

Youseﬁ, J. and Hamilton-Wright, A.

Classiﬁcation Confusion within NEFCLASS Caused by Feature Value Skewness in Multi-dimensional Datasets.

DOI: 10.5220/0006033800210029

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 21-29

ISBN: 978-989-758-201-1

in interpretation.

We provide a study based on an easily repro-

ducible synthetic data distributions, in order to allow

deeper insights into the data analysis. We argue that

the skewed data, in terms of feature value distribu-

tion, cause a higher misclassiﬁcation rate in classi-

ﬁcation learning algorithms. We further argue that

distribution sensitive discretization methods such as

CAIM and MME result in greater improvements in

the classiﬁcation accuracy of the NEFCLASS classi-

ﬁer as compared to using the original EQUAL-WIDTH

technique.

The next section of this paper contains a short re-

view of the NEFCLASS classiﬁer and three discretiza-

tion methods that will be used to perform the clas-

siﬁcation task is presented. Section 3 describes the

methodology of our study, and in section 4 the ex-

perimental results and statistical analysis are given.

Finally, conclusions are presented.

2 BACKGROUND

2.1 Discretization

A discretization process divides a continuous numeri-

cal range into a number of covering intervals where

data falling into each discretized interval is treated

as being describable by the same nominal value in

a reduced complexity discrete event space. In fuzzy

work, such intervals are then typically associated with

the support of fuzzy sets, and the precise placement in

the interval is mapped to the degree of membership in

such a set.

Discretization methods are categorized into super-

vised and unsupervised algorithms. EQUAL-WIDTH

intervals (Chemielewski and Grzymala-Busse, 1996),

EQUAL-FREQUENCY intervals, such as k-means

clustering (Monti and Cooper, 1999), and Marginal

Maximum Entropy (Chau, 2001; Gokhale, 1999) are

examples of algorithms for unsupervised discretiza-

tion. Maximum entropy (Bertoluzza and Forte, 1985),

ChiMerge (Kerber, 1992), CAIM (Kurgan and Cios,

2004), and URCAIM (Cano et al., 2016) are some ex-

amples of supervised algorithms that take class label

assignment in a training data set into account when

constructing discretization intervals.

In the following discussion, the three discretiza-

tion methods, that we have chosen for the experi-

ments are described. To demonstrate the partitioning

we used a skewed dataset with 45 training instances

and three classes, with sample discretizations shown

Fig. 1. The subﬁgures within Fig. 1 each show the

same data, with the green, red and blue rows of dots

(a) EQUAL-WIDTH

(b) MME

Figure 1: Three discretization techniques result in different

intervals produced on the same three-class data set.

(top, middle and bottom) within each ﬁgure describ-

ing the data for each class in the training data.

2.1.1 EQUAL-WIDTH

The EQUAL-WIDTH discretization algorithm divides

the observed range of continuous values for a given

feature into a set number of equally sized intervals,

providing a simple mapping of the input space that is

created independent of both the distribution of class

and of the density of feature values within the input

space (Kerber, 1992; Chemielewski and Grzymala-

Busse, 1996).

Fig. 1a demonstrates the partitioning using

EQUAL-WIDTH intervals; note that there is no clear

relation between classes and intervals, and that the in-

tervals shown have different numbers of data points

within each (21, 19 and 5 in this case).

2.1.2 MME

Marginal Maximum Entropy, or MME, based dis-

cretization (Chau, 2001; Gokhale, 1999) divides the

dataset into a number of intervals for each feature,

where the number of points is equal for all of the

intervals, under the assumption that the information

of each interval is expected to be equal. Fig. 1b

shows the MME intervals for the example three-class

dataset. Note that the intervals in Fig. 1b do not

cover the same fraction of the range of values (i.e., the

widths differ), being the most dense in regions where

there are more points. The same number of points

(15) occur in each interval.

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

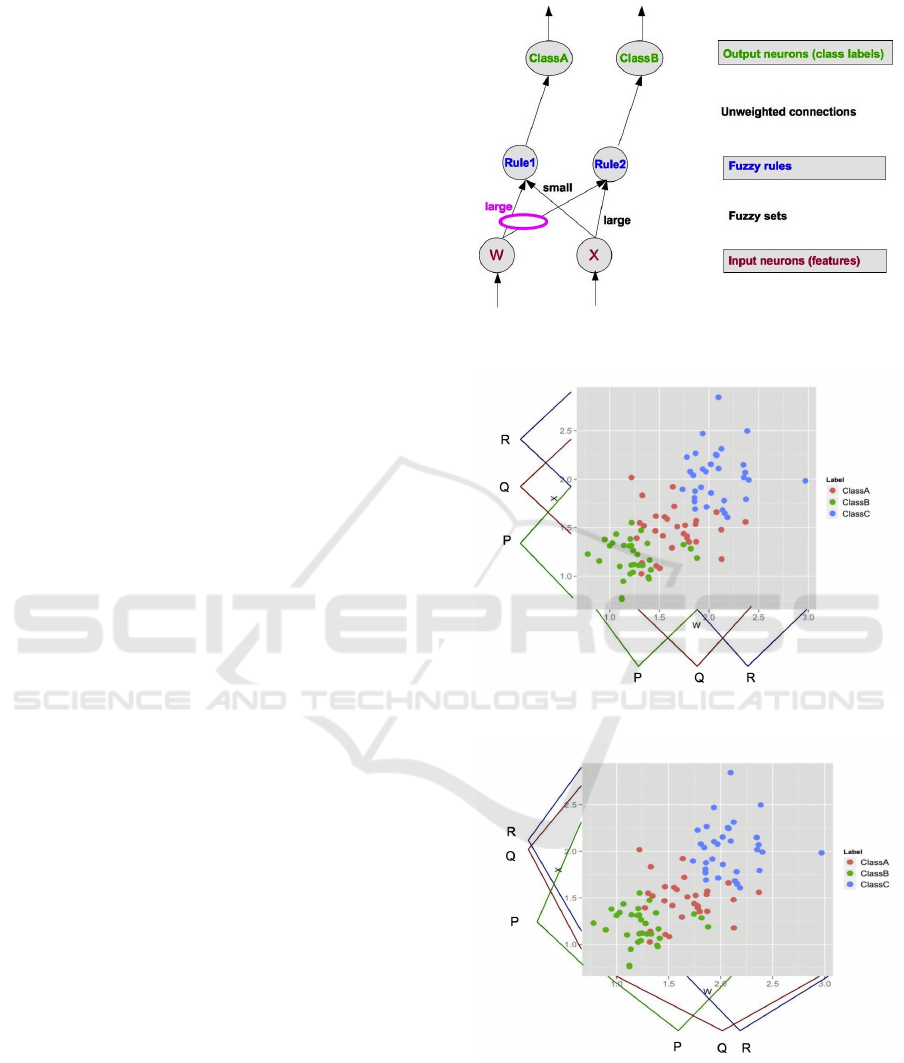
2.1.3 CAIM

CAIM (class-attribute interdependence maximiza-

tion) discretizes the observed range of a feature into

a class-based number of intervals and maximizes

the inter-dependency between class and feature val-

ues (Kurgan and Cios, 2004). CAIM discretiza-

tion algorithm divides the data space into partitions,

which leads to preserve the distribution of the original

data (Kurgan and Cios, 2004), and obtain decisions

less biased to the training data.

Fig. 1c shows the three CAIM intervals for our

sample data set. Note how the placement of the dis-

cretization boundaries is closely related to the points

where the densest portion of the data for a particular

class begins or ends.

2.2 NEFCLASS Classiﬁer

NEFCLASS (Nauck et al., 1996; Nauck and Kruse,

1998; Klose et al., 1999) is a neuro-fuzzy classiﬁer

that tunes a set of membership functions that describe

input data and associates these through a rule set with

a set of potential class labels. Training is done in a

supervised fashion based on a training data set.

Fig. 2 shows a NEFCLASS model that classiﬁes

input data with two features into two output classes

by using three fuzzy sets and two fuzzy rules. In-

put features are supplied to the nodes at the bottom

of the ﬁgure. These are then fuzziﬁed, using a num-

ber of fuzzy sets. The sets used by a given rule are

indicated by linkages between input nodes and rule

nodes. If the same fuzzy set is used by multiple rules,

these links are shown passing through an oval, such

as the one marked “large” in Fig. 2. Rules directly

imply an output classiﬁcation, so these are shown

by unweighted connections associating a rule with

a given class. Multiple rules may support the same

class, however that is not shown in this diagram. Rule

weightings are computed based on the degree of asso-

ciation between an input fuzzy membership function

and the rule (calculated based on the degree of associ-

ation in the training data), as well as the level of acti-

vation of the fuzzy membership function, as is typical

in a fuzzy system (Mendel, 2001, Chapter 1).

In Fig. 3a, a set of initial fuzzy membership func-

tions describing regions of the input space are shown,

here for a two-dimensional problem in which the

fuzzy sets are based on the initial discretization pro-

duced by the EQUAL-WIDTH algorithm. As will be

demonstrated, NEFCLASS functions work best when

these regions describe regions speciﬁc to each in-

tended output class, as is shown here, and as is de-

scribed in the presentation of a similar ﬁgure in the

Figure 2: A NEFCLASS model with two inputs, two rules,

and two output classes.

(a) Initial fuzzy set membership functions in NEFCLASS, pro-

duced using EQUAL-WIDTH discretization

(b) Results of tuning the above membership functions to bet-

ter represent class/membership function information

Figure 3: Fuzzy membership functions before and after

training data based tuning using the NEFCLASS algorithm.

classic work describing this classiﬁer (Nauck et al.,

1996, pp. 239).

As is described in the NEFCLASS overview pa-

Classiﬁcation Confusion within NEFCLASS Caused by Feature Value Skewness in Multi-dimensional Datasets

per (Nauck and Kruse, 1998, pp. 184), a relationship

is constructed through training data based tuning to

maximize the association of the support of a single

fuzzy set with a single outcome class. This implies

both that the number of fuzzy sets must match the

number of outcome classes exactly, and in addition,

that there is an assumption that overlapping classes

will drive the fuzzy sets to overlap as well.

Fig. 3a shows the input membership functions as

they exist before membership function tuning, when

the input space is partitioned into EQUAL-WIDTH

fuzzy intervals.

Fig. 3b demonstrates that during the fuzzy set tun-

ing process, the membership function is shifted and

the support is reduced or enlarged, in order to better

match the coverage of the data points belonging to

the associated class, however as we will see later, this

process is strongly informed by the initial conditions

set up by the discretization to produce the initial fuzzy

membership functions.

3 METHODOLOGY

This paper has two objectives. The ﬁrst is to char-

acterize how the NEFCLASS classiﬁcation accuracy

degrades as data skewness increases. The second

is to evaluate alternative discretization methods to

counteract the performance problems in skewed data

domains. To support this second goal we will

evaluate maximum marginal entropy (MME) (Chau,

2001; Gokhale, 1999) and the supervised, class-

dependent discretization method CAIM (Kurgan and

Cios, 2004).

We carried out two different set of experiments. In

the ﬁrst experiment, denoted as the effect of skewness

of feature values, we evaluate unmodiﬁed NEFCLASS

behaviour when dealing with different level of skew-

ness.

In the second experiment, denoted as the effect of

discretization, we investigate the classiﬁcation accu-

racy of a modiﬁed NEFCLASS classiﬁer upon employ-

ing the three different discretization techniques. The

MME and CAIM methods are not part of the stan-

dard NEFCLASS implementation, therefore we im-

plemented two modiﬁed versions of NEFCLASS clas-

siﬁer, each utilizing one of these two discretization

methods. Experiments were then performed on syn-

thesized datasets with different levels of feature val-

ues skewness.

Results from the experiments are presented in

terms of misclassiﬁcation rates, which are equal to the

number of misclassiﬁed data instances divided by the

total number of instances in the testing dataset.

3.1 Datasets

Three synthesized datasets were used for experi-

ments. All the synthesized data sets used describe

classiﬁcation problems within a 4-dimensional data

space containing distributions of data from three sep-

arate classes.

Our data was produced by randomly generating

numbers following the F-distribution with different

degrees of freedom chosen to control skew. The F-

distribution (Natrella, 2003) has been chosen as the

synthesis model because the degree of skew within

an F-distribution is controlled by the pairs of degrees

of freedom speciﬁed as a pair of distribution control

parameters. This allows for a spectrum of skewed

data distributions to be constructed. We designed

the datasets to present different levels of skewness

with increasing skew levels. Three pairs of degrees

of freedom parameters have been used to generate

datasets with different levels of skewness, including

low, medium, and high-skewed feature values. After

initial experiments datasets with degrees of freedom

(100, 100) was chosen to provide data close to a nor-

mal distribution, (100, 20) provides moderate skew,

and (35, 8) provides high skew.

A synthesized data set consisting of 1000 ran-

domly generated examples consisting of four-feature

(W , X , Y , Z) F-distribution data for each of three

classes was created. The three classes (ClassA,

ClassB and ClassC) overlap, and are skewed in the

same direction. The size of datasets were designed to

explore the effect of skewness when enough data is

available to clearly ascertain data set properties. Ten-

fold cross validation was used to divide each dataset

into training (2700) and testing (300 point) sets in

which an equal number of each class is represented.

We have taken care to ensure that all datasets used

have a similar degree of overlap, and same degree of

variability.

Fig. 4 shows the skewness of each dataset for

each feature. From these ﬁgures one can see that the

LOW-100,100 data is relatively symmetric, while the

MED-100,20 and HIGH-35,8 data show an increas-

ing, and ultimately quite dramatic, skew.

4 RESULTS AND DISCUSSION

4.1 The Effect of Skewness on

Classiﬁcation Accuracy

In this section, we discuss how feature value skewness

affects the classiﬁcation accuracy of the NEFCLASS

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

W X Y Z

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

(a) LOW-100,100

W X Y Z

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

(b) MED-100,20

W X Y Z

Skewness Value

0 1 2 3 4

ClassA

ClassB

ClassC

Figure 4: Skewness by label and feature for the three syn-

thetic datasets.

classiﬁer. We begin by applying the NEFCLASS clas-

siﬁer to the synthesized datasets with our three differ-

ent levels of skewness: low, medium, and high. Our

null hypothesis is that the misclassiﬁcation rate ob-

served for NEFCLASS are equal in all three datasets.

As mentioned earlier, NEFCLASS will attempt to

tune the fuzzy membership functions provided by the

initial EQUAL-WIDTH discretization to associate the

support of each fuzzy set unambiguously with a single

class. As our skewed data sets overlap substantially,

this is a difﬁcult task for the NEFCLASS classiﬁer.

Figs. 5 and 6 show the relationship between the

distribution of input data values in feature X, and the

placement of the ﬁnal membership function by the

NEFCLASS classiﬁer when using the EQUAL-WIDTH

discretization method for the three datasets LOW-

100,100, MED-100,20 and HIGH-35,8.

Figs. 5a, 5b, and 5c illustrate the density functions

for the LOW-100,100, MED-100,20 and HIGH-35,8

data sets, respectively. As can be seen in 5a, the fea-

ture values in this case are centrally tended and gen-

erally symmetric, providing an approximation of a

Normal distribution, though observable skew is still

present, as shown in Fig. 4a. In Fig. 5b, tails are ob-

servable as the mean of feature values are pulled to-

wards the right while the median values remain sim-

ilar to those in 5a, for a moderately skewed distribu-

tion. In Fig. 5c, the feature values exhibit longer tails

than normal, indicating a highly skewed distribution.

Fig. 5 and 6 allows comparison between a data

distribution and the representation of fuzzy sets for

this feature in this distribution, displayed immediately

below. For example, Fig. 5a can be compared with

Fig. 6a. Similar vertical comparisons are able to be

made for Figs. 5b and 5c.

Fig. 6a illustrates the placement of initial fuzzy

sets and ﬁnal membership functions with the EQUAL-

WIDTH discretization method for dataset LOW-

100,100. As can be seen, the same number of fuzzy

sets with equal support are constructed, and after tun-

ing the membership functions are shifted and the sup-

ports are reduced or enlarged, in order to better match

the distribution of class-speciﬁc feature values. The

dotted line indicates the initial fuzzy sets and the solid

line indicates the ﬁnal placement of the fuzzy sets.

Fuzzy sets have been given the names “P”, “Q”

and “R” in these ﬁgures, rather than more tradi-

tional linguistic labels such as “small”, “medium” and

“large” because of the placement associations with

the classes, and the assignment of class names to

fuzzy sets lies within the NEFCLASS training algo-

rithm, and is not under user control. For this reason,

it is not possible to assign names a priori that have any

linguistic meaning. The choices NEFCLASS makes in

terms of which fuzzy set is used to represent a partic-

ular class is part of the underlying performance issue

explored in this paper, as will be shown.

As one can see in comparing Fig. 6a with 5a,

NEFCLASS has chosen to associate fuzzy set P with

ClassB, set Q with ClassA, and fuzzy set R with

ClassC based on this EQUAL-WIDTH initial dis-

cretization. The associations are not as clear with data

exhibiting higher skew, as shown in Figs. 6b and 6c, in

which NEFCLASS is attempting to set two, and then

three, fuzzy membership functions to essentially the

Classiﬁcation Confusion within NEFCLASS Caused by Feature Value Skewness in Multi-dimensional Datasets

0 1 2 3 4 5

0.0 0.5 1.0 1.5 2.0

ClassA

ClassB

ClassC

(a) LOW-100,100

0 2 4 6 8

0.0 0.5 1.0 1.5 2.0

ClassA

ClassB

ClassC

(b) MED-100,20

0 5 10 15

0.0 0.5 1.0 1.5 2.0

ClassA

ClassB

ClassC

Figure 5: Density plots for feature X for all datasets.

0 1 2 3 4 5

0.0 0.2 0.4 0.6 0.8 1.0

(a) LOW-100,100

0 2 4 6 8

0.0 0.2 0.4 0.6 0.8 1.0

(b) MED-100,20

0 5 10 15

0.0 0.2 0.4 0.6 0.8 1.0

Figure 6: Fuzzy Sets and Membership Functions constructed by EQUAL-WIDTH for feature X of all datasets.

0 1 2 3 4 5

0.0 0.2 0.4 0.6 0.8 1.0

(a) LOW-100,100

0 2 4 6 8

0.0 0.2 0.4 0.6 0.8 1.0

(b) MED-100,20

0 5 10 15

0.0 0.2 0.4 0.6 0.8 1.0

Figure 7: Fuzzy Sets and Membership Functions constructed by MME for feature X of all datasets.

0 1 2 3 4 5

0.0 0.2 0.4 0.6 0.8 1.0

(a) LOW-100,100

0 2 4 6 8

0.0 0.2 0.4 0.6 0.8 1.0

(b) MED-100,20

0 5 10 15

0.0 0.2 0.4 0.6 0.8 1.0

Figure 8: Fuzzy Sets and Membership Functions constructed by CAIM for feature X of all datasets.

same support and with the same central peak. This,

of course, limits or entirely destroys the information

available to the rule based portion of the system, and

is therefore unsurprisingly correlated with a higher

number of classiﬁcation errors.

The analysis of fuzzy sets and memberships for

feature X in dataset LOW-100,100 shows that all of

three fuzzy sets are expanded in terms of their sup-

port. As shown in Fig. 6a, the support of fuzzy sets

Q and R share identical support, as deﬁned by the ob-

served range of the training data. In addition, sets

Q and R are deﬁned by a nearly identical maximum

point, rendering the distinction between them moot.

Similarly, in Fig. 6b, we observe identical maxima

and support for sets P and Q, however R is set apart

with a different, but substantially overlapping, sup-

port and a clearly distinct maxima.

This confusion gets only more pronounced as the

degree of skew increases, as is clear in Fig. 6c, rep-

resenting the fuzzy sets produced for HIGH-35,8, in

which all fuzzy sets P, Q and R share identical sup-

port deﬁned by the range of the observed data. In

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

Table 1: Mean and standard deviation of misclassiﬁcation rates and median of number of rules for each classiﬁer trained on

three synthesized dataset.

Discretization Dataset

LOW-100,100 MED-100,20 HIGH-35,8

Mean and SD for

Misclassiﬁcation Rates

EQUAL-WIDTH 22.63 ± 1.07 65.30 ± 3.38 63.07 ± 6.77

MME 25.67 ± 1.85 33.73 ± 1.64 42.30 ± 2.78

CAIM 24.13 ± 2.72 34.30 ± 1.52 42.37 ± 3.08

Median for

Number of Rules

EQUAL-WIDTH 49.00 34.50 15.00

MME 44.00 50.00 46.00

CAIM 53.50 51.50 45.00

Table 2: M-W-W results comparing the misclassiﬁcation rates based on level of skew.

LOW-100,100 MED-100,20

Discretization vs. vs.

MED-100,20 HIGH-35,8 HIGH-35,8

EQUAL-WIDTH 2.9 × 10

−11

∗ 2.9 × 10

−11

∗ .9300

MME 2.9 × 10

−11

∗ 2.9 × 10

−11

∗ .0001∗

CAIM 2.9 × 10

−11

∗ 2.9 × 10

−11

∗ .0001∗

* signiﬁcant at 99.9% conﬁdence (p < .001)

addition, all the fuzzy sets in this example are deﬁned

by a nearly identical maximum point.

It is perhaps surprising that difference in the pro-

portion of data in the tails of the distribution are not

represented more directly here, however this is largely

due to the fact that the EQUAL-WIDTH discretization

technique is insensitive to data density, concentrating

instead purely on range.

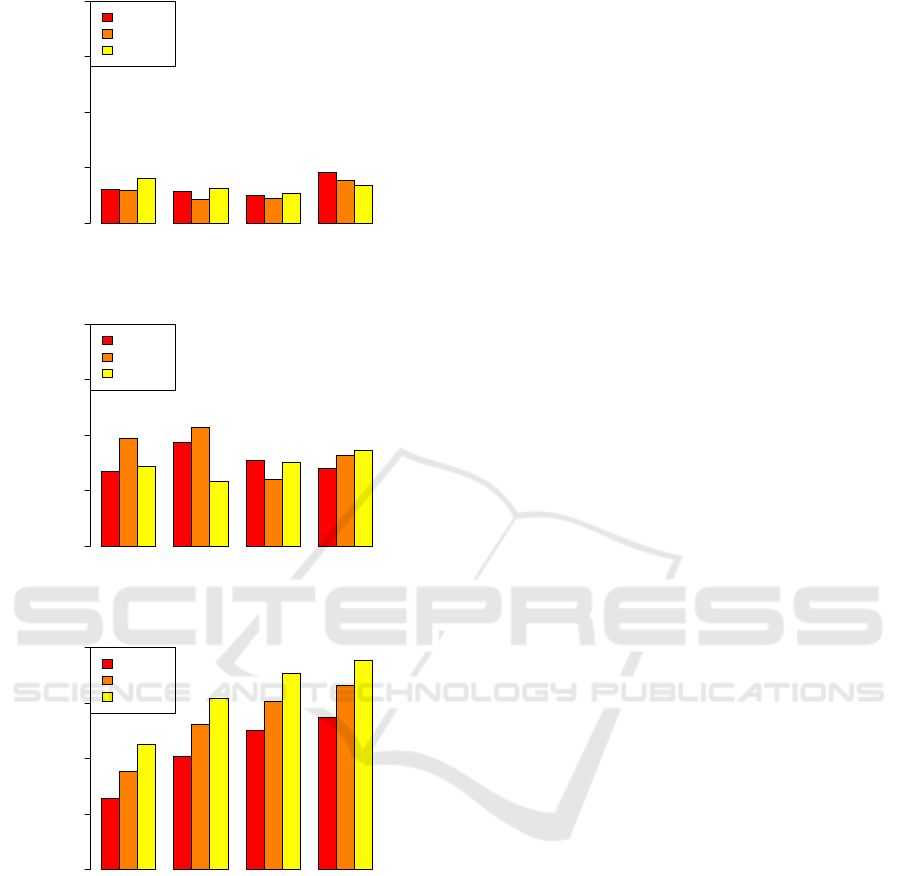
Table 1 reports the misclassiﬁcation rates (as mean

± standard deviation), as well as the median number

of fuzzy rules obtained by each classiﬁer, using each

discretization technique, and for each dataset. The re-

sults have been calculated over the 10 cross-validation

trials. As shown in Table 1, LOW-100,100 achieved

the lowest misclassiﬁcation rate and the lowest vari-

ability. The results also show considerably larger

variability in the misclassiﬁcation rate of HIGH-35,8,

compared to MED-100,20. The decrease in the

number of rules produced using the EQUAL-WIDTH

method shows that less information is being captured

about the data set as skewness increases. As there

is no reason to assume that less information will be

required to make a successful classiﬁcation, this de-

crease in the number of rules is therefore an contribut-

ing cause for the increase in the misclassiﬁcation rate

noted for EQUAL-WIDTH in Figs 9a.

Fig. 9 shows a graphical summary of the differ-

ences between the misclassiﬁcation rates and number

of rules observed for each discretization method.

An exploration of the normality of the distribu-

tion of misclassiﬁcation rates using a Shapiro-Wilks

test found that a non-parametric test was appropri-

ate in all cases. To explore the statistical validity

of the differences between observed misclassiﬁcation

rates of NEFCLASS classiﬁers for different data sets

and using different discretization techniques, Mann-

Whitney-Wilcoxon (M-W-W) tests were performed.

By running a M-W-W test on the misclassiﬁca-

tion rates for each pair of skewed data sets, the results

shown in Table 2 were obtained. The M-W-W test re-

sults shows that there is a signiﬁcant difference for al-

most all levels of skewness, the only exceptions being

the MED-100,20 and HIGH-35,8 distributions when

the EQUAL-WIDTH discretization method has been

used. We therefore reject the null hypothesis and con-

clude that the NEFCLASS classiﬁcation accuracy was

signiﬁcantly affected by feature value skewness in the

majority of cases.

4.2 The Effect of Discretization

Methods

In this section, we investigate how the choice of dis-

cretization method affects the classiﬁcation accuracy

of a NEFCLASS based classiﬁer, when dealing with

datasets with various degrees of skew. We compare

the results for our new NEFCLASS implementations

using MME and CAIM with the results of the de-

fault EQUAL-WIDTH discretization strategy. The null

hypothesis is that there will be no difference in the ob-

served misclassiﬁcation rates.

Fig. 7 illustrates the placement of initial fuzzy sets

and ﬁnal membership functions when using the MME

discretization method for each of the three datasets.

As can be seen in this ﬁgure, the same number of

Classiﬁcation Confusion within NEFCLASS Caused by Feature Value Skewness in Multi-dimensional Datasets

●

●●

●

100

1. Low−100_100

2. Medium−100_20

3. High−35_8

(a) EQUAL-WIDTH

100

1. Low−100_100

2. Medium−100_20

3. High−35_8

(b) MME

●●

●

100

1. Low−100_100

2. Medium−100_20

3. High−35_8

Figure 9: Summary of misclassiﬁcation rates and number

of rules for EQUAL-WIDTH, MME and CAIM.

fuzzy sets with unequal support are constructed. Sim-

ilarly, in Fig. 8, the fuzzy membership functions pro-

duced using CAIM discretization are shown. The

CAIM algorithm constructed three fuzzy sets for all

features for our test data, however as the algorithm

is free to choose a differing number of discretiza-

tion intervals based on the observed data (Kurgan and

Cios, 2004), for other applications this may vary from

feature to feature. All fuzzy sets generated had dis-

tinct support, range, and a different centre value deﬁn-

ing the triangular membership functions, though there

was still a strong degree of similarity between some

sets, as shown in the representative data displayed in

Fig. 8.

As shown in Figs. 7 and 8, the ﬁnal placement

of support for fuzzy the ﬁrst membership function,

P, is different from the support for Q and R, in con-

trast with the very similar fuzzy set deﬁnitions of

EQUAL-WIDTH shown in Fig. 6. This will preserve a

greater degree of differentiation between the informa-

tion captured in each fuzzy set. A comparison be-

tween the results for MME and CAIM for HIGH-

35,8 (not shown graphically in the paper) indicated

that the choice of the triangular membership functions

produced by CAIM for HIGH-35,8 were slightly dif-

ferent, but the choice of the triangular membership

functions produced by MME were nearly identical.

As the difference between the support of the fuzzy

membership functions and the centre points increases,

the learning phase is more able to create meaningful

new rules. This therefore leads to a lower number

of classiﬁcation errors. The larger number of rules

generated by MME and CAIM for MED-100,20 and

HIGH-35,8 is summarized in Table 1.

Table 3: M-W-W results comparing the misclassiﬁcation

rates based on discretization method.

EQUAL-WIDTH MME

Dataset vs. vs.

MME CAIM CAIM

LOW-100,100 .0020∗ .2500 .1600

MED-100,20 .0001∗ .0001∗ .5000

HIGH-35,8 .0001∗ .0001∗ .9100

* signiﬁcant at 99.9% conﬁdence (p < .001)

As shown in Table 3, M-W-W results identify

the signiﬁcance of the difference in misclassiﬁcation

rates for EQUAL-WIDTH versus MME and CAIM at

medium and high skew, where very low p values are

computed. In the case of LOW-100,100, a signiﬁ-

cant difference is observed when comparing EQUAL-

WIDTH to MME, however with a signiﬁcantly greater

p value (.002). Note that there is no signiﬁcant differ-

ence in misclassiﬁcation performance between MME

and CAIM.

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

5 CONCLUSIONS

The results of this study indicate that the NEFCLASS

classiﬁer performs increasingly poorly as data feature

value skewness increases. Further, this study indi-

cates that the choice of initial discretization method

affects the classiﬁcation accuracy of NEFCLASS clas-

siﬁer, and that this effect is very strong in skewed data

sets. Utilizing MME or CAIM discretization meth-

ods in the NEFCLASS classiﬁer improved classiﬁca-

tions accuracy.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the support of

NSERC, the National Sciences and Engineering Re-

search Council of Canada, for ongoing grant support.

REFERENCES

Au, W., Chan, K., and Wong, A. (2006). A fuzzy approach

to partitioning continues attributes for classiﬁcation.

IEEE Transactions on Knowledge and Data Engineer-

ing, 18:715–719.

Bertoluzza, C. and Forte, B. (1985). Mutual dependence of

random variables and maximum discretized entropy.

The Annals of Probability, 13(2):630–637.

Cano, A., T., N. D., Ventura, S., and Cios, K. J. (2016).

urcaim: improved caim discretization for unbalanced

and balanced data. Soft Computing, 33:173–188.

Changyong, F., Hongyue, W., Naiji, L., Tian, C., Hua, H.,

Ying, L., and Xin, M. (2014). Log-transformation and

its implications for data analysis. Shanghai Arch Psy-

chiatry, 26(2):105–109.

Chau, T. (2001). Marginal maximum entropy partition-

ing yields asymptotically consistent probability den-

sity functions. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 23(4):414–417.

Chemielewski, M. R. and Grzymala-Busse, J. W. (1996).

Global discretization of continuous attributes as pre-

processing for machine learning. International Jour-

nal of Approximate Reasoning, 15:319–331.

Chittineni, S. and Bhogapathi, R. B. (2012). A study on the

behavior of a neural network for grouping the data.

International Journal of Computer Science, 9(1):228–

234.

Gokhale, D. V. (1999). On joint and conditional entropies.

Entropy, 1(2):21–24.

Hubert, M. and Van der Veeken, S. (2010). Robust classi-

ﬁcation for skewed data. Advances in Data Analysis

and Classiﬁcation, 4:239–254.

Kerber, R. (1992). ChiMerge discretization of numeric at-

tributes. In Proceedings of AAAI-92, pages 123–12,

San Jose Convention Center, San Jose, California.

Klose, A., N

urnberger, A., and Nauck, D. (1999). Im-

proved NEFCLASS pruning techniques applied to a

real world domain. In Proceedings Neuronale Netze

in der Anwendung, University of Magdeburg. NN’99.

Kurgan, L. A. and Cios, K. (2004). CAIM discretization al-

gorithm. IEEE Transactions on Knowledge and Data

Engineering, 16:145–153.

Liu, Y., Liu, X., and Su, Z. (2008). A new fuzzy approach

for handling class labels in canonical correlation anal-

ysis. Neurocomputing, 71:1785–1740.

Mansoori, E., Zolghadri, M., and Katebi, S. (2007). A

weighting function for improving fuzzy classiﬁca-

tion systems performance. Fuzzy Sets and Systems,

158:588–591.

Mendel, J. M. (2001). Uncertain Rule-Based Fuzzy Logic

Systems. Prentice-Hall.

Monti, S. and Cooper, G. (1999). A latent variable model

for multivariate discretization. In The Seventh Interna-

tional Workshop on Artiﬁcial Intelligence and Statis-

tics, pages 249–254, Fort Lauderdale, FL.

Natrella, M. (2003). NIST SEMATECH eHandbook of Sta-

tistical Methods. NIST.

Nauck, D., Klawonn, F., and Kruse, R. (1996). Neuro-Fuzzy

Systems. John Wiley and Sons Inc., New York.

Nauck, D. and Kruse, R. (1998). NEFCLASS-X – a soft

computing tool to build readable fuzzy classiﬁers. BT

Technology Journal, 16(3):180–190.

Peker, N. E. S. (2011). Exponential membership func-

tion evaluation based on frequency. Asian Journal of

Mathematics and Statistics, 4:8–20.

Qiang, Q. and Guillermo, S. (2015). Learning transforma-

tions for clustering and classiﬁcation. Journal of Ma-

chine Learning Research, 16:187–225.

Tang, Y. and Chiu, C. (2004). Function approximation via

particular input space partition and region-based ex-

ponential membership functions. Fuzzy Sets and Sys-

tems, 142:267–291.

Zadkarami, M. R. and Rowhani, M. (2010). Application of

skew-normal in classiﬁcation of satellite image. Jour-

nal of Data Science, 8:597–606.

Classiﬁcation Confusion within NEFCLASS Caused by Feature Value Skewness in Multi-dimensional Datasets