EDA-based Decomposition Approach for Binary LSGO Problems
Evgenii Sopov
Department of Systems Analysis and Operations Research, Siberian State Aerospace University, Krasnoyarsk, Russia
Keywords: Large-Scale Global Optimization, Problem Decomposition, Estimation of Distribution Algorithm, Binary
Genetic Algorithm.
Abstract: In recent years many real-world optimization problems have had to deal with growing dimensionality.
Optimization problems with many hundreds or thousands of variables are called large-scale global
optimization (LSGO) problems. Many well-known real-world LSGO problems are not separable and are
complex for detailed analysis, thus they are viewed as the black-box optimization problems. The most
advanced algorithms for LSGO are based on cooperative coevolution schemes using the problem
decomposition. These algorithms are mainly proposed for the real-valued search space and cannot be applied
for problems with discrete or mixed variables. In this paper a novel technique is proposed, that uses a binary
genetic algorithm as the core technique. The estimation of distribution algorithm (EDA) is used for collecting
statistical data based on the past search experience to provide the problem decomposition by fixing genes in
chromosomes. Such an EDA-based decomposition technique has the benefits of the random grouping methods
and the dynamic learning methods. The EDA-based decomposition GA using the island model is also
discussed. The results of numerical experiments for benchmark problems from the CEC competition are
presented and discussed. The experiments show that the approach demonstrates efficiency comparable to
other advanced techniques.
1 INTRODUCTION
Evolutionary algorithms (EAs) have proved their
efficiency at solving many complex real-world
optimization problems. However, their performance
usually decreases when the dimensionality of the
search space increases. This effect is called the “curse
of dimensionality”. Optimization problems with
many hundreds or thousands of objective variables
are called large-scale global optimization (LSGO)
problems.
There exist some classes of optimization
problems that are not hard for either classical
mathematical approaches or more advanced search
techniques (for example, linear programming). At the
same time, real-world optimization problems are
usually complex and not well-studied, so they are
viewed as black-box optimization problems even the
objective has analytical representation (mathematical
formula). Black-box LSGO problems have become a
great challenge even for EAs as we have no
information about the search space to include it into a
certain algorithm. Another challenge is
nonseparability that excludes a straightforward
variable-based decomposition. Nevertheless, some
assumption can be done, and there exist many
efficient LSGO techniques for the continuous search
space (Mahdavi et al., 2015).
Many real-world optimization problems encode
different complex structures and contain variables of
many different types, which cannot be represented
only by real values. In this case binary genetic
algorithms (GAs) can be used. As we can see from
papers, there is a lack of LSGO approaches using the
GA as the core technique.
In this paper a novel LSGO technique using a GA
with a decomposition based on the estimation of
distribution algorithm (EDA) is proposed. The binary
EDA is used to present a statistic of the past search
experience of the GA and to predict the values of
problem subcomponents that are being fixed to
decrease the problem dimensionality.
The rest of the paper is organized as follows.
Section 2 describes related work. Section 3 describes
the proposed approach. In Section 4 the results of
numerical experiments are discussed. In the
Conclusion the results and further research are
discussed.
132
Sopov, E.
EDA-based Decomposition Approach for Binary LSGO Problems.
DOI: 10.5220/0006034301320139
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 132-139
ISBN: 978-989-758-201-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
There exist a great variety of different LSGO
techniques that can be combined in two main groups:
non-decomposition methods and cooperative
coevolution (CC) algorithms. The first group of
methods are mostly based on improving standard
evolutionary and genetic operations. But the best
results and the majority of approaches are presented
by the second group. The CC methods decompose
LSGO problems into low dimensional sub-problems
by grouping the problem subcomponents. CC
consists of three general steps: problem
decomposition, subcomponent optimization and
subcomponent coadaptation (merging solutions of all
subcomponents to construct the complete solution).
The problem decomposition is a critical step. There
are many subcomponent grouping methods,
including: static grouping (Potter and De Jong, 2000),
random dynamic grouping (Yang et al., 2008) and
learning dynamic grouping (Liu and Tang, 2013;
Omidvar et al., 2014). A good survey on LSGO and
methods is proposed in (Mahdavi et al., 2015). As we
can observe in papers, almost all studies are focused
on continuous LSGO, and there is a lack of
techniques for binary (or other discrete)
representations.
The EDA is a stochastic optimization technique
that explores a space of potential solutions by
building and sampling explicit probabilistic models.
The estimated distribution can be used for improving
standard search techniques. There exist some hybrid
EDA-EA approaches for LSGO (Dong et al., 2013;
Wang and Li, 2008). These hybrid EDA-EA
techniques are also designed for continuous LSGO.
The most widely known competition on LSGO
has been held within the IEEE Congress on
Evolutionary Computation (CEC) since 2008. As we
can see from the last competition, the majority of
proposed methods are based on the random dynamic
grouping and continuous search techniques.
3 PROPOSED APPROACH
3.1 EDA-based Decomposition
The main idea of the LSGO problem decomposition
methods is based on the divide-and-conquer approach
which decomposes the problem into single-variable
or multiple-variable low dimensional problems. In
this case, only part of the variables are used in the
search process; the rest are fixed and their values are
defined using some strategy (for example, values
from the best-found solution are used).
The finding of an appropriate decomposition is
part of the general search process. It is obvious and
has been presented in many studies that the best
performance is achieved with separable LSGO
problems. In the case of non-separable problems, the
performance strongly depends on the decomposition
strategy.
In this work, we will formulate the following
requirements for the proposed decomposition
method:
 The grouping should be dynamic to realize the
“exploration and exploitation” strategy.
 The grouping should be random to avoid the
greedy search and the local convergence.
 The grouping should be based on the past
search experience of the whole population (to
provide the global search options).
 The grouping should be adaptively scalable to
provide efficient decomposition at every stage
of the search process.
As is known, GAs do not collect a statistic of the
past generations in an explicit form, but it is contained
in the genes of individuals in the population. One of
the ways to present the statistic is to evaluate the
distribution of binary values as in the binary EDA.
The following probability vector can be used (1):

(

)
=

(

)
,

(

)
,…,

(

)
,


(

)
=
(


=1
)
=
1






,=1,
(1)
where t is the number of the current generation, 

is
the probability of a one-value for the i-th position in
chromosomes of individuals in the last population, 


is the value of the i-th gene of the j-th individual, n is
the chromosome length, and N is the size of the
population.
The distribution calculated at the t-th generation
describes the generalized statistic collected by the GA
in the population. We can also analyse the dynamic
of the statistic over a series of generations. In (Sopov
and Sopov, 2011) a convergence property of the
probability vector components is discussed.
Experiments have shown that for a GA that converges
to the global optima, the probability vector values
converge to one if the corresponding position of the
optimal solution contains a one, and converge to zero
otherwise.
We will use this convergence property to define
the values for fixed genes at the grouping stage. If the
i-th position in a chromosome at the t-th generation is
EDA-based Decomposition Approach for Binary LSGO Problems
133

Figure 1: The dynamic of the probability vector component (the vertical axis is the value of the probability vector
component, the horizontal axis is generation number).
fixed, its value is defined by the corresponding value
of the probability vector (2):



(

)
==
0, 

(

)
<
(
0.5−
)
,

(

)
ϵ(0.5−δ,0.5+)
1, 

(

)
>(0.5+)
(2)
where  is a threshold (a confidence level), ∈
(0,0.5).
We will explain the proposed approach using
Figure 1. The diagram visualizes an arbitrary
component of the probability vector for an arbitrary
run of a GA on the Rastrigin function. For the chosen
gene the corresponding value of the optimal solution
is equal to zero. As we can see from Figure 1, the GA
starts with random initialization, thus the value of the
probability vector is equal to 0.5. At the first
generations the GA actively explores the search space
and number of 1’s and 0’s genes are almost equal,
thus the value of the probability vector is still about
0.5. After that, the GA locates a promising region in
the search space and increases the number of 0’s in
this position, thus the value of the probability vector
decreases towards zero.
The confidence level  is a parameter that defines
a threshold for the probability value around 0.5, when
we cannot make a decision about the gene value.
Although a decision about fixed variables is made
by stand-alone components, the estimated
distribution contains information about the problem
solving in general. Thus the method is not focused
only on separable LSGO problems.
Next we need to define the number of variables
that will be fixed. There exist many strategies. For
example, the splitting-in-half method divides an n-
dimensional problem into two n/2 subcomponents. In
general, we will define the number of fixed variables
as a percentage of the chromosome length and will
denote it as . The value of  can be constant or can
change during the run of the algorithm. The variables
and corresponding components of the probability
vector are fixed for some predefined number of
generations, which is called an adaptation period
(denoted as 

). The list of fixed components is
randomly defined.
In this paper, the straight-forward approach is
used,  and 

are predefined and constant.
The main advantage of such EDA-based
decomposition is that we do not lose the previously
collected statistic as we fix components of the
probability vector. The GA solves the problem of
reduced dimensionality and updates the probability
only for active components. After each adaptation
period we will randomly fix other components, and
the previously fixed components will continue
updating their saved values.
3.2 The GA with EDA-based
Decomposition for LSGO
We will describe the proposed LSGO algorithm in
detail.
First, we need to encode the initial problem into a
binary representation. The standard binary or Grey
code can be used. A chromosome length n is defined.
Next, specific parameters of the EDA-based
decomposition and the chosen GA, maximum number
of fitness evaluations (MaxFE) or maximum number
of generations (MaxGEN) are defined. The maximum
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
134

number of generations can be substituted with any
other stop condition (for example, time-based
condition).
Finally, the following algorithm is used:
Input: n, N, , , 

, MaxFE, the
GA operators’ parameters.
Initialization:
Randomly generate a population of N
individuals of the length n.
Calculate P(0) using formula (1).
Main loop.
Until MaxFE is reached:
1. Problem decomposition stage: Start
new adaptation period. Fix random 
components in chromosomes and in the
probability vector.
2. Subcomponent optimization stage:
Run the GA for 

generations:
a. Fitness evaluation. Set
values in fixed positions of chromosomes
according to P(t) using formula (2).
b. Perform selection, crossover
and mutation operations.
c. Create next generation, update
the probability vector P(t) for active
components.
Output: the best-found solution.
3.3 Parallel Modification with
Self-Configuration
Many proposed LSGO approaches with the
subcomponent grouping are based on cooperative
coevolution. In this case, many populations are used,
which evolve different groups of subcomponents. The
cooperation is used on the fitness evaluation step to
define the values of components that were fixed
during the algorithm run. Usually, components of the
best individuals from other populations are used.
We will introduce many parallel populations
using the following scheme. At the main loop, the
total population of size N is divided into K
populations of size M, where =∙. For each
population the problem decomposition and the
subcomponent optimization steps are independently
performed. Thus each population can be viewed as an
island with its own decomposition strategy. When the
adaptation period is over, all individuals from all
populations are collected back into the total
population and the summary statistic is updated. This
step can be viewed as the cooperation.
As is known, the island model GA can outperform
the standard single-population GA for many complex
optimization problems (Gonga et al., 2015). We can
also decrease the computational time by
implementing the GA with a parallel multi-core or
multi-processor computer.
We will use the following approach for self-
configuration of the GA parameters. First, we define
a list of different genetic operators: selection types,
crossover types and values of mutation intensity.
Next, we set probabilities for each operator to be
chosen. All probabilities are initialized with equal
values. During the GA run, we define a combination
of genetic operators, which is used for producing
offspring according to the given probabilities
distribution. Finally, after each generation we
redistribute the probabilities in order to increase
probabilities of operators that have produced
offspring with better fitness values. More detailed
information about the approach can be found in
(Semenkin and Semenkina, 2012).
Also we will provide additional interaction of
subpopulation in the island model using concept
proposed in (Sopov, 2015). We will increase the size
of island with the best performance over some
predefined number of generations (adaptation
period). The migration operation will copy the current
best-found solution to each island to equate the start
positions of all population for the next adaptation
period.
4 EXPERIMENTAL RESULTS
To estimate the proposed approach performance, we
have used 15 large-scale benchmark problems from
the CEC’2013 Special Session and Competition on
Large-Scale Global Optimization (Li et al., 2013a).
These problems represent a wider range of real-world
large-scale optimization problems and provide
convenience and flexibility for comparing various
evolutionary algorithms specifically designed for
large-scale global optimization. There are 3 fully-
separable problems (denoted as f1-f3), 8 partially
separable problems (f4-f7 with a separable
subcomponent and f8-f11 with no separable
subcomponents), 3 problems with overlapping
subcomponents (f12-f14), and 1 non-separable
problem (f15).
The experiment settings are:
 Dimensions for all problem are D=1000;
 The standard binary encoding is used with
accuracies: =0.1 for f1, f4, f7, f8 and f11-15,
=0.05 for f3, f6 and f10, and =0.01 for f2, f5
and f9;
EDA-based Decomposition Approach for Binary LSGO Problems
135

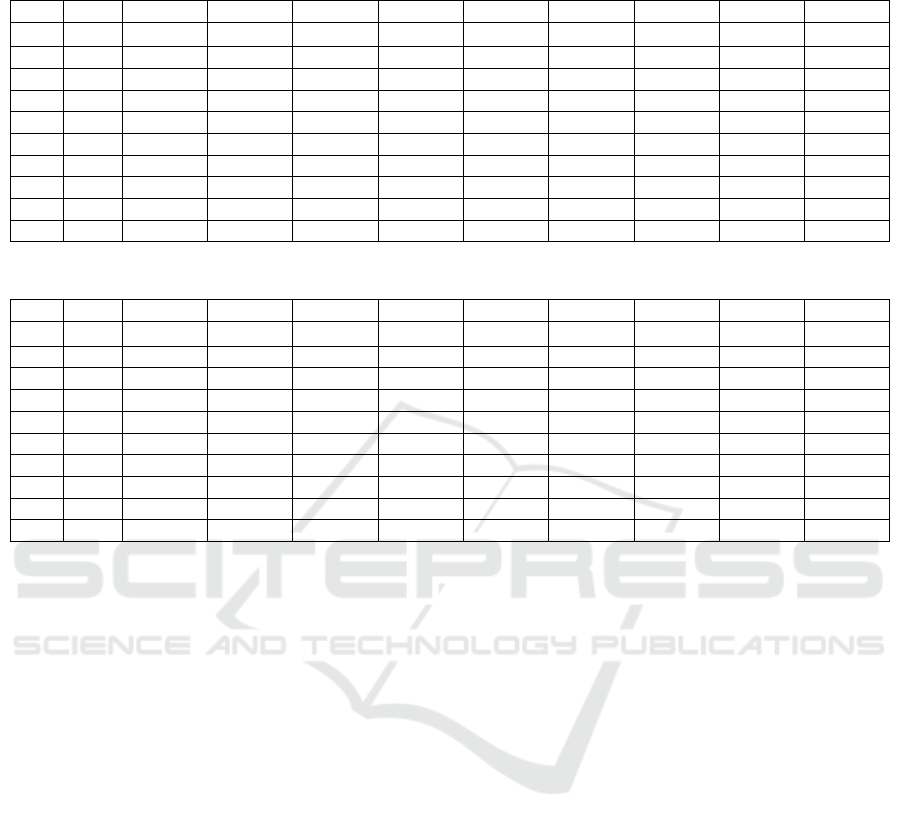
Table 1: Experimental results for the f1 problem and the EDA-based decomposition with the single-population GA.

25 25 25 50 50 50 75 75 75

0.05 0.15 0.25 0.05 0.15 0.25 0.05 0.15 0.25
1.2e5 Best 2.08E+07 1.98E+07 1.72E+07 1.89E+07 1.50E+07 1.59E+07 1.98E+07 1.53E+07 1.76E+07
Mean 6.13E+07 5.97E+07 6.81E+07 8.95E+07 4.98E+08 7.32E+07 8.30E+07 8.72E+07 7.23E+07
StDev 3.31E+07 2.90E+07 2.70E+07 3.74E+07 2.98E+07 3.51E+07 3.66E+07 3.93E+07 3.34E+07
6.0e5 Best 1.99E+03 2.11E+03 1.71E+03 2.55E+04 8.23E+03 1.50E+03 1.23E+04 9.20E+03 9.00E+03
Mean 2.71E+04 2.53E+04 2.22E+04 3.47E+04 2.19E+04 1.99E+04 3.88E+04 2.51E+04 3.02E+04
StDev 9.47E+03 9.36E+03 7.90E+03 1.85E+04 1.68E+03 7.08E+03 1.85E+04 1.20E+04 1.69E+04
3.0e6 Best 9.32E-05 8.02E-05 7.63E-05 4.50E-05 4.59E-05 7.11E-05 6.73E-05 5.19E-05 6.34E-05
Mean 4.00E-04 4.23E-04 4.51E-04 5.01E-04 5.68E-04 4.98E-04 4.02E-04 3.80E-04 3.56E-04
StDev 2.24E-04 2.09E-04 2.19E-04 2.08E-04 4.29E-04 2.11E-04 1.95E-04 1.65E-04 1.82E-04
Table 2: Experimental results for the f1 problem and the EDA-based decomposition with the island GA.

25 25 25 50 50 50 75 75 75

0.05 0.15 0.25 0.05 0.15 0.25 0.05 0.15 0.25
1.2e5 Best 1.76E+07 1.79E+07 1.73E+07 1.62E+07 1.56E+07 1.63E+07 1.62E+07 1.42E+07 1.45E+07
Mean 4.90E+07 4.95E+07 5.61E+07 5.72E+07 5.34E+07 5.39E+07 6.16E+07 5.50E+07 5.23E+07
StDev 3.04E+07 3.01E+07 2.23E+07 3.15E+07 2.98E+07 2.12E+07 2.41E+07 2.98E+07 2.44E+07
6.0e5 Best 8.68E+03 8.61E+03 8.41E+03 7.72E+03 7.58E+03 7.65E+03 8.50E+03 7.00E+03 6.89E+03
Mean 1.85E+04 1.79E+04 2.07E+04 2.17E+04 2.15E+04 1.77E+04 1.81E+04 2.21E+04 1.99E+04
StDev 8.60E+03 9.33E+03 1.07E+04 1.28E+04 1.68E+03 8.12E+03 1.18E+04 9.19E+03 1.68E+03
3.0e6 Best 5.78E-05 5.92E-05 5.46E-05 5.09E-05 5.00E-05 4.91E-05 5.47E-05 4.59E-05 4.95E-05
Mean 6.13E-04 5.45E-04 5.17E-04 5.51E-04 5.06E-04 5.40E-04 5.98E-04 5.68E-04 5.44E-04
StDev 2.47E-04 2.37E-04 2.19E-04 2.24E-04 4.29E-04 2.21E-04 2.40E-04 4.29E-04 2.22E-04
 For each problem the best, mean, and standard
deviation of the 25 independent runs are
evaluated;
 Maximum number of fitness evaluations is
MaxFE=3.0e+6;
 The performance estimation is performed for
the number of fitness evaluations equal to
1.2e+5, 6.0e+5 and 3.0e+6.
The EDA-based decomposition GA settings are:
 Population sizes are N=1000 for the single-
population version, N=500 for the island
version with 3 islands, and N=400 for 5 islands;
 The adaptation period is 

=100;
 The probability threshold is =0.05, 0.15 and
0.25;
 Numbers of fixed components are =25%,
50% and 75% of the chromosome length.
All algorithms have been implemented in Visual
Studio C++ using the OpenMP for parallel computing
with multi-core PC. Free C++ source codes of the
benchmark problems are taken from
(http://goanna.cs.rmit.edu.au/~xiaodong/cec13-lsgo/
competition/lsgo_2013_benchmarks.zip, 2013).
We have carried out the above-mentioned
experiments and have established the following. In
the case of single population, the best performance on
average is achieved with 50% fixed components and
=0.15. In the case of the island model, the best
results are obtained by the 5 island model with 75%
fixed components and =0.15. Almost for every
considered value of parameters, the island model
outperforms the single population version of the
algorithm.
Let’s discuss it in detail. We have estimated the
algorithm performance for each benchmark problem
varying the percentage of fixed components () and
the confidence level value (). The results for the f1
problem are presented in Table 1 and 2. Table 1
contains the results obtained with the single-
population algorithm, and. Table 2 contains results
obtained with the 5 island GA. As we can see from
Tables, the island model version outperforms the
single-population version almost for all combinations
of parameters.
We have visualized the best-found value
depending on the  and the  parameters for each of
3 numbers of fitness evaluations. The best-found
value has been normalized to [0, 1] interval and
averaged over all benchmark problems. The
dependences are presented in Figures 2 and 3. As we
can see from Figures, the best performance on
average is obtained with high percentage of fixed
components. In the case of single population, the best
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
136

Figure 2: Performance of the single-population algorithm via the and the parameters change for MaxFE={1.2e+5, 6.0e+5,
3.0e+6}.
Figure 3: The Performance of the 5 island algorithm via the and the parameters change for MaxFE={1.2e+5, 6.0e+5,
3.0e+6}.
components. In the case of single population, the best
combination is (=50%, =0.15) for the
MaxFE=1.2e+5, but it shifts to (=50%, =0.25) for
the MaxFE=6.0e+5 and 3.0e+6. In the case of the
island model, the best combinations are (=75%,
=0.25) for the MaxFE=1.2e+5 and (=75%,
=0.15) for the MaxFE=6.0e+5 and 3.0e+6. Our
hypothesis is that the algorithm requires different
parameters settings for different stages of the search
process. In further work, an adaptive parameters
tuning will be introduces and investigated.
The experimental results for the best found
settings are presented in Table 3. The summary
results are compared with other techniques presented
at the CEC’13 competition. The algorithms are
DECC-G (differential evolution (DE) based
cooperative coevolution (CC) with random dynamic
grouping) (Yang et al., 2008), VMO-DE (variable
mesh optimization using differential evolution) (Li et
al., 2013b), CC-CMA-ES (Covariance Matrix
Adaptation Evolution Strategy using Cooperative
Coevolution) (Liu and Tang, 2013), MOS (Multiple
Offspring Sampling (MOS) based hybrid algorithm)
(LaTorre et al., 2013), and SACC (smoothing and
auxiliary function based cooperative coevolution)
(Wei et al., 2013). We have averaged the performance
estimates of all algorithms over all problems and have
ranked algorithms by the Best and the Mean values.
The results are in Table 4.
As we can see from Table 4, the proposed
approach has taken 4th place by the Best criterion and
5th place by the Mean value. We should note that all
algorithms except the proposed are specially designed
for continuous LSGO problems. The EDA-based
decomposition GA does not use any knowledge about
search space. Moreover, the chromosome length in
the binary algorithm is greater than in the case of the
continuous space. Nevertheless, the EDA-based
decomposition GA outperforms the CC-CMA-ES by
two measures and the DECC-G by the Best value on
average.
Our hypothesis is that the proposed approach will
be a good tool for solving complex real-world LSGO
problems, which usually contain not only continuous
variables, but mixed-type variables and can represent
arbitrary complex structures. Further investigations
of the algorithm structure and parameters can
probably improve its performance. In particular, the
 value can be adjusted adaptively during the
algorithm run using information about the probability
vector convergence.
EDA-based Decomposition Approach for Binary LSGO Problems
137

Table 3: Experimental results for the EDA-based decomposition GA with 5 islands and =75%.
f1 f2 f3 f4 f5 f6 f7 f8
1.2e5 Best 1.42E+07 9.63E+03 1.08E+02 1.39E+11 6.11E+14 2.90E+05 7.05E+08 3.97E+15
Mean 5.50E+07 1.06E+04 4.52E+01 9.15E+11 7.17E+14 7.78E+05 2.76E+09 2.71E+16
StDev 2.98E+07 1.53E+03 1.44E+01 5.63E+11 7.45E+08 2.61E+05 1.44E+09 6.77E+15
6.0e5 Best 6.89E+03 9.11E+03 3.04E+00 1.95E+10 3.07E+14 5.21E+05 2.01E+08 2.09E+14
Mean 1.99E+04 1.25E+04 1.30E+01 9.07E+10 5.03E+14 6.05E+05 9.41E+08 2.18E+15
StDev 1.68E+03 1.18E+03 6.32E-01 6.03E+10 2.50E+07 2.60E+05 7.56E+08 1.52E+15
3.0e6 Best 4.59E-05 1.82E+03 2.94E-05 6.60E+09 7.59E+14 6.25E+04 7.65E+07 4.49E+13
Mean 5.68E-04 3.34E+03 4.81E-01 2.32E+10 9.75E+14 4.75E+05 2.53E+08 3.64E+14
StDev 4.29E-04 2.54E+02 2.28E-01 1.14E+10 2.18E+06 3.35E+05 8.35E+07 5.21E+14
f9 f10 f11 f12 f13 f14 f15 Average
1.2e5 Best 1.08E+09 8.87E+06 1.46E+11 3.87E+06 2.66E+10 1.88E+11 3.61E+07 3.05E+14
Mean 1.80E+09 7.14E+07 3.47E+11 4.36E+08 2.98E+10 5.78E+11 2.69E+08 1.85E+15
StDev 4.27E+08 1.57E+07 2.25E+11 7.89E+08 1.12E+10 3.67E+11 9.91E+07 4.52E+14
6.0e5 Best 6.42E+08 7.91E+06 1.34E+10 2.40E+03 6.28E+09 5.68E+10 1.80E+07 3.44E+13
Mean 1.25E+09 1.38E+07 9.84E+10 6.66E+03 1.47E+10 1.03E+11 2.43E+07 1.79E+14
StDev 5.21E+08 1.65E+07 1.18E+11 5.53E+03 4.83E+09 6.70E+10 8.68E+06 1.02E+14
3.0e6 Best 4.15E+08 6.18E+06 2.60E+10 7.72E+02 8.02E+09 1.42E+10 2.40E+07 5.36E+13
Mean 8.06E+08 1.61E+07 7.01E+10 2.30E+03 1.27E+10 1.69E+11 3.05E+07 8.93E+13
StDev 1.72E+08 7.89E+06 4.29E+10 2.41E+03 2.96E+09 4.81E+10 5.13E+06 3.47E+13
Table 4: LSGO approaches comparison.
Algorithm SACC MOS VMO-DE DECC-G
C
C-CMA-ES EDA-GA
Best 9.80E+12 2.17E+11 4.90E+13 5.80E+13 6.25E+13 5.36E+13
Ranking
by Best
2 1 3 5 6 4
Mean/
StDev
8.0E+13/
5.08E+13
5.33E+11/
2.04E+11
5.32E+13/
4.81E+12
7.7E+13/
1.02E+13
8.58E+13/
2.39E+13
8.93E+13/
3.47E+13
Ranking
by Mean
4 1 2 3 6 5
5 CONCLUSIONS
In this paper a novel technique for LSGO that uses a
binary GA with EDA-based decomposition is
proposed. The EDA is used for collecting statistical
data based on the past search experience to predict the
convergence of subcomponents and to decrease the
problem dimensionality by fixing some genes in
chromosomes. We have compared a single population
and the island model implementations of the
algorithm. The best results have been obtained with
the island model version. It yields state-of-the-art
LSGO techniques, but the performance is
comparable. The advantage of the proposed approach
is that it can be applied to problems with arbitrary
representations and it needs no a priori information
about the search space.
In further work, more detailed analysis of the
EDA-based decomposition GA parameters will be
provided. A self-configuration will be introduced into
the algorithm.
ACKNOWLEDGEMENTS
The research was supported by the President of the
Russian Federation grant (MK-3285.2015.9).
REFERENCES
Dong, W., Chen, T., Tino, P., Yao, X., 2013. Scaling up
estimation of distribution algorithms for continuous
optimization. IEEE Trans. Evol. Comput. 17 (6). pp.
797–822.
Gonga Y.-J., Chena, W.N., Zhana, Zh.-H., Zhanga, J., Li,
Y., Zhange, Q., Lif, J.-J., 2015. Distributed evolution-
nary algorithms and their models: A survey of the state-
of-the-art. Applied Soft Computing, 34. pp. 286–300.
LaTorre, A., Muelas, S., Pena, J.-M., 2013. Large scale
global optimization: experimental results with MOS-
based hybrid algorithms. In 2013 IEEE Congress on
Evolutionary Computation (CEC). pp. 2742–2749.
Li, X., Tang, K., Omidvar, M.N., Yang, Zh., Qin, K., 2013a.
Benchmark functions for the CEC 2013 special session
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
138

and competition on large-scale global optimization.
Technical Report, Evolutionary Computation and
Machine Learning Group, RMIT University, Australia.
Li, X., Tang, K., Omidvar, M.N., Yang, Zh., Qin, K.,
2013b. Technical report on 2013 IEEE Congress on
Evolutionary Computation Competition on Large Scale
Global Optimization. [online] Available at:
http://goanna.cs.rmit.edu.au/~xiaodong/cec13-
lsgo/competition/lsgo-competition-sumary-2013.pdf.
Liu, J., Tang, K., 2013. Scaling up covariance matrix
adaptation evolution strategy using cooperative
coevolution. In Intelligent Data Engineering and
Automated Learning – IDEAL 2013. pp. 350–357.
Springer.
Mahdavi, S., Shiri, M.E., Rahnamayan, Sh., 2015.
Metaheuristics in large-scale global continues
optimization: A survey. Information Sciences, Vol.
295. pp. 407–428.
Omidvar, M.N., Li, X., Mei, Y., Yao, X., 2014. Cooperative
co-evolution with differential grouping for large scale
optimization. IEEE Trans. Evol. Comput. 18 (3). pp.
378–393.
Potter, M., De Jong, K.A., 2000. Cooperative coevolution:
an architecture for evolving coadapted subcomponents.
Evol. Comput. 8 (1). pp. 1–29.
Semenkin, E.S. and Semenkina, M.E., 2012. Self-
configuring Genetic Algorithm with Modified Uniform
Crossover Operator. Advances in Swarm Intelligence.
Lecture Notes in Computer Science 7331. Springer-
Verlag, Berlin Heidelberg. pp. 414-421.
Sopov, E., 2015. A Self-configuring Metaheuristic for
Control of Multi-Strategy Evolutionary Search. ICSI-
CCI 2015, Part III, LNCS 9142. pp. 29-37.
Sopov, E., Sopov, S., 2011. The convergence prediction
method for genetic and PBIL-like algorithms with
binary representation. In IEEE International Siberian
Conference on Control and Communications, SIBCON
2011. pp. 203-206.
Test suite for the IEEE CEC’13 competition on the LSGO.
[online] Available at: http://goanna.cs.rmit.edu.au/
~xiaodong/cec13-lsgo/competition/lsgo_2013_bench
marks.zip.
Wang, Y., Li, B., 2008. A restart univariate estimation of
distribution algorithm: sampling under mixed gaussian
and lévy probability distribution. In IEEE Congress on
Evolutionary Computation, CEC 2008 (IEEE World
Congress on Computational Intelligence). pp. 3917–
3924.
Wei, F., Wang, Y., Huo, Y., 2013. Smoothing and auxiliary
functions based cooperative coevolution for global
optimization. In 2013 IEEE Congress on Evolutionary
Computation (CEC). pp. 2736–2741.
Yang, Zh., Tang, K., Yao, X., 2008. Large scale
evolutionary optimization using cooperative
coevolution. Inform. Sci. 178 (15). pp. 2985–2999.
EDA-based Decomposition Approach for Binary LSGO Problems
139