
Skip Search Approach for Mining Probabilistic Frequent Itemsets
from Uncertain Data
Takahiko Shintani, Tadashi Ohmori and Hideyuki Fujita
Graduate School of Informatics and Engineering, The University of Electro-Communications, Tokyo, Japan
Keywords:
Frequent Itemset, Probabilistic Data, Uncertain Data.
Abstract:
Due to wider applications of data mining, data uncertainty came to be considered. In this paper, we study
mining probabilistic frequent itemsets from uncertain data under the Possible World Semantics. For each tuple
has existential probability in probabilistic data, the support of an itemset is a probability mass function (pmf).
In this paper, we propose skip search approach to reduce evaluating support pmf for redundant itemsets. Our
skip search approach starts evaluating support pmf from the average length of candidate itemsets. When an
evaluated itemset is not probabilistic frequent, all its superset of itemsets are deleted from candidate itemsets
and its subset of itemset is selected as a candidate itemset to evaluate next. When an evaluated itemset is
probabilistic frequent, its superset of itemset is selected as a candidate itemset to evaluate next. Furthermore,
our approach evaluates the support pmf by difference calculus using evaluated itemsets. Thus, our approach
can reduce the number of candidate itemsets to evaluate their support pmf and the cost of evaluating support
pmf. Finally, we show the effectiveness of our approach through experiments.
1 INTRODUCTION
One of important problems in data mining is
a discovery of frequent itemsets within a large
database(Agrawal and R.Srikant, 1994; Han et al.,
2000). Due to wide applications in frequent item-
set mining, data uncertainty came to be consid-
ered(Aggarwal and Yu, 2009). For example, data col-
lected by sensor device are noisy. The locations of
users obtained through GPS systems are not precise.
The user activities that were estimated from the ac-
celeraion sensor data are underspecified. The uncer-
tain data is the probabilistic database which each item
and/or transaction has a probability value, called at-
tribute uncertainty model and tuple uncertainty model
respectively. On the probabilistic database, frequent
itemsets are probabilistic. The support of an itemset
is a random variable. Several algorithms for mining
frequent itemsets from uncertain data have been pro-
posed. In (Chuim et al., 2007; Leung et al., 2007;
Leung et al., 2008; Aggarwal et al., 2009; Wang
et al., 2013; MacKinnon et al., 2014; Cuzzocrea
et al., 2015), the frequent itemsets are detected by
their expected support count. However, it is reported
that many important itemsets are missed by using ex-
pected support(Zhang et al., 2008).
By using the Possible Worlds Semantics (PWS),
we can interpretprobabilistic databases(Dalvi and Su-
ciu, 2004). A possible world means the case where
a set of transactions occurs. We can find frequent
itemsets under PWS by counting their support counts
from every possible world. Since the enormous num-
ber of possible worlds have to be considered, this is
impractical. The approximate algorithms for finding
frequent itemsets from the attribute uncertain model
and tuple uncertain model were proposed(Wang et al.,
2012; Leung and Tanbeer, 2013), but these algo-
rithms cannot find exact solutions. In (Zhang et al.,
2008), the algorithm for finding exact solutions of fre-
quent items were proposed, but this algorithm can-
not handle itemsets. The algorithms for finding exact
solution of probabilistic frequent itemsets were pro-
posed in (Bernecker et al., 2009; Sun et al., 2010).
The bottom-up manner algorithm finds frequent item-
sets in ascending order of length like Apriori algo-
rithm(Agrawal and R.Srikant, 1994). This algorithm
can prune candidate itemsets by Apriori down-closed
property. The dynamic programing (DP)(Bernecker
et al., 2009) and divide-and-conquer (DC)(Sun et al.,
2010) for evaluating the support probability were pro-
posed. DP and DC evaluate the support probabil-
ity from scratch, so its cost is high. In (Sun et al.,
2010), the top-down manner algorithm, TODIS, was
proposed. TODIS can evaluate the support probabil-
174
Shintani, T., Ohmori, T. and Fujita, H.
Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data.
DOI: 10.5220/0006035401740180
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 174-180
ISBN: 978-989-758-203-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: Example of PDB.
TID Transaction Existential Prob.
T
1
{a, e, f, g} 0.7
T
2
{a, b, e, g} 1.0
T
3
{b, c, h, i, j} 0.5
T
4
{b, d, f, h, j} 0.8
ity function by inheriting a superset of the itemset, but
it involves evaluating many redundant itemsets.
In this paper, we study mining probabilistic fre-
quent itemsets from uncertain data in the tuple un-
certainty model under PWS by extending our previ-
ous study(Tateshima et al., 2015). We propose skip
search approach to avoid evaluating redundant item-
sets which becomes probabilistic infrequent. Our skip
search approach starts to evaluate the support prob-
ability from the average length of itemsets. When
the evaluated itemset is not probabilistic frequent, it’s
super-itemset is evaluated next. When the evaluated
itemset is probabilistic frequent, its sub-itemset is
evaluated next. Moreover, our skip search approach
evaluates the support probability function efficiently
by difference calculus. We show the effectiveness of
our skip search approach by experiments.
This paper is organized as follows. In the next sec-
tion, we explain the problem of mining probabilistic
frequent itemsets. In section 3, we propose our skip
search approach. Performance evaluations are given
in section 4. Section 5 concludes this paper.
2 MINING PROBABILISTIC
FREQUENT ITEMSETS
First, we introduce basic concepts of frequent item-
sets on exact databases. Let L = {i
1
, i
2
, . . . , i
m
} be a
set of literals, called items. Let D = {t
1
,t
2
, . . . ,t
n
} be
a set of transactions, where each transaction t is a set
of items such that t ⊆ I . A transaction has an asso-
ciated unique identifier called TID. A set of items
X ⊆ I is called an itemset. Itemset X is a sub-itemset
of itemset Y if and only if X is a subset of Y. Y is
called a super-itemset of X. We say each transaction
t contains an itemset X, if X ⊆ t. The itemset X has
support s in D if s transactions contain X, here we
denote s = sup(X).
In the tuple uncertainty model, each transaction
t
i
has an existential probability p
i
. Here 0 < p
i
≤ 1.
Existential probability indicates the probability of the
transaction occurs. Example of probabilistic database
(PDB) in tuple uncertainty model is shown in Table
1. Table 1 consists of ten items with four transac-
tions. For example, T
1
denotes that the probability of
Table 2: Possible worlds for Table 1.
W Occurred transactions Prob. P(W)
W
1
T
2
0.03
W
2
T
1
, T
2
0.07
W
3
T
2
, T
3
0.03
W
4
T
2
, T
4
0.12
W
5
T
1
, T
2
, T
3
0.07
W
6
T
1
, T
2
, T
4
0.28
W
7
T
2
, T
3
, T
4
0.12
W
8
T
1
, T
2
, T
3
, T
4
0.28
a transaction {a, e, f, g} occurs is 0.7.
We can interpret PDB by using PWS. Table 2
shows all possible worlds for PDB in Table 1. Here,
the probability of a possible world W
i
is denoted as
P(W
i
), the sum of them is 1(=
∑
i
P(W
i
)). For exam-
ple,W
2
denotes the case where T
1
and T
2
occur,T
3
and
T
4
do not occur. The probability of W
2
is calculated
as follows: P(W
2
) = p
T
1
∗ p
T
2
∗(1− p
T
3
)∗(1− p
T
4
) =
0.7∗ 1.0∗ (1 − 0.5) ∗ (1− 0.8) = 0.07.
Since there are many possible worlds and each
possible world has a probability, the support of an
itemset becomes a random variable. We denote f
X
(k)
as the probability mass function(pmf) of an itemset X
at sup(X) = k(k ≥ 0). For example, itemset {b, h} is
contained in T
3
and T
4
. When both T
3
and T
4
occur,
sup({b, h}) becomes 2. The possible worlds where
both T
3
and T
4
occur are W
7
and W
8
, f
{b,h}
(2) =
P(W
7
) + P(W
8
) = 0.4. When either T
3
or T
4
oc-
curs, sup({b, h}) becomes 1. The possible worlds
where either T
3
or T
4
occurs are W
3
,W
4
,W
5
and W
6
,
f
{b,h}
(1) = P(W
3
) + P(W
4
) + P(W
5
) + P(W
6
) = 0.5.
When neither T
3
nor T
4
occurs, sup({b, h}) becomes
0. The possible worlds where neither T
3
nor T
4
occurs
are W
1
and W
2
, f
{b,h}
(0) = P(W
1
) + P(W
2
) = 0.1.
In PDB, we define that an itemset X is probabilis-
tic frequent if the following equation is satisfied.
Pr(sup(X) ≥ minsup) ≥ minprob (1)
Here, Pr(sup(X) ≥ minsup) is the sum of the prob-
ability that sup(X) is minsup or more. minsup
and minprob are user-specified minimum thresholds
of the support and the probability. For example,
Pr(sup({b, h}) = f
{b,h}
(2) + f
{b,h}
(1) = 0.9 when
minsup = 1. If minprob = 0.7, {b, h} is probability
frequent.
The problem of mining probabilistic frequent
itemsets is to find all itemsets that satisfy equation 1
on the assumption that we are given minsup, minprob
and PDB.
In (Sun et al., 2010), the bottom-up manner al-
gorithm, a-Apriori, was proposed. The p-Apriori
finds probabilistic frequent itemsets in ascending or-
der of length like Apriori. In the first pass (pass
Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data
175

1), the support pmf(spmf) for each item are eval-
uated. All the items which satisfy equation 1 are
picked out. These items are called probabilistic fre-
quent 1-itemsets. Here after, k-itemset is defined
a set of k items. The second pass, the 2-itemsets
are generated using probabilistic frequent 1-itemsets,
which are called candidate 2-itemsets. Then spmf
for each candidate 2-itemsets are evaluated, the prob-
abilistic frequent 2-itemsets which satisfy equation
1 are determined. In k-th pass, the candidate k-
itemsets are generated by using probabilistic frequent
(k − 1)-itemsets, spmf for each candidates are evalu-
ated, and the probabilistic frequent k-itemsets are de-
termined. The candidate generation is same as Apri-
ori. This iteration terminates when the probabilistic
frequent itemset becomes empty. The dynamic pro-
graming(DP) algorithm(Bernecker et al., 2009) and
divide-and-conquer(DC) algorithm(Sun et al., 2010)
for evaluating spmf have been proposed. These algo-
rithms do not examine possible worlds. By examin-
ing all transactions in PDB for each candidateitemset,
DC evaluated spmf. The DC divides D into D
1
and
D
2
, spmf of X is evaluated by the convolution of f
X,1
and f
X,2
.
f
X
(k) =
k
∑
i=0
f
X,1
(i) ∗ f
X,2
(k− i) (2)
Here, f
X, j
(here, j = 1 or 2) is the pmf of sup(X)
in D
X, j
. The p-Apriori reduces the number of can-
didate itemsets by pruning with the Apriori down-
closed property. However, all transactions in PDB
have to be examined to evaluate spmf for each item-
set.
Next, we explain the top-down manner algorithm,
TODIS(Sun et al., 2010). The TODIS evaluates spmf
of itemsets efficiently by inheriting spmf from their
super-itemsets. Since TODIS starts spmf evaluations
from the longest itemset, all potentially probabilis-
tic frequent itemsets have to be identified on ahead.
These itemsets are called candidate itemsets. It can-
not be probabilistic frequent that an itemset does not
satisfy minsup without considering existential proba-
bility. By ordinary frequent itemset mining algorithm
such as Apriori, TODIS generates all candidate item-
sets which satisfy minsup without considering exis-
tential probability. Hereafter, an itemset which satisfy
minsup without considering existential probability is
called a count frequent itemset. For each candidate
itemset, TODIS also generates id-list, which is uti-
lized to evaluate spmf. An id-list of itemset X is a set
of TIDs which contains X. We denote id-list of item-
set X as L
X
. Then, TODIS evaluates spmf of every
candidate itemsets in a top-down manner. First, the
spmf of the longest candidate itemsets is evaluated by
DC algorithm. Afterward, the spmf of candidate item-
sets are evaluated in descending order of their length.
The spmf of a candidate itemset is evaluated by inher-
iting spmf of its super-itemset. Here, we show evalu-
ating the spmf of a candidate itemset X. The spmf of
an itemset Z is denoted as f
Z
. Assume that an itemset
Y is a super-itemset of X, and f
Y
is known. f
X
is eval-
uated from transactions L
X
. Since X is a sub-itemset
of Y, L
X
⊇ L
Y
. f
X
can be evaluated from transactions
in L
Y
and L
X
\ L
Y
. Let T
0
, . . . , T
n−1
be a set of trans-
actions in L
X
\ L
Y
. f
X
can be evaluated by convolving
T
0
, . . . , T
n−1
to f
Y
. Here, let p
i
be probability that T
i
occurs, q
i
(= 1− p
i
) be probability that T
i
does not oc-
cur. Let f
Z
(k) be f
Z
at sup(Z) = k. Let f
i
Z
(k) be spmf
that convolved f
Z
from T
0
to T
i
. If any transactions
does not occur, k = 0. f
X
(0) is calculated as
f
X
(0) = f
n−1
Y
(0) = f
Y
(0) ∗ Π
n−1
m=0
q
m
(3)
If k ≥ 1, f
i+1
Y
(k) is the sum of the case that T
i+1
occurs
at f
i
Y
(k− 1) and T
i+1
does not occur at f
i
Y
(k). f
i+1
Y
(k)
is calculated as
f
i+1
Y
(k) = f
i
Y
(k− 1) ∗ p
i+1
+ f
i
Y
(k) ∗ q
i+1
(4)
f
X
(k) is the spmf of sup(X) = k that convolved f
Y
(k)
from T
0
to T
n−1
, so we can calculate f
X
(k) by repeat-
ing Equation 4 from i = 0 to n− 1. Thus, f
x
is evalu-
ated by inheriting f
Y
using Equation 3 and 4. The top-
down manner algorithm efficiently evaluates spmf of
an itemset by inheriting the spmf of its super-itemsets.
However, the spmf of all candidate itemsets has to be
evaluated. Even if the evaluated candidate itemset is
not probabilistic frequent, this algorithm cannot avoid
to evaluate of spmf for its super-itemsets. Because all
super-itemsets have already been evaluated.
3 SKIP SEARCH APPROACH
In this section, we describe the way to evaluating
spmf by inheriting the spmf of sub-itemsets. Then,
we explain the skip search approach for avoiding to
evaluate spmf for redundant candidate itemsets.
3.1 Evaluating Spmf by Inheriting
Sub-itemset
TODIS evaluates spmf of candidate itemsets in de-
scending order, so all candidate itemsets can be eval-
uated spmf by inheriting spmf of its super-itemset.
When the order to evaluate spmf is not one way, it
is not enough. We can evaluate spmf of a candi-
date itemset by deconvolving spmf of its sub-itemset.
Here, we propose the way to evaluate spmf by inher-
iting spmf of sub-itemset. Assume that an itemset Y
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
176

is a sub-itemset of a candidate itemset X, and f
Y
is
known. f
X
is evaluated from transactions in L
X
. Since
X is a super-itemset of Y, L
X
⊆ L
Y
. Let T
0
, . . . , T
n−1
be a set of transactions in L
Y
\ L
X
. The spmf of X can
be evaluated by deconvolving T
0
, . . . , T
n−1
to the spmf
of Y. Here, let p
i
be the probability that T
i
occurs,
q
i
(= 1− p
i
) be the probability that T
i
does not occur.
Let f
X
(k) be the spmf of X at sup(X) = k. Let f
i
Y
(k)
be the spmf of sup(Y) = k that deconvolved f
Y
from
T
0
to T
i
. If any transactions does not occur, k = 0.
f
Y
(0) is calculated as
f
Y
(0) = f
0
Y
(0) ∗ q
0
(5)
f
0
Y
(0) is calculated as
f
0
Y
(0) =
f
Y
(0)
q
0
(6)
We can calculate f
i+1
Y
(0) by deconvolving f
i
Y
(0) with
T
i+1
f
i+1
Y
(0) =
f
i
Y
(0)
q
i+1
(7)
f
X
(0) can be calculated by deconvolving f
Y
(0) from
T
0
to T
n−1
.
f
X
(0) = f
n−1
Y
(0) = f
Y
(0) ∗ Π
n−1
m=0
1
q
m
(8)
If k ≥ 1, k transactionsoccur. When f
Y
is deconvolved
with T
0
, f
Y
(k) is calculated as
f
Y
(k) = f
0
Y
(k) ∗ q
0
+ f
0
Y
(k− 1) ∗ p
0
(9)
Thus,
f
0
Y
(k) =
f
Y
(k) − f
0
Y
(k− 1) ∗ p
0
q
0
(10)
When f
Y
is deconvolved with T
0
, . . . , T
i
, f
i
Y
(k) is cal-
culated as
f
i
Y
(k) = f
i+1
Y
(k) ∗ q
i+1
+ f
i+1
Y
(k− 1) ∗ p
i+1
(11)
Thus,
f
i+1
Y
(k) =
f
i
Y
(k) − f
i+1
Y
(k− 1) ∗ p
i+1
q
i+1
(12)
f
X
(k) can be calculated by deconvolving f
Y
(k) from
T
0
to T
n−1
, so we can calculate f
X
(k) by repeating
Equation 8 to 12 from i = 0 to n− 1.
This difference calculus by inheriting sub-itemset
can be applied to p-Apriori. When pass k ≥ 2, spmf
of candidate itemsets can be evaluated by inheriting
their sub-itemsets. Since p-Apriori finds probabilis-
tic frequent itemsets in ascending order of the length
of itemsets, all sub-itemsets have already been evalu-
ated. We can evaluate spmf of a candidate k-itemset
by inheriting its sub-itemsets.
3.2 Order to Evaluate Spmf of
Candidate Itemsets
The skip search approach evaluates spmf in a bidi-
rectional way so that we can avoid to evaluate spmf
of probabilistic infrequent itemsets by Apriori down-
closed property. Assume that the spmf of candidate
itemset X was evaluated. If X is not probabilistic
frequent, we can omit to evaluate spmf of all super-
itemset of X. Because an itemset whose sub-itemsets
are not probabilistic frequent cannot be probabilistic
frequent. Since our skip search approach starts evalu-
ating spmf from the average length of candidate item-
sets, it’s super-itemsets that have not been evaluated
spmf are remaining. When X is probabilistic infre-
quent, a sub-itemset of X in candidate itemsets is se-
lected as a candidate itemset to evaluate spmf next.
The spmf of this itemset is evaluated by difference
calculus in section 3.1. When X is probabilistic fre-
quent, spmf of all sub-itemsets of X in candidate item-
sets are evaluated. A super-itemset of X in candidate
itemsets is selected as the candidate itemset to eval-
uate spmf next, since it has a potential to be proba-
bilistic frequent. The spmf of this itemset is evaluated
same as TODIS. Hereby, our skip search approach can
omit evaluations for redundant candidate itemsets.
Here, we show the procedure to select a candidate
itemset evaluating spmf next.
An itemset X in candidate itemsets is selected at
random. Here, the length of X is close to the aver-
age length of candidate itemsets. Then, the spmf
of X is evaluated.
If X is probabilistic frequent:
An itemset Y which is super-itemset of X in
candidate itemsets is selected. The length of
Y is close to the median length of X and the
longest super-itemset of X.
If X is not probabilistic frequent:
An itemset Y
′
which is sub-itemset of X in can-
didate itemsets is selected. The length of Y
′
is
close to the median length of X and the shortest
unevaluated sub-itemset of X.
If all sub-itemset and super-itemset have been al-
ready evaluated:
An itemset is selected at random.
3.3 Procedure of Skip Search Approach
Here, we describe the procedure of skip search ap-
proach.
Step1. Set of candidate itemsets C , that of evaluat-
ing itemsets E and that of probabilistic frequent
itemsets F are initialized to the empty set.
Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data
177

Step2. All count frequent itemsets are inserted to C ,
and their id-lists are generated.
Step3. A candidate itemset c ∈ C is selected from
candidate itemset set at random.
Step4. f
c
is evaluated from L
c
. If a super-itemsets
or sub-itemsets of c exists in E , f
c
is evaluated by
inheriting it. Then, c is deleted from C .
• If c is probabilistic frequent, c is inserted into
F . When any sub-itemset c
′
of c has not been
evaluated yet, f
c
′
is evaluated, inserted into F
and deleted from C . A super-itemset of c in C
is selected as the candidate itemsets evaluating
spmf next.
• If c is not probabilistic frequent, all super-
itemset of c are deleted from C . A sub-itemset
of c in C is selected as the candidate itemsets
evaluating spmf next.
• If super-itemset and sub-itemset do not exist in
C , a candidate itemset in C is selected from
candidate itemset set at random.
Step5. If the candidate itemset evaluating spmf next
is empty, this procedure terminates. Otherwise,
step4 is repeated.
In skip search approach, candidate itemsets which
are selected at random cannot be evaluated by inherit-
ing their super/sub-itemsets. The spmf of these item-
sets are evaluated by algorithm DP or DC, it is costly.
To solve this problem, we propose another approach,
“skip search approach from maximal”. A maximal
candidate itemsets(Bayardo, 1998) is selected in Step
3. In Step 4, candidate itemsets which are sub-itemset
of selected maximal candidate itemset are evaluated.
This procedure can avoid using DC in Step 4. The
spmf of maximal candidate itemsets have to be evalu-
ated by DC, and most of these itemsets are not prob-
abilistic frequent. However, the cost of evaluating
them by DP or DC is relatively small. Because the
support of these itemset is small. Example of the or-
der to evaluate spmf in skip search approach from
maximal is shown in Figure 1. First, a maximal
candidate itemset {a, b, c, d, e} is selected and eval-
uated. Then a candidate itemset {a, c, d} which is
a sub-itemset of {a, b, c, d, e} is selected and eval-
uated. Since {a, c, d} is not probabilistic frequent,
{a, b, c, d} and {a, c, d, e} which are super-itemsets of
{a, c, d} are deleted. We can omit to evaluate spmf
of {a, b, c, d} and {a, c, d, e}. Next, {a, d} which is
a sub-itemset of {a, c, d} is selected and evaluated.
{a, d} is probabilistic frequent, so spmf of all its sub-
itemsets, {a} and { d}, are evaluated. Then, {a, d, e}
which is a super-itemset of {a, d} is selected as a can-
didate itemset to evaluate next. When all sub-itemsets
Figure 1: Example of the order to evaluate spmf in skip
search approach from maximal.
of {a, b, c, d, e} were evaluated, other maximal candi-
date itemset, for example {d, e, f}, is selected as a
candidate itemset to evaluate next.
This enhance is effective when all candidate item-
sets and their id-lists cannot fit in memory. Since the
information of a maximal candidate itemset and its
sub-itemsets is required in Step 4, we can reduce the
size of memory usage.
4 PERFORMANCE EVALUATION
We evaluated the performance of skip search ap-
proaches by comparing with the top-down manner
algorithm, TODIS, and the bottom-up manner algo-
rithm, p-Apriori. In experiments, p-Apriori evaluates
spmf by ihneriting sub-itemsets described in section
3.1, that is more efficient than using DC. This algo-
rithm is denoted as “p-Apriori w diffcalc” in experi-
mantal results. In skip search approaches and TODIS,
the count frequent itemsets are found by Apriori algo-
rithm. In experimental results, the naive skip search
approach is denoted as “skip”. The skip search ap-
proach described in section 3.3 is denoted as “skip f
max”.
To evaluate the performance of our approach,
synthetic data emulating retail transactions are used,
where the generation procedure is based on the
method described in (Agrawal and R.Srikant, 1994).
The average length of a transaction is 40, the average
length of a frequent itemset is 10, and the dataset size
N is 500k. For each transaction, we set the existential
probability with a Gaussian distribution.
Figure 2 shows the execution time varying
minsup. Here, minprob was set to 0.3. When minsup
is small, the difference between the execution time of
skip search approaches and TODIS. Since the aver-
age length of probabilistic frequent itemsets becomes
long for small minsup, the number of candidate item-
sets which skip search approaches can omit to evalu-
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
178
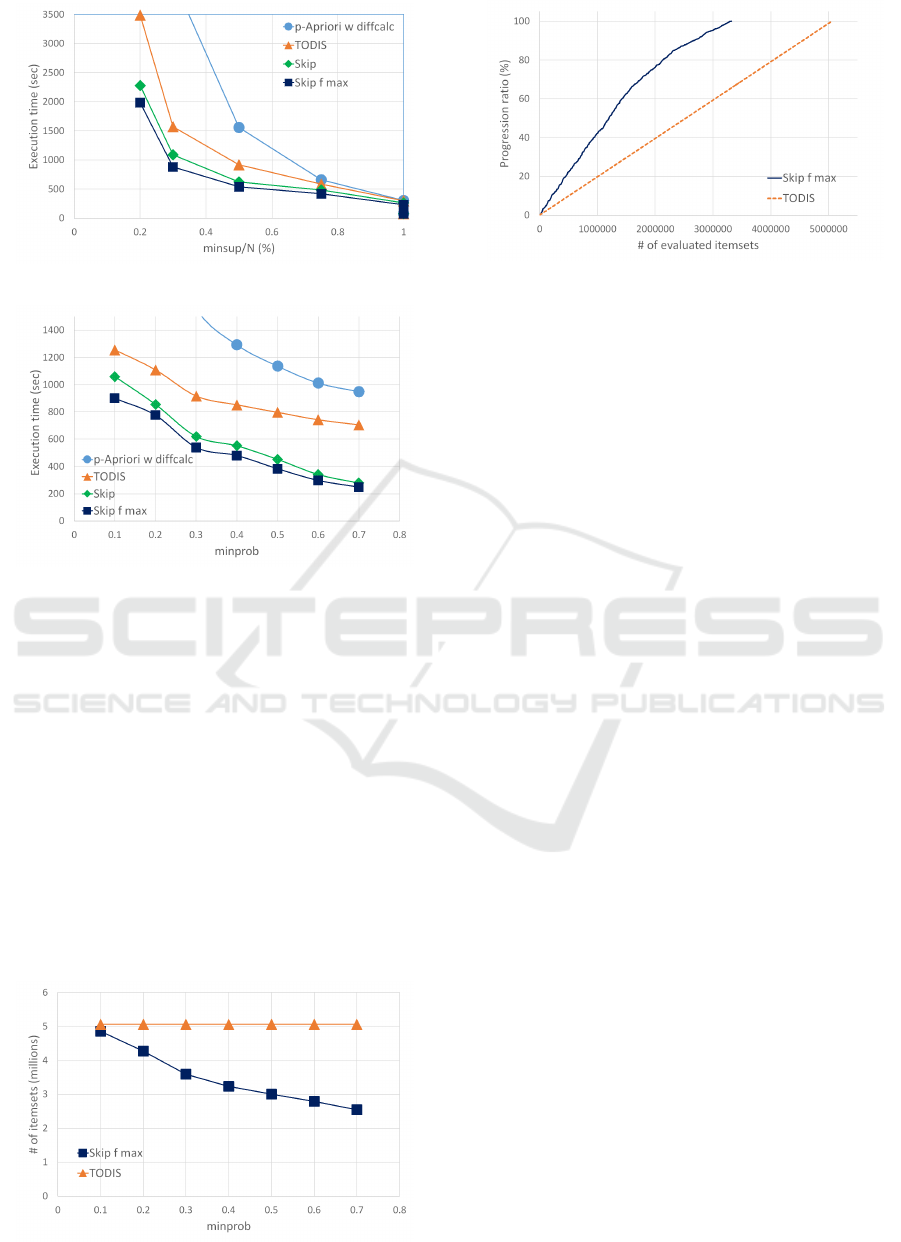
Figure 2: Execution time varying minsup.
Figure 3: Execution time varying minprob.
ate spmf increases.
Figure 3 shows the execution time varying
minprob. Here, minsup was set to 0.003. Our skip
search approaches significantly outperform other al-
gorithms. As the minimum probability decreases, the
difference of the execution time between skip search
approaches and TODIS shrinks. In this experiment,
minsup is fixed, so the number of candidate itemsets
is constant (Figure 4). When minprob is small, the
ratio of the number of omitted candidate itemsets be-
comes small. Thus, the difference of the execution
time becomes small. The difference of the execu-
tion time between skip and skip f max becomes small
for large minprob. The number of probabilistic fre-
quent itemsets becomes smaller asminprob increases.
Since the number of probabilistic infrequent itemsets
Figure 4: Number of evaluated itemsets varying minprob.
Figure 5: Progression ratio.
is large, the difference between skip and skip f max
becomes small.
Figure 5 shows the progression ratio of skip f max
and TODIS. The horizontal axis is the number of
itemsets which have been evaluated their spmf, the
vertical axis is the progression ratio. The progres-
sion ratio means the ratio of itemsets either proba-
bilistic frequent or not havebeen confirmed. Here, the
minimum support threshold and the minimum proba-
bility threshold are set to 0.003 and 0.3 respectively.
TODIS evaluates the spmf of candidate itemsets one
by one in descending order, so its progression ratio
becomes linear. In skip f max, its progression ratio
becomes linear when an evaluated candidate itemset
is probabilistic frequent. However, when an evalu-
ated candidate itemset is not probabilistic frequent, its
super-itemsets are deleted at a time, so the gradient of
progression ratio significantly increases.
5 CONCLUSIONS
In this paper, we proposed skip search approach for
mining probabilistic frequent itemsets under the Pos-
sible Worlds Semantics. By starting spmf evalua-
tion from the average length of candidate itemsets
for each maximal itemset and its sub-itemsets, our
skip search approach can omit to evaluate redundant
itemsets which become probabilistic infrequent. It
can evaluate spmf efficiently by inheriting spmf from
its sub/super-itemsets. Performance evaluations show
our skip search approach from maximal can attain
good performance.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number JP25280022 and JP26330129.
This work was supported by CREST, Japan Sci-
ence and Technology Agency.
Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data
179

REFERENCES
Aggarwal, C., Li, Y., and Wang, J. (2009). Frequent pattern
mining with uncertain data. In 15th ACM SIGKDD In-
ternational Conference on Knowledge Discovery and
Data Mining.
Aggarwal, C. and Yu, P. (2009). A survey of uncertain data
algorithms and applications. In IEEE Transactions on
Knowledge and Data Enginerring.
Agrawal, R. and R.Srikant (1994). Fast algorithm for min-
ing association rules. In 20th International Confer-
ence on Very Large Data Bases.
Bayardo, R. (1998). Efficiently mining long patterns from
databases. In 1998 ACM SIGMOD International Con-
ference on Management of Data.
Bernecker, T., Kriegel, H., Renz, M., Verhein, F., and Zue-
fle, A. (2009). Probabilistic frequent itemset mining in
uncertain databases. In 15th ACM SIGKDD Interna-
tional Conference on Knowledge Discovery and Data
Mining.
Chuim, C., Kao, B., and Hung, E. (2007). Mining fre-
quent itemsets from uncertain data. In 11th Pacific-
Asia Conference on Knowledge Discovery and Data
Mining.
Cuzzocrea, A., Leung, C., and MacKinnon, R. (2015). Ap-
procimation to expected support of frequent itemsets
in mining probabilistic sets of uncertain data. In 19th
Annual Conference in Knowledge-Based and Intelli-
gent Information and Engineering Systems.
Dalvi, N. and Suciu, D. (2004). Efficient query evaluation
on probabilistic databases. In 13th International Con-
ference on Very Large Data Bases.
Han, J., Pei, J., and Y.Yin (2000). Mining frequent patterns
without candidate generation. In 2000 ACM SIGMOD
International Conference on Management of Data.
Leung, C., Carmichael, C., and Hao, B. (2007). Efficient
mining of frequent patterns from uncertain data. In
Workshops of 7th IEEE International Conference on
Data Mining.
Leung, C., Mateo, M., and Brajczuk, D. (2008). A tree-
based approach for frequent pattern mining from un-
certain data. In 12th Pacific-Asia Conference on
Knowledge Discovery and Data Mining.
Leung, C. and Tanbeer, S. (2013). Puf-tree: a compact tree
structure for frequent pattern mining of uncertain data.
In 17th Pacific-Asia Conference on Knowledge Dis-
covery and Data Mining.
MacKinnon, R., Strauss, T., and Leung, C. (2014). Disc:
efficient uncertain frequent pattern mining with tight-
ened upper bound. In Workshops of 14th IEEE Inter-
national Conference on Data Mining.
Sun, L., Cheng, R., Cheung, D., and Cheng, J. (2010).
Mining uncertain data with probabilistic gurantees.
In 16th ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining.
Tateshima, H., Shintani, T., Ohmori, T., and Fujita, H.
(2015). Skip search approach for mining frequent
itemsets from uncerdain dataset. In DBSJ Japanese
Journal.
Wang, L., Cheung, D., and Cheung, R. (2012). Effi-
cient mining of frequent item sets on large uncertain
databases. In IEEE Transactions on Data Engineer-
ing.
Wang, L., Feng, L., and Wu, M. (2013). At-mine: an ef-
ficient algorithm of frequent itemset mininf on uncer-
tain dataset. In Journal of Computers.
Zhang, Q., Li, F., and Yi, K. (2008). Finding frequent items
in probabilistic data. In 14th ACM SIGKDD Interna-
tional Conference on Knowledge Discovery and Data
Mining.
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
180
