Diversifying Techniques & Neutrality in Genetic Algorithms

Seamus Hill and Colm O’Riordan

College of Engineering & Informatics, National University of Ireland, Galway, Ireland

Keywords:

Neutral Theory, Genetic Drift, Neutrality, Genotype, Phenotype, Genetic Algorithms.

Abstract:

This paper examines the implicit maintenance of diversity within a population through the inclusion of a

layered genotype-phenotype map (GP-map) in a Genetic Algorithm (GA), based on the principal of Neutral

theory (Kimura, 1968). The paper compares a simple GA (SGA), incorporating a variety of diversifying tech-

niques, to the multi-layered GA (MGA) as proposed by the authors. The MGA creates a neutral representation

by including a layered GP-map based on the biological concepts of Transcription and Translation. In standard

GAs, each phenotype is represented by a distinct genotype. However by allowing a higher number of alleles to

encode phenotypic information on the genotype, one can create a situation where a number of genotypes may

represent the same phenotype. Through this process one can introduce the idea of redundancy or neutrality

into the representation. This representation allows for adaptive mutation (hot spots) and silent mutation (cold

spots). This combination enables the level of diversity to dynamically adjust during the search, and directs the

search towards closely related neutral sets. Previous work has shown that introducing this type of representa-

tion can be beneﬁcial; in this paper we show how this representation is useful at introducing and maintaining

diversity. Here we compare the performance of the MGA against traditional diversifying techniques used in

conjunction with a SGA over a fully deceptive changing landscape.

1 INTRODUCTION

Genetic algorithms are search mechanisms based on

Darwinian principals. However, simple genetic algo-

rithms (SGA), through the representation used, im-

plement a process of evolution without including the

concept of neutral mutations. That is, representations

in SGA do not adopt the notion of Neutral theory.

Neutral theory can be described as a situation where

the size of the search space is increased, without an

equivalent increase in the solution space. This al-

lows silent mutations to occur, where a mutated in-

dividual, at the genotypic level, can still represent the

same phenotype. Kimura’s work indicated that the

vast majority of mutations are caused by genetic drift

rather than selection (Kimura, 1968). With this in

mind, while natural selection is an important feature

in the evolutionary process, only a fraction of DNA

changes result in adaptation. This means that the ma-

jority of mutations taking place are phenotypically

silent (Kimura, 1983). The motivation is to develop

a tunable, synonymous, non-trivial GA representation

which incorporates neutrality and to compare the im-

plicit diversity created by the representation with that

of a SGA, using a variety of diversifying techniques.

The contribution is to examine the use of a GA which

is designed to implicitly maintain diversity within the

population through its representation and to analyse

the impact of the representation on population evolu-

tion. The paper is laid out as follows: Section 2 gives

a brief background to Neutral theory and the use of

neutrality in GAs. Section 3 outlines the genotype-

phenotype map (GP-map) used in the paper, while

Section 4 describes the experiments undertaken. Sec-

tion 5 outlines and analyses the results and Section 6

concludes.

2 BACKGROUND

Previous research on the use of neutrality in evolu-

tionary search produced mixed results. Smith et al.

(Smith et al., 2001) highlighted the effect of neutral

networks on the evolutionary search and concluded

that neutrality does not provide an advantage. Ebner

et al. (Ebner et al., 2001) examined the use of mu-

tation and found that high levels of mutation could

be sustained through the presence of neutral net-

works. They also identiﬁed that neutral networks as-

sist in maintaining diversity in the population, which

could prove useful over changing landscapes. Simi-

lar results were also found in (Grefenstette and Cobb,

140

Hill, S. and O’Riordan, C.

Diversifying Techniques & Neutrality in Genetic Algorithms.

DOI: 10.5220/0006036201400147

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 140-147

ISBN: 978-989-758-201-1

1993). Research carried out by Yu and Miller (Yu and

Miller, 2001) illustrated that through the incorpora-

tion of neutrality, mutation may or may not be adap-

tive depending on the gene in question. They also

examined neutrality using the OneMax problem, with

results indicating that neutrality is advantageous as it

allows the absorption of destructive mutations. Other

research in the area includes (Hill and O’Riordan,

2105) which looked at the population dynamics of

neutrality using a deceptive problem over a changing

landscape. Results indicated that neutrality had a pos-

itive impact, allowing the search to escape local op-

tima following the environmental changes. Problem

difﬁculty also impacted on the usefulness of neutral-

ity, as shown in (Hill and O’Riordan, 2104) and (Hill

and O’Riordan, 2013).

3 GENOTYPE-PHENOTYPE

MAPPING (GP-MAP)

In relation to redundancy, Information Theory pro-

vides a measurement of information. The information

contained in a sequence, measured in Bits B, can be

deﬁned as the number of bits b required to represent

that given information. In other words you need to

be able to distinguish between the Bits, which repre-

sent the amount of information and the bits, which are

used to represent the information (Rothlauf, 2002). If

b > B, then your representation incorporates an ele-

ment of redundancy. With regard to the multi-layered

mapping of the MGA and using the notation out-

lined in (Rothlauf, 2002), as you progress through

the layers, the level of redundancy alters. In the tran-

scription layer, which maps |φ

| (the genotype space)

→ |φ

| (the DNA space) → |φ

| (the RNA space),

k = 1 (where k represents the order of the phenotypic

building block) and there is no redundancy, therefore

b = B and k

= 1 (where r can be deﬁned as the num-

ber of genotypic building blocks of length kk

used

to represent a phenotypic building blocks of length

k). In this paper, the chromosome length, l

= 24 and

|φ

| = 2

. The DNA space |φ

| consists of characters

selected from a 4 character alphabet, with the DNA

string l

= 12 and k = 3. Therefore, |φ

| = 4

also

|φ

| = |φ

| and l

= l

(the RNA string) . The trans-

lation layer which maps |φ

| → |φ

| (the phenotype

space), introduces redundancy into the mapping. In

the translation layer, b > B, r = 1, k

= 3 and k = 1.

The RNA building blocks have size kk

and the re-

dundancy is uniform. As k represents the order of

the phenotypic building blocks, there are 2

different

phenotypes, which are represented by 4

different

RNA strings. In other words, there are 4

differ-

ent possibilities to encode a single phenotypic bit and

|φ

| = 2

. In this paper, the phenotype string l

= 4.

Although the redundancy is uniform, the Hamming

distances are not minimal and therefore the redun-

dancy is not linear.

Figure 1: 6-bit MGA Representation Mapping.

In summary, |φ

| = {0,1}

where l

is the geno-

type length. The transcription phase maps |φ

| →

|φ

| → |φ

|. Where: |φ

| = {A,C, G,T}

with the

following mappings: 00 → A; 01 → C; 10 → G and

11 → T. A bijective mapping maps |φ

| → |φ

where: |φ

| = {A,C, G,U}

. U is biologically in-

spired and has no impact on the evolution unless we

include operators at this level. Following transcrip-

tion, the translation phase takes place, mapping the

RNA space to a phenotype space |φ

|, |φ

| → |φ

where: |φ

| = {0,1}

l/c

, c is the cardinality chosen at

initialisation to create a translation table, which maps

3 characters to a phenotype bit (either 0 or 1). The

level of redundancy is determined by c, in this paper

c = 6 (see Figure 1), and implies |φ

| > |φ

| as c > 1.

Missense mutation or substitution refers to a change

in one amino acid in a protein, arising from a point

mutation in a single nucleotide. Missense mutation in

nature is carried out at the RNA level. In relation to

the MGA, the Missense mutation mapping is as fol-

lows: A → U, C → G, G → A and U → C. The varia-

tion operators, one-point crossover and single-point

mutation occur at the genotype level prior to tran-

scription and missense mutation takes place before

translation. This mapping implicitly maintains related

genetic diversity within the population, thus allowing

the occupation by the population, of a greater number

of neutral networks. This is possible as adaptive mu-

tation occurs at c locations (hot zones) on the chro-

mosome. The effect of this is to allow silent muta-

tion to occur at l

− c locations (cold zones), which

allows 2

−c

genotypes represent the same phenotype.

This increases the level of diversity within the popu-

lation and allows the creation of neutral sets, which

self-organise during evolution.

Diversifying Techniques & Neutrality in Genetic Algorithms

141

4 EXPERIMENT SET UP

Solutions and sub-solutions are normally lost in a

SGA population for three reasons: selection pressure,

selection noise and operator disruption. Selection

pressure occurs as the result of the selection process,

with less ﬁt solutions disappearing from the popula-

tion. Selection noise is the result of the variance of

the selection process due to random choices between

identically ﬁt solutions. Operator disruption takes

place through the implementation of the crossover

and mutation operators which possess the ability to

destroy good solutions. In an attempt to avoid prema-

ture convergence, techniques for diversifying a pop-

ulation generally attempt to reduce individually or in

combination with one another, selection pressure, se-

lection noise or operator disruption (Mahfoud, 1995).

Diversity within a population can serve a number

of purposes, such as delaying convergence (note that

premature convergence can be deﬁned as the conver-

gence to non-global optima) in order to promote ex-

ploration. Hence the maintenance of diversity within

a population is a desirable feature for GAs. Diver-

siﬁcation methods capable of reducing all three cri-

teria, selection noise, selection pressure and operator

disruption exist. The problem lies in the fact that re-

ducing all three criteria to arbitrarily low levels re-

sults in the GA carrying out little or no useful search

(Mahfoud, 1995). The maintenance of diversity for its

own sake is undesirable; what is required is diversity

that promotes good strings (Goldberg and Richard-

son, 1987).

By comparing the performance of the MGA with a

SGA containing a number of diversifying techniques,

we can evaluate the diversity maintenance mecha-

nism implicit in the MGA representation. With re-

gard to the three mechanisms for promoting diversity,

the theory would suggest that Stochastic Universal

Selection (SUS) offers the ability to minimise selec-

tion noise, ﬁtness scaling can decrease selection pres-

sure and lower rates of crossover and mutation can

reduce operator disruption (Mahfoud, 1995). How-

ever it is worth remembering that a relationship exists

between convergence and diversity in a GA popula-

tion. If there is no operator disruption and no selection

pressure, then the GA will maintain its initial popula-

tion and won’t perform any meaningful search. Also

with regard the mutation operator, as mutation rates

increase, the diversity produces is usually not useful

as the GA is approaching random search.

In this paper a four-bit changing deceptive land-

scape as outlined in (Hill and O’Riordan, 2105) was

used. Although this landscape is relatively small in

terms of the search space, it was chosen as it allows

the dynamics of the population evolution to be stud-

ied. The parameters chosen are outlined in Table

1. Over the set of experiments designed to examine

various diversifying techniques, we altered the selec-

tion mechanisms and scaling methods of the SGA.

We also conducted a number of experiments where

we increased the SGA’s variation operators. The mo-

tivation for these changes is to vary the selection

noise, selection pressure and operator disruption for

the SGA, thereby examining the impact of the inclu-

sion of well understood diversifying techniques into

the SGA, which in turn are then compared with the

performance of the MGA.

Table 1: Parameters Used.

Parameters MGA SGA

Runs 10 10

Generations 200 200

Population P 20 20

Crossover P

0.7 0.7

Mutation P

1/l 1/l

Missense Mutation 0.2 No

Selection Mechanisms Tournament Various

Scaling Methods No Various

In Section 5 we outline the results of the ex-

periments conducted. The selection noise experi-

ments explore the use of Stochastic Remainder Se-

lection (SRS) and SUS. The selection pressure exper-

iments examine Linear, Window, Sigma Truncation

and Boltzmann scaling techniques and niching tech-

niques, such as, crowding and Incest Reduction. Fi-

nally, the operator disruption experiments look at the

impact of increasing rates of crossover and mutation.

20 40 60 80 100 120 140 160 180 200

Fitness

Generations

SGA & MGA 4-bit Deceptive Problem - Online/Offline Performance Analysis

MGA Off-line Performance

MGA On-line Performance

SGA Off-line Performance

SGA On-line Performance

Figure 2: SGA & MGA On-line/Off-line.

5 RESULTS

Figure 2 illustrates the off-line (averaged best ﬁtness)

and on-line (averaged ﬁtness) performance for both

the SGA and the MGA. The results indicate that the

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

142

changing 4-bit deceptive landscape initially proved

equally easy for both the SGA and the MGA, as they

both located the global optimum. This is shownby the

off-line performance of both GAs up to the change

of landscape at generation 50. After the landscape

changes, the SGA becomes trapped on the local op-

timum, while the MGA succeeds in locating the new

global optimum. To analyse the results statistically,

in this paper we used a Wilcoxon signed rank test to

compare the off-line results of the SGA and MGA,

and similarly to compare the on-line performances of

both the SGA and MGA. The results indicated that

the off-line results for both GAs were statistically

signiﬁcant with a p-value < 2.2e

−16

. Similarly the

on-line results were also statistically signiﬁcant (p-

value < 2.2e

−16

5.1 Neutral Networks

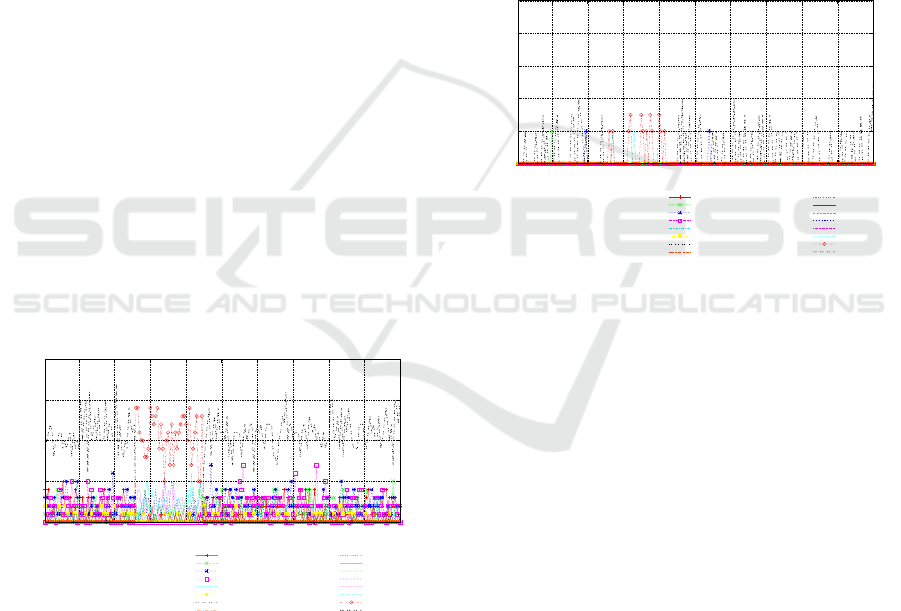
The neutral networks representing various ﬁtness val-

ues are shown in Figure 3. Before the landscape

changes at generation 50, the most prominent neu-

tral network represents the global optimum pheno-

type (1111). As the population evolves, the MGA,

through its M : 1 representation, allows the size of

neutral networks to adapt as the population evolves.

The next largest neutral networks represent the phe-

notypes (0111), (1110), (1101) and (1011), which

are the four genotypes closest in Hamming distance

to the optimum, indicating that the MGA’s population

evolves towards neighbouring neutral sets.

20 40 60 80 100 120 140 160 180 200

Number of Genotypes of Similar Fitness

Generations

MGA 4-bit Deceptive Problem - Genotype Fitness Representation Per Generation

Fitness 0 (0001 & 1000)

Fitness 2 (1011 & 0100)

Fitness 4 (1101 & 0010)

Fitness 6 (1110 & 0001)

Fitness 8 (1100 & 0011)

Fitness 10 (1010 & 0101)

Fitness 12 (1001 & 0110)

Fitness 14 (0110 & 1001)

Fitness 16 (0101 & 1010)

Fitness 18 (0011 & 1100)

Fitness 20 (1000 & 0111)

Fitness 22 (0100 & 1011)

Fitness 24 (0010 & 1101)

Fitness 26 (0001 & 1110)

Fitness 28 (0000 & 1111)

Fitness 30 (1111 & 0000)

Figure 3: Neutral Networks - Number of Genotypes with

Similar Fitness.

As the landscape changes the largest neutral net-

work represents the new local optimum (1111), as

this was the global optimum at the time of the change.

As the search continues the MGA’s population es-

capes the local optimum and has located the global

optimum. At this point, the most prominent neutral

network represents the phenotype (0000) (the new

global optimum). Also, the MGA population has

evolved towards a different group of neutral sets rep-

resenting the phenotypes (0001), (0010), (0100) and

(1000), all close, phenotypically, in Hamming dis-

tance to the global optimum.

Figure 4 looks at the composition of the neutral

sets, examining the number of identical genotypes in

each set. The ﬁgure indicates that there is a high de-

gree of diversity maintained within each neutral set,

with low numbers of identical genotypes present. The

number of identical genotypes representing the global

optimum varying between 2 and 4, illustrating the im-

pact of the M : 1 representation on the population.

Overall, the results indicate that the representation,

implicitly maintains useful building blocks within the

population, which promotes good strings and assist in

improving the adaptability of the MGA.

20 40 60 80 100 120 140 160 180 200

Number of Similar Genotypes

Generations

MGA 4-bit Deceptive Problem - Genotype M:1 Representation Per Generation

Fitness 0 (0001 & 1000)

Fitness 2 (1011 & 0100)

Fitness 4 (1101 & 0010)

Fitness 6 (1110 & 0001)

Fitness 8 (1100 & 0011)

Fitness 10 (1010 & 0101)

Fitness 12 (1001 & 0110)

Fitness 14 (0110 & 1001)

Fitness 16 (0101 & 1010)

Fitness 18 (0011 & 1100)

Fitness 20 (1000 & 0111)

Fitness 22 (0100 & 1011)

Fitness 24 (0010 & 1101)

Fitness 26 (0001 & 1110)

Fitness 28 (0000 & 1111)

Fitness 30 (1111 & 0000)

Figure 4: Neutral Networks - Identical Genotype.

5.2 Selection Noise

As outlined by DeJong (De Jong, 1975), the vari-

ance of selection is one of the main contributors to

the idea of convergence. In order to examine selec-

tion variance or selection noise, we compare a number

of selection mechanisms designed to reduce selection

noise, namely SRS and SUS. With SRS, the ﬁtness of

an individual f

is divided by the average ﬁtness of the

population

f. For each string i where f

f is greater

than 1.0, the integer part of the number deﬁnes the

number of copies of the individual are put forward for

crossover. For example an individual with a ﬁtness

value of 1.45, places one copy forward for crossover

and then has a 0.45 chance of putting a second copy

forward.

SUS on the other hand, is optimal with respect to

efﬁciency, bias (that is, the distance from the RWS

in relation to expected value) and the spread (range

of possible individuals put forward for crossover)

(Baker, 1985). SUS simulates a roulette wheel sim-

ilar to RWS. However, while RWS spins the wheel n

times (n = populationsize), SUS spins the wheel once,

using n uniformly spaced pointers at the edge of the

Diversifying Techniques & Neutrality in Genetic Algorithms

143

wheel. SUS has zero bias, is very efﬁcient and min-

imises the spread and is regarded as the lowest noise

selection scheme.

20 40 60 80 100 120 140 160 180 200

Fitness

Generations

SGA (SRS & SUS) & MGA 4-bit Deceptive Problem - Online/Offline Performance Analysis

MGA Off-line Performance

MGA On-line Performance

SGA (SRS) Off-line Performance

SGA (SRS) On-line Performance

SGA (SUS) Off-line Performance

SGA (SUS) On-line Performance

Figure 5: Selection Noise On-line/Off-line.

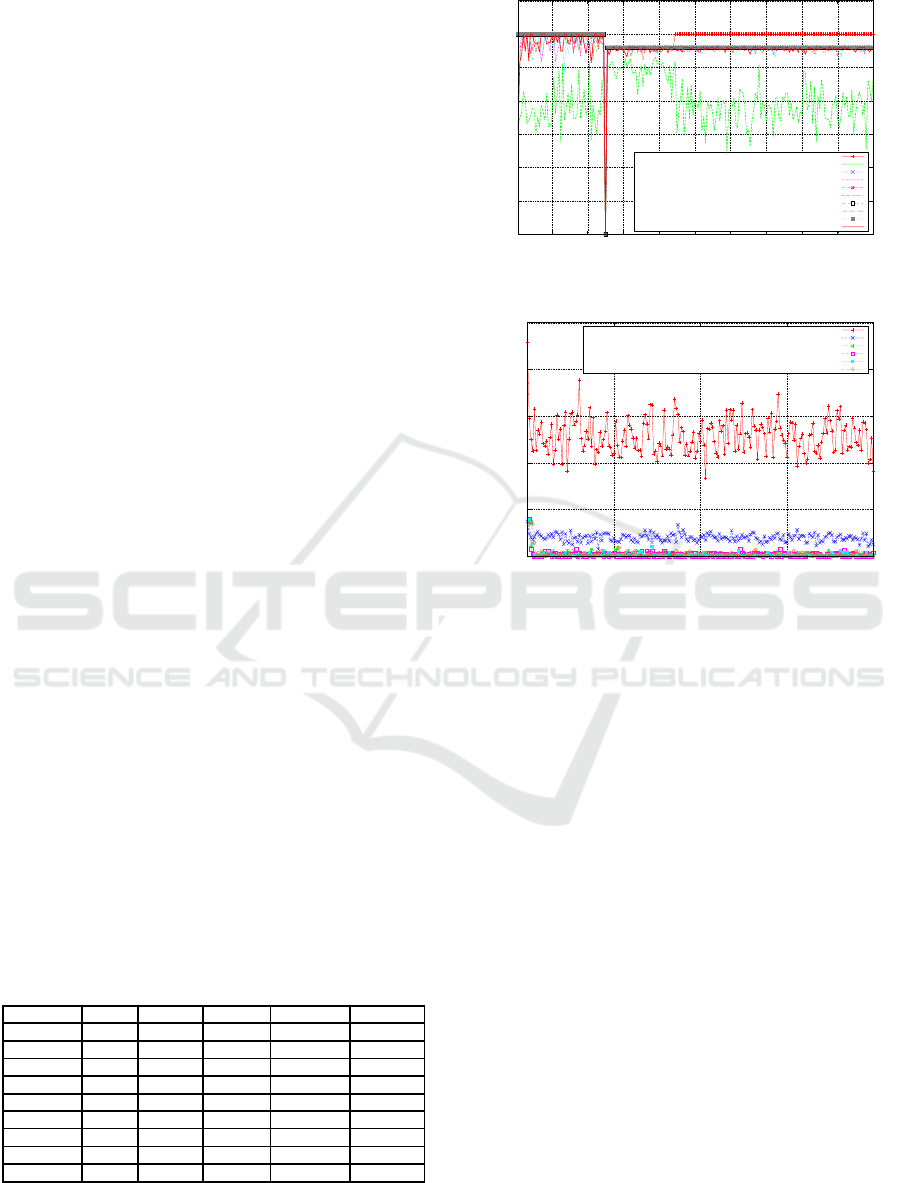
Figure 5 indicates that the SGA (with SRS and

SUS individually included), located the local opti-

mum in the initial population, (see the off-line per-

formances) due in part to the level of diversity (illus-

trated by the SGA on-line performance). However,

the population converges prematurely as the search

continues and diversity is quickly eliminated from

the population. Once the landscape changes, because

the population, for both the SRS and SUS SGAs,

were trapped on the deceptive local optimum, they

automatically located to new global optimum and re-

mained there for the duration of the search. The MGA

on the other hand located the global optimum both be-

fore and after the landscape change.

Table 2: Off-Line & On-Line Selection p-values.

Off-Line SRS SUS MGA

SRS − 0.04131 0.09138

SUS 0.04131 − 0.4005

On-Line

SRS − 0.2732 < 2.2e

−16

SUS 0.2732 − < 2.2e

−16

The statistical analysis of the results between the

MGA and the SGA are shown in Table 2 and indi-

cate that the off-line and on-line performance of SRS

and SUS are quite similar to one-another. Comparing

the MGA’s off-line results to those of the SRS SGA,

shows a less signiﬁcant result than that of the off-line

MGA and SUS SGA. The on-line performance of the

MGA differs signiﬁcantly from both of the SGAs.

Figure 6, illustrates the rate of convergence within

the population and shows both the SGA (using SRS)

and the SGA (using SUS) converging quickly. The

MGA maintains a higher degree of diversity, both at a

phenotypic and genotypic level which assists in suc-

cessfully locating the global optimum, both before

and after the landscape change, as the level of diver-

sity maintained allows the search to escape from the

local optimum.

500

1000

1500

2000

2500

0 50 100 150 200

Hamming Distance

Generations

Selection Noise SGA & MGA - Genotype & Phenotype Convergence

MGA Genotype Hamming Distance

MGA Phenotype Hamming Distance

SGA (SRS) Genotype Hamming Distance

SGA (SUS) Genotype Hamming Distance

Figure 6: Selection Noise Convergence Rate.

5.3 Selection Pressure

With selection, the extraordinary individuals within

a population will begin to dominate the population

quite quickly and premature convergence will be-

gin to take hold. Even if there is signiﬁcant di-

versity within a population, late in a run, the pop-

ulation’s average ﬁtness (on-line) may be close to

the population’s best ﬁtness (off-line). This leads

to a situation where the search for improvement be-

comes a “random-walk among the mediocre” (Gold-

berg, 1989).

5.3.1 Scaling Techniques

Fitness scaling has been used to overcome this prob-

lem. We now examine ﬁtness scaling diversifying

techniques aimed at reducing the selection pressure

within the population:

• Linear scaling adjusts the ﬁtness values of all

individuals within the population, such that the

ﬁttest individual receives a ﬁxed number of ex-

pected offspring and therefore prevents it from

reproducing too frequently. The ﬁtness function

′

= axf

+ b is used where a and b are normally

selected so to allow the average individual receive,

on average, one offspring copy, and the best re-

ceives the speciﬁed number of copies (normally

two). This method may return a negative ﬁtness

value.

• Window scaling, ﬁtness is scaled by subtracting

from the raw ﬁtness, the lowest ﬁtness of any in-

dividual in the past number of scaling window

generations. The ﬁtness function is f

′

= f

− f

where w is the window size and is typically some-

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

144

where between 2 and 10 and f

is the worst value

observed in the w most recent generations.

• Sigma Truncation avoids returning negative ﬁt-

ness values for individuals within the population

and incorporates problem dependant information

into the scaling mechanism. The ﬁtness of an indi-

vidual fi

′

is calculated as follows: f

′

= f

− (

f −

cxσ), where c is a small integer value between 1

and 5,

f is the average rawﬁtness and σ is the pop-

ulation standard deviation. Negative values for f

are avoided as any result f < 0 is set to zero. Indi-

viduals where f

< c standard deviation from the

average ﬁtness value are not selected.

• Boltzmann tournament selection procedure is de-

rived and implemented to give stable distribu-

tions within a population. It also creates another

niching mechanism for forming and sizing stable

subpopulations of individuals according to differ-

ences among them, if the cooling process is not

taken to the limit. Boltzmann scaling is expressed

as f

′

= e

and selection pressure is low when

the control parameter T is high.

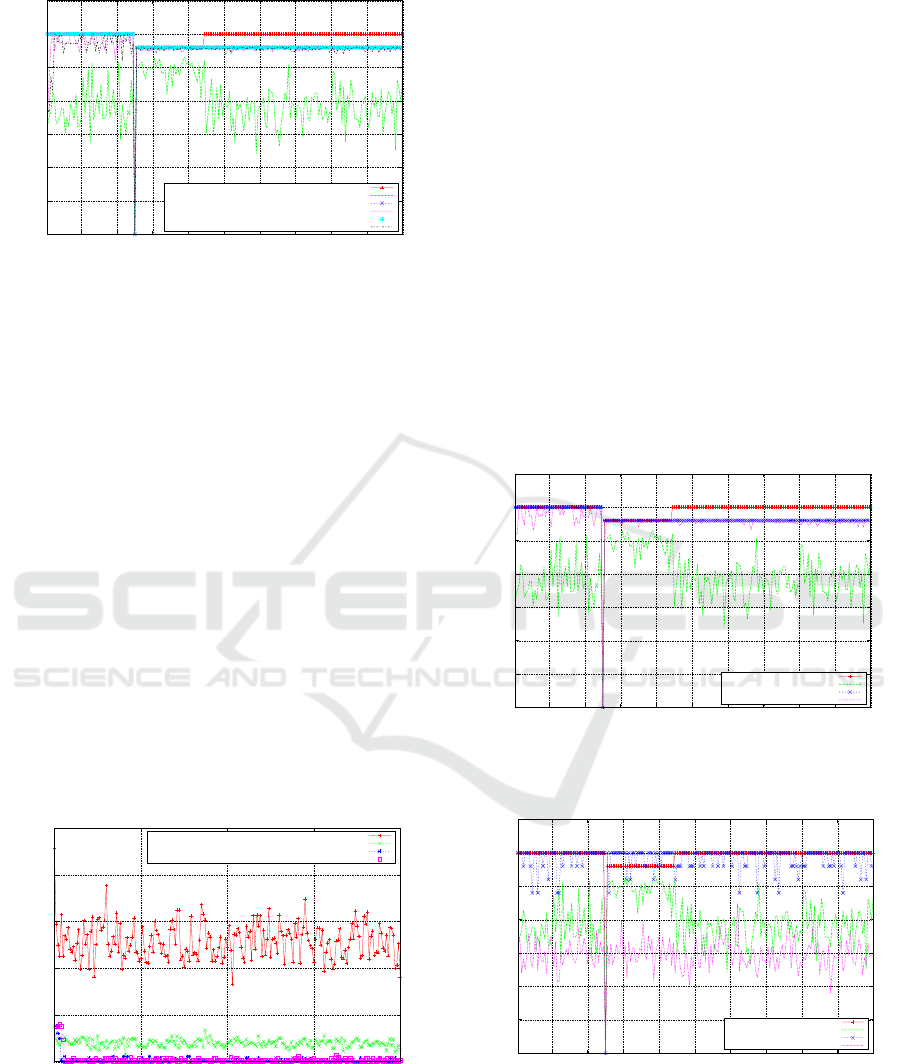
The results of the scaling experiments are illustrated

in Figure 7 and Table 3. These results indicate that

the SGA using various scaling techniques, fails to

maintain enough diversity within the population to

avoid premature convergence. The statistical results

indicate that differences between the various scaling

methods, for these experiments, are minimal. The

most signiﬁcant results are between the MGA and the

SGA using each of the scaling mechanisms. Figure

8, gives an overview of the rate of convergence as-

sociated with the SGA (incorporating scaling mecha-

nisms) and the MGA. The graph illustrates that Lin-

ear, Window, Sigma Truncation and Boltzmann SGA

loose diversity very quickly in the search, which re-

sults in the failure of the SGA to adapt after the land-

scape changes. The MGA implicitly maintains a level

of diversity within the population which assists in

adapting and locating the global optimum before and

after the landscape change.

Table 3: Off-Line & On-Line Scaling p-values.

Off-Line Linear Window Sigma T. Boltzmann MGA

Linear − 1 0.5807 0.5716 < 2.2e

−16

Window 1 − 0.5807 0.5716 < 2.2e

−16

Sigma T. 0.5807 0.5807 − 1 < 2.2e

−16

Boltzmann 0.5716 0.5716 1 − < 2.2e

−16

On-Line

Linear − 0.9319 0.1071 0.6711 < 2.2e

−16

Window 0.9319 − 0.04809 0.9433 < 2.2e

−16

Sigma T. 0.1071 0.04809 − 0.1353 < 2.2e

−16

Boltzmann 0.6711 0.9433 0.1353 − < 2.2e

−16

20 40 60 80 100 120 140 160 180 200

Fitness

Generations

SGA (Scaling) & MGA 4-bit Deceptive Problem - Online/Offline Performance Analysis

MGA Off-line Performance

MGA On-line Performance

SGA (Linear) Off-line Performance

SGA (Linear) On-line Performance

SGA (Window) Off-line Performance

SGA (Window) On-line Performance

SGA (Sigma Truncation) Off-line Performance

SGA (Sigma Truncation On-line Performance

SGA (Boltzmann) Off-line Performance

SGA (Boltzmann) On-line Performance

Figure 7: Selection Pressure On-line/Off-line.

500

1000

1500

2000

2500

0 50 100 150 200

Hamming Distance

Generations

SGA (Boltzmann) & MGA - Genotype & Phenotype Hamming Distance

MGA Genotype Hamming Distance

MGA Phenotype Hamming Distance

SGA Linear Scaling Genotype Hamming Distance

SGA Window Scaling Genotype Hamming Distance

SGA Sigma Truncation Scaling Genotype Hamming Distance

SGA Boltzmann Scaling Genotype Hamming Distance

Figure 8: Selection Pressure Convergence Rate.

5.3.2 Niching Techniques

Niching can be deﬁned as an approach which en-

courages a number of distinct groups of genotypes to

develop and remain in the population, with reduced

pressure from the GA to converge towards a single

type of genotype. Crowding involves a form of nich-

ing of the population. With crowding, as implemented

in this paper, before crossover or mutation, normal

ﬁtness weighted selection is used to select members

for the next generation. Crossover then takes place

on individuals selected randomly from this set. Af-

ter individuals have been selected for crossover, the

offspring are created as usual. For each offspring,

crowding factor, in this case 2, members of the sur-

vivors are selected randomly and the Hamming dis-

tance of each genotype from the offspring is calcu-

lated for 2 individuals. The offspring the replaces

whichever survivor is nearest in Hamming distance.

Incest reduction is used in conjunction with crowding

and introduces a mechanism to reduce the percent-

age of crossover between similar genotypes. After

being selected, pairs are then selected for crossover

by choosing the ﬁrst parent at random from the list

of selected individuals, then choosing a pre-deﬁned

(incest-reduction) number of possible candidates for

Diversifying Techniques & Neutrality in Genetic Algorithms

145

20 40 60 80 100 120 140 160 180 200

Fitness

Generations

SGA (Niching) & MGA 4-bit Deceptive Problem - Online/Offline Performance Analysis

MGA Off-line Performance

MGA On-line Performance

SGA (Crowding) Off-line Performance

SGA (Crowding) On-line Performance

SGA (Incest Reduction) Off-line Performance

SGA (Incest Reduction) On-line Performance

Figure 9: Niching On-line/Off-line.

the other parent randomly. The Hamming distance

of each candidate from the ﬁrst parent and the one

with the greatest Hamming distance is selected for

crossover.

The results of the SGA performance with crowd-

ing and Incest reduction are shown in Figure 9. The

results indicate that the performance of the SGA with

crowding are very similar to those of the SGA incor-

porating Incest reduction (off-line p-value = 0.03351

and the on-line p-value= 0.1663). Both niching tech-

niques fail to the escape the local optimum. The MGA

results differ, in that the diversity maintained within

the population allows the search escape the deceptive

trap. Comparing the MGA off-line and on-line results

statistically against both of the niching techniques,

indicated a high statistically signiﬁcant difference in

performance. In relation to the rate of convergence.

Unlike the MGA, the niching techniques outlined,

lose diversity early in the search (see Figure 10), mak-

ing it difﬁcult for the SGA to adapt and escape the

local optimum when the environment changed.

500

1000

1500

2000

2500

0 50 100 150 200

Hamming Distance

Generations

SGA & MGA - Genotype & Phenotype Convergence

MGA Genotype Hamming Distance

MGA Phenotype Hamming Distance

SGA Crowding Genotype Hamming Distance

SGA Incest Reduction Genotype Hamming Distance

Figure 10: Niching Techniques Convergence Rate.

5.4 Operator Disruption

For the operator disruption experiments, we increased

the rate of P

and P

(see Figures 11 and 12 respec-

tively). Examining the results of increasing the rate

of crossover to 0.90, the SGA located the global op-

timum early in the search but failed to adapt once the

landscape changed. The results of increasing the rate

of mutation to 0.50, illustrate that the search is be-

ing directed by randomness, with the SGA constantly

moving to and from the global optimum, shownby the

off-line performance. The result also shown a very

large degree of change in the on-line performance.

The increased crossover results, both off-line and on-

line were signiﬁcantly different from the MGA results

(off-line p-value = 2.2e

−16

and on-line p-value =

0.0003238). The results using mutation also indicated

a statistically signiﬁcant difference. The mutation off-

line results indicate that increased mutation rates are

statistically closer to the MGA results, however as the

on-line results indicate, the search was driven by ran-

domness and failed to produce good strings, meaning

the diversity maintained wasn’t useful in terms of a

search algorithm.

20 40 60 80 100 120 140 160 180 200

Fitness

Generations

SGA (Increased Crossover) & MGA 4-bit Deceptive Problem - Online/Offline Performance Analysis

MGA Off-line Performance

MGA On-line Performance

SGA Off-line Performance

SGA On-line Performance

Figure 11: Operator Disruption (Crossover) On-line/Off-

line.

20 40 60 80 100 120 140 160 180 200

Fitness

Generations

SGA (Mutation 0.50) & MGA 4-bit Deceptive Problem - Online/Offline Performance Analysis

MGA Off-line Performance

MGA On-line Performance

SGA Off-line Performance

SGA On-line Performance

Figure 12: Operator Disruption (Mutation) On-line/Off-

line.

Regarding to the maintenance of diversity within

the population, Figure 13 outlines the impact of oper-

ator disruption. Increasing crossover failed to main-

tain diversity within the population, which converged

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

146

quickly. The mutation experiment increased the level

of diversity within the population, but as mentioned

above, the search was directed by randomness. This

random diversity failed to assist in the search.

500

1000

1500

2000

2500

0 50 100 150 200

Hamming Distance

Generations

SGA & MGA - Genotype & Phenotype Convergence

MGA Genotype Hamming Distance

MGA Phenotype Hamming Distance

SGA Increased Crossover Genotype Hamming Distance

SGA Increased Mutation Genotype Hamming Distance

Figure 13: Operator Disruption Convergence Rate.

6 CONCLUSION

The results presented, illustrate that through the

implementation of Neutral theory, as proposed by

Kimura (Kimura, 1968), the genotype-phenotype

mapping of the MGA allows for a tunable, non-trivial,

many-to-one relationship. By adopting this approach,

convergence at a phenotypic level can be achieved,

but genetic diversity is maintained at a genotypic

level. Through the MGA’s multi-layered genotype-

phenotype mapping, adaptive (hot spots) and silent

(cold spots) mutations become possible. This phe-

nomenon allows neutral networks evolve within the

population. The MGA, as a result of genetic drift,

convergeson neutral sets close to one another in Ham-

ming space, which assists in relation to the adaptive-

ness of the MGA to changing environments. The

results indicate that neutrality, as introduced by the

MGA mapping, maintains a level of diversity within

the population, which assists in searching dynamic

landscapes as the diversity maintained by the MGA

promotes good strings. When compared to a SGA in-

corporating a number of diversifying techniques, the

implicit maintenance of diversity by the MGA proved

successful in searching the deceptive dynamic land-

scape. The MGA, as a result of genetic drift, con-

verges on neutral sets close to one another in Ham-

ming space.

REFERENCES

Baker, J. E. (1985). Adaptive Selection Methods for Genetic

Algorithms. In Proc. of the International Conference

on Genetic Algorithms and Their Applications, pages

101–111, Pittsburgh, PA.

De Jong, K. A. (1975). An Analysis of the Behavior of a

Class of Genetic Adaptive Systems. PhD thesis, Uni-

versity of Michigan, Ann Arbor. Dissertation Ab-

stracts International 36(10), 5140B; UMI 76-9381.

Ebner, M., Langguth, P., Albert, J., Shackleton, M., and

Shipman, R. (2001). On Neutral Networks and Evolv-

ability. In IEEE Congress on Evolutionary Computa-

tion (CEC). IEEE Press.

Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-

timization, and Machine Learning. Addison-Wesley

Publishing Company, Inc., Reading, MA.

Goldberg, D. E. and Richardson, J. (1987). Genetic Al-

gorithms with Sharing for Multimodal Function Opti-

mization. In Proceedings of the Second International

Conference on Genetic Algorithms on Genetic algo-

rithms and their application, pages 41–49, Hillsdale,

NJ, USA. L. Erlbaum Associates Inc.

Grefenstette, J. J. and Cobb, H. G. (1993). Genetic Algo-

rithms for Tracking Changing Environments. In Proc.

of the 5th Int. Conf. on Genetic Algorithms and their

Applications, pages 523–530. Morgan Kaufmann.

Hill, S. and O’Riordan, C. (2013). Analysing the im-

pact of dimensionality and diversity in a multi-layered

genotype-phenotype mapped GA. In CEC. Cancun,

Mexico.

Hill, S. and O’Riordan, C. (2104). Altering the granularity

of neutrality in a multi-layered genetic algorithm. In

6th International Conference on Evolutionary Com-

putation Theory and Applications ECTA Rome, Italy.

Hill, S. and O’Riordan, C. (2105). Examining the impact of

neutral theory on genetic algorithm population evolu-

tion. In 7th International Conference on Evolutionary

Computation Theory and Applications ECTA Lisbon,

Portugal.

Kimura, M. (1968). Evolutionary Rate at the Molecular

Level. Nature, 217(1):624–626.

Kimura, M. (1983). The Neutral Theory of Molecular Evo-

lution. Cambridge University Press.

Mahfoud, S. W. (1995). Niching Methods for Genetic Algo-

rithms. PhD thesis, University of Illinois at Urbana-

Champaign, Champaign, IL, USA. UMI Order No.

GAX95-43663.

Rothlauf, F. (2002). Representations for Genetic and Evo-

lutionary Algorithms. Springer-Verlag.

Smith, T., Husbands, P., and O’Shea, M. (2001). Neu-

tral networks and evolvability with complex genotype-

phenotype mapping. In Proceedings of the 6th Euro-

pean Conference on Advances in Artiﬁcial Life, ECAL

01, pages 272–281, London, UK. Springer-Verlag.

Yu, T. and Miller, J. (2001). Neutrality and the evolvability

of boolean function landscape. In Genetic Program-

ming, Proceedings of EuroGP2001, volume 2038 of

LNCS, pages 204–217. Springer-Verlag.

Diversifying Techniques & Neutrality in Genetic Algorithms

147