Success Prediction System for Student Counseling using Data Mining

org Frochte and Irina Bernst

Dept. of Electrical Engineering and Computer Science,

Bochum University of Applied Sciences, 42579 Heiligenhaus, Germany

Keywords:

Data Mining, Classiﬁcation, Supervised Learning, Information Privacy, Tertiary Education.

Abstract:

A framework how to use data mining of central exam data for the prediction of student success in bachelor

degree courses is presented. For the prediction a supervised learning approach is used based on successful

and unsuccessful student biographies. We develop a trafﬁc light rating system and present results for two

different kinds of bachelor degree courses; one in economics and one in engineering. We discuss applications

for students and student counseling institutions as well as the limitations dealing with information privacy

aspects, especially under the conditions regarding data mining in Germany.

1 INTRODUCTION

The application ﬁeld of knowledge discovery from

data bases is wide. One of these interesting ﬁelds

arises in the education system.

1.1 Research Questions and

Contributions

In this paper we apply techniques from knowledge

discovery from data bases to build a prediction sys-

tem, which can be helpful in the context of student

counseling. With this we mean institutions or persons

in the tertiary education that offer counseling to help

students work through their difﬁculties and ﬁnd ways

of managing their study and life situation.

The ﬁrst contribution of our work relates to the

construction of a framework for a success prediction

system on the degree course level. We discuss the

question of the relevant feature space including prac-

tical issues. This system is based on some static pa-

rameters concerning the qualiﬁcations of the student,

but mainly on the dynamic behavior during his study.

It uses data bases that naturally occur during the stu-

dent’s time at a university. The most important data

source we are considering is the data base of the exam

ofﬁce, in which the data accumulates after every ex-

amination period. In the case a student signs on a reg-

ular course exam, additional data is being collected

whether he or she passes, fails or withdraws. In the

case the student chooses to not sign on a course this

is recorded as well. So our approach doesn’t need any

additional data collection like e.g. surveys at all.

Other contributions of our research relate to the

development of a trafﬁc light rating system based on

the approach above. This provides a practical case

study for our approach.

1.2 Related Work

In the context of knowledge discovery from educa-

tional data bases the term Educational Data Mining is

nowadays used more and more. The work (Romero

and Ventura, 2007) provides a good survey on this

topic in the early years from 1995 to 2005. Often this

covers approaches contributing to theories of learning

or the learning sciences or as well the prediction of the

student’s future learning behavior. As in (Baker and

Yacef, 2009) this has often a kind of low level context.

This means in most cases the Educational Data Min-

ing community tends to consider student modeling on

the level of courses or single learning activities.

In this work – with a whole degree course as level

for the prediction – we consider a higher level of

abstraction concerning learning activities. A quite

closely related work is (Osmanbegovi

c and Sulji

2012), in which different learning techniques were

compared concerning the success in the course Busi-

ness Informatics. The work was based on 257 data

records and achieved a prediction accuracy between

71.2% and 76.65% depending on the used technique.

More to the initial conditions focuses the work

(Kova

c, 2010). It mainly uses socio-demographic

features like age, gender, ethnicity, education, work

Frochte, J. and Bernst, I.

Success Prediction System for Student Counseling using Data Mining.

DOI: 10.5220/0006036401810188

In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 181-188

ISBN: 978-989-758-203-5

181

status, and disability. Beyond this, aspects like the

fact, whether a bachelor of business or bachelor of

applied science is aimed, are used. Therefore, the pre-

diction here is mainly independent of the students’ be-

havior during their study. The CART approach used

in (Kova

c, 2010) was based on 453 data records

and reaches an overall percentage of correct classi-

ﬁcation of 60.5%. In (Jishan et al., 2015) the goal is

a prediction model for the ﬁnal grade. The used data

set contains 181 instances from a course titled Nu-

merical Analysis at North South University, Dhaka,

Bangladesh. The highest accuracy of about 75% was

reached using Artiﬁcial Networks and Naive Bayes

classiﬁcation.

2 KNOWLEDGE DISCOVERY IN

EXAM DATA BASES AND USE

CASES

We use Knowledge Discovery in Data Bases accord-

ing to (Fayyad et al., 1996) and apply this concept to

the demands of exam data bases especially in Ger-

many or states with similar restrictions concerning

data protection and informational self-determination.

Germany has quite strict laws concerning which,

where and by whom data is processed. For example,

aspects like the social background or migration back-

ground is not covered for data collection and process-

ing by (Law of the FRG, 2016). Therefore, the sug-

gested framework tries to be most careful concerning

this issue and shows, how it is still possible to pro-

vide a tool for student counseling based on exam data

records with these limitations.

2.1 Suggested Framework

Because of the discussed limitations we developed the

following processing work ﬂow. As ﬁgure 1 illus-

trates, the starting point is the data base of the ex-

amination ofﬁce of a university. It contains all data

about a student that a university has. To keep the data

maximum secure in a ﬁrst step, the data of relevant

features is anonymized and copied to a new data base.

This is a full automatic process that can be performed

on the computer system of the examination ofﬁce in a

regular schedule. Therefore, the risk of stolen data or

illegal use is the same as before. At this point the sug-

gested process does not contain any new party or en-

vironment. The features are discussed more detailed

in section 2.2 as well as the necessary preprocessing

of the data. The last preprocession step yields a train-

ing set from which a prediction system is built. The

resulting system, e.g. a multilayer perceptron (MLP),

is trained. The important aspect is that most software

systems based on machine learning algorithms – after

they have been trained – can act independently of the

used training data base. For example, in artiﬁcial neu-

ral networks like multilayer perceptron knowledge is

compressed in the weights w

i j

of each layer, which

means a few matrices of double values. Concerning

data security it is impossible to reconstruct a single

record of the training data base from these matrices.

Therefore, a trained system can be distributed with-

out interfering with data protection issues among e.g.

other institutions of a university.

While after the completed training the software

unit itself does not contain personal data of the stu-

dents from the training set, it of course still needs the

input data vector of the student it should predict the

study success for. Thus, for this software system there

are at least two applications.

1. Use as personal advisor or alarm system for

the students themselves. If a student signs in for the

alarm system every exam period, his behavior can be

rated and he may receive a feedback in terms of a traf-

ﬁc light rating system. Red would mean that he or

she should consider seeking for help, e.g. at a stu-

dent counseling ofﬁce. Green means everything is

ﬁne, and yellow is obviously in between. For the stu-

dent that might mean to watch carefully his own steps

and to consider what was different compared to the

last green semester. If the last exam period was red,

yellow could mean, that someone is on the right way

and things are getting better.

2. Use as tool for the counseling ofﬁces. In the

same way as a single student can use it for himself it

can also act as second opinion for professional coun-

selors. This is always possible, because a counselor

can access the student’s data during counseling.

If the current law allows it, of course it would be

possible to e.g. process the data of all students a coun-

selor is responsible for and to seek for candidates,

who might need additional support. In countries, in

which this is not automatically possible by law, there

is in general the option to ask students for a permis-

sion, when they sign in for the university. Because

this will be non-obligatory, only a subset of students

will be covered by this usage scenario.

2.2 Practical and Data Quality Issues

After the introduction of the bachelor and master de-

gree programs in association with the Bologna Pro-

cess the universities in Germany have built up a wide

range of different degree courses. All of them use

the European Credit Transfer and Accumulation Sys-

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

182

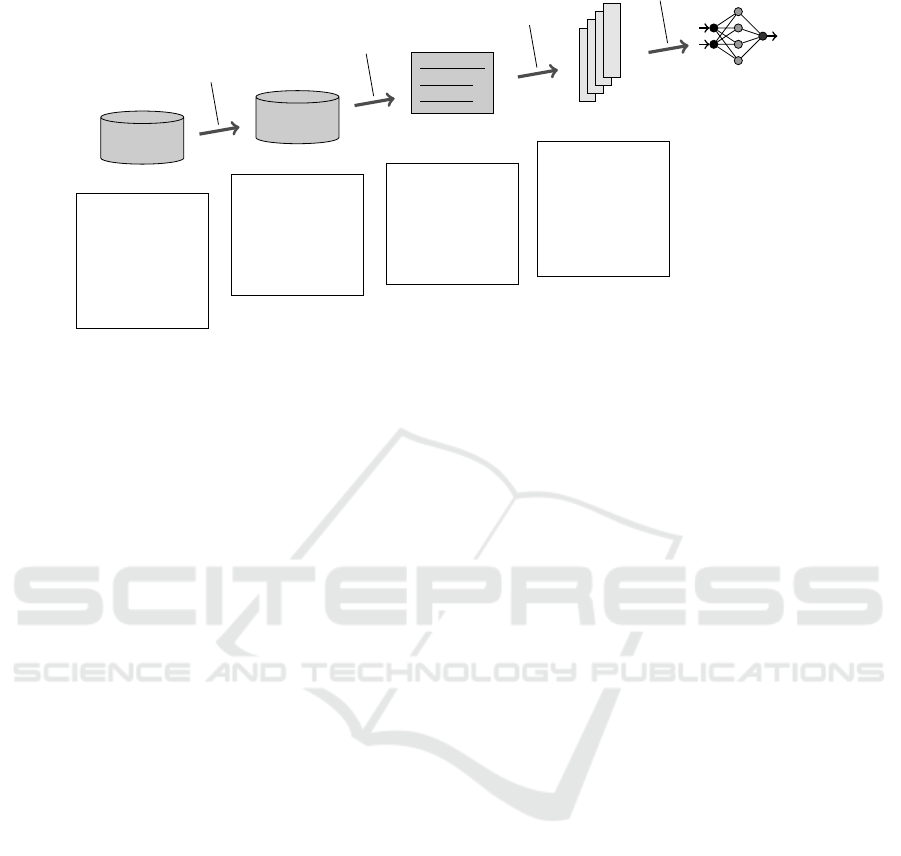
Database

exam. auth.

Target Data

Personalized Data

Anonymized Data

Conditioned

anonym. Data

Numerical

Training Set

Trained

Prediction System

Max Muster

Freiwald Gymnasium

Final Grade: 3.1

Maths 1: 3.0

Maths 2: failed

(2. Exam. Attempt)

Exam. Withdrawal: 1

Electronics: ’null’

. . .

#1F65121 Gymnasium

Final Grade: 3.1

Maths 1: 3.0

Maths 2: failed

(2. Exam. Attempt)

Exam. Withdrawal: 1

Electronics: ’null’

. . .

#1F65121 Gymnasium

Abschlussnote: 3.1

Maths 1: 3.0

Maths 2: failed

(2. Exam. Attempt)

Exam. Withdrawal: 1

Electronics: ’n.a.’

. . .

#1F65121

3.1

3.0

-1

. . .

Selection

Preprocessing

Transformation

Machine Learning & Data Mining

Figure 1: Knowledge Discovery in Exam Data Bases according to (Fayyad et al., 1996).

tem (ECTS). One semester corresponds to 30 ECTS

credits. Today there are about 18,000 degree courses.

Some of them only differ in details, some differ to-

tally. Nevertheless, most of them are descendants of

traditional diploma degree courses. In engineering for

example there are about ﬁve types: civil engineer-

ing, electrical engineering, mechanical engineering,

mechatronics and depending on the deﬁnition com-

puter science.

So one might expect the level of supersets of de-

gree courses to be a reasonable level for learning ap-

proaches. Considering this in detail it yields that this

level is not very promising for our approach. The rea-

son is that for the presented prediction system the dif-

ferences between the degree courses are hard to be

modeled. For example, let us suppose several uni-

versities provide a degree course for electrical engi-

neering. These degree courses all contain foundation

courses, e.g. in mathematics, physics. But all of the

degree courses will have different exam regulations.

Most of them might limit the number of trials to three,

some not. Some will provide grades for the courses,

some just attributes like passed or failed. Some even

might have rules like you need m of n foundation

courses etc. All of these aspects might change the

behavior of the students in the system and therefore

effects the learning methods. Beyond this, a degree

course is in these terms a moving target. Every 5th

up to 7th year the universities have to evaluate their

degree courses and in general change some aspects.

Therefore, it is reasonable to look for features that

are independent of the particular degree course. From

a scientiﬁc point of view we suggested – in addition

to the exam data records – also to analyze the impact

of personal data features, like gender/sex and year of

birth. Also other studies analyzed personal features,

like (Jirjahn, 2007) that indicates a strong correlation

between success and the age when a person starts to

study as well as the grade of the qualiﬁcation for uni-

versity entrance. The age is again an important fac-

tor in (Mosler and Savine, 2004). Beyond this, the

published results indicate that the gender is not a rel-

evant feature for the tertiary education level. Other

social economic features might be very important for

the success in the German university system as (Erdel,

2010) indicates. Beside existing data bases Erdel used

a survey, which in opposite to (Mosler and Savine,

2004) indicates that both, age and gender, are very

important. In general, considering the OECD studies,

e.g. (OECD, 2010) p. 43 – 45 and 95, one could ex-

pect that at least in Germany more social economic

features have a signiﬁcant impact.

Nevertheless, because of legal concerns it has not

been possible to include these social economic fea-

tures in our data base. Therefore, we were restricted

especially concerning sex/gender aspects. The age is

not directly included, but we were allowed to use both

data records, the year of the qualiﬁcation for univer-

sity entrance and the starting year of degree course,

which together correlate with the age. Therefore age

is weakly included.

We concentrate our study on two very different de-

gree courses: A bachelor degree in economics and

one in engineering. They differ much concerning

their structure and size of the data records.

After eliminating incomplete or obviously cor-

rupt data, the sample comprised 952 students of eco-

nomics and 261 of engineering. All of theses samples

are completed degree course biographies labeled for

this particular degree course with success or dropout.

Dropout means that the student left the degree course

at this particular university. Right now it is not pos-

Success Prediction System for Student Counseling using Data Mining

183

sible to track the students after they left a single uni-

versity. So some of them might leave e.g. because of

personal reasons following their cohabitation partner

to another town and continue their studies there. In

the new university these biographies again cause data

sets, which may lead to issues as shown in section 4.3.

2.3 Feature Selection

We prepared our training set, which contains 952 stu-

dents of economics and 261 of engineering, with the

following features, partitioned into two categories.

The ﬁrst are the static features, which will be constant

during the whole degree course biography:

1. Grade of the qualiﬁcation for university entrance

2. Year of the qualiﬁcation for university entrance

3. Kind of entrance qualiﬁcation

4. Starting year of degree course

The best categories are the dynamic features,

which means that these values will change after ev-

ery examination period based on the behavior of the

student:

5. Success coefﬁcient =

Number of successful exams

Number of possible exams

6. Mean grade of all successful exams

7. Number of exam trials

8. Number of withdrawals

9. Sum of reached ECTS

As we will see in section 4.1 these features are highly

diagnostic compared to the static features above.

With these features one has the possibility to

model very different types of students. For exam-

ple, we do not have the information, whether a stu-

dent considers himself as part-time student. Germany

has no tuition fees, so this is quite common. But a

successful part-time student can be modeled with our

feature set as well. This group could be classiﬁed by a

low number of withdrawals and a good mean grade in

contradiction to an average success coefﬁcient, which

directly correlates with the number of exam trials and

a low sum of reached ECTS compared to the semester.

Therefore, we could also classify unsuccessful and

successful part-time students.

To select the features one must keep in mind that

in general e.g. the signiﬁcance tests for a single fea-

ture might differ from one degree course to another.

To illustrate this let us consider the grade of the qual-

iﬁcation for university entrance.

The results in table 1 and table 2 make us – inde-

pendent of the used method – conclude that with a sig-

niﬁcance level of 5% we can reject the null hypothesis

Table 1: Signiﬁcance Test (Pearson).

Pearson’s linear

correlation coefﬁcient p-Value

Economic -0.0875 0.0074

Engineering -0.2393 0.0001

Table 2: Signiﬁcance Test (Spearman).

Spearman’s rank

correlation coefﬁcient p-Value

Economic -0.0734 0.0246

Engineering -0.2399 0.0001

for both degree courses. Therefore, there is a correla-

tion between the grade of the qualiﬁcation for univer-

sity entrance and the chance to successfully graduate

in the degree course. The correlation for the economic

degree course is much weaker than for the engineer-

ing course. The suggested explanatory model is that

the engineering degree course has stronger dependen-

cies to teaching contents at school, e.g. physics or

mathematics.

Features like kind of entrance qualiﬁcation are on

the other hand more important for degree courses at a

university of applied sciences than at traditional uni-

versities. At a traditional university this feature is

nearly always the identical constant value for all stu-

dents. This assumption does not hold for universities

of applied sciences, where the students have a broader

spread of entrance qualiﬁcations.

Nevertheless, in all cases we analyzed that the suc-

cess coefﬁcient (feature no. 5) is the most important

feature and this is very robust over all degree courses.

3 SUPERVISED LEARNING AND

TRAFFIC LIGHT RATING

SYSTEM

In this section we describe the approach of using the

supervised learning for developing a predictive sys-

tem of the students’ success and based on this the traf-

ﬁc light rating system.

3.1 Supervised Learning Approach

For our approach we need a data set with students,

who already have completed a bachelor degree course

or have chosen to dropout. As a result, we have a data

base with labeled training and testing data.

We present results for two different training

methods. On the one hand a common multilayer per-

ceptron (MLP) with one input layer, two hidden layers

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

184

and one output layer. All neurons used sigmoid func-

tions and the weights have been trained using back-

ward propagation. On the other hand we have got the

discriminant function analysis as statistical method

for behavior prediction or classiﬁcation of objects.

While the MLP is used as function approximation

between the values 0 for dropout and 1 for alumnus

using the features described above, the discriminant

function analysis works a bit differently: Its goal is to

analyze the group differences, meaning the investiga-

tion of the two groups of students with regard to the

given features.

Both methods were used as follows to predict the

success of the student in the particular bachelor de-

gree course. As discussed in section 2.2 the degree

courses are quite different. To avoid a new feature

space for every degree course we trained a single sys-

tem for every semester of every degree course. The

training per semester includes peculiarities of the spe-

ciﬁc semester in the speciﬁc degree course into the

achieved model of the learning system. So if e.g. the

ﬁrst two semesters are quite hard with a big drop rate

and the following four ones are – for the remaining

students – smoother, then this behavior is included

in the models. This has a lot of advantages, e.g. it

avoids explicitly modeling the examination regula-

tions and other speciﬁc aspects of the degree course.

Of course, this also has disadvantages mainly that for

a new course program developed after the evaluation

cycle discussed in section 2.2 it is still open, how to

transfer the achieved knowledge to a derived degree

course.

3.2 Trafﬁc Light Rating System

In section 2.3 we proposed a model with nine fea-

tures that primarily conduces to success concerning

the classiﬁcation of the students. The use of the meth-

ods from section 3.1 with these features leads to the

approach for the trafﬁc light rating system:

1. The trained system receives the nine features from

section 2.3 for a particular student.

2. The dropout probability for the student is calcu-

lated according to section 3.1.

3. The trafﬁc light rating system takes the dropout

probability of the previous semester into account.

The weighted linear extrapolation of dropout

probabilities P

of the semester i and P

i−1

of the

previous semester i − 1 yields

= P

+ α · (P

−

i−1

) with the coefﬁcient α ∈ [0, 1]. Thus, the sys-

tem is based on calculation of the dropout proba-

bility trend. For the ﬁrst semester we use

= P

4. To illustrate the prediction in trafﬁc lights, the

range of

from 0 to 1 is divided into three areas:

The ﬁrst area (green) is from 0 to 0.35, the second

area (yellow) from 0.35 to 0.65 and the third area

(red) from 0.65 to 1.

4 RESULTS

We compared the different methods and approaches.

The results are shown for the test set, which prevents

over-ﬁtting effects. As we will show below, it turns

out that the total prediction accuracy is mainly deﬁned

by the selected features.

The results of the test sets may differ depending

on the selected data records. For example, a test set

based on 15% of the total data sets are just 39 data

sets in engineering. To provide meaningful results the

systems were trained multiple times with randomly

selected sets, evaluated concerning the achieved ac-

curacy, and afterwards all of the results were arith-

metically averaged.

In the tables below the value of correctly classi-

ﬁed alumnus means, how many of the persons, who

according to the data base ﬁnished the degree course,

were correctly classiﬁed as alumnus; the same for the

ones, who dropout of the degree course independent

of the speciﬁc reasons.

4.1 Results using Discriminant

Function Analysis

We start with the results achieved on discriminant

function analysis. In all tests, see e.g. table 3, it turned

out that the discriminant function analysis as method

on this problem set tends to be signiﬁcantly more cor-

rect for the alumnus subset than for the dropout sub-

set.

Table 3: Prediction after the ﬁrst semester prediction.

Course Correctly Classiﬁed

Total Alum. Dropout

Economics 76% 79% 68%

Engineering 82% 88% 80%

Let us assume for the application scenario that we

have a degree course with 30% dropout rate and about

200 freshmen. The system would classify about 110

of the alumnus set correctly and send 30 to the coun-

seling. On the other hand about 40 of the dropout set

would be correctly classiﬁed and 20 would be mis-

classiﬁed. Under these conditions the system does

not work entirely satisfactorily, because 70 persons

would maybe be asked to seek for an appointment at

the counseling ofﬁce, while 57% will really need it.

Success Prediction System for Student Counseling using Data Mining

185

For engineering with the higher rates it turns out bet-

ter. Under the same conditions 122 alumni are classi-

ﬁed correctly and 18 would be sent to the counseling

by mistake. On the other hand 48 dropouts would be

detected correctly. There we end up with about 73%

of the 66 persons, who will be sent for counseling and

really need a counseling appointment.

These are the rates and the prediction accuracy in

the ﬁrst semester. As table 4 below shows, this accu-

racy will rise, if one considers higher semesters.

Table 4: Prediction accuracy for different semesters.

Semester

Correctly Classiﬁed

Economics Engineering

1 76% 83%

2 78% 85%

6 82% 89%

Nevertheless, for student counseling mainly the

ﬁrst two semesters are of major interest. If the sys-

tem receives data for the second semester, the student

will have studied about one year and have already set

the course for another half year.

Another aspect that table 4 shows, is that both de-

gree courses differ concerning the prediction quality,

whereas both gain about 6% points from the ﬁrst to

the sixth semester.

The prediction quality between both degree

courses differs between 6% and 7% points. The rea-

son is not the size of the data base because the number

of data records for economics is higher. One reason

might be that students of the economic degree course

might be more heterogeneous compared to the engi-

neering students and therefore the missing social eco-

nomic features might have a higher impact here.

Beyond this, for the economic degree course the

static features provide no additional information – in

opposite to some other degree courses. If one just uses

the static features for the prediction, we receive the re-

sults shown in table 5. So in economics one can see

Table 5: Prediction after the ﬁrst semester using feat. 1 – 4.

Course Correctly Classiﬁed

Total Alum. Dropout

Economics 53% 47% 65%

Engineering 65% 64% 65%

that guessing is nearly as effective as using the predic-

tion system. It turned out that these features have not

enough information for this course. For the engineer-

ing course on the other hand the output is beyond the

rates achieved in (Kova

c, 2010) for static features.

So for this course they provide useful information.

4.2 Results for the First Semester using

a Feedforward Neural Network

With the following results we would like to emphasize

that the model for the prediction is quite simple and

up to this level its success mainly depends on the data

base and its quality.

To do this we used a multilayer perceptron (MLP)

with two hidden layers of equal length as an alterna-

tive to the discriminant function analysis. As table 6

and 7 indicate, it is possible to model the main be-

havior with three neurons in both layers. Raising the

number of neurons up to ten in each layer only leads

to small changes. After that point the results for the

studied six semesters of both bachelor degree courses

won’t improve anymore or will get even worse on the

respective testing set.

Table 6: MLP for Economics (1. Semester).

Hiddenlayer Correctly Classiﬁed

1 2 Total Alumnus Dropout

3 3 75% 76% 73%

10 10 76% 77% 72%

Comparing table 6 and 3, both approaches reach

about the same rate for correct classiﬁcation on the

total set. The only signiﬁcant difference is about their

behavior on the two subsets of successful alumnus

and dropouts. The multilayer perceptron tends to be

more correct for the dropouts and the discriminant

function analysis for the alumnus.

Table 7: MLP for Engineering (1. Semester).

Hiddenlayer Correctly Classiﬁed

1 2 Total Alumnus Dropout

3 3 85% 79% 88%

10 10 85% 80% 87%

The same is true for the results in table 7. Beyond

this, for this degree course the multilayer perceptron

produces slightly better results compared to the dis-

criminant function analysis.

4.3 Application on Trafﬁc Light Rating

System

Now we demonstrate the application of this prediction

approach to the trafﬁc light rating system described in

section 3.2.

Figure 2 shows the estimated dropout probabil-

ity (blue graph) and the suggested trafﬁc light system

with α = 0.5. The two students are members of the

test set and ﬁnish this degree course as alumni.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

186

Figure 2: Trafﬁc light rating for alumni in economics.

The trafﬁc light rating considers the dropout prob-

ability for all semesters as low. The provided feed-

back was correct all of the time. Even the yellow sign

for student 2 is reasonable, because of the changing

of the dropout probability. In this case the student

managed it on his / her own, but the yellow sign with

a still quite low dropout probability would provide a

good feedback.

In ﬁgure 3 we see different time lines, which

are all marked as dropout in the data base. Student

4 dropped out after the third semester. After that

Figure 3: Trafﬁc light rating for dropouts in economics.

point the dropout probability is 1. Student 3 is an

example for unusual behavior that makes it hard to

achieve higher certainty rates. After a bad start it be-

came better and better, but ended with a dropout in

a higher semester. The cause might be a shift to an-

other university or personal reasons. In these cases a

third group like continues studies elsewhere or similar

could be helpful.

The same experiments were performed for the en-

gineering degree course. Two alumni students are

shown in ﬁgure 4. The system works in general ﬁne

as shown e.g. for student 5. However, there are ex-

ceptional cases as shown with student 6. Here, the

reason is that the student changed the degree course.

In such a case the data has all the ECTS credits that

have been transferred from the former degree course

listed in one semester. Other features like the trials

(often being set to 1) suffer as well. So this data set is

very hard to predict by a learning system, because it

is highly irregular.

Figure 4: Trafﬁc light rating for alumni in engineering.

4.4 Benchmark of the Results

In this section we will discuss, whether the achieved

results meet already the considered use cases and how

they can be seen in comparison to the results in the re-

lated work section. We considered two main applica-

tion cases, the ﬁrst one as tool for a personal advisor

and the second one as tool for a counseling ofﬁce.

The results for the engineering degree course are

very promising. With the prediction accuracy of the

MLP it should be possible to use the developed pre-

diction system at least as a ﬁrst ﬁlter for a counseling

Success Prediction System for Student Counseling using Data Mining

187

ofﬁce as to the question, which students might need

further attention. Because the counselors as profes-

sionals will be able to bring the output of the algo-

rithm into line with their experience, the rate will be

good enough.

Probably most of the students would be able to

balance the statistical rating of the system against

their personal appraisal. Nevertheless, for some stu-

dents a misclassiﬁcation of the tool might encourage

them with their wrong opinion or even unsettle per-

sons with a low self conﬁdence. Therefore, we con-

sider the results as still not good enough for the appli-

cation in the suggested use case as personal advisor

but as a reasonable tool for counseling ofﬁces.

If we compare the results of the overall percentage

of correct classiﬁcation of 60.5% in (Kova

c, 2010),

76.65% (Osmanbegovi

c and Sulji

c, 2012) and 75% in

(Jishan et al., 2015) the reached classiﬁcation rate for

the bachelor degree course in economics with 75%-

76% is in a good region. The rates of 85% using MLP

and 82% with the discriminant function analysis for

the degree course in engineering are very good.

5 CONCLUSION AND FUTURE

PROSPECTS

In this paper, we proposed an approach for the success

prediction of a whole bachelor degree course. The

proposed key idea was to learn on a mixture of static

features and dynamic features. With this we intro-

duced a novel feature set and it is beyond this possible

to model every bachelor degree course independent of

the current subject area. The achieved results of this

generic approach are at least in the common interval

of related results or even better.

In addition, several avenues of future work have

been identiﬁed which we expect to offer further im-

provements. To improve the percentage of correct

classiﬁcation we assume social economic features in

contradiction with an improved tracking of dropout

students. Another open question is, if it will be pos-

sible to transfer knowledge of old bachelor degree

courses to a reﬁned version after the evaluation phase.

Beyond this, one has to keep in mind that the alumnus

set is bigger than the dropout group in contradiction

with the fact the all approaches are less accurate on

this subset. This is an issue for the counseling ofﬁce

usage scenario because of the subset of alumnus clas-

siﬁed as dropouts. These persons will unnecessarily

tie up capacities. Therefore one future prospect is to

develop a second stage in which just the persons clas-

siﬁed as dropout are evaluated again.

Due to the promising results with further research

concerning these aspects we expect that knowledge

discovery in exam data bases will become a very im-

portant tool in student counseling and academic qual-

ity control.

ACKNOWLEDGEMENTS

We would like to thank C. Kaufmann, P. Bouillon &

S. R

usche for support and discussion. This work is

supported by a grant from the MIWF NRW.

REFERENCES

Baker, R. S. and Yacef, K. (2009). The state of educational

data mining in 2009. JEDM-Journal of Educational

Data Mining, 1(1):3–17.

Erdel, B. (2010). Welche Determinanten beeinﬂussen

den Studienerfolg? Technical report, Friedrich-

Alexander-Universit

at Erlangen-N

urnberg - School of

Business and Economics.

Fayyad, U., Piatetsky-Shapiro, G., and Smyth, P.

(1996). From data mining to knowledge discovery in

databases. AI magazine, 17(3):37.

Jirjahn, U. (2007). Welche Faktoren beeinﬂussen den

Erfolg im wirtschaftswissenschaftlichen Studium.

Schmalenbachs Zeitschrift f

ur betriebswirtschaftliche

Forschung, 59(3):286–313.

Jishan, S. T., Rashu, R. I., Haque, N., and Rahman, R. M.

(2015). Improving accuracy of students’ ﬁnal grade

prediction model using optimal equal width binning

and synthetic minority over-sampling technique. De-

cision Analytics, 2(1):1–25.

Kova

c, Z. J. (2010). Early prediction of student success:

mining students enrolment data. In Proceedings of In-

forming Science & IT Education Conference (InSITE),

pages 647–665. Citeseer.

Law of the FRG (2016). Hochschulstatistikgesetz (hstatg).

http://www.gesetze-im-internet.de/hstatg 1990/

BJNR024140990.html.

Mosler, K. and Savine, A. (2004). Studienaufbau und Stu-

dienerfolg von K

olner Volks-und Betriebswirten im

Grundstudium. Technical report, Discussion papers

in statistics and econometrics.

OECD (2010). PISA 2009 Results: Overcoming Social

Background. OECD Publishing.

Osmanbegovi

c, E. and Sulji

c, M. (2012). Data mining ap-

proach for predicting student performance. Economic

Review Journal of Economics and Business, 10(1).

Romero, C. and Ventura, S. (2007). Educational data min-

ing: A survey from 1995 to 2005. Expert systems with

applications, 33(1):135–146.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

188