
A Quantum Field Evolution Strategy
An Adaptive Surrogate Approach
J
¨
org Bremer
1
and Sebastian Lehnhoff
2
1
Department of Computing Science, University of Oldenburg, Uhlhornsweg, Oldenburg, Germany
2
R&D Division Energy, OFFIS – Institute for Information Technology, Escherweg, Oldenburg, Germany
Keywords:
Evolution Strategies, Global Optimization, Surrogate Optimization, Quantum Potential.
Abstract:
Evolution strategies have been successfully applied to optimization problems with rugged, multi-modal fitness
landscapes, to non linear problems, and to derivative free optimization. Usually evolution is performed by
exploiting the structure of the objective function. In this paper, we present an approach that harnesses the
adapting quantum potential field determined by the spatial distribution of elitist solutions as guidance for the
next generation. The potential field evolves to a smoother surface leveling local optima but keeping the global
structure what in turn allows for a faster convergence of the solution set. We demonstrate the applicability
and the competitiveness of our approach compared with particle swarm optimization and the well established
evolution strategy CMA-ES.
1 INTRODUCTION
Evolution Strategies have shown excellent perfor-
mance in global optimization especially when it
comes to complex multi-modal, high dimensional,
real valued problems (Kramer, 2010; Ulmer et al.,
2003). A major drawback of population based algo-
rithms is the large number of objective function evalu-
ations. Real world problems often face computational
efforts for fitness evaluations; e. g. in Smart Grid load
planning scenarios, fitness evaluation involves simu-
lating a large number of energy resources and their
behaviour (Bremer and Sonnenschein, 2014).
We propose a surrogate approach that harnesses
a continuously updating quantum potential field de-
termined by elitist solutions. On the one hand side,
the quantum field exploits global information by ag-
gregating over scattered fitness information similar to
scale space approaches (Horn and Gottlieb, 2001; Le-
ung et al., 2000), on the other side by continuously
adapting to elitist solutions, the quantum field surface
quickly flattens to a smooth surrogate for guiding fur-
ther sampling directions. To achieve this, the surro-
gate is a result of Schr
¨
odinger’s equation of which a
probability function is derived that determines the po-
tential function after a clustering approach (cf. (Horn
and Gottlieb, 2001)). We associate minima of the po-
tential field, created in denser regions of good solu-
tions’ positions with areas of interest for further inves-
tigation. Thus, offspring solutions are generated with
a trend in descending the potential field. By harness-
ing the quantum potential as a surrogate, we achieve
a faster convergence with less objective function calls
compared with using the objective function alone. In
lieu thereof the potential field has to be evaluated at
selected point. Although a fine grained computation
of the potential field would be a computationally hard
task in higher dimensions (Horn and Gottlieb, 2001),
we achieve a better overall performance because we
need to calculate the field only at isolated data points.
The paper starts with a review of using quan-
tum mechanics in computational intelligence and in
particular in evolutionary algorithms; we briefly re-
cap the quantum potential approach for clustering
and present our adaption for integration into evolu-
tion strategies. We conclude with an evaluation of the
approach with the help of several well-known bench-
mark test functions and demonstrate the competitive-
ness to two competitive algorithms: particle swarm
optimization (PSO) and co-variance matrix adaption
evolution strategy (CMA-ES).
2 RELATED WORK
Several evolutionary algorithms have been introduced
to solve nonlinear complex optimization problems
with multi-modal, rugged fitness landscapes. Each
Bremer, J. and Lehnhoff, S.
A Quantum Field Evolution Strategy - An Adaptive Surrogate Approach.
DOI: 10.5220/0006037000210029
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 21-29
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
21

of these method has its own characteristics, strengths
and weaknesses. A common characteristics in all EAs
is the generation of an offspring solution set in order
to explore the characteristics of the objective function
in the neighbourhood existing solutions. When the
solution space is hard to explore or objective evalu-
ations are costly, computational effort is a common
drawback for all population-based schemes. Many
efforts have been already spent to accelerate conver-
gence of these methods. Example techniques are: im-
proved population initialization (Rahnamayan et al.,
2007), adaptive populations sizes (Ahrari and Shariat-
Panahi, 2013) or exploiting sub-populations (Rigling
and Moore, 1999).
Sometimes a surrogate model is used in case
of computational expensive objective functions
(Loshchilov et al., 2012) to substitute a share of objec-
tive function evaluations with cheap surrogate model
evaluations. The surrogate model represents a learned
model of the original objective function. Recent ap-
proaches use Radial Basis Functions, Polynomial Re-
gression, Support Vector Regression, Artificial Neu-
ral Network or Kriging (Gano et al., 2006); each ap-
proach with individual advantages and drawbacks.
At the same time, quantum mechanics has in-
spired several fields of computational intelligence
such as data mining, pattern recognition or optimiza-
tion. In (Horn and Gottlieb, 2001) a quantum me-
chanics based method for clustering has been in-
troduced. Quantum clustering extends the ideas of
Scale Space algorithms and Support Vector Cluster-
ing (Ben-Hur et al., 2001; Bremer et al., 2010) by
representing an operator in Hilbert space by a scaled
Schr
¨
odinger equation that yields a probability func-
tion as result. The inherent potential function of the
equation that can be analytically derived from the
probability function is used to identify barycenters of
data cluster by associating minima with centers. In
(Weinstein and Horn, 2009a) this approach has been
extended to a dynamic approach that uses the fully
fledged time dependant variant of the Schr
¨
odinger
equation to allow for a interactive visual data mining
especially for large data sets (Weinstein et al., 2013).
We adapted and extended the quantum field part
of the clustering approach to optimization and use
the potential function to associate already found so-
lutions from the objective domain with feature vec-
tors in Hilbert space; but with keeping an emphasis of
the total sum (cf. (Horn and Gottlieb, 2001)) and thus
with keeping in mind all improvements of the ongo-
ing optimum search.
(Rapp and Bremer, 2012) used a quantum po-
tential approach derived from quantum clustering
to detect abnormal events in multidimensional data
streams. (Yu et al., 2010) used quantum clustering
for weighing linear programming support vector re-
gression. In this work, we derive a sampling method
for a pµ`λq-ES from the quantum potential approach
originally used for clustering by (Horn and Gottlieb,
2002).
A quantum mechanical extension to particle
swarm optimization has been presented e.g. in (Sun
et al., 2004; Feng and Xu, 2004). Here particles move
according to quantum mechanical behavior in contrast
to the classical mechanics ruled movement of parti-
cles in standard PSO. Usually a harmonic oscillator
is used. In (Loo and Mastorakis, 2007) both meth-
ods quantum clustering and quantum PSO have been
combined by deriving good particle starting positions
from the clustering method first. For the simulated
Annealing (SA) approach also a quantum extension
has been developed (Suzuki and Nishimori, 2007).
Whereas in classical SA local minima are escaped by
leaping over the barrier with a thermal jump, quantum
SA introduces the quantum mechanical tunneling ef-
fect for such escapes.
We integrated the quantum concept into evolution
strategies; but by using a different approach: we har-
ness the information in the quantum field about the
so far gained success as a surrogate for generating the
offspring generation. By using the potential field, in-
formation from all samples at the same time is con-
densed into a directed generation of the next genera-
tion.
3 THE SCHR
¨
ODINGER
POTENTIAL
We start with a brief recap of the Schr
¨
odinger po-
tential and describe the concept following (Horn and
Gottlieb, 2002; Horn and Gottlieb, 2001; Weinstein
and Horn, 2009b). Let
Hψ ” p´
σ
2
pot
2
∇
2
`V px
x
xqqψpx
x
xq “ Eψpx
x
xq (1)
be the Schr
¨
odinger equation rescaled to a single free
parameter σ
pot
and eigenstate ψpx
x
xq. H denotes the
Hamiltonian operator corresponding to the total en-
ergy E of the system. ψ is the wave function of the
quantum system and ∇
2
denotes the Laplacian differ-
ential operator. V corresponds to the potential energy
in the system. In case of a single point at x
x
x
0
Eq. (1)
results in
V “
1
2
σ
2
pot
px
x
x ´x
x
x
0
q
2
(2)
E “
d
2
(3)
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
22

(a) (b) (c) (d)
(e) (f) (g) (h)
(i) (j) (k) (l)
Figure 1: Function (left column) and exemplary evolution (after 1, 3 and 8 iterations) of the quantum potential that guides the
search for minima for the test functions: Alpine, Goldstein-Price and Himmelblau (from top to bottom).
with d denoting the dimension of the field. In this case
ψ is the ground state of a harmonic oscillator. Given
an arbitrary set of points, the potential at a point x
x
x can
be expressed by
V px
x
xq “ E `
σ
2
pot
2
∇
2
ψ
ψ
“ E ´
d
2
`
1
2σ
2
pot
ψ
ÿ
i
px
x
x ´x
x
x
i
q
2
e
´
px
x
x´x
x
x
i
q
2
2σ
2
pot
.
(4)
In Eq. (4) the Gaussian wave function
ψpx
x
xq “
ÿ
i
px
x
x ´x
x
x
i
q
2
e
´
px
x
x´x
x
x
i
q
2
2σ
2
pot
(5)
is associated to each point and summed up. Please
note that the bandwidth parameter (usually named σ,
cf. (Horn and Gottlieb, 2002)) has been denoted σ
pot
to discriminate the bandwidth of the wave function
and the variance σ in the mutation used in the evo-
lutions strategy later. In quantum mechanics, usually
the potential V px
x
xqis given and solutions or eigenfunc-
tions ψpx
x
xq are sought. In our approach we are already
given ψpx
x
xq determined by a set of data points. The
set of data points is given by elitist solutions. We then
look for the potential V pxq whose solution is ψpx
x
xq.
The wave function part corresponds with the
Parzen window estimator approach for data clustering
(Parzen, 1962) or with scale-space clustering (Leung
et al., 2000) that interprets this wave function as the
density function that could have generated the under-
lying data set. The maxima of this density function
correspond therefore with data centers.
In quantum clustering and by requiring ψ to be the
ground state of the Hamiltonian H the potential field
V establishes a surface that shows more pronounced
minima (Weinstein and Horn, 2009b). V is unique up
to a constant factor. By setting the minimum of V to
zero it follows that
E “ ´min
σ
2
pot
2
∇
2
ψ
ψ
. (6)
A Quantum Field Evolution Strategy - An Adaptive Surrogate Approach
23

With this convention V is determined uniquely with
0 ď E ď
d
2
. In this case, E is the lowest eigenvalue of
the operator H and thus describes the ground state.
V is expected to exhibit one or more minima
within some region around the data set and grow
quadratically on the outside (Horn and Gottlieb,
2002). In quantum clustering, these minima are as-
sociated with cluster centers. We will interpret them
as balance points or nuclei where the minimum of an
associated function f lies if the set of data points that
defines V is a selection of good points (in the sense of
a good fitness according to f ).
4 THE ALGORITHM
We start with a general description of the idea. In our
approach we generate the quantum potential field of
an elitist selection of samples. Out of a sample of
λ solutions the best µ are selected according to the
objective function. These µ solutions then define a
quantum potential field that exhibits troughs at the
barycenters of good solution taking into account all
good solutions at the same time. In the next step this
potential field is used to guide the sampling of the next
generation of λ offspring solutions from which the
next generation is selected that defines the new field.
In this way, the potential field continuously adapts in
each iteration to the so far found best solutions.
The advantage of using the potential field results
from its good performance in identifying the barycen-
ters of data points. Horn and Gottlieb (Horn and Got-
tlieb, 2001) demonstrated the superior performance
compared with density based approaches like Scale
Space or Parzen Window approaches (Roberts, 1997;
Parzen, 1962). Transfered to optimization this means
the quantum potential allows for a better identification
of local optima. As they can be explored faster they
can be neglected earlier which in turn leads to a faster
convergence of the potential field towards the global
optimum (cf. Figure 1).
Figure 1 gives an impression of the adaption pro-
cess that transforms the quantum field into an easier
searchable function. Each row shows the situation af-
ter 1, 3 and 8 iterations for different 2-dimensional ob-
jective functions. The left column displays the origi-
nal objective function; from left to right the evolving
potential field is displayed together with the respec-
tive offspring solutions that represent the so far best.
The minimum of the potential field evolves towards
the minimum of the objective function (or towards
more than one optimum if applicable).
Figure 2 shows the approach formally. Starting
from an initially generated sample X equally dis-
X – tx
x
x
i
„ Upx
lo
, x
up
q
d
u, 1 ď i ď n
repeat
S Ð H
repeat
x
x
x
z
– x
x
x
i
P X , i „ Up1, |X |q
s
s
s „ N px
x
x
z
, σ
2
q
if p ď e
V px
x
x
z
q´V ps
s
sq
, p „Up0, 1q then
S
S
S ÐS
S
S Ys
s
s
end if
until |S| ““ λ
V ÐV pS, σ
pot
q
X Ð selectpS, f , µq
σ Ð σ ¨ω
until }f px
best
q´ f px
˚
q} ď ε
Figure 2: Basic scheme for the Quantum Sampling ES Al-
gorithm.
tributed across the whole search domain defined by
a box constraint in each dimension. Next, the off-
spring is generated by sampling λ points normally
distributed around the µ solutions from the old gen-
eration with an each time randomly chosen parent
solution as expectation and with variance σ
2
that
decreases with each generation. We use a rejec-
tion sampling approach with the metropolis criterion
(Metropolis et al., 1953) for acceptance applied to the
difference in the potential field between a new candi-
date solution and the old solution. The new sample is
accepted with probability
p
a
“ minp1, e
∆V
q. (7)
∆V “ V px
old
q´V px
new
q denotes the level difference
in quantum field. A descent within the potential field
is always accepted. A (temporary) degradation in
quantum potential level is accepted with a probabil-
ity P
a
(eq. 7) determined by the level of degradation.
As long as there exists at least one pair tx
x
x
1
, x
x
x
2
u Ă
S with x
x
x
1
‰ x
x
x
2
, the potential field has a minimum at
x
x
x
1
with x
x
x
1
‰x
x
x
1
^x
x
x
1
‰x
x
x
1
. Thus, the sampling will find
new candidates. The sample variance σ
2
is decreased
in each iteration by a rate ω. Finally, for the next iter-
ation, the solution set X is updated by selecting the µ
best from offspring S.
The process is repeated until any stopping crite-
rion is met; apart from having come near enough the
minimum we regularly used an upper bound for the
maximum number of iterations (or rather: number of
fitness evaluations respectively).
5 RESULTS
We evaluated our evolution strategy with a set of
well known test functions developed for benchmark-
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
24
0 100 200 300 400
500
10
´10
10
´7
10
´4
10
´1
iterations
log error
plain
quantum
Figure 3: Comparing the convergence of using the quantum
field as surrogate with the plain approach working on the
objective function directly. For testing, the 2-dimensional
Alpine function has been used.
ing optimization heuristics. We used the follow-
ing functions: Alpine, Goldstein-Price, Himmelblau,
Bohachevsky 1, generalized Rosenbrock, Griewank,
Sphere, Booth, Chichinadze and Zakharov (Ulmer
et al., 2003; Ahrari and Shariat-Panahi, 2013; Him-
melblau, 1972; Yao et al., 1999); see also appendix
A. These functions represent a mix of multi-modal, 2-
dimensional and multi-dimensional functions, partly
with a huge number of local minima and steep as
well as shoal surroundings of the global optimum and
broad variations in characteristics and domain sizes.
Figure 1 shows some of the used functions (left
column) together with the respective evolution of the
quantum potential field that guides the search towards
the minimum at p0, 0q for the Alpine function and
p0, ´1q for Goldstein-Price; the Himmelblau function
has four global minima which are all found. The fig-
ure also shows the evolution of the solution popula-
tion. In the next step, we tested the performance of
our approach against competitive approaches.
First, we tested the effect of using the quantum
field as adaptive surrogate compared with the same
update strategy working directly on the fitness land-
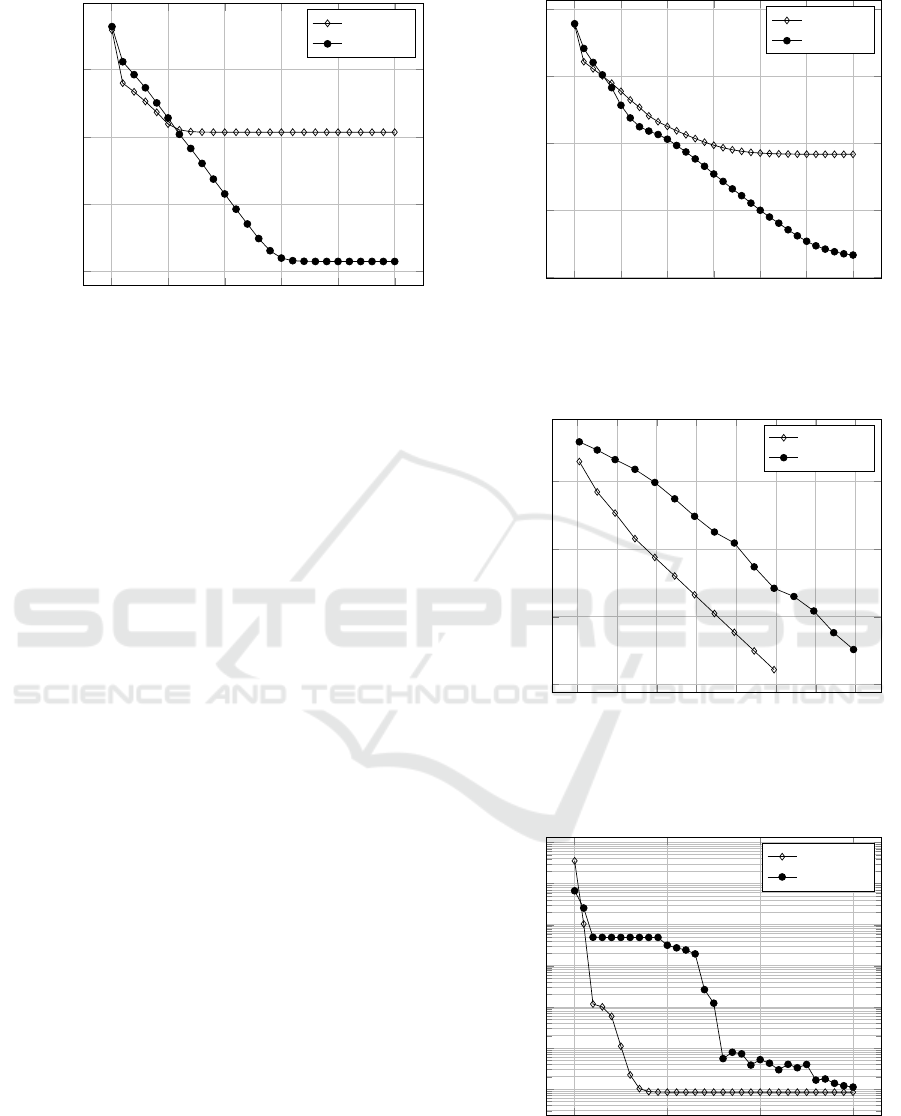
scape of the objective function. Figure 3 shows the
convergence of the error on the Alpine test function
for both cases. Although the approach with surrogate
converges slightly slower in the beginning it clearly
outperforms the plain approach without quantum sur-
rogate. Figure 4 shows the same effect for the 20-
dimensional case. Both results show the convergence
of the mean error for 100 runs each.
In a next step, we compared our approach
with two well-known heuristics: particle swarm
optimization (PSO) from (Kennedy and Eber-
hart, 1995) and the covariance matrix adaption
0
500
1,000
1,500
2,000
2,500
3,000
10
´6
10
´4
10
´2
10
0
10
2
iterations
log error
plain
quantum
Figure 4: Convergence of using the quantum field as sur-
rogate compared to the plain approach. Depicted are the
means of 100 runs on the 20-dimensional Alpine function.
0 20 40
60
80 100 120 140
10
´22
10
´15
10
´8
10
´1
iterations
log error
quantum
CMA-ES
Figure 5: Comparing the convergence (means of 100
runs) of CMA-ES and the quantum approach on the 2-
dimensional Booth function.
0
500
1,000
1,500
10
´2
10
´1
10
0
10
1
10
2
10
3
10
4
iterations
log error
quantum
CMA-ES
Figure 6: Comparing the convergence of CMA-ES and the
quantum approach on the 20-dimensional Griewank func-
tion on the domain r´2048, 2048s
20
. Both algorithms have
been stopped after 1500 iterations.
A Quantum Field Evolution Strategy - An Adaptive Surrogate Approach
25

evolution strategy (CMA-ES) by (Hansen, 2011).
Both strategies are well-known, established, and
have been applied to wide range of optimiza-
tion problems. We used readily available and
evaluated implementations from Jswarm-PSO
(http://jswarm-pso.sourceforge.net) and commons
math (http://commons.apache.org/proper/commons-
math).
All algorithms have an individual, strategy spe-
cific set of parameters that usually can be tweaked to
some degree for a problem specific adaption. Never-
theless, default values that are applicable for a wide
range of functions are usually available. For our ex-
periments, we used the following default settings. For
the CMA-ES, the (external) strategy parameters are
λ, µ, w
i“1...µ
, controlling selection and recombination;
c
σ
and d
σ
for step size control and c
c
and µ
cov
control-
ling the covariance matrix adaption. We have chosen
to set these values after (Hansen, 2011).
λ “ 4 `t3 lnnu, µ “
„
λ
2
, (8)
w
w
w
i
“
lnp
λ
2
`0.5q´lni
ř
j“1
µ
λ
2
`0.5q´lni
, i “ 1, . . . , µ (9)
C
c
“
4
n `4
, µ
cov
“ µ
e
f f , (10)
C
cov
“
1
µ
cov
2
pn `
?
2q
2
`
ˆ
1 ´
1
µ
cov
˙
min
ˆ
1,
2µ
cov
´1
pn `2q
2
`µ
cov
˙
,
(11)
These settings are specific to the dimension N of the
objective function. An in-depth discussion of these
parameters is also given in (Hansen and Ostermeier,
2001).
For the PSO, we used values of 0.9 for the weights
and 1 for the inertia parameter as default setting (Shi
and Eberhart, 1998).
For the quantum field strategy, we empirically
found the following values as a useful setting for a
range of objective functions. The initial mutation
variance has been set to σ “ d{10 for an initial di-
ameter d of the search space (domain of the objec-
tive function). The shrinking rate of the variance has
been set to ω “ 0.98 and the bandwidth in the poten-
tial equation (4) has been set to σ
pot
“ 0.4. For the
population size we chose µ “ 10 and λ “ 50 if not
otherwise stated.
First, we compared the convergence of the quan-
tum strategy with the CMA-ES. Figure 5 shows a
first result for the 2-dimensinal Booth function (with
a minimum of zero). The quantum approach has been
stopped at errors below 1 ˆ10
´21
to avoid numeri-
cal instabilities. The used CMA-ES implementation
has a similar condition integrated into its code. Com-
paring iterations, the quantum approach converges
faster than CMA-ES. Figure 5 shows the result for
the 20-dimensional Griewank function with a search
domain of r´2049, 2048s
20
. Here, the quantum ap-
proach achieves about the same result as the CMA-ES
within less iterations. Comparing iterations does not
yet shed light on performance.
As the performance is determined by the number
of operations that have to be conducted in each itera-
tion, the following experiments consider the number
of function evaluation calls rather than iterations. Ta-
ble 1 shows the results for a bunch of 2-dimensional
test functions. For each test function and each al-
gorithm the achieved mean (averaged over 100 runs)
solution quality and the needed number of function
evaluations is displayed. The solution quality is ex-
pressed as the error in terms of remaining difference
to the known global optimum. As stopping criterion
this time each algorithm has been equipped with two
conditions: error below 5 ˆ10
´17
and a given budget
of at most 5 ˆ10
7
evaluations. For the quantum ap-
proach two counts of evaluation functions are given,
because due to the nature of surrogate approaches a
share of function evaluations is substituted by surro-
gate evaluations. Thus, total evaluations refers to the
sum of function and surrogate evaluations.
The results show that CMA-ES is in general un-
beatable in terms of function evaluations whereas the
quantum approach in half of the cases gains the more
accurate result. The PSO succeeds for the Griewank
and the Chichinadze function. For the 20-dimensional
cases in Table 2 the quantum approach gains the most
accurate result in most of the cases. The CMA-ES
winning margin of a low number of evaluations de-
creases compared with the quantum approach, but is
still prominent. Nevertheless, the number of neces-
sary function evaluations for the quantum approach
can still be reduced when using a lower population
size. But, such tuning is subject to the problem at
hand. On the other hand, notwithstanding the low
number of objective evaluations, the CMA-ES needs
higher processing time for high-dimensional prob-
lems due to the fact that CMA-ES needs – among oth-
ers – to conduct eigenvalue decompositions of its co-
variance matrix (Opn
3
q) with number of dimensions n
(Knight and Lunacek, 2007). Table 3 gives an expres-
sion for necessary computation (CPU-) times (Java 8,
2.7 GHz Quadcore) for the 100-dimensional Sphere
function for CMA-ES and a quantum approach with
reduced populations size (µ “ 4, λ “ 12).
All in all, the quantum approach is competitive to
the established algorithms and in some cases even su-
perior.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
26

Table 1: Results for comparing CMA-ES, PSO and the quantum approach with a set of 2-dimensional test functions. The
error denotes the remaining difference to the known optimum; obj. evaluations and total evaluations refer to the number of
conducted function evaluations and the sum of function and quantum surrogate evaluations respectively. The latter is only
applicable to the quantum approach.
problem algorithm error obj. evaluations total evaluations
Alpine
CMA-ES 3.954 ˆ10
´12
˘ 4.797 ˆ10
´12
746.38 ˘ 90.81 n/a
PSO 5.543 ˆ10
´9
˘ 3.971 ˆ10
´8
500000.00 ˘ 0.00 n/a
quantum 8.356 ˆ10
´16
˘ 4.135 ˆ10
´16
99363.00 ˘ 66100.02 198996.53 ˘ 132200.50
Griewank
CMA-ES 2.821 ˆ10
2
˘ 2.254 ˆ10
2
174.22 ˘ 137.63 n/a
PSO 4.192 ˆ10
´4
˘ 1.683 ˆ10
´3
500000.00 ˘ 0.00 n/a
quantum 6.577 ˆ10
´3
˘ 5.175 ˆ10
´3
201361.50 ˘ 47207.02 472348.75 ˘ 94420.25
GoldsteinPrice
CMA-ES 0.459 ˆ10
1
˘ 1.194 ˆ10
2
613.96 ˘ 203.03 n/a
PSO 1.698 ˆ10
0
˘ 1.196 ˆ10
1
500000.00 ˘ 0.00 n/a
quantum 1.130 ˆ10
0
˘ 1.255 ˆ10
1
250000.00 ˘ 0.00 500012.75 ˘ 3.48
Bohachevsky1
CMA-ES 3.301 ˆ10
´2
˘ 1.094 ˆ10
´1
672.70 ˘ 59.91 n/a
PSO 1.626 ˆ10
´10
˘ 1.568 ˆ10
´9
500000.00 ˘ 0.00 n/a
quantum 4.707 ˆ10
´16
˘ 3.246 ˆ10
´16
39641.50 ˘ 1672.63 87548.03 ˘ 3377.00
Booth
CMA-ES 4.826 ˆ10
´17
˘ 1.124 ˆ10
´16
605.68 ˘ 49.55 n/a
PSO 5.985 ˆ10
´14
˘ 3.743 ˆ10
´13
500000.00 ˘ 0.00 n/a
quantum 5.695 ˆ10
´16
˘ 2.957 ˆ10
´16
33696.00 ˘ 1357.07 68283.18 ˘ 2711.51
Chichinadze
CMA-ES 0.953 ˆ10
1
˘ 4.125 ˆ10
1
698.44 ˘ 200.31 n/a
PSO 0.226 ˆ10
0
˘ 2.247 ˆ10
´1
500000.00 ˘ 0.00 n/a
quantum 1.327 ˆ10
1
˘ 8.376 ˆ10
0
50.00 ˘ 0.00 180.68 ˘ 12.63
Table 2: Results for comparing CMA-ES, PSO and the quantum approach with a set of 20-dimensional test functions with the
same setting as in Table 1.
problem algorithm error obj. evaluations total evaluations
Rosenbrock
CMA-ES 1.594 ˆ10
7
˘ 6.524 ˆ10
7
10678.60 ˘ 6514.47 n/a
PSO 1.629 ˆ10
10
˘ 1.759 ˆ10
10
50000000 ˘ 0.00 n/a
quantum 3.884 ˆ10
7
˘ 1.470 ˆ10
8
23291850.00 ˘ 3166.67 50001008.27 ˘ 557.53
Griewank
CMA-ES 5.878 ˆ10
1
˘ 1.082 ˆ10
2
8734.48 ˘ 7556.50 n/a
PSO 1.429 ˆ10
2
˘ 3.539 ˆ10
2
50000000 ˘ 0.00 n/a
quantum 2.267 ˆ10
´3
˘ 3.973 ˆ10
´3
6929090.0 ˘ 974963.9 17269617.9 ˘ 1949920.8
Zakharov
CMA-ES 9.184 ˆ10
´16
˘ 1.068 ˆ10
´15
8902.24 ˘ 845.05 n/a
PSO 7.711 ˆ10
1
˘ 5.961 ˆ10
1
50000000 ˘ 0.00 n/a
quantum 8.978 ˆ10
´17
˘ 9.645 ˆ10
´18
1021370.00 ˘ 4802.47 2962737.19 ˘ 10126.34
Spherical
CMA-ES 1.200 ˆ10
´15
˘ 1.258 ˆ10
´15
8678.80 ˘ 912.13 n/a
PSO 2.637 ˆ10
0
˘ 7.517 ˆ10
0
50000000 ˘ 0.00 n/a
quantum 8.943 ˆ10
´17
˘ 1.036 ˆ10
´17
973750.00 ˘ 4243.53 2674716.70 ˘ 8844.04
Alpine
CMA-ES 9.490 ˆ10
´12
˘ 3.331 ˆ10
´11
15196.48 ˘ 570.76 n/a
PSO 4.021 ˆ10
0
˘ 2.442 ˆ10
0
50000000 ˘ 0.0 n/a
quantum 9.272 ˆ10
´17
˘ 5.857 ˆ10
´18
1867830.0 ˘ 3795.41 4771580.5 ˘ 8390.4
A Quantum Field Evolution Strategy - An Adaptive Surrogate Approach
27

Table 3: Comparing computational performace of CMA-ES and quantum approach with the 100-dimensional Sphere function.
algorithm error total evaluations CPU time / nsec.
CMA-ES 1.593 ˆ10
´16
˘ 1.379 ˆ10
´16
129204.4 ˘ 18336.1 5.189 ˆ10
10
˘ 6.918 ˆ10
9
quantum 9.861 ˆ10
´17
˘ 1.503 ˆ10
´18
161172.8 ˘ 626.8 4.029 ˆ10
9
˘ 1.040 ˆ10
8
6 CONCLUSION
We introduced a novel evolution strategy for global
optimization that uses the quantum potential field de-
fined by elitist solutions for generating the offspring
solution set.
By using the quantum potential, information about
the fitness landscape of scattered points is condensed
into a surrogate for guiding further sampling instead
of looking at different single solutions; one at a time.
In this way, the quantum surrogate tries to fit the
search distribution to the shape of the objective func-
tion like CMA-ES (Hansen, 2006). The quantum sur-
rogate adapts continuously as the optimization pro-
cess zooms into areas of interest.
Compared with a population based solver and
CMA-ES as established evolution strategy, we
achieved a competitive and sometimes faster conver-
gence with less objective function calls. We tested
our method on ill-conditioned problems as well as on
simple problems finding it performing equally good
on both.
REFERENCES
Ahrari, A. and Shariat-Panahi, M. (2013). An improved
evolution strategy with adaptive population size. Op-
timization, 64(12):1–20.
Ben-Hur, A., Siegelmann, H. T., Horn, D., and Vapnik, V.
(2001). Support vector clustering. Journal of Machine
Learning Research, 2:125–137.
Bremer, J., Rapp, B., and Sonnenschein, M. (2010). Sup-
port vector based encoding of distributed energy re-
sources’ feasible load spaces. In IEEE PES Confer-
ence on Innovative Smart Grid Technologies Europe,
Chalmers Lindholmen, Gothenburg, Sweden.
Bremer, J. and Sonnenschein, M. (2014). Parallel tempering
for constrained many criteria optimization in dynamic
virtual power plants. In Computational Intelligence
Applications in Smart Grid (CIASG), 2014 IEEE Sym-
posium on, pages 1–8.
Feng, B. and Xu, W. (2004). Quantum oscillator model of
particle swarm system. In ICARCV, pages 1454–1459.
IEEE.
Gano, S. E., Kim, H., and Brown II, D. E. (2006). Compar-
ison of three surrogate modeling techniques: Datas-
cape, kriging, and second order regression. In Pro-
ceedings of the 11th AIAA/ISSMO Multidisciplinary
Analysis and Optimization Conference, AIAA-2006-
7048, Portsmouth, Virginia.
Hansen, N. (2006). The CMA evolution strategy: a compar-
ing review. In Lozano, J., Larranaga, P., Inza, I., and
Bengoetxea, E., editors, Towards a new evolutionary
computation. Advances on estimation of distribution
algorithms, pages 75–102. Springer.
Hansen, N. (2011). The CMA Evolution Strategy: A Tuto-
rial. Technical report.
Hansen, N. and Ostermeier, A. (2001). Completely deran-
domized self-adaptation in evolution strategies. Evol.
Comput., 9(2):159–195.
Himmelblau, D. M. (1972). Applied nonlinear program-
ming [by] David M. Himmelblau. McGraw-Hill New
York.
Horn, D. and Gottlieb, A. (2001). The Method of Quantum
Clustering. In Neural Information Processing Sys-
tems, pages 769–776.
Horn, D. and Gottlieb, A. (2002). Algorithm for data clus-
tering in pattern recognition problems based on quan-
tum mechanics. Phys Rev Lett, 88(1).
Kennedy, J. and Eberhart, R. (1995). Particle swarm op-
timization. In Neural Networks, 1995. Proceedings.,
IEEE International Conference on, volume 4, pages
1942–1948 vol.4. IEEE.
Knight, J. N. and Lunacek, M. (2007). Reducing the space-
time complexity of the CMA-ES. In Genetic and Evo-
lutionary Computation Conference, pages 658–665.
Kramer, O. (2010). A review of constraint-handling tech-
niques for evolution strategies. Appl. Comp. Intell.
Soft Comput., 2010:1–19.
Leung, Y., Zhang, J.-S., and Xu, Z.-B. (2000). Clustering
by scale-space filtering. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 22(12):1396–
1410.
Loo, C. K. and Mastorakis, N. E. (2007). Quantum poten-
tial swarm optimization of pd controller for cargo ship
steering. In Proceedings of the 11th WSEAS Inter-
national Conference on APPLIED MATHEMATICS,
Dallas, USA.
Loshchilov, I., Schoenauer, M., and Sebag, M. (2012). Self-
adaptive surrogate-assisted covariance matrix adapta-
tion evolution strategy. CoRR, abs/1204.2356.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N.,
Teller, A. H., and Teller, E. (1953). Equation of state
calculations by fast computing machines. The Journal
of Chemical Physics, 21(6):1087–1092.
Mishra, S. (2006). Some new test functions for global opti-
mization and performance of repulsive particle swarm
method. Technical report.
Parzen, E. (1962). On estimation of a probability den-
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
28

sity function and mode. The Annals of Mathematical
Statistics, 33(3):1065–1076.
Rahnamayan, S., Tizhoosh, H. R., and Salama, M. M.
(2007). A novel population initialization method for
accelerating evolutionary algorithms. Computers &
Mathematics with Applications, 53(10):1605 – 1614.
Rapp, B. and Bremer, J. (2012). Design of an event en-
gine for next generation cemis: A use case. In Hans-
Knud Arndt, Gerlinde Knetsch, W. P. E., editor, Envi-
roInfo 2012 – 26th International Conference on Infor-
matics for Environmental Protection, pages 753–760.
Shaker Verlag. ISBN 978-3-8440-1248-4.
Rigling, B. D. and Moore, F. W. (1999). Exploitation of
sub-populations in evolution strategies for improved
numerical optimization. Ann Arbor, 1001:48105.
Roberts, S. (1997). Parametric and non-parametric un-
supervised cluster analysis. Pattern Recognition,
30(2):261–272.
Shi, Y. and Eberhart, R. (1998). A modified particle swarm
optimizer. In International Conference on Evolution-
ary Computation.
Sun, J., Feng, B., and Xu, W. (2004). Particle swarm
optimization with particles having quantum behav-
ior. In Evolutionary Computation, 2004. CEC2004.
Congress on, volume 1, pages 325–331 Vol.1.
Suzuki, S. and Nishimori, H. (2007). Quantum annealing
by transverse ferromagnetic interaction. In Pietronero,
L., Loreto, V., and Zapperi, S., editors, Abstract Book
of the XXIII IUPAP International Conference on Sta-
tistical Physics. Genova, Italy.
Ulmer, H., Streichert, F., and Zell, A. (2003). Evolu-
tion strategies assisted by gaussian processes with im-
proved pre-selection criterion. In in IEEE Congress
on Evolutionary Computation,CEC 2003, pages 692–
699.
Weinstein, M. and Horn, D. (2009a). Dynamic quantum
clustering: A method for visual exploration of struc-
tures in data. Phys. Rev. E, 80:066117.
Weinstein, M. and Horn, D. (2009b). Dynamic quan-
tum clustering: a method for visual exploration of
structures in data. Computing Research Repository,
abs/0908.2.
Weinstein, M., Meirer, F., Hume, A., Sciau, P., Shaked,
G., Hofstetter, R., Persi, E., Mehta, A., and Horn, D.
(2013). Analyzing big data with dynamic quantum
clustering. CoRR, abs/1310.2700.
Yao, X., Liu, Y., and Lin, G. (1999). Evolutionary program-
ming made faster. IEEE Trans. Evolutionary Compu-
tation, 3(2):82–102.
Yu, Y., Qian, F., and Liu, H. (2010). Quantum clustering-
based weighted linear programming support vector re-
gression for multivariable nonlinear problem. Soft
Computing, 14(9):921–929.
APPENDIX
Used test functions (Ulmer et al., 2003; Ahrari and
Shariat-Panahi, 2013; Himmelblau, 1972; Yao et al.,
1999; Mishra, 2006).
Alpine:
f
1
px
x
xq “
n
ÿ
i“1
|x
i
sinpx
i
q`0.1x
i
|, (12)
´10 ď x
i
ď 10 with x
x
x
˚
“ p0, . . . , 0q and f
1
px
x
x
˚
q “ 0.
Goldstein-Price:
f
2
px
x
xq “p1 `px
1
`x
2
`1q
2
¨
p19 ´14x
1
`2x
2
1
´14x
2
`6x
2
x
2
`3x
2
2
qq¨
p30 `p2x
1
´3x
2
q
2
¨
p18 ´32x
1
`12x
2
1
`48x
2
´36x1x2 `27x2
2
qq,
(13)
´2 ď x
1
, x
2
ď 2 with x
x
x
˚
“ p0, ´1q and f
2
px
x
x
˚
q “ 3.
Himmelblau:
f
3
px
x
xq “ px
2
1
`x
2
´11q
2
`px
1
`x
2
2
´7q
2
(14)
´10 ď x
1
, x
2
ď 10 with f
3
px
x
x
˚
q “ 0 at four identical
local minima.
Bohachevsky 1:
f
4
px
x
xq“x
2
1
`2x
2
2
´0.3 cosp2πx
1
q´0.4cosp4πx
2
q`0.7,
(15)
´100 ď x
1
, x
2
ď100 with x
x
x
˚
“p0, 0qand f
4
px
x
x
˚
q“ 0.
Generalized Rosenbrock:
f
5
px
x
xq “
n´1
ÿ
i“1
pp1 ´x
i
q
2
`100px
i`1
´x
2
i
q
2
q, (16)
´2048 ď x
i
ď 2048 with x
x
x
˚
“ p1, . . . , 1q f
5
px
x
x
˚
q “ 0.
Griewank:
f
6
px
x
xq “ 1 `
1
200
n
ÿ
i“1
x
2
i
´
n
ź
i“0
cosp
x
i
?
i
q, (17)
´100 ď x
i
ď 100 with x
x
x
˚
“ p0, . . . , 0q f
6
px
x
x
˚
q “ 0.
Zakharov:
f
7
px
x
xq “
n
ÿ
i“1
x
2
i
`p
n
ÿ
i“1
0.5ix
i
q
2
`p
n
ÿ
i“1
0.5ix
i
q
4
, (18)
´5 ď x
i
ď 10 with x
x
x
˚
“ p0, . . . , 0q f
7
px
x
x
˚
q “ 0.
Sphere:
f
8
px
x
xq “
n
ÿ
i“1
x
2
i
, (19)
´5 ď x
i
ď 5 with x
x
x
˚
“ p0, . . . , 0q f
8
px
x
x
˚
q “ 0.
Chichinadze:
f
9
px
x
xq “ x
2
1
´12x
1
`11 `10cospπx
1
{2q
`8sinp5πx
1
q´p1{5q
0.5
e
´0.5px
2
´0.5q
2
,
(20)
´30 ďx
1
, x
2
ď30 with x
x
x
˚
“p5.90133, 0.5q f
9
px
x
x
˚
q“
´43.3159.
Booth:
f
1
0px
x
xq “ px
1
`2x
2
´7q
2
p2x
1
`x
2
´5q
2
, (21)
´20 ď x
1
, x
2
ď 20 with x
x
x
˚
“ p1, 3q f
9
px
x
x
˚
q “ 0.
A Quantum Field Evolution Strategy - An Adaptive Surrogate Approach
29
