Neighborhood Strategies for QPSO Algorithms to Solve Benchmark

Electromagnetic Problems

Anton Duca

, Laurentiu Duca

, Gabriela Ciuprina

and Daniel Ioan

Politehnica University of Bucharest, Faculty of Electrical Engineering, Bucharest, Romania

Politehnica University of Bucharest, Faculty of Computer Science, Bucharest, Romania

Keywords: PSO, QPSO, Neighborhood Strategies, Optimization, Electromagnetic Field.

Abstract: Several neighborhood strategies for QPSO algorithms are proposed and analyzed in order to improve the

performances of the original methods. The proposed strategies are applied to some of the most well known

QPSO algorithms such as the QPSO with random mean, the QPSO with Gaussian attractor and of course the

basic QPSO. To prevent the premature convergence and to avoid being trapped in local minima the

neighborhoods are dynamically changed during the optimization process. For testing the efficiency of the

neighborhood techniques two benchmark optimization problems from the electromagnetic field computation

have been chosen, Loney’s solenoid and TEAM22.

1 INTRODUCTION

The PSO (Particle Swarm Optimization) algorithms

are part of stochastic optimization methods which

use a population of candidate solutions that evolve

over time. Comparable in terms of performance with

the genetic algorithms, these algorithms are problem

independent and are suitable for solving difficult

optimization problems where the analytical

expression of the objective function is not known.

First proposed by Kennedy and

(Kennedy,

Eberhart, 1995)

, the original PSO (classic) has its

root in biology and is inspired by social behavior

within fish schools or bird flocks. Each particle in

the swarm (population) is characterized by its

current position and velocity. The position

encapsulates the potential solution of the

optimization problem, while the velocity influences

how that position will be changed at the next

iteration.

The main issues of the classical PSO are the high

probability to get stuck in a local minimum and the

large number of iterations required to find the global

solution. Over time, to improve the performance of

the PSO algorithm several solutions have been

proposed in the literature (Ciuprina et al., 2002), but

the most efficient options currently available are

based on SPSO (Standard PSO) (Bratton, Kennedy,

2007) (Clerc, 2012) and QPSO (Quantum-behaved

PSO) (Sun et al., 2004).

The SPSO and QPSO algorithms have been

successfully used to solve a variety of problems,

such as (Li et al., 2007) (Zhang, Zuo, 2013), but also

to solve electromagnetic optimization problems

(Mikki, Kishk, 2006) (Coelho, 2007) (Coelho,

Alotto, 2008). In (Mikki, Kishk, 2006) authors

solve the LAA problem (Linear Antenna Array)

proposing a method for the optimal control of the

QPSO algorithm parameters. In (Coelho, 2007) and

(Coelho, Alotto, 2008) the author makes a

comparison between the PSO and QPSO algorithms

for the TEAM22 problem and the Loney's solenoid

problem. Even if the solutions mentioned in

(Coelho, Alotto, 2008) do not mention/verify the

quench condition, the conclusions of both articles

highlight the superiority of the QPSO algorithms

over the PSO.

Although the latest QPSO versions proposed by

Sun&others (Xi et al., 2008) (Sun et al., 2011) (Sun

et al., 2012) are better than the SPSO algorithm

when optimizing CEC benchmark functions, in case

of statistical studies conducted on electromagnetic

optimization problems the SPSO algorithm is more

stable (Duca et al., 2014) (Duca et al., 2014, 2). In

some cases the performance offered by the QPSO

based algorithms provide better solutions (smaller

values of the objective function) but statistically the

QPSO based methods are outperformed by the SPSO

algorithm, which provides a smaller mean and a

148

Duca, A., Duca, L., Ciuprina, G. and Ioan, D.

Neighborhood Strategies for QPSO Algorithms to Solve Benchmark Electromagnetic Problems.

DOI: 10.5220/0006040901480155

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 148-155

ISBN: 978-989-758-201-1

smaller standard deviation.

To improve the QPSO algorithms performances

when solving electromagnetic problems this paper

proposes and studies several neighborhood

strategies.

Starting from the idea used in SPSO, in the

current paper different neighborhood strategies are

applied to enhance the performances of the best

QPSO algorithms available at present time, QPSO-

WM (weighted mean) (Xi et al., 2008), QPSO-GA

(Gaussian attractor) (Sun et al., 2011), QPSO-RO

(ranking operator) (Sun et al., 2012), QPSO-RM

(random mean) (Sun et al., 2012), and basic (Sun et

al., 2004). To avoid the premature convergence and

local minima the neighborhoods are dynamically

changed during the optimization process. The

influence of the change frequency over the

performances is analyzed for each neighborhood

scheme and each QPSO algorithm. The tests are

carried for two benchmark electromagnetic

optimization problems, Loney’s solenoid and

TEAM22.

2 QPSO ALGORITHMS

Unlike PSO and SPSO algorithms, where the

particle trajectories are according to Newton's

mechanic laws, QPSO is a quantum system

proposed by Sun & others (Sun et al., 2004). In

QPSO the behavior of each particle is described by a

wave function Ψ (Schrödinger's equation) |Ψ|

being

the probability density function for the particle

position. On the other hand, while in the PSO

algorithm the particles converge to the solution

through the global best position, in QPSO the

particles exert a greater influence on each other

through an average of the personal best positions, so

the probability to get stuck in a local minimum is

smaller.

The coordinate j for a particle i at the step (t + 1)

is given by:

)1ln()()(

)()1(

jijij

jiji

utxtm

tptx







(1)

)()1(

)()(

,,,

txtp

jGBji

jiPBjiji







(2)

where p is called attractor, u and α are random

generated numbers uniformly distributed in the

interval [0, 1) (for each component of a particle),

and β is a contraction–expansion factor linearly

decreased at each iteration with values between 1

and 0.5. The particles in a QPSO algorithm exert

great influence on each other through a mean best

(m) calculated using the formula:



















niPB

iPB

tmtmtmtm

)(

),(

)](),(),([)(



(3)

where M is the swarm size (the number of particles)

and n is the number of coordinates for the position

of a particle.

During time, to enhance the performances of the

QPSO several variants have been proposed. The

most effective QPSO based algorithms available

today are: QPSO with weighted mean (QPSO-WM),

QPSO with Gaussian attractor (QPSO-GA), QPSO

with ranking operator (QPSO-RO), and QPSO with

random mean (QPSO-RM).

In QPSO-WM (Xi et al., 2008), at each iteration,

the particles are sorted according to their fitness

values. Each particles is assigned a weight (α)

related to its ranking position (better solution means

larger weight), to enforce an elitism behavior. The

mean is calculated as a weighted sum as follows:



















niPBni

iPBi

txtx

1,1,

)(),(

)(





(4)

For improving the convergence, diversify the

swarm, and escaping the local minima, in (Sun et al.,

2011) the authors propose a new QPSO-GA

algorithm which changes the attractor (p) from the

position formula to a Gaussian probability

distribution. The new attractor (np) is evaluated with

the formula:

))(),(()(

,,,

tpmtpNtnp

jijjiji





(5)

)1ln()()(

)()1(

jijij

jiji

utxtm

tnptx











(6)

where N is a function with Gaussian distribution. In

the beginning the particles are scattered in a wider

space, and the standard deviation is larger, while in

the late stage of the search the particles converge

toward the mean, and the standard deviation

decreases toward zero.

In (Sun et al., 2012), the authors demonstrate

using the probabilistic metric spaces theory that

QPSO can converge to a global optimum, and

propose two new improvements QPSO-RM and

QPSO-RO. The QPSO-RM algorithm replaces the

mean best position with a personal best position of a

random selected particle. This change diversifies the

Neighborhood Strategies for QPSO Algorithms to Solve Benchmark Electromagnetic Problems

149

swarm and enhances the ability of the global search.

Unlike the previous algorithms, where the

particles move toward global best, in the QPSO-RO

each particle is guided by its personal best and the

personal best of a random selected particle. The

selected particle is chosen from the particles with a

better fitness value, and its selection is based on a

ranking operator. The formula for the attractor

becomes:

)()1(

)()(

,,,

txtp

jqPBji

jiPBjiji







(7)

where q is the random selected particle with a better

fitness value.

3 QPSO NEIGHBORHOOD

STRATEGIES

Three different neighborhood strategies are proposed

and analyzed for combining with the QPSO

algorithms, one with unidirectional links and two

with bidirectional links between particles.

For the first strategy, which is inspired from

Clerc’s SPSO (Clerc, 2012), the particles of the

swarm are connected, each connection representing

a unidirectional link between two particles. A

unidirectional link has an informed and an informing

particle, the informed particle knowing the position

and the personal best of the second particle. Thus,

each informed particle has a set of informing

particles called neighborhood (Figure 1). This

strategy will be referred as INF (from

informed/informing).

Figure 1: INF neighborhood strategy for a swarm with 6

particles and 3 informants.

Figure 2: Subswarm neighborhood strategy for a swarm

with 6 particles and 2 subswarms.

When adapted to our QPSO algorithms, the INF

strategy will compute for each particle the mean

only using particle’s neighborhood, and the attractor

using the local best a from the same neighborhood.

In the case of QPSO-RO/RM the random chosen

particles for mean and attractor components will

only be from the neighborhood.

If for a given number of iterations the current

structure of the INF swarm does not improve the

global best the structure is regenerated randomly.

The pseudocode for this strategy is the following:

;generate links between particles

noImprovmentSteps=0

foreach iteration

foreach particle i

;calculate localbest for Ni

;calculate medium for Ni

;calculate attractor for Ni

;calculate new position

;evaluate

foreach particle i

;update position

;update personal best

;calculate global best

if (global best was improved)

noImprovmentSteps=0

else

noImprovmentSteps ++

if (noImprovmentSteps==MAX)

;generate new links

noImprovmentSteps=0

For the second and third strategies the swarm is

divided into subswarms. The subswarms are disjoint

meaning there are no connections between particles

belonging to different subswarms. Inside a

subswarm the particles are fully connected, one

particle has as neighbors all the other particles

(Figure 2).

Just as for the first strategy, the subswarms are

(126)

(345)

(1236)

(12346)

(3456)

(1245)

(125)

(3456)

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

150

dynamically changed during the optimization

process if the global best is not improved for several

iterations. The particles are assigned to subswarms

randomly, each subswarm having a fixed number of

particles.

The second strategy will compute the attractor of

each particle using the local best of the belonging

subswarm (or particles inside it, in case of QPSO-

RO), while the third strategy will use the global best.

For both strategies the mean will be evaluated

(generated in case of QPSO-RM) only using

particles inside the corresponding subswarm. The

second strategy will be reffered as SS-LB while the

third strategy will be reffered as SS-GB (from

subswarm with local/global best).

The pseudocode for the second strategy (similar

for third strategy) is the following:

;generate subswarms

noImprovmentSteps=0

foreach iteration

foreach subswarm SSj

;calculate localbest

;calculate medium

foreach particle i in SSj

;calculate attractor

;calculate new position

;evaluate

foreach particle i

;update position

;update personal best

;calculate global best

if (global best was improved)

noImprovmentSteps=0

else

noImprovmentSteps ++

if (noImprovmentSteps==MAX)

;generate subswarms

noImprovmentSteps=0

4 ELECTROMAGNETIC

PROBLEMS

The QPSO based algorithms have been tested on

two electromagnetic benchmark problems defined

by the COMPUMAG community.

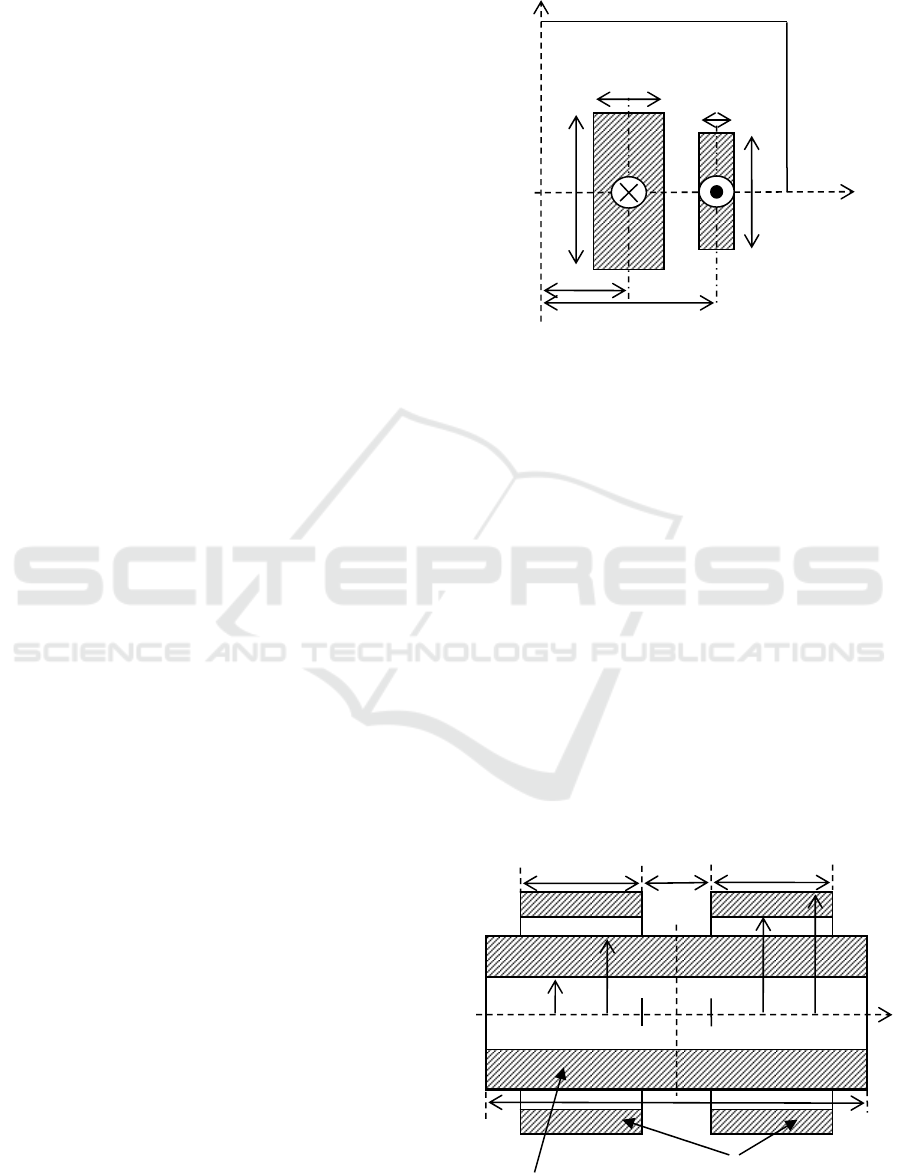
4.1 The TEAM22 Problem

Two coaxial coils carry current with opposite

directions (Figure 3), operate under superconducting

conditions and offer the opportunity to store a

significant amount of energy in their magnetic

fields, while keeping within certain limits the stray

field (Ioan et al., 1999). An optimal design should

couple the energy to be stored by the system with a

minimum stray field into one objective function.

Figure 3: TEAM22 problem configuration.

The objective function has as parameters, the

radii (R), the heights (h) , the thicknesses (d) and the

current densities (J). Besides domain restrictions, the

problem must take into account that the solenoids do

not overlap each other, and the superconducting

material should not violate the quench condition that

links together the value of the current density and

the maximum value of magnetic flux density.

The evaluation method of the objective function

is based on the Biot-Savart-Laplace formula in

which the elliptic integrals are computed by using

the King algorithm and numerical integration as in

(TEAM22, 2015).

4.2 The Loney’s Solenoid

The Loney's solenoid benchmark problem,

formulated in (Di Barba et al., 1995) consists of a

main coil and two identical correction coils, having

fixed dimensions (Figure 4).

Figure 4: Loney’s solenoid problem configuration.

main coil correcting coils

line a 11

line b 11

points

(0,10)

(10,0)

z (axis of rotation)

Neighborhood Strategies for QPSO Algorithms to Solve Benchmark Electromagnetic Problems

151

A constant current flows through the coils such

that their current density is the same. The aim is to

produce a constant magnetic flux density in the

middle of the main coil. The parameters to be

optimized are the length of the correction coils (s)

and the axial distance between them (l).

The objective function is of minmax type, i.e.

minimize the maximum difference between the

values of the magnetic flux density along a straight

segment in the middle of the main solenoid, i.e.

minimize (B

max

- B

min

)/B

, where B

is the magnetic

field density in the middle of the main coil. The

maximum and minimum values are sought along the

segment [-z

]. Tests done by the authors of this

benchmark revealed that the problem is non convex

and ill conditioned (Di Barba, Savini, 1995). The

electromagnetic field problem is easily solved, in a

magnetostatic regime, by discretizing the coils in

elementary coils without thickness and by applying

well known analytical formulas for the field along

the solenoid axis.

5 RESULTS

To solve the electromagnetic optimization problems

four QPSO based algorithms have been considered

QPSO-WM, QPSO-Gauss, QPSO-RM and QPSO-

RO. After a preliminary study, QPSO-Gauss and

QPSO-RM, together with the basic QPSO, have

been chosen for further testing. Each of the three

mentioned QPSO algorithms have been adapted and

combined with each of the described neighborhood

strategies, INF, SS-LB and SS-GB. Further more,

for each combination have been analyzed the

influence over the performances of the structure

change frequency.

Tables 1 and 2 (see Appendix section) present

the solution fitness values for 30 independent tests

(runs), each run having different random values for

the initial population. For each test the swarm size

was 32, and the stop criteria was the maximum

number of iterations equivalent to 2560 objective

function evaluations. Mean-best is the average of the

best solutions (minimum values) obtained at each of

the 30 runs, while Min-best (Max-best) is the

minimum (maximum) of the minimum values

obtained at each run. The number of informants for

INF strategy was 3, and the number of subswarms

for SS-LB(GB) was 4. Two different frequencies

were tested, a low frequency (LF) of 10 iterations,

and a high frequency (HF) which meant change at

each iteration if the global best was not improved.

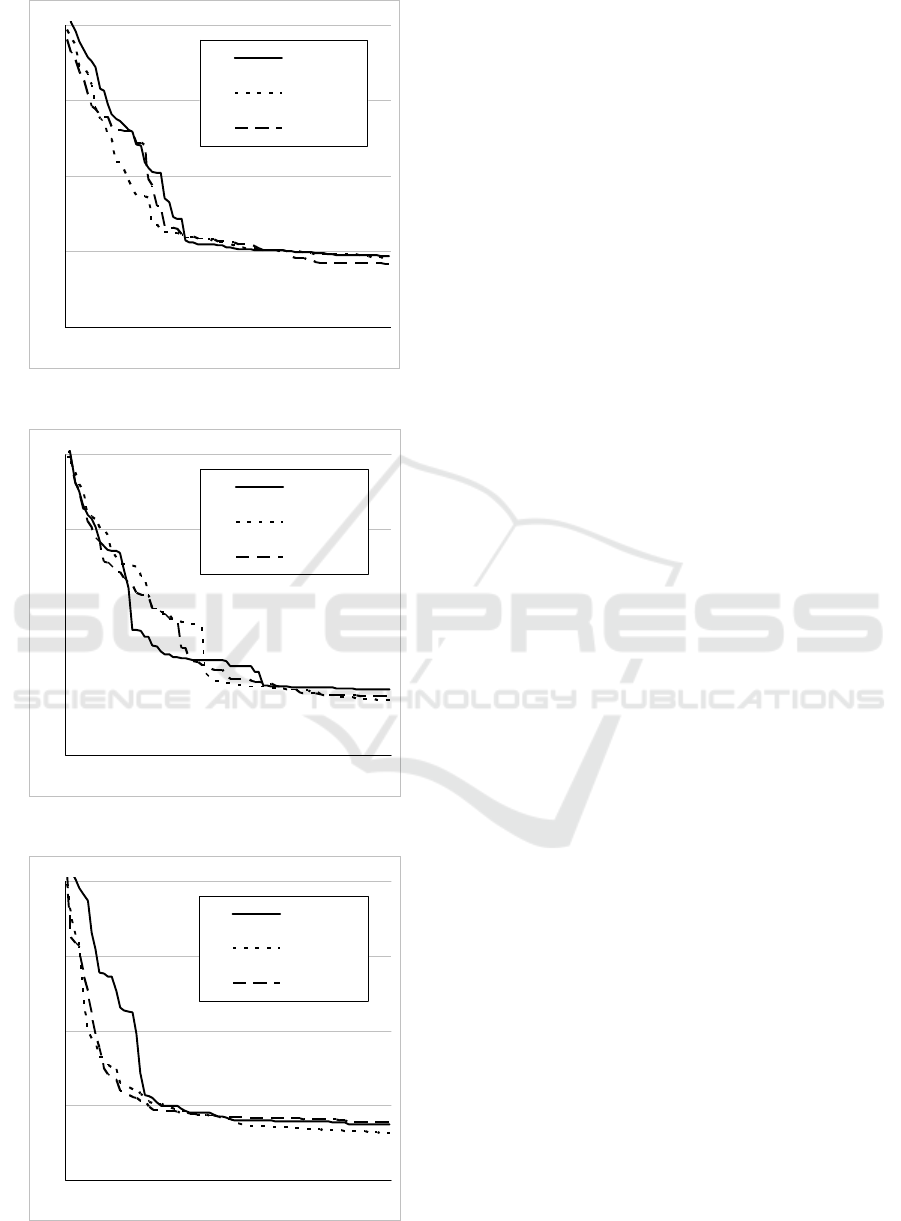
Mean - best OF value (QPSO)

1.E-08 1.E-07 1.E-06 1.E-05 1.E-04

1 1019283746556473

classic

SS-LB-LF

INF-HF

Figure 5: QPSO mean for Loney.

Mean - best OF value (QPSO-RM)

1.E-08 1.E-07 1.E-06 1.E-05 1.E-04

1 1019283746556473

classic

SS-LB-LF

SS-GB-HF

Figure 6: QPSO-RM mean for Loney.

Mean - best OF value (QPSO-Gauss)

1.E-08 1.E-07 1.E-06 1.E-05 1.E-04

1 1019283746556473

classic

SS-LB-LF

INF-HF

Figure 7: QPSO-Gauss mean for Loney.

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

152

Mean - best OF value (QPSO)

1.E-03 1.E-02 1.E-01 1.E+00 1.E+01

1 1019283746556473

classic

SS-LB-HF

SS-GB-LF

Figure 8: QPSO mean for TEAM22.

Mean - best OF value (QPSO-RM)

1.E-03 1.E-02 1.E-01 1.E+00 1.E+01

1 1019283746556473

classic

SS-LB-LF

INF-HF

Figure 9: QPSO-RM mean for TEAM22.

Mean - best OF value (QPSO-Gauss)

1.E-03 1.E-02 1.E-01 1.E+00 1.E+01

1 1019283746556473

classic

SS-LB-LF

SS-GB-HF

Figure 10: QPSO-Gauss mean for TEAM22.

For the Loney’s solenoid benchmark, the classic

algorithms performances are always improved when

the algorithms are enhanced with neighborhood

strategies. The most stable combinations (smallest

mean-best, and standard deviation) are QPSO-RM

with SS-LB-LF, and QPSO-Gauss with INF-HF.

The overall best solution, which is among the best

found in the literature (by our knowledge), was

obtained with QPSO-RM with SS-LB-LF. In terms

of frequency, while for the SS-LB strategy the low

frequency is better, for SS-GB and INF strategies the

high frequency provides better results.

For the TEAM22 benchmark the algorithms with

neighborhood strategies provide most of the time

better mean and standard deviation values, but the

improvement for the best solution is not as

significant as in the case of Loney’s solenoid.

Surprisingly, the best solution is obtained with the

classic version of the basic QPSO, which offers a

solution close to the well known best from the

literature (1.8 E-3) (TEAM22, 2015). The most

stable combinations are QPSO-Gauss with SS-GB-

HF (LF), QPSO-RM with SS-LB-LF(HF), and

QPSO with SS-GB-LF. Regarding the frequency

change of particles connections, the small

frequencies are suitable for obtaining better mean

values while high frequencies lead to better standard

deviations.

The improvements obtained with the algorithms

enhanced with neighborhood strategies can also be

seen from mean-best evolution during the

optimization process. Besides the fact that statistical

mean values are smaller, the neighborhood enhanced

algorithms are more stable having a smoother

evolution while the classic algorithms evolve (with

some exceptions) in slopes.

6 CONCLUSIONS

The present paper studied the efficiency of

neighborhood strategies when applied to QPSO

based algorithms to solve benchmarks

electromagnetic problems.

Three different neighborhood have been

proposed and analyzed, one with unidirectional and

two with bidirectional particle connections. In the

first strategy, inspired from Clerc’s SPSO, each link

has an informant and an informed particle, thus each

particle has its own neighborhood containing the

informants. The other two strategies divide the

swarm into disjoint subswarms and use to calculate

the attractors the local best of the subswarm or the

global best. For all the strategies the connections are

Neighborhood Strategies for QPSO Algorithms to Solve Benchmark Electromagnetic Problems

153

dynamically changed, reset and randomly

regenerated, if the solution is not improved for

several iterations.

These strategies have been applied to the best

QPSO algorithms available, such as QPSO-RM,

QPSO-Gauss or basic QPSO, and were tested on two

problems from electromagnetism, namely TEAM22

and Loney’s solenoid.

In case of Loney’s solenoid benchmark the

QPSO algorithms enhanced with neighborhood

strategies significantly improve the results for each

of the combinations. The enhanced QPSO

algorithms provide much small mean and standard

deviation values. In the same time the overall best

solution obtained with a QPSO-RM with SS-LB is

one of the best solutions available in the literature.

In case of TEAM 22 problem the enhanced

QPSO algorithms performed better in terms of

stability providing smaller mean and standard

deviation values. However, the best solution is given

surprisingly by the basic QPSO.

For both testing problems the frequency of

structure (connections) change has also been studied.

A low frequency was more suitable for the SS-LB

strategy. For the other two strategies a higher

frequency leads most of the times to better results,

but the optimal frequency also depends on the QPSO

algorithm.

ACKNOWLEDGEMENTS

This work has been supported by the Politehnica

University of Bucharest in the frame of the project

UPB Grant of Excellence, no. 254/2016, the

Romanian Government in the frame of the PN-II-

PT-PCCA-2011-3 program, grant no. 5/2012

(managed by CNDI– UEFISCDI, ANCS), and in the

frame of RO-BE bilateral project, grant no xx/2016.

REFERENCES

Bratton, Kennedy, 2007. Defining a standard for particle

swarm optimization. Proceedings of the IEEE Swarm

Intelligence Symposium, 2007.

Ciuprina, Ioan, Munteanu, 2002. Use of intelligent-particle

swarm optimization in electromagnetics. IEEE

Transactions on Magnetics, vol. 38 (2), pp. 1037-

1040.

Clerc, 2012. Standard particle swarm optimization. Open

access archive HAL (http://clerc.maurice.free.fr/pso/

SPSO_descriptions.pdf).

Coelho, 2007. A novel Gaussian quantum-behaved

particle swarm optimizer applied to electromagnetic

design, IET Science, Measurement & Technology 1,

pp. 290–294.

Coelho, Alotto, 2008. Global optimization of

electromagnetic devices using an exponential

quantum-behaved particle swarm optimizer, IEEE

Transactions on Magenetics 44, pp. 1074–1077.

Di Barba, Gottvald, Savini, 1995. Global optimization of

Loney’s solenoid: A benchmark problem. Int. J. Appl.

Electromagn. Mech., vol. 6, no. 4, pp. 273–276.

Di Barba, Savini, 1995. Global optimization of Loney’s

solenoid by means of a deterministic approach. Int. J.

Appl. Electromagn. Mech., vol. 6, no. 4, pp. 247–254.

Duca, Duca, Ciuprina, Yilmaz, Altinoz, 2014, PSO

Algorithms and GPGPU Technique for

Electromagnetic Problems, in the International

Workshops on Optimization and Inverse Problems in

Electromagnetism (OIPE), Delft, The Netherlands.

(under review process, to be published by an ISI

indexed journal).

Duca, Rebican, Janousek, Smetana, Strapacova, 2014.

PSO Based Techniques for NDT-ECT Inverse

Problems. In Electromagnetic Nondestructive

Evaluation (XVII), vol. 39, pp. 323 - 330. Capova, K.,

Udpa, L., Janousek, L., and Rao, B.P.C. (Eds.), IOS

Press, Amsterdam.

Ioan, Ciuprina, Szigeti, 1999. Embedded stochastic-

deterministic optimization method with accuracy

control. IEEE Transactions on Magnetics, vol. 35 , pp.

1702-1705.

Kennedy, Eberhart, 1995. Particle swarm optimization.

Proceedings of IEEE International Conference on

Neural Networks, pp. 1942-1948.

Li, Wang, Hu, Sun, 2007. A new QPSO based BP neural

network for face detection, Fuzzy Information and

Engineering, Advances in Soft Computing 40,

Springer.

Mikki, Kishk, 2006. Quantum particle swarm optimization

for electromagnetics, IEEE Transactions on Antennas

and Propagation 54, pp. 2764–2775.

Sun, Feng, Xu, 2004, Particle swarm optimization with

particles having quantum behavior, in: IEEE

Proceedings of Congress on Evolutionary

Computation, pp. 325–331.

Sun, Fang, Palade, Wua, Xu, 2011. Quantum-behaved

particle swarm optimization with Gaussian distributed

local attractor point, Applied Mathematics and

Computation 218, pp. 3763–3775.

Sun, Wua, Palade, Fang, Lai, Xu, 2012.

Convergence

analysis and improvements of quantum-behaved

particle swarm optimization, Information Sciences

193, pp. 81–103.

TEAM22 benchmark problem, 2015.

http://www.compumag.org/jsite/team.html.

Xi, Sun, Xu, 2008. An improved quantum-behaved

particle swarm optimization algorithm with weighted

mean best position, Applied Mathematics and

Computation 205, pp. 751–759.

Zhang, Zuo, 2013. Deadline Constrained Task Scheduling

Based on Standard-PSO in a Hybrid Cloud, Advances

in Swarm Intelligence, Springer.

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

154

APPENDIX

Table 1: Objective function values and standard deviation for Loney’s solenoid.

Algorithm

Min-best

OF value

Max - best

OF value

Mean - best

OF value

Standard

deviation

QPSO

classic 9.73E-09 1.13E-06 7.72E-08 2.03E-07

SS–LB–LF 4.09E-09 1.78E-07

3.04E-08 3.47E-08

SS–LB–HF 9.89E-09 2.05E-07 3.87E-08 3.63E-08

SS–GB–LF 1.02E-08 5.99E-07 6.47E-08 1.19E-07

SS–GB–HF

3.87E-09

2.38E-06 1.21E-07 4.30E-07

INF–LF 9.29E-09 3.33E-07 4.07E-08 5.99E-08

INF–HF 8.64E-09

1.71E-07

3.33E-08 3.47E-08

QPSO

classic 6.02E-09 4.04E-07 3.99E-08 7.33E-08

SS–LB–LF

1.05E-10 1.80E-08 1.07E-08 5.33E-09

SS–LB–HF 2.89E-09 8.23E-08 2.42E-08 1.52E-08

SS–GB–LF 1.17E-10 4.13E-07 3.84E-08 9.68E-08

SS–GB–HF 3.93E-09 2.55E-07 2.64E-08 4.85E-08

INF–LF 1.32E-08 3.78E-07 6.77E-08 8.62E-08

INF–HF 7.41E-09 2.21E-07 4.37E-08 5.15E-08

QPSO

Gauss

classic 8.03E-09 2.17E-07 3.01E-08 4.08E-08

SS–LB–LF 4.33E-09 5.28E-08 1.93E-08 1.04E-08

SS–LB–HF

1.88E-09

7.95E-08 2.18E-08 1.40E-08

SS–GB–LF 7.09E-09 4.29E-07 4.03E-08 7.91E-08

SS–GB–HF 1.23E-08 1.39E-07 3.43E-08 3.17E-08

INF–LF 1.02E-08 8.76E-08 2.44E-08 1.73E-08

INF–HF 1.25E-08

3.47E-08 1.92E-08 5.34E-09

Table 2: Objective function values and standard deviation for TEAM 22.

Algorithm

Min - best

OF value

Max - best

OF value

Mean - best

OF value

Standard

deviation

QPSO

classic

2.23E-03

2.76E-02 8.68E-03 6.46E-03

SS–LB–LF 4.69E-03 3.17E-02 8.78E-03 5.84E-03

SS–LB–HF 4.48E-03 1.65E-02 7.71E-03 3.15E-03

SS–GB–LF 3.85E-03

1.06E-02 6.76E-03 1.93E-03

SS–GB–HF 3.65E-03 2.71E-02 7.46E-03 5.08E-03

INF–LF 5.21e-03 3.38e-01 3.46e-02 7.82e-02

INF–HF 4.12e-03 3.56e-02 1.17e-02 8.71e-03

QPSO

classic 3.09E-03 2.17E-02 7.31E-03 4.85E-03

SS–LB–LF 3.50E-03 1.40E-02

5.33E-03

2.55E-03

SS–LB–HF 4.53E-03

9.31E-03

6.11E-03

1.26E-03

SS–GB–LF

2.78E-03

1.77E-02 6.37E-03 4.01E-03

SS–GB–HF 3.64E-03 1.01E-02 6.16E-03 1.80E-03

INF–LF 3.21e-03 9.48e-03 5.93e-03 1.81e-03

INF–HF 3.65e-03 1.02e-01 1.24e-02 2.15e-02

QPSO

Gauss

classic 2.66E-03 9.54E-03 5.53E-03 1.54E-03

SS–LB–LF

2.58E-03

8.95E-03

4.27E-03

1.56E-03

SS–LB–HF 4.10E-03 9.25E-03 6.35E-03 1.54E-03

SS–GB–LF 4.54E-03 1.17E-02 6.76E-03 2.18E-03

SS–GB–HF 4.61E-03

7.65E-03

5.95E-03

8.79E-04

INF–LF 4.40e-03 9.86e-03 6.71e-03 1.73e-03

INF–HF 4.08e-03 1.69e-02 7.16e-03 3.08e-03

Neighborhood Strategies for QPSO Algorithms to Solve Benchmark Electromagnetic Problems

155