
Linked Genes Migration in Island Models
Marcin Michal Komarnicki and Michal Witold Przewozniczek
Department of Computational Intelligence, Wroclaw University of Science and Technology, Wroclaw, Poland
Keywords: Island Models, Coevolution, Genetic Algorithms, Linkage Learning, Messy Coding.
Abstract: Island Models (IMs) divide the whole population into many coevolving subpopulations, which periodically
exchange fractions of their individuals. Some IMs, exchange probabilistic models built during the
subpopulations evolution. The use of many coevolving subpopulations helps to preserve the population
diversity, which makes it less likely to get stuck in the local optima. Another promising research direction in
the Evolutionary Computation field is the Linkage Learning. The knowledge about gene dependencies can
be used in many different ways that improve the overall method effectiveness. Therefore, this paper
proposes the Gene Pattern Based Island Model (GePIM) that uses the multi-population nature of IMs to
generate the linkage information. GePIM also introduces a new type of migration based on exchanging
linked gene groups, instead of exchanging the whole individuals or probabilistic models.
1 INTRODUCTION
Evolutionary Algorithms (EAs) are well-known
methods capable of solving hard computational
problems. Many different EAs were proposed, all of
them have their pros and cons. During the recent
years, the research toward proposing universal and
beneficial mechanisms for EAs has gained an
increasing attention. Among these universal
mechanisms, the coevolution of many subpopula-
tions can be found (Chang, 2015; Dahzi et al., 2008;
Fidrysiak and Przewozniczek, 2015; Fieldsend,
2014; Kurdi, 2016; Leitão et al., 2015; Kwasnicka
and Przewozniczek 2011; Przewozniczek et al.,
2015; Skolicki, 2008; Walkowiak et al., 2013;
Zhang et al., 2007). Island Models (IMs) improve
the performance of Genetic Algorithms (GAs) by
better preservation of population diversity (Kurdi,
2016; Leitão et al., 2015; Skolicki and De Jong,
2007; Skolicki, 2008). IMs allow for decreasing the
negative influence of preconvergence (Kwasnicka
and Przewozniczek, 2011; Watson and Pollack,
1999; Watson, 2006). Due to the higher diversity,
more potentially valuable Building Blocks (BBs)
remain in the population. Usually, the more BBs can
be processed by a GA-based method, the greater is
the chance of reaching the breakthrough and finding
more valuable solutions than in the case of fast
converging methods.
As stated above, in general, the better diversity
preservation improves the overall GA effectiveness.
However, it does not seem enough to make the
valuable BBs exist in a population (Kwasnicka and
Przewozniczek, 2011; Skolicki, 2008). The method
must also use mechanisms that allow for effective
BBs processing. As shown in the literature, not all
BBs are equally effectively processed by classical
EA operators like crossover. Therefore, the Linkage
Learning (LL) techniques became popular. The LL
methods try to discover the possible gene
dependencies during their run (so-called linkage
discovery). The knowledge about linkage is used
later on to improve the method effectiveness. For
instance, during the crossover operation only linked
genes can be exchanged between individuals instead
of using classical single point or uniform crossover
operators. Therefore, the LL techniques are often
shown to be beneficial to many different EA types
(Omidivar et al., 2014).
IMs use many coevolving subpopulations to
improve the overall population diversity (Skolicki,
2008). To ensure the communication between
separated subpopulations (called islands) the
migration operator is used. During the migration, all
subpopulations (isolated for the most of the method
run) usually exchange individuals with one another.
In some papers, the probabilistic models that were
built by separate islands are exchanged (delaOssa et
al., 2004; Muelas et al., 2014). The migration is, in
fact, supposed to exchange BBs that are carried by
migrated individuals or probabilistic models
(Skolicki, 2008; Watson, 2006). The question is: if
30
Komarnicki, M. and Przewozniczek, M.
Linked Genes Migration in Island Models.
DOI: 10.5220/0006042300300040
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 30-40
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

we want to exchange BBs why don’t we exchange
BBs instead of exchanging other data structures that
are supposed to carry them? Therefore, this paper
proposes a new type of migration: the Linked Gene
Groups Migration (LGGM). During the LGGM only
linked gene groups (which are assumed to be BBs)
are migrated. To show the potential of the new
migration operator, the Gene Pattern Based Island
Model (GePIM) that incorporates the LGGM and the
LL techniques is proposed.
The remainder of the paper is organized as
follows. In the second section, the related work is
presented. The third section describes GePIM. The
description of the performed experiments and their
analysis is presented in Section 4. Finally, the last
section concludes and summarizes the paper.
2 RELATED WORK
In the recent years, the LL became an important part
of evolutionary computation research. The idea
behind LL is to find potential gene dependencies
during an EA run and use this knowledge to improve
the overall method effectiveness. Many different
ways have been proposed for linkage information
gathering, storing, and use. Therefore, the next
subsections contain a brief introduction to recent
research on the LL and IMs.
2.1 Linkage Learning
One of the first classifications for the LL methods
was proposed in (Chen et al., 2007a). The LL
concerns three main fields: the way the good and the
bad linkage are distinguished, linkage representation
and linkage storage. According to the first
classification field, the good and the bad linkage
may be distinguished only on the base of fitness
value (unimetric way) or some additional criteria
may also be taken into consideration (multimetric
way). The typical unimetric way of good and bad
linkage distinguish may be found in Multi
Population Pattern Searching Algorithm (MuPPetS)
(Kwasnicka and Przewozniczek, 2011). The
multimetric approach may be found in Bayesian
Optimization Algorithm (BOA) (Pelikan et al.,
1999; Pelikan et al., 2006). The linkage may be
represented in a virtual or a physical way. If the
linkage is represented by graphs, matrices, gene
patterns (Kwasnicka and Przewozniczek, 2011;
Pelikan et al., 1999; Pelikan et al., 2006), or other
data structures then the virtual representation is
used. If the linkage is being represented as physical
genes locations in the chromosome (i.e., genes that
are close to one another are considered to be linked)
then physical linkage representation is being used.
The typical example of physical linkage
representation is messy coding (Goldberg et al.,
1993; Kwasnicka and Przewozniczek, 2011).
Finally, the linkage may be stored in two different
ways: centralized and distributed. The centralized
way is used when linkage information is stored in
some globally accessible database (i.e., the complete
linkage information in the database may be accessed
at any method operation). On the other hand, the
messy coding is a typical example for distributed
linkage information storing (each individual possess
its own linkage information that is used only for the
operations that include this individual).
Another classification of LL techniques, also
called Decomposition Strategies, was proposed in
(Yu et al., 2009). The three main linkage generation
ways are pointed: perturbation, interaction adapta-
tion, and model building. In (Omidivar et al., 2014)
this list was supplemented by random methods. All
techniques are discussed below. This paper defines
another decomposition strategy which was not
distinguished before although the methods that use it
are present in the literature - the evolution results
comparison.
Perturbation. These methods perturb the
genotype. The fitness value changes caused by
perturbations are analysed to detect the possible
interactions between genes. The example of this
strategy is the Probabilistically Complete
Initialization (PCI) phase of fast messy GA (fmGA)
(Goldberg et al., 1993) and Differential Grouping
(Omidivar et al., 2014).
Interaction Adaptation. The methods that use
this linkage discovery technique are capable of
evolving the gene order in the chromosome. This
decomposition strategy is used during the
evolutionary process.
Model Building. These methods, also called
Estimation of Distribution Algorithms (EDAs),
construct the probabilistic model on the base of
promising individuals in the population. The
examples of such methods are BOA and hBOA
(Pelikan et al., 1999; Pelikan et al., 2006).
Random Methods. These methods use the most
simple linkage generation strategy – the linkage is
generated randomly. The new linkage may be
generated again after some evolutionary method
iterations (in such case the quality of linkage is not
controlled at all) (Yang et al., 2008). Another
possibility is to generate new linkage information
when the information used so far is found not useful
Linked Genes Migration in Island Models
31

(Chen et al., 2007a; Fidrysiak and Przewozniczek,
2015). Note that such decomposition strategy is
quite primitive, but still may be more effective than
the use of typical linkage-blind operators like the
uniform or the single point crossover operators
(Przewozniczek, 2015).
Evolution Results Comparison. This decom-
position strategy class was not distinguished before
but seems necessary since the already proposed list
does not cover all possibilities that may be found in
the EA literature. The methods that use this
decomposition strategy compare the individuals that
are the results of different evolution processes. For
instance, evolution results produced by various
islands may be compared (Skolicki, 2008). Another
way is used in MuPPetS (Kwasnicka and
Przewozniczek, 2011; Przewozniczek et al., 2015;
Walkowiak et al., 2013). In MuPPetS, a perturbation
to a particular genotype is introduced. Then this
perturbed genotype is optimized by an evolutionary
process. The linkage information is generated on the
base of differences between the genotype before
perturbation and after evolutionary optimization of
the perturbed genotype.
Linkage information is used in many different
ways. The most common one is to improve the
effectiveness of crossover operators (Chen et al.,
2007a; Fidrysiak and Przewozniczek, 2015;
Goldberg et al., 1993; Kwasnicka and
Przewozniczek, 2011). Other ways may include the
population initialization (Goldberg et al., 1993;
Kwasnicka and Przewozniczek, 2011; Pelikan et al.,
1999; Pelikan et al., 2006) and gene grouping in
Cooperative Coevolution (Omidivar et al., 2014).
Note that some of the proposed LL techniques may
be hardly useful in practice. For instance, in
(Omidivar et al., 2014) the proposed LL technique
assumes that identified groups of genes are fully
separable. It seems doubtful that a method built on
such assumptions will be capable of effectively
solving the real-life problems – usually, the BBs are
not fully separable (Pelikan et al., 2006; Skolicki,
2008; Watson and Pollack, 1999).
2.2 Island Model
In IMs (Kurdi, 2016; Leitão et al., 2015; Skolicki
and De Jong, 2007; Skolicki, 2008) the population is
divided into subpopulations called islands. For each
island (subpopulation), a separate evolutionary
process is executed. The evolutionary operations are
restricted to islands, so individuals from different
islands cannot interact freely. The islands commu-
nicate with one another usually by migrating whole
individuals. Such model improves the diversity of
the whole population and thus makes it less
vulnerable to preconvergence.
An interesting direction of research in the IM
field is the hybridization of IM and EDAs (delaOssa
et al., 2004; Muelas et al., 2014). EDAs build the
probabilistic models during their run which are used
to generate offspring. The IM and EDA hybrids
exchange probabilistic models instead of exchanging
individuals. However, the question of how to
effectively combine the exchanged models remains
open. Therefore, in this paper, we concentrate on
exchanging detected building blocks instead of
exchanging models or individuals.
In some of the papers another way of
understanding IMs may be found (Skolicki and De
Jong, 2007; Skolicki, 2008). IMs may be interpreted
as a two-level system, where islands are higher level
individuals and interactions between them are a part
of high-level evolution. This interpretation is close
to the idea of Compositional Evolution (Watson,
2006) defined as “evolutionary processes involving
the combination of systems or subsystems of semi-
independently preadapted genetic material”. Skolicki
(Skolicki, 2008) points out that lower evolution level
of IMs is used to produce BBs while the higher level
is used to exchange them. Therefore, IMs should be
suitable to solve problems built from multiple
subsolutions. Note that similar, two-level method
construction, is becoming more and more popular
and is typical not only for GA-based methods. For
instance, MuPPetS (Kwasnicka and Przewozniczek,
2011; Przewozniczek et al., 2015; Przewozniczek,
2016) uses a dynamically changed number of messy
individual subpopulations, which exchange data
using LL. In (Alves, 2015; Kwasnicka and
Przewozniczek, 2011; Kim and Choi, 2015) GA-
based methods, with many coevolving subpopula-
tions, were proposed. The idea of multiple subpopu-
lations may also be found in papers concerning
Particle Swarm Optimization (PSO) (Chang, 2015;
Dahzi et al., 2008; Fidrysiak and Przewozniczek,
2015; Fieldsend, 2014; Zhang et al., 2007),
Differential Evolution (DE) (Wang et al., 2015;
Zavoianu et al., 2015), and others (Omidivar et al.,
2014; Yang et al., 2008).
3 GENE PATTERN BASED
ISLAND MODEL
In this section, the description of the proposed Gene
Pattern Based Island Model (GePIM) is presented.
As pointed in the former sections, the migration in
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
32

IMs is used to exchange the BBs between islands.
Therefore, the main motivation behind GePIM is to
exchange linked gene groups instead of exchanging
individuals or probabilistic models.
3.1 Gepim Overview
The general GePIM procedure is presented in Figure
1. The method framework is typical for IMs. The
main differences are the introduction of LL
mechanisms and the use of linked genes.
1: it
←
1;
2: for each island:
3: initialize(island);
4: evaluate(island);
5: while (!stopCondition):
6: for each island:
7: select(island);
8: crossover(island);
9: mutate(island);
10: evaluate(island);
11: if (it % retrievalFreq = 0):
12: retrieveLinkage();
13: if (it % migrationFreq = 0):
14:
migrateLinkedGeneGroups();
15: for each island:
16: evaluate(island);
17: it
←
it + 1;
18: return bestIndividual;
Figure 1: The general GePIM procedure.
As shown in Figure 1, first all subpopulations
(islands) are randomly initialized. Then all
subpopulations are processed like in the standard
GA (sGA). In the case of GePIM, the uniform
crossover operator is used as it is not dependent on
gene order. The probability of mutation is checked
for every single gene separately. If the mutation
occurs then the gene value is flipped. The linkage
information retrieval and the LGGM are performed
with frequencies defined by a user. These two
operations are described in the next two subsections.
3.2 Linkage Information Retrieval
The linkage information is stored in a form of gene
patterns (Kwasnicka and Przewozniczek, 2011). A
gene pattern is a set of gene positions that are
expected to be dependent on one another. A gene
pattern of length l is denoted as {p
1
, p
2
, …, p
l
},
where p
i
is the ith gene position. For example, the
gene pattern {1, 4, 6} marks three genes: first,
fourth, and sixth. Here, gene patterns are created by
comparing two individuals and selecting only those
genes that are different. Therefore, lengths of gene
patterns are not fixed. For example, for the
comparison of 001100 and 010101 individuals, the
gene pattern is {2, 3, 6}, because the genotypes are
different at the second, third, and sixth position.
Assuming that two individuals have different
genotypes and are well evolved (they cannot be
easily improved by a typical evolutionary process),
some of their genotype differences may have a
considerable impact on fitness. The existence of the
specific good gene values only in one individual
may be caused by difficulties in obtaining such
sequence. It may be supposed that these genes
depend on one another.
Therefore, in IMs, it seems reasonable to
compare individuals from different islands to
produce linkage. The objective is to compare
individuals that are well evolved, so only the best
individuals from each island are taken into account.
For each island, two types of the best individual can
be defined. The first is the current best individual
(i.e., the best individual in the island’s population).
The other is the best individual found so far on a
particular island. The current best individual and the
best individual found so far can, but do not have to,
be the same.
To retrieve the linkage information, comparisons
between the best individuals from all islands are
made. Each island provides two best individuals:
current and the best found so far. All possible pairs
are checked. Therefore,
2
2 N
C
comparisons are made,
where N is the number of islands. Each comparison
produces a single gene pattern. Comparing two best
individuals from the same island could provide a
useful gene pattern since they may represent
different local optima. A single gene pattern may
contain gene positions from different BBs.
Especially in the early method stage when all islands
are the most diversified due to the random
initialization. Thus, not every gene pattern generated
in the above way will be a valuable one. Note that in
every LL method the linkage information does not
have to be perfect. It is as good as it improves the
performance of the whole method. A wider
discussion on this topic may be found in (Kwasnicka
and Przewozniczek, 2011).
Each newly created gene pattern is added to a
global gene patterns storage, called gene pattern
pool. A size of a gene pattern pool cannot exceed a
user defined maximum size. If a maximum size is
reached then every new gene pattern replaces a
randomly selected gene pattern from the gene
pattern pool. The above mechanism of replacing
randomly chosen gene patterns by new gene patterns
Linked Genes Migration in Island Models
33

is adopted from (Kwasnicka and Przewozniczek,
2011). The motivation behind this mechanism is
quite straightforward. It is very hard (if not
impossible) to distinguish the linkage information
that is useful on the current method stage, from the
useless one. Therefore, it seems reasonable to assu-
me that useful linkage information will be generated
more times and will replace the useless one.
3.3 Linked Gene Groups Migration
Operator
During a classic migration, individuals are migrated
between islands. Note that even if migrated
individuals provide some new BBs to an island, it
may be hard to exchange them with other
individuals. New BBs can be easily destroyed by
classical crossover operators. For example, if the
optimal problem solution is 11111111 then even if
the population contains individuals 01010101 and
10101010, obtaining the individual representing the
best solution is highly unlikely.
The above drawback can be avoided by
migrating linked genes instead of individuals or
probabilistic models. Genes marked by a single gene
pattern are supposed to be linked. To perform the
Linked Gene Groups Migration (LGGM), two
islands are selected first. Then, the defined number
of best-fitted individuals from both islands is
selected. The individuals that migrate their genes are
called ‘source individuals’ while the individuals
from the island that receives the linked genes are
called ‘receiving individuals’. The source and
receiving individuals are paired in the way that the
best source individual sends its genes to the best
receiving individual, the second best source
individual sends its genes to the second best
receiving individual and so on. For each source-
receiving individuals pair, the gene pattern is
selected randomly from the gene pattern pool that
contains gene patterns created during the linkage
information retrieval phase. Finally, all genes from
the source individual, marked by the chosen gene
pattern replace proper genes in the receiving
individual. For example, if the 01010101 is the
receiving individual, the 10101010 is the source
individual and the {1, 3, 5, 7} gene pattern was
selected for this migration then after such operation
the genotype of receiving individual will be as
follows: 11111111.
3.4 Summary
GePIM is an example of IM, which uses the LL
technique. The linkage information is used during
(and only during) the LGGM operation. This
improves the method effectiveness. The method is
not dependent on gene order since the uniform
crossover operator is used.
The GePIM classification as an LL method is as
follows. GePIM uses the unimodal way of good and
bad linkage distinguish, the linkage information
representation is virtual and is stored in a centralized
way. The evolution results comparison is used as a
decomposition strategy.
4 THE RESULTS
In this section, the results of performed experiments
are presented. In the first subsection the competing
methods choice is presented, then the problems used
for tests and the stop condition are discussed. The
tuning procedure, obtained results, and their
discussion are described in the latter subsections. All
methods were coded in C++. Whenever it was
possible, the methods shared the same pieces of
code. All experiments were conducted on HP Elite
Desk800 3.4 GHz 8GB RAM server with Intel Core
i7-4770 CPU and Windows 7 64-bit installed. For
each test case, ten independent runs were executed.
Complete results, source codes of all competing
methods, and configuration files are available at:
http://mp2.pl/download/ai/20160531_gepim.zip.
4.1 Competing Methods Choice
Four methods were chosen to compete with GePIM.
The classical Island Model (IM) was chosen to
check how significant is the improvement caused by
changes proposed in this paper. sGA was chosen to
check if the difference between the simple and more
evolved methods is significant. Both, classical IM
and sGA use (same as GePIM) the uniform
crossover operator and the gene flip mutation
checked for every gene separately. Finally, BOA
(Pelikan et al., 1999) and MuPPetS (Kwasnicka and
Przewozniczek, 2011) methods were chosen as the
literature review points them as highly effective
ones. BOA is effective when used for solving the
deceptive functions concatenations, while MuPPetS
was shown capable of effective solving both:
theoretical (Kwasnicka and Przewozniczek, 2011)
and practical problems (Przewozniczek, 2015;
Walkowiak et al., 2013).
BOA (Pelikan et al., 1999) is an LL method that
builds a Bayesian network to represent gene
dependencies. At each iteration, a Bayesian network
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
34

is generated on the base of a set of best individuals.
In the next iteration, new individuals are created on
the base of Bayesian network. BOA was shown to
use a relatively low number of Fitness Function
Evaluations (FFE) when compared to other
evolutionary methods. However, in the case of
BOA, the main part of computation load is
consumed not for the fitness value computation, but
on Bayesian tree generation. In this paper the same
Bayesian network construction algorithm as in
(Kwasnicka and Przewozniczek, 2011; Pelikan et al.,
1999) is used. The time complexity of this algorithm
is O(k
2
kn
2
N + kn
3
), where n is the problem size, N is
the size of the dataset, and k is the maximum
allowed indegree (the tree depth).
MuPPetS (Kwasnicka and Przewozniczek, 2011)
is a relatively new proposition of LL method. It uses
a flexible number of coevolving virus populations.
The viruses are messy-coded individuals (Goldberg
et al., 1993; Kwasnicka and Przewozniczek, 2011),
but purpose and way of use are different than in the
classical messy coded individuals case. The number
of virus subpopulations is increased when the
method is stuck and decreased after reaching a
breakthrough. This feature makes the method
capable of automatically adjusting itself to the
current evolution state. The linkage information is
extracted with the use of evolution results
comparison strategy.
4.2 The Test Problems and Stop
Condition
As discussed in the previous subsection the
computation load used by BOA is mainly dependent
on Bayesian network construction, not on fitness
value computation. Therefore, FFE is not a fair
computation measure for BOA. A detailed analysis
of the dependency between FFE and the computa-
tion time used by BOA may be found in (Kwasnicka
and Przewozniczek, 2011). Therefore, in this paper,
the computation time (7200 seconds) was used as a
stop condition. The stop condition was checked after
each method iteration. Thus, the overall computation
time could be slightly greater than 7200 seconds.
The time-based stop condition favors the methods
that spend most of the computation load for fitness
value computation. The proper analysis of FFE and
computation time dependency is given at the end of
Section 4.4.
All experiments were executed in a repeatable
environment without any other resource consuming
processes running. Three different kinds of test
problems were chosen: the deceptive functions
concatenations, the Knapsack, and the MAX-2SAT
problem.
4.2.1 Mixed Deceptive Functions
Concatenations
Eight different deceptive functions were used to
build the deceptive functions concatenations. They
are presented in Table 1. The value of the deceptive
function is dependent on unitation u (the number of
‘1’s in the genotype).
Table 1: Used deceptive functions definitions.
u
3-bit
(3l)
3-bit
(3lh)
3-bit
(3h)
3-bit
(3hh)
5-bit
(5l)
5-bit
(5lh)
5-bit
(5h)
5-bit
(5hh)
0 0.33 0.98 3.33 9.80 0.4 0.99 4 9.88
1 0.17 0.49 1.67 4.90 0.3 0.74 3 7.41
2 0 0 0 0 0.2 0.49 2 4.94
3 1 1 10 10 0.1 0.25 1 2.47
4NANANANA 0 0 0 0
5 NA NA NA NA 1 1 10 10
To each deceptive functions concatenation, the
tale function was added. The tale is the OneMax
function and is defined as follows: Tale(length) =
u/length, where u is the unitation and length is the
tale function gene number. The test cases used in the
experiments are defined in Table 2 according to
Table 1 and the tale definition. The number of bits
necessary to encode the complete problem solution
was 600 for all used concatenations.
Table 2: Used deceptive functions concatenations.
TC no. Definition
1 50*3l + 30*5l + Tale(300)
2 50*3lh + 30*5lh + Tale(300)
3 15*3l + 35*3h + 9*5l + 21*5h + Tale(300)
4 15*3lh + 35*3hh + 9*5lh + 21*5hh + Tale(300)
5 60*5l + Tale(300)
6 60*5lh + Tale(300)
7 18*5l + 42*5h + Tale(300)
8 18*5lh + 42*5hh + Tale(300)
The definitions of the above test cases were
adopted from (Kwasnicka and Przewozniczek,
2011). Note that frequently, when the deceptive
functions concatenations are used, the glued
deceptive blocks are identical (Goldberg et al., 1993;
Pelikan et al., 1999; Pelikan et al., 2006). Such a
Linked Genes Migration in Island Models
35

practice may be found surprising since deceptive
functions concatenations are supposed to mimic the
existence of BBs in the problem. It seems a
reasonable assumption that, usually, a problem is
built from many BBs (Watson and Pollack, 1999;
Watson, 2006). Nevertheless, the assumption that
these BBs are identical seems unjustified. Therefore,
mixed deceptive functions concatenations were
proposed (Kwasnicka and Przewozniczek, 2011).
The test problems include a tale which is a part that
should be easy to optimize by any GA-based
method. Note that it was shown that some of the
methods (e.g., fmGA) considered effective in
solving the problems built from deceptive functions
concatenations are ineffective when the deceptive
blocks are not identical (Kwasnicka and
Przewozniczek, 2011).
4.2.2 The Knapsack Problem
The Knapsack problem is a common tool used to test
the effectiveness of methods that use the binary
coding. Most of the test instances of the knapsack
problem can be solved in pseudo-polynomial time
using dynamic programming, but it is possible to
generate instances that are hard to solve (Pisinger,
2005). In the performed experiments, only such
hard-to-solve instances were used. The set of hard
instances and their solutions was downloaded from
http://www.diku.dk/~pisinger/largecoeff_pisinger.tg
z. For each instance the solution time that indicates
its hardness was provided. Six of the hardest
instances corresponding to the greatest value of the
solution time were chosen for tests:
“knapPI_3_500_10000000_76” (test case (TC) no.:
9; bit length: 500), “knapPI_3_500_10000000_92”
(10; 500), “knapPI_3_1000_10000000_73” (11;
1000), “knapPI_4_500_10000000_13” (12; 500),
“knapPI_4_1000_10000000_22” (13; 1000),
“knapPI_4_1000_10000000_49” (14; 1000).
4.2.3 The MAX-2SAT Problem
The MAX-2SAT problem is the specific kind of the
MAX-SAT problem, because the given conjunctive
normal form (CNF) formula is the conjunction of
clauses of two literals. Instances of the MAX-2SAT
problem can be generated using a planted solution
model (Watanabe and Yamamoto, 2010). In this
model, for each instance, a solution that is very
likely to be optimal is provided. Thus, a large
number of instances can be created and
experimentally checked if they are hard to solve.
Four instances were generated with the use of
planted solution model and used during the
experiments: test case no. 15 (p=0.1243; r=0.0311;
bit length: 500), 16 (p=0.1492; r=0.0373; 500), 17
(p=0.0553; r=0.0138; 1000), 18 (p=0.0691;
r=0.0173; 1000). The p and r variable values
reported for the MAX-2SAT problem instances are
the parameters used to generate the instances by the
planted model.
4.3 The Tuning Procedure
All methods were tuned with the use of the same
tuning procedure. The initial settings were proposed,
on the basis of the literature review. Then, each
parameter was optimized separately in a greedy way
– if a parameter change improves the results then the
change is accepted. The tuning was made for the
following deceptive functions concatenations: 5, 6,
7, 8. These functions are supposed to be the most
challenging test cases to solve. Therefore, if the
tuning procedure causes each method to propose the
results of quality as good as possible for these
problems, then the methods should also perform
well for the other test cases. During tuning, two
independent runs were executed, for each test case.
Similar tuning procedure can be found in
(Kwasnicka and Przewozniczek, 2011,
Przewozniczek et al., 2015).
The complete initial and final configurations of
all competing methods are given in Tables 3, 4, 5, 6,
and 7. The parameter tuning order was the same as
the parameter order in the tables.
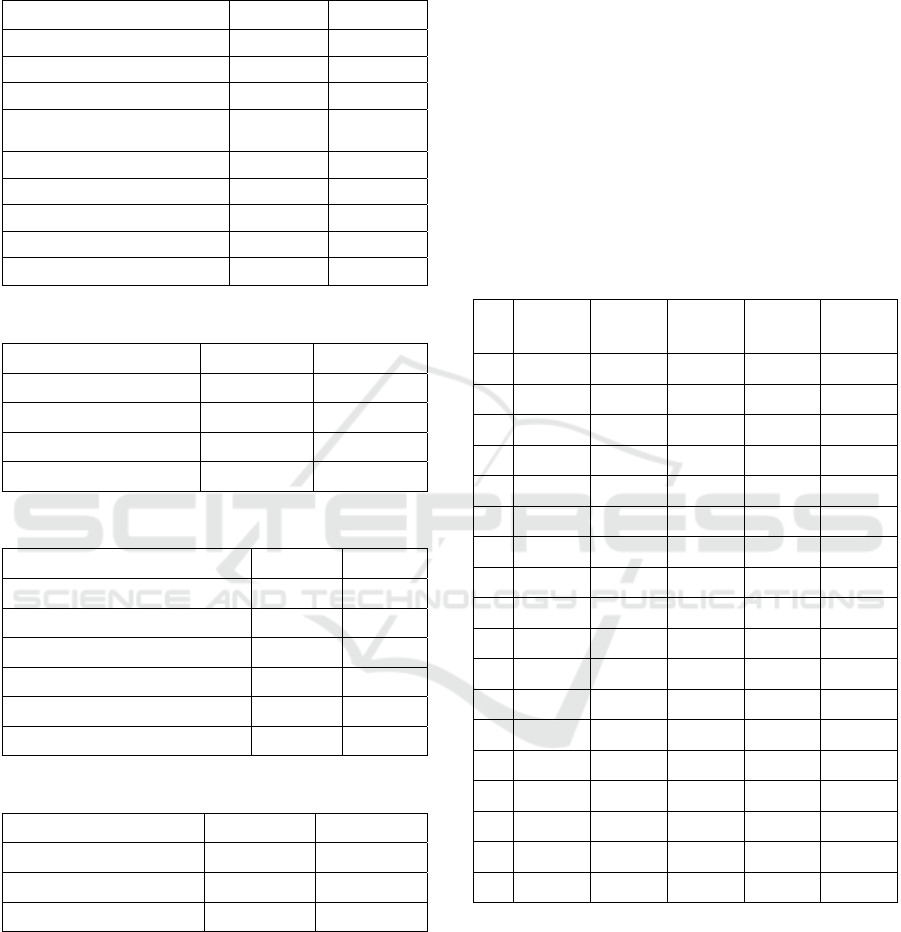
Table 3: GePIM configuration.
Parameter Initial value Final value
Crossover 0.6 0.3
Population size per island 400 200
Number of islands 10 30
Migration frequency 200 50
Number of migrating
Individuals
40 40
Gene pattern pool size 300 300
Linkage information retrieval
freq.
100 500
Mutation 1 / length 1 / (3 * length)
As presented in Table 3, the most significant
change of initial GePIM configuration made by
tuning was the increase of the LGGM frequency and
decrease the frequency of linkage gathering. It
seems that it is more beneficial for GePIM to
exchange BBs more often and collect the linkage
information when the current and the overall best
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
36
individual are well evolved, which should increase
the gathered linkage quality.
Table 4: MuPPetS configuration.
Parameter Initial value Final value
Gene pattern pool size 200 200
Minimal pattern size 3 3
Virus generation number 5 10
Virus population per
competetive template
400 180
Cut probability 0.05 0.16
Splice probability 0.5 0.16
Mutation 0.1 0.02
Remove gene probability 0.1 0.02
Add gene probability 0.1 0.02
Table 5: BOA configuration.
Parameter Initial value Final value
Population size 80000 50000
Bayesian tree level 4 4
Parents percentage 50 40
Offspring percentage 50 60
Table 6: Classical IM configuration.
Parameter Initial value Final value
Crossover 0.7 0.5
Population size per island 400 400
Number of islands 10 50
Migration frequency 200 50
Number of migrating individuals 40 40
Mutation 1 / length 1 / length
Table 7: sGA configuration.
Parameter Initial value Final value
Crossover 0.7 0.4
Population size 400 800
Mutation 1 / length 2 / length
4.4 The Methods Comparison
As mentioned, for each test case ten independent
runs were performed. In Table 8 the average solution
quality for each test case is presented. In the case of
deceptive functions concatenations, the quality
measure was the best solution unitation percentage:
UnitPerc(X
best
) = u(X
best
)/len, where X
best
is the best-
found individual, u(X
best
) is its unitation, and len is
the genotype length. Unitation percentage informs
how similar is the best-found individual to the global
optimum and is typical for deceptive functions
concatenations (Fidrysiak and Przewozniczek, 2015;
Goldberg et al., 1993; Kwasnicka and
Przewozniczek, 2011; Pelikan et al., 2006). For the
Knapsack and the MAX-2SAT problems, the quality
measure was the proportion of the best-found
solution and the global optimum values. Due to the
space limitations, the standard deviation was not
reported. However, for all the test cases the standard
deviation was rather low (usually below 0.01). The
average time presented in Table 9 informs how fast
the final solution was found.
Table 8: The average solution quality comparison.
TC
no.
GePIM
[%]
Classical
IM [%]
sGA
[%]
BOA
[%]
MuPPetS
[%]
1 99.92 87.87 98.62
100.00 100.00
2 99.25 63.75 58.55 97.90
99.50
3 99.50 87.90 98.28
100.00
99.70
4
99.45
63.12 58.31 95.20 99.20
5
100.00
75.36 98.63
100.00 100.00
6 97.25 52.26 50.07
100.00
98.30
7
100.00
76.07 86.16
100.00 100.00
8 97.75 53.33 50.50 94.20
98.10
9
100.00 100.00
99.96
100.00
99.99
10
100.00 100.00
99.98
100.00
99.99
11
100.00 100.00
99.96 99.01 99.95
12
100.00 100.00 100.00 100.00 100.00
13
100.00 100.00 100.00
99.99
100.00
14
100.00 100.00 100.00
99.99 99.96
15
100.00 100.00
99.91
100.00
99.93
16
100.00 100.00
99.95
100.00
99.93
17
100.00 100.00
99.95 86.70 99.96
18
100.00
99.99 99.94 86.10 99.99
For deceptive functions concatenations Classical
IM and sGA performed worse than all other three
methods for every single instance. BOA for two
cases proposed the solutions of relatively low quality
(for test case number 8 and 4 the average solution
quality is only 94.2 and 95.2 respectively).
Therefore, the best methods for this problem class
are GePIM and MuPPetS, while MuPPetS is slightly
better. For the Knapsack and the MAX-2SAT
problems, all methods report high quality-results,
Linked Genes Migration in Island Models
37

Table 9: The average time comparison.
TC no.
GePIM
[s]
Classical
IM [s]
sGA
[s]
BOA
[s]
MuPPetS
[s]
1-8 300 2624 3040 3622 4886
9-14 643 2151 1890 4410 2534
15-18 1035 3253 2941 5485 427
but GePIM and classical IM are the best. Note that
BOA reported results of very low quality for 17th
and 18th test case. To encode solutions to these test
cases 1000 genes is necessary. For such a large gene
number, the computation load spent by BOA for
building the Bayesian network (it is built at every
iteration) rises significantly and makes the method
ineffective. Similar situation, in which BOA was
unable to handle the problems encoded with large
gene number was already observed and discussed in
(Kwasnicka and Przewozniczek, 2011).
The worst solution quality for each test case type
group is reported in Table 10. The comparison
confirms that GePIM and MuPPetS are the only two
methods that guarantee the highest solution quality
for all problem types.
Table 10: The comparison of the worst solution quality for
each test case type.
GePIM
[%]
Classical
IM [%]
sGA
[%]
BOA
[%]
MuPPetS
[%]
Dec.
func.
95.00 51.67 49.83 90.00
96.00
Knap
sack
100.00 100.00
99.95 98.89 99.93
MAX-
2SAT
100.00
99.98 99.77 85.96 99.77
To confirm the statistical significance of solution
quality differences the Wilcoxon statistical test was
used. The p-values reported by this test are presented
in Table 11. The tests were performed on the results
of all runs, rounded if necessary, to the sixth most
significant position. The results obtained confirm the
analysis presented above – GePIM significantly
outperforms all competing methods except MuPPetS
for the deceptive functions concatenations case.
In Figure 2 the dependency between the computation
time and FFE for all competing methods is
presented. The comparison is done for deceptive
functions concatenations test cases (80 runs per
method). Similar comparisons may be found in (Cai
and Wang, 2015; Kwasnicka and Przewozniczek,
2011; Przewozniczek et al., 2015; Saha et al., 2010,
Suganthan et al., 2005).
Table 11: The solution quality comparisons on the base of
p-values reported by Wilcoxon test.
Null hypothesis:
GePIM...
better or
equal
worse or
equal
equal
Classical
IM
DF
1
0 0
KS 0.50 0.50
1
M2S
0.85
0.16 0.33
sGA
DF
1
0 0
KS
1
0 0
M2S
1
0 0
BOA
DF 0.59 0.41
0.83
KS
0.99
0 0
M2S
1
0 0
MuPPetS
DF 0.24
0.76
0.49
KS
1
0 0
M2S
1
0 0
Figure 2: Average FFE per second for deceptive functions
concatenations.
As shown in Figure 2 the dependency between
FFE and computation time is highly repeatable – the
standard deviation value is low. The sGA is capable
of doing the highest FFE number per second. This is
an expected result since sGA does not do many
computation load consuming operations other than
fitness calculation. The high number of FFE per
second is also understandable for MuPPetS and
Classical IM. GePIM does about 50% of FFE done
by Classical IM. This difference is a result of
frequent migrations, which require many sorting
operations. Finally, the average number of FFE per
second for BOA is about 30 times lower than in the
GePIM case, which confirms the previous reasoning
that the FFE number is not a suitable computation
load measure for BOA.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
38

5 CONCLUSIONS AND FURTHER
WORK
In this paper, the proposition of the Linked Gene
Groups Migration for Island Models was presented.
The GePIM method, an IM using the proposed
LGGM was shown to be an effective tool when
compared to other evolutionary methods. Despite its
simplicity, GePIM was able to compete successfully
with MuPPetS and BOA methods.
The main fields that should be concerned in the
future work are as follows:
the application of GePIM to other problems
than those considered in this paper,
further LGGM development,
employing in GePIM other LL techniques
than used in this paper,
combining the LGGM, the LL and dynamic
subpopulation number control
(Przewozniczek, 2016).
The further research in the above directions
should allow proposing new and more effective
evolutionary methods.
REFERENCES
Alves, H. N. 2015. A Multi-population Hybrid Algorithm
to Solve Multi-objective Remote Switches Placement
Problem in Distribution Networks. In Journal of
Control, Automation and Electrical Systems, 25, 5,
545-555.
Cai, Y., Wang, J. 2015. Differential evolution with hybrid
linkage crossover. In Information Sciences, 320, 244-
287.
Chang, W.D. 2015. A modified particle swarm
optimization with multiple subpopulations for
multimodal function optimization problems. In
Applied Soft Computing, 33, 170-182.
Chen, Y., Peng. W, Jian M. 2007a. Particle Swarm
Optimization With Recombination and Dynamic
Linkage Discovery. In IEEE Transactions on Systems,
Man and Cybernetics, Part B: Cybernetics, 37, 6,
1460-1470.
Chen, Y., Sastry, K., Goldberg, D.E. 2007b. A Survey of
Linkage Learning Techniques in Genetic and
Evolutionary Algorithms. In IlliGAL Report No.
2007014, Illinois Genetic Algorithms Laboratory.
Dahzi, W., Wu, C.H., Ip, W.H., Wang, D., Yan, Y. 2008.
Parallel multi-population Particle Swarm Optimization
Algorithm for the Uncapacitated Facility Location
problem using OpenMP. In IEEE Congress on
Evolutionary Computation, 124-128.
delaOssa, L., Gámez, J.A., Puerta, J.M. 2004. Migration of
Probability Models Instead of Individuals: An
Alternative When Applying the Island Model to
EDAs. In Lecture Notes in Computer Science (PPSN
2004), 3242, 242-252.
Fidrysiak, B., Przewozniczek, M. 2015. Towards Finding
an Effective Way of Discrete Problems Solving: the
Particle Swarm Optimization, Genetic Algorithm and
Linkage Learning Techniques Hybrydization. In
Proceedings of the 7th International Joint Conference
on Computational Intelligence, 228-236,
DOI=10.5220/000559660228023.
Fieldsend, J. E. 2014. Running Up Those Hills: Multi-
Modal Search with the Niching Migratory Multi-
Swarm Optimiser. In IEEE Congress on Evolutionary
Computation, 2593-2600.
Goldberg, D.E., Deb, K., Kargupta, H., Harik, G. 1993.
Rapid, Accurate Optimization of Difficult Problems
Using Fast Messy Genetic Algorithms. In Prcs. 5th
International Conference on Genetic Algorithms, 55-
64.
Kim, H.H., Choi, J.Y. 2015. Pattern generation for multi-
class LAD using iterative genetic algorithm with
flexible chromosomes and multiple populations. In
Expert Systems with Applications, 42, 833–843.
Kurdi, M. 2016. An effective new island model genetic
algorithm for job shop scheduling problem. In
Computers and Operations Research, 67, 132-142.
Kwasnicka, H., Przewozniczek, M. 2011. Multi
Population Pattern Searching Algorithm: a new
evolutionary method based on the idea of messy
Genetic Algorithm. In IEEE Transactions on
evolutionary computation, 15, 5, 715-734.
Leitão, A., Pereira, F.B., Machado, P. 2015. Island models
for cluster geometry optimization: how design options
impact effectiveness and diversity. In Journal of
Global Optimization, 63, 677-707.
Muelas, S., Mendiburu, A., LaTorre, A., Peña, J.-M. 2014.
Distributed Estimation of Distribution Algorithms for
continuous optimization: How does the exchanged
information influence their behavior? In Information
Sciences, 268, 231-254.
Omidivar, M.N., Li, X., Mei, Y., Yao, X. 2014.
Cooperative Co-evolution with Differential Grouping
for Large Scale Optimization. In IEEE Transactions
on evolutionary computation, 18, 378-393.
Pisinger, D. 2005. Where are the hard knapsack problems?
In Compuers and Operation Research. 32, 9, 2271-
2284.
DOI=http://dx.doi.org/10.1016/j.cor.2004.03.002.
Pelikan, M., Goldberg, D.E., Cantu-Paz, E. 1999. BOA:
The Bayesian Optimization Algorithm. In IlliGAL
Report No. 99003.
Pelikan, M., Sastry, K., Butz, M.V., Goldberg, D.E. 2006.
Hierarchical BOA on Random Decomposable
Problems. In MEDAL Report No. 2006001.
Przewozniczek, M., Goscien, R., Walkowiak, K.,
Klinkowski, M. 2015. Towards Solving Practical
Problems of Large Solution Space Using a Novel
Pattern Searching Hybrid Evolutionary Algorithm -
An Elastic Optical Network Optimization Case Study.
In Expert Systems with Applications, 42, 7781-7796.
Linked Genes Migration in Island Models
39

Przewozniczek, M. 2015. Towards finding an effective
uniform and single point crossover balance for
optimization of Elastic Optical Networks. In The
Proceedings Of The Second European Network
Intelligence Conference.
Przewozniczek, M., 2016. Active Multi Population
Pattern Searching Algorithm for Flow Optimization in
Computer Networks – the novel coevolution schema
combined with linkage learning. In Information
Sciences, 355-356, 15-36.
Saha, A., Datta, R., Deb, K. 2010. Hybrid gradient
projection based Genetic Algorithms for constrained
optimization. In IEEE Congress on Evolutionary
Computation, 1-8.
Skolicki, Z., De Jong, K. 2007. The importance of a two-
level perspective for island model design. In
Proceedings of the IEEE Congress on Evolutionary
Computation, 4623–4630.
Skolicki, Z. 2008. Linkage in Island Models. In Lecture
Notes in Computer Science, 157, 41-60.
Suganthan, P., Hansen, N., Liang, J., Deb, K., Chen, Y.,
Auger, A., Tiwari, S. 2005. Problem definitions and
evaluation criteria for the CEC 2005 special session on
real-parameter optimization. In Technical Report, 1-
50, Nanyang Technol Universiy, Singapore.
Walkowiak, K., Przewozniczek, M., Pająk, K. 2013.
Heuristic Algorithms for Survivable P2P Multicasting.
In Applied Artificial Intelligence, 27, 4, 278-303.
Wang, J., Zhang, W., Zhang, J. 2015. Cooperative
Differential Evolution With Multiple Populations for
Multiobjective Optimization. In IEEE Transactions on
Cybernetics, DOI: 10.1109/TCYB.2015.2490669 (in
press).
Watanabe, O., Yamamoto, M. 2010. Average-case
analysis for the MAX-2SAT problem. In Theoretical
Computer Science, 411, 1685-1697.
DOI=http://dx.doi.org/10.1016/j.tcs.2009.12.020.
Watson, R.A., Pollack, J.B. 1999. Hierarchically
Consistent Test Problems for Genetic Algorithms. In
Proceedings of 1999 Congress on Evolutionary
Computation, CEC-99, 2.
Watson, R.A. 2006. Compositional Evolution: The impact
of Sex, Symbiosis and Modularity on the Gradualist
Framework of Evolution. In Vienna Series in
Theoretical Biology. MIT Press.
Yang, Z., Tang, K., Yao, X. 2008. Large scale
evolutionary optimization using cooperative
coevolution. In Information Sciences, 178, 2986–2999.
Yu, T., Goldberg, D.E., Sastry, K., Lima, C.F., Pelikan,
M. 2009. Dependency structure matrix, genetic
algorithms, and effective recombination. In
Evolutionary Computation, 17, 595-626.
Zavoianu, A.-C., Lughofer, E., Bramerdorfer, G.,
Amrhein, W., Klemen, E. P. 2015. DECMO2: a robust
hybrid and adaptive multi-objective evolutionary
algorithm. In Soft Computing, 19, 12, 3551-3569.
Zhang, J., Huang, D.-S., Liu, K.-H. 2007. Multi-Sub-
Swarm Optimization Algorithm for Multimodal
Function Optimization. In IEEE Congress on
Evolutionary Computation, 3215-3220.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
40
