Numerical Simulation and Experimental Scheme for Monitoring

Hoof Wall Structure and Health in Sport Horses

K. Hanstorp

, B. M. Mihiretie

, M. Karlsteen

, A. Rosén

, M. Sundin

, D. Cederkrantz

H. Otterberg

, Å. Hinton

and B. Berg

Department of Physics, Göteborg University, SE-41296, Göteborg, Sweden

Department of Physics, Chalmers University of Technology, SE-41296, Göteborg, Sweden

Hot Disk AB, Chalmers Science Park, SE-41288, Göteborg, Sweden

Ale Animal Clinic, Ale, Sweden

Keywords: Equestrian Sport, Hoof Structure, Hoof Capsule Damages, Numerical Simulation, Finite Element Method,

Heat Conduction, Thermal Conductivity, Transient Curve.

Abstract: This study provides a computational model developed to demonstrate the possibility of monitoring hoof

structure and health in equestrian sport. This is achieved by employing finite element simulation of three-

dimensional heat flow from a surface heat source into a hoof structure while simultaneously sensing the

surface temperature. The time evolution of the recorded surface temperature, transient curve, is used to

investigate hoof structure and predict its intactness by comparing these curves for three different models.

We have observed differences between the transient curves obtained from a normal hoof structure, a hoof

structure containing a foreign material and hoof capsule subjected to wall separation. An experimental

method for probing hoof profile was briefly discussed. It uses temperature sensor/heat source. The method

can determine the thermal conductivity of the hoof along the hoof structure from the recorded transient

curve. Thus, it displays the hoof structure by utilizing the thermal conductivity variation between the hoof

parts.

1 INTRODUCTION

In all equestrian sports, the well-being of the horse is

fundamental. Frequently the horse struggles with

hoof problems. Often it is hard to detect the

underlying damages hidden in the internal of the

hoof. The hoof is composed of an external hoof

capsule connected with the internal pedal bone by

horny and fleshy plates (Nassau, 2004). Hoof

capsule damages of different degrees are common in

most horses. Injuries such as wall separation,

submural infections and crack are caused by various

factors including environmental conditions and

specific athletic endeavours (Moyer, 2003),

particularly the latter could disproportionally affect

athletic horses. Here we discuss a computational

method to monitor the status of a hoof by

determining the presence or absence of foreign

object in the structure. This is realized using thermal

waves. The use of thermal wave for health care

inspection can be achieved in several ways: the first

one is thermography. It is a direct imaging of heat

pattern on the surface of objects or scene (Ibarra-

Castanedo, 2013). A second method requires the

recording of the surface temperature to deduce the

thermal transport property of the material,

commonly referred as an inverse problem. The

method proposed in this study belongs to the latter

group. It works by supplying constant heat on the

surface of the object and recording the change in

temperature on the heat source and then predicting

the property of the sample from the recording.

In this work, COMSOL Multiphysics software is

employed to determine the numerical solution of the

temperature distribution of a hoof due to external

heat source and the change in temperature on the

heat source due to its contact with the hoof. The

model consists of concentric heat source placed on

the hoof wall structure and provides constant heat

for few minutes. The change in temperature on the

heat source and the temperature distribution of the

hoof is then retrieved. The above information can be

used to determine the presence or absence injury

(foreign materials or change in structural properties)

in the hoof.

Hanstorp, K., Mihiretie, B., Karlsteen, M., Rosén, A., Sundin, M., Cederkrantz, D., Otterberg, H., Hinton, Å. and Berg, B.

Numerical Simulation and Experimental Scheme for Monitoring Hoof Wall Structure and Health in Sport Horses.

DOI: 10.5220/0006043601710175

In Proceedings of the 4th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2016), pages 171-175

ISBN: 978-989-758-205-9

171

An experimental approach to investigate the

structural profile of the hoof wall is also included.

The general experimental technique implemented is

referred as hot disk method (Gustafsson, 1991). The

method measures the thermal transport property of

materials by only recording the change in

temperature on the sensor. A recent extension of this

method enables it to thermally profile a material

along its depth. This approximation scheme and

some examples are included in the reference (Sizov,

2016). Further detail examples and description on

the experimental limitation and capabilities of

structural profiling of materials along their structure

is shown in (Mihiretie, 2016).

This contributes in understanding of hoof wall

defects and could potentially help horses to have

longer athletic careers and life.

2 MODEL

Three different models were designed to represent

the situations in a healthy hoof and damaged hooves.

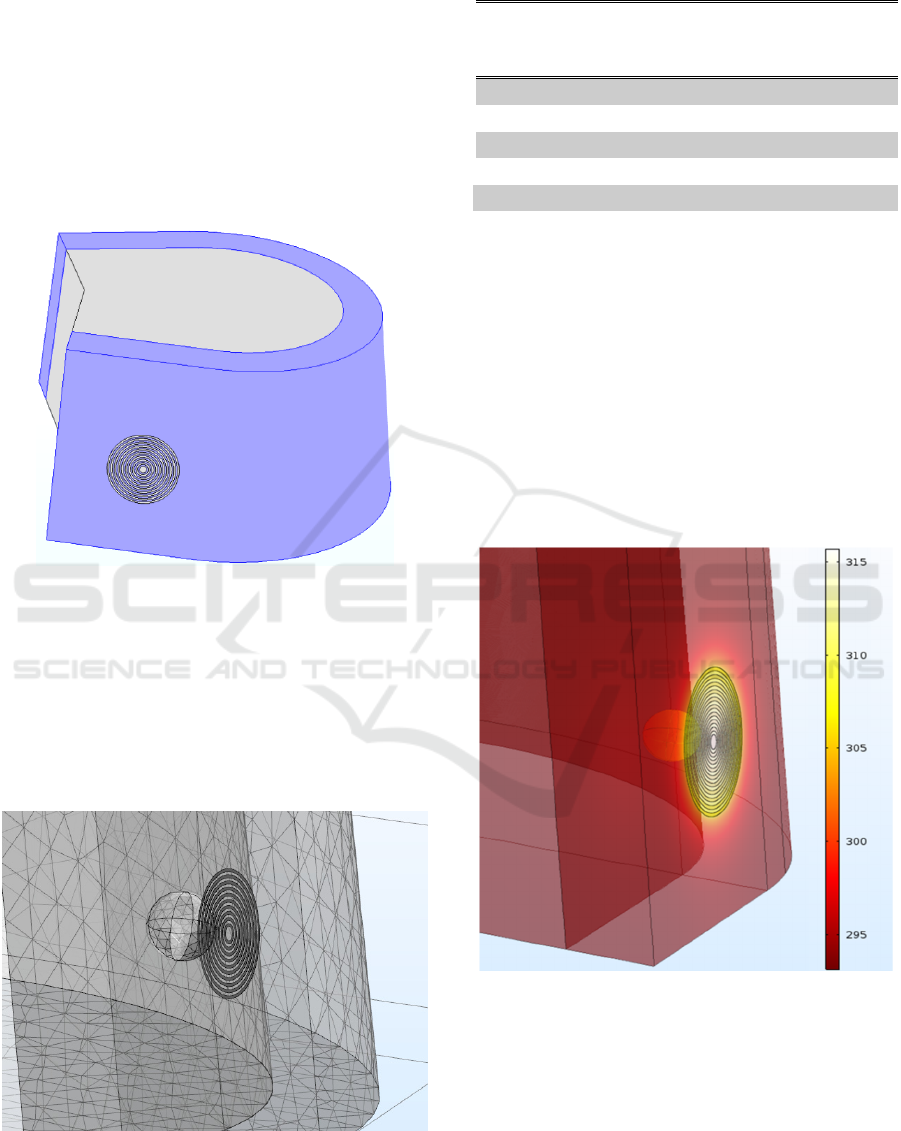
I. Normal hoof structure, fig.1.

II. Hoof structure with a foreign material inside

the hoof capsule, fig.2.

III. Hoof capsule subjected to separation of wall.

Model I, represents a healthy hoof structure. It

consists of three parts: hoof wall; bone and heat

source. The external keratin material (hoof wall),

surrounds the internal bone structure and the double

spiral heat source (nickel wire) is placed on the

outside surface of hoof capsule. In model II, a

spherical foreign material is included in addition to

the parts listed in model I. The foreign material

assume the role of an infected part that developed

some sort of fluid (pus) inside the hoof capsule.

Thermal wave from the heat source travels through

the hoof wall before it spreads to the bone structure.

In model III, since the inside part of the hoof wall is

exposed to air to represent wall separation, the heat

wave is exposed to convective cooling from the

inside part of the hoof capsule.

The models are generated using COMSOL

Multiphysics V.5.2, the software uses the finite

element method to describe the complex problem

with a linear system of equations. This is achieved

by dividing the geometry of the problem at hand into

several subdivisions (elements), called meshing.

Then the relevant quantity is approximated at each

node of the element. Finally the solution for each

element can be collected to form global solution for

the entire geometry (Tabatabaian, 2014). The

validation of COMSOL's heat transfer modules is

documented in different studies (Gerlich, 2013,

Suarez, 2014).

The aim of the simulation is to demonstrate the

utility of the finite element analysis in the

investigation of monitoring the structural integrity of

hooves. This is realized by studying the thermal

response of the hoof structure.

The governing equation that describes transient

heat transfer in solids can be expressed as follows:

 ∙

(,)



=∇∙(∙∇

(

, 

)

+) (1)

Where  is the volumetric specific heat of the

material, T is temperature, t is the test time, K is

thermal conductivity, r is position vector and Q is

the heat source per unit volume.

It is difficult to solve eqn. 1 analytically for the

present geometry, thus a mathematical tool for

numerical solving of such partial differential

equations is employed, using COMSOL.

COMSOL consists of different modules, thus a

typical simulation starts by choosing the physics and

study type. In this study, heat transfer module with

time dependent study is used. Simulation time vector

was introduced for the transient measurement, in the

closed interval [0,320s], with increments of 0.1s

during which a constant power of 0. 5 W is used. For

solving, default solver is used.

Defining the geometry and type of materials

follows naturally. Here they are defined to represent

the different hoof status expressed in the model I-III.

Finally, applying appropriate meshing, boundary and

initial conditions comes to effect. The initial

temperature considered for the entire system was set

to be at room temperature (293.15K), and the

following boundary conditions are considered:

• Extremities of the model are insulated.

.  = 0 (2)

Where  is normal vector and  is the heat flux

by conduction.

• Thermal contact boundary condition is set

between the heat source and the hoof wall and

also between the hoof capsule and the bone.

−



. 



=−ℎ

(





−



)

+



(3a)

−



. 



=−ℎ

(





−



)

+

(

1 + 

)





(3b)

Where h is the conductance; u (up) and d

(down) subscripts refers to the two sides of the

contact.

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

172

• The heat source is defined using thin

concentric elements with over all heat

transfer rate.

• Heat loss due to convection is considered

in the case of wall separation.



=−ℎ

(





−

)

(4)

Where q



is convective heat flux and 



is external temperature.

• Physics controlled finer mesh element size

is adapted for all the domains.

Figure 1: Model of hoof structure. The external blue

structure is hoof capsule (keratin). The internal sliver part

is the bone. The heat source represented by the concentric

circles is placed on the side of the hoof wall.

The second model shown in fig. 2 consist of

spherical object in the hoof capsule filled with fluid.

It represents a possible pus caused by infection. In

the simulation the thermal properties of such fluid is

assumed to be similar to that of water.

Figure 2: Meshed geometry showing the concentric heat

source placed on the hoof surface and spherical foreign

object inside the hoof capsule. Normal size meshing of

COMSOL is used.

Table 1: Characteristic of materials used in the simulation.

Material

Thermal

Conductivit

y W/(m.K)

Heat

capacity

J/(kg.K)

Density

(kg/m

)

Keratin 0.45 2000 1200

Bone 0.32 1313 1908

Nickel 90.7 445 8900

Fluid 0.6 4187 1000

Air 0.03 1005 1.2

The properties of keratin and bone were determined

in a separate experiment (Gustavsson, 1994)

whereas, the properties of the rest materials were

imported from COMSOL material list.

3 RESULT AND DISCUSSION

As explained in sec. 2, heat transfer mode and

transient analysis in conduction of heat in solids

have been chosen. The temperature distribution of

the hoof after constant heat supply from source for

320 seconds on a hoof with fluid is shown in fig.3.

Figure 3: Temperature distribution of the hoof (K), at t

=320 sec., with spherical foreign material in the hoof

capsule, model II. Initial temperature of the hoof was

293.15 K.

The highest temperature (315 K, fig.3) which is at

the heat source drops to room temperature as one

goes away from the source.

The heat supplied from the source propagates

into the hoof and cause change in temperature along

Numerical Simulation and Experimental Scheme for Monitoring Hoof Wall Structure and Health in Sport Horses

173

the way. The way heat leaves the source depends on

the thermal property of the hoof composition. Thus,

computing the time evolution of the heat source,

transient curve, one can predict the composition of

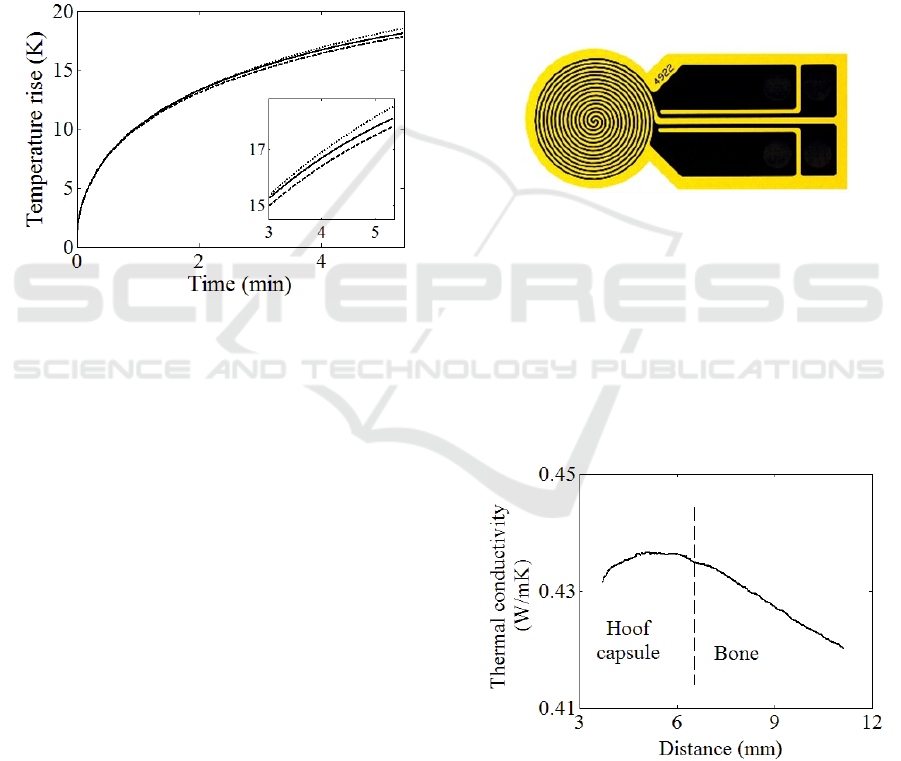
the hoof profile. Fig. 4 shows transient curve of the

heat source. The three curves represent the three

different models discussed in sec. 2. The top dotted

line is obtained from hoof subjected to separation of

wall (Model III) whereas the middle solid line is the

transient curve for heat source placed on the healthy

hoof (model I) and the dashed line (Model II) is

retrieved from a hoof with a foreign material inside.

The curves represent the average change in

temperature on the heat source volume in time.

Figure 4: Temperature rise as a function of time. Each

transient curve represents different models. Solid, dashed

and dotted lines represent model I, model II and model III

respectively. Inset: includes only measurements after 3

minute.

The presence of air (model III) instead of bone

inhibits propagation of heat, as air is less thermal

conductor, resulting higher temperature rise on the

heat source compared to the case of a normal hoof

composition (model I). However, in the case of

model II, the fluid is more thermal conducting than

hoof which enhance heat conduction resulting lower

temperature on the source. The clear distinction

between the three curves in fig. 4 occurred due to the

presence of different composition in the hoof

structure. Thus, comparing the transient curve of a

particular hoof with the one obtained from a healthy

hoof, it is possible to predict the intactness of a

given hoof.

4 EXPERIMENTAL WORK

The experiment part of this study consist of thermal

profiling using a transient plane source technique

called hot disk method (Gustafsson, 1991). It is an

ISO standard technique for testing thermal transport

properties of materials (ISO22007, 2008). The

technique works by using a sensor that can supply

constant heat source to the hoof and simultaneously

record the change in temperature. The thermal

conductivity of the material is calculated from the

recorded temperature. The hot disk thermal

constants analyser can detect temperature

differences with an accuracy better than 0.1 mK by

utilising highly sensitive components (ISO22007,

2008). The sensor is made from double spiral nickel

wire covered with thin polymer, kapton, fig. 5.

A special application of hot disk technique enables

to approximate the thermal conductivity of the

material along the heat wave penetration depth

(Mihiretie, 2016), fig. 6.

Figure 5: A hot disk sensor. Spiral wire nickel covered

with polymer kapton.

Applying this technique to horse hoof requires to

place the sensor on the hoof surface and record the

change in temperature on the sensor as current pass

through the sensor. Such experimental profiling was

performed on conserved dead horse hoof. To keep

the hoofs preserved all the measurements were

performed in a fridge with a temperature of around 7

degrees Celsius.

Figure 6: Thermal conductivity profile of conserved hoof.

This hoof capsule is about 7 mm thick. Repetitive

measurements are reproducible.

The experimental work was realized on a healthy

conserved horse hoof. It reveals the hoof profile.

The thermal conductivity plot demonstrate that the

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

174

hoof capsule has higher thermal conductivity than

the bone. The thermal conductivity starts to decrease

as the heat wave reaches the bone structure. This

gradual drop instead of sharp change at the interface

is due to the fact that the calculation method uses an

averaging technique. It is also worth to note that

information about the part near the outer wall is

missing due to interference from thermal contact

resistance.

Experimental and modelling parameters were

designed to be equivalent to each other, for instance

the double spiral nickel wires were represented by

concentric circles in the simulation. However, direct

comparison between experiment and simulation is

left for future work. This requires the simulation to

be expressed in terms of thermal conductivity

instead of transient curve. The work is in progress

with this aspect.

5 CONCLUSION

In this article, a computational model supported by

experimental work to thermally profile horse hoof is

presented. The findings from the simulation show

that by using the temperature rise curve of the heat

source one can monitor the structural composition of

the hoof. It is also possible to differentiate between

wall separation and a fluid contained in the hoof by

comparing with the transient of a normal hoof. The

experimental measurement revealed the hoof

structure.

REFERENCES

Gerlich, V., Sulovská, K., and Zálešák, M., 2013.

COMSOL Multiphysics validation as simulation

software for heat transfer calculation in buildings:

Building simulation software validation. Measurement

46, 2003–2012.

Gustafsson, S. E., 1991. Transient plane source techniques

for thermal conductivity and thermal diffusivity mea-

surements of solid materials. Rev. Sci. Instrum. 62, 3.

Gustavsson, M., Karawacki, E., and Gustafsson, S. E.,

1994. Thermal conductivity, thermal diffusivity and

specific heat of thin samples from transient

measurements with hot disk sensors. Rev. Sci.

Instrum. 62, 12.

Ibarra-Castanedo, C., Tarpani, J., and Maldague, X. P. V.,

2013. Nondestructive testing with thermography. Eur.

J. Phys. 34, S91-S109.

ISO 22007-2:2008. Plastics - Determination of thermal

conductivity and thermal diffusivity - Part 2: Transient

plane heat source (hot disc) method.

Mihiretie, B., Cederkrantz, D., Karlsteen, M., Sundin, M.,

Rosen, A., Otterberg, H., Hinton, Å., Berg, B., 2016.

Thermal depth profiling of materials for defect

detection using hot disk technique. AIP Advances, 6,

085217.

Moyer, W., 2003. Hoof wall defects: chronic hoof wall

separations and hoof wall cracks. Vet Clin Equine, 19,

463 – 477.

Sizov, A., Cederkrantz, D., Salmi, L., Rosén, A.,

Jacobson, L., Gustafsson, S. E., and Gustavsson, M.,

2016. Thermal conductivity versus depth profiling of

inhomogeneous materials using the hot disc technique.

Rev. Sci. instrum. 87, 074901.

Suarez, V., Hernández Wong, J., Nogal, U., Calderón, A.,

Rojas-Trigos, J.B., Juárez, A.G., Marín, E., 2014.

Study of the heat transfer in solids using infrared

photothermal radiometry and simulation by COMSOL

Multiphysics. Applied Radiation and Isotopes 83, 260–

263.

Tabatabaian, M., 2014. COMSOL for Engineers. Mercury

Learning and Information.

Van Nassau, R., 2004. Hoof problems: Hoof Construction,

Trimming and Shoeing, Hoof problems and solutions.

Kenilworth Press.

Numerical Simulation and Experimental Scheme for Monitoring Hoof Wall Structure and Health in Sport Horses

175