DynaGrow – Multi-Objective Optimization for Energy Cost-efﬁcient

Control of Supplemental Light in Greenhouses

Jan Corﬁxen Sørensen

, Katrine Heinsvig Kjaer

, Carl-Otto Ottosen

and Bo Nørregaard Jørgensen

The Maersk Mc-Kinney Moller Institute, University of Southern Denmark, Campusvej 55, 5230 Odense M, Denmark

Department of Horticulture, Aarhus University, Kirstinebjergvej 10, 5792 Aarslev, Denmark

Keywords:

Multi-Objective Optimization, Greenhouse Climate Control, Supplemental Light, Weather Forecast, Electric-

ity Cost, Decision Support, Energy Saving.

Abstract:

The Danish greenhouse horticulture industry utilized 0.8 % of the total national electricity consumption in

2009 and it is estimated that 75 % of this is used for supplemental lighting. The increase in energy prices is

a challenge for growers, and need to be addressed by utilizing supplemental light at low prices without com-

promising the growth and quality of the crop. Optimization of such multiple conﬂicting objectives requires

advanced strategies that are currently not supported in existing greenhouse climate control systems. It is costly

to incorporate advanced optimization functionality into existing systems as the software is not designed for

such changes. The growers can not afford to buy new systems or new hardware to address the changing

objectives. DynaGrow is build on top of existing climate computers to utilize existing infrastructure. The

greenhouse climate control problem is characterized by non-linearity , stochasticity, non-convexity, high di-

mension of decision variables and an uncertain dynamic environment. Together, these mathematical properties

are handled by applying a Multi-Objective Evolutionary Algorithm (MOEA) for discovering and exploiting

critical trade-offs when optimizing the greenhouse climate. To formulate advanced objectives, DynaGrow

integrates local climate data, electricity energy price forecasts and outdoor weather forecasts. In spring 2015,

one greenhouse experiment was executed to evaluate the effects of DynaGrow. The experiment was run as

three treatments in three identical greenhouse compartments. One treatment was controlled by a standard con-

trol system and the other three treatments were controlled by different DynaGrow conﬁgurations. A number

of different plant species and batches were grown in the three treatments over a season. The results from

DynaGrow treatment demonstrated that it was clearly possible to produce a number of different sales-ready

plant species and at the same time optimize the utility of supplemental light at low electricity prices without

compromising product quality.

1 INTRODUCTION

In 2009, Danish horticulture industry consumed 0.8

% of the total national electricity and 75 % of this

consumed energy was estimated to come from sup-

plemental light alone.

Several countries are at present time in a transition

towards non-fossil renewable energy sources such as

wind turbines. The large contribution of energy from

renewable energy sources results in irregular electric-

ity production, that leads to ﬂuctuation in the elec-

tricity prices. An increased electricity price is a chal-

lenge for the horticulture industry that is positioned in

a highly competitive market. A spot market electricity

price structure has been introduced in the Scandina-

vian countries to provide an incentive for industry to

utilize energy in cost effective hours where the supply

of energy is plentiful (Nord Pool, 2016).

Existing ﬁxed rate supplemental light control

strategies are in contradiction to the ﬂexible price

structure. Fixed rate light-plans often consume en-

ergy at hours that are costly. The ﬁxed rate strate-

gies only plan according to the ﬁxed time periods

and do not take price structures into account. How-

ever, changing the light patterns may have severe ef-

fects on how the cultivar reacts. For example, neg-

ative effects could be bud dormancy, delayed leaf

development, stem elongation, late seed germination

and early ﬂower initiation (Thomas and Vince-Prue,

1997). Hence, there is a need to optimize the util-

ity of supplemental light to ensure that the light-plans

represent the cheapest electricity prices and promote

Sørensen, J., Kjaer, K., Ottosen, C-O. and Jørgensen, B.

DynaGrow – Multi-Objective Optimization for Energy Cost-efﬁcient Control of Supplemental Light in Greenhouses.

DOI: 10.5220/0006047500410048

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 41-48

ISBN: 978-989-758-201-1

a high quality of the produced cultivar.

This paper proposes a system DynaGrow that in-

tegrates local climate data, electricity price and out-

door weather forecasts to formulate advanced control

objectives. The core of the system is a customized

Multi-Objective Evolutionary Algorithm (MOEA),

that searches for coordinated Pareto-optimal light-

plans that fulﬁl the speciﬁed climate control objec-

tives. DynaGrow is a features-oriented software sys-

tem divided into a number of features. Each feature

encompasses an individual unit of software function-

ality and is implemented as loosely coupled plug-in

modules. The feature-oriented separation of Dyna-

Grow makes it relatively strait-forward to integrate to

existing hardware devices and conﬁgure the system to

optimize different objectives. Each set of objectives

are strictly separated and can be conﬁgured to fulﬁll

the speciﬁc climate control requirements given by the

problem domain. Present time, DynaGrow supports

two different climate control hardware platforms and

support 37 different objectives (Sørensen et al., 2011).

Related work is shortly summarized in Section 2

Section 3 describes the different elements of Dyna-

Grow and how they are connected. The most impor-

tant control objectives optimized in the presented ex-

periment, are formulated and detailed in Section 4.

How the DynaGrow core is implemented as a genetic

MOEA is described in Section 5. Section 6 describes

the experiment that evaluate DynaGrow by growing

three different cultivars based on three different cli-

mate control settings. The results of the experiment is

described in Section 7. Next, the discussion reﬂects

on how well DynaGrow optimized the identiﬁed ob-

jectives of the climate control problem. Last, Sec-

tion 9 summarizes the article.

2 RELATED WORK

Research literature describes independent models that

can contribute to an optimized greenhouse production

and cut the energy consumption through development

of intelligent control strategies. Aaslyng et. al created

the foundation for a component-based climate con-

trol system IntelliGrow that optimizes the greenhouse

climate (Aaslyng et al., 1996). The results showed

that it was possible to reduce energy consumption by

more than 20 %. Subsequently, there have been sev-

eral projects in which the models and control strate-

gies have been optimized (Aaslyng et al., 1999; Lund

et al., 2006). The IntelliGrow concept is documented

by Aaslyng et al. in (Aaslyng et al., 2005). Kjaer et

al. developed the DynaLight system that provides a

search-based approach to ﬁnd the most cost-efﬁcient

use of supplemental light, based on a predeﬁned set-

point of Daily Photosynthesis Integral (DPI), fore-

casted solar light and the spot-market electricity price

(Kjaer and Ottosen, 2011; Kjaer et al., 2012; Clausen

et al., 2012). The DynaLight algorithm is tightly in-

tegrated with the weather and electricity forecast ser-

vices and does not support optimization multiple ob-

jectives.

None of the mentioned approaches support Pareto

optimization of multiple independently developed ob-

jectives, to generate a coordinated set of setpoints that

can be effectuated by the greenhouse climate control

system. DynaGrow is the only approach that supports

optimization of multiple objectives that are based on

weather and electricity price forecasts.

3 DynaGrow

DynaGrow is designed to control climate-related

growth factors by sensing and manipulating the

greenhouse climate through the use of sensors and ac-

tuators. The physical setting of DynaGrow is a com-

bination of a control machine, a number of connection

domains and a controlled domain (Figure 1). The con-

trol machine consists of the DynaGrow software run-

ning on a PC, that is connected to a set of climate con-

trollers. The climate controllers are connected to sen-

sors and actuators (Connection Domains) that interact

with the indoor climate of the greenhouse (Controlled

Domain). A connection domain can act as a sensor

or an actuator. Sensors provide measured input infor-

mation m in form of input variables i to the control

machine. Contrary, actuators inﬂuence the physical

phenomenon c in the controlled domain according to

output variables o provided by the machine.

Control Machine

Controlled Domain

Connection Domains

Sensors (S)

Actuators (A)

Environment (E)

DynaLight NG

Controller

Figure 1: DynaGrow system overview.

The output of DynaGrow is determined by the

system’s control objectives that typically incorporates

models of the physical environment. For example, a

model of the photosynthesis process of a given plant

in a greenhouse. Control objectives are formulated

over a set of input variables i and output variables

o, connecting the control machine with the connected

domains. The control objectives are evaluated contin-

uously in cycles by the machine, and is integrated into

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

the control process. Each cycle is triggered at speciﬁc

time intervals. For each control cycle, the system per-

ceives the environment through its sensors variable i,

optimizes the control objectives and changes the en-

vironment through its actuators to obtain the desired

objective of the system. The result of a control cy-

cle is a set of output variables o (setpoints) that are

written to the actuators.

The control objectives are optimized using the

CONTROLEUM-GA to guarantee a Pareto optimal

trade-off between the multiple control objectives

within computational tractable time (Ghoreishi et al.,

2015). The CONTROLEUM-GA is a multi-objective

genetic algorithm that incorporates domain speciﬁc

variables and operators to solve dynamic optimiza-

tion problems. The support for domain speciﬁc vari-

ables and operators, enable the algorithm to converge

fast enough to optimize a larger number of objectives

within each optimization cycle of DynaGrow.

4 OBJECTIVES

This section describes the most important objectives

optimized in the DynaGrow experiment described in

this article. Each control objective function can be

formulated either as a minimization cost function or

as a constraint. The objective function evaluates op-

tions proposed by the MOEA during the optimization

process. The option argument is passed over by the

MOEA and is a data-structure that contains a set of

input variables i and output variables o that connects

the control machine to the connection domains. In

the pseudo-code, variables starting with an upper case

letter represent information from the option provided

by the MOEA. Lower case variables represent result

variables used in the objective function.

SPARBAL(option)

1 lightPlanSum = CALCPARSUM(LightPlan,LampPAR)

2 balance =

5 ×ParDLI −(ParHist + ParFuture + lightPlanSum)

3 return balance

The PAR Light Sum Balance objective

(SPARBAL) minimizes a Photosynthetically Ac-

tive Radiation (PAR) sum balance, see Line 2. PAR

designates the spectral wave band of solar radiation

from 400 to 700 nanometers that photosynthetic

organisms are able to utilize for photosynthesis. The

balance is calculated over a ﬁve days time-window

deﬁned by current day, two days in the past and

two days in the future. The PAR Integral Today

and Past Two Days (ParHist) input is derived from

historical data stored by DynaGrow. Data for the

Expected Natural PAR Sum Remaining Day and

Future Two days (ParFuture) input is provided by

Conwx Intelligent Forecast Systems (Conwx, 2016).

The PAR Day Light Integral (ParDLI) input speciﬁes

the average goal to be achieved over the ﬁve days

period and is provided by the grower. The total light-

plan PAR sum (lightPlanSum) variable is calculated

based on the Installed Lamp PAR (LampPAR) input

and the number of suggested light intervals in the

LightPlan output. The balance is then calculated

as the difference between the provided goal and the

total of ParHist, ParFuture and the lightPlanSum.

At the end of each day, the ParHist input will be

updated with data from the past days. Similarly, the

ParFuture input will be updated with data from next

day. That is, the balance is calculated based on a ﬁve

days sliding window.

SCHEAPLIGHT(option)

1 cost =

∑

i=1

LightPlan.Switch

× ElForecasts.Price

(TotalLoad × LpTimeslot

)

2 return cost

The Prefer Cheap Light objective

(SCHEAPLIGHT) is speciﬁed as a cost func-

tion that minimizes the price of the Light-plan

(LightPlan) based on El. Spot and Prognosis Prices

(ElCompPrices). The electricity spot market price

forecast is provided by Nord Pool and the longer

three day prognosis is provided by Energi Danmark

(Nord Pool, 2016; Energi Danmark, 2016). The

Total Lamp Load (TotalLoad) is calculated as the

Installed Lamp Effect (InstLampEffect) multiplied

by the Greenhouse Size (GreenhouseSize). The

index i is the time-slot index of the LightPlan. For

each light time-slot i, the sub-cost is calculated as

the Total Lamp Load (TotalLoad) multiplied by the

light-plan time-slot interval T

and the electricity price

ElForecasts.Price

. The total cost of the Light-plan

(LightPlan) is then the sum of all the sub-costs for

each of the light intervals (LightPlan.Switch

). The

LightPlan.Switch

is zero for light switched off and

one for when the supplemental light is lit.

5 IMPLEMENTATION

The CONTROLEUM-GA function shows the pseudo-

code for the genetic algorithm implementation used

by the core of DynaGrow. Note that the line numbers

break and continue in places where sub-functions are

called from CONTROLEUM-GA ().

DynaGrow – Multi-Objective Optimization for Energy Cost-efﬁcient Control of Supplemental Light in Greenhouses

CONTROLEUM-GA(time,oldPop)

1 if oldPop.isNotEmpty

2 for each oldSolution ∈ oldPop

3 ADD-NONDOMSOLUTION(

COPY(time, solution))

4 for i = 0 to POPSIZE

5 ADD-NONDOMSOLUTION(D-INIT(time))

17 while isNotTerminated

18 for i = 0 to i ≤ POPSIZE

19 if RANDOM-DOUBLE() < MUTATIONRATE

20 child = S-MUTATE(RANDOM(pop))

27 else

28 child = S-CROSSOVER(RANDOM(pop),

RANDOM(pop))

34 ADD-NONDOMSOLUTION(child)

The CONTROLEUM-GA function has two argu-

ments: 1) a time-stamp time for when the algorithm

is executed, and 2) the population oldPop from previ-

ous executions. The time-stamp time is used for dy-

namic optimization problems that use the start time of

the optimization. The algorithm is separated into the

following phases: Initialization, Ranking, Mutation,

Crossover and Termination.

Initialization: A population consist of a number of

non-dominated Pareto optimal solutions. Each so-

lution is represented by a data-structure that has a

collection of objective results solution.objectives and

decision variables solution.variables. A solution can

have multiple different types of domain speciﬁc vari-

ables; e.g., temperature, CO

and light-plan. In this

work we focus on the light-plan variable. Line 1

checks if the previous population oldPop is empty.

The population oldPop is empty the ﬁrst time the al-

gorithm is executed. If the population oldPop exists

from previous executions, it is copied into the new

non-dominated population pop (Line 3). A domain

speciﬁc initialization operator D-INIT is implemented

for each type of decision variable (Line 5). For exam-

ple, the supplemental light-plan is initialized by the

domain speciﬁc initialization operator that is an im-

plementation of the D-INIT function. For example the

different time resolutions of light-plans are encoded

in the light-plan variable.

CONTROLEUM-GA Line 17 test if the evolution

should terminate. Evolution is terminated after a

speciﬁed time limit, after a number of generations or

when the population is stable.

Ranking: The function ADD-

NONDOMSOLUTION sorts all solutions in the

population pop according to the Pareto domi-

nance relation (Line 8). That is, the objectives

are ranked given the proposed decision variables

solution.variables. The results of the evaluations are

assigned to the objective values solution.objectives

for each proposed solution. Only non-dominated

solutions are added to the population pop.

ADD-NONDOMSOLUTION(newSolutionA)

6 for each oldSolutionB ∈ pop

7 ﬂag =

8 PARETO-COMPARE(newSolutionA, oldSolutionB)

9 if f lag

= =

ADOMINATESB

10 REMOVE(oldSolutionB,pop)

11 elseif f lag

= =

BDOMINATESA

12 return f alse

13 elseif DISTANCE(newSolutionA, oldSolutionB) < EPS

14 return f alse

15 ADD(newSolutionA, pop)

16 return true

The function PARETO-COMPARE compares

if a solution newSolutionA dominates a solution

oldSolutionB or visa verse. If solution newSolutionA

dominates solution oldSolutionB then solution

oldSolutionB is removed from the population pop

(Line 10). Contrary, if solution oldSolutionB domi-

nates solution newSolutionA then it is not added to the

population pop (Line 12). Two solutions are deﬁned

as the same, if the Euclidean DISTANCE between

two solutions in the objective space, is less than the

level of signiﬁcance deﬁned by constant EPS. In case

newSolutionA is the same as oldSolutionB then it is

not added to the population pop (Line 14).

Mutation: For each generation, solutions are ran-

domly selected a number of times for mutation. The

number of mutations is determined by the constants

MUTATIONRATE and POPSIZE. For example, if

POPSIZE is 100 and MUTATIONRATE is 50 % then

50 randomly selected solutions are mutated. If a mu-

tation results in a non-dominated solution then it is

added to the population pop.

S-MUTATE(solution)

21 i = RANDOM-INT()

22 solution. variables[i] = D-MUTATE(solution.variables[i])

Mutation is applied at solution level and domain

variable level. At solution level a random decision

variable is selected for mutation in Line 21 using a

generic uniform mutation (UM) operator. Each de-

cision variable has its own domain speciﬁc mutation

operator D-MUTATE. The D-MUTATE operator is ap-

plied on the randomly selected variable in Line 22.

D-MUTATE-LIGHT shows the implementation of D-

MUTATE for a light plan variable. The selected light

plan variable is copied and a randomly selected index

in the plan is negated. That is, if the light state for the

selected index was ON, then after mutation it will be

set to OFF.

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

D-MUTATE-LIGHT(lightPlan)

23 l p = COPY(lightPlan, TIMEINTERVAL)

24 i = RANDOM-INT(l p. size)

25 l p[i] = ¬l p[i]

26 return l p

Implementations of D-MUTATION operators in-

corporate domain knowledge to ensure that the val-

ues of the decision variables are always viable. In

case of the light plan variable, the D-MUTATION-

LIGHT incorporate knowledge about time-resolution

and which index of the light plan that is viable for

change (Line 23 and 24). For example, if a light inter-

val only can change once for a given period of time, or

if a light state is always ﬁxed, then it is implemented

in the implementation of the D-MUTATE function for

the given variable. Each domain mutation operator

deﬁnes a range for a speciﬁc type of decision variable

(temperature, energy, CO

, etc.). The intersection of

these ranges deﬁnes the viability space of the decision

variable.

Crossover: Solutions are randomly selected for

crossover for a number of iterations. The number

of crossover iterations is determined by the constant

POPSIZE. Crossover is applied at solution and deci-

sion variable level. The solution level crossover func-

tion S-CROSSOVER is called in CONTROLEUM-GA

Line 28.

S-CROSSOVER(solutionA,solutionB)

29 i = RANDOM-INT(solutionA. variables. size)

30 solutionA. variables[i] =

D-CROSSOVER(solutionA.variables[i],

solutionB. variables[i])

31 for j = i + 1 to j < solutionA.variables. size − 1

32 solutionA. variables[ j] = solutionB.variables[ j]

33 return solutionA

Random variables from two solutions solutionA

and solutionB are selected for crossover at decision

variable level using a generic one-point crossover op-

erator (Line 29,30). At the other variables from the

selected index i + 1 till last index from solutionB is

copied to solutionA.

The domain speciﬁc D-CROSSOVER operator is

applied on the selected decision variables in Line 30.

The D-CROSSOVER function is the domain speciﬁc

crossover operator for two light plans lightPlanA

and lightPlanB. In the DynaGrow experiment, the

two light plans are crossed by a standard one-point

crossover operator but more complex outputs requires

more knowledge encoded into the output datastruc-

ture.

6 EXPERIMENT

In February 2015 a greenhouse experiment was exe-

cuted to evaluate the cost effectiveness and the quali-

ties of the DynaGrow software. The experiment was

executed as three treatments in three identical green-

house compartments. The ﬁrst treatment (S SON-T)

was executed by a standard control system with SON-

T lamps and ﬁxed day length of 18 hours. The sec-

ond treatment (DG SON-T) was equipped with SON-

T lamps but controlled by DynaGrow. The third treat-

ment (DG LED) was equipped with LED lamps and

was controlled by DynaGrow. For both the Dyna-

Grow compartments the control cycle was set to 5

minutes.

The PAR Day Light Integral provided by natural

light was on average approximately 12 mol m

−2

−1

and the DLI goal for all of the evaluated control strate-

gies was set to 8 mol m

−2

−1

The cost of the energy, used for supplemental

light, was calculated based on when the light was lit

and the price of electricity for that speciﬁc time. The

electricity prices was for the west part of the Danish

electricity grid (DK1). Each compartment is 76 m

and in the SON-T compartments there is 16 lamps in-

stalled. A SON-T lamp has an effect of 600 Watt.

That is, the installed effect for the SON-T compart-

ments is (16 × 600 W )/76 m

= 126 W /m

. In com-

parison, a LED lamp has an effect of 190 W and the

LED compartment has 38 LED lamps installed. The

total installed effect for the LED compartment is then

(38 × 190 W )/76 m

= 95 W /m

The granularity of the SON-T light-plans was

set to one hour due the physical properties of the

lamps. A SON-T lamp can not tolerate to be switched

ON/OFF to often due to heating. The granularity of

the LED light-plans was set to 15 minutes as LED

lamps tolerate to be lit in short intervals.

Roses, Kalanchoe and Chili batches were grown

in the three treatments over the season, to evaluate the

effect of the different light-plans. The cultivars were

harvested a maturation, meaning that plants from the

different treatments were sometimes harvested at dif-

ferent times.

7 RESULTS

Figure 2 illustrates the light-plans, effectuated for

each of the compartments, together with the electric-

ity prices provided from the Nord Pool power spot

market (Nord Pool, 2016). The light-plan for the S

SON-T compartment has ﬁxed rates as expected from

the standard ﬁxed rate light control strategy.

DynaGrow – Multi-Objective Optimization for Energy Cost-efﬁcient Control of Supplemental Light in Greenhouses

El [EUR/MWh]

Plan [ON/OFF]

Feb 05 Feb 12 Feb 19 Feb 26

(a) Standard SON-T

El [EUR/MWh]

Plan [ON/OFF]

Feb 05 Feb 12 Feb 19 Feb 26

(b) DynaGrow SON-T

El [EUR/MWh]

Plan [ON/OFF]

Feb 05 Feb 12 Feb 19 Feb 26

Figure 2: Comparison of light-plans optimized by different

strategies in February 2015.

Figure 2a shows that the ﬁxed rate light-plan

clearly requires supplemental light at hours where the

electricity price is high.

In contrast, the DG SON-T light-plan is quite dif-

ferent to the S SON-T light plan. Figure 2b illustrates

the DG SON-T light-plan for the same experiment

period. The DG SON-T light-plan has the same

one hour granularity as the S SON-T light-plan but

expensive supplemental light hours are avoided. That

is, the CONTROLEUM-GA has clearly optimized the

SCHEAPLIGHT objective in order to generate

the DG SON-T light-plan.

The DG LED light-plan is similar to the DG SON-

T light-plan as both light-plans are optimized by same

MOEA with same objectives, see Figure 2c. The dif-

ferences between the DG SON-T and DG LED light-

plans are the granularity of the generated light-plans

and the energy consumed by the different type of

lamps. The ﬁner granularity (15 minutes) of the DG

LED light-plans can be observed February 20-23 in

Figure 2c.

Table 1: Energy results of the experiment February 2015.

Control Energy

[KWh]

Energy

[%]

Cost

[e ]

Cost

[%]

S SON-T 4139.2 100 127.0 100

DG SON-T 2482.6 40 62.4 51

DG LED 1828.5 56 45.3 64

Table 1 provides a summary of the experimental

energy results for February 2015. The total energy

consumed by the S SON-T treatment (control) was

4139.2 KW h and was set as the reference. The DG

SON-T the DG LED treatments consumed 40 % and

56 % less energy compared to the reference, respec-

tively. Furthermore, the total cost of S SON-T light-

plan (reference) was 127 e. The DG SON-T and LED

treatments was 51 % and 64 % cheaper than the ref-

erence, respectively.

Table 2: Light hours and DLIs of the experiment February

2015.

Control Average

DLI

[mol

−2

−1

]

DLI

[%]

Suppl.

Light

hours

[h]

Suppl.

Light

[%]

S SON-T 8.5 100 432.3 100

DG SON-T 6.5 19 259.3 40

DG LED 6.5 19 253.3 41

Table 2 shows the experimental DLI results for the

three compartments in February 2015. For the refer-

ence S SON-T treatment, supplemental light was lit in

432.3 hours. In comparison, supplemental light was

lit for 259.3 and 253.3 for the DG SON-T and DG

LED treatments, respectively. That is, the DG SON-

T and DG LED treatments had respectively 40 % and

41 % less supplemental light hours than the reference.

The DLI goal for each treatment was 8 mol m

−2

−1

Additionally, the average DLI for the S SON-T treat-

ment was higher than the DG SON-T and DG LED

treatments. The two DynaGrow treatments obtained

the same average DLI of 6.5 mol m

−2

−1

which is

19 % lower than the reference and 1.5 mol m

−2

−1

lower than the DLI goal.

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

DLI [mol m

-2

-1

]

Feb 05 Feb 12 Feb 19 Feb 26

(a) S SON-T

DLI [mol m

-2

-1

]

Feb 05 Feb 12 Feb 19 Feb 26

(b) DG SON-T and “DG LED”

Figure 3: PAR light sum comparison from tree experimental

compartments optimized by different strategies in February

2015.

Figure 3 shows the accumulated DLIs for each of

the treatments. The DG SON-T and DG LED DLIs

are similar but the S SON-T DLIs are in average

higher which corresponds to the results in Table 2.

The properties of the cultivars was reported for

Roses, Kalanchoe and Chili by measuring the rela-

tive growth rate (RGR), relative dry weight (RDW)

and the number of ﬂowers. In general the results

are reﬂecting that plant growth was related to the cli-

mate conditions of the treatments with species and

genotype-speciﬁc differences. All the plants grew

well in the three climates and reached maturation

within acceptable time. Figure 4 is pictures of Kalan-

choe (Simone) grown under the S SON-T (left), DG

SON-T (Middle) and DG LED (Right) treatments.

Further details about the results of growing the differ-

ent cultivars in irregular light conditions can be found

in work by Ottosen et al (Kjaer et al., 2012; Kjaer and

Ottosen, 2011; Kjaer et al., 2011). Last, is was con-

cluded that all the grown cultivars was in a sales-ready

quality.

Figure 4: Kalanchoe (Simone) as a result of the S SON-

T (left), DG SON-T (Middle) and DG LED (Right) treat-

ments.

8 DISCUSSION

The DG SON-T and LED treatments was 51 % and

64 % cheaper than the reference, respectively (Ta-

ble 1). In euro, that is a saving of 81.7 e per month

in the best case for a compartment of 76 m

. In Den-

mark, some industrial growers have greenhouse facil-

ities that is more than 65000 m

and the documented

energy saving can have a huge potential economical

impact. It’s important to emphasise that the price

calculation does not include rates for Public Service

Obligations (PSO), but is based purely on the spot

market prices and the theoretical installed effect in

each compartment.

Figure 5: Optimistic outdoor light forecast (bell curve) and

the actual outdoor light data for February 11-18.

The lower DG SON-T and DG LED DLIs was

not expected as similar effect (light intensity) should

have been installed in the S SON-T treatment. The

equal DG SON-T and DG LED DLIs indicate that

the optimization of PAR Light Sum Balance objec-

tive has been achieved but with a too low goal. A

reason for the lower DLI can be explained by the nat-

ural light forecast provided by the external service.

The cost calculation in the SPARBAL objective de-

DynaGrow – Multi-Objective Optimization for Energy Cost-efﬁcient Control of Supplemental Light in Greenhouses

pends on a precise outdoor light forecast, see SPAR-

BAL Section 3.

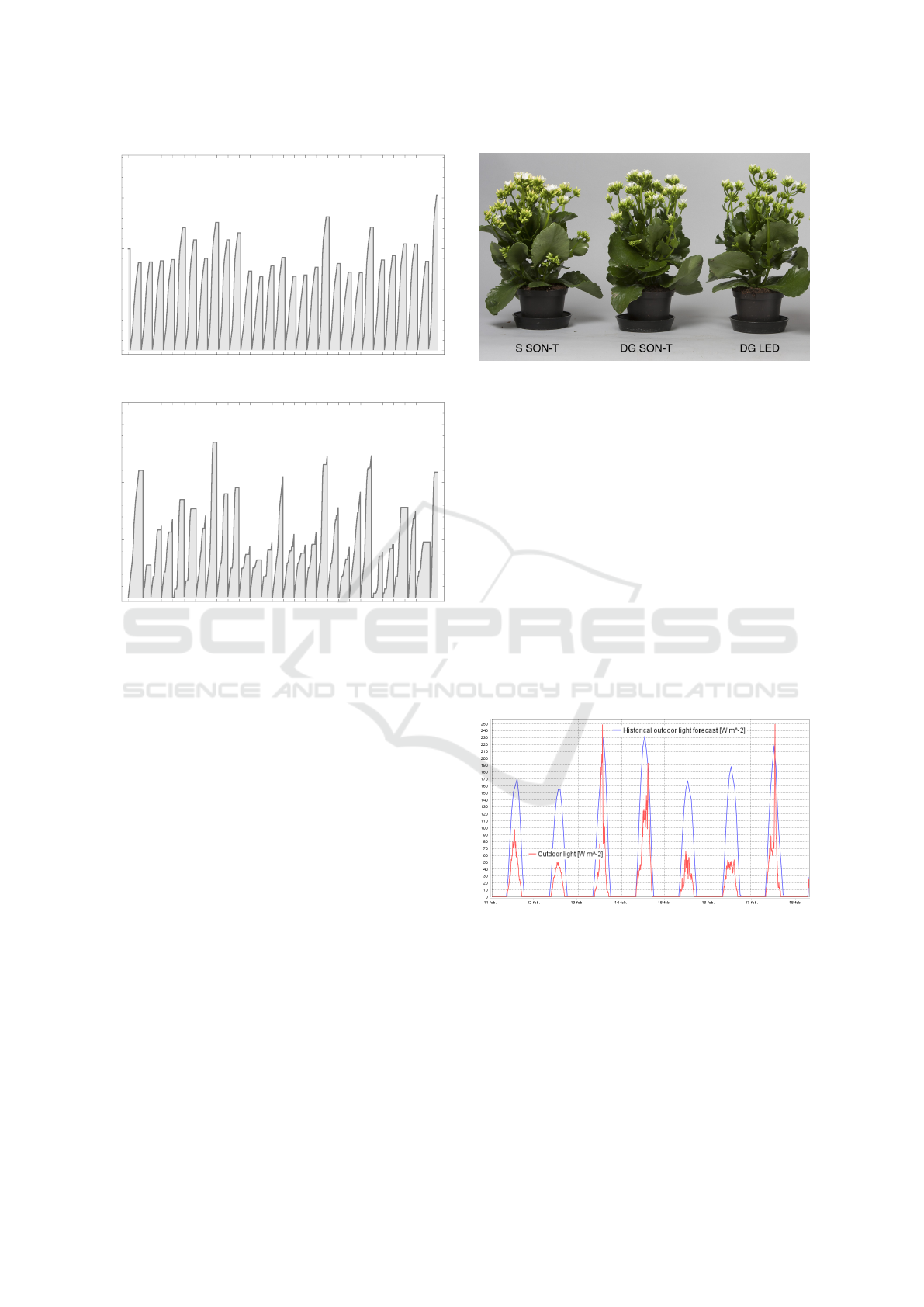
Figure 5 illustrates the time-series of the outdoor

light forecast and the actual outdoor light. The time-

series reveal that the outdoor light forecast has a ten-

dency to be too optimistic. An optimistic light fore-

cast will inﬂuence the sliding window balance in the

SPARBAL objective as the ParFuture will promise

more light than is the actual light. If the ParFuture

is optimistic over several days, like illustrated in the

time-series in Figure 5 (February 11-18), then the av-

erage of the ParDLI will never be achieved within the

sliding window. That is, the result will be a lower

average DLI as indicated by Table 2.

9 CONCLUSION

The increasing energy prices is a challenge for grow-

ers and need to be addressed by utilizing supplemen-

tal light when electricity prices are low and without

compromising the growth and quality of the crop. Op-

timization of such multiple conﬂicting objectives re-

quires advanced strategies that are currently not sup-

ported in existing greenhouse climate control sys-

tems.

The result of the winter experiment 2015 demon-

strates that DynaGrow utilizes supplemental light

at low electricity prices without compromising the

growth and quality of the crop compared to standard

ﬁxed rate supplemental light control. It was possible

to produce a number of different cultivars where the

supplemental light (SON-T or LED), the temperature

and CO

was controlled by the DynaGrow software.

The energy savings are achieved in relation to a con-

trol treatment with a ﬁxed day length, but only if the

DLI is comparable between the treatments.

In Denmark, DynaGrow will have a high impact

on cost in the beginning and end of the growing sea-

son, when there is a huge potential for optimizing the

supplemental light.

There is an unexplored potential to optimize the

utilization of supplemental light, temperature, CO

humidity and other climate variables simultaneously

by formulating multiple advanced control objectives

based on models already available from the extensive

horticultural literature.

The results clearly demonstrate, that DynaGrow

supports a dynamic climate control strategy by op-

timizing multiple control objectives that results in a

cost-effective control of the greenhouse climate.

REFERENCES

Aaslyng, J. M., Ehler, N., and Jakobsen, L. (2005). Climate

Control Software Integration with a Greenhouse En-

vironmental Control Computer. Environmental Mod-

elling and Software 20, 20(5):521–527.

Aaslyng, J. M., Ehler, N., Karlsen, P., Høgh-Schmidt, K.,

and Rosenqvist, E. (1996). Decreasing the Environ-

mental Load by a Photosynthetic based System for

Greenhouse Climate Control. Acta Horticulturae: In-

ternational Symposium on Plant Production in Closed

Ecosystems (ISHS), 1(440):105–110.

Aaslyng, J. M., Ehler, N., Karlsen, P., and Rosenqvist, E.

(1999). IntelliGrow: A Component-based Climate

control System for Decreasing the Greenhouse Energy

Consumption. Acta Horticulturae, (507):35–41.

Clausen, A., Soerensen, J. C., Jørgensen, B. N., Kjaer,

K. H., and Ottosen, C.-O. (2012). Integrating Com-

mercial Greenhouses in the Smart Grid with De-

mand Response based Control of Supplemental Light-

ing. International Conference on Agriculture, Envi-

ronment, Energy and Biotechnology(ICAEEB 2014).

Conwx (2016). Conwx intelligent forecasting systems.

http://www.conwx.com.

Energi Danmark (2016). Energi danmark electricity fore-

casts. http://www.energidanmark.dk.

Ghoreishi, S. N., Sørensen, J. C., and Jørgensen, B. N.

(2015). Enhancing State-of-the-art Multi-objective

Optimization Algorithms by Applying Domain Spe-

ciﬁc Operators. In IEEE Symposium on Computa-

tional Intelligence in Dynamic and Uncertain Envi-

ronments (IEEE CIDUE’15), page 8, Cape Town,

South Africa. IEEE Computational Intelligence Soci-

ety (CIS).

Kjaer, K. H. and Ottosen, C.-O. (2011). Growth of Chrysan-

themum in Response to Supplemental Light Provided

by IrregularLight Breaks during the Night. Journal

of the American Society for Horticultural Science,

136:3–9.

Kjaer, K. H., Ottosen, C.-O., and Jørgensen, B. N. (2011).

Cost-efﬁcient light control for production of two cam-

panula species. Scientia Horticulturae, 129(4):825–

831.

Kjaer, K. H., Ottosen, C.-O., and Jørgensen, B. N. (2012).

Timing growth and development of Campanula by

daily light integral and supplemental light level in a

cost-efﬁcient light control system. Scientia Horticul-

turae.

Lund, J. B., Rosenqvist, E., Ottosen, C. O., and Aaslyng,

J. M. (2006). Effect of a Dynamic Climate on En-

ergy Consumption and Production of Hibiscus rosa-

sinensis L. in Greenhouses. HortScience, 41(2):384–

388.

Nord Pool (2016). Nord pool spot market electricity prices.

http://www.nordpoolspot.com.

Sørensen, J. C., Jørgensen, B. N., Klein, M., and De-

mazeau, Y. (2011). An agent-based extensible cli-

mate control system for sustainable greenhouse pro-

duction. Agents in Principle, Agents in Practice, 14th

International Conference, PRIMA 2011, Wollongong,

Australia, 7047:218–233.

Thomas, B. and Vince-Prue, D. (1997). Photoperiodism in

Plants. Elsevier Science Direct.

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications