
A New Distance on a Specific Subset of Fuzzy Sets
Majid Amirfakhrian
Department of Mathematics, Central Tehran Branch, Islamic Azad University, Tehran, Iran
Keywords:
Fuzzy Sets, Fuzzy Numbers, Fuzzy LR Sets, Generalized LR Fuzzy Number, Value, Ambiguity.
Abstract:
In this paper, first we propose a definition for fuzzy LR sets and then we present a method to assigning distance
between these form of fuzzy sets. We show that this distance is a metric on the set of all trapezoidal fuzzy sets
with the same height and all trapezoidal fuzzy numbers and is a pseudo-metric on the set of all fuzzy sets.
1 INTRODUCTION
There are lots of works that the authors investigated
fuzzy sets, in order to find the nearest approximation
of an arbitrary fuzzy numbers. Approximation of a
fuzzy number can be done in three ways. Some au-
thors assigned a single crisp number to a fuzzy num-
ber as a ranking method. In this case many infor-
mation of the fuzzy number will be lost. The other
method is using an interval as an approximations of a
fuzzy number (Chanas, 2001; Grzegorzewski, 2002),
But, in this case, the modal value (the core with height
1) of the fuzzy number will be lost. In some works
such as (Abbasbandy and Asady, 2004; Delgado et al.,
1998; Grzegorzewski and Mr ´owka, 2005), the authors
tried to solve an optimization problem in order to ob-
tain a trapezoidal fuzzy number as a nearest approxi-
mation. Some works were done on approximation of
a fuzzy number (Anzilli et al., 2014; Ban et al., 2011;
Cano et al., 2016). Some distances and their prop-
erties were done in (Abbasbandy and Amirfakhrian,
2006a; Abbasbandy and Amirfakhrian, 2006b).
In this work we introduce a fuzzy LR set and we
present a distance to find the nearest trapezoidal fuzzy
set to an arbitrary LR fuzzy set. The motivation be-
hind this distance is trying to compare fuzzy sets of
special format and the same height.
The structure of the this paper is as follows. In
Section 2 the basic concepts of our work are intro-
duced, then we introduce LR fuzzy set. In Section 3
we introduce a distance over all fuzzy LR sets with
the same height and we named it h-source distance,
which is a metric on the set of all trapezoidal LR fuzzy
set, with the same height. In Section 4 the nearest
trapezoidal fuzzy number to an arbitrary trapezoidal
LR fuzzy set was introduced and a simple method for
computing it, was presented. Section 5 contains some
numerical examples.
2 PRELIMINARIES
Let F(R) be the set of all normal and convex fuzzy
numbers on the real line.
Definition 2.1. A generalized LR fuzzy number ˜u
with the membership function µ
˜u
(x),x ∈R can be de-
fined as
µ
˜u
(x) =
l
˜u
(x) , a ≤ x ≤ b,
1 , b ≤ x ≤ c,
r
˜u
(x) , c ≤ x ≤ d,
0 , otherwise,
(2.1)
where l
˜u
(x) is the left membership function that is
an increasing function on [a,b] and r
˜u
(x) is the right
membership function that is a decreasing function on
[c,d]. Furthermore we want to have l
˜u
(a) = r
˜u
(d) = 0
and l
˜u
(b) = r
˜u
(c) = 1. In addition, if l
˜u
(x) and r
˜u
(x)
are linear, then ˜u is a trapezoidal fuzzy number which
is denoted by (a,b,c, d). If b = c, we denoted it by
(a,c, d), which is a triangular fuzzy number.
For 0 < α ≤ 1; α-cut of a fuzzy number ˜u is de-
fined by,
[ ˜u]
α
= {t ∈ R | µ
˜u
(t) ≥ α}. (2.2)
Definition 2.2. (Voxman, 1998), A continuous func-
tion s : [0,1] −→[0, 1] with the following properties is
a regular reducing function :
1. s(r) is increasing.
2. s(0) = 0,
3. s(1) = 1,
4.
R
1
0
s(r)dr =
1
2
.
Amirfakhrian, M.
A New Distance on a Specific Subset of Fuzzy Sets.
DOI: 10.5220/0006047900830087
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 83-87
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
83

In (Chong-Xin and Ming, 1991), the authors rep-
resented a fuzzy number ˜u by an ordered pair of func-
tions (u(r), u(r)):
The parametric form of a fuzzy number is shown
by ˜v = (v(r),v(r)), where functions v(r) and v(r); 0 ≤
r ≤ 1 satisfy the following requirements:
1. v(r) is monotonically increasing left continuous
function.
2. v(r) is monotonically decreasing left continuous
function.
3. v(r) ≤ v(r) , 0 ≤ r ≤ 1.
4. v(r) = v(r) = 0 for r < 0 or r > 1.
Definition 2.3. (Voxman, 1998), The value and am-
biguity of a fuzzy number ˜u are defined by
Val( ˜u) :=
Z
1
0
s(r)[u(r) + u(r)]dr, (2.3)
and
Amb( ˜u) :=
Z
1
0
s(r)[u(r) −u(r)]dr, (2.4)
respectively.
Definition 2.4. A fuzzy set ˜u is a generalized LR
fuzzy set, if there exist a positive number h ∈ (0,1]
such that
µ
˜u
(x) =
l(x), a ≤ x ≤ b,
h, b ≤ x ≤ c,
r(x), c ≤ x ≤d,
0, otherwise.
(2.5)
where l(x) is nondecreasing on [a,b] and r(x) is
nonincreasing on [c,d] such that l(a) = r(d) = 0 and
l(b) = r(c) = h. If h = 1 then ˜u is an LR fuzzy number.
In addition, if l(x) and r(x) are linear, then
˜u is a trapezoidal fuzzy set which is denoted by
(a,b, c,d, h). In this case if b = c, we denote it by
(a,b, d,h), which is a trapezoidal LR fuzzy set. Also
if Let TF(R) and T F
h
(R) be the set of all trapezoidal
fuzzy numbers and all trapezoidal LR fuzzy set with
height h on R, respectively:
T F(R) = {(a, b,c,d) : a < b ≤c < d},
T F
h
(R) = {(a,b,c,d, h) : a < b ≤c < d}.
(2.6)
Definition 2.5. A function s ∈C[0,h] with the follow-
ing properties is a source function
1. s(α) ≥ 0, α ∈ [0,h]
2. s(0) = 0,
3. s(h) = h,
4.
R
h
0
s(α)dα =
1
2
h
2
.
For an LR fuzzy set ˜u and α ∈[0, h] we define u(α)
and u(α) as follows
u(α) = inf{x|µ
˜u
(x) ≥ α}, 0 ≤ α < h, (2.7)
u(α) = sup{x|µ
˜u
(x) ≥ α}, 0 ≤α < h. (2.8)
For a trapezoidal fuzzy set which is denoted by
˜u = (a,b,c,d, h), we have
u(α) = a +
b−a
h
α, (2.9)
u(α) = d −
d−c
h
α. (2.10)
Definition 2.6. We define Value and Ambiguity of an
LR fuzzy set ˜u by the following relations:
1. V
h
( ˜u) =
R
h
0
s
h
(α)[u(α) + u(α)]dα,
2. A
h
( ˜u) =
R
h
0
s
h
(α)[u(α) −u(α)]dα.
Definition 2.7. Let s be a source function, then I
s,h
defined bellow is source number with respect to s.
I
s,h
=
Z
h
0
s(α)αdα. (2.11)
Lemma 2.1. For an arbitrary source function s over
(0,h], we have I
s,h
<
1
2
h
3
.
Proof. By using Mid-point Theorem, the proof is
straightforward.
3 h-SOURCE DISTANCE
BETWEEN FUZZY LR SETS
Definition 3.1. For two LR fuzzy sets ˜u and ˜v, with
same heights h, we define h-source distance D as fol-
lows,
D( ˜u, ˜v) =
1
2
|
V
h
( ˜u) −V
h
( ˜v)
|
+
|
A
h
( ˜u) −A
h
( ˜v)
|
+ h
3
d
H
([ ˜u]
h
,[ ˜v]
h
)
.
where d
H
is Hausdorff metric, and [ ˜w]
h
=
{x|µ
˜w
(x) ≥ h} is the h-cut of fuzzy number ˜w.
Theorem 3.1. For ˜u, ˜v, ˜w in LR fuzzy sets, the h-
source distance, D, satisfies the following properties:
1. D( ˜u, ˜u) = 0,
2. D( ˜u, ˜v) = D( ˜v, ˜u),
3. D( ˜u, ˜w) ≤ D( ˜u, ˜v) + D( ˜v, ˜w).
source distance between fuzzy numbers defined
in (Abbasbandy and Amirfakhrian, 2006b) is a spe-
cial case of h-source distance.
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
84

Example 3.1. Let µ
˜u
(x) =
h , x = a,
0 , otherwise,
,
µ
˜v
(x) =
h , x = b,
0 , otherwise.
D( ˜u, ˜v) =
1
2
(h
3
|a −b|+ h
3
|a −b|) = h
3
|a −b|.
In this case if ˜u and ˜v are two crisp real numbers:
µ
˜u
(x) = χ
{a}
, µ
˜v
(x) = χ
{b}
, then
D( ˜u, ˜v) = |a −b|.
For the set of all LR fuzzy sets with the same
height, we have the following theorem.
Theorem 3.2. For ˜u, ˜v, ˜u
0
, ˜v
0
∈ T F
h
(R) and nonnega-
tive real number k, h-source distance D satisfies the
following properties:
1. D(k ˜u,k ˜v) = kD( ˜u, ˜v),
2. D( ˜u + ˜v, ˜u
0
+ ˜v
0
) ≤ D( ˜u, ˜u
0
) + D( ˜v, ˜v
0
).
4 NEAREST APPROXIMATION
OF LR FUZZY SETS
In this section we use h-source distance to find the
nearest approximation of an arbitrary fuzzy set. We
start with a theorem on set of all fuzzy sets with the
same height.
Theorem 4.1. Let ˜u, ˜v ∈ T F
h
(R), then D( ˜u, ˜v) = 0, if
and only if ˜u = ˜v.
Proof. If ˜u = ˜v, from Theorem 3.1 we have D( ˜u, ˜v) =
0. Let ˜u = (a
u
,b
u
,c
u
,d
u
,h) and ˜v = (a
v
,b
v
,c
v
,d
v
,h)
are two trapezoidal fuzzy sets. If D( ˜u, ˜v) = 0 then
a) max{h
3
|
c
u
−c
v
|
,h
3
|
b
u
−b
v
|
} = 0,
b) V
h
( ˜u) = V
h
( ˜v),
c) A
h
( ˜u) = A
h
( ˜v).
(4.1)
From (a), we have max {h
3
|
b
u
−a
u
|
,h
3
|
b
v
−a
v
|
}= 0
and hence a
u
= a
v
and b
u
= b
v
. From (b) and (c)
V
h
( ˜u) + A
h
( ˜u) = 2
Z
h
0
s(α)u(α)dα
= 2
Z
h
0
s(α)v(α)dα
= V
h
( ˜v) + A
h
( ˜v), (4.2)
V
h
( ˜u) −A
h
( ˜u) = 2
Z
h
0
s(α)u(α)dα
= 2
Z
h
0
s(α)v(α)dα
= V
h
( ˜v) −A
h
( ˜v), (4.3)
and hence
(
d
u
h
2
2
−
d
u
−c
u
h
I
s,h
=
d
v
h
2
2
−
d
v
−c
v
h
I
s,h
,
a
u
h
2
2
+
b
u
−a
u
h
I
s,h
=
a
v
h
2
2
−
b
v
−a
v
h
I
s,h
.
(4.4)
By considering θ = h
3
−2I
s,h
, the system 4.4 is equiv-
alent to the following relations:
hd
u
θ + 2c
u
I
s,h
= hd
v
θ + 2c
v
I
s,h
,
ha
u
θ + 2b
u
I
s,h
= ha
v
θ + 2b
v
I
s,h
.
(4.5)
Since b
u
= b
v
and c
u
= c
v
, using Lemma 2.1, we
have a
u
= a
v
and d
u
= d
v
, hence ˜u = ˜v.
Corollary 4.2. h-source distance, D, is a metric on
T F
h
(R), for a fixed height h.
Proof. By Theorems 3.1 and 4.1 the proof is clear.
Corollary 4.3. Let ˜u be an arbitrary LR fuzzy set
with height h. Let
t =
Z
h
0
u(α)s(α)dα, t =
Z
h
0
u(α)s(α)dα.
The nearest trapezoidal fuzzy set of ˜u is ˜v =
(a
v
,b
v
,c
v
,d
v
,h), where
a
v
=
1
( h
3
−2I
s,h
)
(−2b
v
+ 2ht), (4.6)
b
v
= u(h), (4.7)
c
v
= u(h), (4.8)
d
v
=
1
( h
3
−2I
s,h
)
(−2c
v
+ 2ht). (4.9)
Lemma 4.4. For an arbitrary LR fuzzy set ˜u with
height h, the nearest trapezoidal fuzzy set exists and it
is unique.
Proof. By Corollary 4.3 the proof is clear.
5 NUMERICAL EXAMPLES
In this section we present some numerical examples
using the proposed method.
Example 5.1.
Let ˜u = (e
r
,e
2−r
),
1
2
and s(r) = r. The
nearest trapezoidal fuzzy set of ˜u is ˜v =
24 −14
√
e,
√
e,e
3/2
,24e
2
−38e
3/2
. In Fig-
ure 1, ˜u and ˜v are shown by solid and dashed lines,
respectively.
Example 5.2.
Let ˜u = (e
r
,e
2−r
), and s(r) = r. The nearest triangular
fuzzy number of ˜u is ˜v = (6 −2e,e,2e(3e −7)). In
Figure 2, ˜u and ˜v are shown by solid and dashed lines,
respectively.
A New Distance on a Specific Subset of Fuzzy Sets
85
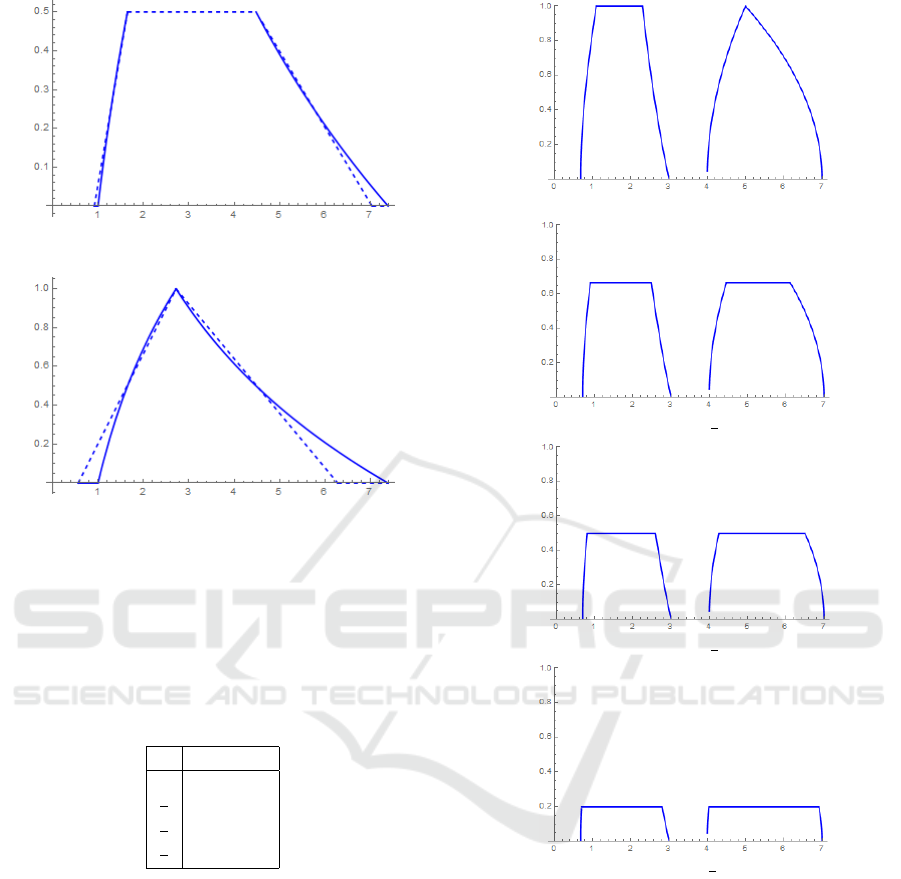
Figure 1: The nearest trapezoidal fuzzy set.
Figure 2: The nearest fuzzy number.
Example 5.3.
Let ˜u
h
= (ln(2 + r
2
,4 −ln(1 + r), h) and ˜v
h
= (r
2
+
1,5 −2r
2
,h). Using s(r) = r, the values of h-distance
D( ˜u
h
, ˜v
h
) between the fuzzy sets are shown in Table 1
for various values of h . See Figure 3.
Table 1: ˜u
h
and ˜v
h
for various values of h.
h D( ˜u
h
, ˜v
h
)
1 3.95069
2
3
1.49782
1
2
0.76366
1
5
0.09769
6 CONCLUSIONS
In this work we presented a method to find the nearest
trapezoidal fuzzy set of an arbitrary LR fuzzy set with
the same height. The nearest fuzzy set was found by
using a new distance between fuzzy sets. Numerical
examples shows that this method is acceptable.
(a) h = 1
(b) h =
2
3
(c) h =
1
2
(d) h =
1
5
Figure 3: ˜u
h
and ˜v
h
for various values of h.
REFERENCES
Abbasbandy, S. and Amirfakhrian, M. (2006a). The nearest
approximation of a fuzzy quantity in parametric form.
Applied Mathematics and Computation.
Abbasbandy, S. and Amirfakhrian, M. (2006b). The near-
est trapezoidal form of a generalized left right fuzzy
number. Journal of Approximate Reasoning.
Abbasbandy, S. and Asady, B. (2004). The nearest trape-
zoidal fuzzy number to a fuzzy quantity. Applied
Mathematics and Computation.
Anzilli, L., Facchinetti, G., and Mastroleo, G. (2014).
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
86

A parametric approach to evaluate fuzzy quantities.
Fuzzy Sets and Systems.
Ban, A. I., Coroianu, L., and Khastan, A. (2011). Condi-
tioned weighted lr approximations of fuzzy numbers.
Fuzzy Sets and Systems.
Cano, Y. C., Bez-Snchez, A. D., Romn-Flores, H., and
Rojas-Medar, M. (2016). On the approximation of
compact fuzzy sets. Computers and Mathematics with
Applications.
Chanas, S. (2001). On the interval approximation of a fuzzy
number. Fuzzy Sets and Systems.
Chong-Xin, W. and Ming, M. (1991). Embedding problem
of of fuzzy number space: Part i. Fuzzy Sets and Sys-
tems.
Delgado, M., Vila, M. A., and Voxman, W. (1998). On
a canonical representation of fuzzy numbers. Fuzzy
Sets and Systems.
Grzegorzewski, P. (2002). Nearest interval approximation
of a fuzzy number. Fuzzy Sets and Systems.
Grzegorzewski, P. and Mr ´owka, E. (2005). Trapezoidal ap-
proximations of fuzzy numbers. Fuzzy Sets and Sys-
tems.
Voxman, W. (1998). Some remarks on distance between
fuzzy numbers. Fuzzy Sets and Systems.
A New Distance on a Specific Subset of Fuzzy Sets
87
