EvoloPy: An Open-source Nature-inspired Optimization Framework in

Python

Hossam Faris

, Ibrahim Aljarah

, Seyedali Mirjalili

, Pedro A. Castillo

and Juan J. Merelo

Department of Business Information Technology, King Abdullah II School for Information Technology,

The University of Jordan, Amman, Jordan

School of Information and Communication Technology, Grifﬁth University, Nathan, Brisbane, QLD 4111, Australia

ETSIIT-CITIC, University of Granada, Granada, Spain

Keywords:

Evolutionary, Swarm Optimization, Metaheuristic, Optimization, Python, Framework.

Abstract:

EvoloPy is an open source and cross-platform Python framework that implements a wide range of classical

and recent nature-inspired metaheuristic algorithms. The goal of this framework is to facilitate the use of

metaheuristic algorithms by non-specialists coming from different domains. With a simple interface and

minimal dependencies, it is easier for researchers and practitioners to utilize EvoloPy for optimizing and

benchmarking their own deﬁned problems using the most powerful metaheuristic optimizers in the literature.

This framework facilitates designing new algorithms or improving, hybridizing and analyzing the current ones.

The source code of EvoloPy is publicly available at GitHub (https://github.com/7ossam81/EvoloPy).

1 INTRODUCTION

In general, nature-inspired algorithms are population-

based metaheuristics which are inspired by different

phenomena in nature. Due to their stochastic and non-

deterministic nature, there has been a growing interest

in investigating their applications for solving complex

problems when the search space is extremely large

and when it is impossible to solve them with conven-

tional search methods (Yang, 2013).

In general, nature-inspired algorithms can fall into

two main categories: Swarm Intelligence and Evolu-

tionary Algorithms. Swarm intelligence algorithms

simulate the natural swarms such as ﬂocks of birds,

ant colonies, and schools of ﬁshes. Popular algo-

rithms that fall in this category are Particle Swarm

Optimization (PSO) (Kennedy and Eberhart, 1995),

and Ant Colony Optimization (ACO) (Koro

sec and

Silc, 2009). More recent Swarm intelligence algo-

rithms include Cuckoo Search (CS) (Yang and Deb,

2009), Grey Wolf Optimizer (GWO) (Mirjalili et al.,

2014), Multi-Verse Optimizer (MVO) (Mirjalili et al.,

2016), Moth-ﬂame optimization (MFO) (Mirjalili,

2015), Whale Optimization Algorithm (WOA) (Mir-

jalili and Lewis, 2016), Bat Algorithm (BAT) (Yang,

2010b), Fireﬂy Algorithm (FFA) (Yang, 2010a), and

many others. Most of Swarm intelligence algorithms

reach the best solution by exchanging the information

between the swarm’s individuals.

On the other hand, evolutionary-based algorithms

are inspired by some concepts from the Darwinian

theory about evolution and natural selection. Such

algorithms include Genetic algorithm (GA) (Hol-

land, 1992), Genetic Programming (GP)(Koza, 1992),

and Evolution Strategy (ES) (Beyer and Schwefel,

2002). These algorithms maintain different strategies

to evolve and ﬁnd good solutions for difﬁcult prob-

lems based on evolutionary operators like mutation,

crossover and elitism.

An important twist in the research ﬁeld was made

when the No Free Lunch Theorem (NFL) was re-

leased (Wolpert and Macready, 1997; Ho and Pepyne,

2002). NFL states that no algorithm is superior to

all other algorithms when considering all optimiza-

tion problems. This means that if an algorithm A out-

performs another algorithm B on some type of opti-

mization problems then algorithm B outperforms A

in another types of problems. Since the release of

NFL, researchers and practitioners have developed

a wide range of metaheuristic algorithms and inves-

tigated their applications in different types of chal-

lenging optimization problems. In the last decade,

most of the researchers implemented and shared their

proposed optimizers in Matlab (Yang, 2010a; Yang,

2010b; Mirjalili et al., 2014; Mirjalili, 2015). This is

due to its simplicity and ease of use. However, Matlab

Faris, H., Aljarah, I., Mirjalili, S., Castillo, P. and Merelo, J.

EvoloPy: An Open-source Nature-inspired Optimization Framework in Python.

DOI: 10.5220/0006048201710177

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 171-177

ISBN: 978-989-758-201-1

171

is a commercial and expensive software and portabil-

ity is a big issue.

In this paper, we introduce EvoloPy which is

a framework written in Python that provides well-

regarded and recent nature-inspired optimizers. The

goal of the framework is to take the advantage of

the rapidly growing scientiﬁc community of Python

and provide a set of robust optimizers as free and

open source software. We believe that implementing

such algorithms in Python will increase their popular-

ity and portability among researchers. Moreover, the

powerful libraries and packages available in Python

will make it more feasible to apply metaheuristic al-

gorithms for solving complex problems on a much

higher scale.

2 RELATED WORK

Today, many different nature-inspired optimization li-

braries and frameworks are available. Some of them

are developed for special type of nature-inspired op-

timization like GEATbx (Hartmut Pohlheim, 2006),

which is a framework that contains many variants

of the Genetic Algorithms, and Genetic Program-

ming. GEATbx is implemented in MATLAB envi-

ronment and provides many global optimization ca-

pabilities. The authors in (Matthew Wall, 1996) de-

veloped GAlib library, which contains a set of C++

genetic algorithm tools and operators for different op-

timization problems. In addtion, GAlib is built on

UNIX platforms and is implemented to support dis-

tributed/parallel environments.

In (Fortin et al., 2012), the authors developed a

novel evolutionary computation Python framework

called DEAP to simplify the execution of many op-

timization ideas with parallelization features. The

DEAP Framework includes many nature-inspired al-

gorithms with different variations such as: GA, GP,

ES, PSO, Differential Evolution (DE), and multi-

objective optimization. In addition, DEAP includes

Benchmarks modules containing many test functions

for evaluations. In (Wagner and Affenzeller, 2004),

the authors present a generic optimization environ-

ment named HeuristicLab, which is implemented

using C# language. HeuristicLab is a framework

for heuristic, evolutionary algorithms, and machine

learning. HeuristicLab includes many algorithms

such as: Genetic Programming, Age-layered Popu-

lation, Structure (ALPS), Evolution Strategy, Genetic

Algorithm, Island Genetic Algorithm, Particle Swarm

Optimization, Relevant Alleles Preserving GA, and

many others.

In (Durillo and Nebro, 2011), jMetal is devel-

oped, which is a framework that contains many meta-

heuristic algorithms implemented in Java language.

The authors employ the object-oriented architecture

to develop the framework. jMetal includes many

features such as: multi-objective algorithms, paral-

lel algorithms, constrained problems, and different

representations of the problem variables. In (Ca-

hon et al., 2004; Humeau et al., 2013), the authors

present a white-box object-oriented framework called

ParadisEO. ParadisEO is developed by integrating

Evolving Objects (EO) - which is an C++ evolution-

ary computation framework - and many distributed

metaheuristics including local searches (LS), and hy-

bridization mechanisms.

Most of the existing optimization and metaheuris-

tic based frameworks include classical evolutionary

and nature-inspired algorithms such as: GA, GP, PSO

and ES. However few of them implement recent meta-

heuristic algorithms. In contrast to previous frame-

works, we propose our framework as an initiative to

keep an implementation of the recent nature-inspired

metaheuristics as well as the classical and well re-

garded ones in a single open source framework. To

the best of our knowledge, EvoloPy framework is the

ﬁrst tool that implements most of these algorithms in

Python language. EvoloPy is designed in an efﬁcient

way to solve computationally expensive optimization

functions with very high dimensions.

Our own research group has been involved on the

development of many metaheuristic libraries, from

EO (Merelo-Guerv

os et al., 2000) to, lately, Algo-

rithm::Evolutionary (Merelo-Guervs et al., 2010) and

NodEO (Merelo Guerv

os, 2014). These libraries have

been mainly focused on evolutionary algorithms. The

library we present in this paper has a wider breadth

and, besides explores the possibilities of a new lan-

guage, Python. We will explain this election next.

3 WHY PYTHON?

Python is a general purpose scripting language which

has a clear and simple syntax. With the rapid de-

velopment of mature, advanced and open source sci-

entiﬁc computing libraries and packages, Python be-

came as one of the most popular and powerful lan-

guages for scientiﬁc computing. Moreover, Python

has cross-platform runability, which works with dif-

ferent operating systems, and has ability to access li-

braries written in different programming languages

and computing environments. Python also can sup-

port small-form devices, embedded systems, and mi-

crocontrollers. In addition, Python needs very mini-

mal setup procedure to start with. Python uses modu-

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

172

lar and object based programming, which is a popular

methodology to organize classes, functions, and pro-

cedures into hierarchical namespaces. All these rea-

sons have turned Python to be a popular language in

a huge community of scientists.

4 FRAMEWORK OVERVIEW

EvoloPy provides a set of classical and recent nature-

inspired metaheuristic optimizers with an easy-to-use

interface. The framework incorporates four main

components which are described as follows:

• The Optimizer: this is the main interface of the

framework in which the users can select a list of

optimizers to run in their experiment. Using this

interface, the user can conﬁgure common parame-

ters for the algorithms like the maximum number

of iterations for each run, the size of the popula-

tion and the number of runs. In addition, a list of

benchmark problems can be selected.

• The metaheuristic algorithms: simply this part in-

cludes the list of implemented optimizers in the

framework. At the time of writing this paper,

the following eight algorithms have been imple-

mented:

– Particle Swarm Optimization (PSO)

– Fireﬂy Algorithm (FFA) (Yang, 2010a)

– Gray Wolf Optimizer (GWO)(Mirjalili et al.,

2014)

– Whale Optimization Algorithm (WOA) (Mir-

jalili and Lewis, 2016)

– Multi-Verse Optimizer (MVO) (Mirjalili et al.,

2016)

– Moth Flame Optimizer (MFO) (Mirjalili, 2015)

– Bat Algorithm (BAT) (Yang, 2010b)

– Cuckoo Search Algorithm (CS) (Yang and Deb,

2009)

• Benchmark functions and problem deﬁnitions:

This part includes a set of benchmark problems

commonly used in the literature for the purpose

of comparing different metaheuristic algorithms.

Any new user-deﬁned cost function could be

added to this list.

• Results management: this component is responsi-

ble for exporting the results and storing them in

one common CSV ﬁle.

5 DESIGN ISSUES

Most of nature-inspired metaheuristics are

population-based algorithms. These algorithms

start by randomly initializing a set of individuals

each of which represents a candidate solution.

Conventionally, in most of state-of-art evolutionary

algorithms frameworks, populations are implemented

as 2-dimensional arrays while individuals are im-

plemented as 1-dimensional arrays. For example an

individual I and a population P can be represented as

given in equations 1 and 2.

= [

... x

] (1)

P =







... x







(2)

In EvoloPy, Numpy is chosen to deﬁne and repre-

sent the populations and individuals in the optimizers.

Numpy is an open-source extension to Python that pro-

vides common scientiﬁc computing and mathematical

routines as pre-compiled and fast functions. NumPy

also supports large multidimensional arrays and ma-

trices and it offers a varied range of functions to han-

dle and perform common operations on these arrays.

Numpy has many things in common with Matlab. This

makes it easier for researchers who are familiar with

Matlab to use EvoloPy.

The core data structure ndarray (abbreviation for

N-dimensional array) in Numpy is used to deﬁne 1-

dimensional and 2-dimensional arrays that represent

individuals and populations, respectively. For exam-

ple, to deﬁne a randomly generated initial population

with 50 individuals and 100 dimensions the following

python line of code can be used

initialPop = np.random.rand(50,100)

Moreover, with Numpy it is possible to perform

vector operations in simple and compact syntax. For

example, one of the common operations used in many

metaheuristic algorithms is to check the boundaries of

the elements of the individuals after updating them.

This can be performed all at once with Numpy as fol-

lows:

newPop=numpy.clip(oldPop, lb, ub)

Where lb and ub are the upper and lower bounds

respectively.

To demonstrate the main components of EvoloPy

framework we use the UML representation. A class

diagram illustrating the EvoloPy components and

their relationships is presented in Figure 1. The

EvoloPy framework consists of eleven classes, three

EvoloPy: An Open-source Nature-inspired Optimization Framework in Python

173

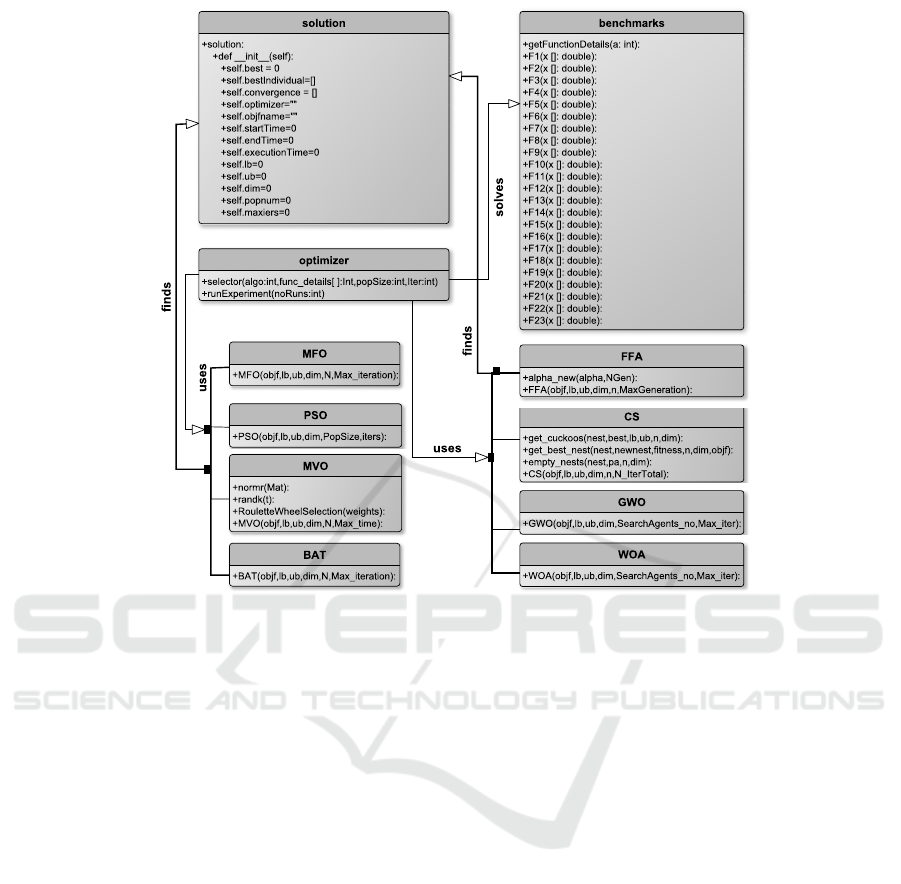
Figure 1: Class diagram of the EvoloPy framework.

of them for coordinating and simplifying the opti-

mization process, namely; optimizer, benchmarks,

and solution. On the other hand, the other eight

classes represent the actual nature-inspired optimiz-

ers. The core ﬂow of EvoloPy relies in that an op-

timizer solves a benchmark using one or more opti-

mizers to ﬁnd global solutions. We have used generic

classes names in the framework in order to make it

very easy to ﬂow and general enough to be modiﬁed

and usable.

6 COMPARISON WITH MATLAB

In this section we compare the metaheuristic algo-

rithms implemented so far in EvoloPy with their peers

in Matlab based on their running time. The idea

here is to measure the running time of the main loop

of each algorithm in EvoloPy and Matlab with an

equal number of function evaluations. The experi-

ments were performed on a personal machine with

an Intel(R) Core(TM) i5-2400 CPU at 3.10Ghz and

a memory of 4 GB running Windows 7 professional

32bit operating system. In all experiments, the popu-

lation size and the number of iterations were set to 50,

and 100, respectively for all algorithms. In order to

study the effect of the size of the problem on the run-

ning time of the algorithms, all optimizer were exe-

cuted using different dimension lengths ranging from

a small number of 50 elements reaching up to 20,000

in both implementations, Matlab and EvoloPy. Note

that the dimension length here indicates the number

of elements in a single individual or in another words,

the number of variables in the objective function. All

optimizers were applied to minimize the unimodal

function given in Equation 3.

f (x) =

n−1

∑

i=0

(

i−1

∑

j=0

)

(3)

The results of EvoloPy and Matlab implementa-

tions are shown in Figure 2. It can be noticed that

with small dimension sizes there is no signiﬁcant dif-

ference in the running time between the two imple-

mentations. In most of the optimizers and up to a di-

mension size of 500 the running time was less than

250 second. However, for higher sizes, the difference

in the running time remarkably increases. On a di-

mension length of 20,000 the ratio is around 1:2 for

most of the optimizers.

The efﬁcient running time of EvoloPy compared

to Matlab implementation when applied for solving

problems with large number of variables can be ex-

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

174

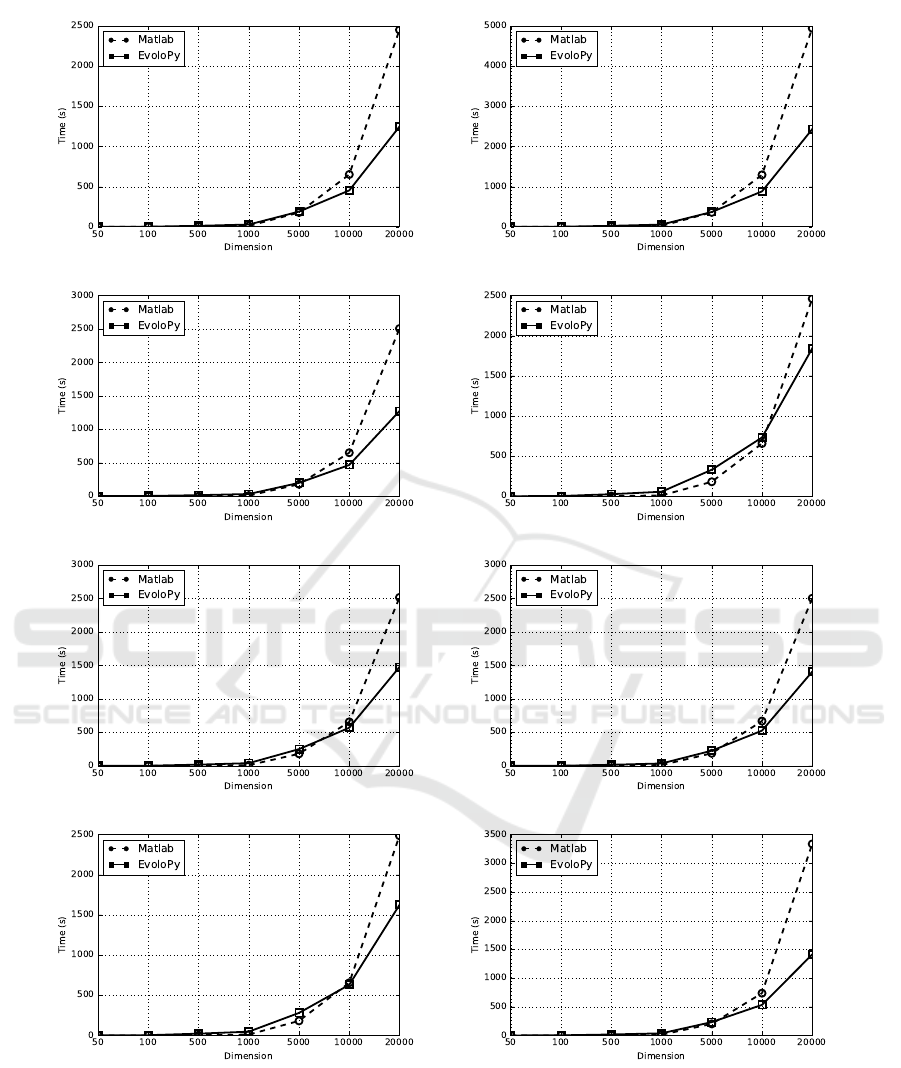
(a) BAT (b) CS

(e) MFO (f) MVO

(g) PSO (h) WOA

Figure 2: Comparison of running time between the metaheuristic optimizers in EvoloPy and Matlab based on the running

time of the main iteration.

plained due to the use of the powerful N-dimensional

array object NumPY to represent individuals and popu-

lations.

7 CONCLUSIONS AND FUTURE

WORK

EvoloPy is a framework written in Python that pro-

vides and maintains classical and recent nature-

EvoloPy: An Open-source Nature-inspired Optimization Framework in Python

175

inspired metaheuristic algorithms. Being coded in

Python with its NumPy extension, the implemented

algorithms are boosted by the powerful and efﬁcient

multi-dimensional objects. In comparison with Mat-

lab, EvoloPy shows more efﬁciency in terms of run-

ning time for problems with high dimension and large

number of variables. This proves that the open source

tool Python should be considered over and preferably

other proprietary tools for carrying out experiments in

metaheuristics, and, for that matter, scientiﬁc comput-

ing in general, because besides being free and gratis,

it offers better efﬁciency and, inherently to its open

source nature, reproducibility.

The ﬁrst steps after this paper will be to carry out

a proﬁling of the tool to identify inefﬁciencies and

make it run faster. After that, more recent and robust

metaheuristic algorithms are planned to be added to

the framework. It is also interesting to expand the

experiments presented in this paper to include a com-

parison with Matlab or other implementations based

on more challenging and sophisticated optimization

functions rather than simple ones.

ACKNOWLEDGEMENTS

This paper has been supported in part by

http://geneura.wordpress.comGeNeura Team,

projects TIN2014-56494-C4-3-P (Spanish Ministry

of Economy and Competitiveness).

REFERENCES

Beyer, H.-G. and Schwefel, H.-P. (2002). Evolution strate-

gies – a comprehensive introduction. Natural Com-

puting, 1(1):3–52.

Cahon, S., Melab, N., and Talbi, E.-G. (2004). Par-

adiseo: A framework for the reusable design of paral-

lel and distributed metaheuristics. Journal of Heuris-

tics, 10(3):357–380.

Durillo, J. J. and Nebro, A. J. (2011). jmetal: A java frame-

work for multi-objective optimization. Advances in

Engineering Software, 42:760–771.

Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A., Parizeau,

M., and Gagn

e, C. (2012). DEAP: Evolutionary algo-

rithms made easy. Journal of Machine Learning Re-

search, 13:2171–2175.

Hartmut Pohlheim (2006). Geatbx - the genetic and evolu-

tionary algorithm toolbox for matlab.

Ho, Y.-C. and Pepyne, D. L. (2002). Simple explana-

tion of the no-free-lunch theorem and its implica-

tions. Journal of optimization theory and applications,

115(3):549–570.

Holland, J. (1992). Genetic algorithms. Scientiﬁc American,

pages 66–72.

Humeau, J., Liefooghe, A., Talbi, E.-G., and Verel, S.

(2013). ParadisEO-MO: From Fitness Landscape

Analysis to Efﬁcient Local Search Algorithms. Re-

search Report RR-7871, INRIA.

Kennedy, J. and Eberhart, R. (1995). Particle swarm op-

timization. In Neural Networks, 1995. Proceedings.,

IEEE International Conference on, volume 4, pages

1942–1948 vol.4.

Koro

sec, P. and

Silc, J. (2009). A distributed ant-based al-

gorithm for numerical optimization. In Proceedings

of the 2009 workshop on Bio-inspired algorithms for

distributed systems - BADS 09. Association for Com-

puting Machinery (ACM).

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press, Cambridge, MA, USA.

Matthew Wall (1996). Galib: A c++ library of genetic al-

gorithm components.

Merelo Guerv

os, J. J. (2014). NodEO, a evo-

lutionary algorithm library in Node. Tech-

nical report, GeNeura group. Available at

http://ﬁgshare.com/articles/nodeo/972892.

Merelo-Guerv

os, J.-J., Arenas, M. G., Carpio, J., Castillo,

P., Rivas, V. M., Romero, G., and Schoenauer, M.

(2000). Evolving objects. In Wang, P. P., editor,

Proc. JCIS 2000 (Joint Conference on Information

Sciences), volume I, pages 1083–1086. ISBN: 0-

9643456-9-2.

Merelo-Guervs, J.-J., Castillo, P.-A., and Alba, E. (2010).

Algorithm::Evolutionary, a ﬂexible Perl mod-

ule for evolutionary computation. Soft Computing,

14(10):1091–1109. Accesible at http://sl.ugr.es/000K.

Mirjalili, S. (2015). Moth-ﬂame optimization algorithm: A

novel nature-inspired heuristic paradigm. Knowledge-

Based Systems, 89:228 – 249.

Mirjalili, S. and Lewis, A. (2016). The whale optimization

algorithm. Advances in Engineering Software, 95:51

– 67.

Mirjalili, S., Mirjalili, S. M., and Hatamlou, A. (2016).

Multi-verse optimizer: a nature-inspired algorithm for

global optimization. Neural Computing and Applica-

tions, 27(2):495–513.

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey

wolf optimizer. Advances in Engineering Software,

69:46 – 61.

Wagner, S. and Affenzeller, M. (2004). The heuristiclab op-

timization environment. Technical report, University

of Applied Sciences Upper Austria.

Wolpert, D. H. and Macready, W. G. (1997). No free lunch

theorems for optimization. Evolutionary Computa-

tion, IEEE Transactions on, 1(1):67–82.

Yang, X.-S. (2010a). Fireﬂy algorithm, stochastic test func-

tions and design optimisation. Int. J. Bio-Inspired

Comput., 2(2):78–84.

Yang, X.-S. (2010b). A new metaheuristic bat-inspired

algorithm. In Gonz

alez, J. R., Pelta, D. A., Cruz,

C., Terrazas, G., and Krasnogor, N., editors, Na-

ture Inspired Cooperative Strategies for Optimiza-

tion (NICSO 2010), pages 65–74, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Yang, X.-S. (2013). Metaheuristic optimization: Nature-

inspired algorithms and applications. In Studies in

ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications

176

Computational Intelligence, pages 405–420. Springer

Science Business Media.

Yang, X. S. and Deb, S. (2009). Cuckoo search via levy

ﬂights. In Nature Biologically Inspired Computing,

2009. NaBIC 2009. World Congress on, pages 210–

214.

EvoloPy: An Open-source Nature-inspired Optimization Framework in Python

177