
Evolving Art using Aesthetic Analogies
Evolutionary Supervised Learning to Generate Art with Grammatical Evolution
Aidan Breen and Colm O’Riordan
Computational Intelligence Research Group, National University of Ireland Galway, Galway, Ireland
Keywords:
Genetic Algorithms, Evolutionary Art and Design, Genetic Programming, Hybrid Systems, Computational
Analogy, Aesthetics.
Abstract:
In this paper we describe an evolutionary approach using models of human aesthetic experience to evolve
expressions capable of generating real-time aesthetic analogies between two different artistic domains. We
outline a conceptual structure used to define aesthetic analogies and guide the collection of empirical data
used to build aesthetic models. We also present a Grammatical Evolution based system making use of aes-
thetic models with a heuristic based fitness calculation approach to evaluate evolved expressions. We demon-
strate a working model that has been designed to implement this system and use the evolved expressions to
generate real-time aesthetic analogies with input music and output visuals. With this system we can generate
novel artistic visual displays, similar to a light show at a music concert, which can react to the musician’s
performance in real-time.
1 INTRODUCTION
Analogy is the comparison of separate domains. The
process of analogy has strong applications in com-
munication, logical reasoning, and creativity. A hu-
man artist will often take some source material as
inspiration and create an equivalent, or related art
piece in their chosen artistic domain. This process of
metaphor is the equivalent of making an artistic anal-
ogy and has been used successfully in a literal form by
artists like Klee (Klee, 1925), Kandinsky (Kandinsky
and Rebay, 1947) and more recently Snibbe (Snibbe
and Levin, 2000). Similar approaches are often taken
in a less direct form by stage lighting designers or film
soundtrack composers.
Our aim is to make computational analogies be-
tween the domains of music and visuals by making
use of aesthetic models, computational analogy, and
grammatical evolution.
This work has direct practical applications for live
performance and stage lighting design. The work in
this paper may also have less direct applications in
user interface and user experience design with par-
ticular use in the automatic generation of user inter-
faces and subconscious feedback mechanisms. Be-
yond these application domains, our research motiva-
tion also includes gaining insight into aesthetics and
analogical reasoning.
1.1 Creating Aesthetic Analogies
One of the major challenges of computational art is to
understand what makes an art piece good. Indeed the
cultural and contextual influences of an art piece may
define what makes it emotive, such as Duchamp’s
Fountain (Cameld, 1990) or Ren Magritte’s The
Treachery of Images (Magritte, 1928), but beyond
that we rely on the aesthetics of an object to decide
if it is pleasurable to perceive. Aesthetics provide an
objective description of this perception. We use this
objective description as a tool upon which to build our
analogies.
Every domain has its own aesthetic measures —
musical harmony, visual symmetry, rhythm and com-
binations thereof. In some cases, these measures can
be used to describe objects in more than one do-
main. Symmetry, for example, can describe both a
visual image, and a phrase of music. The example we
demonstrate in this paper is harmony. Musical har-
mony can be measured by the consonance or disso-
nance of musical notes. Visual harmony can be mea-
sured directly as the harmony of colours.
The analogy we are hoping to create is described
as follows: Given some musical input with harmony
value x, a mapping expression can be created to gen-
erate a visual output with a harmony value y such that
x ' y. Furthermore, we posit that when performed to-
Breen, A. and O’Riordan, C.
Evolving Art using Aesthetic Analogies - Evolutionary Supervised Learning to Generate Art with Grammatical Evolution.
DOI: 10.5220/0006048400590068
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 59-68
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
59

gether, both input music and output visuals will cre-
ate a pleasing experience. In other words, can we take
music and create a visual with a similar harmony and
will they go together?
For this simple example, it is clear that a suit-
able expression could be created by hand with some
knowledge of music and colour theory. However, if
we extend the system to include more aesthetic mea-
sures, such as symmetry, intensity, contrast or gran-
ularity, defining an analogy by use of a mapping ex-
pression becomes far more complex. While develop-
ing a system to capture more complex mappings is
beyond the scope of this paper, we aim to build the
system such that it may be extended to do so.
1.2 Grammatical Evolution and
Mapping Expressions
A genetic algorithm (GA) provides a useful method
of traversing an artistic search space, as demonstrated
by Boden and Edmonds in their 2009 review (Boden
and Edmonds, 2009). Grammatical evolution (GE)
(O’Neil and Ryan, 2003), in particular allows us to
provide a simple grammar which defines the struc-
ture of mapping expressions which can be evolved us-
ing a GA. This allows us to flexibly incorporate aes-
thetic data, operators and constants while producing
human readable output. Importantly, we make no as-
sumptions about the relationships between input and
output. This approach does not restrict the output to
any rigid pattern; potentially allowing the creation of
novel and interesting relationships between any two
domains, music and visuals or otherwise.
No single set of mapping expressions would be
capable of creating pleasing output in every circum-
stance. In this respect, we intend to find suitable ex-
pressions for a specific input, such as a verse, chorus
or phrase. Expressions may then be used in real-time
when required and would handle improvisation or un-
expected performance variations. Expressions pro-
duced by Grammatical Evolution are naturally well
suited to this task as they can be stored or loaded when
necessary, and evaluated in real-time.
1.3 Contributions and Layout
The main contribution of this work is an implementa-
tion of Grammatical Evolution using music and em-
pirically developed aesthetic models to produce novel
visual displays. Secondary contributions include a
structural framework for aesthetic analogies used to
guide the gathering of data and development of evo-
lutionary art using mapping expressions, and prelim-
inary results produced by our implementation of the
system.
The layout of this paper is as follows. Section 2
outlines related work in the areas of computational
analogy, computational aesthetics, and computational
art. Section 3 introduces our proposed method in-
cluding a general description of our analogy structure,
aesthetic models and the structure of our evolution-
ary system. Section 4 presents the details of our im-
plementation in two distinct phases, the evolutionary
phase (Section 4.1) and the evaluation phase (Section
4.2). Our results are presented in Section 5 followed
by our conclusion in Section 6 including a brief dis-
cussion of future work (Section 6.1).
2 RELATED WORK
“Analogy underpins language, art, music, invention
and science” (Gentner and Forbus, 2011). In par-
ticular, Computational Analogy (CA) combines com-
puter science and psychology. CA aims to gain some
insight into analogy making through computational
experimentation. As a research domain, it has been
active since the late 1960s, accelerated in the 1980s
and continues today. Computational analogy sys-
tems historically fall into three main categories: sym-
bolic systems, connectionist systems and hybrid sys-
tems. Symbolic systems make use of symbolic logic,
means-ends analysis and search heuristics. Connec-
tionist systems make use of networks with spreading
activation and back-propagation techniques. Hybrid
systems often use agent based systems taking aspects
of both symbolic and connectionist systems. For fur-
ther reading, see (French, 2002) and (Hall, 1989).
Birkhoff is often cited as one of the first to
consider aesthetics from a scientific point of view.
His simplistic ‘aesthetic measure’ formula M = O/C
was simply the ratio of order (O) to complexity (C)
(Birkhoff, 1933). Of course, this is over simplified
and abstract, but it did begin a long running discus-
sion on aesthetics and how we can use aesthetics to
learn about the higher functions of human cognition.
More recently, the discussion has been reignited
by Ramachandran who has outlined a set of 8 ‘laws
of artistic experience’ (Ramachandran and Hirstein,
1999). In this paper a number of factors are out-
lined which may influence how the human brain per-
ceives art. Some of these factors are measurable, such
as contrast and symmetry, but others remain more
abstract such as the grouping of figures. Nonethe-
less, it has inspired further discussion (Goguen, 1999;
Huang, 2009; Hagendoorn, 2003; Palmer et al.,
2013).
Within specific domains, heuristics can be formal-
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
60
ized and used to generate derivative pieces in a partic-
ular style or to solve particular challenges in the cre-
ation of the art itself. GAs in particular have proven
to be quite effective due to their ability to traverse a
large search space. In music for example, GAs have
been used to piece together particular musical phrases
(Todd and Werner, 1999), generate complex rhyth-
mic patterns (Eigenfeldt, 2009) or even generate en-
tire music pieces (Fox and Crawford, 2016). Similar
systems have also been used to create visuals (Heidar-
pour and Hoseini, 2015; Garca-S
´
anchez et al., 2013),
sculpture (Bergen and Ross, 2013) and even poetry
(Yang et al., 2016).
Indeed the use of aesthetic measures in combi-
nation with GAs has also been reviewed (den Heijer
and Eiben, 2010) and an approach has been outlined
to demonstrate the potential application of Multi-
Objective Optimization to combine these measures
(den Heijer and Eiben, 2011). While the system does
produce computational art that may be described as
aesthetic, it is also limited strictly by the aesthetic
measures used, without any artistic context.
It is clear that computational systems can work in
tandem with aesthetics to generate art and explore the
possible applications of computational intelligence.
Up to this point however, popular approaches have
been remarkably rigid. Our work aims to explore a
more flexible approach and perhaps discover a more
natural artistic framework through analogy.
3 PROPOSED METHOD
3.1 Analogy Structure
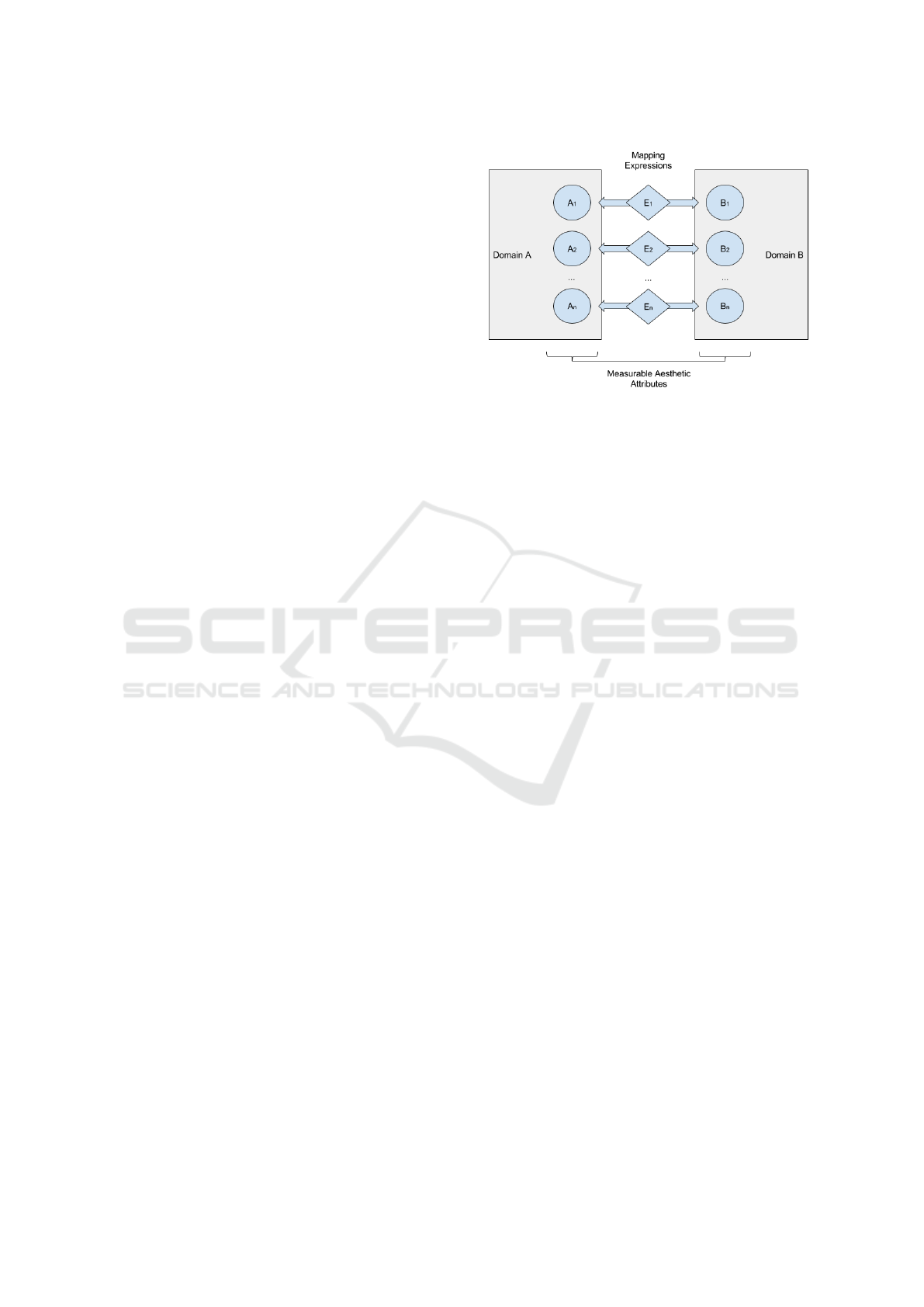
We make use of a conceptual structure to provide a
basis for our aesthetic data and analogies. The struc-
ture is shown in Figure 1 with measurable aesthetic at-
tributes in separate domains which are connected by
a set of mapping expressions which may be evolved
using grammatical evolution. The implementation in
this paper uses a single attribute in each domain, how-
ever, the structure is not restricted to a bijective map-
ping.
Some aesthetic attributes may be more suitable
than others for use in a structure as described in Fig-
ure 1. Harmony is selected for use in this paper as it
has a strong impact on the overall aesthetic quality of
an art piece, and can be measured quite easily in sep-
arate domains. In music, the harmony of notes being
played is often referred to as the consonance — or
conversely, dissonance — of those notes. While the
timbre of notes has an impact, an estimate can be ob-
tained from pitch alone. In the visual domain, colour
Figure 1: Analogy structure overview. The Mapping Ex-
pressions, E
1
to E
n
, are encoded as chromosomes and
evolved using the genetic algorithm.
harmony, or how pleasing a set of colours are in com-
bination, can be measured as a function of the posi-
tions of those colours in some colour space. This pro-
vides a convenient and understandable starting point.
Consonance values for any two notes have been
measured (Malmberg, 1918; Kameoka and Kuriya-
gawa, 1969; Breen and O’Riordan, 2015) and nu-
merous methods have been proposed that suggest a
consonance value can be obtained for larger sets of
notes (Von Helmholtz, 1912; Plomp and Levelt, 1965;
Hutchinson and Knopoff, 1978; Vassilakis, 2005).
The simplest general approach is to sum the conso-
nances for all pairs of notes in a set. This provides a
good estimation for chords with the same number of
notes and can be normalized to account for chords of
different cardinalities.
For this preliminary implementation, we enforce
a number of restrictions. Firstly, we restrict the num-
ber of inputs to two musical notes at any one time.
This simplifies the grammar and allows us to more
easily analyse the output mapping expressions. Sec-
ondly, musical harmony is calculated using just 12
note classes within a single octave. This helps to
avoid consonance variations for lower frequencies.
Figure 2 shows the consonance values for note pairs
used based on results by Breen and O’Riordan (Breen
and O’Riordan, 2015).
Similarly, colour harmony values can be measured
and modelled (Chuang and Ou, 2001; Szab
´
o et al.,
2010; Schloss and Palmer, 2011). While the harmony
of more than 2 colours may be obtained with a sim-
ilar approach to music chords, the pattern in which
colours are displayed adds an extra level of complex-
ity. To combat this, we assume our visual display is
not a strict two dimensional image, but rather a pair
of lights emitting coloured light into some space. For
example, a pair of LED stage lights for a small musi-
Evolving Art using Aesthetic Analogies - Evolutionary Supervised Learning to Generate Art with Grammatical Evolution
61

2 4
6
8 10
2
4
6
8
Semitone offset
Average Consonance Ranking
Musical Consonance Values
Figure 2: Consonance Values for musical intervals used to
calculate musical Harmony Values.
60
120 180 240 300
5
6
7
Degree Offset
Average Harmony Ranking
Colour Harmony Values
Figure 3: Average Colour Harmony values.
cal performance. Figure 3 shows the average harmony
values for colour pairs based on our own study of 30
individuals based on the approach taken by Breen and
O’Riordan (Breen and O’Riordan, 2015).
3.2 Evolutionary System
Our evolutionary approach is based upon Grammat-
ical Evolution. We use a Genetic Algorithm (GA)
to evolve mapping expressions based upon a given
grammar. The evolved expression allows us to create
a real time system rather than a single visual output.
In this way, any particular performance is not limited
to a strict musical input thereby allowing improvisa-
tion, timing and phrasing variation, and handling of
human error. Other advantages of this particular GA
approach include the flexibility by which we can in-
corporate aesthetic data and the human readability of
the output expression.
Mapping expressions are evolved by using an in-
dividual chromosome to guide the construction of a
symbolic expression by use of the given grammar.
The following is an example of a symbolic expres-
sion representing a nested list of operators (addition
and multiplication) and parameters (2, 8 and 5) using
prefix notation.
(+ 2 (* 8 5))
The grammar defines the structure of an expres-
sion using terminal and non-terminal lexical opera-
tors. Terminals are literal symbols that may appear
within the expression. Non-terminals are symbols
that can be replaced. Non-terminals often represent
a class of symbols such as operators of a specific car-
dinality, other non-terminals, or specific terminals.
Beginning with a starting non-terminal, each value
in the chromosome is used in series as the index of
the next legal terminal or non-terminal. This mapping
continues until either the expression requires no more
arguments, or a size limit is reached. If the chromo-
some is not long enough to complete the expression,
we simply begin reading from the start of the chro-
mosome again. See the appendix for further details
on expression encoding.
Calculating the fitness of any mapping expression
without some guidelines would be extremely subjec-
tive. In our implementation we take a heuristic ap-
proach that rewards solutions that produce outputs
with a similar normalized aesthetic value as inputs.
An in-depth description of the implemented fitness
function is presented in Section 4.1.
4 IMPLEMENTATION
We now discuss how the structure introduced above
together with the data gathered has been imple-
mented. We demonstrate how the following system
has been used to evolve mapping expressions that
generate a visual output when given a musical input.
The system may be used to generate visuals in time
with music by use of a time synchronized subsystem
utilizing a music synthesizer and visualization server.
4.1 Evolution Phase
Figure 4 shows the structure of the Evolution Phase.
This phase is centred about the GE algorithm. In our
implementation we use a population of 50 chromo-
somes. Chromosomes are stored as 8 bit integer ar-
rays, with values between 0 and 255. A chromosome
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
62

Figure 4: Evolution Phase overview.
length of 60 integer values was used in the work pre-
sented in this paper.
Musical input is taken in the form of Musical In-
strument Digital Interface (MIDI) data. The MIDI
protocol represents digital music signals, originally
designed as a transmission protocol to allow musical
signals to be sent between instruments and synthesiz-
ers. Musical notes are sent as packet pairs (note on
and note off ) containing the note pitch and the ‘veloc-
ity’, or strength of the note which is often translated
to volume. The MIDI protocol also allows data to be
stored as a file with each packet containing a timing
value. We use a file to store a sample musical input
using this format and determine which notes are being
played using the timing value.
Table 1: Grammar terminal operators.
Expression Arguments
Plus 90 degrees 1
Plus 180 degrees 1
Sin 1
Cos 1
Log 1
Addition 2
Subtraction 2
Multiplication 2
Division 2
Music Harmony Constant 2
Visual Harmony Constant 2
Ternary Conditional Operator 3
Table 2: Grammar terminal values.
Expression Range
Constant integer value 0-255
Musical input 1 0-255
Musical input 2 0-255
The implemented grammar contains a list of oper-
ators, and values (variables and constants) which are
presented in Tables 1 and 2. Of note here are the aes-
thetic values for music (input) and visuals which can
be inserted directly into an expression as constants, or
read at run-time as variables. The aesthetic models
use normalized values based on the values shown in
Figures 2 and 3. Aesthetic constant expressions take
two arguments, representing two music notes or two
colour hues, and return the aesthetic value of those
two values.
Our fitness function, as introduced above, aims to
maximize the similarity between input and output har-
mony. The fitness for any n pairs of notes is calculated
as follows, where M is a function representing the mu-
sical harmony of a pair of notes, and V is a function
representing the visual harmony of a pair of colour
hues.
f itness =
1
n
n
∑
i=1
255 − |M(input) −V (out put)| (1)
Both M and V are normalized between 0 and 255,
which produces a fitness range of 0 to 255.
Tournament selection is carried out to select indi-
viduals for evolution. A combination of single point
and double point crossover is used to build a succeed-
ing generation. Elitism is used to maintain the maxi-
mum fitness of the population by promoting the best
performing individuals to the next generation without
crossover or mutation.
Mutation is applied at the gene level. A gene is
mutated by randomly resetting its value. The muta-
tion rate is the probability with which a gene will be
mutated. The mutation rate is varied based on the
number of generations since a new peak fitness has
been reached. This allows us to optimize locally for
a period, and introduce hyper-mutation after an ap-
propriate number of generations without any increase
in peak fitness. We call this the Mutation Threshold.
The standard mutation rate (Mut
1
) is calculated as:
Mut
1
=
0.02
70
α
+ 0.01 (2)
where α represents the number of generations since a
new peak fitness was reached.
After the Mutation Threshold is reached, indicat-
ing a local optima, hyper-mutation (Mut
2
) is intro-
duced to explore further.
Mut
2
= 1.0 (3)
If a fitter solution is discovered, mutation is again
reduced to Mut
1
to allow smaller variations to occur.
Evolution is halted after a Halting Threshold of
generations without an increase of peak fitness has
been reached. Details of the parameters used can be
found in Table 3.
The output of this process is a mapping expression
which, when passed a set of values representing mu-
sic, returns a set of values representing visuals. Vi-
sual data is structured using an augmented form of
the MIDI protocol developed for this implementation.
Evolving Art using Aesthetic Analogies - Evolutionary Supervised Learning to Generate Art with Grammatical Evolution
63

Rather than the pitch of the musical note, we encode
the colour as a value representing its hue. Further de-
tails of the visual generation process can be found in
the appendix.
Table 3: Genetic Algorithm Parameters.
Parameter Value
Population Size 50
Chromosome Length 60
Crossover Rate 0.8
Standard Mutation Rate (Mut
1
) See Equation 2
Hyper-Mutation Rate (Mut
2
) 1.0
Mutation Threshold 100
Halting Threshold 200
Figure 5: Evaluation Phase overview.
4.2 Evaluation Phase
In order to evaluate the performance of an evolved
mapping expression, we must play both music and vi-
suals together. To this end, we have built the evalua-
tion system as outlined in Figure 5.
In order to perform music in synchrony with gen-
erated visuals, an extended MIDI player subsystem
is required. Musical data (MIDI) and visual data are
combined in an extended MIDI file (MIDIX). The ex-
tended MIDI player then parses this file and uses an
internal time synchronization to send MIDI signals to
a music synthesizer and a visualization server in real-
time.
The music synthesizer is a common tool in music
creation and performance. Synthesizers listen for in-
put, often in the form of MIDI signals, and produce
a sound output using some hardware or software. We
use a standard MIDI port to send and receive musical
data to an open source software synthesizer, part of
the Reaper digital audio workstation (Cockos, 2016).
We created the visualization server specifically for
this implementation which listens for signals sent by
the extended MIDI player using http web sockets.
This allows us to generate visuals in real-time and re-
main in synchrony with the music synthesizer.
4.3 Supervised Fitness
Using the evaluation system outlined above, we can
interactively evaluate the performance of a particular
Random Evolved
100
150
200
250
Expressions
Fitness
Fitness of Mapping Expressions
Figure 6: Fitness of 100 randomly generated Mapping Ex-
pressions vs Evolved expressions.
mapping expression. We can either use a static MIDI
file to compare individual expressions or we can use
a live MIDI instrument to send live MIDI signals to
evaluate how it performs with improvised and varying
input.
Expressions that are deemed fit by human supervi-
sion may then be reintroduced to the evolution phase
to continue the process. This step is independent of
the fitness function in order to capture aesthetic re-
sults beyond its capabilities.
5 RESULTS
5.1 Evolutionary Phase
Using the approach outlined above we successfully
evolved mapping expressions capable of mapping
musical input to visual output.
Many of the random seed expressions such as the
following example simply produced constant values:
[’plus180’,[’plus90’,[’sin’, 215]]]
In later generations however, we see more com-
plex expressions producing better fitting results:
[’add’,56, [’mh’,94,[’cos’,’mus2’]]]
Here we see the expression makes use of the in-
put variable mus2 and the musical harmony constant
musicalHarmony (abbreviated here to mh) which pro-
duces a dynamic output. The example chosen here is
one of the smallest expressions created.
Figure 6 demonstrates the distribution of fitness
values for randomly generated expressions versus
evolved expressions. We see the distribution for ran-
dom expressions is heavily skewed towards the min-
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
64
2 4
6
8 10
0
100
200
Input Music Interval
Output Harmony
Mapping Expression Output
Ancestors
Evolved
Target Output
Figure 7: Output of one evolved expression and its ances-
tors compared to target visual harmony.
imum value of 100. This is due to the number of ex-
pressions which produce a constant output. Evolved
expressions however show a much tighter distribution
with significantly higher fitness values.
The distribution of intervals in the input M will af-
fect the fitness of the evolved expression. An evolved
expression may be directly compared to the target vi-
sual harmony by using an equally distributed input.
Our input is a set of 11 note intervals, 1 to 11, ex-
cluding the unison and octave intervals 0 and 12 re-
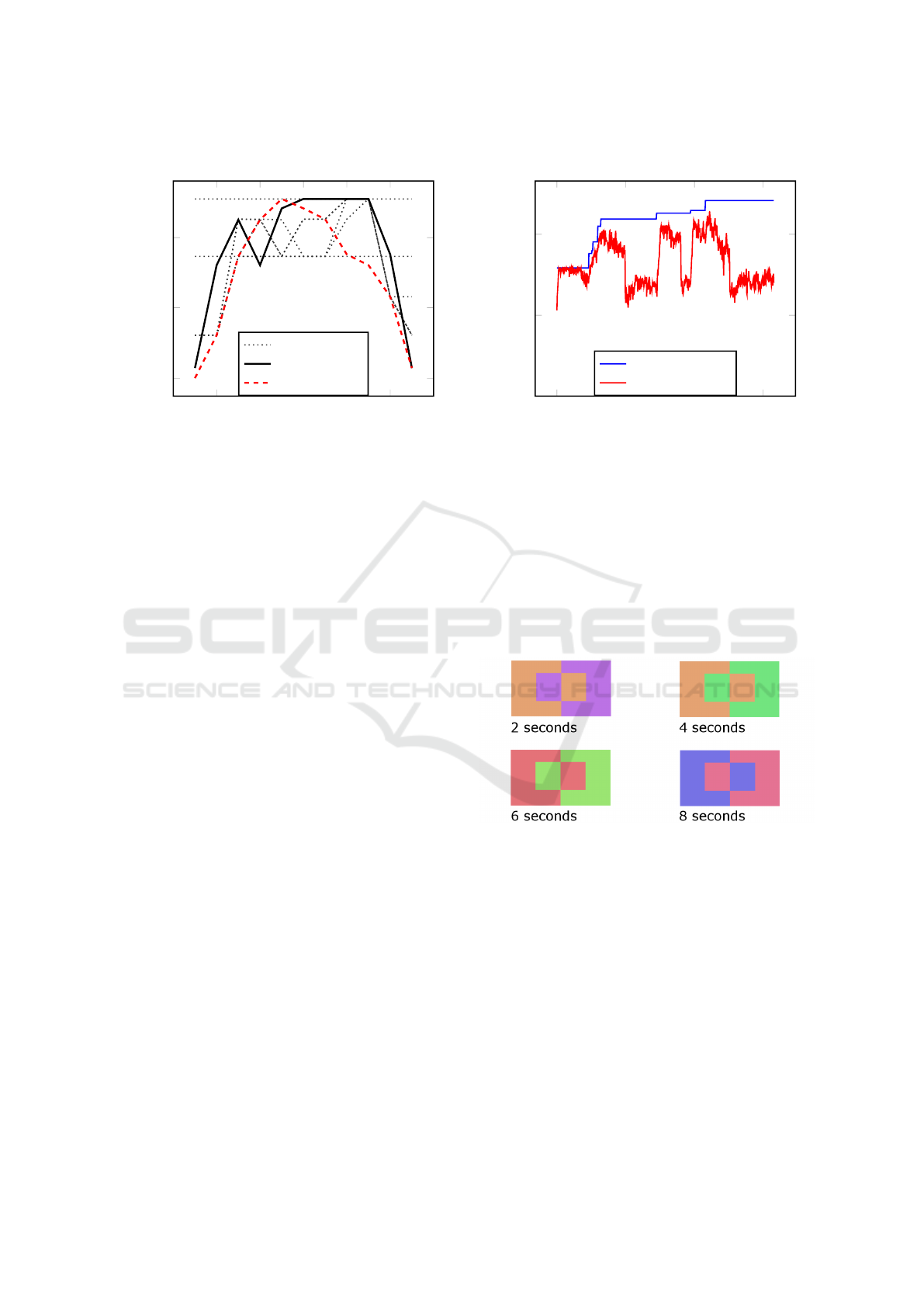
spectively. In Figure 7 we see a demonstration of
this comparison. Previous generations are shown as
dotted lines with the final fittest individual in solid
black. The target output is shown in red. We see
as the generations pass, the output matches the target
more closely. Of note here are the horizontal dotted
lines indicating older generations producing constant
outputs which have been superseded by generations
producing closer matching dynamic outputs.
Figure 8 shows the fitness of a single population
across a number of generations. We see incremen-
tal increases in fitness as local optima are discovered
with low mutation. Hyper-mutation then allows us to
find fitter solutions preventing premature population
convergence at a local optima.
5.2 Evaluation Phase
Preliminary results have been obtained based on the
implementation described in Section 4.2 demonstrat-
ing that a visual display can be produced based on
musical data in real time. The extended MIDI player
was used to play a file containing a 10 second music
piece with intervals of varying harmony. Visuals gen-
erated by a mapping expression were displayed on a
0 200 400
600
100
150
200
Generation
Fitness
Population Fitness
Best Fitness
Average Fitness
Figure 8: Population fitness for 631 generations of a typical
run.
computer screen. Visuals were observed to be in time
with the synthesized music. An example of the visual
display with screenshots taken at 2 second intervals
are shown in Figure 9. The pattern used to display
colours was similar to that used to collect colour har-
mony data.
Initial subjective testing of colours and synchro-
nized music indicates that the analogy does produce a
more enjoyable experience than random colours.
Figure 9: Generated visual display.
6 CONCLUSION
The results obtained from this implementation show
that mapping expressions can be evolved using Gram-
matical Evolution to generate visual displays by use
of musical input data and aesthetic models. Evolved
expressions show a much higher fitness with a tighter
distribution than their random counterparts. Visual
outputs have been evolved with with harmony closely
matching the target output, showing a strong corre-
lation between music and visual aesthetic values. A
population of expressions is presented which demon-
strates how peak fitness increases over time with in-
Evolving Art using Aesthetic Analogies - Evolutionary Supervised Learning to Generate Art with Grammatical Evolution
65

cremental improvements correlated with low muta-
tion rates. Hyper-mutation is also introduced to pre-
vent premature convergence.
Evolved mapping expressions have been used in a
working model with preliminary results showing time
synchronization between input music and output vi-
suals may be possible.
6.1 Future Work
We have shown that mapping expressions can be
evolved using a fitness function based on empirically
developed aesthetic models. However, we have not
evaluated the perceived aesthetic differences between
expressions of varying fitness. Further research is re-
quired to fully evaluate the strength of this correlation.
At present we restrict the number of input musical
notes to simplify the grammar and allow analysis of
the evolved expressions. This clearly limits the appli-
cation of this system greatly. Future iterations should
accommodate varying musical input lengths.
The results presented were obtained using only
one mapping expression between musical consonance
and colour harmony. We have not explored the pos-
sibilities of using multiple mapping expressions in-
corporating many attributes. We believe this will im-
prove the quality of generated visuals dramatically.
As shown in Section 5, the fitness of a population
has certain limitations. We hope to improve the speed
at which fitness increases and also increase the max-
imum fitness achievable by any individual by tuning
the parameters of the genetic operators.
The extended MIDI format has a number of use-
ful applications beyond its use in this implementation.
The format may also be useful for predefined visual
displays and synchronized performances. With this in
mind, we would like to fully define our version of the
protocol and make it available to the public.
In a similar vein, the visualization server, which
uses the extended MIDI format may also be improved.
Most immediately, it should be able to handle all of
the attributes used by mapping expressions to gener-
ate varied and immersing visual displays. Also, the
server is currently restricted to displaying visual dis-
plays on a computer screen, which is not suitable for
a live performance. We hope to develop functionality
to allow the visualization server to accept an extended
MIDI signal and control stage lighting hardware using
industry standard protocols.
6.2 Implementation Evaluation
The outlined system is certainly capable of producing
some visual output. Whether that output is deemed
aesthetically pleasing is still an open question. In or-
der to determine the actual performance of the final
output of the system, we hope to conduct a study with
human subjects. Our hypothesis here is: the system
produces more pleasing visual displays than random
colour changes.
The proposed study would demonstrate if we are
moving in the right direction, however, the overall
goal of this research is to create a system that can cre-
ate art, and perform it. To this end, the success of the
system should be evaluated with a live performance.
ACKNOWLEDGEMENTS
Funded by the Hardiman scholarship, NUIG.
REFERENCES
Bergen, S. and Ross, B. J. (2013). Aesthetic 3D model
evolution. Genetic Programming and Evolvable Ma-
chines, 14(3):339–367.
Birkhoff, G. (1933). Aesthetic Measure. Cambridge Uni-
versity Press.
Boden, M. A. and Edmonds, E. A. (2009). What is genera-
tive art? Digital Creativity, 20(1-2):21–46.
Breen, A. and O’Riordan, C. (2015). Capturing and Rank-
ing Perspectives on the Consonance and Dissonance
of Dyads. In Sound and Music Computing Confer-
ence, pages 125–132, Maynooth.
Cameld, W. A. (1990). Marcel Duchamp’s fountain: Its
history and aesthetics in the context of 1917. Marcel
Duchamp: Artist of the century.
Chuang, M.-C. and Ou, L.-C. (2001). Influence of a holistic
color interval on color harmony. COLOR research and
application, 26(1):29–39.
Cockos (2016). Reaper.
den Heijer, E. and Eiben, A. E. (2010). Comparing aesthetic
measures for evolutionary art. In Applications of Evo-
lutionary Computation, pages 311–320. Springer.
den Heijer, E. and Eiben, A. E. (2011). Evolving art using
multiple aesthetic measures. In Applications of Evo-
lutionary Computation, pages 234–243. Springer.
Eigenfeldt, A. (2009). The evolution of evolutionary soft-
ware: intelligent rhythm generation in Kinetic En-
gine. In Applications of Evolutionary Computing,
pages 498–507. Springer.
Fox, R. and Crawford, R. (2016). A Hybrid Approach to
Automated Music Composition. In Artificial Intelli-
gence Perspectives in Intelligent Systems, pages 213–
223. Springer.
French, R. M. (2002). The computational modeling
of analogy-making. Trends in cognitive sciences,
6(5):200–205.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
66

Garca-S
´
anchez, P., Merelo, J. J., Calandria, D., Pelegrina,
A. B., Morcillo, R., Palacio, F., and Garca-Ortega,
R. H. (2013). Testing the Differences of Using RGB
and HSV Histograms During Evolution in Evolution-
ary Art. ECTA.
Gentner, D. and Forbus, K. D. (2011). Computational mod-
els of analogy. Wiley Interdisciplinary Reviews: Cog-
nitive Science, 2(3):266–276.
Goguen, J. A. (1999). Art and the Brain: Editorial introduc-
tion. Journal of Consciousness Studies, 6(6):5–14.
Hagendoorn, I. (2003). The dancing brain. Cerebrum: The
Dana Forum on Brain Science, 5(2):19–34.
Hall, R. P. (1989). Computational Approaches to Analog-
ical Reasoning : A Comparative Analysis. Artificial
Intelligence, pages 39–120.
Heidarpour, M. and Hoseini, S. M. (2015). Generating
art tile patterns using genetic algorithm. In Fuzzy
and Intelligent Systems (CFIS), 2015 4th Iranian Joint
Congress on, pages 1–4. IEEE.
Huang, M. (2009). The Neuroscience of Art. Stanford Jour-
nal of Neuroscience, 2(1):24–26.
Hutchinson, W. and Knopoff, L. (1978). The acoustic com-
ponent of Western consonance. Journal of New Music
Research, 7(1):1–29.
Kameoka, A. and Kuriyagawa, M. (1969). Consonance the-
ory part I: Consonance of dyads. The Journal of the
Acoustical Society of America, 45(6):1451–1459.
Kandinsky, W. and Rebay, H. (1947). Point and line to
plane. Courier Corporation.
Klee, P. (1925). Pedagogical Sketchbook. Praeger Publish-
ers, Washington.
Magritte, R. (1928). The Treachery of Images. Oil on can-
vas, 231(2):1928–1929.
Malmberg, C. F. (1918). The perception of consonance and
dissonance. Psychological Monographs, 25(2):93–
133.
O’Neil, M. and Ryan, C. (2003). Grammatical evolution.
In Grammatical Evolution, pages 33–47. Springer.
Palmer, S. E., Schloss, K. B., and Sammartino, J. (2013).
Visual aesthetics and human preference. Annual re-
view of psychology, 64:77–107.
Plomp, R. and Levelt, W. J. M. (1965). Tonal consonance
and critical bandwidth. The journal of the Acoustical
Society of America, 38(4):548–560.
Ramachandran, V. S. and Hirstein, W. (1999). The science
of art: a neurological theory of aesthetic experience.
Journal of Consciousness Studies, 6(6):15–35.
Schloss, K. B. and Palmer, S. E. (2011). Aesthetic response
to color combinations: preference, harmony, and
similarity. Attention, Perception, & Psychophysics,
73(2):551–571.
Snibbe, S. S. and Levin, G. (2000). Interactive dynamic
abstraction. In Proceedings of the 1st international
symposium on Non-photorealistic animation and ren-
dering, pages 21–29. ACM.
Szab
´
o, F., Bodrogi, P., and Schanda, J. (2010). Experimen-
tal modeling of colour harmony. Color Research &
Application, 35(1):34–49.
Todd, P. M. and Werner, G. M. (1999). Frankensteinian
methods for evolutionary music. Musical networks:
parallel distributed perception and performace, page
313.
Vassilakis, P. N. (2005). Auditory roughness as means of
musical expression. Selected Reports in Ethnomusi-
cology, 12:119–144.
Von Helmholtz, H. (1912). On the Sensations of Tone as a
Physiological Basis for the Theory of Music. Long-
mans, Green.
Yang, W., Cheng, Y., He, J., Hu, W., and Lin, X. (2016).
Research on Community Competition and Adaptive
Genetic Algorithm for Automatic Generation of Tang
Poetry. Mathematical Problems in Engineering, 2016.
APPENDIX
Expression Encoding
A chromosome is converted to a mapping expres-
sion using the grammar terms — terminals and non-
terminals — shown in tables 1, 2 and 4. Non-
terminals are recursively replaced by terms defined by
the grammar, shown in table 4. Beginning with the
starting non-terminal, the first gene, or element in the
chromosome array, is used to determine its replace-
ment. All legal replacement terms are distributed
across the possible values of the gene. For example,
an Expression non-terminal may be replaced by any
one of the six results shown in table 4. The six re-
placement terms are distributed in six approximately
equal groups across the 256 possible values. If the
chromosome is not long enough to complete an ex-
pression, the process repeats from the first element in
the chromosome array.
The replacement process continues until either an
expression is generated, or a size threshold is reached.
If the size threshold is reached, the expression build-
ing sub-system throws an error which ensures the in-
dividual is given a minimum fitness and the expres-
sion is not evaluated. The size threshold is defined
as a maximum depth of nested expressions, which, in
this work, was approximately 1000.
Generation of Visuals
A sample MIDI file containing pairs of notes of vary-
ing harmony was used to create the visuals displayed
in figure 9. The extended MIDI player loaded the
music file into memory and, using an internal tim-
ing system, sent MIDI messages to the visualization
server and a music synthesizer. The MIDI messages
sent to the music synthesizer were identical to those
in the sample MIDI file, however, the messages sent
Evolving Art using Aesthetic Analogies - Evolutionary Supervised Learning to Generate Art with Grammatical Evolution
67

Table 4: Grammar non-terminals.
Non-terminal Abbr. Result
Start None exp
Expression exp (op1, exp), (op2, exp, exp), (op3, exp, exp, exp), const, var
Single argument operator op1 Any expression in table 1 with 1 argument
Double argument operator op2 Any expression in table 1 with 2 arguments
Ternary operator op3 Conditional operator with 3 arguments, see 1
Constant const A constant integer value, see 2
Variable var Any variable, such as musical inputs, see 2
to the visualization server were augmented based on
a mapping expression. The mapping expression used
to generate the visuals in figure 9 was the fittest in-
dividual of the population shown in figures 7 and 8.
For each pair of notes, the single octave pitch classes
(1-11) were calculated and passed to the mapping ex-
pression as Musical Input 1 and Musical Input 2 (see
table 1). The output value from the mapping expres-
sion, representing a hue offset, was then sent to the
visualisation server as a MIDI message. The visual-
ization server then generated a random base colour
and a second colour offset by the received value.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
68
