Explanation Retrieval in Semantic Networks

Understanding Spreading Activation based Recommendations

Vanessa N. Michalke and Kerstin Hartig

Daimler Center for Automotive IT Innovations (DCAITI), TU Berlin, Ernst-Reuter-Platz 7, Berlin, Germany

Keywords:

Explanation Retrieval, Spreading Activation, Pattern Recognition, Information Retrieval.

Abstract:

Spreading Activation is a well-known semantic search technique to determine the relevance of nodes in a

semantic network. When used for decision support, meaningful explanations of semantic search results are

crucial for the user’s acceptance and trust. Usually, explanations are generated based on the original network.

Indeed, the data accumulated during the spreading activation process contains semantically extremely valuable

information. Therefore, our approach exploits the so-called spread graph, a speciﬁc data structure that com-

prises the spreading progress data. In this paper, we present a three-step explanation retrieval method based on

spread graphs. We show how to retrieve the most relevant parts of a network by minimization and extraction

techniques and formulate meaningful explanations. The evaluation of the approach is then performed with a

prototypical decision support system for automotive safety analyses.

1 INTRODUCTION

Recommender, advisory, and expert systems utilize

available domain information or knowledge, often

in order to help guide decision makers in decision-

making processes (Kaklauskas, 2015). Semantic or

associative networks may be used for representing

such complex knowledge. Spreading activation algo-

rithms support searching those nets semantically, pro-

viding information about relevance of speciﬁc nodes

with respect to the speciﬁed search goals. Spreading

activation algorithms base upon the wavelike distribu-

tion of activation values from nodes to neighbor nodes

throughout the searched network. Consequently, a

node’s level of activation reveals its level of relevance

in the current semantic search.

Semantic search results, such as the ones retrieved

by spreading activation, can be used for providing rec-

ommendations and advices in decision support sys-

tems in various domains, e.g., medical diagnostics

(Alvarez et al., 2011), or automotive safety analyses

(Hartig and Karbe, 2016). In many applications, plau-

sibility and understandability of the search results be-

come important for users, i.e., the decision-makers,

because they need to understand why a certain recom-

mendation or advice was provided. Therefore, expla-

nations of the results are crucial for the user’s accep-

tance and trust in decision support systems. Current

approaches usually identify relevant paths and envi-

ronments by exploiting the original network. This

neglects the valuable ancillary information accumu-

lated during the search process. In this paper, we

present a graph-based method for automatically gen-

erating explanations for semantic search results re-

trieved by applying spreading activation techniques.

Our approach attempts to identify the nodes and edges

that contributed most to the search result we try to ex-

plain. Therefore, we retrieve the most relevant extract

not from the underlying semantic network but from

a speciﬁc graph structure representing the spreading

activation progress during search, i.e., the so-called

spread graph.

The remainder of this paper is structured as fol-

lows. In Section 2, we examine related work in the

areas of spreading activation, recommender systems

and explaining information retrieval results. In Sec-

tion 3, we present our three-step method for the au-

tomated generation of explanations. In Section 4, the

fulﬁllment of explanation goals and the goodness of

the generated explanations will be assessed. Finally,

in Section 5, we summarize our results and present

multiple possibilities to continue research.

2 RELATED WORK

In this section, we introduce the basics of searching

semantic networks by spreading activation and its ap-

Michalke, V. and Hartig, K.

Explanation Retrieval in Semantic Networks - Understanding Spreading Activation based Recommendations.

DOI: 10.5220/0006050502910298

In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 291-298

ISBN: 978-989-758-203-5

291

plication in recommender systems. We then outline

recent research in the area of explanation generation

as a meaningful extension for such systems.

2.1 Spreading Activation

One possibility for identifying and ranking relevant

regions in semantic networks is spreading activa-

tion. In a comprehensive survey, Crestani provides

an overview of its various applications for associa-

tive information retrieval (Crestani, 1997). Techni-

cally, starting from at least one start node, activation

is passed to connected nodes. Thereby, the network is

ﬂooded wave-like, in so-called pulses, until a termi-

nation condition is satisﬁed. The spreading process

is controlled by speciﬁc activation functions, allow-

ing the calculation of different activation values, such

as input and output activation as well as the activa-

tion level of each node. In each pulse, the activation

value a node received is referred to as its input acti-

vation whereas the activation value distributed by a

node is referred to as its output activation. Input ac-

tivation combines activation values potentially trans-

ported by several edges. Therefore, the term trans-

ported activation of an edge corresponds to its actual

activation value passed in a given pulse. The activa-

tion level of a node represents its current relevance

level in the search. Thus, after applying spreading

activation, relevant regions of a network can be iden-

tiﬁed, enabling application-speciﬁc interpretation.

2.2 Recommendations

Today, web-based recommender systems are well-

established, e.g., providing useful suggestions for

products or videos (Jain et al., 2015). One system

that recommends items by using spreading activation

is WebSCSA (Web Search by Constrained Spread-

ing Activation), as described in (Crestani and Lee,

2000). WebSCSA identiﬁes relevant web pages based

on marked pages during a user’s web search. Besides

web-based applications, recommendations in advi-

sory systems support the management of complex

domain-speciﬁc knowledge in enterprises. Such advi-

sory systems may support decision-makers in diverse

domains, e.g., medical diagnostics (Alvarez et al.,

2011), or automotive safety analyses (Hartig and

Karbe, 2016). The importance of high-quality deci-

sions makes explanations especially valuable. There-

fore, such systems are potential candidates for the ex-

planation retrieval method presented in this paper.

2.3 Explanations

The user needs to understand the reasons for a spe-

ciﬁc recommendation to assess its quality (Sinha and

Swearingen, 2002). Explanations can support this un-

derstanding. Reconstructive explanation generation,

as described in (Wick and Thompson, 1992), is con-

sidered an active problem-solving process to explain

any results received by a problem solving component.

Based on the problem solving computations, i.e., the

so-called line-of-reasoning, it generates a so-called

line-of-explanation. For this purpose, the prototype

REX (Reconstructive Explanation System) uses the

shortest path identiﬁed by the A* algorithm (Wick

and Thompson, 1992). The method, presented in this

paper follows the general concepts of reconstructive

explanation generation, but focuses on spreading ac-

tivation as one particular problem solving technique.

In (Forcher et al., 2010), explanations are also cre-

ated by using the shortest path. However, other cri-

teria than the path length must be considered when

searching for the best explanation. (Aleman-Meza

et al., 2005) rank the relationships in semantic net-

works by using conﬁgurable semantic and statistical

criteria like subsumption or popularity. Similar crite-

ria are used for the assessment of relevant paths, iden-

tiﬁed by a modiﬁed bidirectional breadth-ﬁrst search

(Viswanathan and Krishnamurthi, 2012) and a seman-

tic ant colony optimization algorithm (Viswanathan

and Krishnamurthi, 2015). When explaining spread-

ing activation results, an assessment by the presented

criteria is generally applicable. However, we assume

that not limiting explanation retrieval to paths can be

of greater value for meaningful explanations.

In contrast to path-based approaches, subgraph-

based approaches consider potentially relevant ele-

ments across the entire network. Many subgraph-

based approaches extract connection subgraphs from

the original graph and utilize it for their explanation

deduction (Faloutsos et al., 2004; Forcher et al., 2011;

Forcher et al., 2012). Connection subgraphs aim at

describing the relationships between nodes after par-

ticular relevance analyses, e.g., including the appli-

cation of goodness criteria, keyword assignment, or

neighborhood expansion. However, these approaches

utilize the original graph for relevance assessment.

Since semantic search by spreading activation is a

means of relevance assessment of mutual nodes, we

suppose the answer to the question why a node is

highly relevant to another to ground on the spread-

ing activation process itself. Therefore, we propose to

utilize the valuable spreading activation data, i.e., our

spread graph, a speciﬁc graph-based structure repre-

senting logged spreading activation process data.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

292

3 METHOD FOR EXPLAINING

RECOMMENDATIONS

In this paper, we present a method for explaining

spreading activation based recommendations, which

takes advantage of available additional information

from the spreading activation process itself. The

method aims at explaining the reason why a recom-

mendation, i.e., a result node in the searched semantic

network, is considered to be of relevance for the given

start nodes of the spreading activation process. There-

fore, we utilize the data produced during spreading

activation and represent it in a dedicated spread graph

structure. A spread graph is a directed graph illus-

trating the spreading activation process on the original

graph. Nodes in the spread graph represent the state of

their corresponding original graph’s nodes in a certain

spreading pulse. Each edge represents one activation

value distribution step via the corresponding original

graph’s edge. The source(s) of a spread graph are the

start node(s) of the corresponding spreading process.

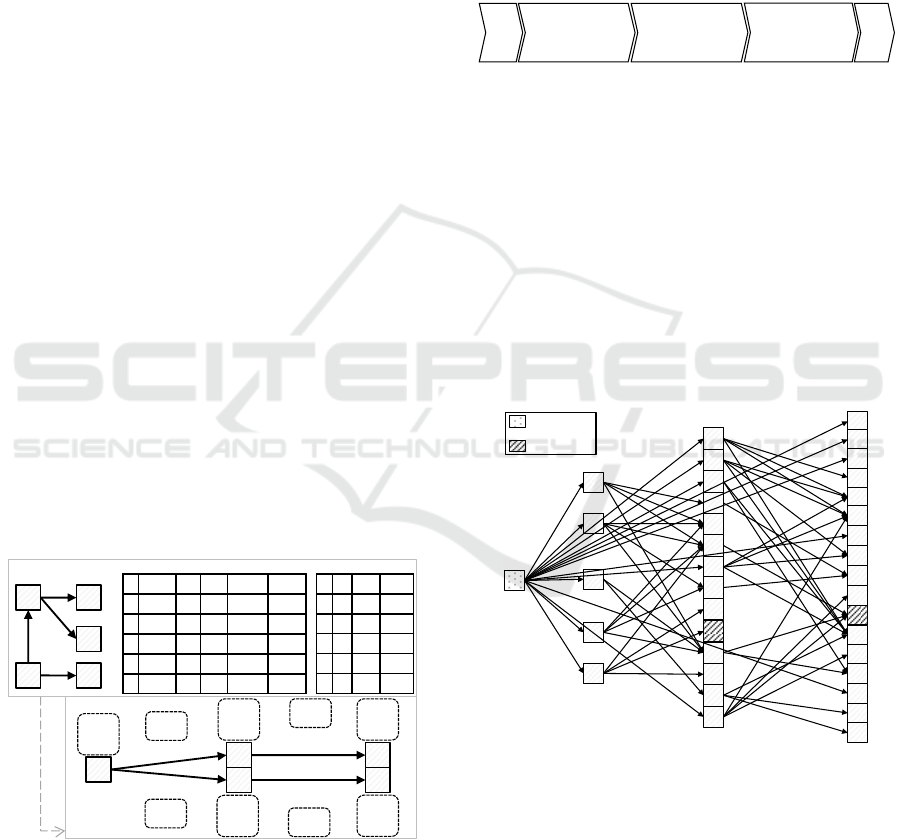
Figure 1 depicts the transformation from the orig-

inal graph to the spread graph as well as two tables il-

lustrating the performed spreading activation steps. In

the left table, each row describes one activation distri-

bution from one node to another in a pulse p including

output o

f rom,p

and transported activation t

edge,p

. The

right table shows the input activation i

v,p

and activa-

tion values a

v,p

for each node after each pulse. The

spread graph combines both the elements from the

original graph and the unrolled spreading activation

steps. Therefore, the spread graph may contain more

than one corresponding element to one original ele-

ment, e.g., v

and v

correspond to v

Original graph and spreading activation steps

‘

‘‘

‘

‘‘

‘

Spread graph

from

via

from,p

edge,p

…

... …

v,p

…

p=2

p=1

…

Figure 1: Transformation to spread graph.

Knowledge-based recommender systems often

utilize ontologies for knowledge representation, for-

mulated in different RDF-based target languages,

from plain RDF to the more expressive Web Ontol-

ogy Language. However, they all base on an underly-

ing RDF Graph, which can be visualized as directed

graph, where the contained statements are represented

by nodes and directed edges (RDF, 2014). The ap-

proach presented in this paper is applicable to any

target structure based on RDF. Usually, a recommen-

dation retrieved by spreading activation is character-

ized by the highest activation value. However, since

the presented approach is capable of explaining every

spreading activation result, the term result node spec-

iﬁes the node an explanation is required for.

Step 1

Minimization

of the

Problem Area

Step 2

Identification

Relevant Groups

Step 3

Pattern Recognition

and Explanation

Creation

Explanation

Recommen-

dation

Generation

Figure 2: Method overview.

Figure 2 illustrates our three-step method for the

explanation of a given recommendation. Initially, we

apply a minimization technique to remove all nodes

from the spread graph that are strictly irrelevant for

the explanation. On base of the resulting minimized

spread graph the most relevant subgraphs, so-called

groups, are identiﬁed in a second step by using com-

plex relevance detection techniques. In a third step,

group-based explanations are created using pattern

recognition. In the following sections, we provide a

detailed description of each step together with a con-

tinuous example.

Pulse 1 Pulse 2 Pulse 3

start node

result node

Figure 3: Example spread graph.

Example: In Figure 3, an example spread graph is

depicted representing the states of each node at each

pulse in a three-pulse spreading activation process.

For example, node 3 receives activation from node 2

in the ﬁrst pulse. The objective of this work is to ex-

plain the detected high relevance of result node 11 for

start node 2. The corresponding original graph and

the remaining spreading data are not depicted since

they are not required for understanding the example.

Explanation Retrieval in Semantic Networks - Understanding Spreading Activation based Recommendations

293

3.1 Minimization of the Problem Area

Since a spread graph represents the entire spreading

activation process, it may contain unnecessary infor-

mation for the explanation of concrete result nodes.

Nodes and edges in the spread graph that do not con-

tribute directly or indirectly to the activation of a re-

sult node, we consider to be strictly irrelevant. This

applies to all nodes and edges that are not part of any

path between start and result nodes. We refer to them

as dead-end elements and propose their removal in or-

der to minimize the problem area. As a result, we re-

trieve a minimized spread graph containing only po-

tentially relevant nodes and edges. Figure 4 illustrates

various dead-end elements, depicted as dashed lines.

start

node

result

node

dead-end

elements

potentially

relevant

elements

Figure 4: Minimization by backtracking.

Technically, the minimization follows the idea of

impact analysis. Starting at the result nodes, all paths

are tracked back in the edges’ opposite direction until

any start node is reached. All elements that are not

part of the detected tracks are dead-end elements and

can be ignored safely. The paths of the backtrack-

ing form the resulting minimized spread graph. Dur-

ing minimization, the activation values of the spread

graph are transferred to the corresponding elements in

the minimized spread graph.

Example: Figure 5 shows the result of minimization

by dead-end removal for the spread graph in Figure 3.

The minimized spread graph only contains potentially

relevant information for the explanation of the result

node 11. For example, node 8 (located between pulse

two and three) is not part of any path that starts at start

node 2 and ends at any result node 11. That means,

node 8 did not contribute anything to the relevance of

node 11 and can be removed.

Pulse 3

Pulse 2 Pulse 1

start node

result node

Figure 5: Example minimized spread graph.

3.2 Identiﬁcation of Relevant Groups

Although a minimized spread graph is usually smaller

than its corresponding spread graph, it still tends to be

too large in order to create a meaningful and concise

textual explanation. Therefore, the goal of this step is

the identiﬁcation of the most relevant subgraphs, so-

called groups, of a minimized spread graph. Their

detection strongly relies on the analysis of previ-

ously collected activation values assigned to the (min-

imized) spread graph. This data allows conclusions

about the relevance of nodes and edges at different

pulses. To identify such groups, we present two sub-

steps: selecting the most relevant nodes and determin-

ing the most relevant paths and groups around them.

3.2.1 The Most Relevant Nodes

Since each node in the minimized spread graph car-

ries a certain relevance, considering all of them in an

explanation poses a very complex task. In order to re-

duce complexity, we introduce the additional parame-

ter n > 0 to deﬁne the expected number of most rele-

vant nodes. The precision n can be conﬁgured by a

user or, alternatively, can be automatically determined

based on speciﬁc properties of the given minimized

spread graph, e.g., the number of represented pulses.

Potential candidates for most relevant nodes are

all nodes in a minimized spread graph that are neither

start nodes, result nodes, or semantically meaningless

nodes such as class or property nodes in RDF-based

semantic networks. Additionally, an application-

speciﬁc ﬁltering of the candidate nodes set is possible.

The relevance of a candidate node is indicated by its

relevance value r. The calculation of r is based on its

input activation because it composes all transported

activation values to the candidate in the given pulse

and, therefore, denotes its relevance. Furthermore,

two properties of the surrounding local network struc-

ture, i.e., connectivity and existence of class nodes,

are used for the calculation. In the following, both are

introduced in detail.

First, class nodes only represent the type of an in-

stance node, for example Ella is of type canary. A

name of an instance can be used together with its

type to raise the comprehensibility of an explanation.

However, types do not add further meaningful infor-

mation to explanations. For that reason, the trans-

ported activation from these nodes to the candidates

is subtracted from the input activation of the candi-

dates, which leads to a reduced relevance value. Ad-

ditionally, the relevance of the candidates that activate

class nodes is slightly reduced to take into account

their special relationship to class nodes.

Second, the connectivity of a candidate inﬂuences

its relevance. A strong distribution of activation is an

indicator for a very broad semantic meaning (Crestani

and Lee, 2000) and, therefore, indicates less rele-

vance for an explanation. On the other side, highly

connected nodes, which receive activation over many

edges, tend to get high input activation values. Never-

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

294

theless, candidates with lower input activation values

might be more relevant for an explanation, e.g., when

the activating edges carried more semantic meaning.

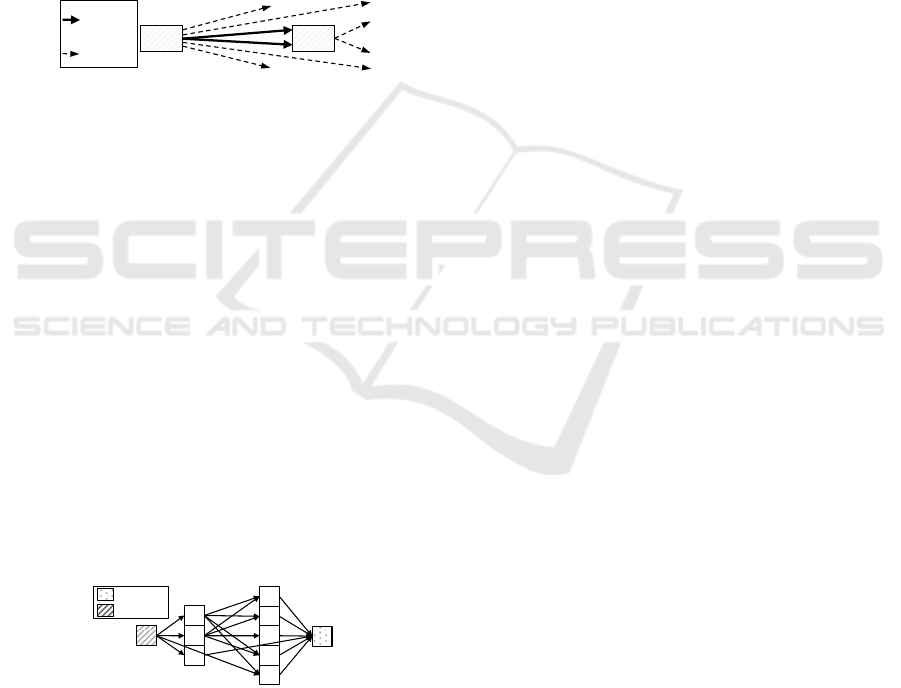
In Figure 6(a), node x receives activation by only two

nodes, whereas in Figure 6(b), node y receives acti-

vation by many nodes. The overall input activation

i of node y exceeds the input activation of node x

by 1. However, node x should be considered to be

more relevant for an explanation than node y. In order

to compare highly connected nodes with other nodes,

the ratio of in- and outgoing edges is considered dur-

ing relevance value computation.

1001

…

t=1

t=500

i=1000

i=1001

(b) (a)

Figure 6: Highly connected nodes.

The relevance of each node is calculated by de-

ﬁned relevance functions based on its input activation

with respect to the beforementioned properties. Then,

the n nodes with the highest relevance values from the

candidate set represent the most relevant nodes.

Example: The input activation and the calculated

relevance values for all candidates in the minimized

spread graph are shown in Figure 7. Start node 2 and

result node 11 are by deﬁnition no candidates as well

as the class nodes 16. Nodes 12 and 3 are the resulting

relevant nodes due to their highest relevance values.

Note, that node 6 has a higher input activation than

node 3. However, regarding the relevance value, node

3 outperforms node 6 because of the connectivity.

relevance value

Pulse 3

Pulse 2 Pulse 1

3,8475 | 0,7695

11,34 | 2,268

1,35 | 0,45

1,8 | 0,9

1,35 | 0,45

class node

input activation

start node

result node

Figure 7: Weighted example minimized spread graph.

3.2.2 The Most Relevant Paths and Groups

The detected most relevant nodes do not form an ex-

planation yet due to missing information about their

relationship to the start and result node(s). This re-

lationship can be clariﬁed through the paths leading

from the result node via a relevant node to a start node

in the minimized spread graph. The problem of ﬁnd-

ing such paths can be transformed into the two prob-

lems of ﬁnding a set of paths between the result and

relevant node and between the relevant and the start

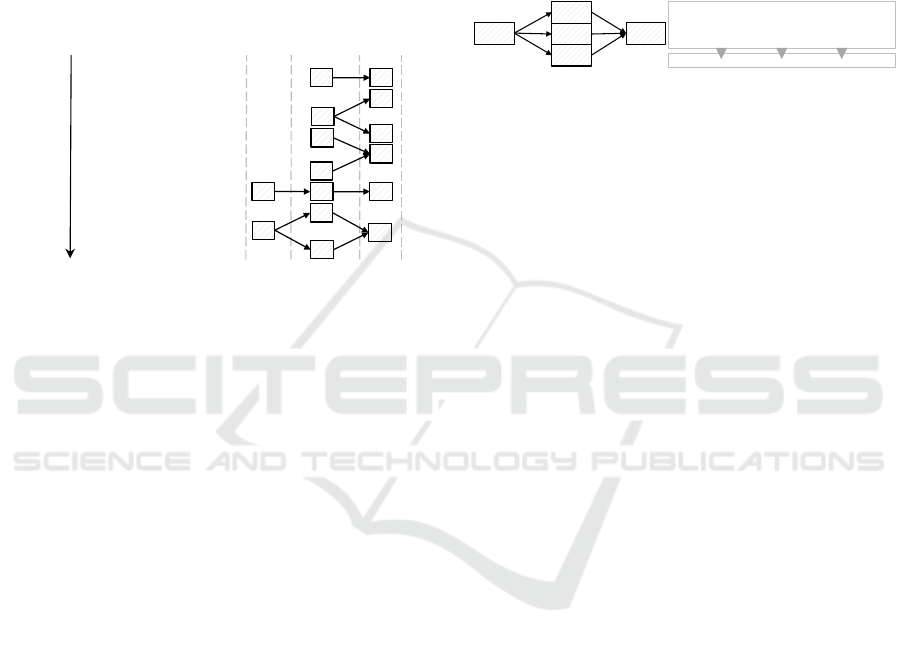
node(s), as shown in Figure 8. We deﬁne an additional

parameter m > 0 for each subproblem, which restricts

the number of paths to identify in order to reduce the

explanation length. This value is either user-speciﬁed

or based on speciﬁc properties.

result

node

relevant

node

relevant

node

start

node

…

result

node

relevant

node

start

node

…

result group

start group

Figure 8: Dividing the path-ﬁnding problem.

For the explanation, we search for the most ex-

pressive and, therefore, the most relevant paths. Since

the transported activation reﬂects the relevance of

an edge, the relevance of a path can be determined

by the sum of transported activation values along its

edges. Thus, the most relevant paths are the longest

paths regarding their overall transported activation.

Generally, ﬁnding a longest path is NP-hard (Uehara

and Uno, 2004). However, directed acyclic graphs,

such as (minimized) spread graphs, allow an efﬁ-

cient solution of the problem. In (Sedgewick and

Wayne, 2011), the authors propose the determination

of longest paths by using a shortest path algorithm

with negated edge weights. We apply this approach

to a Bellman-Ford algorithm. In contrast to origi-

nal graphs, spread graphs support the efﬁcient longest

path search. This is an advantage of the approach pre-

sented in this paper.

Each identiﬁed set of most relevant paths for one

relevant node can be represented as a subgraph of

the minimized spread graph. We call such subgraphs

groups, whereas the group from a result node to a rele-

vant node is called result group and the group from a

relevant node to start node(s) is called start group (see

Figure 8). Distinguishing between these two groups is

a beneﬁt, because it allows customized explanations

for their diverging meaning. While the start group

explains the origin of a relevant node, i.e., the recom-

mendation request, the result group explains its effect,

i.e., recommendation.

Example: Based on the minimized spread graph, the

start and result groups for the relevant nodes 12 and

3 are illustrated in Figure 9. For this example, the

maximum number of paths per group (parameter m)

is restricted to 2. Therefore, the start group of node 12

does not contain all potentially relevant paths.

result group

start group

result group

start group

11 12

12 3

start node

result node

relevant node

Figure 9: Example groups for the relevant nodes.

Explanation Retrieval in Semantic Networks - Understanding Spreading Activation based Recommendations

295

3.3 Pattern Recognition and

Explanation Creation

The beneﬁt of group-based explanations is that we do

not depend on explaining paths as one-dimensional

statements but can take advantage of cross-path in-

formation within the graph. Pattern analysis allows to

linguistically subsume elements in an explanation that

structurally belong together in the underlying group.

This prevents confusing explanations and supports

conciseness, compactness, and comprehensibility.

v‘

…

e‘

No pattern

Multiple outgoing edges

Multiple incoming edges

Chain of three

Diamond

low

priority

high

priority

level level level

Figure 10: Patterns.

We identiﬁed the patterns in Figure 10, which are

prioritized regarding their expressiveness: from low

priority for no speciﬁc pattern to highly prioritized di-

amonds. If no special pattern can be identiﬁed, two

nodes and their connecting edge can be interpreted as

a simple statement of subject, predicate, and object, as

common for semantic networks. In case one node has

at least two outgoing edges to other nodes, the pattern

of multiple outgoing edges applies. Similarly, there is

a pattern for multiple incoming edges. The chain of

three pattern applies whenever there is a sequence of

three nodes connected by unidirectional edges. The

diamond pattern describes two or more equally long

downward paths that split in the ﬁrst node and rejoin

in the last node. However, the level of depth must be

exactly 3 and the nodes of a level and the edges be-

tween the same levels have to be of the same type.

A less restrictive concept for diamond structures was

introduced by (Furnas and Zacks, 1994) in the area

of multi-tree analysis. Since all other patterns are in-

cluded in a diamond, it contains most structural infor-

mation. This makes diamond structures especially ex-

pressive and valuable for explanations. After the pro-

posed pattern recognition, the actual sentence build-

ing process is straightforward. In this work, English

language is used. However, language-speciﬁc appli-

cation is possible. Sentence building follows two ba-

sic principles. First, as many nodes and edges as pos-

sible, that are located on the same depth level in the

pattern, should be subsumed, e.g., utilizing connec-

tion words such as and or using types. Second, the

different levels of a pattern need to be concatenated

to form a sentence, e.g., utilizing connection words

such as which. The generated textual explanation sup-

ports the user to comprehend the reasons for a given

spreading activation based recommendation.

Example: Figure 11 contains a sentence building ex-

ample for the described diamond pattern, which al-

lows to build only one short and more expressive sen-

tence instead of six sentences.

likes

cub B

canary

Ella

cub A

drink

water

has

likes to

The canary Ella has cub A. The canary Ella has

cub B. The canary Ella has cub C. Cub A likes to

drink water. Cub B likes to drink water. Cub C

likes to drink water.

cub C

has

likes to

The canary Ella has cubs, who like to drink water.

Figure 11: Sentence building example based on diamonds.

4 EVALUATION

Evaluating explanations is very challenging since the

most interesting evaluation criterion refers to useful-

ness. Usefulness can only be assessed subjectively,

mostly depending on the experience and preferences

of the observer (Klahold, 2009). In this paper, two

different evaluation approaches are utilized to show

the explanations’ usefulness. The ﬁrst approach ar-

gues on the fulﬁllment of selected explanation goals

as proposed by (Tintarev and Masthoff, 2011). The

second approach evaluates the goodness of explana-

tions by estimating precision, recall, and F-measure.

These measures are common for assessing the good-

ness of recommendations and are applicable to expla-

nations as well (Klahold, 2009).

4.1 Fulﬁllment of the Explanation Goals

In (Tintarev and Masthoff, 2011), the authors propose

an explanation goal dependent evaluation of explana-

tions with goals like transparency, effectiveness, and

efﬁciency. Furthermore, they provide guidelines for

the application-speciﬁc selection of goals and their

evaluation. In this work, we focus on examining the

goals transparency as well as the support of efﬁcient

and effective decisions for users.

Transparency: The proposed explanation generation

process follows a strict and reproducible process, uti-

lizing different intermediate graph structures. Each

intermediate graph is based on its predecessor and

their mutual relationships are deﬁned by transforma-

tion rules. Therefore, an explanation is traceable

backwards through the intermediate graph structures

to the spread graph depicting the spreading activation

process. The result node as well as its corresponding

nodes can be identiﬁed in each single process step.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

296

This supports the user’s understanding of how the sys-

tem works. We therefore consider the proposed expla-

nation generation process to be transparent.

Effectiveness and Efﬁciency: Usually, original

graphs contain much information and spread graphs

tend to be even larger. For example, an original graph

examined in this paper with more than 26 000 nodes

and 138 000 edges leads to a spread graph of 108 000

nodes and 136 000 edges after 6 pulses. Manual trace-

ability of this large amount of data is infeasible. In

contrast, the minimized spread graph only contains 90

nodes and 190 edges, the groups even consist of only

11 nodes and 10 edges. That means, the user retrieves

an immensely reduced data set, which supports an ef-

fective and efﬁcient decision making process.

These arguments show that the generated explana-

tions are adequate to their purpose. The explanations

are transparent and support effective and efﬁcient de-

cisions, which contributes to their usefulness.

4.2 Goodness of the Explanations

To evaluate the explanations’ goodness, we apply the

proposed explanation generation method to results

from the HARvESTer recommender system, which

supports safety experts when performing automotive

safety analyses (Hartig and Karbe, 2016). There,

semantic networks represent real data of completed

automotive safety analyses by an automobile manu-

facturer. For each node and edge of such networks,

the information whether or not it is expected to be

part of an explanation for a given recommendation

is assigned

. Then, an explanation is generated for

the recommendation using the proposed explanation

method. Both results can then be compared regarding

their precision, recall, and calculated F-measure. For

the evaluation, we examine three different requests,

e.g., inquiring malfunctions based on user-given func-

tions, with 4 to 6 pulses. They are performed on four

semantic networks of different sizes listed in Table 1.

Table 1: Sizes of examined networks.

Networks A B C D

# nodes 1800 775 1218 26432

# edges 8779 3426 5319 138773

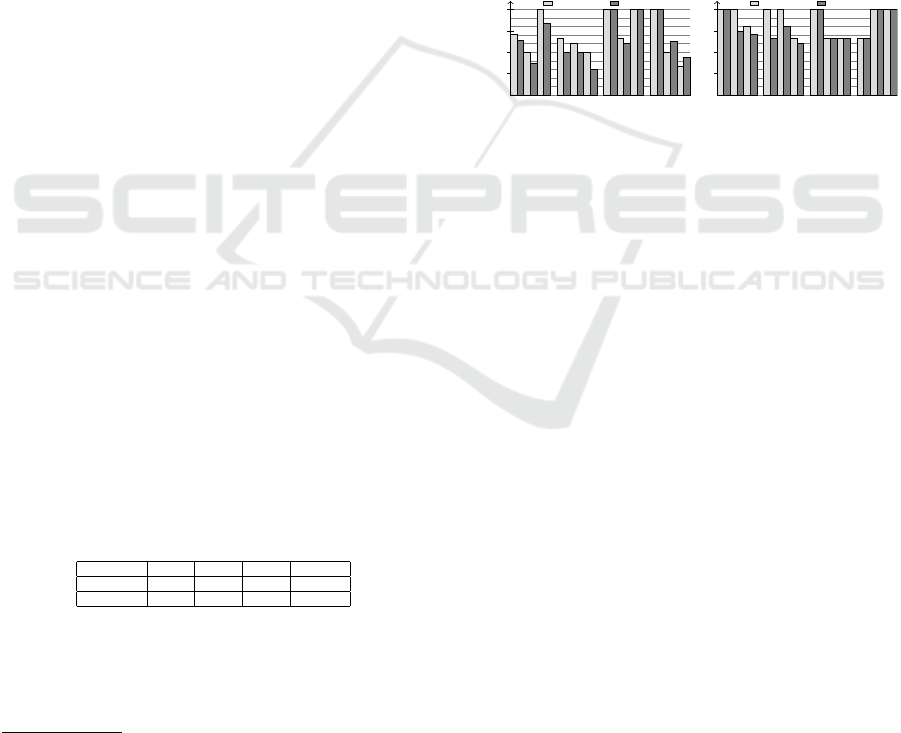
The precision for each request and network is

shown in Figure 12 (left), grouped by nodes (light

gray) and edges (dark gray). The precision results

range from 33% to 100%, where 100% means that

Remark: The assignment of the expected values are de-

termined by one advanced user. Certainly, the evaluations’

reliability can beneﬁt from an assignment by a safety expert

group. For this work, an expert group is not available. This

is planned for extensive future case studies.

the generated explanation contains no false positive

element, i.e., unexpected node or edge. The lower

precision rates, e.g., for network B, are caused by two

main reasons. First, multiple nodes and edges are of-

ten of similar importance. Second, the size of the ex-

planation is restricted by the presented parameters n

and m. Thus, it is possible that only some of several

nodes and edges of similar importance are chosen for

an explanation while other expected nodes and edges

are missing. This explains that receiving 100% is not

always possible. The recall for each request and net-

work is shown in Figure 12 (right). Results range

from 60% to 100%, where 100% means that all ex-

pected nodes or edges are part of a generated expla-

nation, e.g., for request 1 on network C. Lower recall

results are mainly caused by similar important nodes

and edges, resulting in similar good explanations.

Precision

25%

50%

75%

100%

Request

Network

Nodes

Edges

Recall

25%

50%

75%

100%

Nodes

Edges

Figure 12: Precision and recall for nodes and edges.

The quality of an explanation beneﬁts more from

a high rate of expected elements in the explanation

than it loses by additional nodes and edges. There-

fore, recall can be considered to be more important

than precision, i.e., represented by a F

-measure. Its

results range between 62% and 100% with an aver-

age of 84% for nodes and 78% for edges (exclud-

ing outliers). The evaluation shows, especially under-

lined by the high average F-measure, that the content

of the generated explanation generally corresponds to

the expectations. Besides the explanation generation

method, the goodness of an explanation strongly de-

pends on the different user preferences, the expres-

siveness of the underlying knowledge base and the

conﬁguration of the spreading activation algorithm.

5 CONCLUSION AND OUTLOOK

In this paper, we presented a method to retrieve ex-

planations for semantic search results obtained by

spreading activation techniques. The novelty of our

approach is the excessive exploitation of the data ac-

cumulated during the search process instead of uti-

lizing the original network. Therefore, our method

is performed on a speciﬁc graph representing the

spreading process, the so-called spread graph. We

presented our explanation retrieval method in three

steps. Firstly, we introduced a minimization tech-

Explanation Retrieval in Semantic Networks - Understanding Spreading Activation based Recommendations

297

nique for the spread graph in order to remove strictly

irrelevant parts. Secondly, we presented the retrieval

of the most relevant subgraphs, so-called groups,

from the minimized spread graph. Lastly, we de-

scribed pattern recognition techniques to facilitate

meaningful and concise explanation verbalization in

natural language. The evaluation of the approach

showed promising results. For the examined seman-

tic networks, we were able to highlight both the ful-

ﬁllment of the explanation goals and the goodness of

the generated explanations. However, we see much

potential for future research. Since the identiﬁca-

tion of relevant parts in the spread graph is based

on very complex relations, our approach can be re-

ﬁned, e.g., by an additional consideration of more

complex neighborhood inﬂuences. A more extensive

pattern analysis can improve the conciseness of gener-

ated explanations. We furthermore plan on extended

case studies in real-world application environments to

see the beneﬁt of the provided explanations, e.g., the

increasing trust in recommendations. Especially, an

explanation goodness comparison with existing ap-

proaches can emphasize the beneﬁt of our approach.

REFERENCES

Aleman-Meza, B., Halaschek-Weiner, C., Arpinar, I. B.,

Ramakrishnan, C., and Sheth, A. (2005). Ranking

complex relationships on the semantic web. IEEE In-

ternet Computing, 9(3):37–44.

Alvarez, J. M., Polo, L., Jimenez, W., Abella, P., and Labra,

J. E. (2011). Application of the spreading activation

technique for recommending concepts of well-known

ontologies in medical systems. Proceedings of the 2nd

ACM Conference on Bioinformatics, Computational

Biology and Biomedicine (BCB ’11), page 626.

Crestani, F. (1997). Application of spreading activation

techniques in information retrieval. Artiﬁcial Intelli-

gence Review, 11(6):453–482.

Crestani, F. and Lee, P. L. (2000). Searching the web by

constrained spreading activation. Information Pro-

cessing and Management: an International Journal

- Artiﬁcial Intelligence and Information Retrieval,

36(4):585–605.

Faloutsos, C., McCurley, K. S., and Tomkins, A. (2004).

Fast discovery of connection subgraphs. In Proceed-

ings of the tenth ACM SIGKDD international confer-

ence on Knowledge discovery and data mining (KDD

’04), pages 118–127, New York. ACM.

Forcher, B., Agne, S., Dengel, A., Gillmann, M., and Roth-

Berghofer, T. (2012). Towards Understandable Ex-

planations for Document Analysis Systems. In 10th

International Workshop on Document Analysis Sys-

tems(DAS) IAPR, pages 6–10, Gold Cost.

Forcher, B., Roth-Berghofer, T., Sintek, M., and Dengel,

A. (2010). Constructing Understandable Explana-

tions for Semantic Search Results. In 17th Interna-

tional Conference, Knowledge Engineering and Man-

agement by the Masses (EKAW), pages 493–502, Lis-

bon. Springer.

Forcher, B., Roth-Berghofer, T., Sintek, M., and Dengel,

A. (2011). Semantic Logging: Towards Explanation-

Aware DAS. In International Conference on Doc-

ument Analysis and Recognition (ICDAR’11), pages

1140–1144, Beijing. IEEE.

Furnas, G. W. and Zacks, J. (1994). Multitrees: Enriching

and Reusing Hierarchical Structure. In Conference

on Human Factors in Computing Systems (CHI’94),

pages 330–336, Bosten, Massachusetts. ACM.

Hartig, K. and Karbe, T. (2016). Recommendation-

based Decision Support for Hazard Analysis and Risk

Assessment. In 8th International Conference on

Information, Process, and Knowledge Management

(eKNOW ’16), pages 108–111.

Jain, S., Grover, A., Thakur, P. S., and Choudhary, S. K.

(2015). Trends, Problems And Solutions of Recom-

mender System. In International Conference on Com-

puting, Communication and Automation (ICCCA’15),

pages 955–958, Noida. IEEE.

Kaklauskas, A. (2015). Intelligent Decision Support Sys-

tems. In Biometric and Intelligent Decision Making

Support, volume 81, pages 195–220. Springer.

Klahold, A. (2009). Empfehlungssysteme: Recommender

Systems - Grundlagen, Konzepte und L

osungen [Rec-

ommender Systems - Fundamentals, concepts and so-

lutions]. Vieweg + Teubner, Wiesbaden.

RDF (2014). RDF 1.1 Concepts and Abstract Syntax. World

Wide Web Consortium - W3C. Accessed: 15.06.2016.

Sedgewick, R. and Wayne, K. (2011). Algorithms - Fourth

Edition. Addison-Wesley, Boston, Massachusetts.

Sinha, R. and Swearingen, K. (2002). The role of trans-

parency in recommender systems. In Extended Ab-

stracts on Human Factors in Computing Systems (CHI

EA, CHI), pages 830–831, New York. ACM.

Tintarev, N. and Masthoff, J. (2011). Designing and evaluat-

ing explanations for recommender systems. In Ricci,

F., Rokach, L., Shapira, B., and Kantor, P. B., ed-

itors, Recommender Systems Handbook, pages 479–

510. Springer, US.

Uehara, R. and Uno, Y. (2004). Efﬁcient Algorithms for

the Longest Path Problem. In Algorithms and Compu-

tation - 15th International Symposium (ISAAC ’04),

pages 871–883, Hong Kong. Springer.

Viswanathan, V. and Krishnamurthi, I. (2012). Finding rele-

vant semantic association paths through user-speciﬁc

intermediate entities. Human-centric Computing and

Information Sciences, 2(9).

Viswanathan, V. and Krishnamurthi, I. (2015). Finding

relevant semantic association paths using semantic ant

colony optimization algorithm. Soft Computing - A

Fusion of Foundations, Methodologies and Applica-

tions, 19(1):251–260.

Wick, M. R. and Thompson, W. B. (1992). Reconstruc-

tive expert system explanation. Artiﬁcial Intelligence,

54(1-2):33–70.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

298