
Contingency Table Analysis Applying
Fuzzy Number and Its Application
Needs Analysis for Media Lectures
Hiroaki Uesu
Global Education Center, Waseda University, Tokyo, Japan
Keywords: Type-2 Fuzzy Contingency Table, Fuzzy Numbers, Needs Analysis, Kano Model.
Abstract: Generally, we could efficiently analyse the inexact information by applying fuzzy theory. We would extend
contingency table, and propose type-2 fuzzy contingency table. In this paper, we would discuss about type-2
fuzzy contingency table and a needs analysis method applying type-2 fuzzy contingency table.
1 INTRODUCTION
With the spread PCs, tablet PCs and high-capacity
Internet communication, recognition of university
students for the media class has been changed
significantly. In order to the better media class, it is
important to know what students are feeling.
Today, there are some of the needs of the
students, for example, teaching aid, homework,
feedback and so on. In this paper, we propose a
questionnaire analysis that applies type-2 fuzzy
contingency table.
2 FUZZY CONTINGENCY TABLE
Def. 1. Cardinality of Type-1 Fuzzy Set
Consider the type-1 fuzzy set A in universe =
|=1,⋯,
. Cardinality |A| of type-1 fuzzy set
A is defined as follows;
|
|
=
where,
is a membership function of a
type-1 fuzzy set A.
Def. 2. Type-1 Fuzzy ×Contingency Table
Consider the type-1 fuzzy set A in universe =
|=1,⋯,
. The type-1 fuzzy ×
contingency table of type-1 fuzzy set
,⋯,
,
,⋯,
is defined as follows;
where,
=1,
=1
and,
=
∩
∩
=
∙
.
Here, we would expand the definition, we define
a type-2 fuzzy contingency table. For the definition
of type-2 fuzzy contingency table, we need the mean
value of fuzzy numbers, the product value of fuzzy
numbers and the intersection of type-2 fuzzy sets.
Then, we could clarify these definitions.
Def. 3. Mean Value of Fuzzy Numbers
Let
∗
,
∗
,
∗
,…,
∗
be fuzzy numbers with −cuts
∗
=
,
,
,
∈ℝ,0≤≤1
then the mean value
∗
;
∗
=
∗
∈
,
∗
=
1
,
,
1
,
Uesu, H.
Contingency Table Analysis Applying Fuzzy Number and Its Application - Needs Analysis for Media Lectures.
DOI: 10.5220/0006050600930100
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 93-100
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
93

Def. 4. Product Value of Fuzzy Numbers
Let
∗
,
∗
be fuzzy numbers with −cuts
∗
=
,
,
,
∈ℝ,0≤≤1
then the product value
∗
⋅
∗
;
∗
⋅
∗
=
∗
⋅
∗
∈
,
∗
⋅
∗
= min
,
∈
∗
×
∗
⋅
,max
,
∈
∗
×
∗
⋅
Def. 5. Intersection of Type-2 Fuzzy Sets
Consider the type-2 fuzzy sets
,
in universe
=
|=1,⋯,
;
=
,
∗
|=1,…,
,
=
,
∗
|=1,…,
where, let
∗
,
∗
be fuzzy numbers. Then the
intersection
∩
;
∩
=
,
∗
⋅
∗
|=1,…,
Here, we would define the type-2 fuzzy
contingency table by these definitions.
Def. 6. Type-2 Fuzzy m×n Contingency Table
Consider the type-2 fuzzy sets
,⋯,
,
,⋯,
in universe
=
|=1,⋯,
;
=
,
,
,
∗
|=1,…,,
=
,
,
,
∗
|=1,…,
1≤≤,1≤≤
⋯
⋯
⋮ ⋮
⋮
⋯
where, let
be mean value
∗
⋅
∗
of grades of
intersection
,
.
Def. 7. Entropy of Fuzzy Number
Let
∗
be fuzzy numbers with membership
function
∗
, then the entropy
∗
of fuzzy
number
∗
;
∗
=
∗
=
−log−
1−
log
1−
,01
0,
3 ANALYSIS METHOD
The Kano model
[1]
is a theory of product
development and customer satisfaction developed in
the 1980s by Professor Noriaki Kano, which
classifies customer preferences into five categories.
Figure 1: Kano Model Illustrated.
• Must Be (Expected Quality):
Requirement that can dissatisfy (expected, but
cannot increase satisfaction)
• One-Dimensional (Desired Quality):
The more of these requirements that are met,
the more a client is satisfied
• Delighters (Excited Quality):
If the requirement is absent, it does not cause
dissatisfaction, but it will delight clients if
present
• Indifferent:
Client is indifferent to whether the feature is
present or not
• Reverse:
Feature actually causes dissatisfaction
The authors propose a method to analyse Kano
model style questionnaire to the media classroom,
analysed by type-2 fuzzy m×n contingency table.
1. We execute questionnaire, we ask two questions
for one requirement. Two questions are a positive
question and a negative question.
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
94

• Positive question:
“How does customer feel if the requirement
can be met?”
• Negative question:
“ How does customer feel if the requirement
can't be met?”
And, we prepare the answer choices of 13 steps to
each question.
Figure 2: Positive Question and Negative Question.
2. We count the answer of questionnaire by fuzzy
number, and create type-2 fuzzy sets.
For example, when a student
checks for second
step (Fig.3.), we interpret as follows:
The degree of truth of the statement "a student
answers ‘I like it that way’ ” is grade
, the
degree of truth of the statement "a student
answers ‘I am expecting it to be that way’” is
grade
.
Figure 3: Example.
Here, we define a membership function
of the fuzzy number as follows:
=max
0,1−
|
3
−
|
Figure 4: Membership Function
.
3. We create a 5×5 fuzzy contingency table(Table I.)
For example, let
be mean value of grades of
intersection “Expect(Functional)” and
“Neutral(Dysfunctional)”. Consider the type-2
fuzzy sets
,
in universe =
,
. If
“Expect(Functional)” :
=
,
,
,
“Neutral(Dysfunctional)”:
=
,1
,
,
,
then
∩
=
,
∗1
,
,
∗
, and the
membership function of fuzzy number
∗1
and
∗
as follows:
0
0.5
1
0 1/3 2/3 1
Contingency Table Analysis Applying Fuzzy Number and Its Application - Needs Analysis for Media Lectures
95

Table 1: 5×5 Fuzzy Contingency Table.
•
∗1
:
∗
=maxmin
−3+
√
1+36
2
,
7−
√
1+36
2
,0
•
∗
:
∗
=maxmin
−1+
√
1+36
2
,
5−
√
1+36
2
,0
Figure 5: Membership Function
∗
.
Figure 6: Membership Function
∗
.
Fuzzy number
∗1
with −cuts
2
3
∗1
=
+3+2
9
,
−7+12
9
andfuzzy number
∗
with −cuts
1
3
∗
2
3
=
+
9
,
−5+6
9
then, −cuts of
is calculated as follows:
=
+2+1
9
,
−6+9
9
Figure 7: Membership Function
.
4. From 5×5fuzzy contingency table, we create a
cardinality table(Table II.).
0
0.25
0.5
0.75
1
0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.25
0.5
0.75
1
0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.25
0.5
0.75
1
0 0.2 0.4 0.6 0.8 1 1.2 1.4
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
96
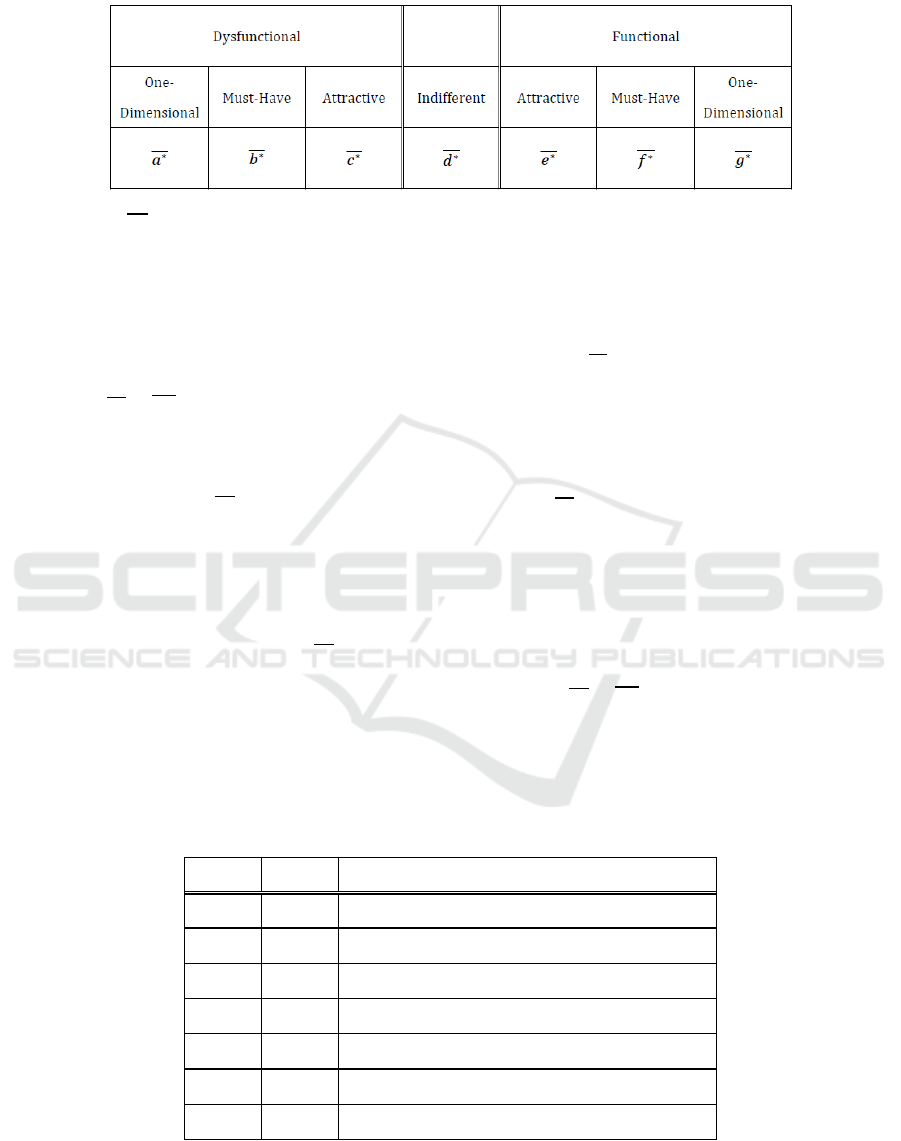
Table 2: Cardinality Table.
Where, Let
∗
be fuzzy numbers with −cuts;
∗
=
,
,
,
∈ℝ,0≤≤1
then,
∗
=
∗
,
∗
=
∗
∈
,
∗
=
,
,
,
,
∗
=
∗
∈
,
∗
=
,
,
,
∗
=
∗
∈
,
∗
=
,
,
,
,
∗
=
∗
∈
,
∗
=
,
,
,
,
∗
=
∗
∈
,
∗
=
,
,
,
,
∗
=
∗
5. From a cardinality table, we calculate the fuzzy weighted average. These weights are as follows:
Table 3: Weight Table.
weight input conclusion
-1 O(N) not actively implement this requirement
- 2/3 M(N) not implement as much as possible this requirement
- 1/3 A(N) can afford to not implement this requirement
0 I can't decided either way
1/3 A(P) can afford to implement this requirement
2/3 M(P) implement as much as possible this requirement
1 O(P) actively implement this requirement
Contingency Table Analysis Applying Fuzzy Number and Its Application - Needs Analysis for Media Lectures
97
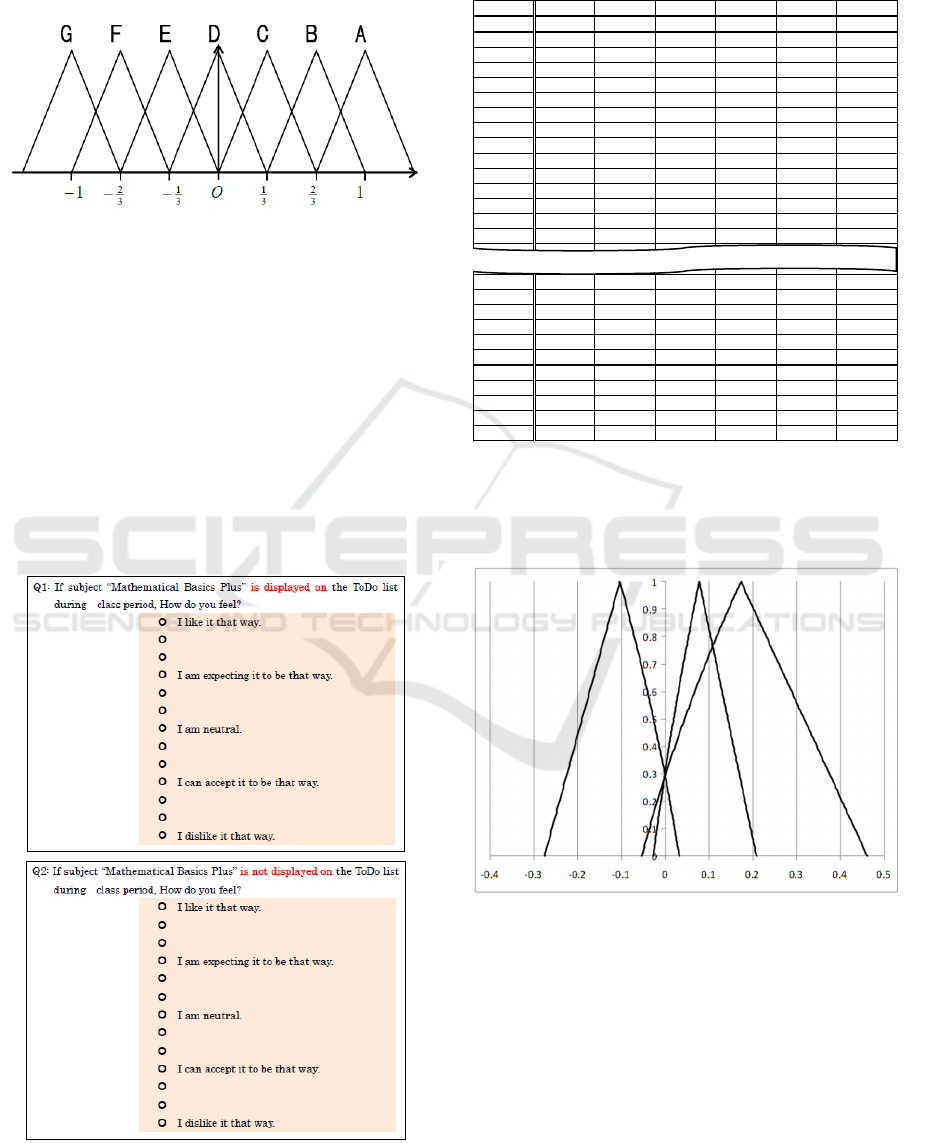
The weight are fuzzy number , the membership
function is defined as follows:
=max
0,1−
|
3
−
|
Figure 8: Membership Functions of weight.
We determine a comprehensive evaluation from
this fuzzy weighted average.
4 APPLICATION
We executed questionnaires about the function for
the media class for 244 students.
Questionnaires:
Q1,Q2 : ToDo list
Q3,Q4 : Reminder Mail
Q5,Q6 : Test’s Deadline
Figure 9: Questionnaires (Q1,Q2).
Then, we obtain the response table(Table IV.).
Table 4: Response Table.
By using the previous method, we obtain a
cardinality table (Table V.).
Next, we calculate the fuzzy weighted average.
Figure 10: Fuzzy Weighted Average.
Then, we determine a comprehensive evaluation
by calculating gravity of this fuzzy weighted average.
No.Q1Q2Q3Q4Q5Q6
17777131
27710477
37747132
4101 1 9103
5777777
6777777
77127738
87711377
911610477
10 1 10 1 10 7 7
11771781
127 7 410131
13 1 10 1 10 10 1
14 1 13 1 13 13 1
15777796
167 7 1107 7
233000000
2342106777
235 1 13 1 13 7 7
2367 7 710122
2377 7 1137 7
238111111
239000000
2407 7 2107 7
241777777
242772777
243776777
2447 7 110102
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
98

Table 5: Cardinality Table (Q1,Q2).
Table 6: Result.
ToDo List
Reminder
Mail
Test’s
Deadline
Weighted
Average
0.078324 0.173297 -0.10338
Center of
Gravity
0.084673 0.188755 -0.11257
Fuzzy
Entropy
0.170076 0.372188 0.222228
5 CONCLUSION
We executed a needs analysis of the students
applying type-2 fuzzy 5 × 5 contingency table. As a
result, it was able to confirm its effectiveness as a
method. Further, we would like to improve
analytical methods in the future.
This paper is a part of the outcome of research
performed under a Waseda University Grant for
Special Research Projects (Project number: 2016B-
310).
REFERENCES
N. Kano, N. Seraku, F. Takahashi, S. Tsuji: Attractive
quality and must-be quality, Journal of the Japanese
Society for Quality Control 14(2), pp. 39-48, 1984 (in
Japanese).
M. Rashid, J. Tamaki, A. M. M. S. Ullah, and A. Kubo: A
Kano Model Based Linguistic Application for
Customer Needs Analysis, International Journal of
Engineering Business Management, Vol.3, No.2, pp.
30-36, 2011.
H. Uesu, S. Takagi: An analysis of students’ needs for
undergraduate mathematics lectures through the Kano
model, Japan Society for Fuzzy Theory and Intelligent
Informatics Soft Science Workshop, pp. 87-88, 2014
(in Japanese).
H. Uesu: Students’ needs analysis for media lectures
applying Kano model, Japan Society for Fuzzy Theory
and Intelligent Informatics Soft Science Workshop,
pp. 89-90, 2014(in Japanese).
H. Uesu: Needs Analysis for Media Lectures Applying
Kano Model, Japan Society for Fuzzy Theory and
Intelligent Informatics Fuzzy System Symposium,
pp. 208-211, 2014(in Japanese).
H. Uesu, S. Kanagawa: Student Needs Analysis Applying
Fuzzy Contingency Table, the 27th Annual
Conference of Biomedical Fuzzy System Association,
pp. 45-46, 2014.
Contingency Table Analysis Applying Fuzzy Number and Its Application - Needs Analysis for Media Lectures
99

H. Uesu: Type-2 Fuzzy Contingency Table Analysis and
its Application the Seventh International Conference
on Dynamic Systems and Applications, 2015.
H. Uesu: Needs Analysis Applying Type-2 Fuzzy
Contingency Table, International Symposium on
Management Engineering 2015
,
pp. 35-38, 2015.
Hiroaki Uesu: Student’s Needs Analysis Applying Type-2
Fuzzy Contingency Table for Media Lectures,
Proceedings of the 28th Annual Conference of
Biomedical Fuzzy Systems Association, pp.293-296
,
2015.
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
100
