Neural Model for the Inﬂuence of Shading on the Multistability of the

Perception of Body Motion

Leonid Fedorov

1,2

, Joris Vangeneugden

and Martin Giese

1,2

Dept. of Cognitive Neurology, CIN, HIH, University of Tuebingen, Tuebingen, Germany

IMPRS for Cognitive and Systems Neuroscience, Tuebingen, Germany

School of Mental Health and Neuroscience, Maastricht, The Netherlands

Keywords:

Action Recognition, Multistable Perception, Biological Motion, Neural Fields, Shading.

Abstract:

Body motion perception from impoverished stimuli shows interesting dynamic properties, such as multista-

bility and spontaneous perceptual switching. Psychophysical experiments show that such multistability dis-

appears when the stimulus includes also shading cues along the body surface. Classical neural models for

body motion perception have not addressed perceptual multistability. We present an extension of a classical

neurodynamic model for biological and body motion perception that accounts for perceptual switching, and

its dependence on shading cues on the body surface. We demonstrate that a set of psychophysical observa-

tions can be accounted for in a unifying manner by a hierarchical neural model for body motion processing

that includes an additional shading pathway, which processes luminance gradients within the individual body

segments. The goal of our model is to explain psychophysics and neural mechanism in the brain.

1 INTRODUCTION

The perception of body motion from image sequences

requires the dynamic integration of complex spatio-

temporal visual patterns. This important visual func-

tion is accomplished by processing within a hierar-

chy of cortical areas along the visual pathway. Psy-

chophysical studies suggest depth cues are important

for biological motion perception (Jackson and Blake,

2010). In absence of such depth information, e.g. in

point-light walkers, body motion perception can be-

come multistable (Vanrie and Verfaillie, 2004). Then

the same stimulus can be perceived as alternating ran-

domly between two interpretations that correspond to

two different walking directions (Vanrie and Verfail-

lie, 2006). Multistabile phenomena has been also in-

vestigated in the context of static ambiguous ﬁgures

and binocular rivalry (Leopold and Logothetis, 1999),

(Blake and Logothesis, 2001), as well as in structure

from motion (Andersen and Bradley, 1998). An ex-

ample of the body motion stimulus that produces such

multistability is shown in Fig. 1A (panel SILHOU-

ETTE). For this stimulus, an articulating silhouette

without intrinsic shading cues, observers perceive the

walker alternately walking obliquely into or out of the

image plane. The two reported percepts correspond to

the unambiguous walking directions indicated in pan-

els TOWARDS and AWAY. The ﬁgure illustrates also

that this perceptual ambiguity disappears when shad-

ing gradients are added to the surface of the walker,

which provide information about the surface orienta-

tion of the body segments and occlusions.

Existing physiologically-inspired neural models

for the processing of body motion and goal-directed

actions (e.g. (Giese and Poggio, 2003), (Lange

and Lappe, 2006), (Escobar and Kornprobst, 2008),

(Jhuang et al., 2007), (Fleischer et al., 2013) and

(Layher et al., 2014)) do not reproduce such multi-

stability, or at least never have investigated this phe-

nomenon. Computer vision and deep learning archi-

tectures for body motion recognition do not address

perceptual multistability. Thus, the study of such phe-

nomena is important for neuroscience, even if such

multistability is often unwanted in technical action

recognition systems.

In the context of low-level vision, perceptual

multi-stability and the underlying neural dynamics

have been extensively studied e.g. in the context of

binocular rivalry (see e.g. (Wilson, 2003)), visual

motion integration (Rankin et al., 2014), or as gen-

eral property of attractor neural networks (Pastukhov

et al., 2013).

The goal of this paper is to extend existing

physiologically-inspired neural models (not computer

Fedorov, L., Vangeneugden, J. and Giese, M.

Neural Model for the Inﬂuence of Shading on the Multistability of the Perception of Body Motion.

DOI: 10.5220/0006054000690076

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 3: NCTA, pages 69-76

ISBN: 978-989-758-201-1

vision algorithms) in a way that accounts for multi-

stability in action perception, where we use as ex-

ample an established model that has been shown to

account jointly for many experimental results in this

area (Giese and Poggio, 2003). We extend it in two

ways: 1) by introduction of a multi-dimensional neu-

ral ﬁeld that accounts for multi-stable behavior by lat-

eral interactions between shape-selective neurons; 2)

by addition of a new pathway that realizes robust pro-

cessing of intrinsic luminance gradients along the sur-

face of the body segments.

The paper is structured as follows: after dis-

cussing related work in the following section, we de-

scribe the developed architecture in section 3. In sec-

tion 4 we show simulation results, illustrating that

the model provides a unifying account for several key

psychophysical results, followed by a brief discussion

in section 5.

2 RELATED THEORETICAL

WORK

Body motion recognition has been a core topic in

computer vision and many technical neural architec-

tures for this purpose have been proposed (Edwards

et al., 2016), (Nguyen et al., 2016), (Ziaeefard and

Bergevin, 2015), (Lee et al., 2014). The goal of that

work is typically a maximization of recognition per-

formance, not a reproduction of perceptual dynamics

of humans. This paper does not contribute to com-

puter vision or machine learning and is entirely fo-

cused on modeling of the brain.

We follow the approach in physiologically-

plausible models of body motion perception, such as

(Giese and Poggio, 2003), (Lange and Lappe, 2006),

(Escobar and Kornprobst, 2008), (Fleischer et al.,

2013), (Layher et al., 2014), while other biological

models in this area (e.g. (Thurman and Lu, 2014)

(Thurman and Lu, 2016)) account for experimental

data without direct relationship to neural mechanisms.

Diverse approaches (see (Tyler, 2011)) have been

proposed for the analysis of shape from shading, but

typically not related to the processing of body mo-

tion. Perceptual dynamics and perceptual switching

have been extensively studied in the context of low-

level vision (reviews see e.g. (Leopold and Logo-

thetis, 1999), (Sterzer et al., 2009), (Pastukhov et al.,

2013)). Multistability in the processing of non-rigid

motion has been rarely studied in neural modeling.

While hierarchical technical algorithms in com-

puter vision typically focus on the problem how the

body motion patterns (e.g. the direction of body

movement) might be distinguished, our model tries

to unify this account with a reproduction of the dy-

namics of perceptual organization in humans which

emerges speciﬁcally for the SILHOUETTE stimulus,

where for the same stimulus two alternating percepts

emerge. This problem is typically not addressed in

technical recognition systems, and to our knowledge

no account for this phenomenon has been given in

biologically-inspired neural models for motion recog-

nition.

3 MODEL ARCHITECTURE

Our model builds on a previous neural model (Giese

and Poggio, 2003), which has been shown to provide

a unifying account for a variety of experimentally

observed phenomena in body motion perception in-

cluding physiological, psychophysical and fMRI data.

The original model included a motion and a form

pathway, processing shape and optic ﬂow features.

The pathways consist of a hierarchy of feature de-

tectors that mimic properties of real cortical neurons.

For the implementation in this paper we used only the

form-pathway and extended it by a multi-dimensional

neural ﬁeld, and a new pathway for the processing of

intrinsic luminance gradients. An extension by in-

clusion of an additional motion pathway is straight-

forward, and will be part of future work.

3.1 Silhouette Pathway

The backbone of our model is a ’silhouette pathway’

(Fig. 1B) that is identical to the the form pathway of

the classical model (Giese and Poggio, 2003). Due

to space limitations, we sketch here only some basics

about this pathway and refer to the original publica-

tion (Giese and Poggio, 2003) with respect to details.

In brief, the form pathway consists of a hierarchy of

layers that process form features of increasing com-

plexity along the hierarchy. More complex features

are formed by combination of the features from pre-

vious layers. Levels that increase feature complex-

ity are interleaved by layers that increase position and

scale invariance by MAX pooling. The highest level

of this shape processing hierarchy is formed by radial

basis function units (called ’snapshot neurons’) that

have been trained with the feature vectors that corre-

spond to keyframes from training movies showing the

recognized action. Each snapshot neuron responds se-

lectively to the body posture that corresponds to time

instance θ (within the gait cycle). In addition, con-

sistent with physiological data (Vangeneugden et al.,

2011), we assume these neurons are view-speciﬁc,

where the variable φ speciﬁes the preferred view an-

NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications

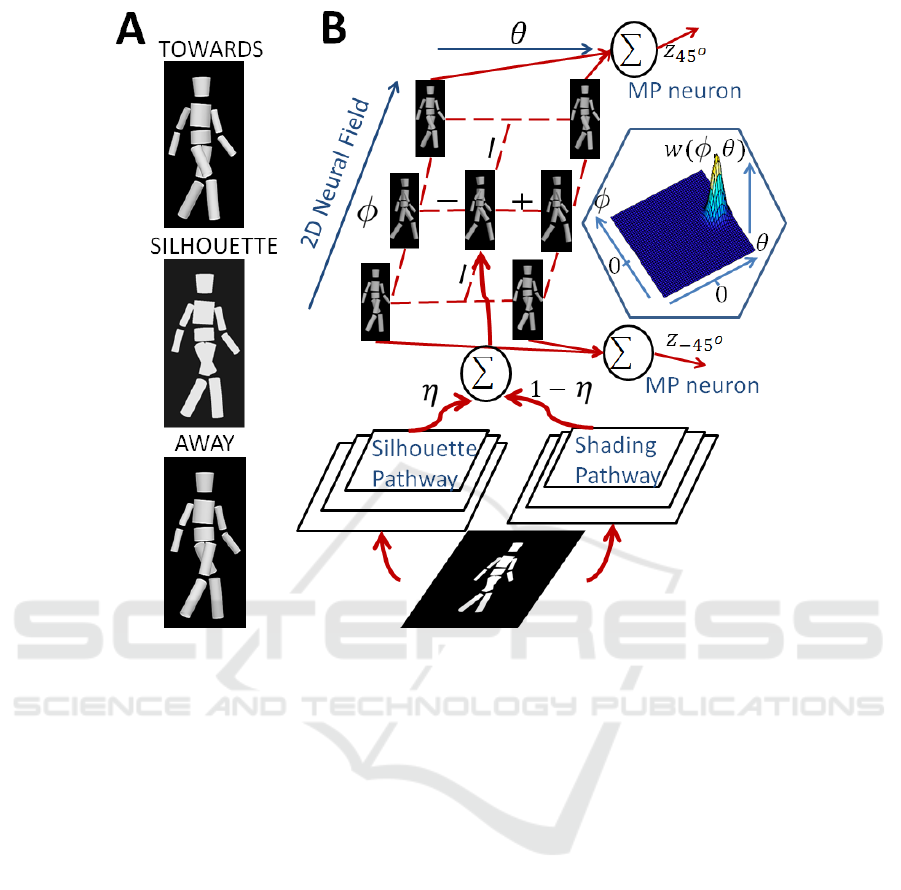
Figure 1: A. Snapshots from movies showing dynamic walker: TOWARDS shaded walker, walking direction 45 deg; SIL-

HOUETTE bistable silhouette walker and AWAY shaded walker, walking direction -45 deg. B. Model architecture. Stimulus

is analyzed by Silhouette and Shading pathways. Their outputs are linearly combined and mapped linearly onto the input of

a 2D dynamic neural ﬁeld that consists of laterally coupled snapshot neurons. Inset shows the lateral interaction kernel of the

ﬁeld. The ﬁeld activity is read out by Motion Pattern (MP) neurons that encode the perceived walking directions ±45 deg.

gle of the neuron. (We assume that the side view of

a walker walking to the right in the image plane de-

ﬁnes the view direction φ = 0). Very similar architec-

tures underlie many other classical and modern neu-

ral and deep models for object recognition, where the

popular deep architectures are typically trained with

much more data and often include many more lay-

ers. Since the goal of this paper is to model the per-

ceptual dynamics, and not to maximize recognition

rate, we used this simple hierachical model, where ex-

tension with modern deep architectures as front-end

seem straight-forward.

3.2 Shading Pathway

The described simple form pathway recognizes body

shape on backgrounds with sufﬁcient contrast. How-

ever, it turned out that with small amounts of training

data it is difﬁcult to accomplish with this architecture

a robust recognition of the silhouette shape together

with a high sensitivity for the luminance shading gra-

dients that disambiguate the depth structure. As one

possible solution to this problem we implemented a

second pathway that is specialized for the processing

of intrinsic shading gradients using physiologically-

plausible operations (Fig. 1B). We do not claim this

is the only possible solution, but it is one that works

with small amounts of training data.

The ﬁrst level of this new pathway overlaps with

the ﬁrst hierarchy level of the silhouette pathway,

described above. It consists of Gabor ﬁlters that

are selective for local orientation features at differ-

ent positions, and for different spatial scales. Let

e,u

(x,y, α, σ) signify the output signal of the even

(e) or uneven (u) Gabor ﬁlter with preferred posi-

tion (x,y), preferred orientation α (we used 8 orienta-

tions), and scale σ (we used 1 scale for the given small

stimuli set). The activations of the uneven Gabor ﬁl-

ters provide a population code for the local luminance

gradients.

By pooling of the responses of the Gabor ﬁl-

ters with the same preferred position over all orien-

tations we obtain position-speciﬁc detectors for con-

tours with the output signals:

Neural Model for the Inﬂuence of Shading on the Multistability of the Perception of Body Motion

C(x, y) = max

{e,u},α,σ

e,u

(x,y, α, σ)|. (1)

This output signal was used to suppress the re-

sponses of the uneven Gabor ﬁlters along the external

contour of the body, exploiting multiplicative gating.

The outer contour of the body typically creates strong

local contrast that dominates the detector responses,

so that the weak intrinsic gradients that signal the 3D

structure cannot be reliably estimated from the neural

responses. A population vector signaling the intrinsic

luminescence gradients is given by the gated signal:

L(x,y, α, σ) = [G

(x,y, α, σ) ·H(λ

−C(x,y))]

. (2)

Here λ

is a positive constant, and the function

H(x) is the Heaviside function, thus H(x) = 1 for x >

0 and H(x) = 0 otherwise.

The next level of the shading pathway consists

of (partially) position-invariant detectors for local lu-

minance gradients. Their responses are computed

by pooling of the gated responses of gradient detec-

tors for the same preferred gradient direction α over

all positions and scales in a quadratic neighborhood

U(x

) of the point (x

) using a maximum opera-

tion, providing the output signals:

D(x,y, α) = max

(x,y)∈U(x

),σ

L(x,y, α, σ). (3)

These position-invariant detectors were deﬁned

for substantially less spatial positions, resulting in

a strong spatial down-sampling (6,480,000 position-

and scale-speciﬁc detectors vs. 648 position-invariant

detector units).

In order to make recognition robust against ﬂuctu-

ating weak features, we selected the strongest features

that provide input to the radial basis function units.

We selected those features that showed the maxi-

mum variance over the training data (where clearly

much more sophisticated feature selections are avail-

able that might lead to better results). We computed

the circular variance of the detectors at position (x,y),

exploiting the (complex) circular mean:

The (complex) circular mean of these responses is

given by:

m(x,y) = (1/K)

∑

k=1

∑

(k)

(x,y, α) exp(iα), (4)

where K is the number of training patterns. A cir-

cular variance measure is then given by the formula:

V (x, y) =

∑

k=1



∑

(k)

(x,y, α) exp(iα) − m(x,y)



(5)

We selected the direction-speciﬁc responses

D(x,y, α) that fulﬁlled the relationship:

V (x, y) > λ

, (6)

where λ

> 0 is a threshold parameter. In total 9

out of 81 feature vectors were selected according to

this criterion.

The next level of the shading pathway is formed

by Gaussian radial basis functions, whose centers

were trained with the feature vectors p

(including

only the selected features) that were generated by in-

dividual keyframes from the training movies. For the

results shown here, the shading pathway was trained

with movies of fully shaded walkers, shown with view

directions −45 deg and 45 deg. In other implementa-

tions, we have realized such models with a continuum

of different views (Fleischer et al., 2013).

The RBF network returns an 50-dimensional out-

put vector R

(t) for each keyframe at time t, where

the components of this vector are given by:

(t) = exp(−λ

||p(t) − p

), (7)

where p(t) is the feature vector for the actual input

frame, and where the components correspond to the

different keyframes and associated training views.

In order to link the shape recognition pathway to

dynamic neurons that reproduce the perceptual dy-

namics, the outputs of the RBF units were mapped

linearly onto a discretely sampled two-dimensional

input activity distribution s

(θ,φ;t) that provides in-

put to the neural ﬁeld that is described below. Signi-

fying by s

(t) the appropriately reordered sampling

points, the linear mapping was given by the equation:

(t) = W(t)R

(t). (8)

The weight matrices W(s) were learned by ridge

regression from a training set that consisted of pairs

of vectors R

(t) for each training keyframe, and a

corresponding vector s

(t) that was computed from

an idealized two-dimensional input activity distribu-

tion s

(θ,φ;t). The idealized activity distribution

was given by a Gaussian peak that was centered at

the keyframe number θ and the corresponding view

φ of the walker (s.b.). A similar input distribution

(θ,φ;t) was computed by a corresponding linear

mapping in the silhouette pathway. The total input

distribution of the neural ﬁeld was then computed

by ’cue fusion’, modeled by a convex combination

of two input distribution functions according to the

equation:

s(θ,φ;t) = ηs

(θ,φ;t) + (1 − η)s

(θ,φ;t), (9)

with 0 ≤ η ≤ 1. Choosing η = 1 one can eliminate

the inﬂuence of the shading pathway.

NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications

3.3 Dynamic Neural Field of Snapshot

Neurons

The core of our model is a dynamic recognition layer

that is implemented as a two-dimensional neural ﬁeld

of Amari type (Amari, 1977), which consists of body

shape-selective neurons that are laterally connected

(Fig. 1B). Consistent with physiological data (Van-

geneugden et al., 2011), we assume that such neurons

encode body shapes that emerge during actions in a

view-speciﬁc manner. In the spatial continuum limit,

we can describe the activity of neurons encoding the

body shape that corresponds to the normalized time θ

(0 ≤ θ ≤ 2π) during the gait cycle and the view angle

φ by the function u(φ,θ,t). The network dynamics is

given by the equation (? signifying a spatial convolu-

tion):

u(φ,θ,t) = −u(φ,θ,t)+ w(φ,θ) ? H(u(φ,θ,t))

+s(φ,θ,t) − h + ξ(φ,θ,t) − c

a(φ,θ,t).

(10)

The input signal s was described above. For the

trained stimulus movies it corresponds to an activity

maximum that moves in θ-direction along the ﬁeld.

The lateral connectivity is speciﬁed by the interac-

tion kernel w(φ,θ) (whose shape is indicated by the

inset in Fig. 1B). It stabilizes a traveling pulse so-

lution in θ-direction and realizes a winner-takes-all

competition in the φ-direction. As consequence, if

multiple views are consistent with the stimulus, one

view is selected by competition. The positive param-

eters τ

and h deﬁne the time scale and the resting

potential of the ﬁeld. The variable ξ(φ, θ,t) deﬁnes a

Gaussian noise process whose statistics was coarsely

adapted to the noise correlations from cortical data

(Giese, 2014). These ﬂuctuations essentially drive the

perceptual switching in the model. Since action per-

ception shows adaptive properties, such as high-level

after-effects and fMRI adaptation, we also included

a neural adaptation process in the model, which re-

duces the activity of snapshot neurons after extended

ﬁring. The corresponding adaptation variable follows

the dynamical equation:

a(φ,θ,t) = −a(φ,θ,t)+ H(u(φ,θ,t)). (11)

The positive constant c

determines the strength of

adaptation(τ

is the time constant). The parameters of

this adaptation dynamics were ﬁtted to experimental

data (Giese, 2014).

The activity of the neurons in the neural ﬁeld was

read out by motion pattern (MP) neurons, which sig-

nal the walking directions perceived in this case as

AWAY from and TOWARDS the observer. These

neurons compute the maximum of the neural ﬁeld ac-

tivity function u(φ,θ,t) over the domains φ > 0 and

φ < 0 in the (φ,θ) space, producing the output signals

and z

−45

4 SIMULATION RESULTS

Testing the model after training with a non-shaded

walker as illustrated in Fig. 1A and 1B, the output

of the shading pathway remained silent because of

the absence of intrinsic luminance gradients in this

stimulus. The silhouette pathway was activated in an

ambiguous way by this stimulus because the stimulus

is consistent with walking in the directions ±45 deg

relative to the image plane. Consistent with simula-

tions described in (Giese, 2014), this stimulus leads

to a bistable solution of the neural ﬁeld that alternates

between two traveling pulse solutions that encode the

spontaneous perceptual switching of a traveling pulse

between the view angles φ = ±45 deg (perception

of TOWARDS or AWAY from the observer). In this

case, the probabilities of the two percepts are almost

identical (Fig. 2B). More detailed simulations show

that the model coarsely reproduces also the switching

time statistics of human perception, comparing it with

experimental data (not yet published (Vangeneugden

et al., 2012)). Fig. 2G shows a histogram of the per-

cept times for the model, and Fig. 2H the percept

times estimated in the psychophysical experiment.

For shaded stimuli (see Figs. 1A TOWARDS and

AWAY), when both pathways are included (η = 0.5),

the model successfully disambiguates the walking di-

rection: For the AWAY stimulus (direction -45 deg)

the output neuron for AWAY remains always acti-

vated while the output neuron for TOWARDS re-

mains silent. If an TOWARDS stimulus is shown (di-

rection 45 deg) the situation is reverse and the TO-

WARDS output neuron is always active (Fig.2 C and

D).

If however the shading pathway is deactivated

(η = 0) again perceptual switching occurs, since the

output of the silhouette pathway is ambiguous, result-

ing in equal percept probabilities for either direction.

The silhouette pathway is not sufﬁciently sensitive to

disambiguate the stimulus robustly based on the avail-

able luminance gradients intrinsic to the body seg-

ments (Fig.2 E-F). This demonstrates the necessity of

the shading pathway in the chosen architecture for the

disambiguation of the percept.

The model makes several veriﬁable experimental

predictions in relation to the time course of the adap-

tation process.

Neural Model for the Inﬂuence of Shading on the Multistability of the Perception of Body Motion

Figure 2: A. Time courses of the activity of motion pattern neurons for depth-ambiguous walker stimulus. B-F. Percept

probability of the motion pattern neurons for the percepts TOWARDS and AWAY for (B) depth-ambiguous walker for model

with both pathways ; (C) shaded −45 deg (AWAY) walker for model with both pathways; (D) same for shaded 45 deg

(TOWARDS) walker; (E) shaded 45 deg (TOWARDS) walker for model without shading pathway; (F) same for shaded 45

deg (TOWARDS) walker; G-H. Histogram of percept times (PT) from experimental data (Vangeneugden et al., 2012) and from

the model. I. Paradigm for testing after-effects in action perception which is compatible with our model. After presentation

of an unambiguous adaptor stimulus (AWAY or TOWARDS), and a ﬁxed Inter-stimulus Interval, an ambiguous test stumulus

(SILHOUETTE) is presented. J. Probability that test stimulus is perceived as walking in the adaptor direction as a function of

the duration of the adaptor.

NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications

An example is illustrated in Fig. 2I that shows

a diagram of a typical adaptation experiment to

demonstrate after-effects in action perception. First,

an unambiguous adaptation stimulus (TOWARDS or

AWAY) is presented to participants, where the dura-

tion of the adaptor (2, 6, 10, 14, 18 or 22 gait cycles)

was varied over different blocks of the experiment.

After this stimulus (and a ﬁxed Inter-stimulus Inter-

val of 2.8 s) an ambiguous test stimulus (SILHOU-

ETTE) is presented for 3 gait cycles, asking for the

perceived walking direction. The predicted results for

such an experiment (from 20 repeated simulations)

are presented in Fig. 2J, which shows the probabil-

ities of the percept for the ambiguous test stimulus

(which was identical in all cases). With increasing

the duration of the adaptor stimulus the probability

that participants perceive the test stimulus as walking

in the same direction as the adaptor decreases. A sig-

niﬁcant decrease of the percept probability (from 0.5

without adaptator presentation) is already perceived

for the shortest adaptor duration of 2 gait cycles, and

we observed a further decrease with longer adaptor

durations (where 1 gait cycle corresponds to 1.4 sec-

onds of stimulus duration). This behavior is consis-

tent with after-effects, as investigated previously for

many modalities (motion, lightness, etc) in low-level

vision. Such after-effects for action perception with a

similar time course have been shown for other types

of action stimuli in the literature (see (Barraclough

and Jellema, 2011), (de la Rosa et al., 2014)), and we

are presently running psychophysical experiments to

verify this prediction of the model in detail.

A further set of experiments that we are presently

running, and for which the model provides quantita-

tive predictions, investigates the interdependence of

the stability of action percepts and the switching times

between the different percepts (which depend on the

mean-ﬁrst passage times of the corresponding attrac-

tors). This extends studies that have been made for

muti-stability of low-level motion perception (Hock

et al., 1993) to the domain of action perception.

5 CONCLUSIONS

To our knowledge, we have described the ﬁrst

biologically-inspired neural model that accounts si-

multaneously for the following properties of body

motion perception: (i) perceptual multi-stability and

switching, (ii) switching time statistics and (iii) the in-

ﬂuence of shading information on the perceptual dy-

namics. We showed that the model reproduces the

psychophysically observed phenomenology and dis-

tributions of the percept times. Since the model is

based on learned templates, these results would trans-

fer trivially to other action patterns with the similar

form of bistability in the view domain.

It is important to stress that the goal of this pa-

per was the modeling of the perceptual dynamics, and

neither the proposal of novel deep shape or action

recognition architecture, nor the claim that the pro-

posed two-pathway architecture is signiﬁcantly bet-

ter for shape recognition. Testing this claim would

require additional experiments with larger data sets,

and was not the focus of this paper. Also it remains to

be shown whether any of the popular recurrent deep

architectures reproduce the details of the human per-

ceptual dynamics.

Future work will have to extend the model for

more stimuli and include more accurate ﬁts of exper-

imental data.

ACKNOWLEDGEMENTS

The ﬁrst author thanks Tjeerd Dijkstra for his insight-

ful commentary on the analysis of the Amari ﬁeld

behavior. Funded by: BMBF, FKZ: 01GQ1002A,

ABC PITN-GA-011-290011, CogIMon H2020 ICT-

644727; HBP FP7-604102; Koroibot FP7-611909,

DFG GZ: KA 1258/15-1.

REFERENCES

Amari, S. (1977). Dynamics of pattern formation in lateral

inhibition type neural ﬁelds. Biological Cybernetics.

Andersen, R. and Bradley, D. (1998). Perception of three-

dimensional structure from motion. Trends in Cogni-

tive Sciences.

Barraclough, N. and Jellema, T. (2011). Visual aftereffects

for walking actions reveal underlying neural mecha-

nisms for action recognition. Psychological Science.

Blake, R. and Logothesis, N. (2001). Visual competition.

Nature Review Neuroscience.

de la Rosa, S., Streuber, S., Giese, M., Buelthoff, H., and

Curio, C. (2014). Putting actions in context: Visual

action adaptation aftereffects are modulated by social

contexts. PLOS One.

Edwards, M., Deng, J., and Xie, X. (2016). From pose to

activity. In Computer Vision and Image Understand-

ing. Elsevier Science Inc.

Escobar, M. and Kornprobst, P. (2008). Action recogni-

tion with a bioinspired feedforward motion processing

model: the richness of center-surround interactions.

In ECCV’08. 10th European Conference on Computer

Vision. Springer Berlin Heidelberg.

Fleischer, F., Caggiano, V., Thier, P., and Giese, M. (2013).

Physiologically inspired model for the visual recog-

Neural Model for the Inﬂuence of Shading on the Multistability of the Perception of Body Motion

nition of transitive hand actions. Journal of Neuro-

science.

Giese, M. (2014). Skeleton model for the neurodynamics

of visual action representations. In Artiﬁcial Neu-

ral Networks and Machine Learning ICANN 2014,

Lecture Notes in Computer Science. Springer Interna-

tional Publishing.

Giese, M. and Poggio, T. (2003). Neural mechanisms for

the recognition of biological movements and action.

Nature Reviews Neuroscience.

Hock, H., Kelso, J., and Schoener, G. (1993). Bistability

and hysteresis in the perceptual organization of appar-

ent motion. Journal of Experimental Psychology: Hu-

man Perception and Performance.

Jackson, S. and Blake, R. (2010). Neural integration of in-

formation specifying human structure from form, mo-

tion, and depth. Journal of Neuroscience.

Jhuang, H., Serre, T., Wolf, L., and Poggio, T. (2007). A bi-

ologically inspired system for action recognition. In

2007 IEEE 11th International Conference on Com-

puter Vision. IEEE.

Lange, J. and Lappe, M. (2006). A model for biological

motion perception from conﬁgural form cues. Journal

of Neuroscience.

Layher, G., Giese, M., and Neumann, H. (2014). Learning

representations of animated motion sequencesa neu-

ral model. In Topics in Cognitive Science. Topics in

Cognitive Science.

Lee, T., Belkhatir, M., and Sanei, S. (2014). A compre-

hensive review of past and present vision-based tech-

niques for gait recognition. In Multimedia Tools and

Applications. Kluwer Academic Publishers.

Leopold, D. and Logothetis, N. (1999). Multistable phe-

nomena: changing views in perception. Trends in

Cognitive Science.

Nguyen, D., Li, W., and Ogunbona, P. (2016). Human de-

tection from images and videos. In Pattern Recogni-

tion. Elsevier Science Inc.

Pastukhov, A., Garca-Rodrguez, P., Haenicke, J., Guilla-

mon, A., Deco, G., and Braun, J. (2013). Multi-stable

perception balances stability and sensitivity. Frontiers

in Computational Neuroscience.

Rankin, J., Meso, A., Masson, G. S., Faugeras, O., and Ko-

rnprobst, P. (2014). Bifurcation study of a neural ﬁeld

competition model with an application to perceptual

switching in motion integration. Journal of Computa-

tional Neuroscience.

Sterzer, P., Kleinschmidt, A., and Rees, G. (2009). The

neural bases of multistable perception. Trends in Cog-

nitive Science.

Thurman, S. and Lu, H. (2014). Bayesian integration of po-

sition and orientation cues in perception of biological

and non-biological forms. Frontiers in Human Neuro-

science.

Thurman, S. and Lu, H. (2016). A comparison of form pro-

cessing involved in the perception of biological and

nonbiological movements. Journal of Vision.

Tyler, C. (2011). Computer Vision: From Surfaces to 3D

Objects. Chapman & Hall/CRC, London, 1st edition.

Vangeneugden, J., de Maziere, P., van Hulle, M., Jaeggli, T.,

van Gool, L., and Vogels, R. (2011). Distinct mecha-

nisms for coding of visual actions in macaque tempo-

ral cortex. Journal of Neuroscience.

Vangeneugden, J., van Ee, R., Verfaillie, K., Wagemans, J.,

and de Beeck, H. (2012). Activity in areas mt+ and

eba, but not psts, allow prediction of perceptual states

during ambiguous biological motion. In Society for

Neuroscience Meeting. Society for Neuroscience.

Vanrie, J. and Verfaillie, K. (2004). Perception of biological

motion: A stimulus set of human point-light actions.

Behavior Research Methods, Instruments, and Com-

puters.

Vanrie, J. and Verfaillie, K. (2006). Perceiving depth in

point-light actions. Perception and Psychophysics.

Wilson, H. (2003). Computational evidence for a rivalry

hierarchy in vision. Proceedings of the National

Academy of Sciences.

Ziaeefard, M. and Bergevin, R. (2015). Semantic human

activity recognition: A literature review. In Pattern

Recognition. Elsevier Science Inc.

NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications